Дистанционный репетитор — онлайн-репетиторы России и зарубежья

КАК ПРОХОДЯТ
ОНЛАЙН-ЗАНЯТИЯ?

Ученик и учитель видят и слышат
друг друга, совместно пишут на
виртуальной доске, не выходя из
дома!

КАК ВЫБРАТЬ репетитора

Выбрать репетитора самостоятельно

ИЛИ

Позвонить и Вам поможет специалист

8 (800) 333 58 91

* Звонок является бесплатным на территории РФ
** Время приема звонков с 10 до 22 по МСК

ПОДАТЬ ЗАЯВКУ

Россия +7Украина +380Австралия +61Белоруссия +375Великобритания +44Израиль +972Канада, США +1Китай +86Швейцария +41

Выбранные репетиторы

Заполните форму, и мы быстро и бесплатно подберем Вам дистанционного репетитора по Вашим пожеланиям.
Менеджер свяжется с Вами в течение 15 минут и порекомендует специалиста.

Отправляя форму, Вы принимаете Условия использования и даёте Согласие на обработку персональных данных

Вы также можете воспользоваться
расширенной формой подачи заявки

Как оплачивать и СКОЛЬКО ЭТО СТОИТ

от
800 до 5000 ₽

за 60 мин.

и зависит

ОТ ОПЫТА и
квалификации
репетитора

ОТ ПОСТАВЛЕННЫХ ЦЕЛЕЙ ОБУЧЕНИЯ
(например, подготовка к олимпиадам, ДВИ стоит дороже, чем подготовка к ЕГЭ)

ОТ ПРЕДМЕТА (например, услуги репетиторовиностранных языков дороже)

Оплата непосредственно репетитору, удобным для Вас способом

Почему я выбираю DisTTutor

БЫСТРЫЙ ПОДБОР
РЕПЕТИТОРА И
ИНДИВИДУАЛЬНЫЙ ПОДХОД

ОПТИМАЛЬНОЕ
СООТНОШЕНИЕ ЦЕНЫ И
КАЧЕСТВА

ПРОВЕРЕНЫ ДОКУМЕНТЫ ОБ ОБРАЗОВАНИИ У ВСЕХ РЕПЕТИТОРОВ

НАДЕЖНОСТЬ И ОПЫТ.
DisTTutor на рынке с 2008 года.

ПРОВЕДЕНИЕ БЕСПЛАТНОГО, ПРОБНОГО УРОКА

ЗАМЕНА РЕПЕТИТОРА, ЕСЛИ ЭТО НЕОБХОДИМО

376490 УЧЕНИКОВ ИЗ РАЗНЫХ СТРАН МИРА

уже сделали свой выбор

И вот, что УЧЕНИКИ ГОВОРЯТ
о наших репетиторах

Чулпан Равилевна Насырова

«

Я очень довольна репетитором по химии. Очень хороший подход к ученику,внятно объясняет. У меня появились сдвиги, стала получать хорошие оценки по химии. Очень хороший преподаватель. Всем , кто хочет изучать химию, советую только её !!!

«

Алина Крякина

Надежда Васильевна Токарева

«

Мы занимались с Надеждой Васильевной по математике 5 класса. Занятия проходили в удобное для обоих сторон время. Если необходимо было дополнительно позаниматься во внеурочное время, Надежда Васильевна всегда шла навстречу. Ей можно было позванить, чтобы просто задать вопрос по непонятной задачке из домашнего задания. Моя дочь существенно подняла свой уровень знаний по математике и начала демонстрировать хорошие оценки.

Мы очень благодарны Надежде Васильевне за помощь в этом учебном году, надеемся на продолжение отношений осенью.

«

Эльмира Есеноманова

Ольга Александровна Мухаметзянова

«

Подготовку к ЕГЭ по русскому языку мой сын начал с 10 класса. Ольга Александровна грамотный педагог, пунктуальный, ответственный человек. Она всегда старается построить занятие так, чтобы оно прошло максимально плодотворно и интересно. Нас абсолютно все устраивает в работе педагога. Сотрудничество приносит отличные результаты, и мы его продолжаем. Спасибо.

«

Оксана Александровна

Наталья Борисовна Карасева

«

Мы восторге от репетитора. Наталья Борисовна грамотный педагог, она любит свою профессию, любит учеников. Занятия с сыном (2 класс), он находится на домашнем обучении, проходят по скайпу в комфортной обстановке. Репетитор умеет заинтересовать ребенка и выстраивает занятие с учетом его способностей, доступно объясняя предметы русский язык и математику.

По результатам занятий можно сразу заметить повышение уровня успеваемости ученика. Наталья Борисовна хороший педагог, умеет быстро найти общий язык с ребенком, внимательная, легко передающая знания ученику. С большим удовольствием будем продолжать наши занятия, т.к. мы всем довольны.

«

Елена Васильевна

Клиентам

• Репетиторы по математике
• Репетиторы по русскому языку
• Репетиторы по химии
• Репетиторы по биологии
• Репетиторы английского языка
• Репетиторы немецкого языка

Репетиторам

• Регистрация
• Публичная оферта
• Библиотека
• Бан-лист репетиторов

Партнеры

• ChemSchool
• PREPY. RU
• Class

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

1.1: Векторы — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

16286

• Том Вайдеман
• Калифорнийский университет, Дэвис

Определение вектора

Для описания природы недостаточно просто присвоить числа физическим величинам. Очень часто физические величины имеют направления. Например, описание движения чего-либо будет неполным, если вы просто укажете, с какой скоростью оно движется. [ Итак, астероид движется со скоростью 35 000 миль в час, но направляется ли он к Земле?! ] Таким образом, мы имеем следующее определение физических величин, обладающих обоими этими свойствами:

Определение: Вектор

Вектор – это величина, имеющая как величину, так и направление.

Мы будем часто представлять векторную величину стрелкой, где направление вектора — это направление, на которое указывает стрелка, а величина вектора представлена ​​длиной стрелки. Это не означает, что векторы — это стрелок — стрелки просто создают удобное геометрическое представление. Таким образом, хотя стрелка, представляющая вектор, может быть 6 см в длину, это не означает, что вектор имеет величину 6 см . Например, вектор может представлять скорость и направление движущегося объекта, и тогда величина вектора даже не выражается в единицах см . Однако если мы нарисуем две стрелки, представляющие одну и ту же величину, и одна из них в два раза длиннее другой, подразумевается, что более длинная стрелка представляет вектор с удвоенной величиной вектора, представленного более короткой стрелкой.

Предупреждение

Невозможно сравнить величины различных физических величин. Если вектор расстояния нарисован в виде стрелки на той же странице, что и стрелка вектора скорости, относительные размеры двух стрелок не имеют смысла.

Есть несколько других вещей, которые мы должны сказать о векторах и стрелках, которые их представляют:

• Расположение стрелки, представляющей вектор, не является отличительной чертой вектора. То есть стрелку, представляющую вектор, можно перемещать по желанию, и пока она не растягивается, не сжимается и не поворачивается, она будет представлять тот же вектор. Простое изменение положения стрелки не меняет ее величины или направления, если ее перемещать осторожно.
• Направления векторов (и, следовательно, направления соответствующих стрелок) могут быть математически изменены на противоположные путем умножения на –1.
• Длина вектора может быть увеличена или уменьшена (масштабирована) посредством умножения на обычное число (называемое скаляром). Если число больше 1, вектор увеличивается в длину, а если меньше 1, то сжимается.

И еще одно… Когда мы пишем символ для векторной величины, мы делаем это с маленькой стрелкой над буквой, например: \(\overrightarrow A\). Предполагается, что переменные с той же буквой, что и заданный вектор, но не содержащие стрелку, представляют величина этого вектора. Так, например, при использовании в том же контексте переменная A представляет величину \(\overrightarrow A\).

Сложение/вычитание векторов

Чтобы математические величины, которые мы называем векторами, имели для нас какое-либо значение, они должны позволять выполнять простые математические операции, такие как сложение. Направленный характер векторов делает сложение намного сложнее, чем простое суммирование двух величин. Оказывается, правильное сложение векторов требует простой геометрии.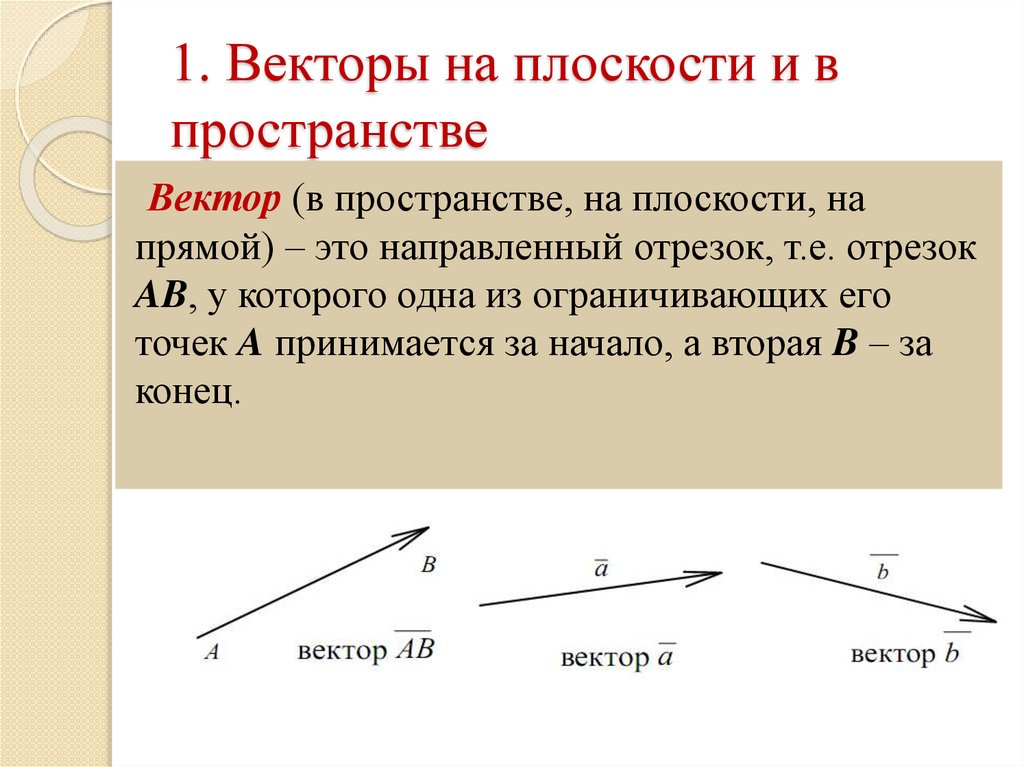 Это происходит так: перенесите один из векторов (параллельно, чтобы не менять его направление) так, чтобы его хвост соприкасался с головой другого вектора. Затем создайте новый вектор таким образом, чтобы его хвост находился на открытом хвосте, а голова — на открытой голове.

Рисунок 1.1.1 — Дополнение графического вектора

Рисунок 1.1.2 — Дополнение вектора

. Что ж, мы можем сделать это, следуя тому же методу, что и для обычных чисел: какой бы вектор мы ни хотели вычесть, мы умножаем на –1, а затем прибавляем результат к другому вектору, что мы делаем, как описано выше. Мы уже знаем, что умножение вектора на –1 меняет его направление на противоположное (и оставляет его величину неизменной), поэтому для нас это четко определенная операция. 92 -2AB \cos \theta\]

Имея все длины катетов треугольника и один из углов (тот, что между \(A\) и \(B\)), мы можем получить другие углы, используя Закон синусов.

Пример \(\PageIndex{1}\)

Значения двух векторов, показанных на диаграмме ниже: \(A=132\) и \(B=145\). Найдите величину и направление (угол, образованный с осью \(х\)) вектора, являющегося разностью этих двух векторов.

Решение

Используя тот факт, что отрицательный вектор — это тот же вектор, указывающий в противоположном направлении, а также сложение векторов «хвост к голове», мы получаем следующую диаграмму для трех векторов:

Угол между \(\overrightarrow A\) и \(\overrightarrow B\), очевидно, равен 65º – 30º = 35º, поэтому для этого треугольника у нас есть длины двух сторон и угол между ними. Следовательно, мы можем найти длину третьей стороны (\(\overrightarrow C\)) по закону косинусов: 9о\номер\]

Если мы повернем \(\overrightarrow C\) против часовой стрелки на этот угол, он будет параллелен \(\overrightarrow A\), если мы затем повернем его назад по часовой стрелке на 30º (угол \(\overrightarrow A\) составляет с осью \(х\), то он будет параллелен оси \(х\). Следовательно, угол \(\overrightarrow C\) с осью \(x\) равен: -81° + 30° = -51° (ниже оси \(x\)). Этот ответ, безусловно, соответствует приведенной выше диаграмме, на которой \(\overrightarrow C\) имеет меньшую величину, чем \(\overrightarrow A\) и \(\overrightarrow B\), и указывает вниз вправо.

Хотя мы можем использовать эти инструменты для математического нахождения суммы двух векторов, оказывается, что есть и другой способ сделать это, не требующий стольких геометрических рассуждений. Этот метод использует три простых факта:

• Мы можем заменить любой отдельный вектор суммой двух (или более) векторов.
• Легко сложить два параллельных вектора.
• Если мы используем прямоугольные треугольники, с тригонометрией работать легче, чем с обычными треугольниками и законом косинусов/синусов.

Хитрость заключается в том, чтобы выбрать две (или три, если необходимо) перпендикулярные оси (они не обязательно должны быть горизонтальными и вертикальными, они должны быть только перпендикулярны друг другу) и разбить каждый вовлеченный вектор в сумму двух перпендикулярные векторы, параллельные этим осям. Длины этих перпендикулярных векторов называются компонентами вектора вдоль этих осей. Возвращаясь к приведенному выше списку преимуществ, помните, что мы можем добавлять подобные компоненты, такие как числа, и мы можем легко определить эти компоненты с помощью тригонометрии.

Рисунок 1.1.3 — Векторные компоненты

Рисунок 1.1.4 — Суммирование векторов с использованием компонентов

333333. те же оси могут быть добавлены. В результате получаются дополнительные компоненты, которые затем необходимо преобразовать в вектор.

Единичные векторы

Таким образом, мы можем использовать перпендикулярные системы координат для описания векторов с точки зрения их компонентов. По сути это означает, что для описания вектора в терминах набора трех осей нам нужно знать три числа. Но может быть полезно выразить эти векторы как единую математическую единицу, и именно здесь понятие 9Приходит единичный вектор 0034 .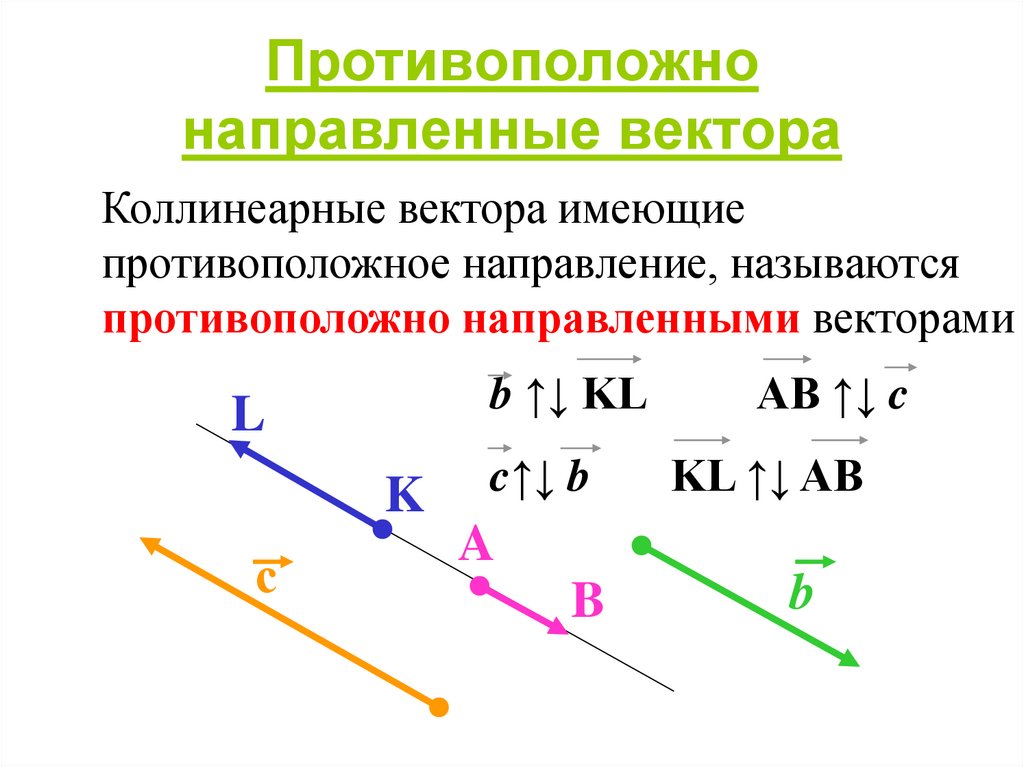 Векторы имеют величину и направление, и с помощью единичных векторов мы можем математически разбить вектор на эти две части. Величина — это просто число (с физическими единицами) без направления, а единичный вектор — это вектор (без единиц), длина которого равна 1, поэтому его можно масштабировать до любой длины, ничего не добавляя к величине. Следовательно, мы можем записать вектор как простое произведение:

\[\overrightarrow A = A\widehat A\]

, где \(\widehat A\) — единичный вектор (обычно произносится как «\(A\)-hat »). Это безразмерный вектор длины 1, указывающий в направлении вектора \(\overrightarrow A\). Значение \(A\) — это число в физических единицах, равное величине. Диаграмма ниже дает графическое описание того, как эта конструкция работает для нескольких распространенных физических векторов. Единичные векторы обеспечивают очень простой шаблон, определяя направление, а величина заполняет шаблон, добавляя обхват и «аромат» (физические единицы) вектора.

Рисунок 1. 1.4 – Единичные векторы и величины

Если мы объединим это понятие с компонентами, мы можем записать любой вектор как сумму компонентов, умноженных на единичные векторы в направлениях трех пространственных измерений. По соглашению мы даем этим единичным векторам имена \(\widehat i\), \(\widehat j\) и \(\widehat k\) для осей \(x\), \(y\) и \(г\) соответственно. В частности, у нас есть:

\[\overrightarrow A = A_x\widehat i + A_y\widehat j + A_z\widehat k \]

Теперь мы можем просто использовать это как математическое представление векторов, и нам вообще не нужно обращаться к геометрии. Например,

\[ \begin{align} \overrightarrow C &= \overrightarrow A + \overrightarrow B \nonumber\\[5pt] &= (A_x\widehat i + A_y\widehat j + A_z\widehat k) + (B_x\widehat i + B_y\widehat j + B_z\widehat k) \nonumber\\[5pt] &= C_x\widehat i + C_y\widehat j + C_z\widehat k\nonumber\\[5pt] &= (A_x+ B_x) \widehat i + (A_y + B_y) \widehat j + (A_z + B_z) \widehat k \end{align}\]

Дает нам тот же результат, что и ранее для компонентов суммы двух векторов. o }\widehat j = 61,3\;\widehat i + 131,4\;\widehat j \end{массив}\nonumber\] 9о} \end{массив}\номер\]

Это соответствует ответу из примера 1.1.1.

---

Эта страница под названием 1.1: Vectors публикуется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Томом Вайдеманом непосредственно на платформе LibreTexts.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Том Вайдеман

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. источник@родной

Ньютоновская механика — Каково значение скольжения вектора силы?

$\begingroup$

Сценарий 1:

Здесь $AB$ — линия действия силы $\underline{u}$, причем $AB$ проходит через центр масс бесконечно длинного жесткого и однородного стержня. Здесь $\vec{CD}=\underline{u}$. Теперь, если $\vec{CD}$ сдвигается и $\vec{CD}$ становится $\vec{EF}=\underline{u}$, физический эффект останется прежним. Другими словами, не имеет значения, действует ли вектор $\underline{u}$ в точке $C$ или в точке $E$, воздействие на стержень останется тем же. Таким образом, в этом сценарии есть польза от существования линии действия $AB$.

Сценарий 2:

Здесь $BA$ — линия действия силы $\underline{u}$, причем $BA$ проходит через центр масс жесткого и однородного стержня. Пусть теперь в точке $O$ стержня действует сила $\vec{OA}=\underline{u}$. Теперь, поскольку сила является скользящим вектором, мы можем скользить $\vec{OA}$, и $\vec{OA}$ становится $\vec{BC}$. Однако у меня есть проблема. В отличие от сценария 1 вектор $\vec{BC}$ не имеет физического смысла/значения, как и вектор $\vec{OA}$. Согласно этому ответу, $\vec{OA}$ можно скользить вдоль линии действия, а $\vec{OA}$ и $\vec{BC}$ действуют на планку одинаково. Однако, повторяю, я считаю, что $\vec{BC}$ не имеет физического смысла, поскольку ни $B$, ни $C$ не являются точками на стержне. $\vec{OA}$ действует на стержне и имеет физический смысл, поскольку $O$ — точка на стержне. Однако $\vec{BC}$ не действует буквально ни на что, в отличие от $\vec{OA}$, так каков же физический смысл смещения вектора $\vec{OA}$ в этом случае?

Мой вопрос:

1. Что означает сдвиг $\vec{OA}$ в сценарии 2?

---

Это может помочь вам ответить на мой вопрос.

• ньютоновская механика
• силы
• векторы
• обозначения
• статика

$\endgroup$

7

$\begingroup$

Слишком длинный комментарий.

1. Сценарий 2:

   Теперь, поскольку сила является скользящим вектором,

   Пожалуйста, внимательно прочитайте мой ответ на ваш предыдущий вопрос, в частности

   3. $\;\ldots$ Здесь, ясно, что $\vec F$ и $\vec{OA}$ — это « свободных вектора».

   и

   Мораль такова: после того, как физический сценарий был математически смоделирован (абстрагирован), система классификации < свободный вектор против скользящий вектор против связанный вектор > не нужен; вместо этого тщательно соблюдая формулировку и условия определений и теорем гарантирует, что выполняемые шаги действительны.

2. Сценарий 1:

   Здесь $AB$ — линия действия силы $\underline{u}$, а $AB$ проходит через центр масс бесконечно длинного твердого тела. и равномерный бар. Здесь $\vec{CD}=\underline{u}$. Теперь, если $\vec{CD}$ сдвигается, и $\vec{CD}$ становится $\vec{EF}=\underline{u}$, физический эффект останется прежним. Другими словами, это не независимо от того, действует ли вектор $\underline{u}$ в точке $C$ или точка $E$,

   В этом (математическом) сценарии, как описано,

   • $\vec{CD}$ и $\vec{EF}$ на самом деле являются одним и тем же объектом;
   • $\vec{CD}$ не «действует» ни в одной конкретной точке (его название не означает, что он действует в точке $C$)
   • о физическом воздействии не может быть и речи (не указано).

$\endgroup$

10

$\begingroup$

Вы понимаете, что теория твердых тел является идеализацией а не реальностью. Реальная сила имеет не только линию действия, но и точку (точки) приложения, а тела упругие, а не жесткие.

Только в контексте этой идеализации можно по-настоящему применить правило скользящих векторов. Вы можете думать о математических силах против реальных сил. Математическая сила имеет величину, направление и линию действия, потому что она также сообщает момент силы (крутящий момент) относительно некоторой контрольной точки.

Именно эта комбинация силы и крутящего момента полностью описывает нагрузку на систему. Любая система сил, производящая одинаковую силу и крутящий момент, неотличима друг от друга (математически). Уравнения движения те же.

Математические силы не имеют точки начала координат, это векторы, принадлежащие где-то вдоль линии действия, где угодно.

На самом деле разумно предположить, что контактная сила действует где-то на поверхности тела (там, где линия действия пересекает тело). Но на другие точки могут действовать и другие силы.

Гравитация действует на все частицы тела, поэтому можно считать, что она сосредоточена в центре масс без ограничения общности (для твердых тел).

Плавучесть, аэродинамические силы, магнетизм могут иметь разные точки, в которых они действуют вдали от центра масс.

Но опять же, когда речь идет о ньютоновской механике, точка, на которую действуют силы, не имеет значения, но имеет значение результирующий крутящий момент относительно точки отсчета. Для динамических задач точкой отсчета должен быть центр масс, но для нединамических (статических) задач он может быть где угодно.

$\endgroup$

0

$\begingroup$

Во-первых, крутящий момент сильно отличается от силы. Крутящий момент является величиной, зависящей от источника, что означает, что он зависит от точки, в которой вы его перемещаете. Если кто-то спросит вас «рассчитать крутящий момент?» Первый вопрос, о какой точке?

Сравните это с силой: Для силы вы можете вычислить результирующую силу, действующую на тело относительно любой точки пространства, и все точки совпадут. Смотрите ответ Джона здесь.

Однако существует один особый случай, когда Крутящий момент становится своего рода независимой от источника величиной: когда результирующая сила равна нулю. Доказательство

Итак, в принципе, если у вас есть тело, движущееся по Земле, вы можете установить начало системы координат в какой-то точке на Марсе и спросить: «Сколько вращается это тело вокруг этой точки на Марсе?».

Когда все это убрано, что значит, что мы можем перемещать вектор силы по всем этим точкам, и крутящий момент сохраняется? В основном это косвенное следствие того факта, что при расчете крутящего момента по определению $\vec{\tau} = \sum \vec{r_i} \times \vec{F_i}$, то, как масса распределяется в пространстве, не имеет значения для расчета.