КАЧЕСТВЕННЫЕ ЗАДАЧИ 11 КЛАСС

САЙТ ПРАКТИКУЮЩЕГО ФИЗИКА

КАЧЕСТВЕННЫЕ ЗАДАЧИ ДЛЯ 11 КЛАССА Качественные задачи курса физики. ЭЛЕКТРОДИНАМИКА Тема: «Магнитное взаимодействие» 1. Каким образом можно обнаружить в пространстве наличие магнитного поля? 2. Молния ударила тв ящик со стальными ножами и вилками. После этого они оказались намагниченными. Как это объяснить? 3.Отклонится ли магнитная стрелка, если её разместить вблизи пучка движущися частиц: а)электронов; б)атомов; в) положительных ионов? 4. Магнитгая стрелка, помещенная возле провода, отклонилась при пропускании по нему тока. За счет какого вида энергии совершена работа, необходимая для поворота стрелки? 5. Как взаимодействуют два воздушных провода троллейбусной линии: ппритягиваются или отталкиваются? 6. Шнур настольной лампы, питаемой постоянным током, поднесли к магнитной стрелке. Окажет ли магнитное поле тока действие на стрелку? 7. Деформируется ли проволочная катушка, если по ней пропускается постоянный ток? 8. Почему сужается струя расплавленного металла при пропускании через неё тока? 9. Сложенный вдвое гибкий провод лежит на столе. Будут ли взаимодействовать части, если по нему пропустить сильный ток?   Тема: «Явление электромагнитной индукции» 1. Сквозь горизонтальное проводящее кольцо падают с одинаковой высоты алюминиевый брусок и магнит. Какой предмет упадет первым? 2. Почему для обнаружения индукционного тока замкнутый проводник лучше брать в виде катушки, а не в виде прямолинейного провода? 3. На вертикальном сердечнике электромагнита лежит монета. Что произойдет, если включить ток в катушке электромагнита? 4. Между двумя любыми точками некоторого контура разность потенциалов равна нулю, а ток в контуре существует. Когда это возможно? 5. Почему иногда недалеко от места удара молнии могут расплавиться предохранители в осветительной сети и повредиться чувствительные приборы? Тема:»Волновые явления» 1. Почему в жидкой или газообразной средах не возникают поперечные волны? 2. Почему в твердых телахмогут распространяться поперечные и продольные волны? Тема: «Свободные электрические колебания в контуре» 1. Могут ли возникнуть свободные колебания в контуре, состящем из конденсатора и активного сопротивления? 2. Как изменится частота колебаний в контуре, если в катушку ввести железный сердечник? Тема:»Трансформатор» 1.Изменится ли соотношение между напряжениями на обмотках трансформатора, если железный сердечник заменить на медный? 2. Ток во вторичной обмотке зависит от сопротивления подключенных приборов. Меняется ли в связи с этим ток в первичной обмотке? 3. Почему трансформатор выходит из строя, если в нём замыкаются накоротко хотя бы два соседних витка? 4. Почему нагруженный трансформатор гудит? 5. Допустимо ли, сняв катушку школьного трансформатора с сердечника, подавать на неё переменное напряжение, указанное на катушке? 6. Изменяется ли мощность тока при преобразовании его в трансформаторе? 7. Почему ненагруженный трансформатор потребляет очень мало энергии? 8. Что может произойти, если случайно подключить трансформатор к источнику постоянного тока? 9. Что произойдет с катушкой трансформатора, если её распрямить, не отключая от сети? 10. Первичная катушка трансформатора присоединена к источнику тока, вторичная же разомкнута. Потребляется ли трансформатором электроэнергия? Тема: «Электромагнитные волны» 1.Во время каких природных явленийобразуются и излучаются электромагнитные волны? 2. Почему зимой и ночью радиоприем лучше, чем летом и днём? 3. Какова причина помех радиоприему от проходящего трамвая? 4. Почему на экране телевизора при появлении летящего вблизи самолёта возникает двойное изображение? 5. Почему нельзя осуществлять радиосвязь между подводными лодками, находящимися на некоторой глубине в океане? 6. Почему радиоприемник в автомобиле работает хуже, когда машина проезжает под мостом или под этакадой? 7. Если включать или выключать свет в комнате, то в радиоприемнике слышны щелчки. Чем они вызваны?   ГЕОМЕТРИЧЕСКАЯ ОПТИКА Тема: «Закон отражения света» 1. Почему в темной комнате видны только те предметы, на которые в данный момент направлен луч фонарика? 2. Почему окна домов всегда кажутся темнее стен, даже если стены окрашены в темный цвет? 3. Отраженный от гладкой поверхности предмета пучок света всегда менее ярок, чем падающий. Почему? 4. Почему в свете фар автомобиля лужа на асфальте кажется водителю темным пятном? 5. Почему, находясь в комнате, трудно увидеть днем свое отражение в оконном стекле? 6. В утренние и предвечерние часы отражение Солнца в спокойной воде ослепительно яркое, а в полдень его можно рассмотреть, не жмурясь. Объясните это явление. 7. Является ли отражение света от киноэкрана диффузным или рассеяным? 8. На поверхности озера или моря против Луны видна сверкающая лунная дорожка. Как она образуется? Можно ли наблюдать лунную дорожку на идеально гладкой, спокойной поверхности воды? Почему дорожка всегда направлена на наблюдателя? Тема: «Изображение в плоском зеркале» 1. На столе лежит зеркало. Как изменится изображение люстры в этом зеркале, если закрыть половину зеркала? 2. Какие печатные буквы алфавита не изменяются при отражении в плоском зеркале? 3. В каком случае поверхность рассеивает падающий на неё свет? Почему? 4. Как изменится расстояние между предметом и его изображением в плоском зеркале, если зеркало переместить в то место, где было изображение? Тема: «Закон преломления света» 1. В каком случае угол преломления луча равен углу падения? 2. Почему изображение предмета в воде всегда менее ярко, чем сам предмет? 3. Почему ложка, поставленная в стакан с водой, кажется изогнутой? 4. Камушки, лежащие на дне водоёма, кажутся колеблющимися, если поверхность воды в водоёме не совсем спокойная. Почему? 5. Если посмотреть на окружающие тела через тёплый воздух, поднимающийся от костра, то они кажутся «дрожащими». Почему? 6. Собирающую оптическую линзу мальчик погрузил в воду. Изменилась ли при этом оптическая сила линзы? 7. Почему, находясь в лодке, трудно попасть копьем в рыбу, плавающую невдалеке? 8. Если читать книгу, держа ее очень близко или очень далеко от глаз, глаза быстро утомляются. Почему? 9. На линзу фотоаппарата села муха. Как это отразится на качестве снимка? 10. Пузырьки воздуха, расположенные на стеблях и листьях подводных растений кажутся серебристо-зеркальными. Почему? 11. Какой дефект зрения «появится» у рыбы, вынутой из воды — близоруклсть или дальнозоркость?   ВОЛНОВАЯ ОПТИКА Тема: «Дисперсия света» 1. Как изменится частота зеленого излучения при переходе света из воздуха в воду? 2. Как изменится длина волны красного излучения при переходе света из воздуха в воду? 3. Как будет выглядеть белая надпись на красном фоне, если осветить её зеленым светом? 4. Какого цвета должно быть стёклышко, сквозь которое можно увидеть зеленую надпись на белой бумаге? 5. Наблюдатель рассматривает сквозь стеклянную призму черную черту на белой бумаге. Что он видит? 6. На листе написано слово «свет» зеленым карандашом. Глядя через какую прозрачную среду нельзя будет прочесть написанное? 7. Белый луч света падает на боковую грань призмы под нулевым углом. Получим ли на экране спектр? 8. Луч света, преломляясь, переходит из стекла в воздух. Как расположатся преломленные лучи различных цветов относительно перпендикуляра к границе сред в точке преломления луча? 9. При получении на экране спектра излучения электрической лампы ее накаливали постепенно с помощью реостата. Какие изменения при этом наблюдали на экране? 10. Имеются призмы из различных материалов, но с одинаковыми преломляющими углами. Чем будут отличаться спектры, получаемые с помощью этих призм? 11. Зеленые лучи переходят из воздуха в воду, при этом длина волны их становится меньше. Какого цвета эти лучи будет воспринимать человек, погрузившись в воду? 12. Изменится ли скорость света, длана волны, частота колебаний при переходе света из воздуха в стекло? Как? 13. С одинаковой ли скоростью проходят к границам атмосферы Земли и Солнца волны красной и фиолетовой части спектра? Одинакова ли их скорость в атмосфере и в любой иной среде? 14. Длина волны красного света в воде равна длине волны зеленого света в воздухе. Какой цвет увидит человек под водой, если вода освещена красным светом? Тема: «Интерференция света» 1. Могут ли интерферировать световые волны, идущие от двух электрических лампочек? 2. Почему крылья стрекоз имеют радужную окраску? 3. Мыльный пузырь играет на солнце всеми цветами радуги. Почему? 4. Если две волны интерферируют друг с другом, то изменяет ли одна волна распространение другой? 5. Почему возникают радужные полосы в тонком слое керосина, плавающем на поверхности воды? 6. Цвета тонких пленок заметно отличаются от цветов радуги. Почему? 7. Лучи белого света падают нормально на тонкую плоскопараллельную прозрачную пластину. Как будет менятья окраска пластины, если увеличить угол падения? Тема: «Дифракция света» 1.На поверхности лазерного диска видны цветные полосы. Как объяснить это явление? 2. Если, прищурив глаза, смотреть на нить накала лампочки, то она кажется окаймленной светлыми бликами. Почему? 3. При изготовлении искусственных перламутровых пуговиц на их поверхность наносят мельчайшую штриховку. Почему после такой обработки пуговица имеет радужную окраску? 4. При освещении тонкой пленки параллельными белыми лучами наблюдается радужная окраска пленки. Чем это объясняется? 5. Почему с помощью микроскопа нельзя увидеть атом? 6. Имеются две тонкие пленки из одинакового материала. При освещении их белым светом, лучи которого перпендикулярны к их поверхности, одна из них кажется красной, а другая — синей? Можно ли сказать, какая из этих пленок толще? 7. Имеются две пленки их одинакового прозрачного материала. При освещении их белым светом, лучи которого перпендикулярны к их поверхности, обе пленки в отраженном свете кажутся зелеными. Можно ли сказать, что их толщина одинакова? 8. Имеется тонкая пленка из прозрачного материала. При её освещении монохроматическим светом, лучи которого перпендикулярны её поверхности, на ней видны параллельные чередующиеся иемные и светлые полосы на равных расстояниях друг от друга. Что можно сказать о толщине такой пленки? 9. Если скозь ресницы смотреть на свет уличного фонаря, вокруг него появляется радужный свет. Чем это объяснить? 10. Почему меняется окраска крыльев насекомого, если его рассматривать под разными углами?   СВЕТОВЫЕ КВАНТЫ Тема: «Давление света» 1.В каком случае давление больше: при падении его на зеркальную поверхность или черную? 2. Если комета видна на небе с вечера, то в какую сторону напрвлен её хвост? 3. Частичка в хвосте кометы приобрела ускорение под действием солнечного света. Поясните причину увеличения её кинетической энергии и сравните энергию падающих и отраженных фотонов. 4. Когда свет падает на поглощающую его поверхность, фотоны перестают существовать. Не противоречит ли это закону сохранения импульса?   АТОМ И АТОМНОЕ ЯДРО Тема: «Квантовые постулаты Бора» 1. Электрон в атоме водорода перешел с четвертого энергетического уровня на второй. Как при этом изменилась энергия атома? Почему? 2. Как изменилась энергия атома водорода, если электрон в атоме перешел с первой орбиты на третью, а потом обратно? 3. Сколько квантов с различной энергией может испустить атом водорода, если электрон находится на третьей орбите? 4. Электрон в атоме водорода перешел с пятого энергетического уровня на второй. Как при этом изменилась энергия атома? Почему? 5. Чем отличается атом, находящийся в стационарном состоянии, от атома в возбужденном состоянии? 6. Одинаковая ли энергия необходима для того, чтобы оторвать от атома гелия: 1)первый электрон; 2)второй электрон? 7. В атоме водорода есть ограничение на минимальное расстояние электрона от ядра. Есть ли ограничение на максимальное расстояние между электроном и ядром? Тема: «Деление ядер урана» 1. Произошел самопроизвольный распад ядра. Выделилась или поглотилась энергия во время этого распада? Ответ обоснуйте. 2. Почему в ядерных реакторах медленные нейтроны более эффективно поглощаются ядрами урана, чем быстрые?   Тема: «Элементарные частицы» 1. Что произойдет, когда электрон столкнется с протоном? 2. При встрече электрона с позитроном, имеющих массу покоя, они превращаются в два фотона, которые массой покоя не обладают. О чем говорит этот факт? 3. И атом водорода, и нейтрон могут распадаться на протон и электрон. Почему же атом водорода не считают элементарной чистицей, а нейтрон причисляют к ним? 4. Допустим, что значительный по массе комок земного вещества, отправленный в глубины космоса, встретился с куском антивещества. Чем должна закончиться такая встреча? 5. В процессе превращения в электромагнитное излучение пары электрон-позитрон никогда не возникает гамма-квант. Проявление какого именно из известных вам законом сохранения можно усмотреть в этом факте? 6. Есть некоторые основания предполагать существование антимиров — скоплений материи, в которых ядра состоят из антипротонов и антинейтронов, а их оболочки из позитронов. Можно проверить эту гипотезу методами спектроскопии?

Главная — на главную  Задачи — расчетные — качественные — эксперимент

Магнитный поток 9 класс онлайн-подготовка на Ростелеком Лицей

Вступление

 

Вспомним, что при изменении параметров магнитного поля вблизи замкнутого проводника в нем возникает ток.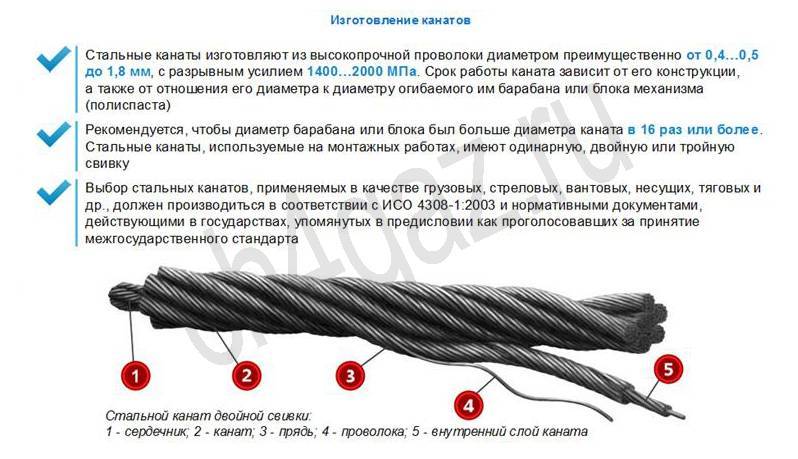 Данный ток получил название тока индукции, а явление – явление электромагнитной индукции.

 

Однако остается вопрос, какие конкретно параметры магнитного поля нам необходимо меня для получения данного эффекта. Для начала проведем эксперимент:

 

Опыт Фарадея

 

 

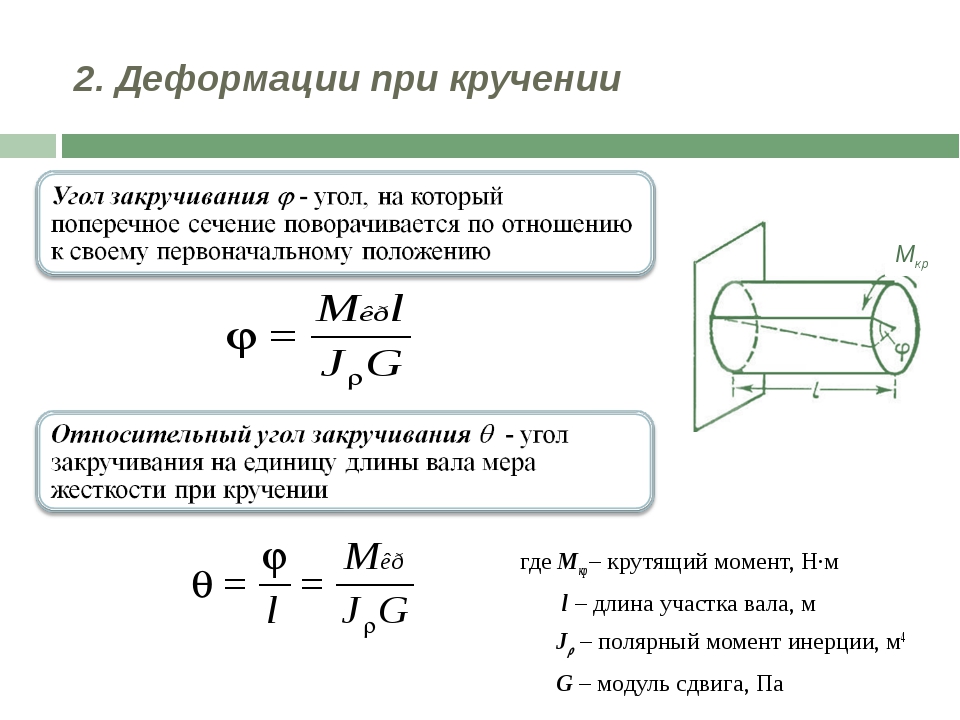
Для его проведения нам необходимо: катушка с большим количеством витков и подключенный к ней амперметр. В ходе проведения опыта обратите внимание на поведение стрелки амперметра (рис. 1).

 

Рис. 1. Опыты Фарадея

Как мы видим, при опускании и вынимании полосового магнита из катушки в ней образуется индукционный ток.

Проанализируем, изменение какого именно параметра привело к наблюдаемому эффекту. При приближении и отдалении магнита от катушки в ней меняется сила магнитного поля.

Таким образом, величиной, которая влияет на образование тока индукции в катушке, является сила магнитного поля.

Вспомним, что она описывается такой величиной, как магнитная индукция. Она является вектором и обозначается  и измеряется в Тл.

 

Второй опыт

 

 

Помещенное перпендикулярно магнитному полю замкнутое проволочное кольцо сжимаем с нескольких сторон, чтобы оно изменило свою форму (рис. 2).

 

Рис. 2. Иллюстрация к опыту

При этом на протяжении процесса деформации в кольце возникает ток индукции. Что же мы изменяли в этот раз?

Теперь изменению подверглась площадь кольца. Конечно же, вместо кольца можно экспериментировать с любым замкнутым проводником.

Контур – замкнутый проводник (рис. 3).

Рис. 3. Контур

 

Принцип работы электрогенератора

 

 

 

Рис. 4. Генератор

Его основными элементами являются (рис. 4):

• катушка, которая может вращаться вокруг своей оси;
• установленный вокруг катушки постоянный магнит.

При вращении катушки в магнитном поле можно увидеть, что лампочка загорается (т. е. в цепи возникает ток индукции).

Из этого опыта можно сделать вывод о том, что явление электромагнитной индукции проявляет себя и при повороте катушки или проводящей рамки в магнитном поле (рис. 5), т. е. при изменении угла между магнитными линиями и плоскостью проводника.

Рис. 5. Иллюстрация к опыту

Все три параметра, изменения которых влияют на величину тока индукции, объединяет физическая величина под названием магнитный поток.

 

Магнитный поток

 

 

В – модуль магнитной индукции поля

 

S – площадь контура

 – характеризует расположение плоскости контура относительно магнитной линии.

Магнитный поток измеряют в Веберах (Вб) и обозначают буквой Ф.

Таким образом, магнитный поток пропорционален модулю магнитной индукции поля, площади контура и зависит от расположения плоскости контура относительно магнитной линии.

 

---

Задача на анализ параметров магнитного потока

Для того чтобы научиться делать выводы об изменении магнитного потока в элементах различных электрических цепей, что может привести к наличию нежелательных индукционных токов, рассмотрим задачу.

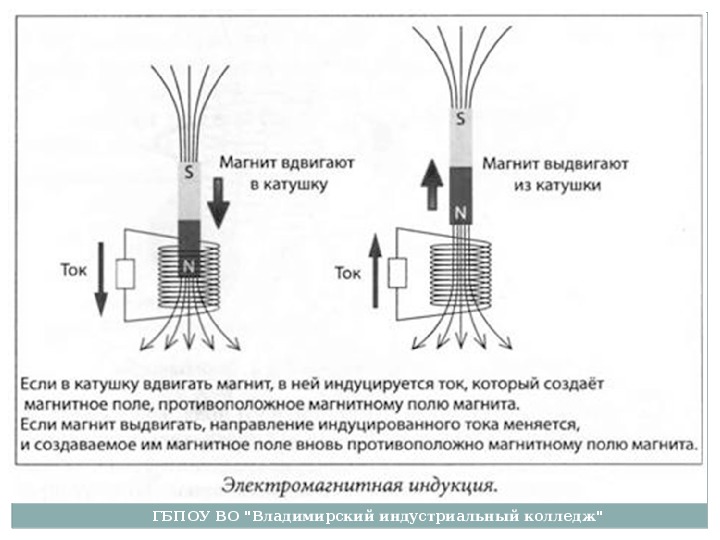
Проволочная катушка со стальным сердечником включена в цепь постоянного тока последовательно с реостатом и ключом (рис. 6).

Рис. 6. Иллюстрация к задаче

Электрический ток, протекающий по веткам катушки,  создает в пространстве вокруг нее магнитное поле (рис. 7). В поле катушки и находится такая же катушка .

Рис. 7. Иллюстрация к задаче

Каким образом можно поменять магнитный поток пронизывающий катушку ? Рассмотрите все возможные варианты.

Вспомним, изменение каких параметров приводит к изменению магнитного потока.

Начнем с изменения индукции магнитного поля катушки .Этого возможно добиться, если изменять силу тока, которая порождает ее магнитное поле. Изменять ток в изображенной цепи можно 2-мя способами:

1. Передвижение ползунка реостата
2. Включение/выключение ключа

Стоит отметить, что изменение значения тока будет наибольшим от максимального до нуля, что приведет к наибольшему изменению магнитного потока в катушке .

Следующим параметром, изменение которого повлияет на значение магнитного потока, является площадь контура. В нашем случае катушки  Но изменить площадь сечения катушки мы не можем. Следовательно, вариант отпадает.

Последним вариантом изменения магнитного потока является поворот катушки  относительно магнитных линий катушки . Для достижения максимального результата изменения повернуть катушку необходимо на 90(рис. 8).

Рис. 8. Иллюстрация к задаче

Что же описывается магнитным потоком?

Как мы уже отметили, он зависит:

• От силы магнитного поля
• От площади контура, через который эти магнитные линии проходят
• От угла расположения между контуром и магнитными линиями

Таким образом, магнитный поток характеризует количество магнитных линий, пронизывающих ограниченный контур.

Это легко проверить.

1. Сравним количество линий, которые пронизывают одинаковый контур, но в различных по силе магнитных полях (рис. 9).

В более сильном поле контур пронизывает больше линий.

Рис. 9. Иллюстрация к задаче

2. Если сравнить количество линий, которые в одном и том же однородном магнитном поле пронизывают различные по площади контуры, то их очевидно больше через больший контур (рис. 10).

Рис. 10. Иллюстрация к задаче

3. Если сравнивать поворот контура в магнитном поле на угол  к магнитным линиям и его расположение вдоль линий, то в первом случае их количество через плоскость контура будет максимально. А во втором магнитные линии будут скользить вдоль контура и не пронизывать его вовсе (рис. 11).

Рис. 11. Иллюстрация к задаче

В указанных примерах большему числу линий через контур соответствовал больший магнитный поток.

В результате отметим, что поскольку величина тока индукции зависит от изменения магнитной индукции, площади контура и от ее ориентации в пространстве, то принято говорить, что она зависит от изменения магнитного потока.

Кроме того, опыты Фарадея показали, что важна скорость изменения магнитного потока. Чем быстрее изменять указанные величины, тем величина индукционного тока будет больше.

Таким образом, можно утверждать, что явление электромагнитной индукции характеризуется скоростью изменения магнитного потока.

---

 

---

Задача на определение условий возникновения индукционного тока

Для того чтобы разобраться со взаимосвязью магнитного потока через контур и явлением электромагнитной индукции в нем, рассмотрим задачу:

Небольшую катушку поступательно перемещают в однородном магнитном поле. Возникает ли в катушке индукционный ток? Ответ обоснуйте.

Рис. 12. Иллюстрация к задаче

Может показаться, что из-за движения катушки могут быть изменения, следствием которых будет являться возникновение тока индукции в ее витках (рис. 12).

Вспомним, что обязательным условием возникновения тока индукции является изменение магнитного потока через витки катушки. Для этого необходимо изменение магнитной индукции через контур катушки. Чего не наблюдается, т. к. по условию поле однородно.

Кроме этого возможно изменение площади сечения катушки, чего также не наблюдается.

Последний возможный вариант – это изменение угла поворота плоскости катушки к магнитным линиям поля, чего, очевидно, также не происходит, поскольку движение поступательное, а значит, никаких поворотов катушки не наблюдается.

Следовательно, делаем вывод – магнитный поток изменяться не будет, соответственно, никакого тока индукции образовываться в витках катушки тоже не будет.

---

 

---

Сравнение магнитного потока с потоком воды

Название изученной нами новой физической величины магнитного потока не случайно. Дело в том, что магнитный поток через контур можно сравнить с потоком воды через кольцо, которое помещено в трубу (рис. 13). (1)

Чем скорость воды больше, тем больше ее проходит через кольцо в единицу времени. (2)

Чем больше площадь кольца, тем, опять-таки, через него протечет больше воды за наблюдаемое время. (3)

Если поворачивать кольцо при его поперечном расположении к потоку воды, через плоскость кольца протечет максимальное количество воды. (4)

Если начать его поворачивать под острым углом к потоку, то воды будет протекать все меньше. (5)

Рис. 13. Сравнение магнитного потока с потоком воды

А при повороте вдоль оттока вода вообще не будет проходить сквозь кольцо, а будет скользить вдоль него. (6)

Аналогичные свойства мы с вами рассмотрели для магнитного потока.

---

 

 

Заключение

 

 

На уроке мы объяснили, какие параметры магнитного поля и контура необходимо менять для наблюдения явления электромагнитной индукции. Мы объединили это в понятие «магнитный поток».

 

 

Список литературы

1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования.
2. Яворский Б. М., Пинский А. А., Основы физики, т. 2., – М., Физматлит., 2003.
3. Элементарный учебник физики. Под ред. Г. С. Ландсберга, Т. 3. – М., 1974.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал «festival.1september.ru» (Источник)
2. Интернет-портал «nvtc.ee» (Источник)
3. Интернет-портал «class-fizika.narod.ru» (Источник)

 

Домашнее задание

1. От чего зависит магнитный поток, пронизывающий площадь плоского контура, помещенного в однородное магнитное поле?
2. Как меняется магнитный поток при увеличении в n раз магнитной индукции, если ни площадь, ни ориентация контура не меняются?
3. Меняется ли магнитный поток при таком вращении контура, когда линии магнитной индукции то пронизывают его. то скользят по его плоскости?

 

Физика пружин | Как производители понимают дизайн пружин

Физика пружин: как производители проектируют пружины, которые работают

Поместите пружину сжатия рядом с листовой пружиной , и вы увидите два очень разных объекта, между которыми мало общего. поверхность. Пружины бывают самых разных форм и размеров, но независимо от того, как они выглядят, все они работают одинаково. Каждая пружина представляет собой эластичный объект , что означает, что она накапливает и высвобождает энергию. Конструкция пружин и их изготовление зависят от глубокого понимания физики пружин.

Процесс производства пружин и оборудование для изготовления пружин немного сложнее, но сами пружины представляют собой простые механизмы, которые ведут себя очень предсказуемо, если вы знаете, чего ожидать. Понимая физику пружин, производители могут точно предсказать, как пружина будет вести себя в реальном мире, прежде чем они включат намоточный станок.

Загрузите нашу бесплатную электронную книгу: Все о пружинах

Закон Гука: Физика пружин

Помимо хранения и высвобождения энергии, еще одним важным аспектом физики пружин является Закон Гука. Закон Гука гласит, что чем больше вы деформируете пружину, тем больше силы потребуется для ее дальнейшей деформации. Используя пример обычной пружины сжатия, чем больше вы сжимаете пружину, тем больше силы потребуется для ее дальнейшего сжатия.

Британский физик Роберт Гук (на фото справа) впервые опубликовал закон в 1678 году, хотя утверждал, что знал о нем почти два десятилетия. Закон был просто сформулирован на латыни, uttensio, sic vis, , что примерно переводится как «как расширение, так и сила». Более современное алгебраическое представление закона: F=kX , где F — сила, k — жесткость пружины , а X — длина деформации.

Если вы посмотрите на график уравнения, вы увидите прямую линию или линейную скорость изменения силы. Из-за этой особенности пружины, подчиняющиеся закону Гука, попадают в категорию пружин с «линейной силой».

Константа пружины

Константа пружины точно определяет, какая сила потребуется для деформации пружины. Стандартной международной (СИ) единицей измерения жесткости пружины является ньютон/метр, но в Северной Америке они часто измеряются в фунтах/дюйм. Более высокая жесткость пружины означает более жесткую пружину, и наоборот.

Жесткость пружины можно определить по четырем параметрам:  

• Диаметр проволоки : диаметр проволоки, входящей в состав пружины
• Диаметр рулона : диаметр каждого рулона, измерение натяжения рулона
• Длина в свободном состоянии : длина пружины в состоянии покоя
• Количество активных витков : количество витков, которые могут свободно расширяться и сжиматься

Материал , из которого изготовлена ​​пружина, также играет роль в определении жесткости пружины наряду с другими физическими свойствами пружины.

Исключения из закона Гука

В мире пружин есть несколько исключений из закона Гука. Например, слишком растянутая пружина растяжения перестанет соответствовать закону. Длина, на которой пружина останавливается по закону Гука, называется пределом упругости .

Пружины переменного диаметра , такие как конические, выпуклые или вогнутые пружины, могут быть свернуты с различными параметрами усилия. Если пружина шаг  (расстояние между витками) постоянно, сила конической пружины будет изменяться нелинейно, а это означает, что она не подчиняется закону Гука. Однако шаг пружины также можно варьировать для получения конических пружин, которые действительно подчиняются закону.

Пружины с переменным шагом являются третьим примером пружины, которая не подчиняется закону Гука. Пружины с переменным шагом часто представляют собой пружины сжатия с постоянным диаметром витка, но с переменным шагом.

Пружины постоянной силы, по отношению к закону Гука, часто являются ложными исключениями . Судя по названию и описанию, пружины постоянной силы , а не , подчиняются закону Гука. В конце концов, если сила, которую они прикладывают, постоянна, как сила может меняться в зависимости от длины пружины? Как упоминалось в нашей публикации о пружинах постоянной силы , материал, из которого изготовлены эти пружины, на самом деле соответствует закону Гука. Отличие состоит в том, что упругая часть пружины с постоянной силой — это только та часть, которая меняется со спиральной на прямую. При вдавливании или вытягивании пружины и изменении диаметра витка действующая сила также изменяется. Это изменение, однако, часто незаметно, потому что изменения диаметра катушки очень малы.

Используя современное оборудование для навивки пружин с ЧПУ AIM , пружины с постоянным усилием можно сконструировать таким образом, чтобы усилие пружины можно было поддерживать постоянным или даже иметь отрицательный градиент при растяжении пружины. Достигнуты отрицательные градиенты порядка 35%.

Почему физика пружин имеет значение при проектировании и производстве пружин

Когда производители производят пружины, они должны знать, как они себя поведут. Очевидно, что та же самая пружина, которая используется для подвески грузовика, не будет работать в шариковой ручке, но во многих механических приложениях мельчайшие различия в поведении пружины будут определять, будет ли система работать или нет.

Например, пружины используются для расширения кровеносных сосудов в медицинских целях. Если жесткость пружины слишком высока или проволока слишком тонкая, пружина может привести к опасному для жизни разрыву. В более широком масштабе системы автомобильной подвески полагаются на чрезвычайно точные пружины, обеспечивающие амортизацию без дестабилизации автомобиля на высоких скоростях.

Все конструктивные характеристики пружины играют роль в определении полезного применения той или иной пружины. Когда производитель настраивает параметры своих станков для намотки пружин, он не просто гадает. Понимая физику пружин, производители могут гарантировать, что они наматывают правильную пружину для работы.

Для подробного ознакомления с типами пружин и их производством загрузите нашу бесплатную электронную книгу

Все о пружинах

моделирование — создание проволочной катушки

спросил 6 лет, 7 месяцев назад

Изменено 4 года, 10 месяцев назад

Просмотрено 6к раз

$\begingroup$

Я хочу создать это: Обратите внимание, что проволока уложена хаотично, поэтому спиральный объект не одно и то же. Есть отличный способ выполнить эту задачу в 3ds max: https://www.youtube.com/watch?v=dAIrlxPUnqM. В основном он деформирует прямой сплайн/кривую, а затем сгибает ее пару итераций (макс. угол более 9000 градусов). Насколько я знаю, Blender не может сгибаться таким образом с помощью простой деформации, только до 360 градусов. Есть ли другой способ сделать обмотку проводов, как на фото?

• моделирование
• модификаторы
• объекты
• преобразования

$\endgroup$

1

$\begingroup$

Вы можете легко создать его с помощью спирали кривой Безье.

1. Активировать дополнение Добавить дополнительные объекты кривой в пользовательских настройках
2. Добавить новую кривую спираль с помощью Shift + A Добавить > Кривая > Добавить спирали кривой: > Archemidian
3. Отрегулируйте число оборотов по желанию, около 8$ должно хватить
4. Отрегулируйте рост радиуса до небольшого значения, примерно одной десятой от общего радиуса, который вы установили.
5. Держите количество вершин на низком уровне, вам не понадобится много вершин, кривая позаботится обо всем остальном.
6. Установите тип Poly и настройте все по желанию, но убедитесь, что вы оставили параметр Height равным $0$
7. Поверните его на $Z$, чтобы его конечная вершина была симметричной, сотрите одну конечную вершину, если необходимо, чтобы они обе начинались и заканчивались в $X=0$

8. В режиме редактирования переместите конечную вершину на 1/10 общего радиуса вниз, а начальную вершину на 1/10 общего радиуса вверх

9. В режиме редактирования продублируйте все и переместите вверх, чтобы концы идеально соединились. Вручную проверьте, что они делают, перемещая вершину по мере необходимости.

10. Теперь продублируйте все и несколько раз увеличьте предыдущую высоту в два раза, чтобы сделать катушку нужной величины.

11. Преобразовать в сетку, чтобы можно было быстро удалить дубликаты и соединить концы, а затем преобразовать обратно в кривую с помощью меню Alt + C
12. В режиме редактирования установите тип кривой на Безье и типы ручек на Автоматически
13. Скос по желанию.
14. Теперь используйте Proportional Edit set to Random fallof type, чтобы переместить или масштабировать вершину и придать ей более грубый случайный вид по желанию.

$\endgroup$

4

$\begingroup$

Вы можете получить это, используя Дополнительные объекты кривой —> Торический узел плюс . Думаю, это самое ленивое решение :).

Включить Дополнительные объекты кривой в настройках пользователя ( Ctrl + Alt + U ).

Нажмите Shift + A —> Curve —> Torus Knot Plus , чтобы добавить спираль и поиграть с ее настройками. Добавьте еще один, измените его настройки (чтобы он немного отличался от предыдущего) и масштабируйте его, чтобы провод выглядел более плотным.

ПРИМЕЧАНИЕ: Вы можете использовать пропорциональное редактирование , чтобы сделать провод более грязным.