Определение осевого момента инерции тела методом физического маятника

Цель работы: освоение метода экспериментального определения момента инерции вращающегося тела с помощью дополнительного груза.

1. Краткая теория

Теория данной работы практически совпадает с теорией, изложенной в пункте 1 описания лабораторной работы №1.2.2. Поэтому прежде чем приступить к работе, конспектируйте указанный теоретический материал.

2. Описание методики измерения и лабораторной установки

Приборы и принадлежности: цилиндр или шар с прикрепленным дополнительным грузом, штангенциркуль, секундомер.

На практике часто возникает необходимость в определении осевого момента инерции тела, вращающегося относительно оси, проходящей через его центр инерции. Тело находится в этом случае в уравновешенном состоянии и не способно совершать колебания вокруг оси вращения. Однако, если к исследуемому телу прикрепить вспомогательный груз mо (вне оси вращения), то состояние безразличного равновесия системы под действием силы тяжести дополнительного груза заменяется состоянием устойчивого равновесия.

В этом случае исследуемое тело с дополнительным грузом можно рассматривать как физический маятник. Период колебаний такого физического маятника можно вычислить по формуле:

T = 2π

J           ,

[(mо  + m)gL]

откуда момент инерции J системы относительно оси вращения:

T 2 (m

+ m )gL

J =      о          ,           (27)

4π 2

где m – масса исследуемого тела, L – расстояние центра инерции системы относительно оси вращения.

20

Для  определения момента инерции  исследуемого тела  J m    из

общего момента инерции системы J  необходимо вычесть момент инерции дополнительного груза относительно общей оси колебания J    :

0

J m  = J − J m

.           (28)

В качестве дополнительного груза обычно берут однородные тела правильной геометрической формы, момент инерции которых относительно оси симметрии можно точно вычислить. Например, цилиндр или шар, моменты инерции, которых приведены в таблице 1 теоретической части работы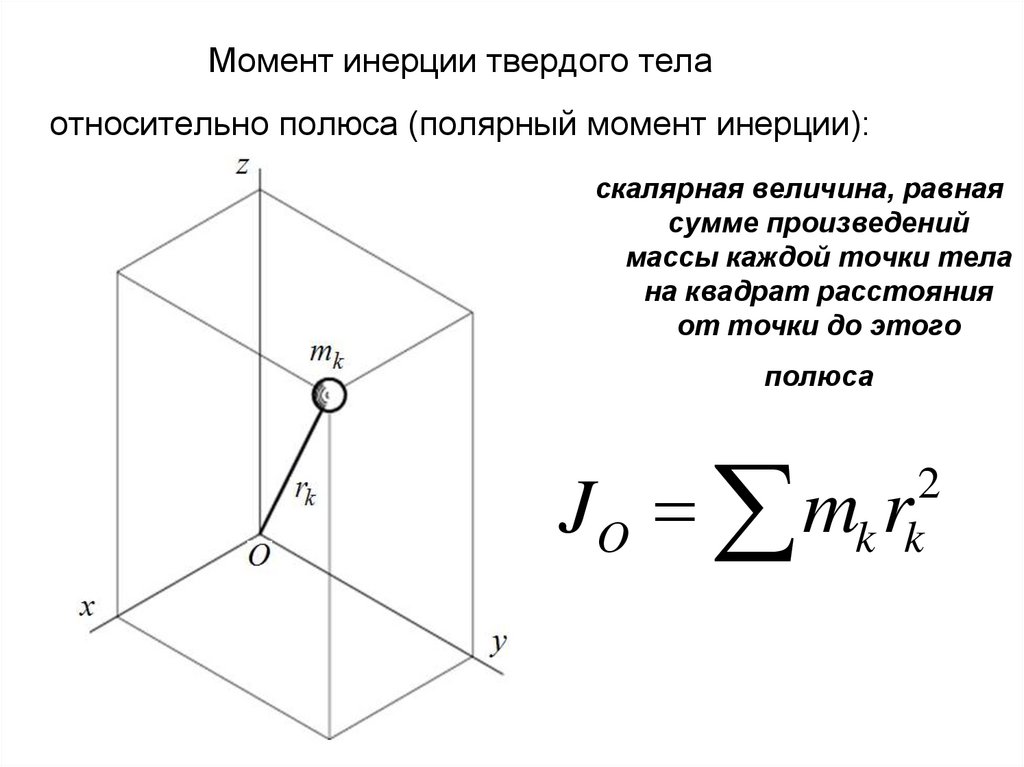 № 1. 2.1.

Момент инерции дополнительного груза можно вычислить по теореме Штейнера (10).

Координата центра инерции нахо — l

дится по формуле:

Чтобы  иметь  возможность  проверить результаты экспериментального определения момента инерции тела, в данной работе применяются тела в виде диска (рис. 6) или шара.

r

Fт

Рис. 6. Физический маятник с дополнительным грузом

3. Измерения и обработка результатов измерений

Вид физического маятника для исследования задается преподавателем.

1.   С помощью штангенциркуля измерьте диаметры исследуемого тела D и дополнительного груза d в трех разных сечениях и определите радиусы  R и r.  Вычислите расстояние l между центрами инерции тел.

2.   Измерив время определенного количества колебаний (в пределах 5−10), определите период колебаний системы,. Измерения проводите три раза для разного количества колебаний.

3.   По формуле (29) по среднему значению l вычислите расстояние от оси вращения до центра инерции L.

Массы считаются заданными.

21

4.   По формуле (27) вычислите момент инерции системы J для каждого измерения.

5.   По средним значениям r  и l  вычислите момент инерции дополнительного груза

J           по формуле (10).

0

6.   Рассчитайте момент инерции исследуемого тела J m

по формуле (28). Результаты измерений и расчетов занесите в таблицу 4.

Результаты измерений и расчетов

Таблица 4

№ опыта	R, м	r, м	l, м	L, м	Т, с	J, кг⋅м2	Jmo, кг⋅м2	Jm, кг⋅м2	∆J, кг⋅м2
1 2 3
Ср.

7.   Вычислите доверительный интервал для момента инерции исследуемого тела:

коэффициент Стьюдента, (строгое определение ∆J m

производится по методу косвенных измерений).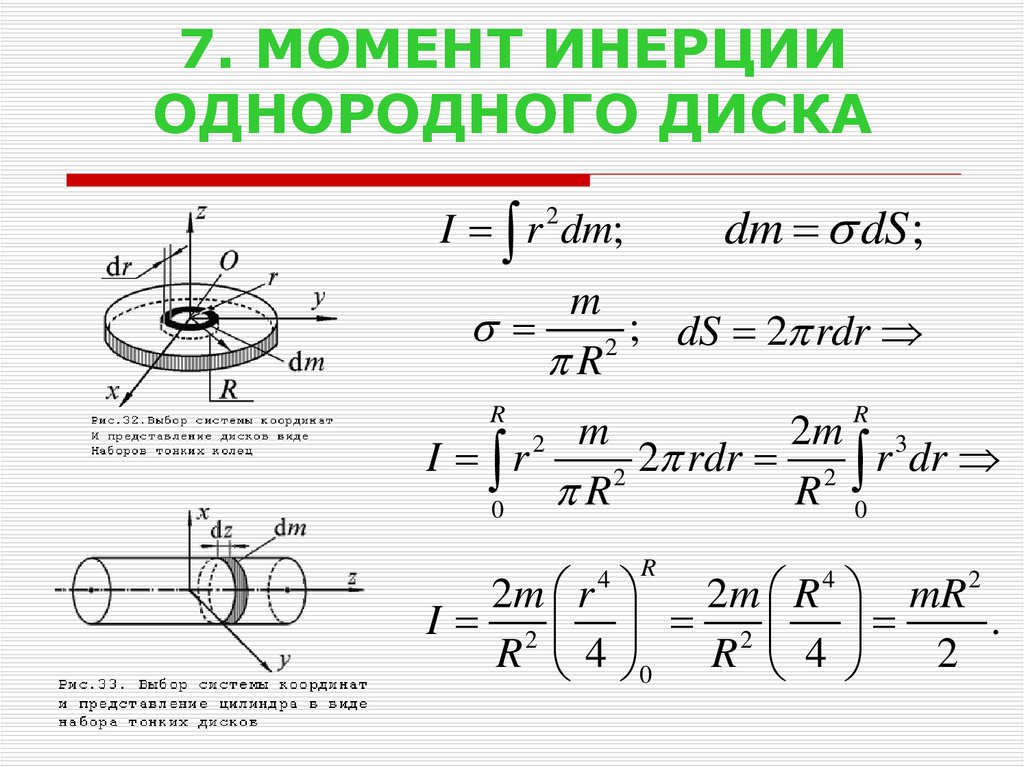

Результат занесите в последнюю ячейку тал. 4.

8.   Вычислите момент инерции исследуемого тела, по формуле,

приведенной в табл. 1  и сравните с экспериментальным значением.

Контрольные вопросы

1.   Дайте определение физического маятника.

2.   В чем заключается суть метода определения момента инерции тела методом дополнительного груза?

3.   Что называется моментом инерции? Сформулируйте и запишите теорему Штейнера.

4.   Что называется центром инерции тела?

22

Материал взят из методических указаний Динамика твердого тела (Биктагиров В.В.)

Определение момента инерции тела по методу крутильных колебаний

ЛАБОРАТОРНАЯ РАБОТА 1-06

 

ОПРЕДЕЛЕНИЕ МОМЕНТА  ИНЕРЦИИ ТЕЛА ПО

МЕТОДУ КРУТИЛЬНЫХ КОЛЕБАНИЙ

 

Цель работы: определение момента инерции тела методом крутильных колебаний, проверка справедливости теоремы Гюйгенса–Штейнера.

Приборы и принадлежности: лабораторная установка, грузы сферической формы, электронный секундомер, штангенциркуль, весы и разновески.

ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ

 

Поступательное и вращательное движения являются частными проявлениями общего процесса механического движения материи.  Физическое единство отражается в аналогии математической формы записи законов, описывающих эти виды движения. Основной закон динамики поступательного движения описывается выражением

_{.                         (1)}

Величина m – масса тела – выражает численно меру инертности тела, т.е. его способность изменять состояние поступательного движения под действием силы F. Основной закон динамики вращательного движения твердого тела, вращающегося вокруг оси симметрии тела, записывается в виде

_{,                          (1а)}

где L — момент импульса тела; j — вектор углового перемещения; e — угловое ускорение; M — момент силы.

Коэффициент пропорциональности J носит название момента инерции. Момент инерции является мерой инерции тела во вращательном движении и определяет способность тела изменять состояние вращательного движения под действием момента  силы M.

Размерность момента инерции в системе СИ – [кг×м²]. Исходя из размерности момента инерции, можно дать определение момента инерции материальной точки относительно оси вращения в виде

J_i = m_{i,                                           (2)}

где r_i – радиус вращения материальной точки, а m_i – ее масса. Масса реального тела представляется в виде суммы масс материальных точек, его составляющих. Аналогично этому, момент инерции тела есть совокупность моментов инерции его частей, рассматриваемых как материальные точки:

J = _{.                                           (3)}

Для тел правильной геометрической формы суммирование (а в пределе – интегрирование) по (3) дает следующие результаты для моментов инерции, вычисленных относительно оси, проходящей через центр симметрии этих тел:

обруч J = mr²;

диск J = _mr²;

шар J = _mr²;

здесь r – радиус соответствующих тел, а m – их масса.

Если необходимо рассчитать момент инерции тела относительно оси АА, не проходящей через центр симметрии, но параллельной ей (рис. 1), можно воспользоваться теоремой Гюйгенса–Штейнера: «Момент инерции тела J

АА относительно любой оси АА параллельной оси ОО, проходящей через центр симметрии тела, равен моменту инерции  J_оо  этого тела  относительно оси ОО,  сложенному с величиной ml²; l — расстояние между осями АА и ОО; m – масса тела

J_AA = J_oo + ml².                                            (4)

Используя формулы (3) и (4), можно аналитически рассчитать момент инерции любого тела, условно разделяя его на составные части правильной геометрической формы и определяя расстояния, на которых они находятся от общей оси вращения тела. В случаях, когда аналитическое определение момента инерции затруднено сложностью формы тела или неоднородностью распределения массы, его определяют опытным путем, что является одной из целей настоящей работы.

 

ТЕОРИЯ МЕТОДА ОПРЕДЕЛЕНИЯ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА И ПРОВЕРКИ ТЕОРЕМЫ  ГЮЙГЕНСА–ШТЕЙНЕРА

 

 Тело, момент инерции которого необходимо определить относительно некоторой  оси вращения ОО, проходящей через центр симметрии С тела, жестко скрепляют с этой осью. Если концы оси фиксировать, тело с осью можно рассматривать как крутильный (торсионный) маятник (рис. 2). Выведенный из состояния равновесия маятник будет совершать колебания с периодом

_{.                           (5)}

Здесь κ (каппа) называется коэффициентом угловой жесткости или модулем кручения подвеса (оси). Численно κ**выражает величину момента силы, возникающего в материале при его закручивании на единичный угол. Для тела, момент инерции J_оо которого необходимо определить в опыте, период колебаний будет иметь величину Т₀

_{.                                  (5а)}

Если коэффициент угловой  жесткости известен, то J_oo легко определить из формулы (5а). Однако часто коэффициент угловой жесткости неизвестен. Тогда для определения момента инерции тела J_oo, чтобы исключить из формулы (5а) κ, поступают следующим образом: добавляют к телу, момент инерции которого определяют, дополнительное тело правильной геометрической формы, момент инерции J которого относительно оси ОО маятника легко вычислить по теореме Гюйгенса–Штейнера. Период колебаний такого усложненного маятника станет равным

_{.                                           (6)}

Из уравнений (5а) и (6) выражаем искомый момент инерции J_oo

_{.                                        (7)}

Если в качестве дополнительного  груза использовать два одинаковых шара, массы m₀ и радиуса r каждый, расположенных симметрично относительно оси маятника ОО, то момент инерции J будет записан, применяя теорему Гюйгенса–Штейнера, в виде

_{.                                            (8)}

Здесь m – общая масса двух шаров; l – расстояние между осью ОО и центром каждого шара.

С учетом (8) получаем формулу для  искомого момента инерции

_{.                               (9)}

Подчеркнем, что формула (9) позволяет  определить момент инерции J_oo крутильного маятника при условии, что теорема Гюйгенса – Штейнера справедлива. Чтобы убедиться в справедливости теоремы, проведем следующие рассуждения. Допустим, что с помощью устройства, изображенного на рис. 4, измерена зависимость периода колебаний маятника Т с дополнительными грузами шарообразной  формы от расстояния   _{между центрами шаров и осью ОО. Построим график зависимости Т² от l². Покажем, что если теорема Гюйгенса – Штейнера справедлива, этот график должен изображаться прямой (рис. 3), пересекающей ось ординат в точке . Наклон этой прямой равен величине . В самом деле, если действительно справедливо, что , формула (6) легко приводится к виду}

то есть Т² = а _{+ С, где ;}

Полученное уравнение  есть уравнение прямой, что доказывает справедливость теоремы Гюйгенса–Штейнера. Наклон этой прямой равен _{, что дает возможность экспериментально определить значение модуля кручения подвеса (оси ОО).}

 Прямая пересекает ось ординат в точке _{, что позволяет рассчитать момент инерции J00 крутильного маятника с точностью,  большей, чем это позволяет формула (9), т.к. для определения J00 в данном случае используется прямая, построенная с учетом погрешностей измерения всех экспериментальных точек.}

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ  УСТАНОВКИ

 

Схема экспериментальной установки для проверки теоремы Гюйгенса–Штейнера и определения момента инерции твердого тела изображена на рис. 4. Тело 1, момент инерции которого J₀₀ необходимо определить, имеет форму шара с кольцом и двумя симметрично расположенными стержнями. Дополнительные грузы 2 – малые шары – надеваются на стержни и могут быть установлены на различных расстояниях l от оси симметрии установки. Ось ОО прикреплена к телу 1 с двух сторон и закреплена в кронштейнах 3. Для приведения системы в колебательно-вращательное движение необходимо приложить момент силы – повернуть двумя руками стержни на угол 8–10°. (При малых углах период колебаний не зависит от амплитуды колебаний).

ЗАДАНИЕ НА ПРОВЕДЕНИЕ ИЗМЕРЕНИЙ

 

1. Проведите измерение периода колебаний Т₀ крутильного маятника без дополнительных грузов не менее 3 раз. Определите его среднеарифметическое значение.
2. Проведите измерение зависимости периода Т крутильного маятника с дополнительными грузами от расстояния l между осью ОО и центром шаров. Измерение периода для каждого значения l проведите не менее 3 раз. Определите среднеарифметическое его значение для каждого l.
3. Постройте график зависимости  _{; убедившись в справедливости теоремы Гюйгенса–Штейнера, определите из графика  модуль кручения подвеса (оси ОО) и момент инерции J00  маятника относительно оси ОО.}
4. Вычислите момент инерции J₀₀ по  формуле (9). Сравните полученные значения J₀₀.
5. Сделайте вывод о справедливости теоремы Гюйгенса–Штейнера и о совпадении момента инерции J₀₀ маятника, рассчитанного по формуле и определенного из графика. В каком случае точность определения J₀₀ больше и почему?

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ РАБОТЫ

 

Для более точного измерения периода необходимо измерить время t не менее как десяти полных колебаний, а затем определить период как

Т = t / N,

где N – число полных колебаний.

Рекомендуется следующий  порядок работы:

1. Определите период колебаний тела Т₀ без дополнительных грузов.
2. Установите дополнительные грузы на концах стержней так, чтобы их край совпадал с краем стержня. В таком положении центры масс шаров будут находиться на расстоянии 0,2 м от оси вращения ОО. Измерьте период Т₁.
3. Измерьте периоды Т₂, Т₃, … Т₆, последовательно передвигая на 2 см шары к центру. Заполните таблицу.
4. Измерьте диаметр шаров-грузов, найдите величину их радиуса. Определите общую массу двух шаров.

 

		l1, м	l2, м	l3, м	l4, м	l5, м	l6, м	Примечание
								r, м =       = 0,023 м   m0, кг =  = 0,18 кг
	Т0, c	Т1, c	Т2,c	Т3, c	Т4, c	Т5, c	Т6, c
1
2
3
Среднее значение периода

 

ВОПРОСЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ И

 ИНДИВИДУАЛЬНОЙ РАБОТЫ

 

1. В чем проявляется физическое единство законов, описывающих поступательное и вращательное движения?
2. В чем проявляется отличие  момента инерции от массы тела?
3. Сформулируйте теорему Гюйгенса–Штейнера. Можно ли изменять ориентацию оси АА?
4. В каких случаях является затруднительным аналитический расчет момента инерции тела? Как поступают в этом случае?
5. Под действием касательной силы F диск массой m и радиусом R приобретает угловое ускорение e относительно оси, проходящей через центр инерции диска. При каких значениях массы и радиуса диска может быть получено прежнее значение углового ускорения e, если касательная вращающая сила уменьшена в k раз. Дайте обоснованный ответ в виде аналитического доказательства.
6. Каков физический смысл коэффициента угловой жесткости или модуля  кручения подвеса?
7. В чем состоит метод дополнительных грузов, используемый в данной работе? Какие дополнительные грузы используются в данной работе?
8. В чем состоит метод проверки справедливости теоремы Гюйгенса – Штейнера, используемый в данной работе?
9. Зависимость Т_{от в предлагаемой работе является линейной? Объясните цели, которые преследуются построением такого графика.}
10. Объясните метод определения модуля кручения подвеса, используемый в данной работе. Как учитывается погрешность измерений данного метода?
11. Какие физические величины должны быть измерены для определения момента инерции цилиндра относительно оси, проходящей параллельно оси симметрии цилиндра?
12. Какие физические величины влияют на период колебаний маятника, используемого в данной работе?
13. Исследуйте зависимость периода колебаний Т от параметров маятника. Имеются ли максимумы и минимумы у Т? 
14. Каким образом размеры стержней, по которым скользят шары, влияют на период колебаний маятника?
15. Докажите, что при углах поворота стержней  маятника на угол, больший, чем 8–10°, период колебаний зависит от амплитуды колебаний.
16. Каким образом влияет амплитуда колебаний на погрешности определения момента маятника инерции и его модуля жесткости подвеса.
17. Предложите наиболее точный метод определения радиуса шаров, используемых в данной работе.
18. Момент инерции маятника определяют графическим и аналитическим путем. В каком случае точность выше и почему?
19. При длительном пребывании в невесомости космонавты обычно худеют. Как можно измерить массы тела космонавтов в невесомости?
20. Как рассчитывают момент инерции шаров, имеющих внутреннюю полость в виде шара, стержня, прямоугольного параллелепипеда?
21. Как измерить момент инерции Земли, Луны?
22. Как измерить орбитальный момент импульса электрона?
23. Как измерить момент инерции молекулы водорода, кислорода.
24. Как измерить начальную (конечную) кинетическую энергию маятника, применяемого в данной работе?
25. Как измерить угловую скорость и угловое ускорение маятника в данной работе?

 

Примечания о моменте инерции твердых тел

Инерция — это характеристика тела, противодействующая любой силе, стремящейся сдвинуть его или, если оно движется, изменить величину или направление его скорости. Инерция твердого тела — это пассивный атрибут, который позволяет телу ничего не делать, кроме как противостоять активным агентам, таким как силы и крутящие моменты. Движущееся тело продолжает двигаться не по инерции, а потому, что нет силы, замедляющей его, изменяющей его траекторию или ускоряющей.

Момент инерции твердых тел

Момент инерции твердых тел определяет, насколько трудно повернуть требовательное тело вдоль определенной оси. Первый закон движения Ньютона гласит, что если тело не подвергается давлению со стороны внешнего источника, известного как сила, оно должно оставаться в состоянии покоя или равномерного движения. Инерция определяется как неспособность материального тела самостоятельно изменять свое состояние покоя или равномерного движения.

Основным свойством материи является инерция. Момент инерции твердого тела — это атрибут массы, влияющий на крутящий момент, необходимый для достижения заданного углового ускорения относительно оси вращения. Это естественный атрибут вещей. Тело сопротивляется любому изменению своего состояния покоя или равномерного прямолинейного движения по инерции. Для данной силы, чем больше масса, тем больше сопротивление движению или больше инерция. При поступательном движении масса тела используется для расчета коэффициента инерции.

Точно так же при вращательном движении тело, которое может свободно вращаться вокруг определенной оси, сопротивляется любому желаемому изменению своего состояния. Величина сопротивления будет определяться массой тела и ее распределением по оси вращения. Момент инерции твердого тела относительно указанной оси является коэффициентом инерции при вращательном движении.

Значение

Значение момента инерции твердого тела следующее:

•   Чем больше концентрация массы вдали от оси, тем больше момент инерции. Момент инерции твердого тела неодинаков по отношению к разным осям вращения.
•   Имеет значение при вращательном движении. Это свойство тела сопротивляться изменению состояния при вращательном движении.
•   Он связан с вращательным движением так же, как масса связана с поступательным движением.

Единица момента инерции

Определив момент инерции твердого тела, теперь мы можем узнать его единицу измерения.

Единица момента инерции твердого тела является составной единицей измерения. В Международной системе (СИ) m измеряется в килограммах, а r измеряется в метрах, при этом I (момент инерции) имеет размерность килограмм-метр в квадрате.

Расчет момента инерции твердого тела

Зная факторы, от которых зависит момент инерции твердого тела, мы можем теперь вычислить момент инерции твердого тела.

Если объект имеет непрерывное распределение массы, момент инерции твердого тела можно вычислить путем интегрирования моментов инерции составляющих его частей. Если dm — масса любой бесконечно малой частицы тела, а r — ее перпендикулярное расстояние от оси вращения, то момент инерции твердого тела относительно оси определяется как:

I= ∫r²dm

Факторы, влияющие на момент инерции

Момент инерции твердого тела зависит от следующих факторов:

•   Индекс массы тела.
•   Размеры и форма корпуса
•   Распределение массы вокруг оси вращения
•   Положение и направление оси вращения по отношению к корпусу.

Момент инерции различных объектов:

Мы знаем, что момент инерции твердого тела зависит от различных факторов.

Следовательно, она различна для разных твердых тел. Момент инерции различных жестких объектов заключается в следующем:

• Стержень — Через центр: 1 ⁄ 12 мл²

— до конца: 1 ~ 3 мл²

• Speera

– Салоу ⁄ 5 м²

–        Полая сфера:  2 ⁄ 3 м²

• Обруч

–        Диаметр обруча:  1 ⁄ 2MR²

— Обруч вокруг симметричной оси: MR²

• Цилиндр

— Сплошной цилиндр или диск, симметричная ось: 1 ⁄2 мр. Прямоугольные объекты

–        Сплошная прямоугольная коробка: 1 ⁄ 12 м (h² + w²)

–        Сплошная прямоугольная пластина: 1 ⁄ 12 м (h² + w²)

• 0 м²r : Кольцо0017 Диск :  1 ⁄ 2 м²

Вывод

Ось вращения влияет на момент инерции. После выбора двух уникальных осей предмет по-разному сопротивляется изменению вращения. Мы устанавливаем новый параметр, известный как радиус вращения, чтобы описать, как масса вращающегося твердого тела распределяется относительно оси вращения. Это связано с моментом инерции и полной массой тела. Стоит отметить, что мы можем написать I = Mk2, где k — размерность длины.

Таким образом, радиус вращения – это расстояние от оси материальной точки, масса которой равна массе всего тела, а момент инерции равен моменту инерции тела относительно оси. В результате на момент инерции влияют не только масса, форма и размеры тела, но и распределение массы внутри тела вокруг оси вращения.

Момент инерции — определение, формула, значение, факты

Что такое момент инерции?

Момент инерции (MOI) — это сопротивляемость тела его угловому ускорению. Момент инерции можно выразить как; I=mk ² , где m — масса тела, а k — радиус вращения.

Момент инерции Определение

Момент инерции – это величина, выражающая тенденцию тела сопротивляться внешнему угловому ускорению, которая может быть рассчитана как сумма произведений массы каждой частицы тела на квадрат расстояния до нее. от оси, вдоль которой он должен вращаться.

Момент инерции Формула

Момент инерции представляет собой резистивную способность поперечного сечения при вращении. Момент инерции также известен как площадь второго момента, которая может быть представлена ​​как ⁿ Σ ₁ A _i y _i , где y — расстояние центра тяжести площади от ее оси

Момент инерции также можно выразить как I=p/ω, где p — угловой момент, а ω — угловая скорость тела.

Момент инерции можно также рассчитать по формуле I=L/ω

Где, I= момент инерции

L= угловой момент

ω= угловая скорость

Единица момента инерции

Как мы знаем, I=mk ²

Итак, единица момента инерции is кг-м ²

Момент инерции — очень важная тема физики, которую необходимо понять, прежде чем применять ее к любым задачам реальной жизни. Момент инерции тела при вращательном движении так же важен, как и масса тела при его поступательном движении. Момент инерции – это свойство сечения, показывающее его способность противостоять вращательному движению.

Момент инерции поперечного сечения показывает сопротивление тела вращению, которое зависит от расстояния накопления массы по поперечному сечению. Момент инерции говорит о свойстве поперечного сечения тела.

Момент инерции твердой сферы

Момент инерции твердой сферы представляет собой присущую ей инерцию, которая обеспечивает сопротивление угловому движению. Момент инерции зависит от распределения массы, и он больше, если распределение массы больше удалено от оси вращения.

Момент инерции для различных форм

Момент инерции для различных форм зависит от расположения массы относительно центра тела. По мере удаления массы от центра тела увеличивается его момент инерции относительно центра, что делает сечение более прочным.

Теорема о параллельной оси

Момент инерции поперечного сечения зависит от оси, вокруг которой вращается поперечное сечение. Итак, если известен момент инерции относительно его центра, то его можно вычислить относительно любой оси, используя две теоремы.

Теорема о параллельных осях используется для расчета момента инерции твердого тела относительно оси, параллельной центральной оси тела

Согласно теореме о параллельных осях: I=I _c +Mh ²

Где I _c — момент инерции, M — масса тела, а h — расстояние между новой осью и центральной осью.

Теорема о перпендикулярной оси

Теорема об перпендикулярной оси используется для расчета момента инерции тела относительно оси, перпендикулярной плоскости тела. Теорема перпендикулярной оси очень полезна для нахождения полярного момента инерции и помогает найти жесткость балки при кручении.

Согласно теореме о перпендикулярной оси; I _Z =I _X +I _Y

Влияние вращения оси на момент инерции

Момент инерции зависит от оси вращения тела, а также зависит от распределения массы по всей площади тела.