Задача 3 — Задачи по электростатике (Физика)
1. Задача 1.3
2. Вариант 11
3. Условие:
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
ε2/ε1=2/1; ε3/ε1=2/1; R0/R=2/1
По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0.
4. Решение:
5. Определим диэлектрическую проницаемость, как функцию радиуса
Для данного варианта .
По теореме Гаусса
и не зависит от диэлектрической проницаемости ε.
Т.к. , то . Поэтому ,
.
Т.к. , а , то , поэтому
, .
Определим поверхностную плотность связанных зарядов
, где — косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности , а для внешней поверхности . Тогда
.
Поэтому , а .
Объёмная плотность связанных зарядов , для полярных координат . Поэтому
, .
Для определения ёмкости вычислим напряжение на его обкладках
Поэтому .
6. Вариант 12
7. Условие:
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
ε2/ε1=3/1; ε3/ε1=1/2; R0/R=2/1
По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0.
8. Решение:
9. Определим диэлектрическую проницаемость, как функцию радиуса
Для данного варианта .
По теореме Гаусса
и не зависит от диэлектрической проницаемости ε,
. Т.к. , то . Поэтому ,
.
Т.к. , а , то , поэтому
, .
Определим поверхностную плотность связанных зарядов
, где — косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности , а для внешней поверхности . Тогда .
Поэтому , а .
Объёмная плотность связанных зарядов , для полярных координат . Поэтому
, .
Для определения ёмкости вычислим напряжение на его обкладках
Поэтому .
10. Вариант 13
11. Условие:
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
ε2/ε1=2/1; ε3/ε1=3/1; R0/R=2/1
По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0.
12. Решение:
Определим диэлектрическую проницаемость, как функцию радиуса
Для данного варианта .
По теореме Гаусса
и не зависит от диэлектрической проницаемости ε.
Т.к. , то . Поэтому ,
.
Т.к. , а , то , поэтому
, .
Определим поверхностную плотность связанных зарядов
, где косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности , а для внешней поверхности .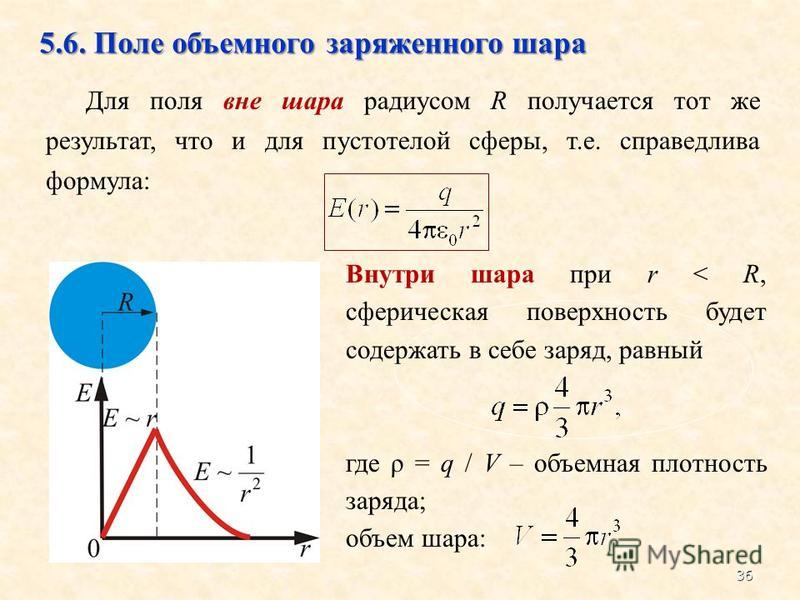 Тогда
Тогда
.
Поэтому , а .
Объёмная плотность связанных зарядов , для полярных координат . Поэтому
, .
Для определения ёмкости вычислим напряжение на его обкладках
Поэтому
.
13. Вариант 14
14. Условие:
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
ε2/ε1=1/2; ε3/ε1=3/1; R0/R=3/1
По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0.
15. Решение:
Определим диэлектрическую проницаемость, как функцию радиуса
Для данного варианта .
По теореме Гаусса
и не зависит от диэлектрической проницаемости ε.
Т.к. , то . Поэтому ,
.
Т.к. , а , то , поэтому
, .
Определим поверхностную плотность связанных зарядов
, где — косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности , а для внешней поверхности . Тогда
.
Поэтому , а .
Объёмная плотность связанных зарядов , для полярных координат . Поэтому
,
.
Для определения ёмкости вычислим напряжение на его обкладках
Поэтому .
16. Вариант 15
17. Условие:
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
ε2/ε1=1/3; ε3/ε1=1/2; R0/R=2/1
По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0.
18. Решение:
Определим диэлектрическую проницаемость, как функцию радиуса
Для данного варианта .
По теореме Гаусса
и не зависит от диэлектрической проницаемости ε,
. Т.к. , то .
Поэтому, .
Т.к. , а , то , поэтому
, .
Определим поверхностную плотность связанных зарядов
, где косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности , а для внешней поверхности . Тогда
.
Поэтому , а .
Объёмная плотность связанных зарядов , для полярных координат . Поэтому
,
.
Для определения ёмкости вычислим напряжение на его обкладках
Поэтому .
19. Вариант 16
20. Условие:
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
Величина диэлектрической проницаемости между обкладками меняется по линейному закону от значения ε1 до ε2 в интервале радиусов от R до R1, и ε3=сonst в интервале радиусов R1 до R0. Построить графически распределение модулей векторов электрического поля E, поляризованности Р и электрического смещения D между обкладками конденсатора. Определить поверхностную плотность зарядов на внутренней и внешней поверхностях диэлектриков, распределение объёмной плотности связанных зарядов ρ’(r), максимальную напряжённость электрического поля Е и ёмкость конденсатора на единицу длины.
ε2/ε1=1/2; ε3/ε1=2/1; R0/R=3/1
По результатам вычислений построить графически зависимости D(r)/D(R), E(r)/E(R), P(r)/P(R), ρ’(r)/ρ’(R) в интервале значений r от R до R0.
21. Решение:
Определим диэлектрическую проницаемость, как функцию радиуса
Для данного варианта .
По теореме Гаусса
и не зависит от диэлектрической проницаемости ε.
Т.к. , то . Поэтому ,
.
Т.к. , а , то , поэтому
, .
Определим поверхностную плотность связанных зарядов
, где косинус угла между нормалью между рассматриваемой поверхностью и поляризованностью, для внутренней поверхности , а для внешней поверхности . Тогда
.
Поэтому , а .
Объёмная плотность связанных зарядов , для полярных координат . Поэтому
Люди также интересуются этой лекцией: Работа продавца. Реклама.
,
.
Для определения ёмкости вычислим напряжение на его обкладках
Поэтому .
| Задача 1.1 | ||||||||||||||||||||||||||||||
Сферический диэлектрический конденсатор имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Заряд конденсатора равен q. Построить графически распределение модулей вектора электрического поля Е, вектора поляризованности Р и вектора электрического смещения D между обкладками конденсатора. Определить поверхностную плотность связанных зарядов на внутренней δ’1 и внешней δ’2 поверхностях диэлектрика, распределение объемной плотности зарядов ρ'(r), максимальные значения напряженности электрического поля Е, векктора электрического смещения D, разность потенциалов U между обкладками и емкость конденсаторов. Функция ε = f(r) для нечетных вариантов имеет вид: Функция ε = f(r) для четных вариантов имеет вид: Таблица 1.1. Значения параметров n и R0/R в зависимости от номера варианта.
| ||||||||||||||||||||||||||||||
| Задача 1.2 | ||||||||||||||||||||||||||||||
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и имеет радиусы внешней и внутренней обкладок R0 и R соответственно. Диэлектрическая проницаемость меняется между обкладками по закону ε = f(r). Построить графически распределение модулей вектора электрического поля Е, вектора поляризованности Р и вектора электрического смещения D между обкладками конденсатора. Функция ε = f(r) для нечетных вариантов имеет вид: Функция ε = f(r) для четных вариантов имеет вид: Таблица 1.2 Номера вариантов в зависимости от параметров n и R0/R
| ||||||||||||||||||||||||||||||
Задача 1.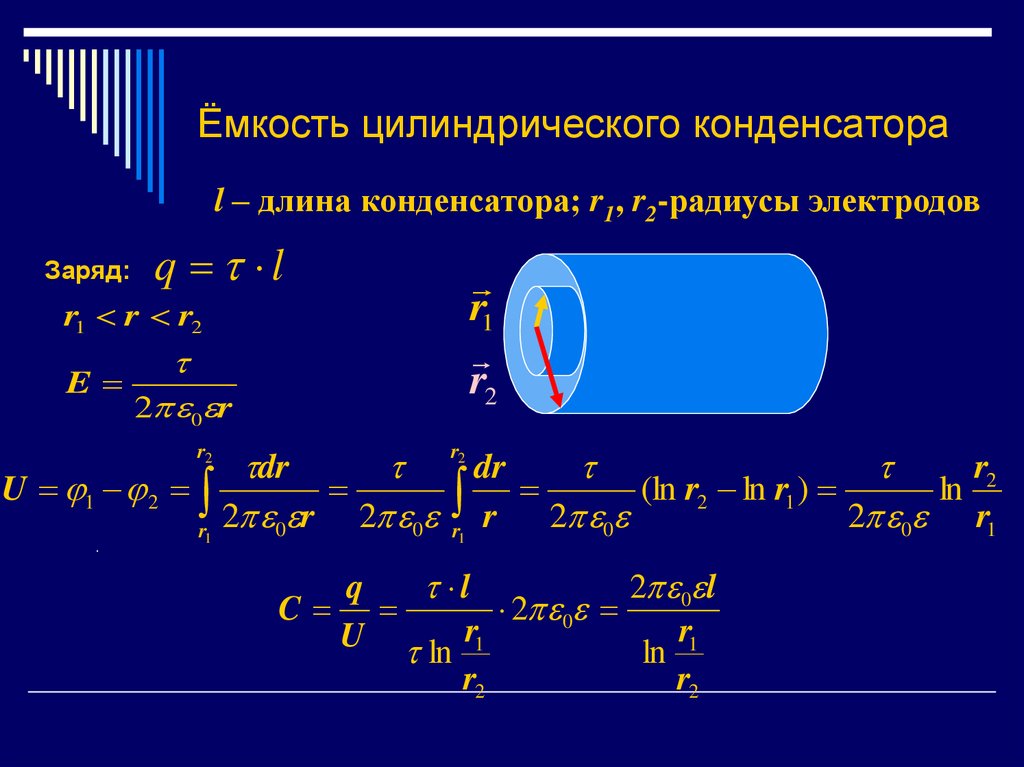 3 3
| ||||||||||||||||||||||||||||||
Цилиндрический бесконечно длинный диэлектрический конденсатор заряжен до разности потенциалов U и расстояние между обкладками равно d. Диэлектрическая проницаемость меняется между обкладками по закону ε = f(y). Построить графически распределение модулей вектора электрического поля E, вектора поляризованности P и вектора электрического смещения D между обкладками конденсатора. Определить емкость конденсатора C на единицу площади, поверхностную плотность связанных зарядов σ Функция ε = f(y) для нечетных вариантов имеет вид: Функция ε = f(y) для нечетных вариантов имеет вид:
| ||||||||||||||||||||||||||||||
| Для всех вариантов. | ||||||||||||||||||||||||||||||
По результатам проведенных вычислений построить графически зависимости D(r)/D(R), E(r)/E(R) в интервале значений r от R до R0 для задач 1.1 и 1.2, и D(y)/D(0), E(y)/E(0) в интервале значений y от 0 до d для задачи 1.3. Все зависимости изобразить на одном графике. | ||||||||||||||||||||||||||||||
Основные формулы электростатики.
| ||||||||||||||||||||||||||||||
Связь между векторами E,D,P: Теорема Гаусса для диэлектрика: Теорема Гаусса для вектора поляризованности P: Связь между напряженностью электрического поля E и потенциалом φ: Емкость конденсатора: | ||||||||||||||||||||||||||||||
| Пример решения задачи 1.1. | ||||||||||||||||||||||||||||||
Определим зависимость модуля вектора E,D,P от радиуса r в предположении, что заряд внутренней и внешней обкладки равен +q и -q соответственно. Для изотропной среды связь между этими векторами определяется известными соотношениями. Тогда, применив теорему Гаусса для сферы радиуса r: Поверхностную плотность связанных зарядов можно определить из соотношения Pn = σ’, например, для нечетных вариантов:
Объемную плотность связанных зарядов определим из уравнения:
В качестве поверхности интегрирования выберем две концентрические сферические поверхности радиусами r и r+dr. d(P4Пr2) =-dq’ где -dq’=ρ'(4Пr2dr) — величина связанного заряда, заключенного между этими сферическими поверхностями. для нечетного варианта: d((R0n — rn)q/4П(R0n + Rn))/r2dr = ρ’ = (-nrn-1)q/4П(R0n + Rn)r2 Емкость конденсатора можно определить найдя разность потенциалов между обкладками: Далее по определению емкости конденсатора C=q/∆φ | ||||||||||||||||||||||||||||||
| Пример решения задачи 1.2. | ||||||||||||||||||||||||||||||
Определим зависимость модуля векторов E,D,P от радиуса r в предположении, что заряд внутренней и внешней обкладки на единицу длины равны +λ и -λ соответственно. Тогда, применив теорему Гаусса для цилиндрической поверхности радиуса r: Поверхностную плотность связанных зарядов можно определить из соотношения Pn = σ’, например, для нечетных вариантов: Объемную плотность связанных зарядов определим из уравнения: В качестве поверхности интегрирования выберем две цилиндрические поверхности радиусами r и r+dr. для нечетного варианта: Емкость конденсатора можно определить найдя разность потенциалов между обкладками: Далее по определению емкости конденсатора на единицу длины: C = λ/∆φ |
электростатика — Электрическое поле вне бесконечно длинного конденсатора
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 287 раз
$\begingroup$
Если мы построим гауссову поверхность, как показано (цилиндр с одним из дисков в отрицательно заряженной пластине конденсатора) и нужно рассчитать поле в точке P, то, поскольку общий заряд внутри поверхности равен нулю, общий поток будет равен нулю.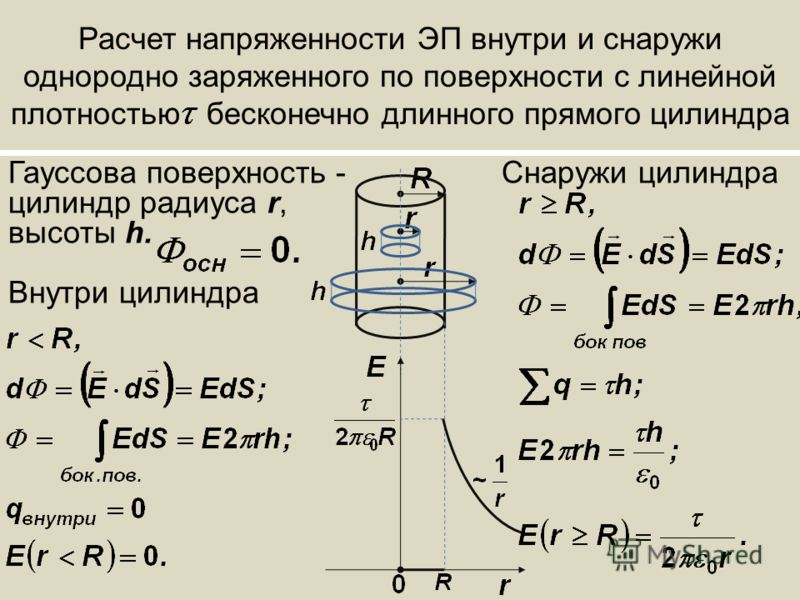 . А электрическое поле во всех точках нормально к плоскости пластин бесконечно длинного конденсатора, а также к дискам цилиндра, поэтому электрическое поле в точке P должно быть равно нулю, но P ближе к положительно заряженной пластине и, следовательно, к плоскости пластины. внешнее электрическое поле должно присутствовать в P. Я не могу разрешить это противоречие, буду признателен за любую помощь.
. А электрическое поле во всех точках нормально к плоскости пластин бесконечно длинного конденсатора, а также к дискам цилиндра, поэтому электрическое поле в точке P должно быть равно нулю, но P ближе к положительно заряженной пластине и, следовательно, к плоскости пластины. внешнее электрическое поле должно присутствовать в P. Я не могу разрешить это противоречие, буду признателен за любую помощь.
- электростатика
- емкость
- закон Гаусса
$\endgroup$
3
$\begingroup$
Бесконечная большая пластина создает перпендикулярное ей однородное электрическое поле. Это означает, что независимо от того, насколько близко или как далеко вы находитесь от этой пластины, вы измеряете одно и то же электрическое поле.
Таким образом, когда вы образуете конденсатор из двух противоположно заряженных пластин, поля между пластинами будут направлены одинаково, а это означает, что у вас есть ненулевое электрическое поле внутри, а поля снаружи пластин будут компенсироваться вне, и у вас есть нулевое электрическое поле снаружи.
$\endgroup$
0
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Емкость концентрических цилиндров – Дэвид Пейс, доктор философии, MBA
Вы здесь: Главная / Физика / Емкость концентрических цилиндров
6 комментариев
В этой теме мы рассчитаем емкость системы концентрических цилиндрических оболочек.
На следующем рисунке представлена геометрия этой темы. Две проводящие и концентрические цилиндрические оболочки бесконечной длины образуют систему с некоторой емкостью, Кл.
Геометрия этой темы. Цилиндрические оболочки бесконечно длинные (хотя и не нарисованные таким образом). Внешняя оболочка имеет радиус b, а внутренняя оболочка имеет радиус a.Начнем с того, что мы можем определить только емкость на единицу длины, C/L, поскольку общая емкость является нереальной величиной. Определение емкости:
, где Q — заряд системы, а V — ее потенциал. Из этого выражения видно, что емкость — это количество заряда, которое может быть сохранено в системе, удерживая ее при потенциале V. Заряд — это количество, которое может храниться отдельно, а не только в целом. Например, в конденсаторе с плоскими пластинами заряд, используемый в
Из этого выражения видно, что емкость — это количество заряда, которое может быть сохранено в системе, удерживая ее при потенциале V. Заряд — это количество, которое может храниться отдельно, а не только в целом. Например, в конденсаторе с плоскими пластинами заряд, используемый в
равно абсолютному значению суммы только на одной из пластин (если бы мы использовали общий заряд, то у нас был бы ноль).
Для определения емкости этой системы разместим некоторый заряд цилиндров. Поместите +Q на центральный цилиндр и -Q на внешний. Чистый заряд системы остается нулевым. Этот заряд будет распределяться по поверхности цилиндров. Наше выражение для емкости на единицу длины этой системы:
, где Q = Q известно (мы подставили его туда сами). Остается определить потенциал V, который сохраняется между цилиндрами при разделении этого заряда.
Поскольку мы знаем, где находится весь заряд в этой системе, можно определить электрическое поле повсюду. Зная электрическое поле E между цилиндрами, можно рассчитать потенциал через соотношение
Зная электрическое поле E между цилиндрами, можно рассчитать потенциал через соотношение
, где оно представляет собой потенциал между конечными точками линии l . Проведенная здесь линия будет проходить по радиальной координате, соединяющей цилиндры. Система симметрична, и эта соединительная линия между цилиндрами представляет собой потенциал между ними во всех точках.
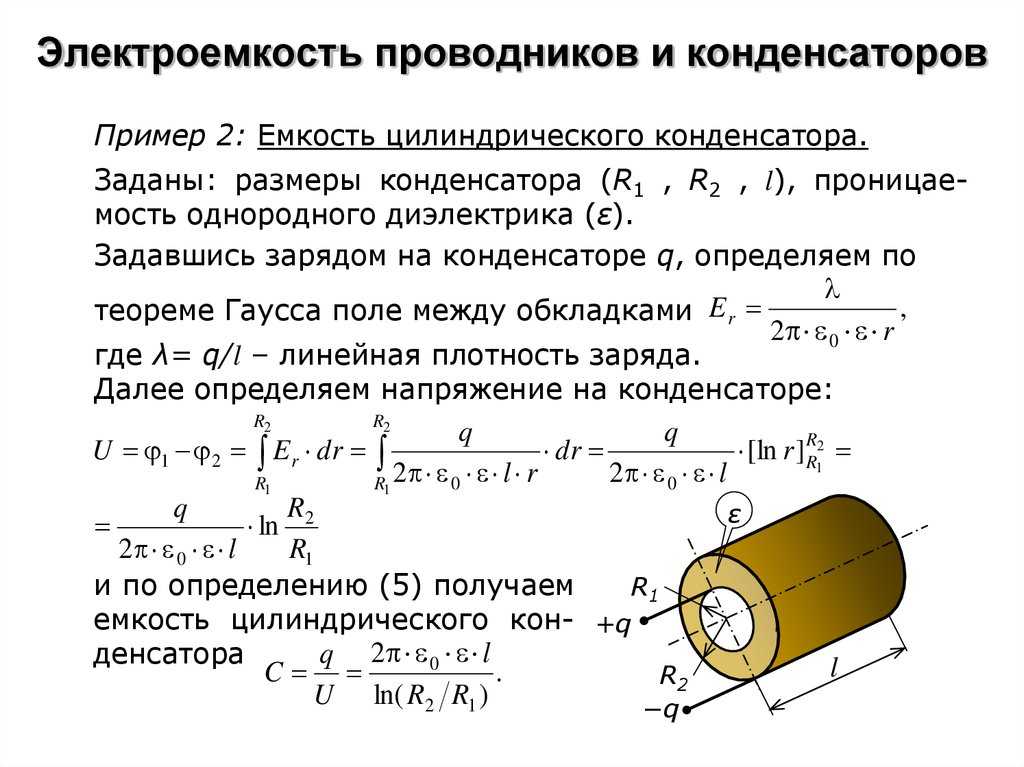
Примером симметрии системы является картина электрического поля внутреннего цилиндра, показанная на рисунке ниже. Бесконечно длинный цилиндр создает однородное электрическое поле вдоль вектора r в цилиндрической системе координат.
Электрическое поле, создаваемое внутренним цилиндром суммарного заряда +Q, полностью направлено по радиальной координате.Возвращаясь к задаче расчета электрического поля, вспомним закон Гаусса,
, где Q enc — полный заряд, заключенный в площади A.
Поскольку мы хотим определить электрическое поле между цилиндрами, необходимо найти поверхность, которая всюду перпендикулярна к нему (т. е. поверхность с нормалью, которая параллельно электрическому полю). Скалярный продукт в приведенном выше выражении в таком случае не равен нулю. На рис. 3 показана поверхность, удовлетворяющая этому требованию. Вектор нормали к поверхности Гаусса, A , всюду параллелен вектору электрического поля.
е. поверхность с нормалью, которая параллельно электрическому полю). Скалярный продукт в приведенном выше выражении в таком случае не равен нулю. На рис. 3 показана поверхность, удовлетворяющая этому требованию. Вектор нормали к поверхности Гаусса, A , всюду параллелен вектору электрического поля.
На приведенном выше рисунке показан только один пример вектора электрического поля. Это поле всюду параллельно радиальному вектору координат. Заряд внешнего цилиндра не вносит вклад в общий заряд, заключенный на поверхности. Вложенный заряд полностью определяется зарядом внутреннего цилиндра. Эта цилиндрическая поверхность является трехмерной и представляет собой еще одну цилиндрическую оболочку. Весь заряд самого внутреннего цилиндра заключен в нашей поверхности, Q enc = +Q.
Элемент дифференциальной площади, d A , может быть переписан в терминах этой геометрии. Общая площадь гауссовой поверхности определяется выражением для площади поверхности цилиндра радиуса r. Поверхность определяется в фиксированном радиальном положении, поэтому для вычисления общей площади необходимы только осевые (z) и азимутальные (Φ) координаты. Это показано ниже.
Общая площадь гауссовой поверхности определяется выражением для площади поверхности цилиндра радиуса r. Поверхность определяется в фиксированном радиальном положении, поэтому для вычисления общей площади необходимы только осевые (z) и азимутальные (Φ) координаты. Это показано ниже.
Возвращаясь к закону Гаусса, решим каждую часть отдельно,
, где последний шаг использует тот факт, что я говорю, что длина бесконечно длинных цилиндров может быть записана как L.
Приравнивание этих результатов приводит к координатный вектор.
, где очень важно помнить об обосновании порядка пределов в интеграле.
Часть определения электрического потенциала состоит в том, что потенциал на бесконечности равен нулю. При вычислении потенциала необходимо выполнять линейное интегрирование, начиная с бесконечности (или как можно дальше) и возвращаясь обратно. Поэтому пределы интегрирования начинаются с самой внешней точки b и заканчиваются в самой внутренней точке.


 Диэлектрическая проницаемость меняется между обкладками по закону ε = f(r).
Диэлектрическая проницаемость меняется между обкладками по закону ε = f(r).



 Для изотропной среды связь между этими векторами определяется известными соотношениями.
Для изотропной среды связь между этими векторами определяется известными соотношениями.
 Тогда уравнение будет иметь вид:
Тогда уравнение будет иметь вид: