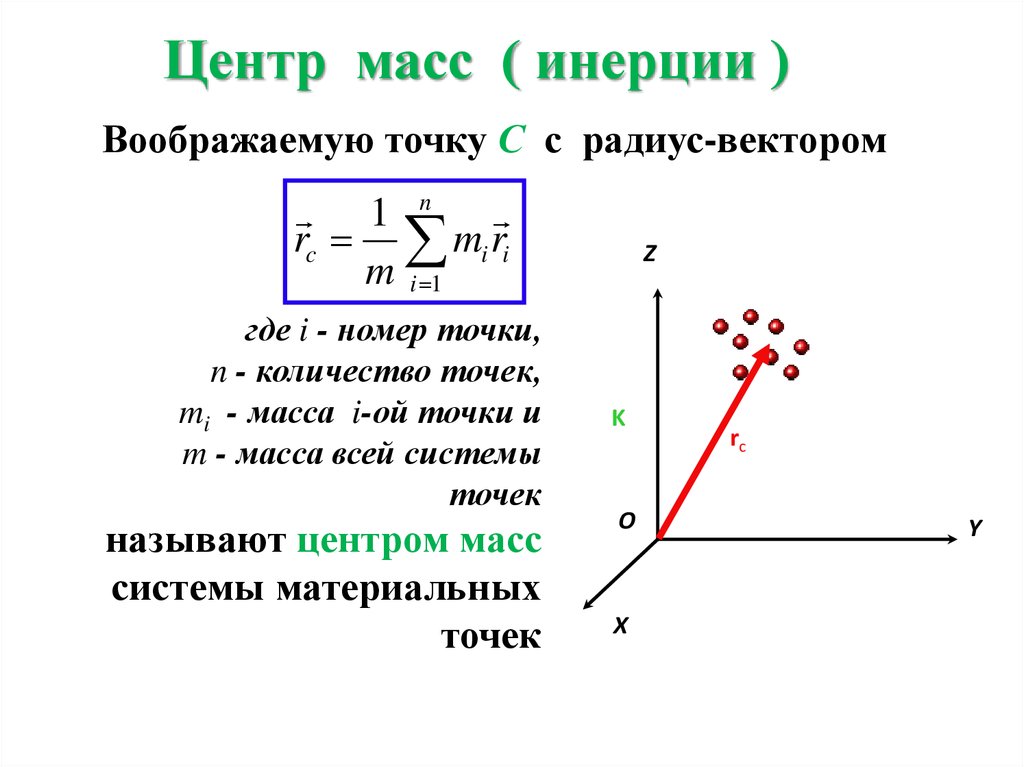
ЦЕНТР МАСС | Энциклопедия Кругосвет
ЦЕНТР МАСС (центр инерции) системы материальных точек – условная (или эквивалентная) точка, представляющая собой одну из геометрических характеристик распределения масс в системе. Пусть – масса -той () точки системы, а ЦЕНТР МАСС (центр инерции) системы материальных точек – условная (или эквивалентная) точка, представляющая собой одну из геометрических характеристик распределения масс в системе. Пусть – масса -той () точки системы, а – радиус-вектор этой точки в некоторой системе координат. Тогда радиус-вектор точки С – центра масс определяется по формуле
,
Понятие центра масс широко используется в различных разделах механики. Например, центр масс тела можно принять в качестве центра тяжести – точки приложения суммарной силы однородного поля тяжести, действующего на тело.
Скорость центра масс, умноженная на суммарную массу системы, – это количество движения (импульс) этой системы.
Ускорение центра масс (по теореме о движении центра масс) определяется суммой внешних по отношению к системе сил, если считать их приложенными к некоторой эквивалентной материальной точке, которая помещена в центр масс и имеет массу .
Количество движения (импульс) материальной точки – векторная динамическая мера ее движения, равная произведению массы этой точки на ее скорость
Количество движения – одно из фундаментальных понятий механики. По второму закону Ньютона скорость изменения количества движения материальной точки равна силе, действующей на эту точку.
Количество движения системы материальных точек – геометрическая сумма количеств движения точек этой системы
Количество движения системы равно количеству движения эквивалентной материальной точки, масса которой равна сумме масс точек системы и которая помещена в центр С масс системы, т.к.
В применении к абсолютно твердому телу это позволяет считать количество движения тела динамической мерой его поступательного движения со скоростью центра масс.
Движение твердого тела может быть представлено в виде суперпозиции (сложения) двух движений: поступательного движения системы координат OXYZ с началом в некоторой точке О тела и вращательного движения тела вокруг точки О относительно системы OXYZ.
Поэтому с точки зрения кинематики скорость каждой точки тела может быть принята в качестве характеристики «поступательного движения» тела. Однако с точки зрения динамики выбор точки С – центра масс тела –предпочтительней, т.к. именно с ее скоростью связано количество движения тела.
Виталий Самсонов
Литература:
Суслов Г.К. Теоретическая механика, М., «Гостехиздат», 1946
Аппель П. Теоретическая механика, тт.1, 2. М., «Физматгиз», 1960
Четаев Н.Г. Теоретическая механика. М., «Наука», 1987
Маркеев А.П. Теоретическая механика. М., «Наука», 1999
Голубев Ю.Ф. Основы теоретической механики. М., Изд-во Моск. Ун-та. 2000
Журавлев В.Ф. Основы теоретической механики. М., «Наука», 2001
Проверь себя!
Ответь на вопросы викторины «Физика»
Что такое изотоп, чему равно число Авогадро и что изучает наука реология?
Пройти тест
Центр масс и центр тяжести тела
Описаны: центр масс (ЦМ) и центр тяжести (ЦТ) твердого тела.
Приведены различные определения ЦМ и ЦТ тела. Показано сходство и различие понятий ЦМ и ЦТ тела.
Для того, чтобы рассчитать момент силы тяжести, создаваемый относительно центров суставов человека при выполнении силовых упражнений, необходимо знать точку, куда приложена сила тяжести. Условно считают, что сила тяжести приложена в центре масс или центре тяжести звена. Давайте познакомимся с этими понятиями более подробно.
Более подробно функционирование опорно-двигательного аппарата человека и биомеханика мышц описаны в книге:
Биомеханика опорно-двигательного аппарата человека
Понятие центра масс (ЦМ) тела
Центром масс тела (центром инерции тела) называется абстрактная точка, положение которой определяется распределением масс в теле. Условно считается, что в этой точке сосредоточена вся масса тела. В твердом теле положение центра масс фиксировано.
Особенность этой точки в том, что её перемещению можно судить о движении всего тела, потому что ЦМ тела движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами.
Это означает, что для описания движения ЦМ тела применимы законы Ньютона, что позволяет значительно упростить биомеханические расчеты.
Тело человека состоит из звеньев: туловища, головы, рук и ног. У каждого звена имеется свой центр масс. Однако звенья тела человека могут перемещаться, поэтому общий центр масс (ОЦМ) тела человека не является фиксированной точкой.
Центр масс твердого тела – особая точка. В этой точке пересекаются линии действия всех внешних сил. Если действующая на твердое тело сила проходит через его ЦМ, тело будет двигаться поступательно. Если действующая на твердое тело сила не будет проходить через его ЦМ, тело будет вращаться вокруг точки, проходящей через ЦМ тела. Поэтому можно дать второе определение центра масс твердого тела.
Центр масс твердого тела – есть неизменно связанная с этим телом точка. При прохождении через эту точку линии действия внешней силы, тело будет двигаться поступательно (рис.
1).
Любое тело можно представить состоящим из множества частиц, на каждую из которых действует сила тяжести. Для любого тела можно найти такую точку О (через которую проходит ось вращения) по отношению к которой сумма моментов силы тяжести, действующих по часовой стрелке, будет равна сумме моментов силы тяжести, действующих против часовой стрелки. Эта точка является центром тяжести тела.
Центр тяжести (ЦТ) твердого тела – это точка, относительно которой сумма моментов силы тяжести, действующих по часовой стрелке равна сумме моментов силы тяжести, действующих против часовой стрелки (рис.2).
Рис.2. Точка С является ЦТ стержня, к которому приложены две силы F1 (F1=m1g) и F2 (F2=m2g)Если твердое тело однородно по плотности, то положение его ЦТ зависит только от его геометрической формы.
Как бы мы не поворачивали твердое тело и не изменяли его положение в пространстве, силы тяжести, действующие на его частицы, останутся вертикальными и параллельными друг другу. Отсюда следует, что центр тяжести твердого тела находится в определенной точке и не меняет своего положения при изменении положения самого тела. Поэтому можно дать несколько другое определение ЦТ твердого тела.
Центр тяжести твердого тела – есть неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующей элементарных сил тяжести частиц данного тела при любом его положении в пространстве.
Если действующая на твердое тело сила проходит через его ЦТ, тело будет двигаться поступательно. Если действующая на твердое тело сила не будет проходить через его ЦТ, тело будет вращаться вокруг точки, проходящей через ЦТ тела. Поэтому можно дать третье определение центра тяжести твердого тела.
Центр тяжести твердого тела – есть неизменно связанная с этим телом точка.
При прохождении через эту точку линии действия внешней силы тело будет двигаться поступательно.
Сила, вызывающая поступательное движение тела, приложена в центре масс этого тела. Следовательно, ЦТ твердого тела совпадает с его центром масс. Поэтому часто центр масс называют центром тяжести. Однако между понятиями центра масс и центра тяжести есть отличие. Понятие центра тяжести справедливо только для твердого тела, находящегося в поле сил тяжести, а понятие центра масс не связано ни с каким силовым полем и справедливо для любого тела (механической системы). В однородном поле тяготения (то есть на Земле) центр тяжести и центр масс тела совпадают.
Определение положения ЦМ и ЦТ твердого телаЦМ твердого тела можно определить аналитическим и инструментальным способами.
Аналитические методы позволяют определить ЦМ на основе формул. При этом большое значение имеет наличие симметрии. При наличии оси симметрии ЦМ тела будет лежать на оси симметрии, а при наличии центра симметрии будет совпадать с ним.
Так, например, для определения ЦМ твердого тела, например, имеющего форму квадрата или прямоугольника достаточно провести две диагонали. Центр масс и центр симметрии будут находится в точке пересечения этих диагоналей (рис.3). У твердого тела, имеющего форму треугольника ЦМ будет находиться в месте пересечения медиан. У твердого тела, имеющего форму круга, ЦМ и центр симметрии будут располагаться в центре круга.
Центр масс твердого тела может находиться вне тела, например, ЦМ диска штанги находится в центре отверстия для грифа (рис.3). Доказательством того, что ЦМ твердого тела может находиться вне тела, может быть следующий эксперимент. Если приложить к диску штанги силу, проходящую через его ЦМ, диск штанги начнет двигаться поступательно. Если приложенная к диску сила не будет проходить через его ЦМ, диск начнет вращаться вокруг точки, положение которой соответствует положению ЦМ.
Рис.3. Расположение ЦМ на плоских фигурах и диске штангиЕсли тело сложной формы, центр масс тела находится методом «разбиения» тела на совокупность тел простой формы.
Инструментальные методы определения положения центра масс (ЦМ) и центра тяжести (ЦТ) плоских тел также достаточно просты. Для этого нужно подвесить тело в какой-либо его точке и провести вертикальную линию, проходящую через точку подвеса. Затем нужно подвесить тело за другую точку и вновь провести вертикальную линию, проходящую через точку подвеса. Точка пересечения проведенных линий и есть ЦТ тела, а также и его ЦМ (рис.4).
Рис.4. Определение ЦТ тела путем его подвешивания в различных положенияхЛитератураХочу рекомендовать очень хорошую книгу по биомеханике, которую написали В.Т. Тураев и В.В. Тюпа – Биомеханика для спринтера. В этой книге Вы найдете все, что нужно знать по биомеханике, независимо от того, каким видом спорта Вы занимаетесь, а спортсмены – спринтеры найдут еще больше нужной для них информации.
С уважением, А.В. Самсонова
Похожие записи:
Сила
Дано определение силы в механике. Описаны факторы, определяющие действие на тело силы: направление, точка приложения и численное значение.
Звенья тела человека как рычаги
Дано описание опорно-двигательного аппарата (ОДА) человека как системы рычагов. Приведен пример расчета силы двуглавой мышцы плеча…
Способ определения положения центров масс (центров тяжести) звеньев тела человека
Описан способ определения положения центров масс (центров тяжести, ЦТ) звеньев тела человека по Вильгельму Брауне и…
Распределение масс в теле человека
Описаны особенности распределения масс в теле человека. Дано понятие геометрии масс тела человека. Показано, что на…
Момент силы и плечо силы
Дано определение момента силы и плеча силы. Определение плеча и момента силы рассмотрено на примерах ОДА человека при…
Масса звеньев тела человека и способы ее оценки
Дано определение массы тела, а также описаны методы оценки массы звеньев тела человека, предложенные В. Брауне и О.
Ньютоновская механика — Момент инерции относительно центра масс
спросил
Изменено 7 лет, 9 месяцев назад
Просмотрено 6к раз
$\begingroup$
Почему момент инерции минимум около центра масс любого твердого тела?
- ньютоновская механика
- момент инерции
$\endgroup$
5
$\begingroup$
Другие ответы очень хороши, поэтому я сосредоточусь на более физическом смысле, на интуиции, а не на математике.
Если мы хотим минимизировать это, нам нужно, чтобы частная производная по $x_0$ и $y_0$ была равна нулю. Это приводит к следующим уравнениям (я показываю это только для $x$#, но то же самое, очевидно, верно и для $y$)
$$\sum_i{m_i \left(-2x_i + 2 x_0\right)}= 0 \подразумевается\\ \sum_i{m_i \cdot x_i} = \sum_i{m_i \cdot x_0}$$
Если разделить на общую массу, выражение слева будет определением центра масс в направлении $x$ — и уравнение говорит нам, что размещение центра вращения в центре масс минимизирует момент инерции.
Этот результат можно с некоторым усилием распространить на трехмерный случай, но обозначения становятся более запутанными, и я не думаю, что это помогает в понимании.
$\endgroup$
$\begingroup$
Вот математическое доказательство вашей проблемы, показывающее, что полярный момент инерции относительно центра тяжести действительно является минимальным, по крайней мере, для ламинарного (2D) твердого тела.
Для твердого тела массой $m$:
Полярный момент инерции относительно общей точки P:
$$I_P = \int\limits_m \left( \vec r_P \cdot \vec r_P \right) dm$$
Нам нужно найти минимальное значение $I_P$ для этого твердого тела.
Вставьте следующее: $\vec r_P = \vec r_G — \vec r_{PG}$
$$I_P = \int\limits_m \left( \vec r_G — \vec r_{PG} \right) \ cdot \left( \vec r_G — \vec r_{PG} \right) dm$$
$$I_P = \int\limits_m \left( \vec r_G \cdot \vec r_G \right) dm — \int\limits_m \left( 2 \vec r_{PG} \cdot \vec r_G \right) dm + \int\limits_m \left( \vec r_{PG} \cdot \vec r_{PG} \right) dm$$ 92 m$ должны быть неотрицательны (квадрат числа, умноженный на массу).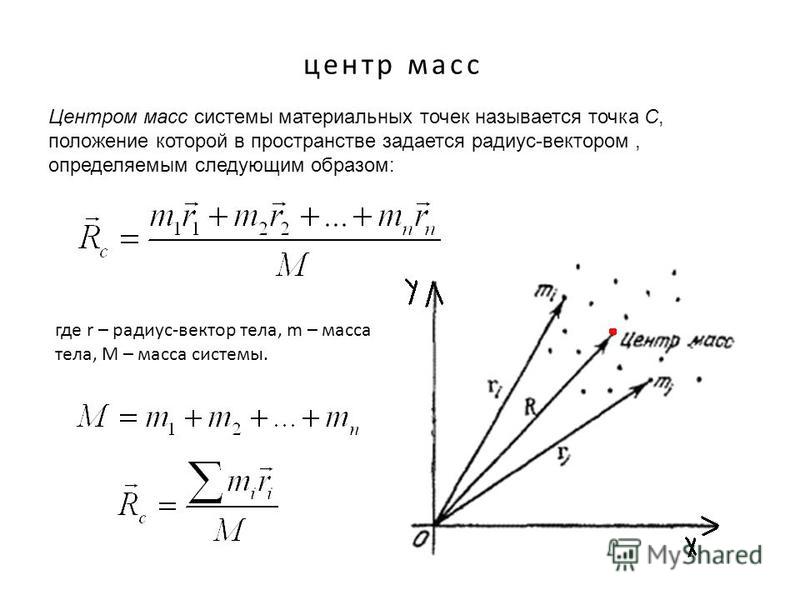
{ext}=I\alpha$.
Таким образом, мы можем заключить, что при расчете чистого крутящего момента относительно центра масс псевдомомент оказывается равным $0$, а чистый крутящий момент остается $I\alpha$, тогда как во всех остальных случаях чистый крутящий момент равен $I \alpha$+ крутящий момент из-за псевдосил
Надеюсь, это ответ на ваш вопрос.
$\endgroup$
11 92\ge0\подразумевается I\ge I_{com}$$
$\endgroup$
определение центра+инерции по The Free Dictionary
Центр+инерции — определение центра+инерции по The Free DictionaryЦентр+инерции — определение центра+инерции в The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
