Что определяет и как записывается закон кулона. Закон Кулона

В электростатике одним из основополагающих является закон Кулона. Он применяется в физике для определения силы взаимодействия двух неподвижных точечных зарядов или расстояния между ними. Это фундаментальный закон природы, который не зависит ни от каких других законов. Тогда форма реального тела не влияет на величину сил. В этой статье мы расскажем простым языком закон Кулона и его применение на практике.

История открытия

Ш.О. Кулон в 1785 г. впервые экспериментально доказал взаимодействия описанные законом. В своих опытах он использовал специальные крутильные весы. Однако еще в 1773 г. было доказано Кавендишем, на примере сферического конденсатора, что внутри сферы отсутствует электрическое поле. Это говорило о том, что электростатические силы изменяются в зависимости от расстояния между телами. Если быть точнее — квадрату расстояния. Тогда его исследования не были опубликованы. Исторически сложилось так, что это открытие было названо в честь Кулона, аналогичное название носит и величина, в которой измеряется заряд.

Формулировка

Определение закона Кулона гласит: В вакууме F взаимодействия двух заряженных тел прямо пропорционально произведению их модулей и обратно пропорционально квадрату расстояния между ними.

Звучит кратко, но может быть не всем понятно. Простыми словами: Чем больший заряд имеют тела и чем ближе они находятся друг к другу, тем больше сила.

И наоборот: Если увеличить расстояние межу зарядами — сила станет меньше.

Формула правила Кулона выглядит так:

Обозначение букв: q — величина заряда, r — расстояние межу ними, k — коэффициент, зависит от выбранной системы единиц.

Величина заряда q может быть условно-положительной или условно-отрицательной. Это деление весьма условно. При соприкосновении тел она может передаваться от одного к другому. Отсюда следует, что одно и то же тело может иметь разный по величине и знаку заряд. Точечным называется такой заряд или тело, размеры которого много меньше, чем расстояние возможного взаимодействия.

Стоит учитывать что среда, в которой расположены заряды, влияет на F взаимодействия. Так как в воздухе и в вакууме она почти равна, открытие Кулона применимо только для этих сред, это одно из условий применения этого вида формулы. Как уже было сказано, в системе СИ единица измерения заряда — Кулон, сокращено Кл. Она характеризует количество электричества в единицу времени. Является производной от основных единиц СИ.

1 Кл = 1 А*1 с

Стоит отметить, что размерность 1 Кл избыточна. Из-за того что носители отталкиваются друг от друга их сложно удержать в небольшом теле, хотя сам по себе ток в 1А небольшой, если он протекает в проводнике. Например в той же лампе накаливания на 100 Вт течет ток в 0,5 А, а в электрообогревателе и больше 10 А. Такая сила (1 Кл) примерно равна действующей на тело массой 1 т со стороны земного шара.

Вы могли заметить, что формула практически такая же, как и в гравитационном взаимодействии, только если в ньютоновской механике фигурируют массы, то в электростатике — заряды.

Формула Кулона для диэлектрической среды

Коэффициент с учетом величин системы СИ определяется в Н 2 *м 2 /Кл 2 . Он равен:

Во многих учебниках этот коэффициент можно встретить в виде дроби:

Здесь Е 0 = 8,85*10-12 Кл2/Н*м2 — это электрическая постоянная. Для диэлектрика добавляется E — диэлектрическая проницаемость среды, тогда закон Кулона может применяться для расчетов сил взаимодействия зарядов для вакуума и среды.

С учетом влияния диэлектрика имеет вид:

Отсюда мы видим, что введение диэлектрика между телами снижает силу F.

Как направлены силы

Заряды взаимодействуют друг с другом в зависимости от их полярности — одинаковые отталкиваются, а разноименные (противоположные) притягиваются.

Кстати это главное отличие от подобного закона гравитационного взаимодействия, где тела всегда притягиваются. Силы направлены вдоль линии, проведенной между ними, называют радиус-вектором. В физике обозначают как r 12 и как радиус-вектор от первого ко второму заряду и наоборот.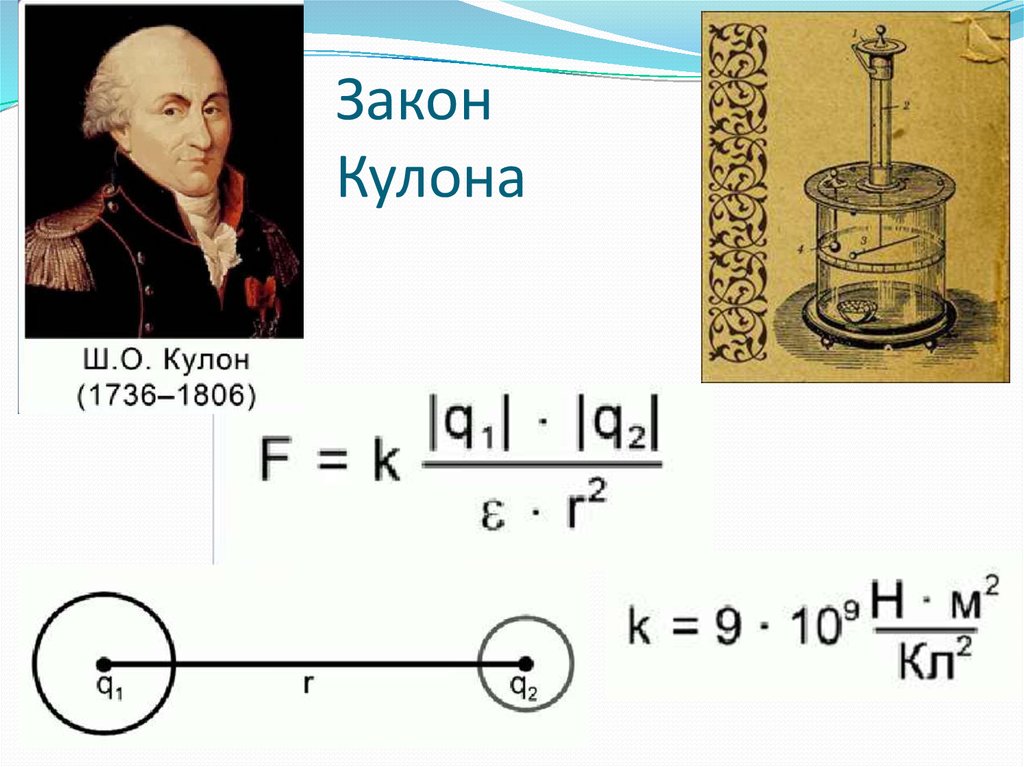 Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:

Сила, приложенная к первому заряду со стороны второго обозначается как F 12. Тогда в векторной форме закон Кулона выглядит следующим образом:

Для определения силы приложенной ко второму заряду используются обозначения F 21 и R 21 .

Если тело имеет сложную форму и оно достаточно большое, что при заданном расстоянии не может считаться точечным, тогда его разбивают на маленькие участки и считают каждый участок как точечный заряд. После геометрического сложения всех получившихся векторов получают результирующую силу. Атомы и молекулы взаимодействуют друг с другом по этому же закону.

Применение на практике

Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод.

С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.

В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы. Рассматривая эти процессы с точки зрения воздействия на точечный заряд группой зарядов, тогда все соотношения закона оказываются справедливыми.

Полезное

В результате долгих наблюдений учеными было установлено, что разноименно заряженные тела притягиваются, а одноименно заряженные наоборот – отталкиваются. Это значит, что между телами возникают силы взаимодействия. Французский физик Ш. Кулон опытным путем исследовал закономерности взаимодействия металлических шаров и установил, что сила взаимодействия между двумя точечными электрическими зарядами будет прямопропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними:

Где k – коэффициент пропорциональности, зависящий от выбора единиц измерений физических величин, которые входят в формулу, а также и от среды, в которой находятся электрические заряды q 1 и q 2 . r – расстояние между ними.

Отсюда можем сделать вывод, что закон Кулона будет справедлив только точечных зарядов, то есть для таких тел, размерами которых вполне можно пренебречь по сравнению с расстояниями между ними.

В векторной форме закон Кулона будет иметь вид:

Где q 1 и q 2 заряды, а r – радиус-вектор их соединяющий; r = |r|.

Силы, которые действуют на заряды, называют центральными. Они направлены по прямой, соединяющей эти заряды, причем сила, действующая со стороны заряда q 2 на заряд q 1 , равна силе, действующей со стороны заряда q 1 на заряд q 2 , и противоположна ей по знаку.

Для измерения электрических величин могут использоваться две системы счисления – система СИ (основная) и иногда могут использовать систему СГС.

В системе СИ одной из главных электрических величин является единица силы тока – ампер (А), то единица электрического заряда будет ее производной (выражается через единицу силы тока). Единицей определения заряда в СИ является кулон. 1 кулон (Кл) – это количество «электричества», проходящего через поперечное сечение проводника за 1 с при токе в 1 А , то есть 1 Кл = 1 А·с.

Коэффициент k в формуле 1а) в СИ принимается равным:

И закон Кулона можно будет записать в так называемой «рационализированной» форме:

Многие уравнения, описывающие магнитные и электрические явления, содержат множитель 4π. Однако, если данный множитель ввести в знаменатель закона Кулона, то он исчезнет из большинства формул магнетизма и электричества, которые очень часто применяют в практических расчетах. Такую форму записи уравнения называют рационализированной.

Величина ε 0 в данной формуле – электрическая постоянная.

Основными единицами системы СГС являются механические единицы СГС (грамм, секунда, сантиметр). Новые основные единицы дополнительно к вышеперечисленным трем в системе СГС не вводятся. Коэффициент k в формуле (1) принимается равным единице и безразмерным. Соответственно закон Кулона в не рационализированной форме будет иметь вид:

В системе СГС силу измеряют в динах: 1 дин = 1 г·см/с 2 , а расстояние в сантиметрах. Предположим, что q = q 1 = q 2 , тогда из формулы (4) получим:

Если r = 1см, а F = 1 дин, то из этой формулы следует, что в системе СГС за единицу заряда принимают точечный заряд, который (в вакууме) действует на равный ему заряд, удаленный от него на расстояние 1 см, с силой в 1 дин. Такая единица заряда называется абсолютной электростатической единицей количества электричества (заряда) и обозначается СГС q . Ее размерность:

Для вычисления величины ε 0 , сравним выражения для закона Кулона, записанные в системе СИ и СГС. Два точечных заряда по 1 Кл каждый, которые находятся на расстоянии 1 м друг от друга, будут взаимодействовать с силой (согласно формуле 3):

В СГС данная сила будет равна:

Сила взаимодействия между двумя заряженными частицами зависит от среды, в которой они находятся. Чтобы характеризовать электрические свойства различных, сред было введено понятие относительной диэлектрической проницательности ε.

Значение ε это различная величина для разных веществ – для сегнетоэлектриков ее значение лежит в пределах 200 – 100 000, для кристаллических веществ от 4 до 3000, для стекла от 3 до 20, для полярных жидкостей от 3 до 81, для неполярных жидкостей от 1,8 до 2,3; для газов от 1,0002 до 1,006.

Также от температуры окружающей среды зависит и диэлектрическая проницаемость (относительная).

Если учесть диэлектрическую проницаемость среды, в которую помещены заряды, в СИ закон Кулона примет вид:

Диэлектрическая проницаемость ε – величина безразмерная и она не зависит от выбора единиц измерения и для вакуума считается равной ε = 1. Тогда для вакуума закон Кулона примет вид:

Поделив выражение (6) на (5) получим:

Соответственно относительная диэлектрическая проницаемость ε показывает, во сколько раз сила взаимодействия между точечными зарядами в какой-то среде, которые находятся на расстоянии r друг относительно друга меньше, чем в вакууме, при том же расстоянии.

Для раздела электричества и магнетизма систему СГС иногда называют системой Гаусса. До появления системы СГС действовали системы СГСЭ (СГС электрическая) для измерения электрических величин и СГСМ (СГС магнитная) для измерения магнитных величин. В первой равной единице принималась электрическая постоянная ε 0 , а второй магнитная постоянная μ 0 .

В системе СГС формулы электростатики совпадают соответствующими формулами СГСЭ, а формулы магнетизма, при условии, что они содержат только магнитные величины – с соответствующими формулами в СГСМ.

Но если в уравнении одновременно будет содержаться и магнитные, и электрические величины, то данное уравнение, записанное в системе Гаусса, будет отличаться от этого же уравнения, но записанного в системе СГСМ или СГСЭ множителем 1/с или 1/с 2 . Величина с равна скорости света (с = 3·10 10 см/с) называется электродинамической постоянной.

Закон Кулона в системе СГС будет иметь вид:

Пример

На двух абсолютно идентичных каплях масла недостает по одному электрону. Силу ньютоновского притяжения уравновешивает сила кулоновского отталкивания. Нужно определить радиусы капель, если расстояния между ними значительно превышает их линейные размеры.

Решение

Поскольку расстояние между каплями r значительно больше их линейных размеров, то капли можно принять за точечные заряды, и тогда сила кулоновского отталкивания будет равна:

Где е – положительный заряд капли масла, равный заряду электрона.

Силу ньютоновского притяжения можно выразить формулой:

Где m – масса капли, а γ – гравитационная постоянная. Согласно условию задачи F к = F н, поэтому:

Масса капли выражена через произведение плотности ρ на объем V, то есть m = ρV, а объем капли радиуса R равен V = (4/3)πR 3 , откуда получаем:

В данной формуле постоянные π, ε 0 , γ известны; ε = 1; также известен и заряд электрона е = 1,6·10 -19 Кл и плотность масла ρ = 780 кг/м 3 (справочные данные). Подставив числовые значения в формулу получим результат: R = 0,363·10 -7 м.

Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна

где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.

В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.

Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид

Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции 1 . Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.

Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов. В математическом анализе разработаны методы такого суммирования, однако в школьный курс физики они не входят. Поэтому, если такая задача и встретится, то суммирование в ней должно легко выполняться на основе тех или иных соображений симметрии. Например, из описанной процедуры суммирования следует, что сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.

Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна

если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.

Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна

где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17.6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.

Рассмотрим теперь решение данных в первой части книги задач.

Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой

Заряды отталкиваются (ответ 2 ).

Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2 ).

Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов при увеличении в раз расстояния между ними уменьшится в раз (задача 17. 1.3 — ответ 4 ).

Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3 ).

При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ 4 ).

При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2 ).

Сила кулоновского взаимодействия (17.1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17. 1.7 — ответ 3 ).

Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (задача 17.1.8 — ответ 2 ).

Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9 ). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4 ).

В системе двух заряженных шариков, связанных нитью (задача 17.1.10 ), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков. Поскольку на каждый из них действуют только кулоновская сила и сила натяжения нити, то из условия равновесия заключаем, что эти силы равны по величине.

Этой величине и будет равна сила натяжения нитей (ответ 4 ). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).

Для нахождения силы, действующей на заряд — в задаче 17.2.2 , используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4 ).

(ответ 3 ).

Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4 . В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17. 4), (17.5)). Имеем = 0 (ответ 3 ).

В задаче 17.2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой

где . Поэтому и результирующая сила равна этому выражению (ответ 2 )

В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы

где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу

Из этих формул следует, что наибольшей сила будет в точке — ответ 1 .

Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины

которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1 ).

Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3 .

Основной закон взаимодействия электрических зарядов был найден Шарлем Кулоном в 1785 г. экспериментально. Кулон установил, что сила взаимодействия между двумя небольшими заряженными металлическими шариками обратно пропорциональна квадрату расстояниямежду ними и зависит от величины зарядови:

где —коэффициент пропорциональности .

Силы, действующие на заряды , являются центральными , то есть они направлены вдоль прямой, соединяющей заряды.

Закон Кулона можно записать в векторной форме :,

где —вектор силы, действующей на заряд со стороны заряда,

Радиус-вектор, соединяющий заряд с зарядом;

Модуль радиус-вектора.

Сила, действующая на заряд со стороныравна,.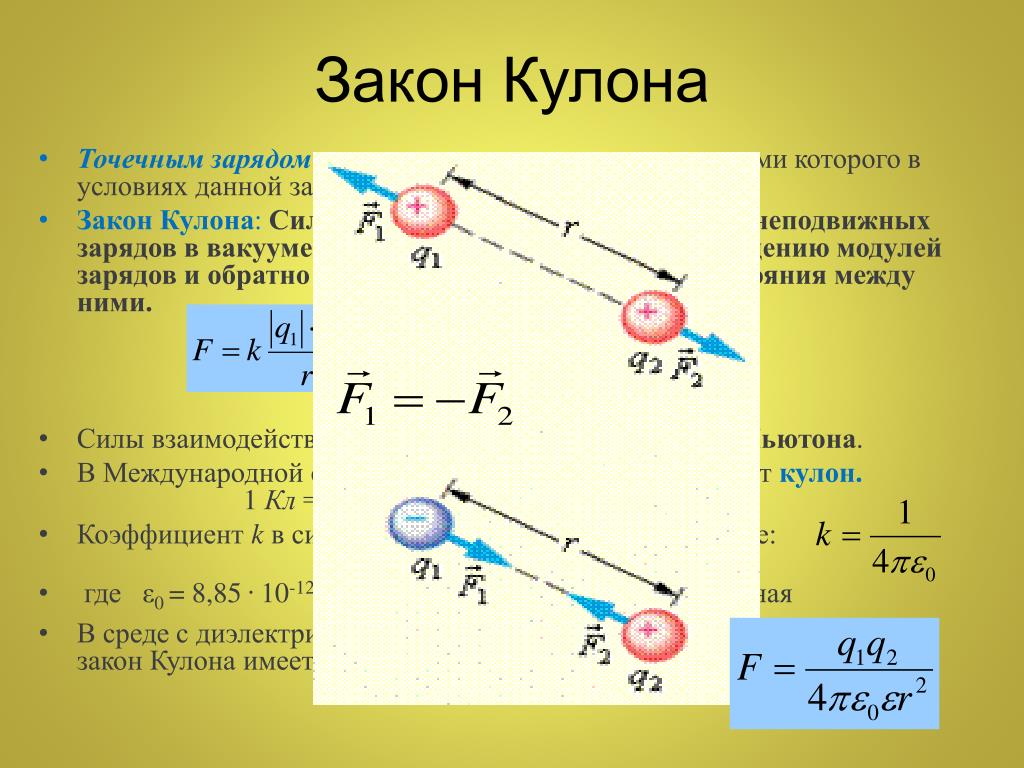

Закон Кулона в такой форме

справедлив только для взаимодействия точечных электрических зарядов , то есть таких заряженных тел, линейными размерами которых можно пренебречь по сравнению с расстоянием между ними.

выражает силу взаимодействия между неподвижными электрическими зарядами, то есть это электростатический закон.

Формулировка закона Кулона :

Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними .

Коэффициент пропорциональности в законе Кулоназависит

от свойств среды

выбора единиц измерения величин, входящих в формулу.

Поэтому можно представить отношением,

где —коэффициент, зависящий только от выбора системы единиц измерения ;

Безразмерная величина, характеризующая электрические свойства среды, называется относительной диэлектрической проницаемостью среды .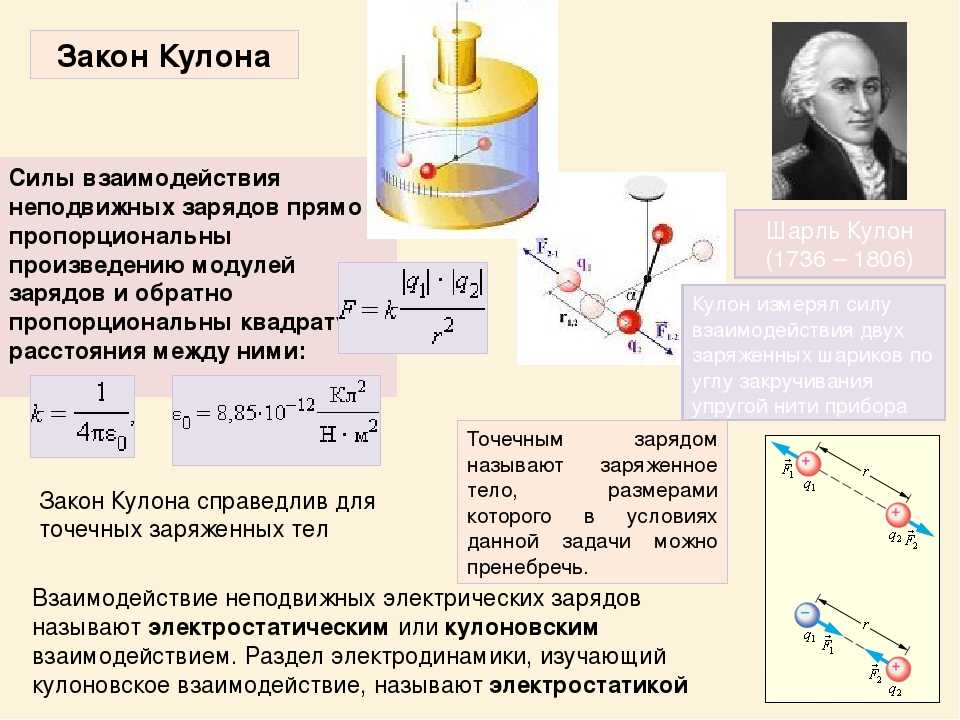 Она не зависит от выбора системы единиц измерения и равна единице в вакууме.

Тогда закон Кулона примет вид:,

для вакуума ,

тогда —относительная диэлектрическая проницаемость среды показывает, во сколько раз в данной среде сила взаимодействия между двумя точечными электрическими зарядами и, находящимися друг от друга на расстоянии, меньше, чем в вакууме.

В системе СИ коэффициент , и

закон Кулона имеет вид :.

Это рационализированная запись закона К улона.

Электрическая постоянная, .

В системе СГСЭ ,.

В векторной форме закон Кулона принимает вид

где —вектор силы, действующей на заряд со стороны заряда ,

Радиус-вектор, соединяющий заряд с зарядом

r –модуль радиус-вектора .

Всякое заряженное тело состоит из множества точечных электрических зарядов, поэтому электростатическая сила, с которой одно заряженное тело действует на другое, равна векторной сумме сил, приложенных ко всем точечным зарядам второго тела со стороны каждого точечного заряда первого тела.

1.3.Электрическое поле. Напряженность.

Пространство, в котором находится электрический заряд, обладает определенными физическими свойствами .

На всякий другой заряд, внесенный в это пространство, действуют электростатические силы Кулона.

Если в каждой точке пространства действует сила, то говорят, что в этом пространстве существует силовое поле.

Поле наряду с веществом является формой материи.

Если поле стационарно, то есть не меняется во времени, и создается неподвижными электрическими зарядами, то такое поле называется электростатическим.

Электростатика изучает только электростатические поля и взаимодействия неподвижных зарядов.

Для характеристики электрического поля вводят понятие напряженности . Напряженность ю в каждой точке электрического поля называется вектор , численно равный отношению силы, с которой это поле действует на пробный положительный заряд, помещенный в данную точку, и величины этого заряда, и направленный в сторону действия силы.

Пробный заряд , который вносится в поле, предполагается точечным и часто называется пробным зарядом.

— Он не участвует в создании поля, которое с его помощью измеряется.

Предполагается, что этот заряд не искажает исследуемого поля, то есть он достаточно мал и не вызывает перераспределения зарядов, создающих поле.

Если на пробный точечный заряд поле действует силой, то напряженность.

Единицы напряженности:

В системе СИ выражение для поля точечного заряда :

В векторной форме:

Здесь – радиус-вектор, проведенный из зарядаq , создающего поле, в данную точку.

Таким образом,векторы напряженности электрического поля точечного заряда q во всех точках поля направлены радиально (рис.1.3)

— от заряда, если он положительный, «исток»

— и к заряду, если он отрицательный «сток»

Для графической интерпретации электрического поля вводят понятие силовой линии или линии напряженности . Это

кривая , касательная в каждой точке к которой совпадает с вектором напряженности .

Линия напряженности начинается на положительном заряде и заканчивается на отрицательном.

Линии напряженности не пересекаются, так как в каждой точке поля вектор напряженности имеет лишь одно направление.

взаимодействие тел, заряженных электрическими зарядами

Физика

12.11.21

10 мин.

Со времён Древней Греции философов интересовало взаимодействие заряженных тел. Закон Кулона, открытый в XVIII веке, математическим языком объясняет, почему предметы, если их наэлектризовать, притягиваются или отталкиваются. Открытие, сделанное французским инженером, является фундаментальным. На основе кулоновских опытов осуществлялись дальнейшие исследования учёных в области электризации тел.

Оглавление:

• Основные понятия
• Формулировка и уравнение
• Историческое значение кулоновского закона

Подготовка к фундаментальному открытию

То, что натёртый шерстью янтарь притягивает лёгкие предметы, заметил философ и математик Фалес Милетский. Однако термин «электричество» — слово «янтарь» на древнегреческом языке пишется, как ήλεχτρоς, произносится как «электрос» — в 1600 году придумал личный врач королевы Англии Елизаветы I. Развитию новой науки способствовало изобретение в 1746 году «лейденской банки», которая позволяла накапливать и сохранять электрический заряд.

Открытию закона Кулона предшествовали работы учёных разных стран:

1. 1747 г. В Америке Б. Франклин теоретически описывает свойства электрических зарядов.
2. 1752 г. Русский учёный Г. В. Рихман экспериментирует с атмосферным электричеством.
3. 1759 г. Ф. Эппиус из Санкт-Петербурга предположил, что величина электрической силы обратно пропорциональна промежутку между заряженными предметами.
4. 1760 г. В Швейцарии Д. Бернулли сконструировал электрометр.
5. 1767 г. Английский естествоиспытатель Дж. Пристли проводит аналогию между законом всемирного тяготения и притяжением электрически заряженных предметов.
6. 1769 г. Шотландский учёный и изобретатель Д. Робинсон определил, что металлические шары, заряженные одинаково, отталкиваются с усилием, которое обратно пропорционально квадрату дистанции между ними.

В восьмидесятых годах XVIII столетия подполковник Шарль Кулон (1736−1806) служил главным интендантом вод и фонтанов французского королевства. В это время инженер исследовал кручение металлических нитей и для опытов смастерил крутильные весы. Устройство оказалось полезным при экспериментах с заряженными шарами. Измерительный прибор помог учёному сформулировать закон, получивший впоследствии его имя.

Как взаимодействуют заряженные частицы

В 1785 году Кулон передал в коллегию парижской Академии наук меморандум, где описал конструкцию и использование электрических весов. В докладе указывалось, что действующая на заряженные шарики сила зависит от удалённости их друг от друга.

Формула открытого закона напоминает уравнение теории всемирного тяготения. Различие состоит в том, что постулаты Ньютона описывают гравитационное взаимодействие тел, которое допускает только притяжение. Аксиома Кулона утверждает, что предметы могут отталкиваться и притягиваться в зависимости от полярности зарядов.

Основные понятия

Электрический заряд — величина, которая характеризует способность физических тел взаимодействовать друг с другом через электрическое или магнитное поле. Подразделяются на плюсовые и минусовые. Одноимённые заряды отталкиваются, величины разноимённых знаков притягиваются.

В математических выражениях заряд обозначается латинскими буквами Q или q. Название единице измерения заряда присвоено в честь учёного — Кулон. На письме отображается как «Кл» (по-русски) или C (в международной системе).

Формулировка и уравнение

Закон Кулона гласит: «На два шара одинакового диаметра, изготовленных из одного материала и имеющих электрический заряд одной полярности, действует отталкивающая сила, величина которой находится в обратно пропорциональной зависимости от квадрата расстояния между центральными точками предметов». Правило справедливо при соблюдении трёх условий:

• размеры шаров намного меньше дистанции между ними, другими словами, заряды должны быть точечными;
• предметы находятся в состоянии покоя;
• эксперимент проводится в вакууме.

Открытие Кулона представляет собой фундаментальный закон. Обнаружение взаимного влияния зарядов произошло во время экспериментальных исследований. Выявленные закономерности получены опытным путём и не исходят из постулатов другого физического закона.

Следующее уравнение описывает взаимодействие двух заряженных частиц в вакууме:

F = k ∙ (q ₁ ∙ q ₂) ∕ r ² ,

где:

F — сила «кулонова взаимодействия»;

k — коэффициент пропорциональности ;

q ₁, q ₂ — заряженность каждого тела;

r — расстояние между телами.

Коэффициент k — величина постоянная и равен 9 ∙ 10⁹. Расчёт производится по формуле:

k = 1 ∕ 4πε₀,

где:

ε₀ — электрическая постоянная, равна 8,85 ∙ 10⁻¹².

Величина силы F зависит от внешнего окружения заряженных тел. Если предметы помещены в пространство, заполненное каким-либо веществом, кулонова сила уменьшается. Учитывая диэлектрическую проницаемость окружающей среды ε, открытие Кулона примет полное математическое выражение в следующем виде:

F = (q ₁ ∙ q ₂) ∕ 4πε₀ε r ² .

Векторная форма закона Кулона :

F ̅₁₂ = [ k ∙ (q ₁ ∙ q ₂) ∕ r ₁₂²] ∙ (r ̄₁₂ ∕ r ₁₂),

где:

F ̅₁₂ — вектор силы, действующей на каждый заряд со стороны другого заряда,

r ̄₁₂ — радиус вектор от первого заряда ко второму; по модулю равен длине промежутка между ними.

Электрическое действие объектов направлено вдоль линии, соединяющей их центры, поэтому если необходимо рассчитать кулонову силу между несколькими предметами, следует проверить, правильно ли изображены взаимодействия заряженных тел.

Историческое значение кулоновского закона

Закон, открытый Шарлем Кулоном, активизировал дальнейшее исследование электрической энергии. Учёный математически оформил взаимодействие заряженных частиц. Его работы легли в основу разделов физики — магнитной статики и электростатики. Научные достижения ускорили применение электротехнических устройств в жизни человечества.

Учёные, изучавшие свойства электричества:

• датский физик Х. К. Эрстед установил взаимосвязь электрических и магнитных полей;
• французский естествоиспытатель Ампер изучал движение электротока;
• англичанин М. Фарадей открыл законы электролиза, создал трансформатор, изготовил первый электродвигатель;
• француз Ш. Огюст разработал методику расчёта единицы заряда, используя величины, которые применяются в механике — расстояние и силу.

Человек, посвятивший жизнь служению отчизне, внушает восхищение и уважение. Но особую благодарность вызывает личность, которая своими трудами расширяет познания человечества о природе. В 1881 году на I Международном конгрессе электриков основным единицам измерения электричества присвоены фамилии исследователей, обнаруживших эти явления. На первом месте в списке стоит имя Кулона.

5.10: Закон Кулона — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

49325

• Эд Витц, Джон В. Мур, Джастин Шорб, Ксавьер Прат-Ресина, Тим Вендорф и Адам Хан
• Цифровая библиотека химического образования (ChemEd DL)

источник графика

источник изображения

Как видно из раздела об орбиталях, энергия электрона в изолированном атоме водорода определяется главным квантовым числом n . Однако причина этого не совсем та же, что и причина, по которой энергия частицы в ящике зависела от целого числа n . В атоме электрон обладает как кинетической энергией (как частица в ящике), так и потенциальной энергией. Потенциальная энергия электрона является результатом силы притяжения между отрицательно заряженным электроном и положительно заряженным ядром.

Когда разноименные заряды (один отрицательный, а другой положительный) притягиваются друг к другу или одинаковые заряды (оба положительные или оба отрицательные) отталкиваются, Закон Кулона управляет силой между ними. Согласно этому закону сила притяжения или отталкивания изменяется обратно пропорционально квадрату расстояния между зарядами. Предположим, что две частицы, одна с зарядом +1 мкКл (микрокулон), а другая с зарядом -1 мкКл, находятся на расстоянии 1 см друг от друга. Сила притяжения между этими двумя зарядами равна 90 Н (ньютон), что примерно равно силе гравитации, действующей на 20-фунтовый груз. Если теперь расстояние между зарядами умножить на коэффициент 100 (увеличение до 1 м), то сила притяжения между двумя зарядами окажется равной разделить на коэффициент 100 в квадрате , т. е. на коэффициент 10 ⁴ . Следовательно, сила уменьшается примерно до веса песчинки. Еще одно стократное увеличение расстояния (до 100 м или около 100 ярдов) уменьшает силу притяжения еще в 10 ⁴ раз, что делает силу практически незаметной.

Как показывает приведенный выше пример, электростатические силы притяжения и отталкивания очень сильны, когда заряды близки, но довольно быстро ослабевают, когда заряды разделяются.

Если расстояние очень велико, электростатическими силами часто можно пренебречь. Это поведение напоминает более знакомый пример притяжения и отталкивания между полюсами магнитов, а также сродни силе гравитации в Солнечной системе. Магнитные силы и гравитационные силы также следуют обратному квадратичному соотношению.

Вторая часть закона Кулона гласит, что сила пропорциональна величине каждого заряда.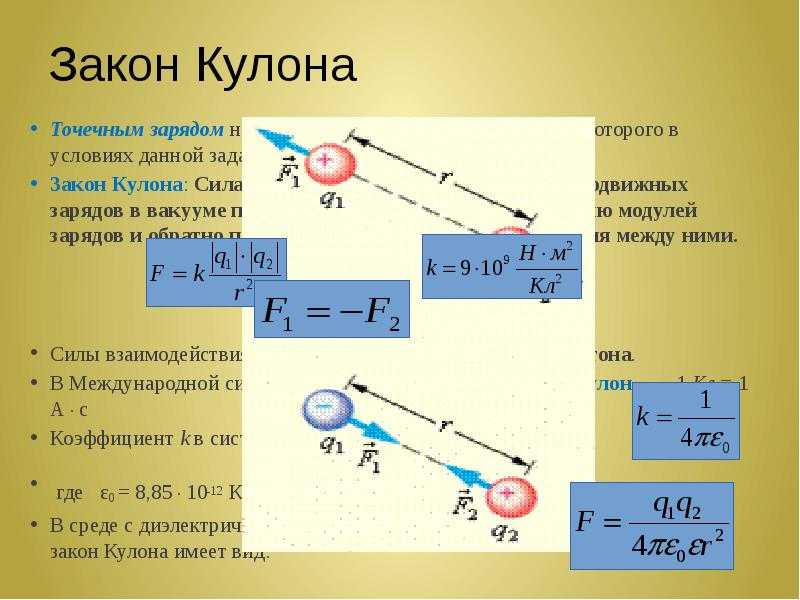 В приведенном выше примере, если один заряд удваивается (до ± 2 мкКл), сила также удваивается, а если 9{2}}\]

, где F — сила, Q ₁ и Q ₂ — заряды, r — расстояние между зарядами. Константа k имеет значение 8,988 × 10 ⁹ N м ² C ^–2 .

Чтобы увидеть это уравнение в действии, проверьте следующее моделирование:

• Эд Витц (Университет Куцтауна), Джон В. Мур (UW-Мэдисон), Джастин Шорб (Колледж Хоуп), Ксавьер Прат-Ресина (Университет Миннесоты в Рочестере), Тим Вендорф и Адам Хан.

---

Эта страница под названием 5.10: Закон Кулона распространяется в соответствии с лицензией CC BY-NC-SA, авторами, ремиксами и/или кураторами являются Эд Витц, Джон У. Мур, Джастин Шорб, Ксавьер Прат-Ресина, Тим Вендорф, и Адам Хан.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ХимПРАЙМ

   Лицензия

   CC BY-NC-SA

   Показать страницу TOC

   № на стр.

2. Теги

   1. Закон Кулона

1.1.1: Закон Кулона — Химия LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

195509

---

Электроны имеют отрицательный (-) заряд и притягиваются к положительному (+) заряду ядра. Электроны в многоэлектронном атоме также отталкиваются друг от друга. Закон Кулона (из классической физики) можно использовать для описания притяжения и отталкивания между любыми заряженными частицами, включая атомарные частицы.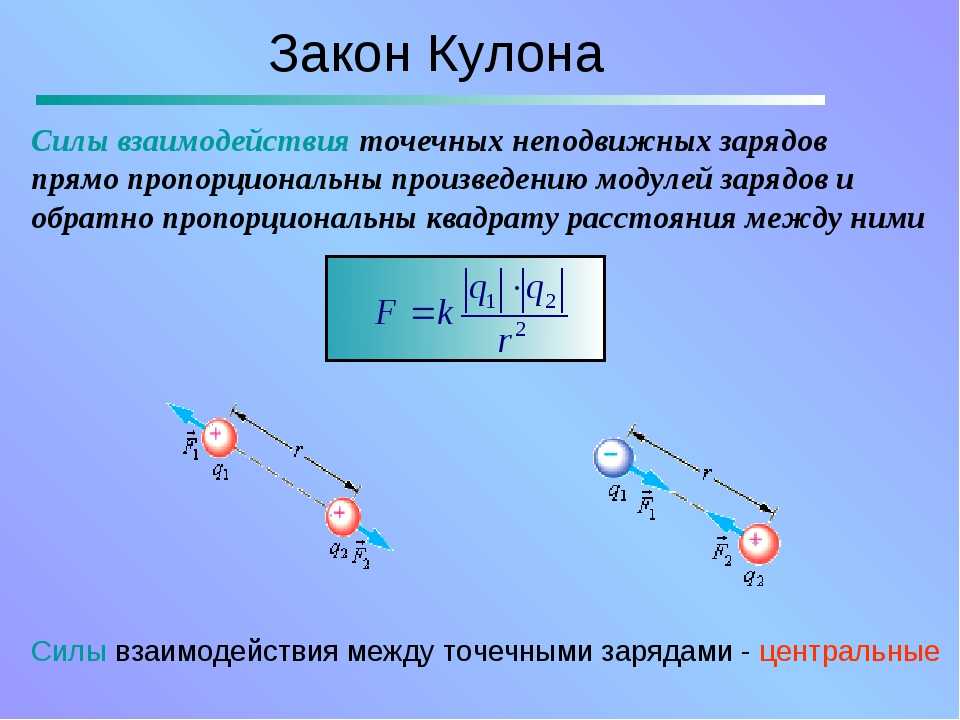 92} \метка{1}\]

Рисунок \(\PageIndex{1}\). Закон Кулона применяется к силе притяжения между ядром и электроном. (CC-BY-NC-SA; Кэтрин Хаас)

Где \(F\) — сила, \(k\) — постоянная Кулона, \(q_1\) и \(q_2\) — заряды двух частиц, а \(r\) — расстояние между частицами. Это соотношение показывает, что сила притяжения или отталкивания между двумя частицами зависит от расстояния ( r ) между частицами, а также знак и величина зарядов на каждой из частиц ( q ). Когда заряды имеют противоположный знак, сила притяжения (отрицательная F ), а если оба заряда имеют один и тот же знак, сила отталкивающая (положительная F ). Величина силы напрямую связана с величиной заряда частиц (более высокий заряд дает более сильную силу) и косвенно связана с расстоянием между частицами (большое расстояние дает более слабое взаимодействие).

Закон Кулона описывает атомы и орбитальные энергии: В большинстве случаев сила притяжения между электроном и ядром намного сильнее, чем сила отталкивания между электронами. W e сосредоточится на более важной силе притяжения между электронами и ядрами .

В атоме наиболее важными факторами, влияющими на силу, рассчитываемую по уравнению Кулона, являются заряд ядра и расстояние от ядра к интересующему электрону. Чем ближе электрон к ядру, тем сильнее сила притяжения (т. е. тем более отрицательным становится F ). Точно так же, чем больше ядерный заряд, тем сильнее сила притяжения. Что касается расстояния (\r\), номер оболочки является наиболее важным фактором, а подоболочка является еще одним фактором (это будет объяснено в этом разделе в разделе Экранирование и проникновение ).

Закон Кулона можно также применить для описания силы отталкивания между двумя электронами. Однако он не полностью объясняет дополнительное и более значительное взаимодействие между несколькими электронами и ядрами, которое происходит в многоэлектронных атомах. Закон Кулона ограничивается описанием системы из двух частиц. Таким образом, этот принцип хорошо работает для описания атома водорода, но закон Кулона — это только часть истории для многоэлектронных атомов.

Проверка на понимание \(\PageIndex{1}\)

Почему 1s-электрон имеет более высокую энергию ионизации, чем 3s-электрон?

Ответить

По мере увеличения номера оболочки расстояние электрона от ядра увеличивается. В оболочке n = 1 электроны находятся максимально близко к ядру. В n = 3 электроны на s-орбитали в среднем намного дальше от ядра, чем на всей 1s-орбитали. (Мы можем увидеть вероятное расстояние электронов, используя функции радиального распределения). Закон Кулона показывает, что противоположные заряды обладают большей силой притяжения, когда они расположены близко друг к другу. Таким образом, 1s-электрон сильнее притягивается к ядру, чем 3s-электрон, а удалить 1s-электрон труднее, поскольку он сильнее притягивается к ядру.

---

Примените закон Кулона, чтобы объяснить, почему основное состояние H равно 1s ¹ , а не 2s ¹ .

Ответить

Сила ( F ) в Законе Кулона аналогична энергии (E) электрона, когда этот электрон взаимодействует с ядром. Когда две частицы сближаются, значение F (сила или энергия) становится более отрицательным, что означает, что частицы сильнее притягиваются друг к другу.

В основном состоянии электроны находятся в конфигурации с самой низкой энергией, что является их наиболее стабильной конфигурацией. Электроны (-) стабилизируются (энергия понижена/более отрицательна) при взаимодействии с ядром (+). Чем ближе электрон к ядру, тем сильнее он притягивается, более стабилизируется и тем сильнее уменьшается его энергия.

---

1.1.1: Закон Кулона распространяется по незадекларированной лицензии и был создан, переработан и/или курирован LibreTexts.