Простые механизмы. Рычаг. Наклонная плоскость. Блоки

 

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: простые механизмы, КПД механизма.

Механизм — это приспособление для преобразования силы (её увеличения или уменьшения).
Простые механизмы — это рычаг и наклонная плоскость.

 

Рычаг.

 

Рычаг — это твёрдое тело, которое может вращаться вокруг неподвижной оси. На рис. 1) изображён рычаг с осью вращения . К концам рычага (точкам и ) приложены силы и . Плечи этих сил равны соответственно и .

Условие равновесия рычага даётся правилом моментов: , откуда

.

 

Рис. 1. Рычаг

 

Из этого соотношения следует, что рычаг даёт выигрыш в силе или в расстоянии (смотря по тому, с какой целью он используется) во столько раз, во сколько большее плечо длиннее меньшего.

Например, чтобы усилием 100 Н поднять груз весом 700 Н, нужно взять рычаг с отношением плеч 7 : 1 и положить груз на короткое плечо. Мы выиграем в силе в 7 раз, но во столько же раз проиграем в расстоянии: конец длинного плеча опишет в 7 раз большую дугу, чем конец короткого плеча (то есть груз).

Примерами рычага, дающего выигрыш в силе, являются лопата, ножницы, плоскогубцы. Весло гребца — это рычаг, дающий выигрыш в расстоянии. А обычные рычажные весы являются равноплечим рычагом, не дающим выигрыша ни в расстоянии, ни в силе (в противном случае их можно использовать для обвешивания покупателей).

 

Неподвижный блок.

 

Важной разновидностью рычага является блок — укреплённое в обойме колесо с жёлобом, по которому пропущена верёвка. В большинстве задач верёвка считается невесомой нерастяжимой нитью.

На рис. 2 изображён неподвижный блок, т. е. блок с неподвижной осью вращения (проходящей перпендикулярно плоскости рисунка через точку ).

 

 

На правом конце нити в точке закреплён груз весом . Напомним, что вес тела — это сила, с которой тело давит на опору или растягивает подвес. В данном случае вес прило жен к точке , в которой груз крепится к нити.

К левому концу нити в точке приложена сила .

Плечо силы равно , где — радиус блока. Плечо веса равно . Значит, неподвижный блок является равноплечим рычагом и потому не даёт выигрыша ни в силе, ни в расстоянии: во-первых, имеем равенство , а во-вторых, в процессе движении груза и нити перемещение точки равно перемещению груза.

Зачем же тогда вообще нужен неподвижный блок? Он полезен тем, что позволяет изменить направление усилия. Обычно неподвижный блок используется как часть более сложных механизмов.

 

Подвижный блок.

 

На рис. 3 изображён подвижный блок, ось которого перемещается вместе с грузом.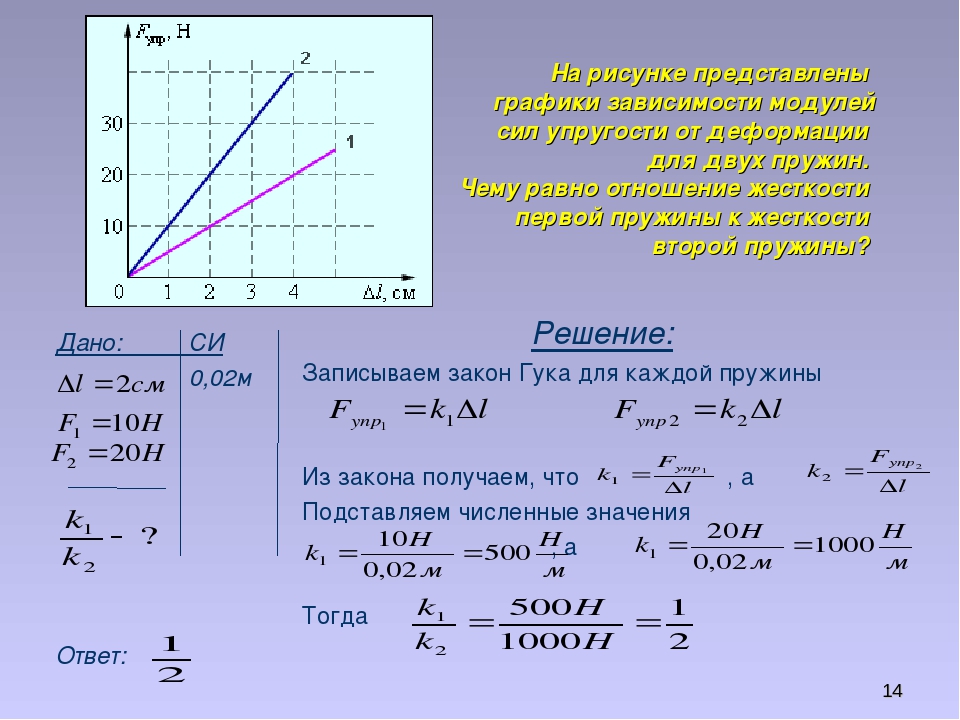 Мы тянем за нить с силой , которая приложена в точке и направлена вверх. Блок вращается и при этом также движется вверх, поднимая груз, подвешенный на нити .

 

 

В данный момент времени неподвижной точкой является точка , и именно вокруг неё поворачивается блок (он бы «перекатывается» через точку ). Говорят ещё, что через точку проходит мгновенная ось вращения блока (эта ось направлена перпендикулярно плоскости рисунка).

Вес груза приложен в точке крепления груза к нити. Плечо силы равно .

А вот плечо силы , с которой мы тянем за нить, оказывается в два раза больше: оно равно . Соответственно, условием равновесия груза является равенство (что мы и видим на рис. 3: вектор в два раза короче вектора ).

Следовательно, подвижный блок даёт выигрыш в силе в два раза. При этом, однако, мы в те же два раза проигрываем в расстоянии: чтобы поднять груз на один метр, точку придётся переместить на два метра (то есть вытянуть два метра нити).

У блока на рис. 3 есть один недостаток: тянуть нить вверх (за точку ) — не самая лучшая идея. Согласитесь, что гораздо удобнее тянуть за нить вниз! Вот тут-то нас и выручает неподвижный блок.

 

 

На рис. 4 изображён подъёмный механизм, который представляет собой комбинацию подвижного блока с неподвижным. К подвижному блоку подвешен груз, а трос дополнительно перекинут через неподвижный блок, что даёт возможность тянуть за трос вниз для подъёма груза вверх. Внешнее усилие на тросе снова обозначено вектором .

Принципиально данное устройство ничем не отличается от подвижного блока: с его помощью мы также получаем двукратный выигрыш в силе.

 

Наклонная плоскость.

 

Как мы знаем, тяжёлую бочку проще вкатить по наклонным мосткам, чем поднимать вертикально. Мостки, таким образом, являются механизмом, который даёт выигрыш в силе.

В механике подобный механизм называется наклонной плоскостью. Наклонная плоскость — это ровная плоская поверхность, расположенная под некоторым углом к горизонту. В таком случае коротко говорят: «наклонная плоскость с углом «.

Найдём силу, которую надо приложить к грузу массы , чтобы равномерно поднять его по гладкой наклонной плоскости с углом . Эта сила , разумеется, направлена вдоль наклонной плоскости (рис. 5).

 

 

Выберем ось так, как показано на рисунке. Поскольку груз движется без ускорения, действующие на него силы уравновешены:

.

Проектируем на ось :

,

откуда

.

Именно такую силу нужно приложить, что двигать груз вверх по наклонной плоскости.

Чтобы равномерно поднимать тот же груз по вертикали, к нему нужно приложить силу, равную . Видно, что , поскольку .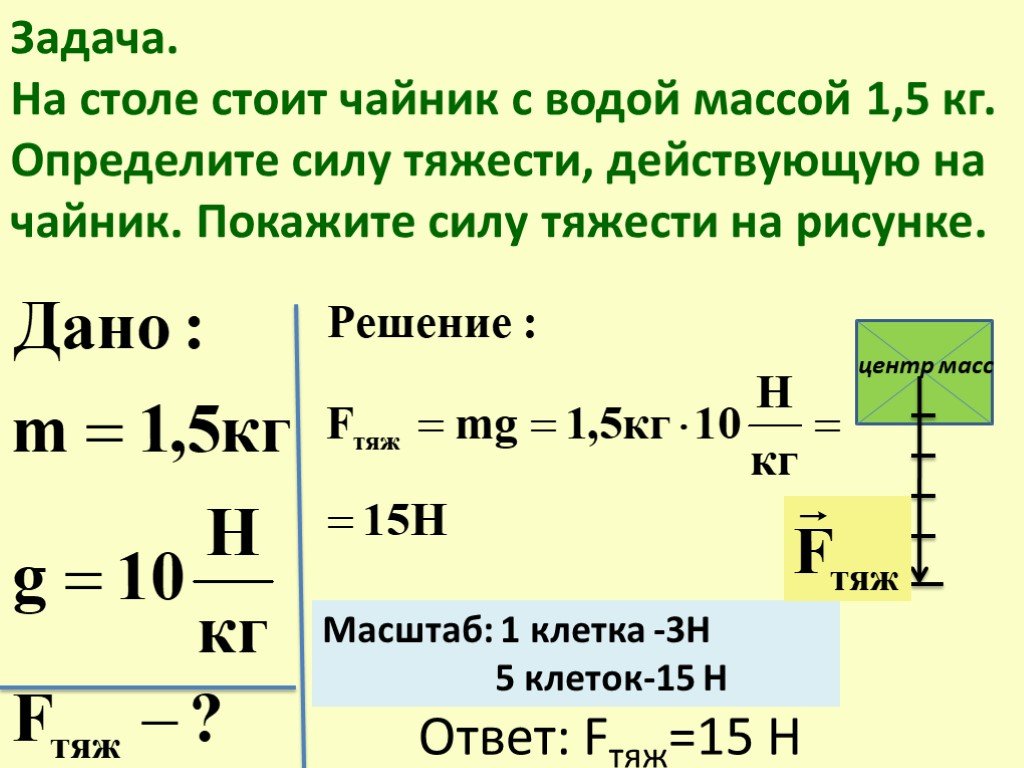 Наклонная плоскость действительно даёт выигрыш в силе, и тем больший, чем меньше угол .

Широко применяемыми разновидностями наклонной плоскости являются клин и винт.

 

Золотое правило механики.

 

Простой механизм может дать выигрыш в силе или в расстоянии, но не может дать выигрыша в работе.

Например, рычаг с отношением плеч 2 : 1 даёт выигрыш в силе в два раза. Чтобы на меньшем плече поднять груз весом , нужно к большему плечу приложить силу . Но для поднятия груза на высоту большее плечо придётся опустить на , и совершённая работа будет равна:

т. е. той же величине, что и без использования рычага.

В случае наклонной плоскости мы выигрываем в силе, так как прикладываем к грузу силу , меньшую силы тяжести. Однако, чтобы поднять груз на высоту над начальным положением, нам нужно пройти путь вдоль наклонной плоскости. При этом мы совершаем работу

т. е. ту же самую, что и при вертикальном поднятии груза.

Данные факты служат проявлениями так называемого золотого правила механики.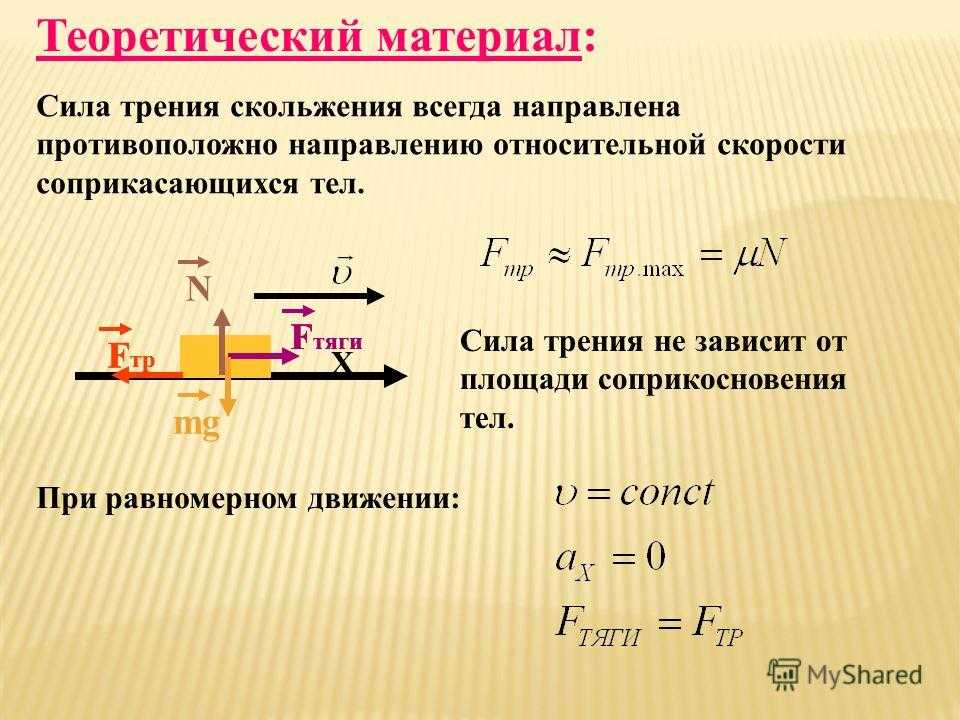

Золотое правило механики. Ни один из простых механизмов не даёт выигрыша в работе. Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии, и наоборот.

Золотое правило механики есть не что иное, как простой вариант закона сохранения энергии.

 

КПД механизма.

 

На практике приходится различать полезную работу A полезн, которую нужно совершить при помощи механизма в идеальных условиях отсутствия каких-либо потерь, и полную работу

Aполн,
которая совершается для тех же целей в реальной ситуации.

Полная работа равна сумме:
-полезной работы;
-работы, совершённой против сил трения в различных частях механизма;
-работы, совершённой по перемещению составных элементов механизма.

Так, при подъёме груза рычагом приходится вдобавок совершать работу по преодолению силы трения в оси рычага и по перемещению самого рычага, имеющего некоторый вес.

Полная работа всегда больше полезной.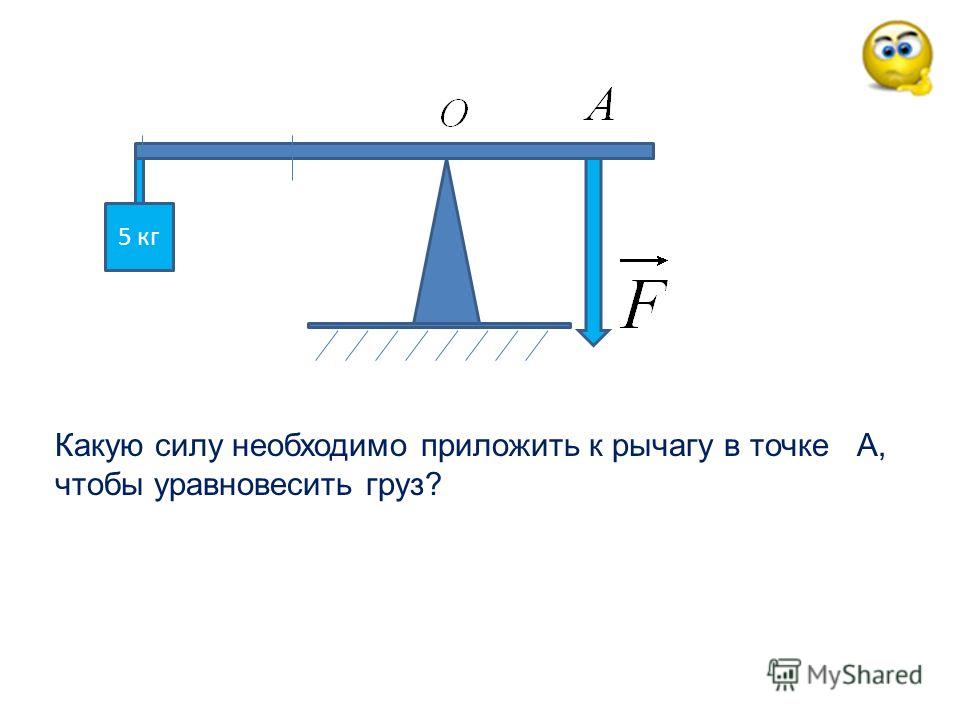 Отношение полезной работы к полной называется коэффициентом полезного действия (КПД) механизма:

=Aполезн/Аполн.

КПД принято выражать в процентах. КПД реальных механизмов всегда меньше 100%.

Вычислим КПД наклонной плоскости с углом при наличии трения. Коэффициент трения между поверхностью наклонной плоскости и грузом равен .

Пусть груз массы равномерно поднимается вдоль наклонной плоскости под действием силы из точки в точку на высоту (рис. 6). В направлении, противоположном перемещению, на груз действует сила трения скольжения .

 

 

Ускорения нет, поэтому силы, действующие на груз, уравновешены:

.

Проектируем на ось X:

. (1)

Проектируем на ось Y:

. (2)

Кроме того,

, (3)

Из (2) имеем:

.

Тогда из (3):

.

Подставляя это в (1), получаем:

.

Полная работа равна произведению силы F на путь, пройденный телом вдоль поверхности наклонной плоскости:

Aполн=.

Полезная работа, очевидно, равна:

Аполезн=.

Для искомого КПД получаем:

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

неужели тормозной путь не зависит от массы авто?

Друзья, в прошлом выпуске я утверждал, что тормозной путь автомобиля не зависит от его массы. Большинство водителей считают, что зависит, и я объяснил, откуда берется это представление. В этой статья я докажу справедливость своего утверждения, прибегнув к физическим понятиям.

Подчеркну, что речь идет о кратчайшем, экстренном, то есть минимально возможном тормозном пути. То есть о тормозном пути при торможении на грани блокировки колес. В современных машинах при таком торможении срабатывает АБС (антиблокировочная система тормозов), а классические машины либо срываются в «юз», либо остаются на грани «юза», в зависимости от действий водителя.

Сначала докажу это «на пальцах». Утяжеляя машину, мы, с одной стороны, увеличиваем ее инертность и осложняем торможение. С другой стороны, мы сильнее прижимаем шины к дороге, увеличиваем сцепление шин с дорогой и повышаем тормозные возможности машины. Эти два эффекта компенсируют друг друга в равной степени, и, в конечном итоге, масса не влияет на длину тормозного пути.

Что такое «масса»?

Для интерсующихся приведу физико-математическое доказательство и вначале кратко расскажу о понятии «масса». Массы в природе две: инертная и гравитационная. Есть, правда, еще и третий вариант – Фелипе Масса, пилот Формулы 1, уже который год выступающий за Ferrari, но сейчас не об этом 🙂

Инертная масса

Инертная масса mи – масса, которая «отвечает» за сопротивление движению тела. Чем тяжелее тело, тем сложнее привести в его движение или остановить, если оно движется.

В механике об этом говорит 2-й закон Ньютона:

a = F/mи

то есть ускорение (замедление) тела пропорционально действующей на него силе и обратно пропорционально инертной массе тела.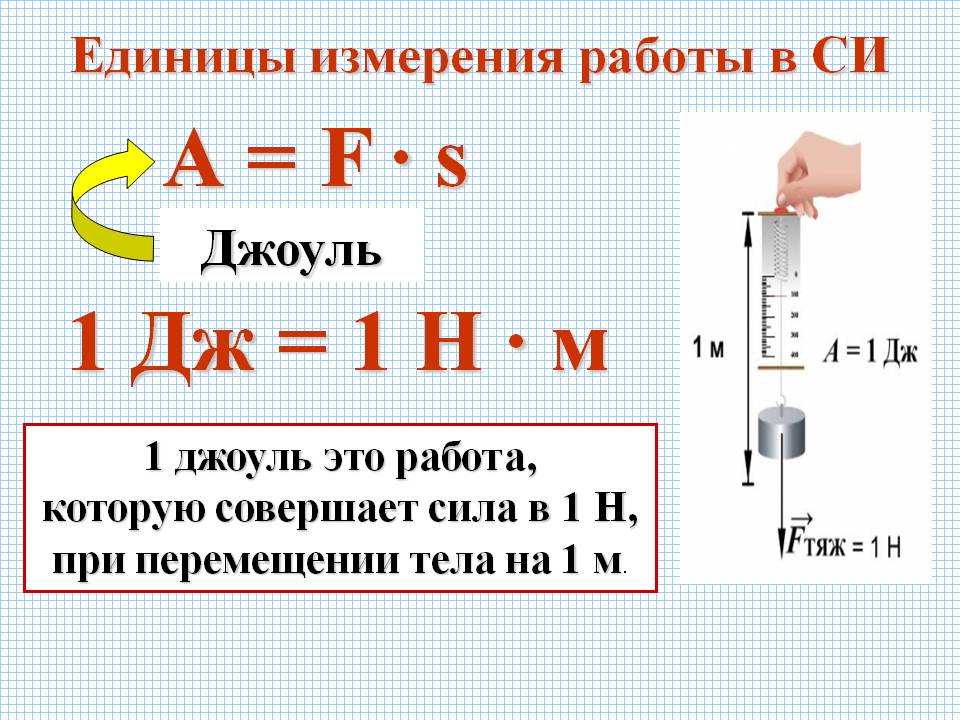 Или в более привычной формулировке этот закон выглядит как

F = mи a

Инертная масса осложняет торможение

Это как раз то, о чем думает большинство водителей: чем тяжелее машина, тем сложнее ее остановить (а также и разогнать) и, якобы, тем длиннее тормозной путь. Остановить машину действительно сложнее, не спорю, но тормозной путь есть возможность сохранить — для этого нужно лишь затратить больше энергии. В этом нам поможет второе понятие массы.

Гравитационная масса

Гравитационная масса mг – масса, которая «отвечает» за взаимное притяжение тел, в частности, за притяжение тел к Земле. Чем тяжелее тело, тем больше сила тяготения и тем сильнее тело давит на опору (пол, дорогу и т.д.).

А об этом в механике говорит закон всемирного тяготения Ньютона:

F = G mг1 mг2/r2

Или, по-русски, сила притяжения двух тел пропорциональна массам (гравитационным) этих тел и обратно пропорциональна квадрату расстояния между ними.

Эта формула упрощается для тела в поле тяготения Земли:

F = mг g

где mг – гравитационная масса тела, а g – ускорение свободного падения, равное 9,81 м/с2

Гравитационная масса помогает торможению

Применительно к разговору о тормозном пути это означает, что чем тяжелее машина, тем сильнее она давит на колеса, тем лучше прижимает их к дороге и тем лучше сцепление шин с дорогой. Ведь, согласно закону Кулона, сила сила трения покоя (в нашем случае — сила сцепления шин с дорогой, она же – «держак» на гоночном жаргоне) пропорциональна весу тела N:

Fтр = k N = k mг g

где mг – гравитационная масса машины, k – коэффициент сцепления шин с дорогой, g – ускорение свободного падения.

Тогда, чем больше масса автомобиля, тем выше сила сцепления шин с дорогой и тем сложнее тормозам заблокировать колеса и пустить машину в «юз» (ну или включить АБС, если она есть).

Одна масса мешает, другая — помогает. Что победит?

В итоге, инертная масса увеличивает инерцию машины, а гравитационная масса улучшает сцепление шин с дорогой и тормозной потенциал машины. Одно удлиняет тормозной путь, а другое пытается укоротить его. Что же победит?

Нам поможет Закон сохранения энергии

На языке физики процесс торможения выглядит как закон сохранения энергии:

mи v2/2 = Fтр s

т.е. кинетическая энергия машины с инертной массой mи и скоростью v при торможении переходит в тепло за счет работы силы трения Fтр, которая затрачивается на замедление машины на участке пути длиной s (собственно, тормозной путь).

Машина тормозит не тормозами, а шинами

Как я уже писал выше, сила трения Fтр равна kmг g – произведение коэффициента трения k, гравитационной массы mг и ускорения свободного падения g. И сразу вопрос: о какой силе трения идет речь? О силе трения колодок о тормозной диск? Или о силе трения шины о дорогу, о «держаке»? Вообще, первопричина торможения – сила трения колодок о диски. Но она не может превышать силу трения между шиной и дорогой: в этом случае шины начинают скользить, и, либо включается АБС, либо машина идет в «юз». После чего любое усиление нажатия на тормоз не дает выигрыша в торможении, и машина продолжает тормозить за счет трения шин о дорогу. Поэтому для случая экстренного торможения нужно считать, что сила трения колодок о диски равна силе сцепления шин с дорогой. И тогда k — коэффициент сцепления шин с дорогой, если шины на грани скольжения, или это коэффициент скольжения шин о дорогу, если колеса заблокированы, и машина тормозит юзом.

Тогда подставим значения силы сцепления Fтр = k mг g в закон сохранения энергии:

mи v2/2 = k mг g S

Инертная и гравитационная массы противодействуют друг другу в равной степени

А теперь ключевой момент! Еще Ньютон доказал, а Эйнштейн в свое время постулировал, что инертная и гравитационные массы равны! На сегодняшний день это проверено многократными экспериментами с высокой степенью точности. Эти массы имеют абсолютно разный физический смысл, но в килограммах это всегда одно и то же!

И тогда заменяем инертную и гравитационную массы на «просто массу»:

m v2/2 = k m g S

Теперь массы можно успешно сократить, и останется:

v2/2 = k g S

Отсюда получаем тормозной путь, не зависящий от массы:

S = v2/(2 k g)

где v – скорость движения машины до начала торможения, k – коэффициент сцепления шин с дорогой, g – ускорение свободного падения.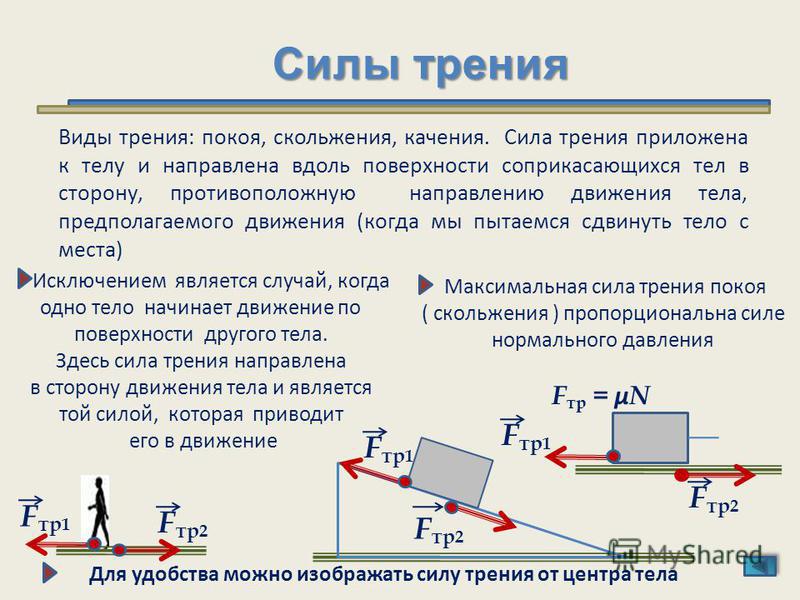

Еще раз смысл: с одной стороны, масса увеличивает инертность машины и создает препятствие тормозам. С другой стороны, масса увеличивает сцепление шин с дорогой и помогает тормозам. Эти два эффекта компенсируют друг друга в равной степени, и, в конечном итоге, масса не влияет на длину тормозного пути.

Скорость зависит только от водителя, g – постоянна, а коэффициент сцепления k зависит от состава резины протектора шины и от качества дорожного покрытия. Выходит, тормозной путь зависит от скорости, качества шины и качества дороги. При этом под качеством шины понимается именно состав резины. А от ширины профиля шины и площади пятна контакта сила сцепления шины с дорогой не зависит, как и не зависит тормозной путь.

Тормоза важны

Поговорим о тормозах. Размеры тормозных дисков, материалы колодок и прочее устройство тормозных механизмов важны для машины, но не могут влиять на тормозной путь напрямую, поскольку он ограничивается сцеплением шин с дорогой. Но хочу отменить следующее. Каждые тормозные механизмы расчитаны на погашение определенной кинетическиой энергии, которая пропорциональна массе и квадрату скорости. Обычно запас тормозов расчитывают так, чтобы даже Форд Фокус остановился с мешком картошки в багажнике со 100 км/ч за те же 40 метров, что и без мешка. Но вот ежели вы в машину загрузите лишних 500 кило, будьте готовы к тому, что ваши тормозные механизмы, рассчитанные под меньшую массу, перегреются и не справятся с задачей, и проедете вы куда больше прежних 40 метров.

Или еще пример. Можно взять Жигули со штатными тормозными дисками и колодками и поставить на нее гоночные слики. А что, на Формулах 1 как раз шины 13-дюймового диаметра, аккурат подойдут 🙂 Конечно, придется серьезно переделать саму машину, но это сейчас не столь важно. Так вот, слики имеют почти вдвое больший коэффициент сцепления с дорогой, а значит для торможения юзом на тормоза Жигулей ляжет нагрузка вдвое больше обычной. И вариантов развития событий тоже два: либо тормоза перегреются с первой же попытки, либо вовсе не смогут довести колеса до грани блокировки… И то, и другое означает для нас увеличение тормозного пути (по сравнению с тормозным путем на этих же сликах и гоночными тормозами) даже для пустой машины. А если ее еще и догрузить как следует, то ситуация еще более усугубится, и тормозной путь таких Жигулей еще как будет зависеть от массы авто.

Таким образом, мы можем говорить о независимости тормозного пути от массы машины, если она соответствует общепринятым нормам безопасности: на машине с загрузкой, не превышающей допустимую производителем, штатные тормоза должны быть способны заблокировать колеса (или включить АБС) на штатных шинах.

Однако главное при торможении — шины

Выходит, и Жигули, и Ferrari затормозят с примерно одинаковым тормозным путем, если тормоза у всех исправны, а на колеса установлены одни и те же шины. Возможна разница за счет разного времени срабатывания тормозной системы, а также за счет разных алгоритмов торможения водителя и АБС. Но эта разница будет куда меньше по сравнению с тем, когда одни и те же Жигули (или Ferrari) будут тормозить сначала на Michelin, а потом на отечественной Каме. Так что главное при торможении — шины!

Выше я уже написал, что в случае торможения на грани скольжения шин под k понимается коэффициент сцепления, а в случае торможения юзом при заблокированных колесах k — коэффициент скольжения шин по дороге. Известно, что трение скольжения всегда меньше трения покоя (сцепления), примерно на 10-15%. Соответственно, машина, тормозящая юзом, как правило, проходит на 10-15% больший путь до полной остановки по сравнению с машиной, тормозящей на грани скольжения. АБС не допускает блокировки колес, поэтому машины с АБС при нажатии тормоза «в пол» тормозят всегда на грани скольжения. А машины без АБС при торможении «в пол» сразу же уходят в юз. Хотя, при должном навыке водитель и без АБС может правильно дозировать усилие на педали и тормозить на грани скольжения. Например, машины в Формуле 1 не оснащены АБС, и пилоты тормозят на грани скольжения, а уход в юз считается ошибкой. Из написанного следует, что при одних и тех же шинах машина с АБС будет тормозить короче, чем машина без АБС юзом, но это справедливо только для гладких и твердых дорог. На рыхлых и неровных покрытиях машины с АБС проигрывают в тормозном пути машинам без АБС.

Кстати, не стоит сравнивать тормозные пути седана и фуры. Это не всегда корректно, поскольку там могут быть конструктивно разные тормоза (у грузовиков даже бывает не гидравлическая, а пневматическая тормозная система с огромной задержкой в срабатывании) и разного качества шины. Лучше всего сравнивать «яблоки с яблоками», то есть одну и ту же машину с разной степенью загрузки. Подробнее об этом читайте в ответе на вопрос гостя нашего сайта о влиянии тормозов.

Легковушка и фура тормозят одинаково

Однако, если время срабатывания тормозов у легковушки и фуры одинаково, и стоят схожие по составу шины, то тормозной путь отличаться не должен. Вот видео, которое подтверждает это (правда, я не понимаю по-немецки, но по смыслу именно то :)):

http://www.myvideo.de/watch/7778214/Bremstest_PKW_LKW_VW_T4_gg_Mercedes_Actros

В заключение скажу, что тормозной путь зависит от веса машины (не будем путать вес и массу), а также от массы прицепа без тормозов, от положения руля. Обо всем этом я расскажу в будущих выпусках.

Как это поможет на практике?

А пока — практический смысл этой статьи.

Используйте качественные шины

Помните, машина тормозит не тормозами, а шинами. Если у вас стоят изношенные или дешевые или просто не соответствующие сезону шины, ваш автомобиль тормозит плохо, и хорошие тормоза ему не помогут. Если вы хотите повысить безопасность и улучшить тормозную динамику машины, не нужно делать тюнинг тормозов и ставить дорогущие тормозные диски, колодки и т.п. Поставьте дорогие качественные шины, и тогда ваша жизнь за рулем будет в большей безопасности.

Тюнинг машины требует профессионального подхода

Если же вы решите «обуть» машину в суперцепкие шины — для гонок ли, или для собственной безопасности, имейте в виду, что это уже вмешательство в конструкцию автомобиля, тюнинг. Одними шинами не обойтись — они потребуют для себя мощных тормозов, а подобрать их и грамотно установить — дело крайне важное и непростое. Так что подходите к тюнингу машины серьезно и пользуйтесь услугами профессионалов, ведь такие вещи не терпят самодеятельности.

Маленькая легкая машина не дает преимуществ при торможении

Выбирая машину при покупке не думайте, что маленький городской автомобильчик будет более безопасный по сравнению с минивэном и тем более фурой лишь потому, что легче и, якобы, лучше тормозит. Не лучше он тормозит, а если и лучше, то масса тут ни при чем. Будьте бдительны, если управляете маленьким авто. Особенно, когда едете сзади фуры: не приближайтесь к ней и не думайте, что в случае чего она будет останавливаться долго, а вы то уж точно успеете остановиться… Сохраняйте безопасную дистанцию, независимо от разницы в массах машин.

Сохраняйте самообладание, управляя загруженной машиной

Если вам предстоит путь на машине с пассажирами и полным багажником, будьте бдительны, но не теряйте самообладание при торможении. Да, вам покажется, что торможение стало хуже. Но это лишь потому, что вы привыкли к другому усилию на педали тормоза.Нажимайте на тормоз сильнее обычного, и машина затормозит так, как вам нужно.  Но и после разгрузки автомобиля не теряйте голову 🙂 — ведь машина станет более чутко отзываться на нажатие педали тормоза, но это иллюзия: тормозной путь не станет короче!

Не перегружайте машину

У каждой машины есть свое предназначение для использования и своя допустимая нагрузка. Если ее превысить, то шины и тормоза могут перегреться, а то и вовсе испортиться. В любом случае, они не справятся с задачей торможения. Тормозной путь заметно увеличится, и это, как вы понимаете, может привести к ДТП.

Учитесь правильно тормозить

Казалось бы, что тут сложного? Но наш тренерский опыт говорит, что многим водителям не хватает плавности и знаний многих тонкостей в повседневном торможении и, наоборот, маловато резкости в экстренном торможении. В общих чертах я написал об этом в статье «Как правильно тормозить?», а если вас интересует практика, то экстренное торможение вы можете отработать на курсе «Зимняя контраварийная подготовка», а постичь все премудрости грамотного торможения на каждый день — на «курсе МВА для водителя: Мастерство Вождения Автомобиля».

сил | Определение и формула

force

Посмотреть все СМИ

Ключевые люди:

Исаак Ньютон Христиан Гюйгенс Сэр Чарльз Вернон Бойз

Похожие темы:

электромагнетизм сила тяжести фундаментальная сила носить трение

Просмотреть весь связанный контент →

сила , в механике любое действие, которое имеет тенденцию поддерживать или изменять движение тела или искажать его. Понятие силы обычно объясняется с точки зрения трех законов движения Исаака Ньютона, изложенных в его Principia Mathematica (1687). Согласно первому принципу Ньютона, тело, находящееся в состоянии покоя или движущееся равномерно и прямолинейно, будет оставаться в этом состоянии до тех пор, пока к нему не будет приложена какая-либо сила. Второй закон гласит, что когда на тело действует внешняя сила, оно вызывает ускорение (изменение скорости) тела в направлении действия силы.

Величина ускорения прямо пропорциональна величине внешней силы и обратно пропорциональна количеству вещества в теле. Третий закон Ньютона гласит, что если одно тело действует на другое тело с такой же силой, то второе тело действует с такой же силой на первое тело. Этот принцип действия и противодействия объясняет, почему сила имеет тенденцию деформировать тело (т. е. изменять его форму), независимо от того, заставляет ли оно двигаться тело. Деформацией тела обычно можно пренебречь при исследовании его движения.

Поскольку сила имеет как величину, так и направление, она является векторной величиной. Представление сил векторами предполагает, что они сосредоточены либо в одной точке, либо вдоль одной линии. Однако это физически невозможно. Например, на нагруженный компонент конструкции приложенная сила создает внутреннюю силу или напряжение, которое распределяется по поперечному сечению компонента. Сила тяжести неизменно распределена по всему объему тела. Тем не менее, когда основное внимание уделяется равновесию тела, обычно справедливо и удобно предполагать, что силы сосредоточены в одной точке. В случае гравитационной силы можно предположить, что весь вес тела сосредоточен в его центре тяжести ( см. гравитация, центр).

Тест «Британника»

Физика и законы природы

Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.

Физики используют ньютон, единицу Международной системы (СИ), для измерения силы. Ньютон — это сила, необходимая для ускорения тела массой один килограмм на один метр в секунду за секунду. Формула F = ma используется для расчета количества ньютонов, необходимого для увеличения или уменьшения скорости данного тела. В странах, до сих пор использующих английскую систему измерения, инженеры обычно измеряют силу в фунтах. Сила в один фунт сообщает объекту весом в один фунт ускорение 32,17 фута в секунду в квадрате.

Редакторы Британской энциклопедии Эта статья была недавно пересмотрена и обновлена ​​Эриком Грегерсеном.

Определение силы в науке

Эта запись была опубликована 30 марта 2022 г. от Anne Helmenstine (обновлено 2 апреля 2022 г. )

---

По определению сила — это толчок или притяжение объекта, который имеет как величину, так и направление.

В физике и других науках сила — это толчок или притяжение массы, которые могут изменить движение объекта. Сила является векторной величиной, то есть имеет как величину, так и направление. Символом силы является заглавная буква F. Известным примером уравнения для силы является второй закон Ньютона:

F = m*a

Здесь F — сила, m — масса, a — ускорение. Этот закон гласит, что результирующая сила равна скорости изменения ее количества движения во времени. Предполагая, что масса постоянна, ускорение объекта (изменение скорости) прямо пропорционально силе и направлению силы.

Единицы силы

Единицей силы в системе СИ является ньютон (Н), который равен килограмму на метр в секунду в квадрате (кг · м/с ² ). Другие общие единицы включают:

• дина
• килограмм-сила (килопонд)
• фунт-сила
• кип
• фунт-сила

история

греческая философия постоянно прикладывала силу. Галилео Галилей и сэр Исаак Ньютон исправили это заблуждение и математически описали силу. Эксперимент Галилея с наклонной плоскостью (1638 г.) математически описывал движение с естественным ускорением. Три закона движения Ньютона (1687 г.) описывают силу в обычных условиях. Теория относительности Эйнштейна расширяет описание явлений, происходящих со скоростью, близкой к скорости света.

Вкратце, три закона движения Ньютона таковы:

1. Движущееся тело остается в движении с постоянной скоростью, если на него не действует внешняя сила. Точно так же тело в состоянии покоя остается в покое, если на него не действует внешняя сила.
2. Сила, действующая на объект, равна произведению массы объекта на его ускорение.
3. Когда один объект воздействует на другой объект, второй объект оказывает равную и противоположную силу на первый.

Примеры сил

Силы окружают нас повсюду в повседневном мире. Например:

• Трение — это сила, противодействующая движению.
• Приложенная сила — это сила, прикладываемая к объекту человеком или другим объектом.
• Центростремительная сила — это сила, действующая на тело, движущееся по круговой траектории, направленной к центру окружности.
• Центробежная сила — это кажущаяся сила, действующая наружу на вращающееся тело.
• Нормальная сила — это сила, действующая на объект, находящийся в контакте с поверхностью.
• Сила тяжести — это сила притяжения между двумя массами. Вес – это ускорение свободного падения, умноженное на массу объекта.
• Сила натяжения — это сила, которая одинаково притягивает два объекта, соединенных веревкой, проволокой или одеждой.
• Сила пружины — это сила, создаваемая растянутой или сжатой пружиной.
• Сила Кориолиса действует перпендикулярно направлению движения и оси вращения на массу, движущуюся во вращающейся системе.
• Электромагнитная сила — это притяжение между противоположными электрическими зарядами или магнитными полюсами или отталкивание одноименных зарядов или магнитных полюсов.

Фундаментальные силы

Четыре фундаментальные силы природы — гравитация, электромагнетизм, сильное взаимодействие и слабое взаимодействие.

• Гравитация — это сила притяжения между двумя массами. Она действует на бесконечном расстоянии, но является самой слабой из фундаментальных сил.
• Электромагнетизм описывает притяжение и отталкивание электрических зарядов и магнитов. Подобно гравитации, она эффективна на бесконечном расстоянии.
• Слабое взаимодействие влияет на некоторые ядерные явления, такие как бета-распад. Его эффективный диапазон составляет всего около 10 ^-18 метров, значит действует в атомном масштабе.
• Сильное взаимодействие очень мощное, но оно действует только на расстоянии около 10 ^-15 метров. Среди прочего, он связывает протоны и нейтроны вместе внутри атомного ядра.