12-г. Сложение и вычитание векторов
- Главная
- Справочник
- Физика
- Книги, лекции и конспекты по физике
- Физика 9 класс
- Введение в кинематику
- 12-г. Сложение и вычитание векторов
§ 12-г. Сложение и вычитание векторов
На уроках геометрии вы уже познакомились с простейшими операциями над векторами: нахождением их суммы и разности. Напомним это.
Сложение векторов. Чтобы найти сумму двух векторов, необходимо: а) параллельным переносом совместить начала векторов; б) дополнить чертёж двумя отрезками так, чтобы получился параллелограмм; в) провести вектор суммы из точки начал векторов в точку соединения дополняющих отрезков (по диагонали параллелограмма).
Проиллюстрируем это правило на примере из § 12-в, когда автомобиль перемещается сначала по вектору AВ1 и затем по вектору В1В2 до поворота на мост (см. чертёж слева). Другими словами, мы ищем вектор суммы или, что то же самое,

Сделаем новые чертежи обсуждаемых векторов (см. ниже). На чертеже «а» применим параллельный перенос и переместим вектор В1В2 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним двумя отрезками СВ2 и В1В2 до образования параллелограмма. На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).
Итак, мы нашли вектор суммы или сумму векторов:
Проверим правильность результата: автомобиль, переместившись из точки А в точку В1, затем переместился из точки В1 в точку В2. Иначе говоря, он совершил перемещение «по» вектору АВ2, который мы только что построили, применив
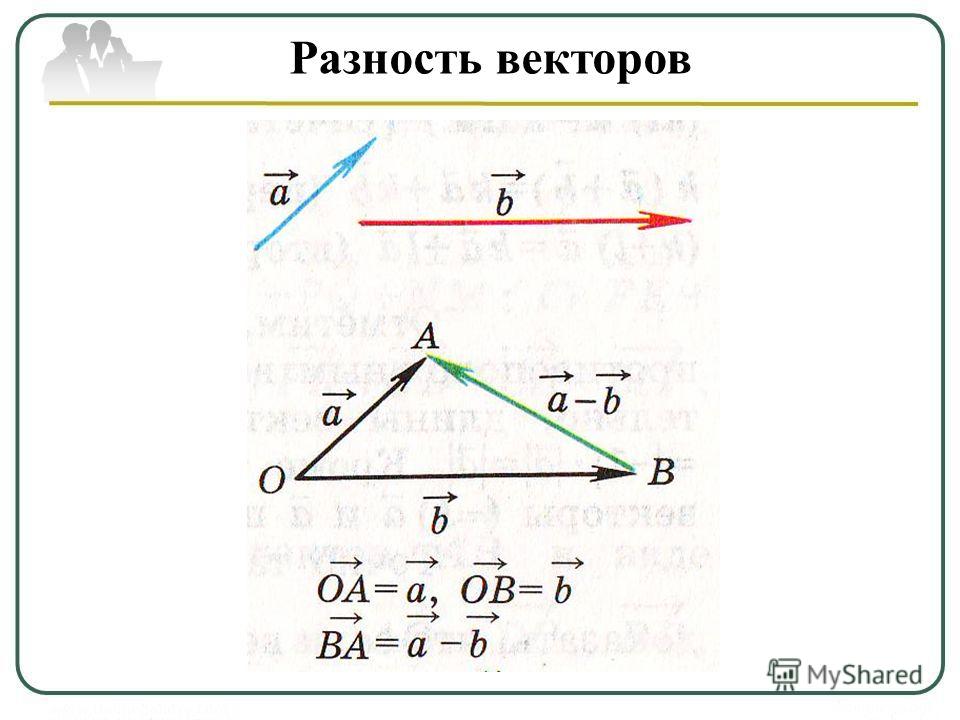
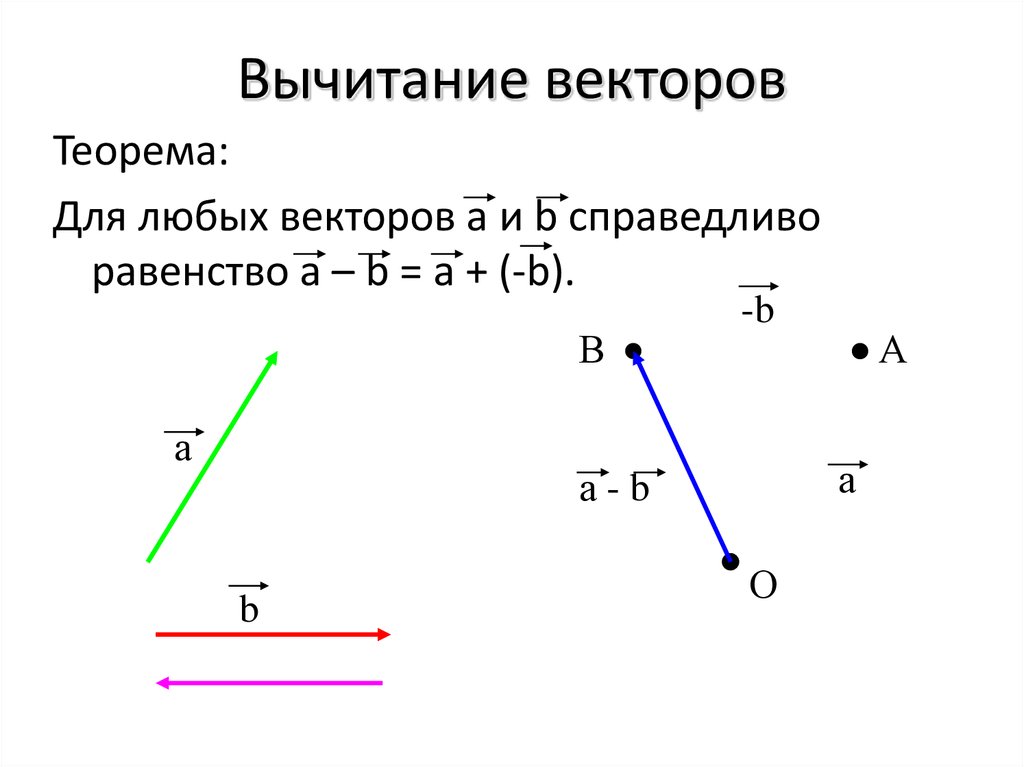
Вычитание векторов. Чтобы найти разность двух векторов, нужно: а) параллельным переносом совместить начала векторов; б) дополнить чертёж отрезком так, чтобы получился треугольник; в) придать отрезку направление от вычитаемого к уменьшаемому, создав вектор разности.
Проиллюстрируем это правило на том же примере из § 12-в, когда автомобиль подъезжает к середине моста. Для этого из вектора полного перемещения АВ3 вычтем перемещение на третьем этапе, вектор B2В3.
Другими словами, сейчас мы ищем вектор разности:
На чертеже «а» применим параллельный перенос и переместим вектор В2В3 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.
Контурной стрелкой показан параллельный перенос найденного вектора разности в точку А. Важно: построенный вектор DВ3 равен искомому вектору разности АВ2. Это, по сути, проверка правильности результата, поскольку этот вектор мы уже находили по правилу параллелограмма.
Заметим, что векторы можно складывать и «треугольником», а вычитать «параллелограммом».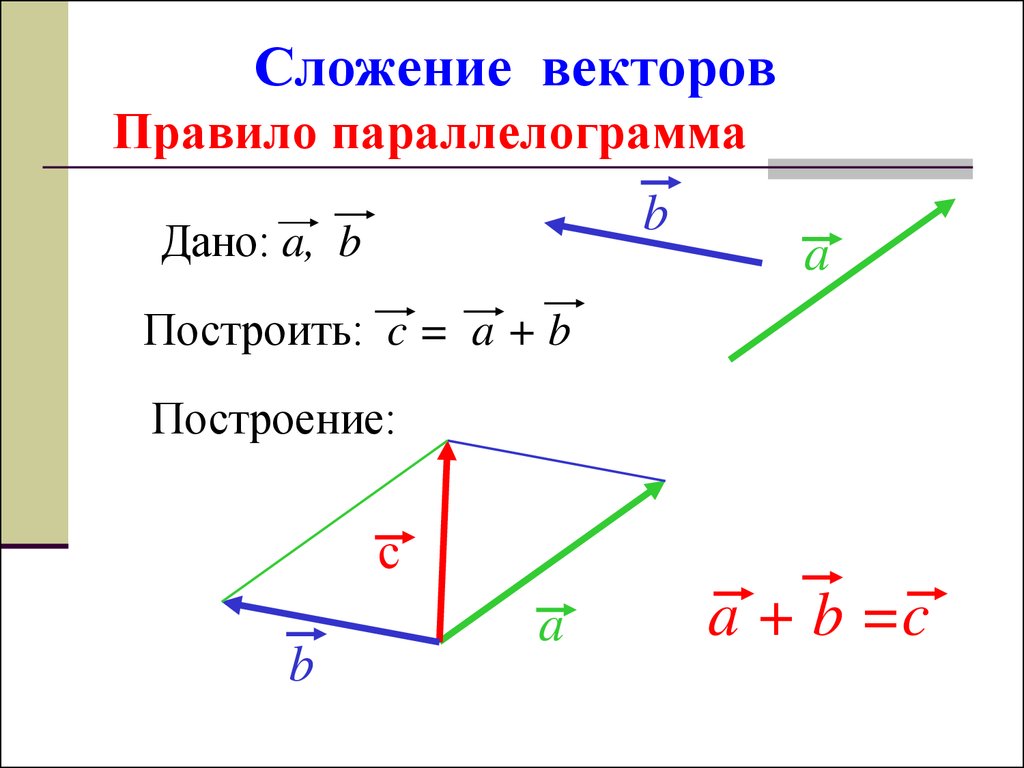 Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде (см. § 12-л, а также § 13-з, § 13-и).
Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде (см. § 12-л, а также § 13-з, § 13-и).
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Введение в кинематику Формулы Физика Теория 9 класс 1233
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
что это такое в геометрии, правила суммы, примеры решения задач
Понятие суммы векторов
Определение 1Вектор в геометрии является таким отрезком, для которого задано направление, а также начало и конец, определенные граничными точками.
Обозначают вектор, например, таким образом: \overrightarrow{AB}. В этом случае началом вектора является точка А, конец обозначен точкой В.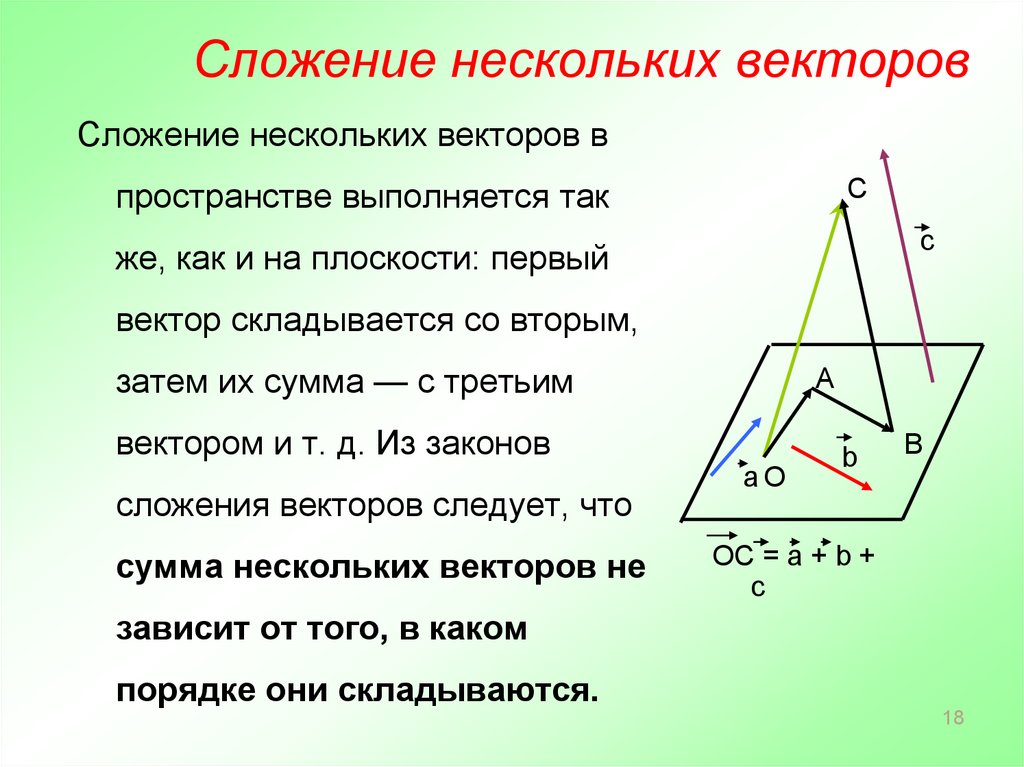 Допускается и такое верное обозначение вектора: \overrightarrow{a}, которое можно встретить в задачах на сложение и вычитание.
Допускается и такое верное обозначение вектора: \overrightarrow{a}, которое можно встретить в задачах на сложение и вычитание.
Источник: shkolkovo.net
В некоторых источниках понятие вектора сформулировано, как движение из точки А в точку В, что можно отметить в конспекте.
Определение 2Длина (или модуль) вектора AB→ представляет собой длину отрезка АВ, который соответствует рассматриваемому вектору:
|AB→|=AB.
Определение 3Нулевой вектор — это вектор со совпадающими началом и концом, то есть нулевым значением длины.
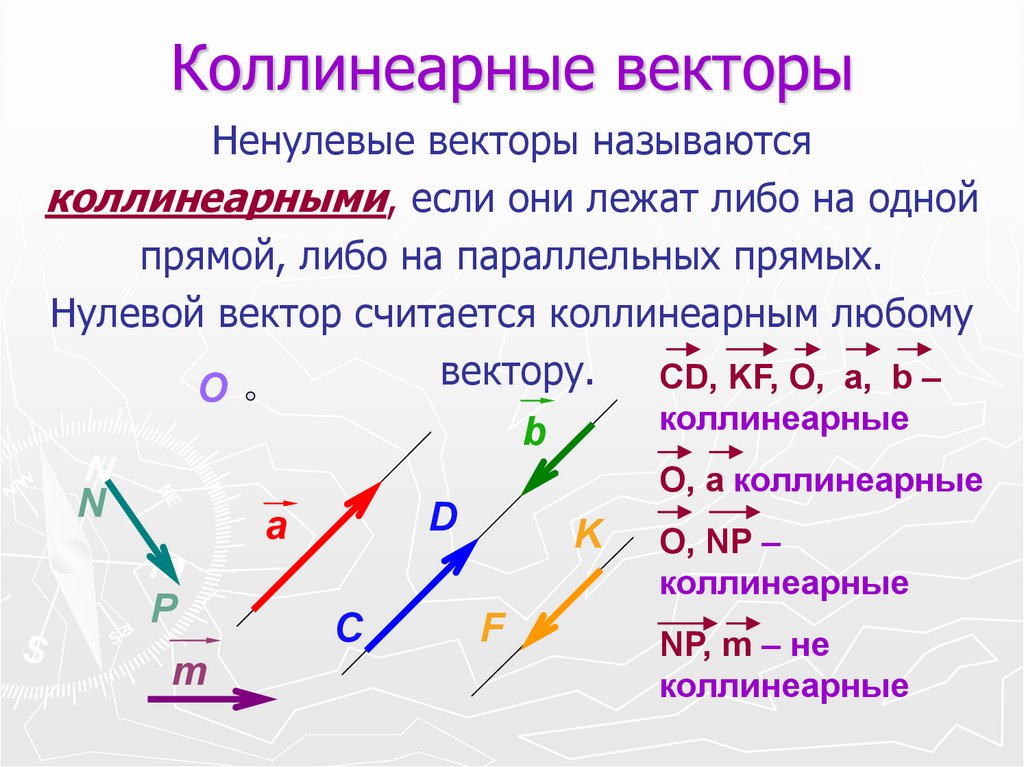
Определение 4Коллинеарные вектора — вектора, расположенные на единой прямой, либо на прямых, которые являются параллельными.
Примеры коллинеарных векторов:
a→,b→ и c→.
Если записанное ранее условие, при котором вектора коллинеарны, не выполняется, вектора называют неколлинеарными. В качестве примера можно представить следующие неколлинеарные вектора:
a→ и d→
Источник: shkolkovo. net
net
Пара векторов, которые коллинеарны друг другу, совпадают по направлению, являются сонаправленными.
На рисунке изображены сонаправленные вектора:
a→ и c→.
Если предыдущее условие, при котором вектора сонаправлены, не выполняется, то такие вектора называют противоположно направленными. Например, противоположно направлены следующие вектора:
a→ и b→.
В задачах на уроке можно встретить следующее обозначение того, как соотносятся между собой вектора:
a→↑↑c→,a→↑↓b→.
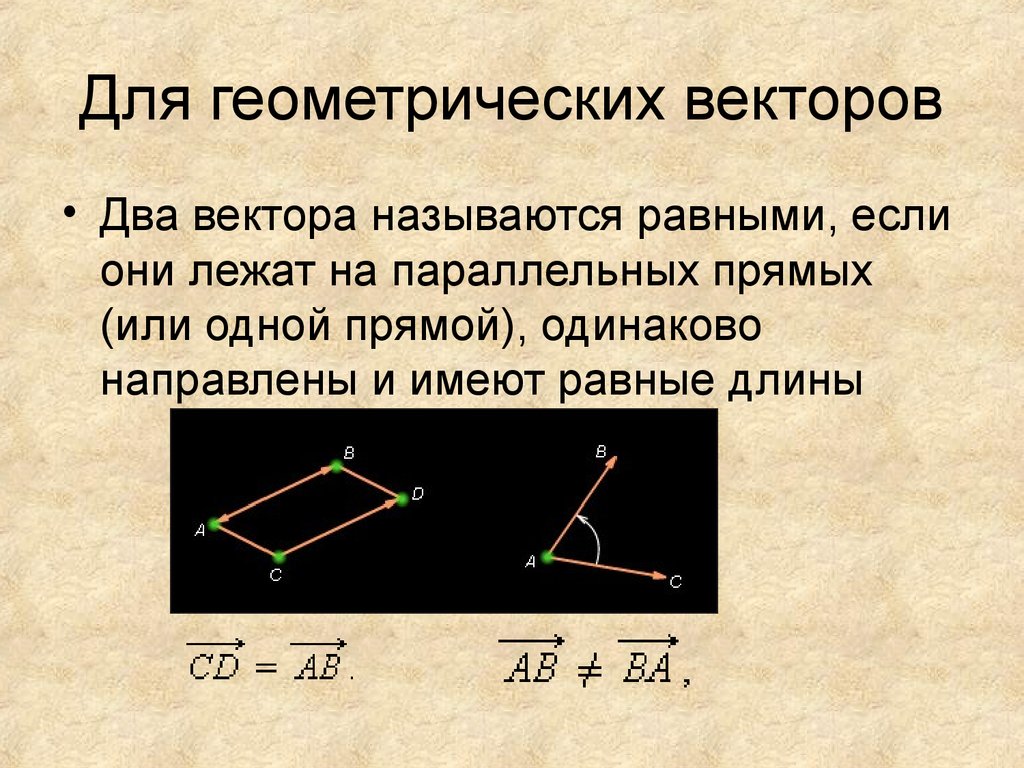
Определение 6Равными векторами являются такие векторы, которые сонаправлены и равны по длине.
Правила нахождения суммы векторов
Формула 1Формула сложения векторов a→=ax;ay и b→=bx;by, которую можно применять в случае решения плоских задач:
a→+b→=ax+bx;ay+by.
Формула 2Формула сложения векторовa→=ax;ay;az и b→=bx;by;bz, которую можно применять в случае решения пространственных задач:
a→+b→=ax+bx;ay+by;az+bz.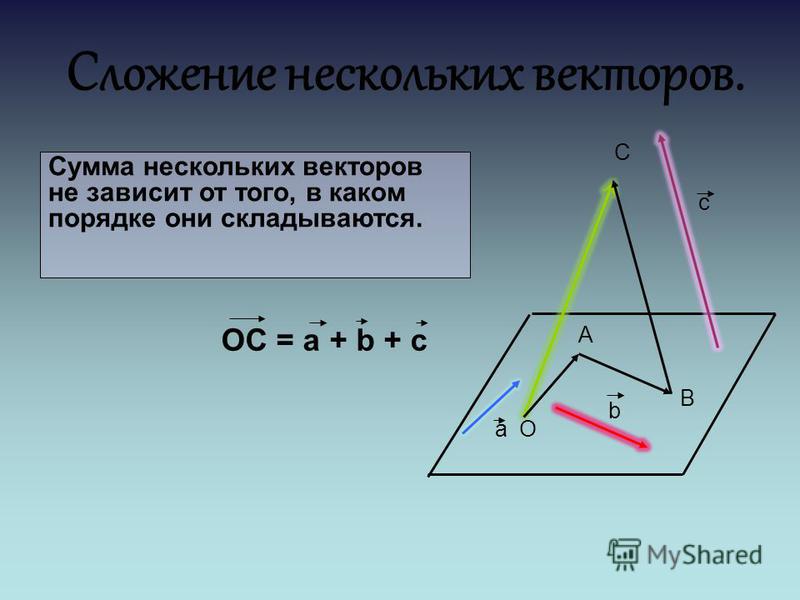
Формула сложения векторов a→=ax;ay;…;an и b→=bx;by;…;bn, которую можно применять в случае решения задач с n-мерными векторами:
a→+b→=ax+bx;ay+by;…;an+bn.
Рассмотрим правила, которые целесообразно использовать при решении заданий в классе и самостоятельно на сложение коллинеарных векторов.
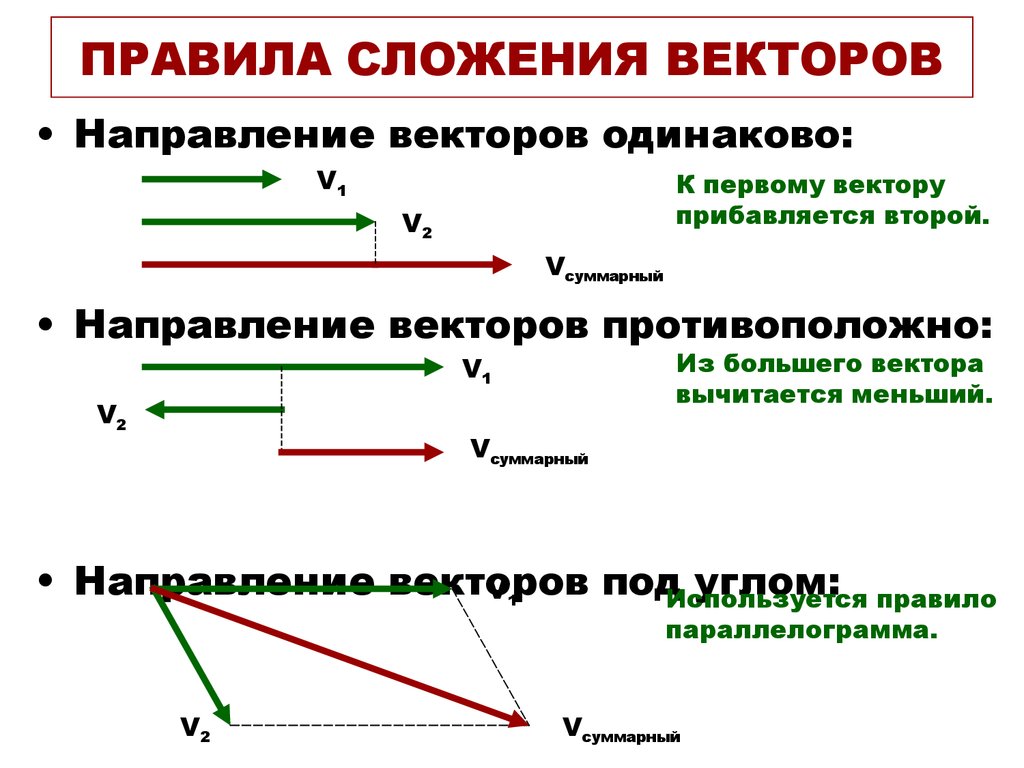
Правило 1При сложении пары сонаправленных векторов требуется отмерить второй вектор от точки, которая является концом первого вектора. Результатом сложения является вектор с началом в точке, которая определяет начало первого вектора, и концом, совпадающим с конечной точкой второго вектора.
Источник: shkolkovo.net
Правило 2При сложении пары противоположно направленных векторов требуется отмерить второй вектор от точки, которая является началом первого вектора. Результатом сложения является вектор с началом в точке, совпадающей с началом для обоих векторов; длиной, равной разности длин векторов; направлением, совпадающим с направлением вектора, который обладает большей длиной.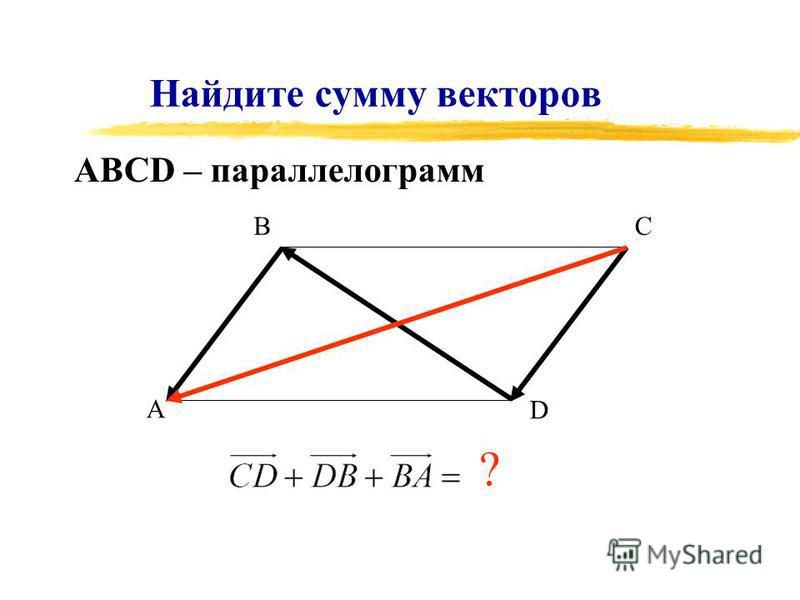
Источник: shkolkovo.net
Существует ряд правил, от знания которых будет зависеть то, насколько легко складываются вектора, не являющиеся коллинеарными.
Правило 3Правило треугольника. Если даны два неколлинеарных вектора a→ и b→, сумму которых нужно вычислить, то необходимо отмерить вектор b→ от конечной точки, принадлежащей вектору a→. Результатом сложения таких векторов a→+b→ является вектор с началом, расположенным в начальной точке вектора a→ и концом, который совпадает с концом вектора b→.
Источник: shkolkovo.net
Правило 4Правило параллелограмма. Если даны два неколлинеарных вектора a→ и b→, сумму которых нужно вычислить, то необходимо отмерить вектор b→ от начальной точки, принадлежащей вектору a→. Результатом сложения векторов a→+b→ является вектор, совпадающий с диагональю, проведенной в параллелограмме, который построен с помощью векторов a→ и b→.
Источник: shkolkovo.net
Действие по сложению векторов обладает рядом характерных свойств. Представим их описание:
- Наличие вектора, который является нейтральным: для какого-либо вектора a→ выполняется следующее: a→+0→=a→.

- Наличие вектора, который является обратным: для какого-либо вектора a→ выполняется следующее: a→+(-a→)=0→.
- Ассоциативность: для каких-либо векторов a→,b→ и c→ выполняется следующее: (a→+b→)+c→=a→+(b→+c→).
- Коммутативность: для каких-либо векторов a→ и b→ выполняется следующее: a→+b→=b→+a→.
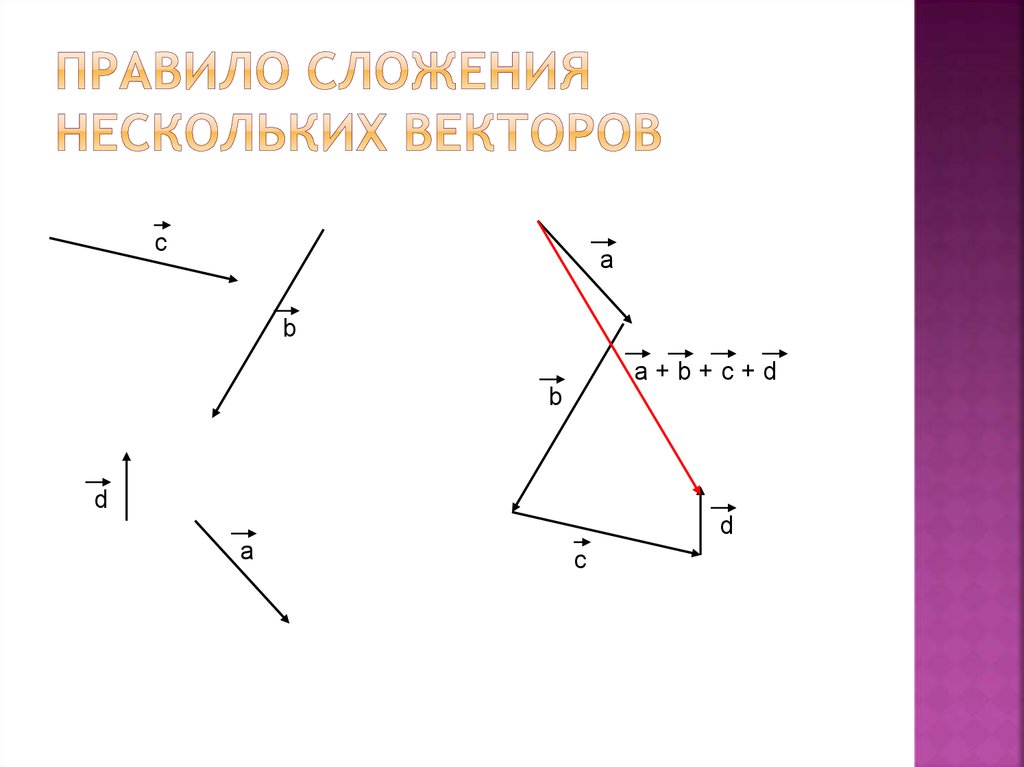
При сложении нескольких векторов следует откладывать их в определенной последовательности: каждый следующий нужно отмерять от точки, которая является концом предыдущего вектора. Результатом сложения данных векторов является вектор с началом, совпадающим с точкой, которая является началом первого вектора, и концом, расположенным в конце последнего вектора:
a1→+a2→+a3→+a4→=a→.
Примеры решения задач
Задача 1Даны два вектора, сумму которых требуется найти:
a→=1;2 и b→=4;8.
Решение
Воспользуемся формулой сложения векторов для плоских задач:
a→+b→=1+4;2+8=5;10
Ответ: 5;10.
Задача 2Даны два вектора, сумму которых требуется вычислить:
a→=1;2;5 и b→=4;8;1.
Решение
Воспользуемся формулой сложения векторов, применимой для решения пространственных задач:
a→+b→=1+4;2+8;5+1=5;10;6
Ответ: 5;10;6.
Задача 3Даны два вектора, которые требуется сложить:
a→=1;2;5;9 и b→=4;8;1;-20.
Решение
Воспользуемся формулой для решения задач с n-мерными векторами:
a→+b→=1+4;2+8;5+1;9+(-20)=5;10;6;-11
Ответ: 5;10;6;-11.
Задача 4Имеется некий прямоугольный треугольник ABC. В нем угол А составляет 90°, точка О обозначает центр окружности, описанной около рассматриваемого треугольника. Вектор А→В имеет координаты 1;1. Координаты вектора А→Сравны-1;1. Требуется определить, чему равна сумма координат вектора OC→.
Решение
Заметим, что в данном случае центр описанной окружности совпадает с серединой гипотенузы, так как вписанный треугольник является прямоугольным. В результате точка О расположена посередине ВС. Выполним соответствующий рисунок:
Источник: shkolkovo.net
В данном случае, справедливо, что:
BC→=AC→-AB→
Таким образом:
BC→={-1-1;1-1}={-2;0}
Заметим, что:
OC→=12BC→
В результате:
OC→={-1;0}
Определим сумму координат вектора OC→:
-1+0=-1
Ответ: -1.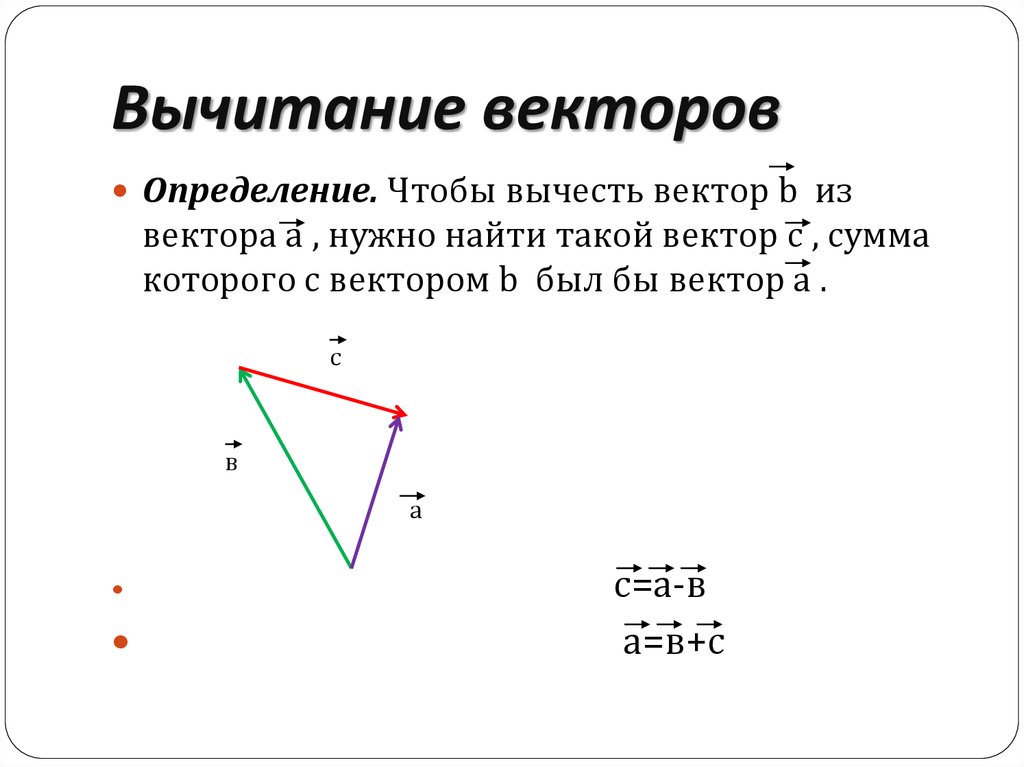
Имеется некая геометрическая фигура в виде многоугольника с четырьмя углами АВСD. На сторонах этого четырехугольника отмерены следующие вектора:
AB→,BC→,CD→,DA→.
Необходимо вычислить длину такого вектора в следующем порядке:
AB→+BC→+CD→+DA→.
Решение
Изобразим геометрическую фигуру, согласно условиям задачи:
Источник: shkolkovo.net
Заметим, что:
AB→+BC→=AC→,AC→+CD→=AD→
В таком случае, можно записать, что:
AB→+BC→+CD→+DA→=AC→+CD→+DA→=AD→+DA→=AD→-AD→=0→.
Длина нулевого вектора, согласно определению, имеет нулевое значение. Исходя из альтернативного понятия, вектор представляет собой перемещение. В таком случае, AB→+BC→ обозначает перемещение из A в B, а далее из B в C. В результате получается перемещение из A в C. В итоге:
AB→+BC→+CD→+DA→=0→
Вывод сделан на основании перемещения из точки А в точку А. Вектор обладает длиной, равной нулю и представляет собой 0→.
Ответ: 0.
Задача 6На рисунке изображен параллелограмм ABCD.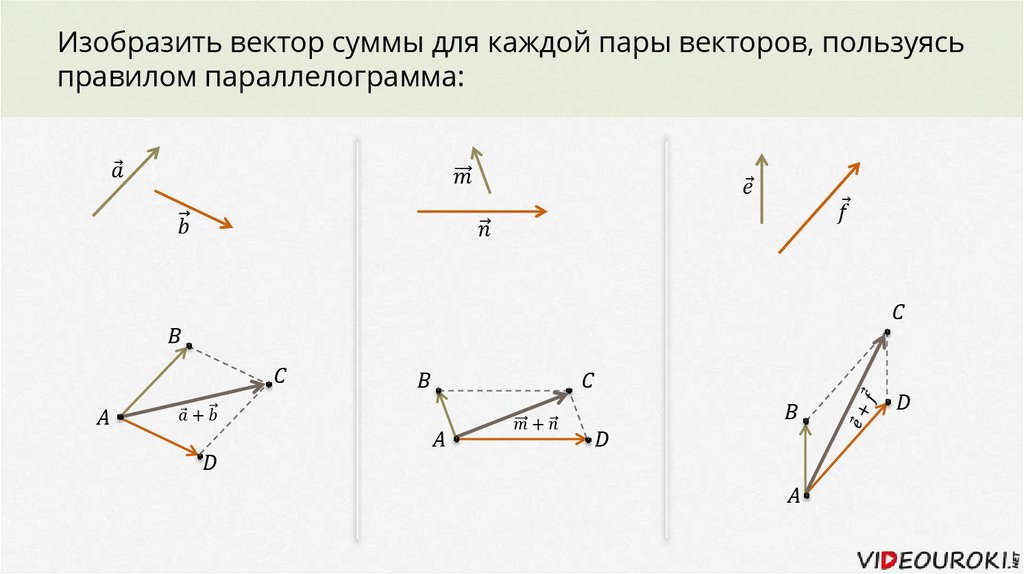 Диагонали данной фигуры, обозначенные, как AC и BD, имеют общую точку пересечения O.
Диагонали данной фигуры, обозначенные, как AC и BD, имеют общую точку пересечения O.
Источник: shkolkovo.net
Предположим, что:
AB→=a→,AD→=b→
В таком случае:
OA→=x·a→+y·b→
Здесь x и y являются какими-то числами. Требуется определить число, которое равно:
x + y.
Решение
OA→=12CA→=12(CB→+BA→)=12(DA→+BA→)=12(-b→-a→)=-12a→-12b→⇒x=-12,y=-12⇒x+y=-1.
Ответ: -1.
Задача 7На рисунке изображен некий параллелограмм ABCD. Точки K и L расположены на сторонах BC и CD соответственно. При этом выполняется следующее соотношение:
BK:KC = 3:1
Точка L расположена на середине стороны CD.
Источник: shkolkovo.net
Предположим, что:
AB→=a→,AD→=b→
В таком случае:
KL→=x·a→+y·b→
Здесь х и y являются какими-то числами. Требуется вычислить такое число, которое равно:
x + y.
Решение
KL→=KC→+CL→=14BC→+12CD→=14AD→+12BA→=14b→-12a→⇒x=-12,y=14⇒x+y=-0,25.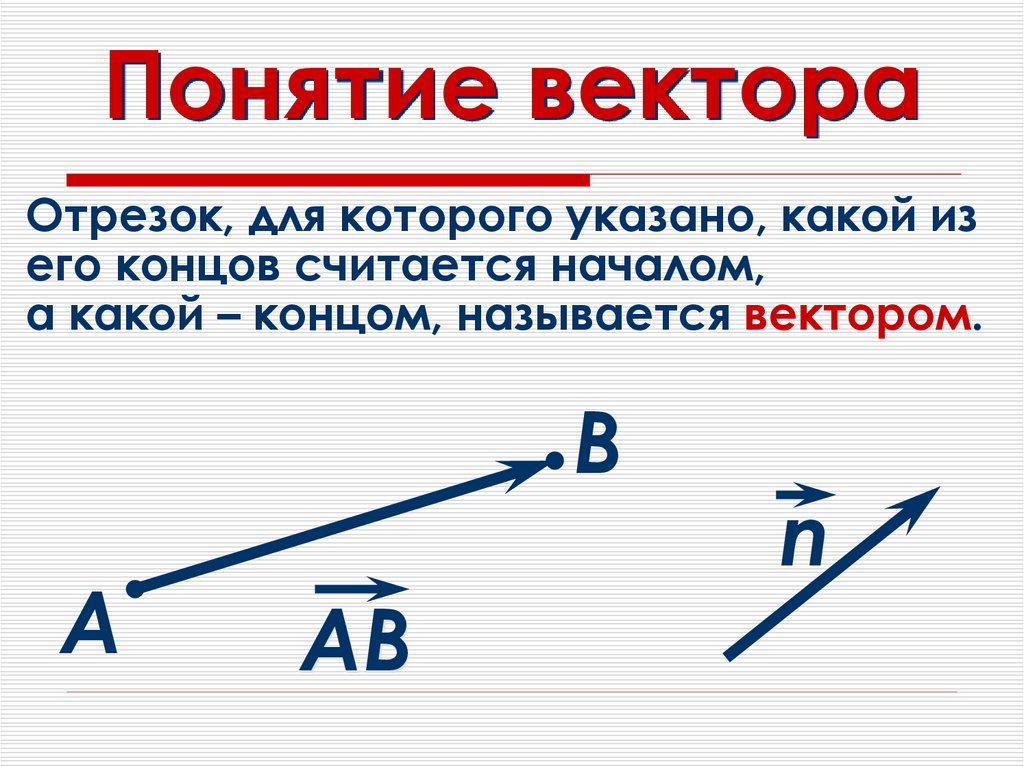
Ответ: -0,25.
Задача 8На рисунке изображен некий параллелограмм ABCD. Точки M и N расположены на сторонах фигуры, обозначенных, как AD и BC соответственно. При этом выполняется следующее условие:
AM:MD = 2:3
BN:NC = 3:1.
Источник: shkolkovo.net
Предположим, что:
AB→=a→,AD→=b→.
В таком случае:
MN→=x·a→+y·b→
Здесь x и y являются какими-то числами. Требуется определить число, которое равно:
x·y.
Решение
MN→=MA→+AB→+BN→=25DA→+AB→+34BC→=-25AD→+AB→+34BC→=-25b→+a→+34b→=a→+720b→⇒x=1,y=720⇒x·y=0,35.
Ответ: 0,35.
Задача 9На рисунке изображен некий параллелограмм ABCD. Точка P расположена на диагонали BD, точка Q принадлежит стороне фигуры CD. При этом выполняется следующее условие:
BP:PD = 4:1
CQ:QD = 1:9.
Источник: shkolkovo.net
Предположим, что:
AB→=a→,AD→=b→
В таком случае:
PQ→=x·a→+y·b→.
Здесь х и y являются какими-то числами. Необходимо вычислить значение числа, которое равно:
Необходимо вычислить значение числа, которое равно:
x·y.
Решение
Ответ: 0,14.
Задача 10На рисунке изображена геометрическая фигура в виде правильного шестиугольника ABCDEF.
Источник: shkolkovo.net
Предположим, что:
AB→=a→,AF→=b→
В таком случае:
BC→=x·a→+y·b→
Здесь x и y являются какими-то числами. Требуется определить число, которое равно:
x + y.
Решение
Согласно условию задания:
Источник: shkolkovo.net
Заметим пересечение отрезков AD, BE и CF в точке O. Данная точка делит рассматриваемые отрезки на две равные части. В данном случае:
BC∥AD
ABCO представляет собой параллелограмм
AF∥BE
ABOF является параллелограммом.
В результате:
BC→=AO→=AB→+BO→=AB→+AF→=a→+b→⇒x=1,y=1⇒x+y=2.
Ответ: 2.
4.3: Геометрический смысл сложения векторов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14519
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9{n}\) — это упорядоченный список чисел.
 {3}\). Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.
{3}\). Каждый из них можно изобразить геометрически, поместив хвост каждого вектора в \(0\) и его точку в \(\left( u_{1}, u_{2}, u_{3}\right)\) и \ (\left(v_{1}, v_{2}, v_{3}\right)\) соответственно. Предположим, мы сдвинем вектор \(\vec{v}\) так, чтобы его хвост оказался в точке \(\vec{u}\). Мы знаем, что это не меняет вектор \(\vec{v}\). Теперь нарисуйте новый вектор от хвоста \(\vec{u}\) до точки \(\vec{v}\). Этот вектор равен \(\vec{u}+\vec{v}\). 9n\) для любого \(n\) дается в следующем определении.Определение \(\PageIndex{1}\): геометрия сложения векторов
Пусть \(\vec{u}\) и \(\vec{v}\) — два вектора. Сдвиньте \(\vec{v}\) так, чтобы хвост \(\vec{v}\) оказался на точке \(\vec{u}\). Затем нарисуйте стрелку, которая идет от хвоста \(\vec{u}\) к точке \(\vec{v}\). Эта стрелка представляет собой вектор \(\vec{u}+\vec{v}\).
Это определение проиллюстрировано на следующем рисунке, на котором \(\vec{u}+\vec{v}\) показан для особого случая \(n=3\) .
Рисунок \(\PageIndex{2}\)
Обратите внимание на параллелограмм, созданный \(\vec{u}\) и \(\vec{v}\) на приведенной выше диаграмме. Тогда \(\vec{u} + \vec{v}\) — направленная диагональ параллелограмма, определяемая двумя векторами \(\vec{u}\) и \(\vec{v}\).
Если у вас есть вектор \(\vec{v}\), его аддитивным обратным \(-\vec{v}\) будет вектор, имеющий ту же величину, что и \(\vec{v}\), но противоположное направление. Когда кто-то пишет \(\vec{u}-\vec{v,}\), это означает \(\vec{u} + \left(-\vec{v}\right)\), как и в случае с действительными числами. Следующий пример иллюстрирует эти определения и соглашения.
Пример \(\PageIndex{1}\): графическое сложение векторов
Рассмотрим следующее изображение векторов \(\vec{u}\) и \(\vec{v}\).
Рисунок \(\PageIndex{3}\)Эскиз рисунка \(\vec{u}+\vec{v},\vec{u}-\vec{v}.\)
Решение
Мы Сначала нарисуйте \(\vec{u}+\vec{v}.\) Начните с рисования \(\vec{u}\), а затем в точке \(\vec{u}\) поместите хвост из \(\vec{v}\), как показано.
Рисунок \(\PageIndex{4}\) Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).Далее рассмотрим \(\vec{u}-\vec{v}.\) Это означает \(\vec{u}+\left( -\vec{v} \ вправо). Вот картинка.
Эта страница под названием 4.3: Геометрическое значение сложения векторов распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) через исходный контент это было отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- source@https://lyryx.

- сложение векторов
- source@https://lyryx.
Результирующий вектор – объяснение и примеры
В векторной геометрии результирующий вектор определяется как:
«Результирующий вектор представляет собой комбинацию или, проще говоря, может быть определен как сумма двух или более векторов, которые имеют свою собственную величину и направление».
В этом разделе мы рассмотрим следующие понятия:
- Что такое результирующий вектор?
- Как найти результирующий вектор?
- Как найти равнодействующую более чем трех векторов?
- Как нарисовать результирующий вектор?
- Какова формула и метод вычисления результирующего вектора?
- Примеры
- Практические вопросы.
Что такое результирующий вектор?Результирующий вектор — это вектор, дающий совокупный эффект всех векторов.
 Когда мы добавляем два или более векторов, результатом является результирующий вектор.
Когда мы добавляем два или более векторов, результатом является результирующий вектор. Давайте рассмотрим эту концепцию на простом практическом примере. Предположим, что имеется балка с двумя лежащими на ней ящиками, как показано на рисунке ниже:
Сможете ли вы рассчитать вес балки и вес двух ящиков? Да! Вы можете, так как вы будете знакомы с концепцией результирующего вектора.
В этом случае результирующий вектор будет суммой сил, действующих на два ящика, т. е. веса ящиков, который будет равен и противоположен весу балки. В этом случае результирующий вектор будет суммой двух сил, поскольку обе они параллельны и направлены в одном направлении.
Предположим, что на плоскости есть три вектора: вектор A, B и C. Результирующее R можно вычислить, сложив все три вектора. Результирующее R можно точно определить, нарисовав правильно масштабированную и точную диаграмму сложения векторов, показанную на рисунке ниже:
A+B+C = R
помощь примера.

Пример 1
Вычислите равнодействующий вектор трех параллельных сил, направленных вверх. ОА = 5Н, ОВ = 10Н и ОС = 15Н.
Solution
As we know that the resultant vector is given as:
R = OA + OB + OC
R = 5 + 10 + 15
R = 30N
Пример 2
Найти результирующий вектор данных векторов OA = (3,4) и ОБ = (5,7).
Решение
Добавление компонентов x для нахождения Rx и компонентов y для расчета RY.
RX=3+5
RX =8
Ry=4+7
Ry =11
Таким образом, результирующий вектор равен R=(8,11)
Как найти результирующие 9014 вектораВекторы можно добавлять геометрически, рисуя их с использованием общего масштаба в соответствии с соглашением «голова к хвосту», которое определяется как
» Соедините хвост первого вектора с началом второго вектора, что даст другой вектор, чья голова соединена с началом второго вектора и хвостом первого вектора.
 ..»
..» …это называется результирующим вектором.
Шаги для нахождения результирующего вектора с использованием правила «голова к хвосту»Ниже приведены шаги, которые необходимо выполнить, чтобы сложить два вектора и найти результирующий вектор:
- Нарисуйте первый вектор в соответствии с выбранным масштабом в заданном направлении.
- Теперь соедините хвост второго вектора с головой первого вектора, нарисованного в заданном масштабе и в заданном направлении.
- Чтобы нарисовать результирующий вектор, соедините хвост первого вектора с головой второго вектора и поместите наконечник стрелки.
- Для определения величины измерьте длину равнодействующей R, и для определения направления измерьте угол равнодействующей с осью x.
Пример 3
Рассмотрим корабль, плывущий под углом 45° к северо-востоку. Затем он меняет курс на 165° к северу. Нарисуйте полученный вектор.
Решение
Результирующий вектор из более чем двух векторовПравила нахождения результирующего вектора или сложения более двух векторов можно распространить на любое количество векторов.

Р = А + В + С +………………………….
Предположим, что имеется три вектора A, B, и C , как показано на рисунках ниже. Чтобы сложить эти векторы, нарисуйте их в соответствии с правилом «голова к хвосту» таким образом, чтобы голова одного вектора совпадала с другим вектором. Таким образом, результирующий вектор задается следующим образом:
R = A + B + C
Примечание: Сложение векторов коммутативно по своей природе; сумма не зависит от порядка сложения.
R = A + B + C=C + B + C
Calculating Resultant Vector Using Rectangular ComponentsFinding a resultant vector using components of a vector известен как аналитический метод; этот метод является скорее математическим, чем геометрическим, и может считаться более точным и точным, чем геометрический метод, т. е. настройка по правилу «голова к хвосту».

Предположим, что имеются два вектора A и B, , образующие углы θA и θB соответственно с положительной осью x. Эти векторы будут разложены на их компоненты. Они будут использоваться для вычисления результирующих компонентов x и y результирующего вектора R, , который будет суммой компонентов x и y двух векторов по отдельности.
R = A + B
R X = A X + B X eq 1
R Y = A Y + B Y eq 2
Since, by rectangular components
R = R x + R x Уравнение 3
теперь, установив значения уравнения 1 и уравнения 2 в уравнении 3
R = (A R = (A X + B X ) + (A Y + B Y )
By rectangular component, the magnitude of the resultant vector is given as
|R | = √ ((Rx )2+( Ry)2)
|R| = √ ((Ax + BX)2+(Ay + BY)2)
По прямоугольным компонентам направление результирующего вектора определяется как:
θ = tan-1 (RY / Rx)
Тот же метод будет применимо для любого количества векторов A, B, C, D …… , чтобы узнать результирующий вектор R.

R = A + B + C + …… C + …… 7 7 7 7 7 9. . = A X + B X + C X + …..
R Y = A Y + B Y + C Y + ……
R = R x + R x
θ = TAN-1 (RY / RX)
Нахождение на основе вектора с использованием параллельного методаДольм 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037 70037. «Если два вектора, действующие одновременно в точке, могут быть представлены смежными сторонами параллелограмма, проведенного из точки, то результирующий вектор представлен диагональю параллелограмма, проходящей через эту точку».
Рассмотрим два вектора A и B , действующие в точке и представленные двумя сторонами параллелограмма, как показано на рисунке.

θ — угол между векторами A и B, и R называется результирующим вектором. Тогда, согласно закону параллелограмма сложения векторов, диагональ параллелограмма представляет собой равнодействующую векторов A и B .
Математическая производная наНиже приведен математический вывод:
R=A+B
Теперь разверните S до T и начертите QT перпендикулярно OT.
Из треугольника OTQ,
SQ2 = OT2+TQ2 EQ 1,4
SQ2 = (OS+ST) 2+TQ2
В треугольнике STQ,
COSθ = ST/SQ
SQCOSθ = ST
, COSθ = ST/SQSQCOSθ = ST
,,,,,,,,,,,,.sinθ=TQ/SQ
TQ=SQsinθ
Уравнение 1.4 дает,
|SQ|=√((A+SQsinθ)2+(SQcosθ)2)
Пусть, SQ=OP=D
|SQ||=√((A+Dsinθ)2+(Dcosθ)2)
Решение приведенного выше уравнения дает
|SQ|= √(A2+2ADcosθ+D2)
Итак, |SQ| дает величину результирующего вектора.

Теперь определяем направление результирующего вектора,
tanφ = TQ/SQ
φ = tan-1 (TQ/OT)
tanφ = TQ/ (OS+ST)
tanφ = Dsinθ/A+ Dcosθ
φ = tan –1(Dsinθ/A+Dcosθ)
Давайте лучше разберемся с помощью примера.
Пример 4
Сила в 12 Н составляет угол 45° с положительной осью x, а вторая сила в 24 Н составляет угол 120° с положительной осью x. Вычислите величину результирующей силы.
Solution
By resolving the vector into its rectangular components, we know that
R X = F 1X + F 2X
R Y = F 1Г + F 2Г
|R| = √ ((Rx )2+( Ry)2) eq 1.1
Вычисление значений |RX| и |RY|,
|Rx| = |F1X| + |F2X| Уравнение 1.2
| f1x | = f1cosθ1
| f1x | = 12cos45
|F1X |=8,48N
|F2X |=F2cosθ2
|F2X |=24cos120
|F2x|= -12N
Подставляя значения в уравнение 1.
 2, получаем
2, получаем| = 8,48+(-12)
|Rx| = -3.52N
Теперь найдем y-компоненту результирующего вектора
|RY| = |F1Y| + |F2Y| Уравнение 1.3
| f1y | = f1sinθ1
| F1Y | = 12SIN45
| F1Y | = 8,48N
| F2Y | = F2 SINθ2
| F2Y | = 24SIN120
| F2Y | = 20,78N
PUT THE THE THEA EQ EQ EQ EQ EQ EQ EQ LISES
. |Рай | = 8,48+20,78|Ry | = 29,26Н
Теперь, помещая значения в уравнение 1.1, чтобы вычислить величину результирующего вектора R ,
|R| = √ ((-3,52 )2+( 29,26)2)
|R| = √ (12,4+856,14)
|R| = 29,5 Н
Таким образом, модуль результирующего вектора R равен 29,5 Н.
Пример 5
Две силы величиной 5 Н и 10 Н наклонены под углом 30°. Вычислите величину и направление результирующего вектора, используя закон параллелограмма.
Решение
При наличии двух сил F 1 = 5 Н и F 2 = 10 Н и угла θ=30o.

Используя формулу,
|R|= √(F12+2F1F2cosθ+F22)
|R|= √ ((5)2+2(5)(10) cos30+(10)2)
|R| =14,54N
φ = tan –1(F2sinθ/F1+F2cosθ)
φ = tan-1 (10sin30/(5+10cos30))
φ = 20,1o
Итак, величина результирующего вектора R — это 14,54 с. ш., а направление — 20,1°.
Практические задачи- Узнайте результирующий вектор следующего векторного параллеля друг другу, указывая в том же направлении
- OA = 12N, OB = 24N ( ANS: 36N)1031033 = 24n ( ANS: 36N)
- 3 = 24N ( ANS: 36N)
- 3. =7N, OB =10N ( Ans: 17N )
- 3 = 24N ( ANS: 36N)
- PQ = (3,8) RQ = (2,4) ( Ans: (5, 12)
- Сила 15 Н образует угол 70° с положительной осью X, а вторая сила 25 Н образует угол 220° с положительной осью X. Рассчитайте величину равнодействующей силы. (
- Вычислите направление результирующего вектора, определенного в задаче № 3.



 Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
Тогда \(\vec{u}+\vec{v}\) — это вектор, полученный в результате рисования вектора от хвоста \(\vec{u}\) до кончика \(\vec{v}\ ).
 Когда мы добавляем два или более векторов, результатом является результирующий вектор.
Когда мы добавляем два или более векторов, результатом является результирующий вектор.  ..»
..» 



 2, получаем
2, получаем
