Сумма ⭐ двух векторов: определение, правило, координаты
Основные понятия
Определение 1Направленный отрезок, то есть отрезок, который имеет длину и определенное направление, носит название вектора.
Обозначается буквенным символом со стрелкой над ним:
Определение 2
Сонаправленные векторы — это векторы, направления которых совпадают (одинаковые по направлению).
Определение 3Противоположно направленные векторы — это векторы, которые направлены в разные стороны.
С векторами можно производить такие операции, как:
- сложение;
- вычитание;
- умножение на число.
Для начала, рассмотрим подробно сложение.
Сложение (сумма) векторов «a + b» — это операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
c=a+b
Вычитание (разность) векторов «a — b» — это операция вычисления вектора c, все элементы которого равны попарной разности соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен:
c=a-b
Сложение векторов может осуществляться по трем правилам:
- Правило параллелограмма.
 Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
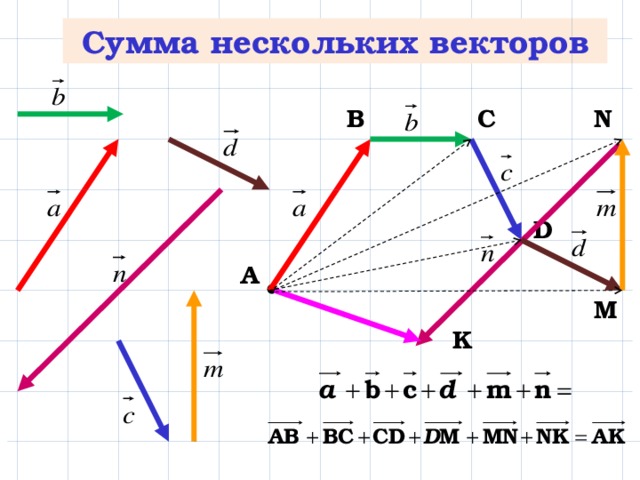
Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов. - Правило многоугольника. Из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее. Когда все векторы отложены, соединим начальную точку с концом последнего вектора и получим сумму нескольких векторов.
- Правило треугольника.
Сумма сонаправленных и противоположно направленных векторов, правило треугольника
Правило треугольника заключается в следующем: для того чтобы сложить два сонаправленных вектора, необходимо из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго. Конечный вектор и будет суммой двух векторов.
Чертеж поможет наглядно объяснить правило:
a+b=AB+BC=AC
AC — сумма векторов.
Разность векторов a и b является суммой векторов a и -b.
Как вычислить координаты суммы двух векторов, пояснение на примерах
Кроме геометрического способа сложения (вычитания) векторов (правила треугольника, параллелограмма, многоугольника), существует способ сложения координат векторов.
Для того чтобы найти координаты суммы двух векторов, нужно сложить их соответствующие координаты по следующей формуле:
Пример 1Найти сумму векторов a(7;5) и b(3;8)
Решение: a+b=(7+3;5+8)=(10;13)
Пример 2Найти сумму координат векторов a(-7;2), b(-3;6), c(6;-5)
Решение: a+b+c=(-7-3+6;2+6-5)=(-4;3)
Примеры решения задач
Пример 3Найти сумму векторов a(1;2), b(7;9)
Решение:a+b=(1+7;2+9)=(8;11)
Пример 4Найти разность координат векторов a(4;-6), b(5;-1)
Решение: a-b=(4-5;-6-(-1))=(-1;-5)
Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. 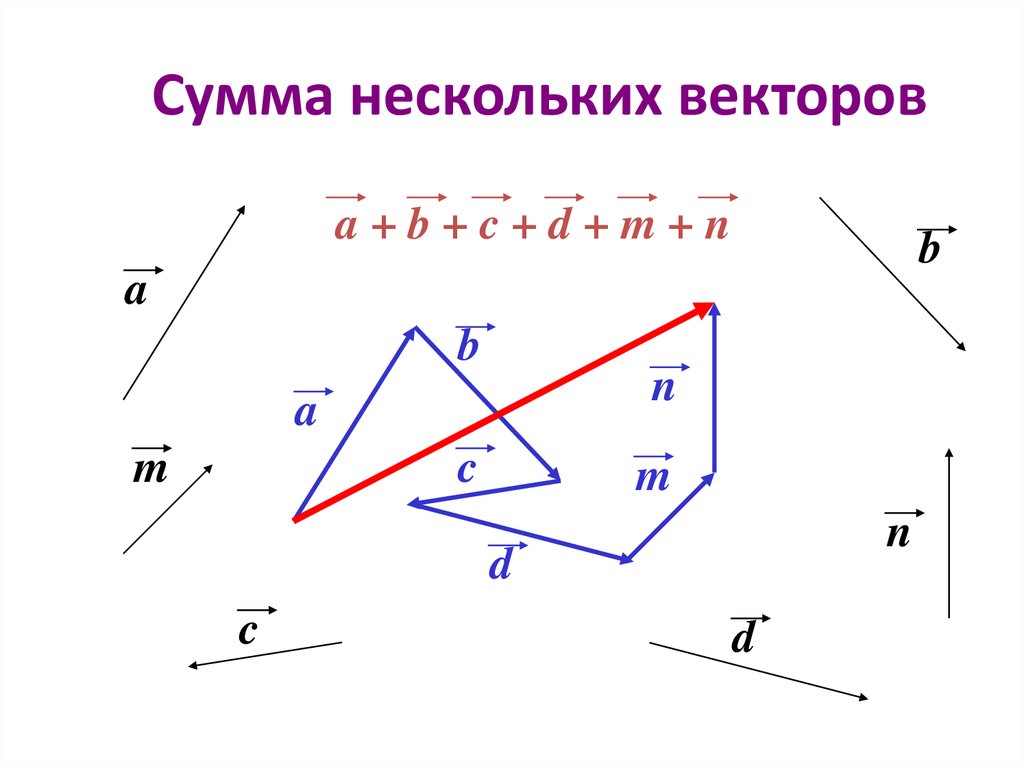 ВЕКТОРНАЯ АЛГЕБРА ВЕКТОРНАЯ АЛГЕБРА2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. 2. Свойства составляющих вектора. 3.  Проекция вектора на ось. Проекция вектора на ось.4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения.  5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. 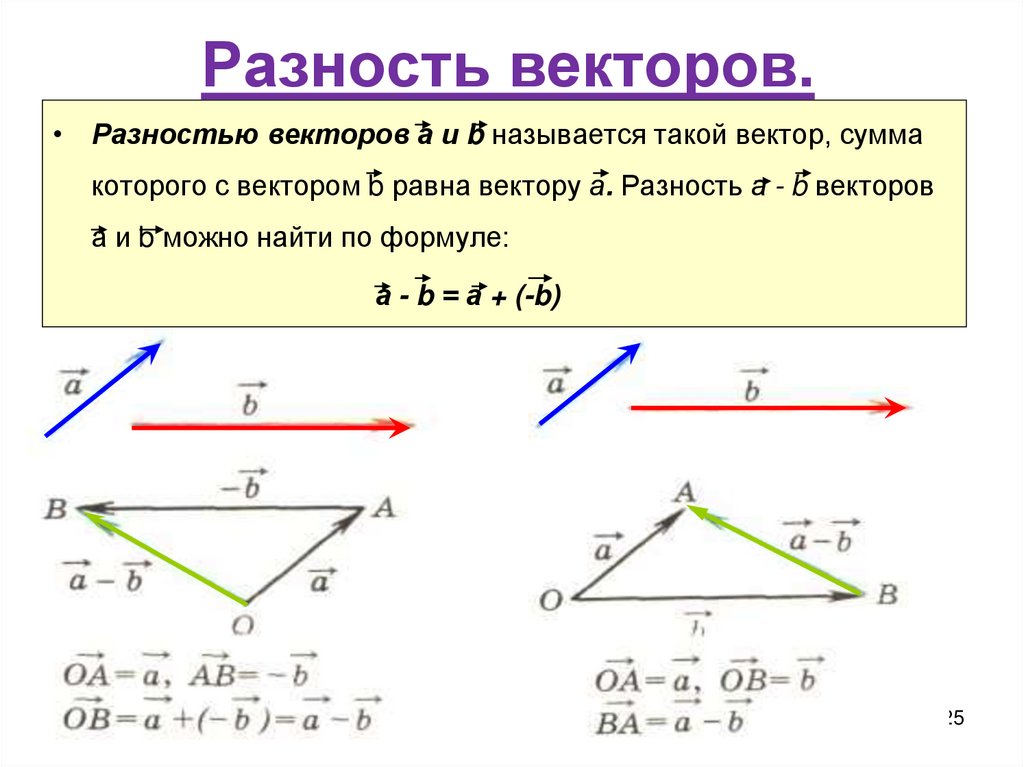 § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 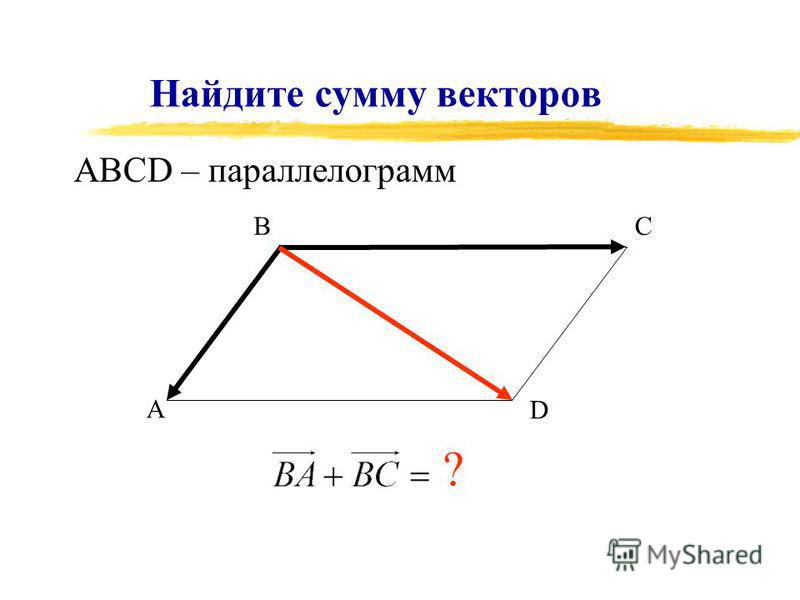 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов. |
Нахождение суммы двух векторов — Криста Кинг Математика
Что значит найти сумму двух векторов?

Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Другими словами, сочетание серого и синего — фиолетовый:
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов. В приведенном выше примере серый + синий = фиолетовый. Мы также можем вычитать векторы. Если вычитается вектор, мы движемся точно в направлении, противоположном исходному вектору. В приведенном ниже примере серый — синий = фиолетовый. Сплошной синий вектор — исходный вектор, но поскольку мы вычитаем, мы движемся в противоположном направлении.
Когда нам заданы числовые значения для векторов, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, и суммируем ???y???? ?-координаты, чтобы получить новую ???y???-координату.
Как найти сумму векторов, в том числе, когда векторы заданы в разных формах
Пройти курс
Хотите узнать больше о Calculus 3? У меня есть пошаговый курс для этого.
 🙂
🙂Еще два примера суммирования векторов
Пример
Найти сумму векторов.
???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???
???u=2i-3j??? и ???v=6i+2j???
Для ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???:
Суммировать векторы ???u=\langle2,1\rangle??? и ???v=\langle-1,5\rangle???, мы просто суммируем ???x???-координаты, чтобы получить новую ???x???-координату, а затем делаем то же самое для ???y???-координат. Мы можем назвать наш новый вектор ???w???.
???w=\langle2+(-1),1+5\rangle???
???w=\langle1,6\rangle???
По сути, объединение двух векторов дает нам тот же результат, что и сложение векторов.
Для ???u=2i-3j??? и ???v=6i+2j???:
Суммировать векторы ???u=2i-3j??? и ???v=6i+2j???, коэффициенты возьмем от нашего ???i??? и ???j??? слагаемых, и складываем их вместе, чтобы найти коэффициенты при этих слагаемых для вектора ???w???.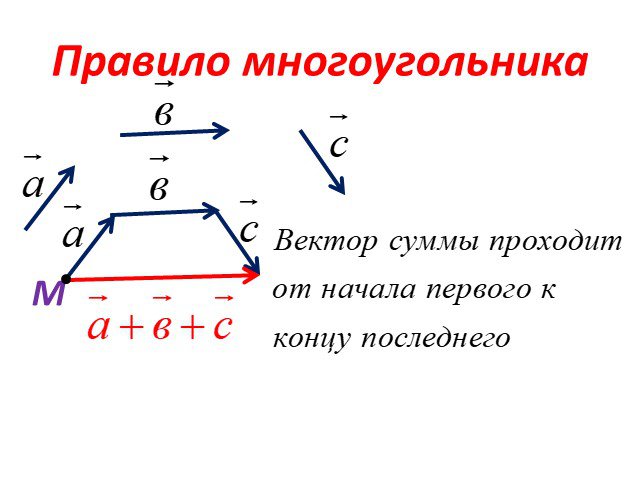
???w=(2+6)i+(-3+2)j???
???w=8i-j???
Мы могли бы также написать вектор ???w=\langle8,-1\rangle???.
Получить доступ к полному курсу Calculus 3
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление iii, исчисление 3, исчисление iii, вычисление 3, векторное исчисление, сумма векторов, добавление векторов, добавление векторов, добавление векторов, вычитание векторов, вычитание векторов
Сложение векторов — Вычитание векторов
Сложение векторов не так просто, как сложение скаляров. Векторы имеют как величину, так и направление, и нельзя просто сложить два вектора, чтобы получить их сумму. Чтобы лучше понять это, давайте рассмотрим пример автомобиля, проехавшего 10 миль на север и 10 миль на юг. Здесь общее пройденное расстояние равно 20 милям, а перемещение равно нулю.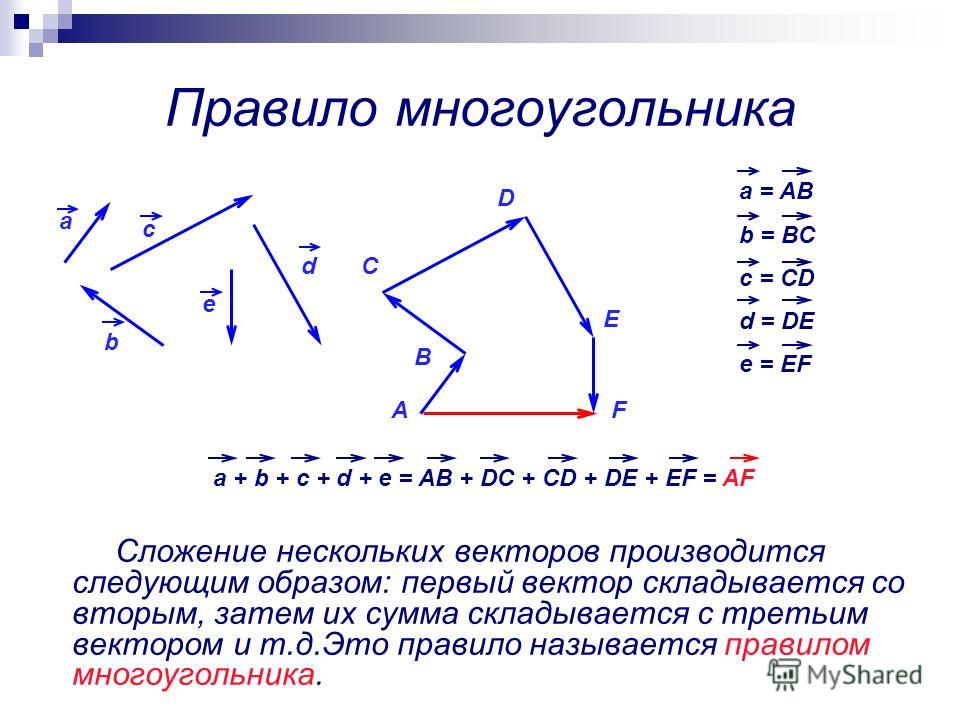 Смещения на север и юг являются векторными величинами, и противоположные направления приводят к тому, что отдельные смещения компенсируют друг друга. В этой статье давайте рассмотрим способы выполнения сложения и вычитания векторов.
Смещения на север и юг являются векторными величинами, и противоположные направления приводят к тому, что отдельные смещения компенсируют друг друга. В этой статье давайте рассмотрим способы выполнения сложения и вычитания векторов.
Содержание
|
Сложение векторов: закон векторов треугольников, параллелограммов и многоугольников
Как уже говорилось, векторы нельзя складывать алгебраически. Ниже приведены несколько моментов, которые следует помнить при добавлении векторов:
Треугольный закон сложения векторов
Сложение векторов выполняется по закону треугольника. Давайте посмотрим, что такое треугольный закон сложения векторов:
Давайте посмотрим, что такое треугольный закон сложения векторов:
Предположим, что есть два вектора, a и b.
Нарисуйте линию AB, представляющую вектор a, где A — хвост, а B — голова. Нарисуйте еще одну линию BC, представляющую вектор b, где B — хвост, а C — голова. Теперь соедините линию AC с A в качестве хвоста и C в качестве головы. Линия AC представляет результирующую сумму векторов a и b. 92~+~2ab~cos~\theta}\end{массив} \)
Где,
a = величина вектора a
b = величина вектора b
θ = угол между векторами a и b
Пусть равнодействующая образует угол Φ с вектором a, тогда:
\(\begin{array}{l}tan\phi= \frac{b~sin~\theta}{a~+~b~cos~\theta}\end{array} \)
Давайте разберемся с этим на примере. Предположим, что два вектора имеют одинаковую величину A и составляют угол θ друг с другом. Теперь, чтобы найти величину и направление равнодействующей, мы будем использовать формулы, упомянутые выше. 92~+~2AA~cos~\theta}=2~A~cos~\frac{θ}{2}\end{массив} \)
Допустим, результирующий вектор составляет угол Ɵ с первым вектором.
\(\begin{array}{l}tan~\phi = \frac{A~sin~θ}{A~+~A~cos~θ} = tan~\frac{θ}{2}\end{ массив} \)
или
\(\begin{array}{l}\theta = \frac{\theta}{2}\end{array} \)
Подробнее: Треугольный закон сложения векторов
Закон параллелограмма сложения векторов
Сложение векторов также можно понимать по закону параллелограмма. Закон гласит: «Если два вектора, действующие одновременно в точке, представлены по величине и направлению двумя сторонами параллелограмма, проведенного из точки, то их равнодействующая по величине и направлению определяется диагональю параллелограмма, проходящей через эту точку. ” 9{-1}[\frac{Q\sin\theta}{P+Q\cos\theta}]\end{массив} \)
Многоугольный закон вектора
Согласно закону сложения векторов многоугольников, если число векторов можно представить по величине и направлению сторонами многоугольника, взятыми в том же порядке, то их равнодействующая представлена величиной и направлением таким образом, что замыкающая сторона многоугольника многоугольник берется в противоположном направлении.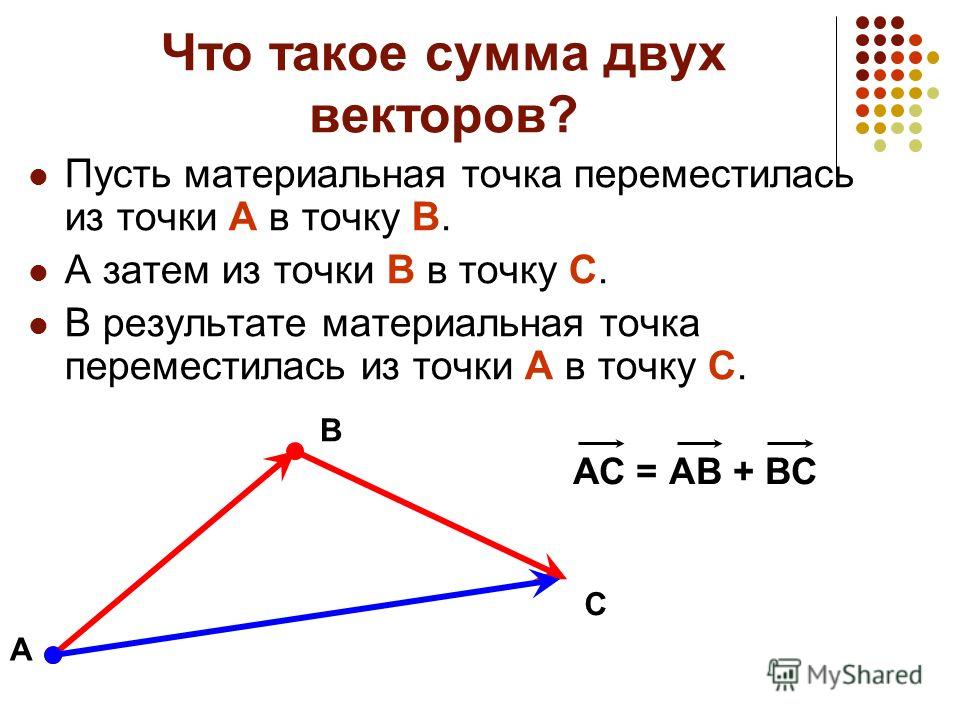
Пусть вектор A, вектор B, вектор C и вектор D являются четырьмя векторами, для которых необходимо получить результирующую.
Рассмотрим треугольник OKL, в котором векторы A и B представлены сторонами OK, KL и взяты в одном порядке. Следовательно, из треугольного закона сложения векторов мы знаем, что замыкающая сторона OL рассматривается в противоположном направлении, так что она представляет результирующие вектора OR и KL.
Следовательно,
\(\begin{array}{l}\vec{OK} + \vec{KL}=\vec{OL}.. eq.1\end{array} \)
Из треугольного закона сложения векторов мы знаем, что треугольник OLM может быть выражен как вектор OM, являющийся результатом векторов OL и LM.
То есть
\(\begin{array}{l}\vec{OL}+\vec{LM}=\vec{OM}\end{array} \)
Из уравнения 1,
\(\begin{array}{l}\vec{OK}+\vec{KL}+\vec{LM}=\vec{OM}.. eq.2\end{array} \)
Опять же, применяя треугольный закон сложения векторов к треугольнику OMN,
\(\begin{массив}{l}\vec{OM}+\vec{MN}+\vec{ON}\end{массив} \)
Из уравнения 2 получаем
\(\begin{array}{l}\vec{OK}+\vec{KL}\end{массив} \)
\(\begin{array}{l}\vec{LM}+\vec{MN}=\vec{ON}. . eq.3\end{array} \)
. eq.3\end{array} \)
Следовательно,
\(\begin{array}{l}\vec{OK}=\vec{A}\end{массив} \)
\(\begin{array}{l}\vec{KL}, \vec{B}\end{массив} \)
\(\begin{массив}{l}\vec{LM}, \vec{C}\end{массив} \)
\(\begin{array}{l}\vec{MN}, \vec{D}\end{массив} \)
Учитывая, что вектор ON=вектор R, уравнение принимает вид
\(\begin{array}{l}\vec{A}+\vec{B}+\vec{C}+\vec{D}=\vec{R}\end{array} \)
Нажмите на видео ниже, чтобы понять применение полигонального закона сложения векторов 92~-~2ab~cos~\theta}\end{массив} \)
вектор (-b) есть не что иное, как вектор b в обратном направлении.
Статьи по теме:
Часто задаваемые вопросы – Часто задаваемые вопросы
Какова максимальная и минимальная сумма двух векторов?
Максимальная сумма двух векторов получается, когда два вектора направлены в одном направлении. Минимальная сумма получается, когда два вектора направлены в противоположные стороны.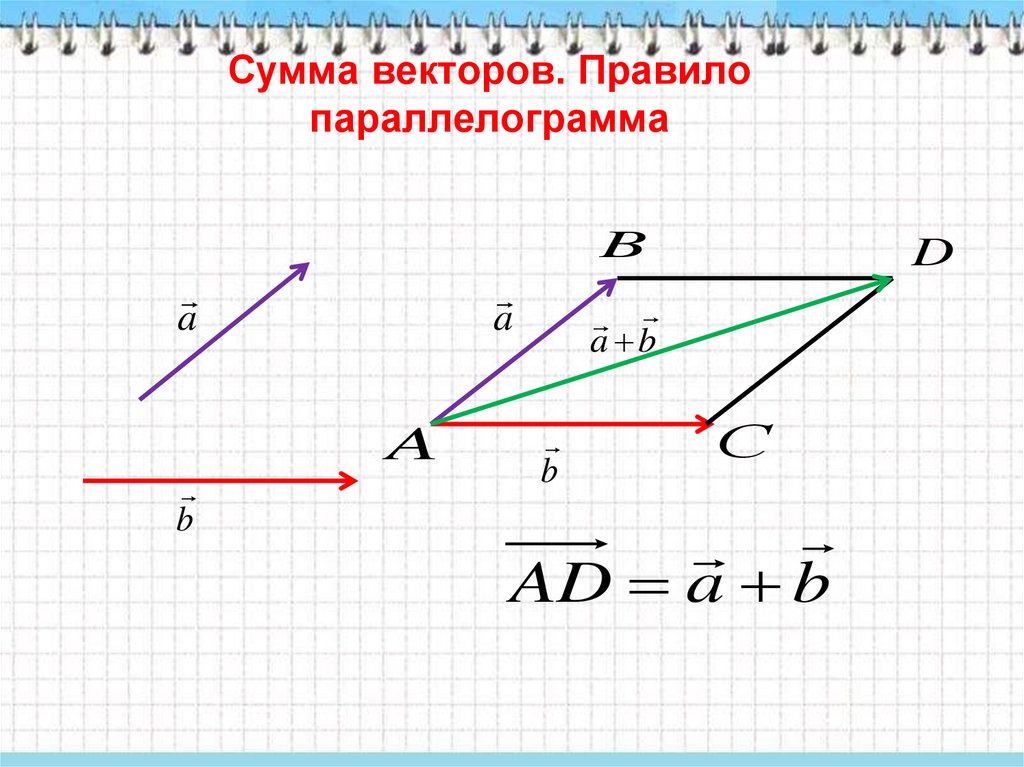


 Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.
Из произвольной точки необходимо отложить два данных вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, будет суммой заданных векторов.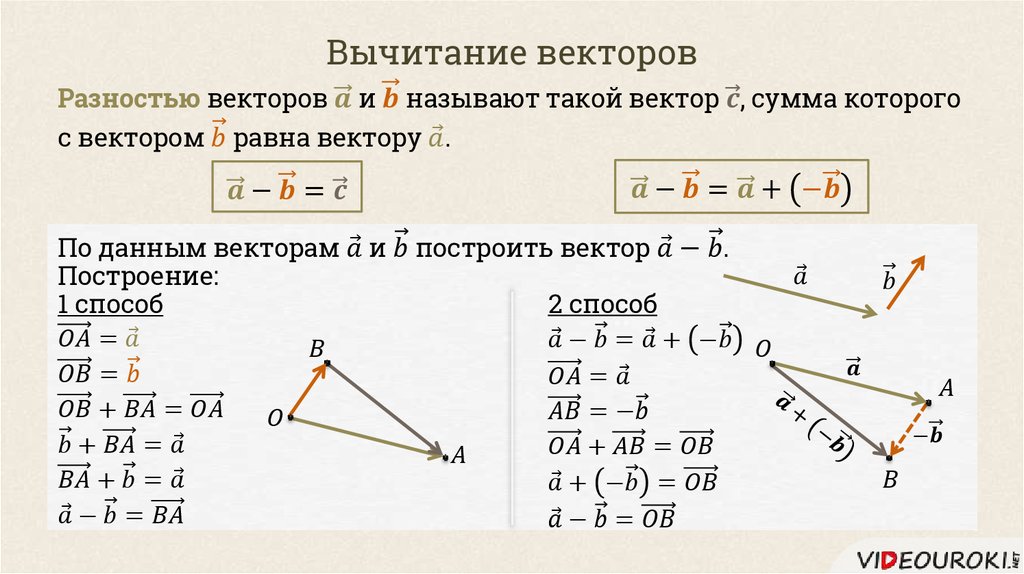 Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с.
Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с.