Введение понятия «средняя плотность» при изучении темы «Плотность» в 7-м классе

В курсе физики 7 класса мы при прохождении темы “ Механическое движение” вводим понятие средней скорости, и при определенном полученном навыке решения задач большинство учащихся с расчетами средней скорости справляются. (Только жаль, что часто при решении ребята сталкиваются с громоздким математическим решением, а они пока к этому не готовы)

Через несколько уроков мы приступаем к введению понятий массы и плотности.

На начальном уровне все основное по данному вопросу в любом учебнике-7 ,в принципе, сказано, но почему мы не оговариваем сразу такой важный закон, как закон сохранения массы? Он нам пригодится для введения понятия средней плотности!

Если растворить сахар в воде, то масса раствора строго равна массе сахара и воды.

При любом дроблении и при растворении масса остается одной и той же.

Формулировка закона: При любых изменениях изолированной системы тел или частиц масса этой системы остается неизменной и равна сумме масс составляющих ее частей.

Так как понятие изолированной системы мы пока не вводим, то можно закон сформулировать проще;

Масса тел до взаимодействия равна массе тел после взаимодействия,т. е. остается неизменной

Математическое выражение закона: m₁ + m₂ + … + m_N =m ^/₁ + m ^/₂ + … + m ^/_N

Границы и условия применимости закона можно пока не вводить

Приоритет в открытии закона сохранения массы вещества принадлежит российскому ученому Михаилу Васильевичу Ломоносову и французу Антуану Лавуазье (Antoine Laurent Lavoisier).

Закон был открыт и сформулирован ими независимо друг от друга на основе анализа многочисленных опытных данных.

В 1756 г. М.В.Ломоносов самостоятельно сформулировал философский принцип сохранения материи и движения: “…все перемены, в натуре случающиеся, такого суть состояния, что сколько чего у одного тела отнимется, столько присовокупится к другому. ..”.

Он считал этот закон одним из основных законов природы!

Примеры проявления закона в природе

1. Явления диффузии
2. Процессы растворения веществ.
3. Дробление и разрушение тел.
4. Глобальный круговорот вещества в биосфере, перенос твердых, жидких и газообразных тел при различных давлениях и температурах, в течение веков и тысячелетий происходит в полном соответствии с законом сохранения массы. Эти же самые слова можно сказать об одном из самых грандиозных процессов – круговороте воды на поверхности земного шара.

Пример:

1) Если взять 1 кг манки, 2 кг гречки, 3 кг пшена и все крупы смешать, то получим массу строго 6 кг

m_см = m_манки + m_гречки + m_пшена = 1 кг + 2 кг +3 кг = 6 кг

2) В пассажирский самолет перед началом рейса погрузили 300 кг продуктов. Изменилась ли масса авиалайнера после того, как в полете все продукты были съедены?

Так как заданий на закон сохранения массы в задачниках нет, то можно предложить ребятам дома самим поработать над их составлением. А из лучших работ составить сборник и вклеить в задачник, которым пользуемся на уроке. Я думаю, что многие ребята захотят в этом поучаствовать.

А теперь о понятии плотность.

При введении этой величины в учебниках почему-то не оговаривается, что речь идет о сплошных телах! И хотя в олимпиадных задачах и в некоторых сборниках предлагаются задачи на нахождение средней плотности (или задачи, связанные с этой величиной) на уроках мы о ней не говорим. А ведь несколько уроков назад было введено понятие средней скорости, так почему по аналогии не ввести понятие средней плотности?

Истинная плотность – отношение массы к объему в абсолютно плотном состоянии (без пор и пустот)

Средняя плотность – физическая величина, определяемая отношением массы материала ко всему занимаемому им объему, включая поры и пустоты.

Средняя плотность не является величиной постоянной и изменяется в зависимости от пористости материала.

Интересно, что средняя плотность играет очень важное значение для человека. Его плавучесть зависит от средней плотности тканей его тела, плотности воды, вдоха и выдоха. Чем меньше средняя плотность тканей тела, тем лучше его плавучесть. При глубоком вдохе пловец, как правило, обладает положительной плавучестью, при полном выдохе – отрицательной, он тонет. Человек способен изменять свою среднюю плотность, регулируя количество воздуха в легких! При полном вдохе средняя плотность человеческого тела становится меньше плотности воды. При выдохе, когда тело теряет плавучесть, человеку приходится создавать подъемную силу движением рук. Получается, что умение плавать – это умение правильно дышать!

Когда вводится понятие выталкивающей силы, может ребятам будет понятнее, почему такие огромные, тяжелые корабли плавают, если поговорить опять о средней плотности корабля и воды! Или привести такой пример: Плотность стекла, из которого сделана бутылка, равна 2200 кг/ м³; плотность воды – 1000 кг/ м³. Следовательно, стекло пойдет ко дну. Но если стеклянная бутылка, наполненная воздухом, плотно закрыта пробкой, она будет плавать на поверхности воды. Масса стеклянной литровой бутылки примерно равна 0,5 кг; масса воздуха, заключенного в ней, — около 0,001 кг, а средняя плотность закупоренной бутылки с воздухом — 501 кг/ м³ (0,5001 кг / 0,001 м³), т.е. вдвое меньше плотности воды!

На уроке можно решить следующие задачи:

Какова плотность смеси глицерина и спирта, если объем спирта составляет половину объема смеси?

Как изменится ответ, если масса спирта составляет половину массы смеси?

Ответ: (900 кг/ м³)

Сплав золота и серебра массой 400г имеет плотность 1,4 · 10⁴ кг/ м³. Полагая объем сплава равным сумме объемов его составных частей, определите массу золота в сплаве.

Ответ: (0,2 кг)

(Примеры данных задач взяты из сборника “Решение ключевых задач по физике для основной школы. 7-9 классы. Гейндешптейн Л.Э., Кирик Л.А., Гельфгат И.М, там же представлены их подробные решения)

Использованная литература:

1. Гейндешптейн Л.Э., Кирик Л.А., Гельфгат И.М. “Решение ключевых задач по физике для основной школы. 7-9 классы. – М.: Илекса, 2006.
2. Детская энциклопедия, том 3 , издательство “Просвещение”, 1966
3. С.Е.Каменецкий, В.П.Орехов “Методика решения задач по физике в средней школе” издательство “Просвещение”, 1986
4. Г.С.Ландсберг “Элементарный учебник физики”, том 3, издательство “Физматлит”, 2000

1.3.2. Определение средней плотности

Средняя плотность – это масса единицы объема материала в естест­венном состоянии.

Среднюю плотность материала определяют отношением массы ( m ) материала ко всему занимаемому им объему (V_мат ), включая имеющиеся в них пустоты и поры (V_пор), и рассчитывают по формуле:

, г/см³ или кг/м³. (5)

Средняя плотность находится в обратной зависимости от пористости материала. Среднюю плотность материалов определяют на изделиях или образцах правильной и неправильной формы в состоянии естественной влажности, в воздушно-сухом и сухом состоянии. Образцы правильной геометрической формы в виде куба, параллелепипеда или цилиндра должны иметь размер по наименьшему измерению не менее 50 мм. Образцы неправильной геометрической формы должны иметь массу не менее 300 г каждый. Среднюю плотность пустотелых изделий определяют на целых изделиях без вычета пустот.

Среднюю плотность определяют не менее чем на трех образцах.

1.3.2.1.Определение средней плотности образцов правильной геометрической формы

Размеры образцов определяют металлической линейкой или штангенциркулем, вычисляют объем. Затем взвешиванием определяют массу образцов.

Среднюю плотность материала вычисляют по формуле:

, г/см

3(6)

где m — масса образца, г;

V_мат — объем образца в естественном состоянии, см³ .

Результаты определения средней плотности заносят в табл. 4.

Таблица 4

Определение средней плотности образцов правильной формы

Номер опыта	Масса образца, m, г	Размеры образца, см	Объем образца, V, см3	Средняя плотность, ρ , г/см3
				полученное значение	среднее значение	по справочным данным

1.3.2.2. Определение средней плотности образцов неправильной формы

Опыт осуществляется с помощью гидростатического взвешивания (рис.

4).

Предварительно взвешенный образец покрывают пленкой из парафина. Затем образец охлаждают и взвешивают, сначала на воздухе, затем на гидростатических весах в воде (рис. 4).

Среднюю плотность материала вычисляют по формуле:

, г/см³(7)

где ρ_воды — плотность воды, 1 г/см ³ ;

ρ_пар — плотность парафина, 0,93 г/см ;

m — масса образца, г;

m₁ — масса парафинированного образца на

воздухе, г;

m₂ — масса парафинированного образца

в воде, г;

m₁ — m₂ — потеря массы в воде, равная

массе вытесненной воды, г

Результаты определения средней плотности материала заносят в табл.

5.

Таблица 5

Определение средней плотности образцов неправильной формы

Номер опыта	Масса образца, m, г	Масса парафинированного образца на воздухе, m1, г	Масса парафинированного образца в воде, m2 , г	Средняя плотность, ρ , г/см3
				полученное значение	среднее значение	по справочным данным

Как усреднить плотность

Обновлено 22 декабря 2020 г.

Кевин Бек

​ Плотность ​ в физике — это мера количества чего-то, что существует в данном физическом пространстве (объеме). В большинстве случаев под «плотностью» принято понимать «плотность массы», но как понятие оно просто описывает, насколько тесно что-то находится.

Плотность населения Гонконга, например, чрезвычайно высока, а в Сибири крайне низка. Но в каждом случае «люди» являются предметом анализа.

Для веществ, состоящих из одного элемента в некотором количестве (например, грамм чистого золота или серебра) или однородной смеси элементов (например, литр дистиллированной воды, который включает водород и кислород в известном фиксированном соотношении ), можно предположить, что значимых изменений плотности в образце нет.

Это означает, что если плотность 60-килограммового однородного объекта перед вами равна 12 кг/л, то любая выбранная малая часть объекта должна иметь это значение своей плотности.

Определение плотности

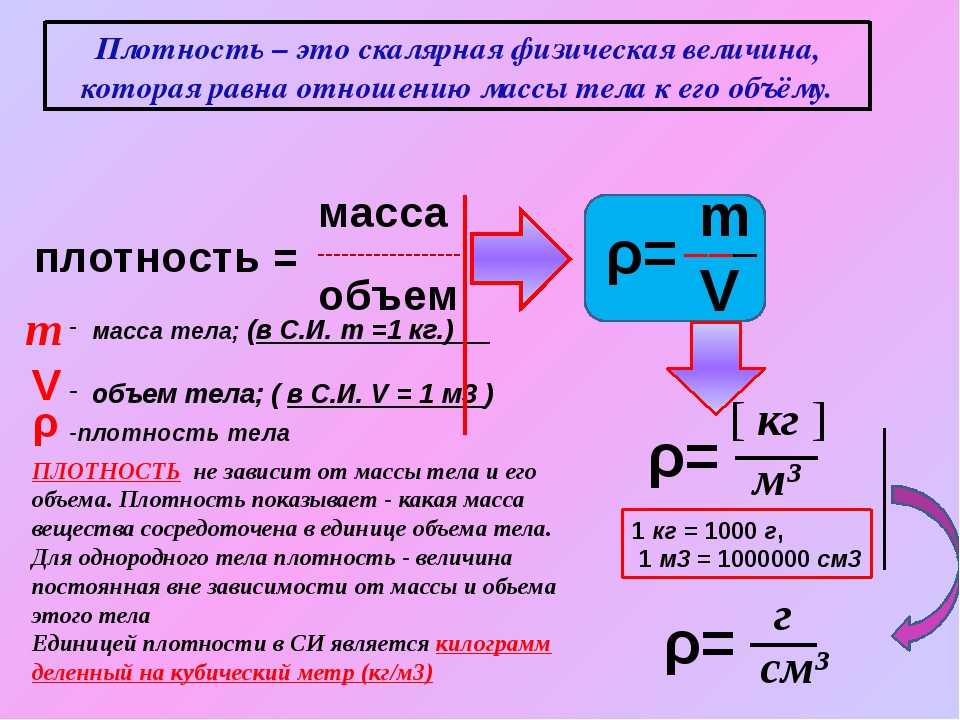
Плотность обозначается греческой буквой ро (ρ) и представляет собой просто массу m , деленную на объем V . Единицами СИ являются кг/м ³ , но г/мл или г/куб.см (1 мл = 1 куб.см) являются более распространенными единицами измерения в лабораторных условиях. Эти единицы фактически были выбраны для определения плотности воды равной 1,0 при комнатной температуре.

• ​ Плотность повседневных материалов: ​ Золото, как и следовало ожидать, имеет очень высокую плотность (19,3 г/куб.см). Хлорид натрия (поваренная соль) составляет 2,16 г/куб.см.

Примеры расчета средней плотности

В зависимости от типа присутствующего вещества или веществ существует несколько способов решения проблемы плотности смеси.

Самый простой случай, когда вам дают набор из N объектов и просят определить среднюю плотность объектов в наборе. Такого рода примеры могут возникать в ситуациях, когда элементы набора относятся к одному и тому же базовому «типу» (например, люди в Англии, деревья в заданном лесу в Монтане, книги в городской библиотеке в Теннесси), но могут очень сильно различаться. в рассматриваемой характеристике (например, вес, возраст, количество страниц).

​ ПРИМЕР: ​ Вам даны три блока неизвестного состава, которые имеют следующие массы и объемы:

• Камень A: 2250 г, 0,75 л
• Камень B: 900 г, 0,50 л
• Камень C : 1850 г, 0,50 л

​ а) Рассчитайте среднее значение плотности камней в наборе. ​

Это делается путем определения плотности каждого камня по отдельности, их сложения и деления на общее количество камней в наборе:

\frac{(2250/0,75) + (900/0,50) + (1650/0,60)}{3} = \frac{(3000 + 1800 + 3700)}{3}=2833\text{ г/л}

​ б) Рассчитайте среднюю плотность комплекса горных пород в целом. ​

В этом случае вы просто делите общую массу на общий объем:

\frac{(2,250 + 900 + 1,850)}{(0,75 +0,50 + 0,50)}=\frac{5,000}{1,75}= 2857\frac{ г/куб.см}

Цифры различаются, потому что породы вносят неодинаковый вклад в эти расчеты.

Формула средней плотности: смесь веществ

​ ПРИМЕР: ​ Вам дан 5-литровый (5000 см3 или мл) кусок материала с другой планеты и сказано, что он состоит из трех сплавленных частей следующих элементов в указанные пропорции по объему:

• Тикстиум (ρ = 15 г/мл): 15%
• Ватериум (ρ = 1 г/мл): 60%
• Тинний (ρ = 0,5 г/мл): 25%

Какова плотность куска в целом?

Здесь вы сначала конвертируете проценты в десятичные дроби и умножаете их на отдельные плотности, чтобы получить среднюю плотность смеси:

(0,15)(15) + (0,60)(1,0) + (0,25)(0,50) = 2,975\text{ г/куб.см}

Химическая лаборатория первокурсников UMass Lowell

 

 

 

Эксперимент

4

 

 

Плотность Определения

 

Обзор

 

Этот эксперимент состоит из трех частей: измерение плотности твердое тело неправильной формы , измеряющее плотность неизвестная жидкая проба и выполнение нескольких измерений плотность вода .

 

 

Этот эксперимент также дает вам возможность попрактиковаться в работе с значимые цифры в измерениях. Для того, чтобы определить плотность материала, необходимо определить массу и объем образца материала. В лаборатории гораздо проще точно определить массу объекта (с помощью весов), чем его заключается в определении объема объекта. Это приводит к некоторой осторожности учет значащих цифр при расчете плотности объекта (масса, деленная на объем).

 

Расчеты:

 

Так как вы делаете несколько определений плотности каждого выборки, можно рассчитать среднее значение для каждого из плотности, среднее отклонение и процентное отклонение. Для обзора расчет средних и процентных отклонений см. в файле справки для эксперимента 1 (или нажмите здесь, чтобы перейти к этому файлу).

Страница отчета 13

Для части C (Плотность дистиллированной воды) обратите внимание, что масса и показания объема должны суммироваться после каждого дополнительного количества из бюретки набирают воду и взвешивают. Например, строка 3b должны представлять общую массу и общий объем после из бюретки извлекается вторая проба (не только увеличенная масса и увеличенный объем после того, как был взят первый образец). Поскольку мы знаем, что плотность воды составляет около 1 г/мл, мы должны увидеть примерно линейная зависимость между массами и объемами.

Плотность твердого тела: стр. 13, часть II A

Предположим, что для твердого образца были записаны следующие данные (см. стр. 13 часть А):

 

 

	Испытание 1	Испытание 2	Испытание 3
Пустой стакан для массы	7,32 г	7,44 г	7,21 г
Стакан для масс + твердый	18,52 г	18,55 г	18,46 г
Объем воды в цилиндре	25,2 мл	24,1 мл	27,3 мл
Объем воды + твердое вещество	30,7 мл	29,2 мл	32,7 мл

 

1.

Объем твердой пробы – расчет Испытание 1

Твердое вещество вызвало повышение уровня воды в испытании 1 с 25,2 до 30,7 мл. Поскольку твердое вещество не реагировало и не растворялось в воды объем твердого вещества в мл представлен только изменение уровня воды. Вычислите объем твердого тела, тогда кликните сюда чтобы проверить свой ответ.

2. Масса твердого образца – расчет Опыт 1

Масса твердого образца равна разнице между масса пустого стакана и масса стакана с твердый. На основании данных таблицы выше рассчитайте массу твердый образец для испытания 1, а затем щелкните здесь, чтобы Проверьте свой ответ.

3. Плотность твердого образца – расчет Испытание 1

Плотность образца представляет собой массу образца, разделенную по объему пробы.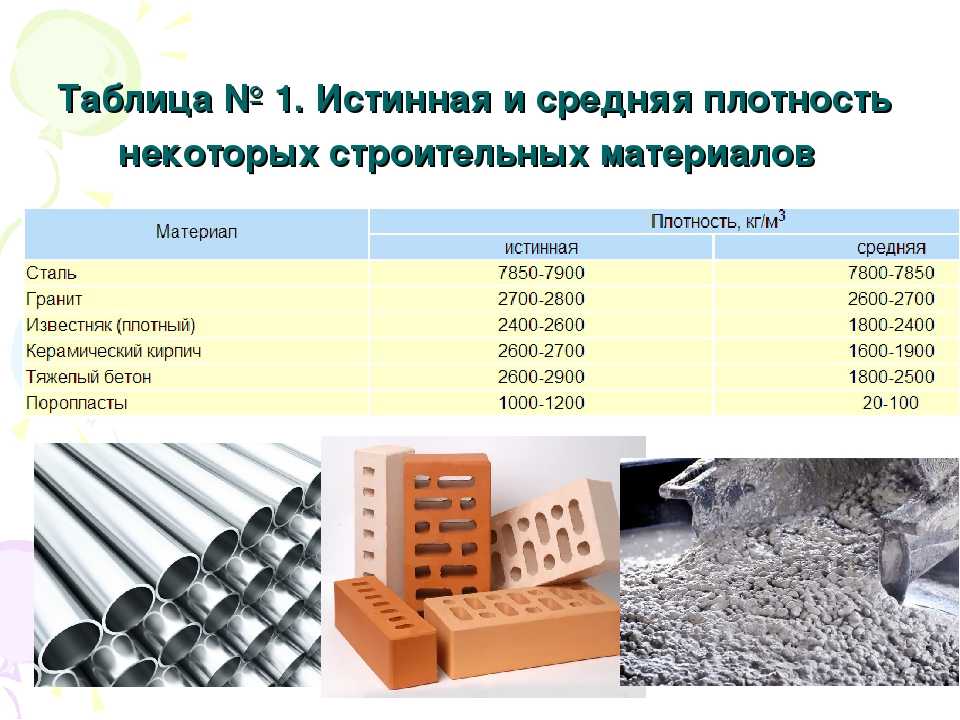 Для твердого образца в испытании 1, рассчитать плотность, затем нажмите здесь, чтобы Проверьте свой ответ. Обратите внимание на значащие цифры!

4. Средняя плотность твердого образца

Помните, что вы должны усреднить плотности, определенные во всех три попытки (а не две).

Для данных в таблице выше три отдельные плотности как рассчитано по данным таблицы (так же, как показано выше для Испытания 1), следующие

 

 

	Испытание 1	Испытание 2	Испытание 3
Плотность	2,0 г/мл	2,2 г/мл	2,1 г/мл

 

 

Тогда средняя (средняя) плотность является суммой трех плотностей разделить на количество испытаний (три). Рассчитать среднее плотность, затем нажмите здесь, чтобы Проверьте свой ответ.

5. Отклонения по плотности

Не забудьте рассчитать отклонения для всех трех испытаний.

Обзор расчетов отклонений см. в Эксперименте 1 (или кликните сюда).

 

 

	Отклонение
Испытание 1	(2,0–2,1) = -0,1 г/мл
Испытание 2	(2,1–2,1) = 0,0 г/мл
Испытание 3	(2,2–2,1) = 0,1 г/мл

 

6.

Среднее отклонение плотности твердого вещества

Не забудьте рассчитать среднее значение по результатам всех трех испытаний.

Обзор расчетов среднего отклонения см. в Эксперименте 1. (или нажмите здесь).

 

 

 

7.

Процентное отклонение плотности твердого вещества

Обзор расчетов процентного отклонения см. в Эксперименте 1. (или нажмите здесь).

 

 

 

 

Плотность жидкости неизвестна: стр. 15, раздел IIB

Помните, что все расчеты должны быть для всех три испытания (не только испытания 1 и 2).

Предположим, что следующие данные были записаны для плотности жидкость неизвестна (см. стр. 14, часть IB):

 

 

	Испытание 1	Испытание 2	Испытание 3
Стакан для масс + жидкость	31,42 г	33,69 г	34,54 г
Объем жидкости	21,6 мл	23,6 мл	23,7 мл
Пустой стакан для массы	7,25 г	7,49 г	7,92 г

 

 

 

1.

Объем жидкой пробы для испытания 1

Здесь нет вычислений. Вы измерили объем непосредственно мерным цилиндром. Том для Испытания 1 (см. таблицу выше) составляет 21,6 мл.

2. Масса пробы жидкости для испытания 1

Это всего лишь разница в массе пустого стакана и стакан с жидкостью в нем! Для испытания 1 в таблице выше рассчитайте массу жидкого образца, затем нажмите здесь, чтобы проверьте свой результат.

3. Плотность жидкого образца для испытания 1

Плотность жидкого образца – это масса образца, деленная на по его объему. Так как масса известна до 4-х значащих цифр, но объем известен только до 3-х значащих цифр, расчетный плотность должна быть выражена только до 3 значащих цифр. Для масса и объем для испытания 1, рассчитайте плотность жидкости пример, затем нажмите здесь, чтобы Проверьте свой ответ.

4. Средняя плотность жидкого образца

Помните, что следует использовать все три испытания (а не только Испытания 1 и 2).

Плотности для трех испытаний (рассчитанные, как показано для 1 выше) и средняя плотность приведены ниже:

 

 

	Испытание 1	Испытание 2	Испытание 3
Плотность	1,12 г/мл	1,11 г/мл	1,12 г/мл

 

 

 

 

5.

Отклонения по плотности

Не забудьте рассчитать отклонения для всех трех испытаний .

 

 

	Испытание 1	Испытание 2	Испытание 3
Отклонение	0,00 г/мл	-0,01 г/мл	0,00 г/мл

 

6.

Среднее отклонение плотности жидкости

Опять же, обязательно используйте все три испытания и помните, что при расчете среднее отклонение это абсолютное значение отклонений, которые следует использовать.

 

 

 

 

 

 

Обратите внимание, что, поскольку наши три плотности действительно согласовывались с каждой другой хорошо, мы получаем среднее отклонение фактически 0,00 г/мл (при учете значащих цифр).

7. Процентное отклонение плотности жидкости

 

 

 

Плотность дистиллированной воды: стр.

15, часть IIC

1. Скорректированная масса и объем после каждого добавления воды

Нам все равно, сколько весит стакан, который вы использовали, и мы неважно, до какого уровня вы наполнили бюретку, прежде чем начать взятие проб воды из него: нам просто нужна масса каждой воды образца и его объема. Помните, что мы для каждого набора данных, которые вы записано в части C на странице 13, мы хотим, чтобы общая совокупная масса и объем после каждого добавления воды (а не только дополнительное количество начиная с предыдущего издания. Для расчета массы после каждого кроме того, вычесть массу пустой мензурки из текущей масса (с текущим количеством воды). Чтобы рассчитать объем после каждого добавления вычитать начальное показание бюретки до того, как какая-либо вода была выдана из текущего показания бюретки в течение конкретного образца.