Шестнадцатеричная система счисления | это… Что такое Шестнадцатеричная система счисления?
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Содержание
|
Применение
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.
Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.
Способы записи
В математике
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и VHDL такие числа указывают так: «16#5A3#».
- В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x».
Например, «0x5A3». - В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бейсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
Например, «0x5A3».В электронных калькуляторах
Б3-34 и ему подобные используют «-», «L», «C», «Г», «E» « » (space) на их экране.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
= 3·1+10·16+5·256 = 3+160+1280 = 144310
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведенной таблицы перевода.
Например:
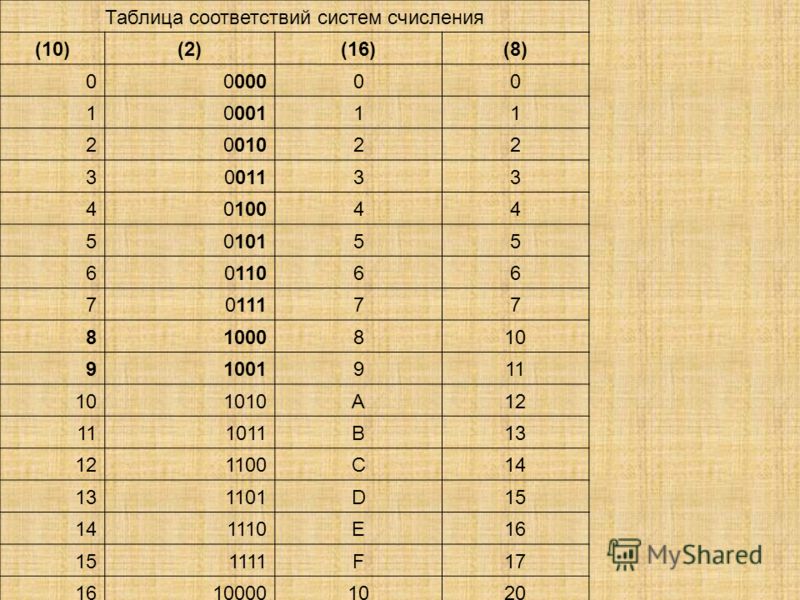
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | ||||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | ||||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
См.
также- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
Шестнадцатеричная система счисления | это… Что такое Шестнадцатеричная система счисления?
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510
Содержание
|
2 Перевод чисел из двоичной системы в шестнадцатеричную и наоборотПрименение
Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Шестнадцатеричный цвет — запись трёх компонент цвета (R, G и B) в шестнадцатеричном виде.
Способы записи
В математике
В математике основание системы счисления принято указывать в десятичной системе в нижнем индексе.
Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и VHDL такие числа указывают так: «16#5A3#».
- В Си и языках схожего синтаксиса, например, в Java, используют префикс «0x». Например, «0x5A3».
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, то для отличия от имён идентификаторов (например, констант) впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бейсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т. д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бейсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как 0xCC, где CC — шестнадцатеричный код символа.
Например, «&h5A3».В электронных калькуляторах
Б3-34 и ему подобные используют «-», «L», «C», «Г», «E» « » (space) на их экране.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
= 3·1+10·16+5·256 = 3+160+1280 = 144310
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведенной таблицы перевода.
Например:
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 | |||
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 | |||
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 | |||
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 | |||
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 | |||
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 | |||
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 | |||
| 7hex | = | 7dec | = | 7 | 0 | 1 | 1 | 1 | |||
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 | |||
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 | |||
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 | |||
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 | |||
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 | |||
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 | |||
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 | |||
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 | |||
См.
также- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
Шестнадцатеричная система счисления — Математические тайны
Определение
Шестнадцатеричная система счисления — это тип системы счисления, базовое значение которого равно 16. Иногда оно также произносится как «hex» . Шестнадцатеричные числа представлены всего 16 символами. Эти символы или значения 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Каждая цифра представляет десятичное значение. Например, D равно десятичному основанию 13.
Шестнадцатеричные системы счисления могут быть преобразованы в другие системы счисления, такие как двоичная (с основанием 2), восьмеричная (с основанием 8) и десятичная системы счисления (с основанием 10). . Концепция системы счисления широко объясняется в программе 9 класса.
.
Список из 16 шестнадцатеричных цифр с их эквивалентным десятичным, восьмеричным и двоичным представлением приведен здесь в виде таблицы, которая поможет в преобразовании системы счисления. Этот список также можно использовать в качестве переводчика или конвертера. 1
Шестнадцатеричная система счисления — BYJUS19FDAШаг 1: ) =
Шаг 2: (1 x 65536) + (9 x 4096) + (15 x 256) + (13 x 16) + (10 x 1)
Шаг 3: (65536+ 36864 + 3840 + 208 + 10) 10
Шаг 4: (106458)₁₀ или 106458
Ссылки
1 Таблица, Преобразования, Примеры». 2022. БАЙЮС . https://byjus.com/maths/шестнадцатеричная система счисления/.
Дополнительная литература
«Арифметические операции с шестнадцатеричными числами — GeeksForGeeks». 2020. GeeksForGeeks . https://www.geeksforgeeks.org/arithmetic-operations-of-hexadecimal-numbers/.
Джастис, Далтон. 2014. «Шестнадцатеричный». SlideServe . https://www.slideserve.com/dalton/hexadecimal.
Видео
Шестнадцатеричная система счисления Шестнадцатеричная система счисления | Применение математических рассуждений | Предварительная алгебра | Академия Хана Какой смысл в шестнадцатеричном формате? (GCSE)
youtube.com/embed/gebgq9o4KW8?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»> Зачем нужны шестнадцатеричная и восьмеричная системы счисления? Очень важно понять причину использования шестнадцатеричной и восьмеричной систем счисления. В этом видео я объяснил необходимость, различные варианты использования шестнадцатеричной и восьмеричной систем счисления, а также преобразование между двоичной, шестнадцатеричной и восьмеричной системами счисления.
⭐ Предлагаю прочитать весь справочник. Другие ссылки можно прочитать полностью, но я оставляю это на ваше усмотрение.
Краткая информация о восьмеричной и шестнадцатеричной системах счисления
Компьютеры созданы человеком, но они работают на языке чисел. Когда мы набираем на компьютере букву, цифру или специальный символ, операционная система преобразует ввод в числа.
Это связано с тем, что компьютер может понимать только позиционную систему счисления, в которой есть некоторые символы, называемые цифрами. Символы, используемые в системе счисления, отображают различные значения.
Величина каждой цифры в числе определяется с помощью цифры, места цифры в числе и основания системы счисления. Существует несколько типов систем счисления, таких как десятичная система счисления, двоичная система счисления и т. д.
В этой статье мы обсудим восьмеричную и шестнадцатеричную системы счисления. Сначала мы поговорим о том, что такое восьмеричная система счисления и ее представление. Затем мы перейдем к обсуждению шестнадцатеричной системы счисления и ее представления.
Восьмеричная система счисления
Восьмеричная система счисления, также известная как октальная, представляет собой систему счисления с основанием 8. В системе используются цифры от 0 до 7. Поэтому, если мы пишем восьмеричное число 10, оно изображает 8, а если мы пишем восьмеричное число 100, оно представляет 64.
Когда мы изучаем десятичную систему счисления, каждый разряд представляется в степени 10. Но когда мы внедряем восьмеричную систему счисления, каждый разряд равен степени 8.
Преобразование восьмеричных чисел довольно просто. Для преобразования восьмеричного числа все, что нам нужно сделать, это сгруппировать двоичные цифры в группу из трех. Примером восьмеричной системы счисления является представление десятичного числа 74. Десятичное представление числа 74 – 1001010. В этой системе перед двоичной цифрой 1 можно поставить два нуля, и теперь мы преобразуем 74 в восьмеричное. Восьмеричное число 112.
Основная характеристика восьмеричной системы счисления состоит в том, что она имеет 8 различных счетных цифр от 0 до 7. В первые дни вычислений восьмеричные числа и восьмеричная система счисления считали входы и выходы. Восьмеричное число было введено для удобного преобразования больших двоичных чисел. Однако восьмеричная система счисления постепенно вымирает из-за более популярной шестнадцатеричной системы счисления.
Представление восьмеричного числа
Система не использует числа или алфавиты выше 8. Кроме того, преобразование восьмеричных чисел в двоичные числа аналогично шестнадцатеричным числам. Восьмеричные числа представляются следующим образом.
Decimal number | 3-bit binary number | Octal number |
0 | 000 | 0 |
1 | 001 | 1 |
2 | 010 | 2 |
3 | 011 | 3 |
4 | 100 | 4 |
5 | 101 | 5 |
6 | 110 | 6 |
7 | 111 | 7 |
8 | 001 000 | 10 (1+0) |
9 | 001 001 | 11 (1 +1) |
При написании 10 или 20 не путайтесь, потому что число 10 и число 20 представляют собой представление с использованием (1+0) и (2+0) в восьмеричной системе счисления.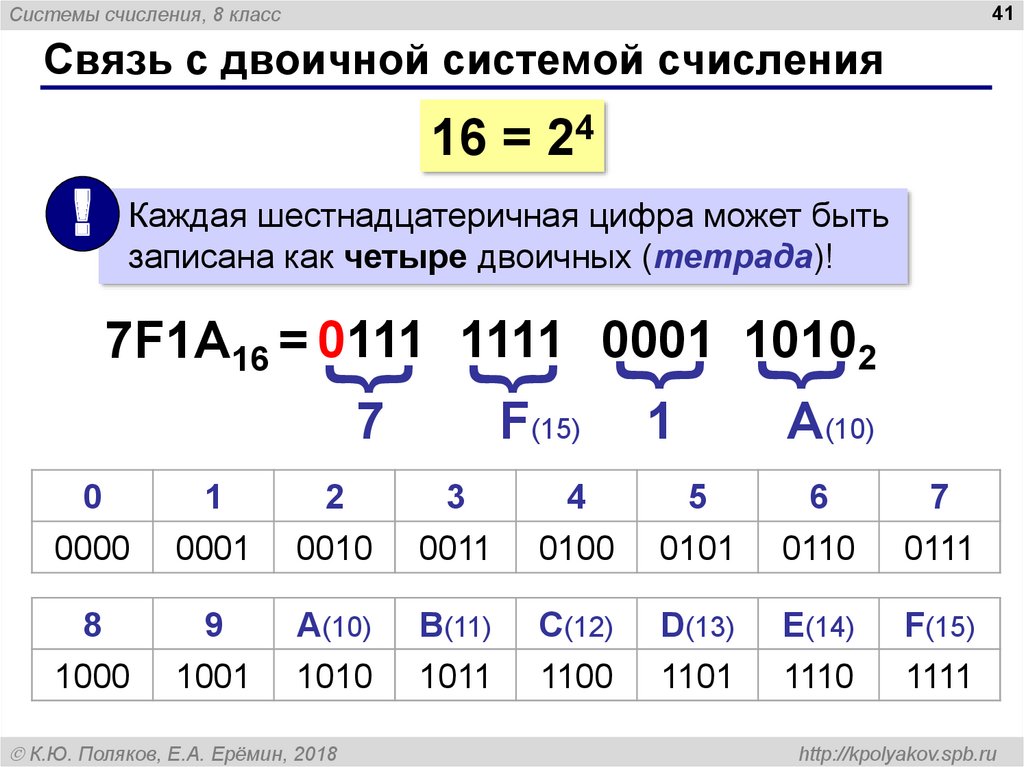
Восьмеричное число равно 8octal. Восьмеричное значение варьируется от 0 до 7.
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — это система счисления, в которой базовое значение равно 16. Это означает, что в шестнадцатеричной системе используется 16 символов. Шестнадцатеричные символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Алфавиты, используемые в шестнадцатеричной системе, представляют собой однобитовое представление десятичные числа 10, 11, 12, 13, 14 и 15. Шестнадцатеричная система требует 4 бита для изображения любой цифры. Поскольку существует так много систем счисления, шестнадцатеричная система счисления обычно обозначается буквой h.
В шестнадцатеричной системе счисления каждая цифра имеет вес, эквивалентный степени 16. Таким образом, в шестнадцатеричной системе счисления каждая цифра в 16 раз ценнее предыдущей. Числовое значение каждой цифры в шестнадцатеричной последовательности получается путем умножения числа в степени 16, которая зависит от положения числа, и последующего прибавления числа к сумме.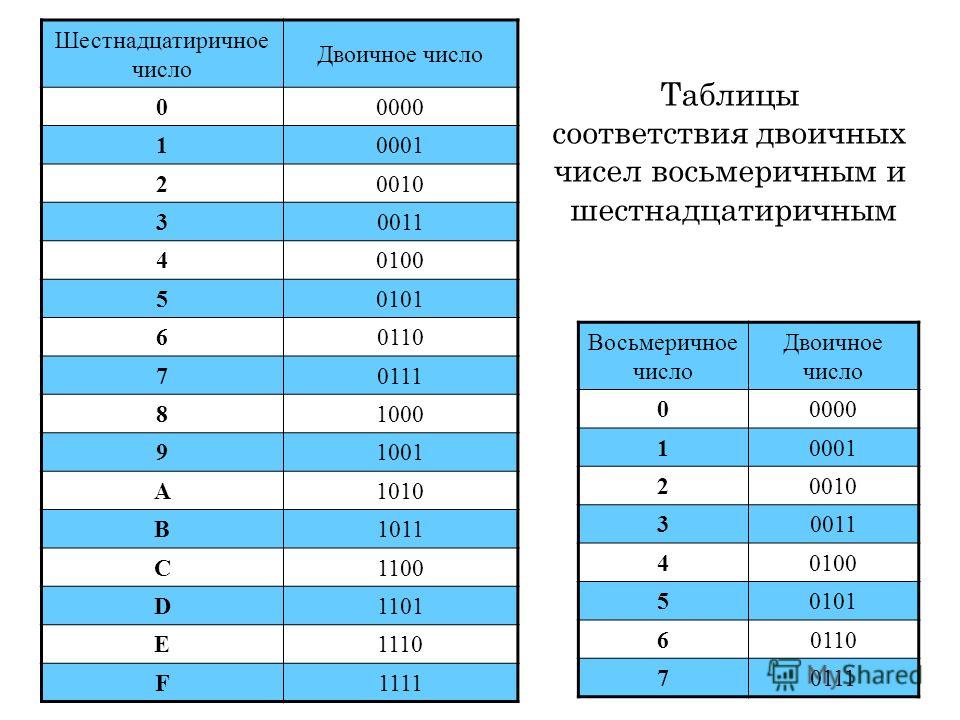
Разработчики программного обеспечения широко используют шестнадцатеричную систему счисления, потому что она удобно представляет двоичные значения.
Представление шестнадцатеричных чисел
Из приведенного выше определения ясно, что шестнадцатеричная система счисления представляет собой набор из 4 битов. Каждый набор битов в шестнадцатеричных числах равен 0 и 15. Шестнадцатеричные числа широко используются в современных компьютерах и цифровых системах, поскольку их удобно интерпретировать.
Представление шестнадцатеричных чисел следующее:
Hex | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Binary | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 |
Hex | 9 | 10 = A | 11 = B | 12 = C | 13 = D 9009 | 7913 = D 9009 | 7913 = D 9009 | 79012215 = F |
Binary | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Основной причиной изобретения шестнадцатеричной системы счисления было решение проблемы преобразования больших двоичных чисел.
