Сферическая аберрация | это… Что такое Сферическая аберрация?
У этого термина существуют и другие значения, см. Аберрация.
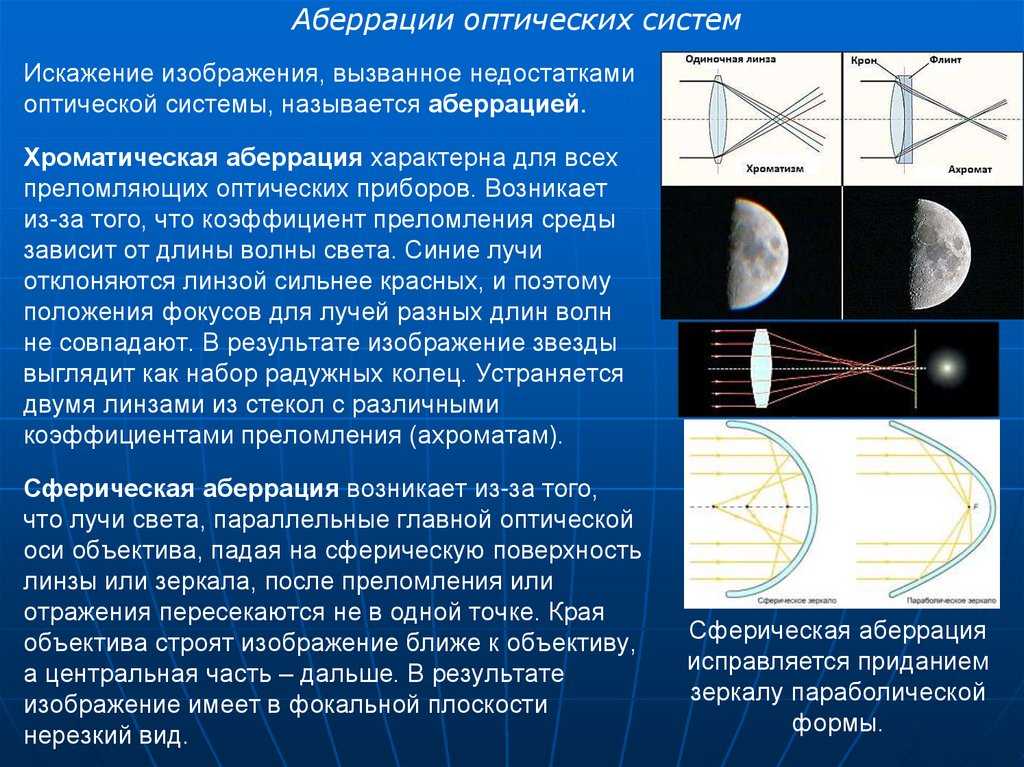
Схема сферической аберрации, где
H, H’ — положения главных плоскостей;
F’ — задняя фокальная плоскость;
f’ — заднее фокусное расстояние;
-δs’ — продольная сферическая аберрация;
δg’ — поперечная сферическая аберрация.
Сфери́ческая аберра́ция — аберрация оптических систем; нарушение гомоцентричности пучков лучей от точечного источника, прошедших через оптическую систему без нарушения симметрии строения этих пучков (в отличие от комы и астигматизма).
Содержание
|
Условия рассмотрения
Сферическую аберрацию принято рассматривать для пучка лучей, выходящего из точки предмета, расположенной на оптической оси. Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Причём, хотя эта аберрация и называется сферической, она характерна не только для сферических поверхностей.
Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Причём, хотя эта аберрация и называется сферической, она характерна не только для сферических поверхностей.
В результате сферической аберрации цилиндрический пучок лучей, после преломления линзой (в пространстве изображений) получает вид не конуса, а некоторой воронкообразной фигуры, наружная поверхность которой, вблизи узкого места, называется каустической поверхностью. При этом изображение точки имеет вид диска с неоднородным распределением освещённости, а форма каустической кривой позволяет судить о характере распределения освещённости. В общем случае, фигура рассеяния, при наличии сферической аберрации, представляет собой систему концентрических окружностей с радиусами пропорциональными третьей степени координат на входном (или выходном) зрачке.
Сферическая аберрация линзы (системы линз) объясняется тем, что её преломляющие поверхности встречают отдельные лучи сколько-нибудь широкого пучка под различными углами. [1] Вследствие чего, более удалённые от оптической оси лучи преломляются сильнее, нежели нулевые[2] лучи, и образуют свои точки схода удалённые от фокальной плоскости.
[1] Вследствие чего, более удалённые от оптической оси лучи преломляются сильнее, нежели нулевые[2] лучи, и образуют свои точки схода удалённые от фокальной плоскости.
Расчётные значения
Расстояние δs’ по оптической оси между точками схода нулевых и крайних лучей называется
Диаметр δ’ кружка (диска) рассеяния при этом определяется по формуле
,
где
- 2h1 — диаметр отверстия системы;
- a’ — расстояние от системы до точки изображения;
- δs’ — продольная аберрация.
Для объектов расположенных в бесконечности
,
где
- f’ — заднее фокусное расстояние.
Для наглядности сферическую аберрацию, как правило, представляют не только в виде таблиц, но и графически.
Графики сферической аберрации:
1a. — продольная сферическая аберрация плоско-выпуклой линзы,
1b.
2. — поперечная сферическая аберрация.
Графическое представление
Обычно приводят графики продольной δs’ и поперечной δg’ сферической аберраций, как функций координат лучей.
Для построения характеристической кривой продольной сферической аберрации по оси абсцисс откладывают продольную сферическую аберрацию δs’, а по оси ординат — высоты лучей на входном зрачке h. Для построения аналогичной кривой для поперечной аберрации по оси абсцисс откладывают тангенсы апертурных углов в пространстве изображений, а по оси ординат радиусы кружков рассеяния δg’
Положительные (собирательные) линзы создают отрицательную сферическую аберрацию, то есть
Комбинируя такие простые линзы, можно значительно исправить сферическую аберрацию.
Зависимость величины продольной сферической аберрации (δs’ ) от формы линзы.
Уменьшение и исправление
Как и другие аберрации третьего порядка, сферическая аберрация зависит от кривизны поверхностей и оптической силы линзы. Поэтому применение оптических стёкол с высокими показателями преломления позволяют уменьшить сферическую аберрацию, посредством увеличения радиусов поверхностей линзы при сохранении её оптической силы.
Уменьшение влияния сферической аберрации
1. диафрагмированием;
2. с помощью дефокусировки.
К тому же, для линз с разной кривизной поверхностей будет иметь значение ориентация линзы относительно хода светового луча. Так, например, сферическая аберрация для плоско-выпуклой линзы, обращенной навстречу лучу своей плоской поверхностью, будет иметь величину бо́льшую, нежели для той же линзы, но встречающей луч своей выпуклой поверхностью.
Заметное влияние на сферическую аберрацию оказывает диафрагмирование объектива (или иной оптической системы), так как при этом отсекаются краевые лучи широкого пучка. Очевидно, что этот способ непригоден для оптических систем, требующих высокой светосилы.
В отдельных случаях небольшая величина сферической аберрации третьего порядка может быть исправлена за счёт некоторой дефокусировки[4] объектива. При этом плоскость изображения смещается к, так называемой, «плоскости лучшей установки», находящейся, как правило, посередине, между пересечением осевых и крайних лучей, и не совпадающей с самым узким местом пересечения всех лучей широкого пучка (диском наименьшего рассеяния)[5]. Это несовпадение объясняется распределением световой энергии в диске наименьшего рассеяния, образующей максимумы освещённости не только в центре, но и на краю.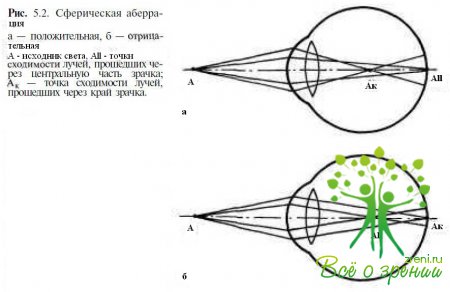
Пересечения лучей возле точки заднего фокуса при остаточной сферической аберрации, соответствующие им диски рассеяния и графики продольной сферической аберрации:
1. — при исправленной сферической аберрации для нулевых и крайних лучей;
Где F’ — задняя фокальная плоскость,
δs’ — расстояние от точки заднего фокуса до точки схода краевых лучей,
— δs’0,7h’ — расстояние от точки заднего фокуса до точки схода «среднезонных» лучей.
Достаточно успешно сферическая аберрация исправляется при помощи комбинации из положительной и отрицательной линз.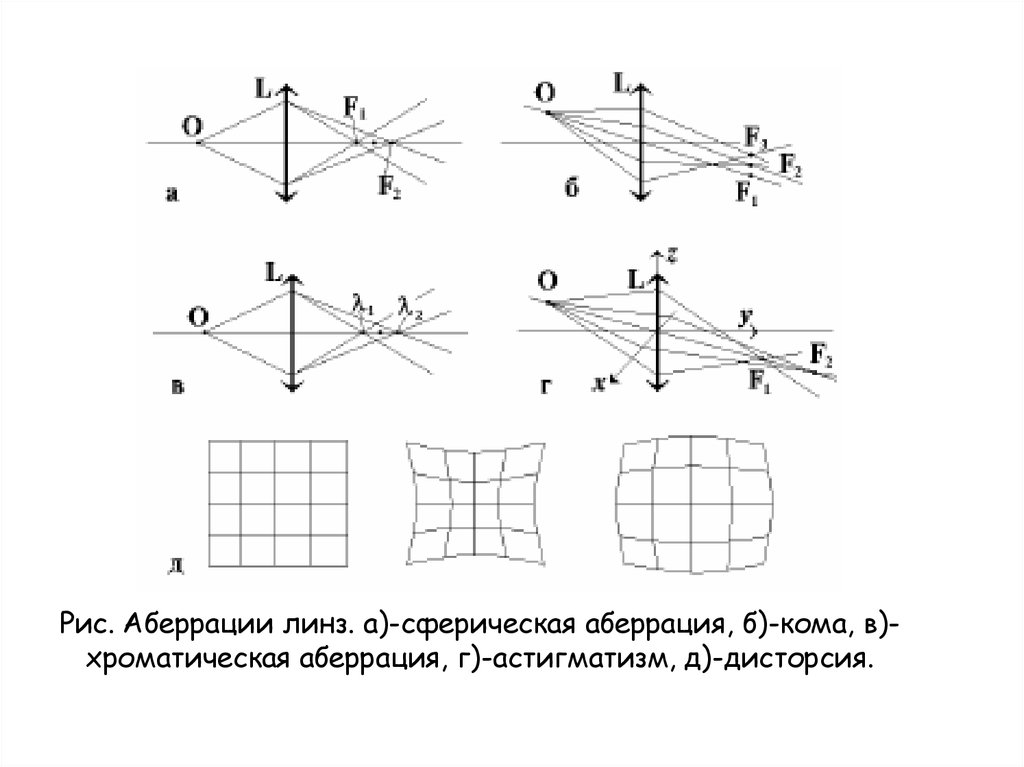 Причём, если линзы не склеиваются, то, кроме кривизны поверхностей компонентов, на величину сферической аберрации будет влиять и величина воздушного зазора (даже в том случае, если поверхности, ограничивающие этот воздушный промежуток, имеют одинаковую кривизну). При этом способе коррекции, как правило исправляются и хроматические аберрации.
Причём, если линзы не склеиваются, то, кроме кривизны поверхностей компонентов, на величину сферической аберрации будет влиять и величина воздушного зазора (даже в том случае, если поверхности, ограничивающие этот воздушный промежуток, имеют одинаковую кривизну). При этом способе коррекции, как правило исправляются и хроматические аберрации.
Строго говоря, сферическая аберрация может быть вполне исправлена только для какой-нибудь пары узких зон, и притом лишь для определенных двух сопряженных точек. Однако, практически исправление может быть весьма удовлетворительным даже для двухлинзовых систем.
Обычно сферическую аберрацию устраняют для одного значения высоты h0 соответствующего краю зрачка системы. При этом наибольшее значение остаточной сферической аберрации ожидается на высоте h
Остаточная сферическая аберрация приводит к тому, что изображение точки так и не станет точечным. Оно останется диском, хотя и значительно меньшего размера, чем в случае не исправленной сферической аберрации.
Для уменьшения остаточной сферической аберрации часто прибегают к рассчитанному «переисправлению» на краю зрачка системы, придавая сферической аберрации краевой зоны положительное значение (δs’ > 0). При этом, лучи, пересекающие зрачок на высоте he[6], перекрещиваются ещё ближе к точке фокуса, а краевые лучи, хотя и сходятся за точкой фокуса, не выходят за границы диска рассеяния. Таким образом, размер диска рассеяния уменьшается и возрастает его яркость. То есть улучшается, как детальность, так и контраст изображения. Однако, в силу особенностей распределения освещённости в диске рассеяния, объективы с «переисправленной» сферической аберрацией, часто, обладают «двоящим» размытием вне зоны фокуса.
В отдельных случаях допускают значительное «переисправление». Так, например, ранние «Планары» фирмы Carl Zeiss Jena имели положительное значение сферической аберрации (δs’ > 0), как для краевых, так и для средних зон зрачка. Это решение несколько снижает контраст при полном отверстии, но заметно увеличивает разрешение при незначительном диафрагмировании.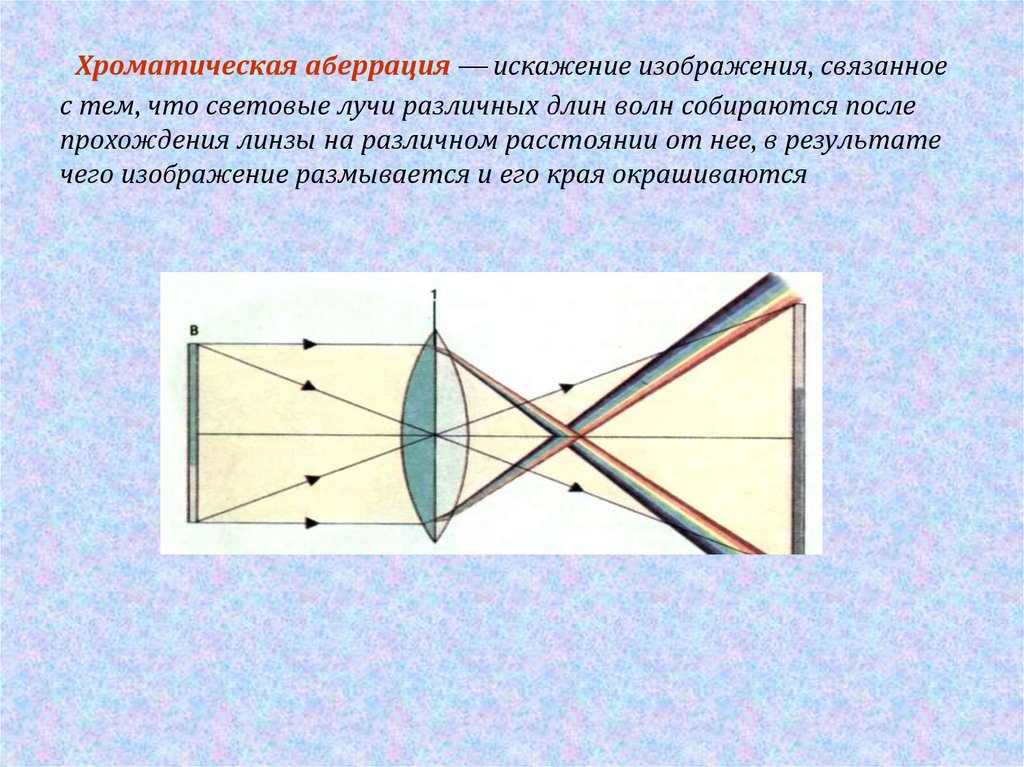
Примечания
- ↑ Или же можно сказать, что оптическая сила сферической линзы неоднородна, и возрастает по мере удаления от оптической оси.
- ↑ Эти лучи, так же, именуются параксиальными лучами.
- ↑ Согласно правилам знаков и ГОСТ 7427-76, преломляющие и отражающие поверхности и разделяющие их среды нумеруются по порядку их следования в направлении распространения света.
- ↑ Согласно теории аберраций, дефокусировка — это аберрация первого, то есть более низкого, порядка.
- ↑ Самое узкое место пересечения всех лучей широкого пучка, проходящего через собирающую линзу, находится слева от точки фокуса на расстоянии ¾
- ↑ Эти лучи иногда именуются среднезонными лучами.
Литература
- Бегунов Б. Н. Геометрическая оптика, Изд-во МГУ, 1966.
- Волосов Д. С., Фотографическая оптика. М., «Искусство», 1971.
- Заказнов Н. П. и др., Теория оптических систем, М.
 , «Машиностроение», 1992.
, «Машиностроение», 1992. - Ландсберг Г. С. Оптика. М.,ФИЗМАТЛИТ, 2003.
- Чуриловский В. Н. Теория оптических приборов, Л., «Машиностроение», 1966.
- Smith, Warren J. Modern optical engineering, McGraw-Hill, 2000.
Сферическая аберрация | это… Что такое Сферическая аберрация?
У этого термина существуют и другие значения, см. Аберрация.
Схема сферической аберрации, где
H, H’ — положения главных плоскостей;
F’ — задняя фокальная плоскость;
f’ — заднее фокусное расстояние;
-δs’ — продольная сферическая аберрация;
δg’ — поперечная сферическая аберрация.
Сфери́ческая аберра́ция — аберрация оптических систем; нарушение гомоцентричности пучков лучей от точечного источника, прошедших через оптическую систему без нарушения симметрии строения этих пучков (в отличие от комы и астигматизма).
Содержание
|
Условия рассмотрения
Сферическую аберрацию принято рассматривать для пучка лучей, выходящего из точки предмета, расположенной на оптической оси. Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Причём, хотя эта аберрация и называется сферической, она характерна не только для сферических поверхностей.
Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Причём, хотя эта аберрация и называется сферической, она характерна не только для сферических поверхностей.
В результате сферической аберрации цилиндрический пучок лучей, после преломления линзой (в пространстве изображений) получает вид не конуса, а некоторой воронкообразной фигуры, наружная поверхность которой, вблизи узкого места, называется каустической поверхностью. При этом изображение точки имеет вид диска с неоднородным распределением освещённости, а форма каустической кривой позволяет судить о характере распределения освещённости. В общем случае, фигура рассеяния, при наличии сферической аберрации, представляет собой систему концентрических окружностей с радиусами пропорциональными третьей степени координат на входном (или выходном) зрачке.
Сферическая аберрация линзы (системы линз) объясняется тем, что её преломляющие поверхности встречают отдельные лучи сколько-нибудь широкого пучка под различными углами.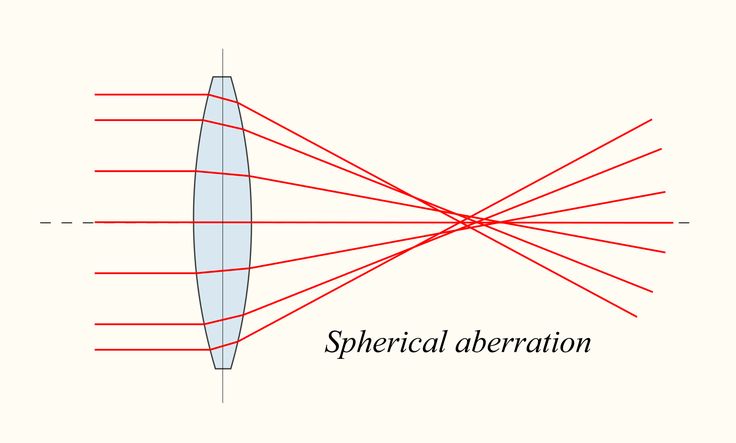 [1] Вследствие чего, более удалённые от оптической оси лучи преломляются сильнее, нежели нулевые[2] лучи, и образуют свои точки схода удалённые от фокальной плоскости.
[1] Вследствие чего, более удалённые от оптической оси лучи преломляются сильнее, нежели нулевые[2] лучи, и образуют свои точки схода удалённые от фокальной плоскости.
Расчётные значения
Расстояние δs’ по оптической оси между точками схода нулевых и крайних лучей называется продольной сферической аберрацией.
Диаметр δ’ кружка (диска) рассеяния при этом определяется по формуле
,
где
- 2h1 — диаметр отверстия системы;
- a’ — расстояние от системы до точки изображения;
- δs’ — продольная аберрация.
Для объектов расположенных в бесконечности
,
где
- f’ — заднее фокусное расстояние.
Для наглядности сферическую аберрацию, как правило, представляют не только в виде таблиц, но и графически.
Графики сферической аберрации:
1a. — продольная сферическая аберрация плоско-выпуклой линзы,
1b. — продольная сферическая аберрация плоско-вогнутой линзы,
— продольная сферическая аберрация плоско-вогнутой линзы,
2. — поперечная сферическая аберрация.
Графическое представление
Обычно приводят графики продольной δs’ и поперечной δg’ сферической аберраций, как функций координат лучей.
Для построения характеристической кривой продольной сферической аберрации по оси абсцисс откладывают продольную сферическую аберрацию δs’, а по оси ординат — высоты лучей на входном зрачке h. Для построения аналогичной кривой для поперечной аберрации по оси абсцисс откладывают тангенсы апертурных углов в пространстве изображений, а по оси ординат радиусы кружков рассеяния δg’
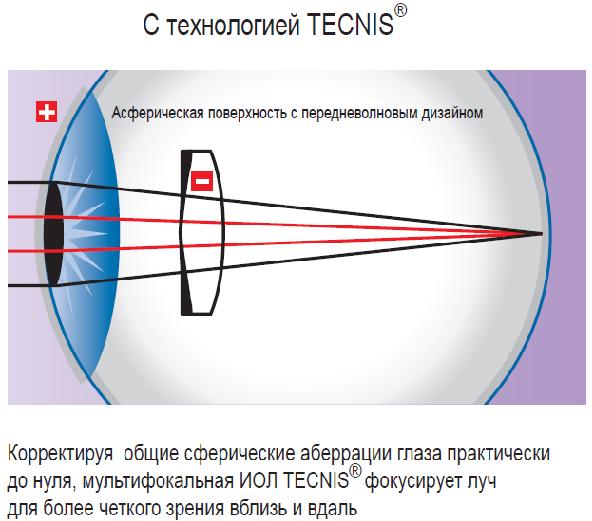
Положительные (собирательные) линзы создают отрицательную сферическую аберрацию, то есть δs’ < 0 для всех зон. Поэтому, на графике, характеристическая кривая продольной аберрации для такой линзы находится слева от оси ординат. Отрицательные (рассеивающие) линзы имеют аберрацию противоположного знака, и соответствующая кривая продольной аберрации будет справа от оси ординат.
Комбинируя такие простые линзы, можно значительно исправить сферическую аберрацию.
Зависимость величины продольной сферической аберрации (δs’ ) от формы линзы.
Уменьшение и исправление
Как и другие аберрации третьего порядка, сферическая аберрация зависит от кривизны поверхностей и оптической силы линзы. Поэтому применение оптических стёкол с высокими показателями преломления позволяют уменьшить сферическую аберрацию, посредством увеличения радиусов поверхностей линзы при сохранении её оптической силы.
Уменьшение влияния сферической аберрации
1. диафрагмированием;
2. с помощью дефокусировки.
К тому же, для линз с разной кривизной поверхностей будет иметь значение ориентация линзы относительно хода светового луча. Так, например, сферическая аберрация для плоско-выпуклой линзы, обращенной навстречу лучу своей плоской поверхностью, будет иметь величину бо́льшую, нежели для той же линзы, но встречающей луч своей выпуклой поверхностью.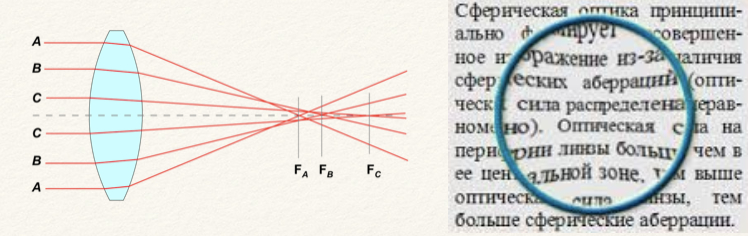 Таким образом, выбор отношения кривизны первой[3] поверхности линзы, к её второй поверхности, так же, будет одним из средств уменьшающих сферическую аберрацию.
Таким образом, выбор отношения кривизны первой[3] поверхности линзы, к её второй поверхности, так же, будет одним из средств уменьшающих сферическую аберрацию.
Заметное влияние на сферическую аберрацию оказывает диафрагмирование объектива (или иной оптической системы), так как при этом отсекаются краевые лучи широкого пучка. Очевидно, что этот способ непригоден для оптических систем, требующих высокой светосилы.
В отдельных случаях небольшая величина сферической аберрации третьего порядка может быть исправлена за счёт некоторой дефокусировки[4] объектива. При этом плоскость изображения смещается к, так называемой, «плоскости лучшей установки», находящейся, как правило, посередине, между пересечением осевых и крайних лучей, и не совпадающей с самым узким местом пересечения всех лучей широкого пучка (диском наименьшего рассеяния)[5]. Это несовпадение объясняется распределением световой энергии в диске наименьшего рассеяния, образующей максимумы освещённости не только в центре, но и на краю. То есть, можно сказать, что «диск» представляет из себя яркое кольцо с центральной точкой. Поэтому, разрешение оптической системы, в плоскости совпадающей с с диском наименьшего рассеяния, будет ниже, несмотря на меньшую величину поперечной сферической аберрации. Пригодность этого метода зависит от величины сферической аберрации, и характера распределения освещённости в диске рассеяния.
То есть, можно сказать, что «диск» представляет из себя яркое кольцо с центральной точкой. Поэтому, разрешение оптической системы, в плоскости совпадающей с с диском наименьшего рассеяния, будет ниже, несмотря на меньшую величину поперечной сферической аберрации. Пригодность этого метода зависит от величины сферической аберрации, и характера распределения освещённости в диске рассеяния.
Пересечения лучей возле точки заднего фокуса при остаточной сферической аберрации, соответствующие им диски рассеяния и графики продольной сферической аберрации:
1. — при исправленной сферической аберрации для нулевых и крайних лучей;
2. и 3. — при «переисправленной» сферической аберрации.
Где F’ — задняя фокальная плоскость,
δs’ — расстояние от точки заднего фокуса до точки схода краевых лучей,
— δs’0,7h’ — расстояние от точки заднего фокуса до точки схода «среднезонных» лучей.
Достаточно успешно сферическая аберрация исправляется при помощи комбинации из положительной и отрицательной линз.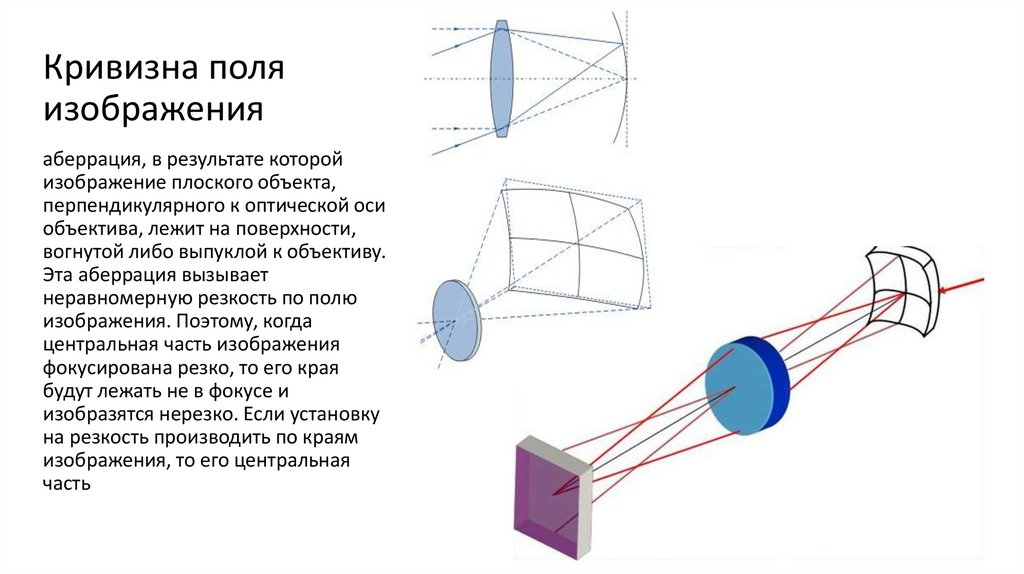 Причём, если линзы не склеиваются, то, кроме кривизны поверхностей компонентов, на величину сферической аберрации будет влиять и величина воздушного зазора (даже в том случае, если поверхности, ограничивающие этот воздушный промежуток, имеют одинаковую кривизну). При этом способе коррекции, как правило исправляются и хроматические аберрации.
Причём, если линзы не склеиваются, то, кроме кривизны поверхностей компонентов, на величину сферической аберрации будет влиять и величина воздушного зазора (даже в том случае, если поверхности, ограничивающие этот воздушный промежуток, имеют одинаковую кривизну). При этом способе коррекции, как правило исправляются и хроматические аберрации.
Строго говоря, сферическая аберрация может быть вполне исправлена только для какой-нибудь пары узких зон, и притом лишь для определенных двух сопряженных точек. Однако, практически исправление может быть весьма удовлетворительным даже для двухлинзовых систем.
Обычно сферическую аберрацию устраняют для одного значения высоты h0 соответствующего краю зрачка системы. При этом наибольшее значение остаточной сферической аберрации ожидается на высоте he определяемой по простой формуле
Остаточная сферическая аберрация приводит к тому, что изображение точки так и не станет точечным. Оно останется диском, хотя и значительно меньшего размера, чем в случае не исправленной сферической аберрации.
Для уменьшения остаточной сферической аберрации часто прибегают к рассчитанному «переисправлению» на краю зрачка системы, придавая сферической аберрации краевой зоны положительное значение (δs’ > 0). При этом, лучи, пересекающие зрачок на высоте he[6], перекрещиваются ещё ближе к точке фокуса, а краевые лучи, хотя и сходятся за точкой фокуса, не выходят за границы диска рассеяния. Таким образом, размер диска рассеяния уменьшается и возрастает его яркость. То есть улучшается, как детальность, так и контраст изображения. Однако, в силу особенностей распределения освещённости в диске рассеяния, объективы с «переисправленной» сферической аберрацией, часто, обладают «двоящим» размытием вне зоны фокуса.
В отдельных случаях допускают значительное «переисправление». Так, например, ранние «Планары» фирмы Carl Zeiss Jena имели положительное значение сферической аберрации (δs’ > 0), как для краевых, так и для средних зон зрачка. Это решение несколько снижает контраст при полном отверстии, но заметно увеличивает разрешение при незначительном диафрагмировании.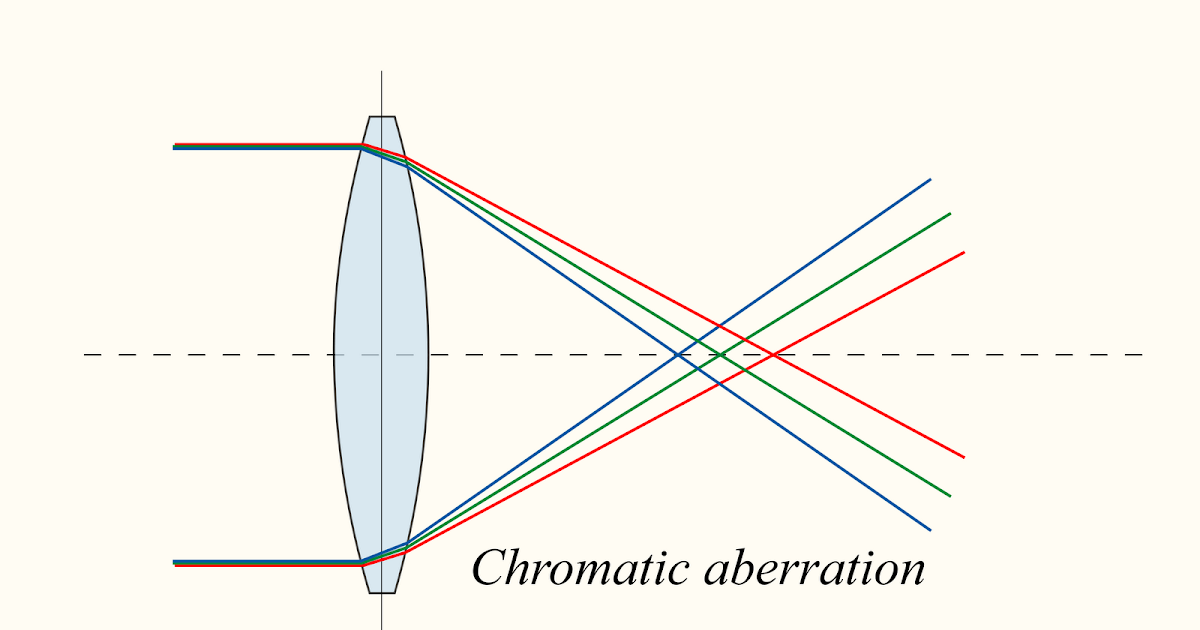
Примечания
- ↑ Или же можно сказать, что оптическая сила сферической линзы неоднородна, и возрастает по мере удаления от оптической оси.
- ↑ Эти лучи, так же, именуются параксиальными лучами.
- ↑ Согласно правилам знаков и ГОСТ 7427-76, преломляющие и отражающие поверхности и разделяющие их среды нумеруются по порядку их следования в направлении распространения света.
- ↑ Согласно теории аберраций, дефокусировка — это аберрация первого, то есть более низкого, порядка.
- ↑ Самое узкое место пересечения всех лучей широкого пучка, проходящего через собирающую линзу, находится слева от точки фокуса на расстоянии ¾δs’.
- ↑ Эти лучи иногда именуются среднезонными лучами.
Литература
- Бегунов Б. Н. Геометрическая оптика, Изд-во МГУ, 1966.
- Волосов Д. С., Фотографическая оптика. М., «Искусство», 1971.
- Заказнов Н. П. и др., Теория оптических систем, М.
 , «Машиностроение», 1992.
, «Машиностроение», 1992. - Ландсберг Г. С. Оптика. М.,ФИЗМАТЛИТ, 2003.
- Чуриловский В. Н. Теория оптических приборов, Л., «Машиностроение», 1966.
- Smith, Warren J. Modern optical engineering, McGraw-Hill, 2000.
Сферическая аберрация
Сферическая аберрацияДля линз со сферическими поверхностями лучи, параллельные оптической оси, но находящиеся на разном расстоянии от оптической оси, не сходятся в одной точке. Для одиночной линзы сферическую аберрацию можно свести к минимуму, согнув линзу в наилучшую форму. Для нескольких объективов сферические аберрации можно устранить путем чрезмерной коррекции некоторых элементов. Использование симметричных дублетов, таких как ортоскопический дублет, значительно снижает сферическую аберрацию. Когда используется понятие главного фокусного расстояния, предполагается, что все параллельные лучи фокусируются на одном и том же расстоянии, что, конечно, верно только при отсутствии аберраций.
| Index Концепции линз Концепции толстых линз | ||||||||||||||||||||||||
| R NAVE |
Сделайте правильный выбор объектива для вашей системы обработки изображений Teledyne Lumenera
Опубликовано 16 декабря 2019 г. Опубликовано в Интересующие вопросы, характеристики и технологии | Теледайн Люменера
Опубликовано в Интересующие вопросы, характеристики и технологии | Теледайн Люменера
Что такое сферическая аберрация и почему она возникает?
Даже при использовании сложной системы линз бывает сложно сфокусировать все изображение. На любой сферической поверхности свет будет преломляться по-разному в зависимости от того, через какую часть поверхности проходит свет. На рисунке 1 ниже свет преломляется под разными углами, где круче кривая на линзе, тем больше угол преломления. В случае объектива камеры, в котором используется сферическое стекло, поверхность у края стекла всегда будет преломлять свет под более крутым углом. Это приведет к тому, что часть падающего света, в первую очередь свет ближе к краю изогнутой поверхности, сфокусируется перед желаемой фокальной плоскостью. Это явление называется сферической аберрацией.
Сферическая аберрация — это нерезкость края изображения. Использование сферического объектива на камере приводит к тому, что свет у края объектива (дальше от оптической оси) сходится ближе к объективу (показано на рисунке 1).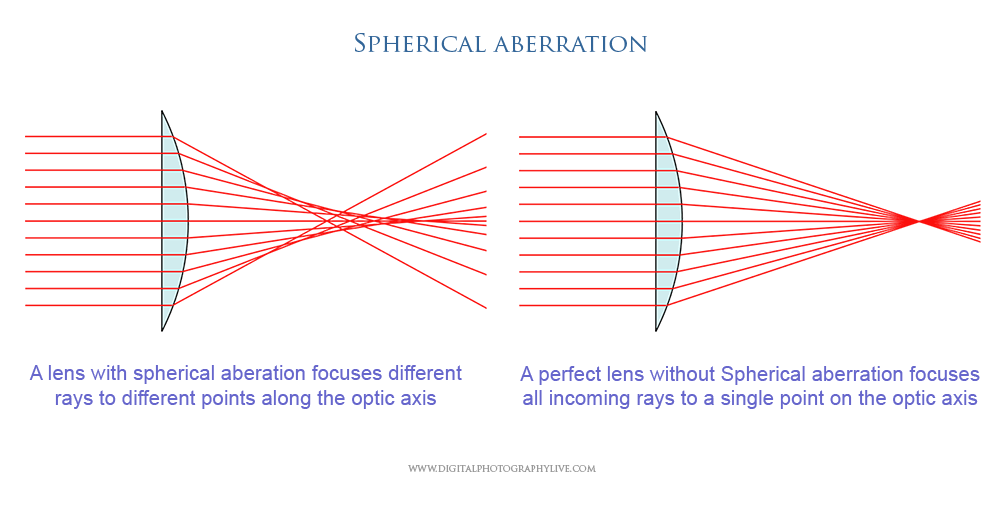 Световые лучи вблизи оптической оси называются параксиальными лучами, а лучи вблизи периферии линзы — краевыми лучами. Следует отметить, что почти вся оптика, встречающаяся в камерах, использует сферические линзы.
Световые лучи вблизи оптической оси называются параксиальными лучами, а лучи вблизи периферии линзы — краевыми лучами. Следует отметить, что почти вся оптика, встречающаяся в камерах, использует сферические линзы.
Это похоже на то, как увеличительное стекло лучше всего фокусируется через центр линзы. На рис. 2 это показано, где схема находится в фокусе рядом с центром, но остальная часть печатной платы, особенно текст, не в фокусе.
Другой пример сферической аберрации можно увидеть на рис. 3, где увеличительное стекло используется для отображения текста в брошюре Teledyne Lumenera. На этом изображении центр текста («Теледин») остается в фокусе. Однако текст не в фокусе по краям изображения. Это преувеличено бочкообразным искажением на рис. 3, но на практике сферическая аберрация может привести к размытию и потере важных данных изображения вблизи краев кадра.
Почему сферическая аберрация имеет значение при работе с изображениями?
Четкость изображения — главная причина, по которой при проектировании системы машинного зрения необходимо учитывать сферическую аберрацию. Без коррекции результирующее изображение может иметь небольшое или даже сильное размытие по краям. В некоторых случаях это может привести к тому, что изображение может «отрезать» жизненно важную часть цели или окружающей среды. Без резкости от края до края процесс анализа изображения может сильно усложниться.
Без коррекции результирующее изображение может иметь небольшое или даже сильное размытие по краям. В некоторых случаях это может привести к тому, что изображение может «отрезать» жизненно важную часть цели или окружающей среды. Без резкости от края до края процесс анализа изображения может сильно усложниться.
В таких приложениях, как точное земледелие, где используется очень широкое поле зрения с большой высоты, очень важно обеспечить постоянную одинаковую резкость по всему периметру. Это особенно верно, когда постобработка выполняется для помощи в анализе, например, NDVI для мониторинга состояния сельскохозяйственных культур, или с использованием программного обеспечения, которое использует преимущества более высокой разрядности для фактического производства самой аналитики. Чтобы понять NDVI и узнать больше о том, почему битовая глубина важна для анализа изображений, прочитайте записи в блоге Teledyne Lumenera «Индексы растительности, измеряющие здоровье растительности с помощью цифровых изображений» и «Углубленный взгляд на битовую глубину».
В аэрофотосъемке программное сшивание используется для объединения изображений в более крупные мозаики. Это можно сделать с несколькими камерами, чтобы умножить количество пикселей, которые захватывают данные изображения. Однако, если задействована сферическая аберрация, это может оказаться затруднительным из-за отсутствия резкости краев. При объединении изображений требуется уровень перекрытия, чтобы обеспечить правильное выравнивание изображений. Если в фокусе недостаточно краев каждого изображения, это повлияет на способность программного обеспечения выравнивать и сшивать изображения. Следовательно, может потребоваться использование большей части каждого изображения для перекрытия, чтобы компенсировать недостаток четкости, эффективно уменьшая количество пикселей, используемых для отображения уникальной информации. Для получения дополнительной информации об использовании нескольких камер в аэрофотосъемке прочитайте наш информационный документ «Использование одной и нескольких камер в аэрофотосъемке».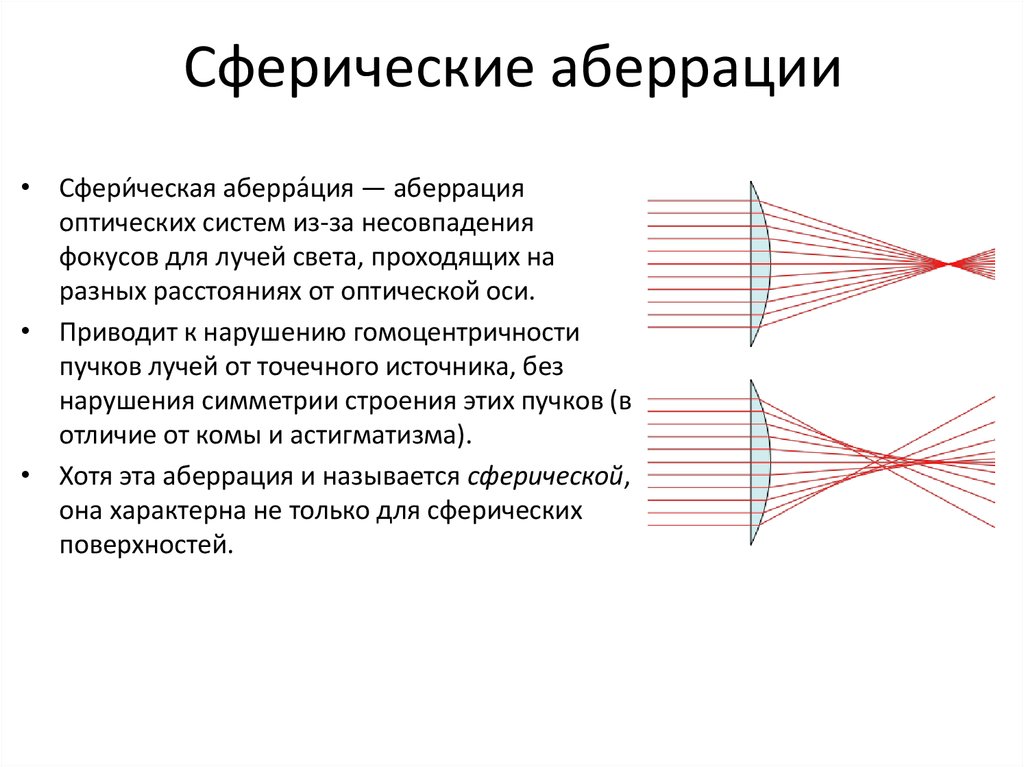
Все сводится к выбору правильной линзы
В ранних оптических системах, в которых использовались одинарные линзы, решение проблемы сферической аберрации заключалось в добавлении небольшой апертуры. Имея узкий путь для прохождения света, расфокусированный свет, исходящий от краев линзы, будет блокироваться, и свет будет проходить только вблизи центра линзы. Это приводит к более четкому изображению, но также снижает яркость. Таким образом, использование системы линз, которая корректирует сферическую аберрацию, помогает предотвратить плохое качество изображения, сохраняя при этом желаемое количество света. Тем не менее, даже с современными конструкциями объективов, которые пытаются скорректировать сферическую аберрацию, использование меньшей диафрагмы по-прежнему является распространенным решением для получения полного кадра в фокусе при достаточном освещении. Чтобы лучше понять, как апертура влияет на формирование изображения, см. запись в блоге Teledyne Lumenera «Улучшение производительности системы обработки изображений с помощью оптимизации апертуры объектива».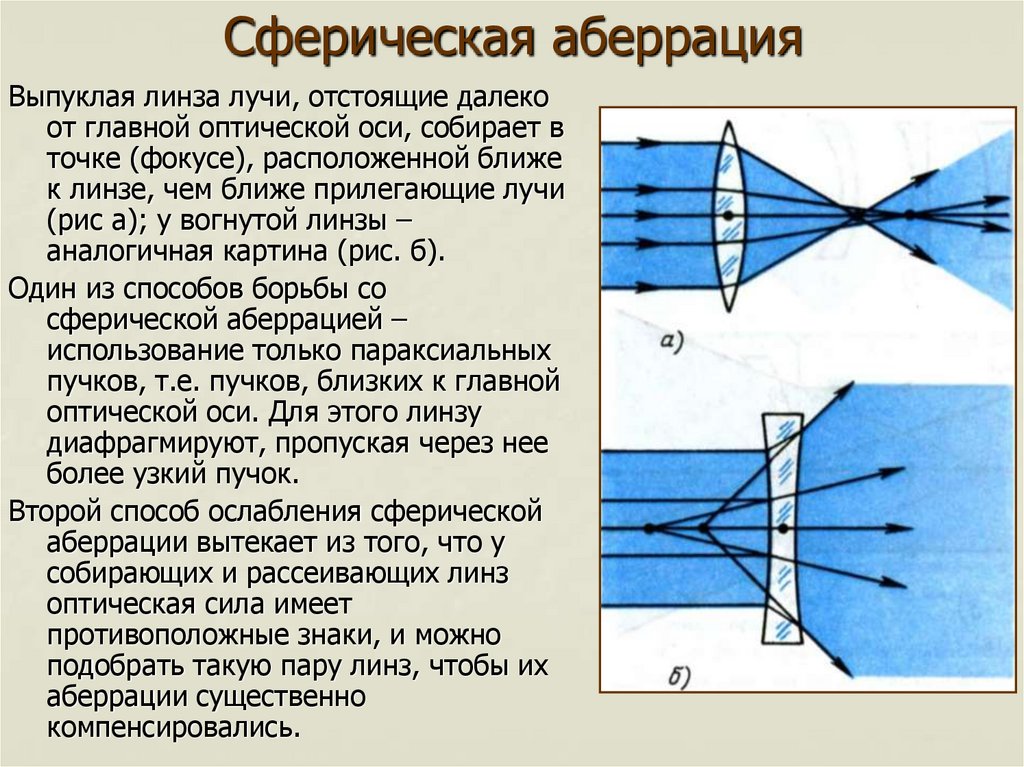
Для промышленных применений может быть сложнее найти решение, когда камера не используется в контролируемых условиях (например, в микроскопии). Производители объективов могут выпускать линзы более высокого качества, которые корректируют несколько типов аберраций, но сферическая аберрация все равно будет до некоторой степени возникать в большинстве систем линз, в которых используется сферическое стекло. Даже если есть поправки, сферическое стекло имеет физическое ограничение фокусировать весь падающий свет в одну точку. Тем не менее, правильная конструкция объектива может в значительной степени скорректировать сферическую аберрацию и создавать изображения, в которых будут запечатлены все важные детали.
Одним из способов корректировки объективом сферической аберрации является регулировка физической формы элементов объектива. Путем шлифовки линзы, чтобы она больше выступала ближе к центру, и внесения некоторых корректировок по краям линза может скорректировать фокусировку на краю и позволить всему свету правильно выровняться.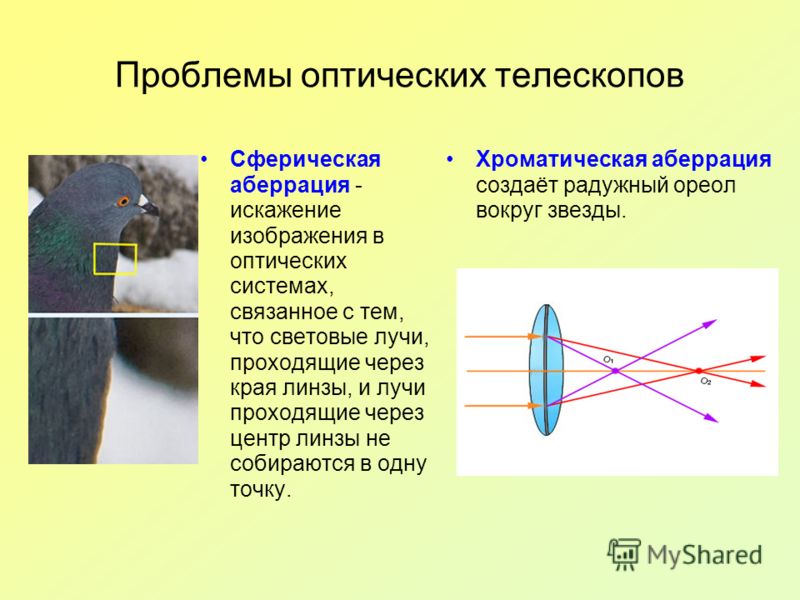 Примером этого является асферическая линза, показанная на рисунке 4. На этом изображении стандартная сферическая линза сравнивается с асферической линзой. Стандартный объектив создает несколько точек фокусировки, но это исправляется введением вместо него асферической линзы, фокусирующей весь свет в одной точке.
Примером этого является асферическая линза, показанная на рисунке 4. На этом изображении стандартная сферическая линза сравнивается с асферической линзой. Стандартный объектив создает несколько точек фокусировки, но это исправляется введением вместо него асферической линзы, фокусирующей весь свет в одной точке.
В зависимости от бюджета выбор объектива будет основываться на множестве факторов, а не только на том, насколько хорошо он может корректировать сферическую аберрацию. Для микроскопии можно приобрести специальную оптику, и даже существуют программные решения для коррекции изображений, такие как INFINITY ANALYZE 7 от Teledyne Lumenera со встроенной коррекцией сферической аберрации. Тем не менее, физические ограничения объектива не могут быть полностью преодолены, из-за множества вариантов объектива никогда не будет одного объектива, который всегда может давать «идеальное» изображение. Любому профессионалу часто необходимы различные типы объективов, поскольку постоянно будут появляться новые цели для изображения и среды, в которых нужно снимать.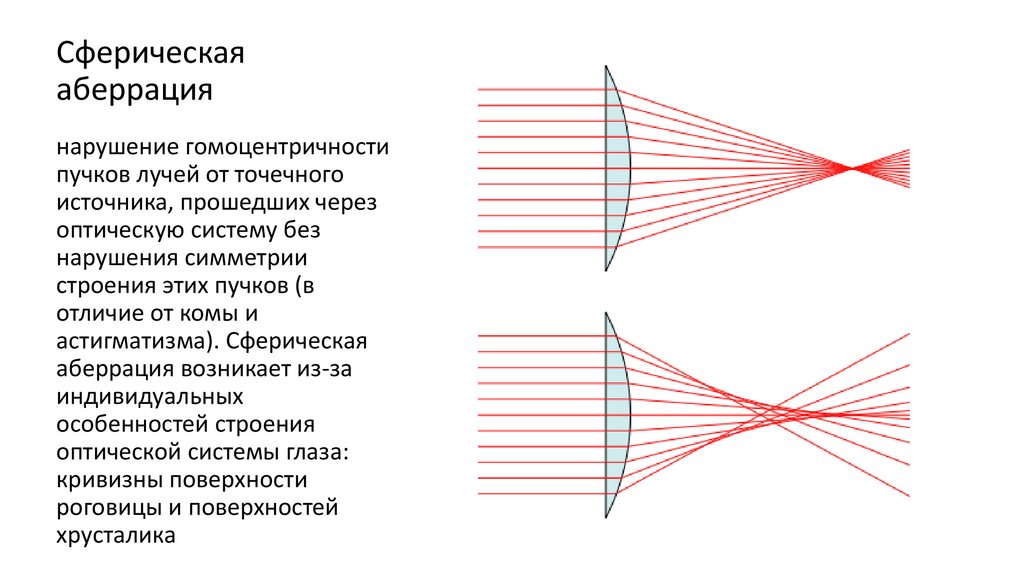


 , «Машиностроение», 1992.
, «Машиностроение», 1992. , «Машиностроение», 1992.
, «Машиностроение», 1992.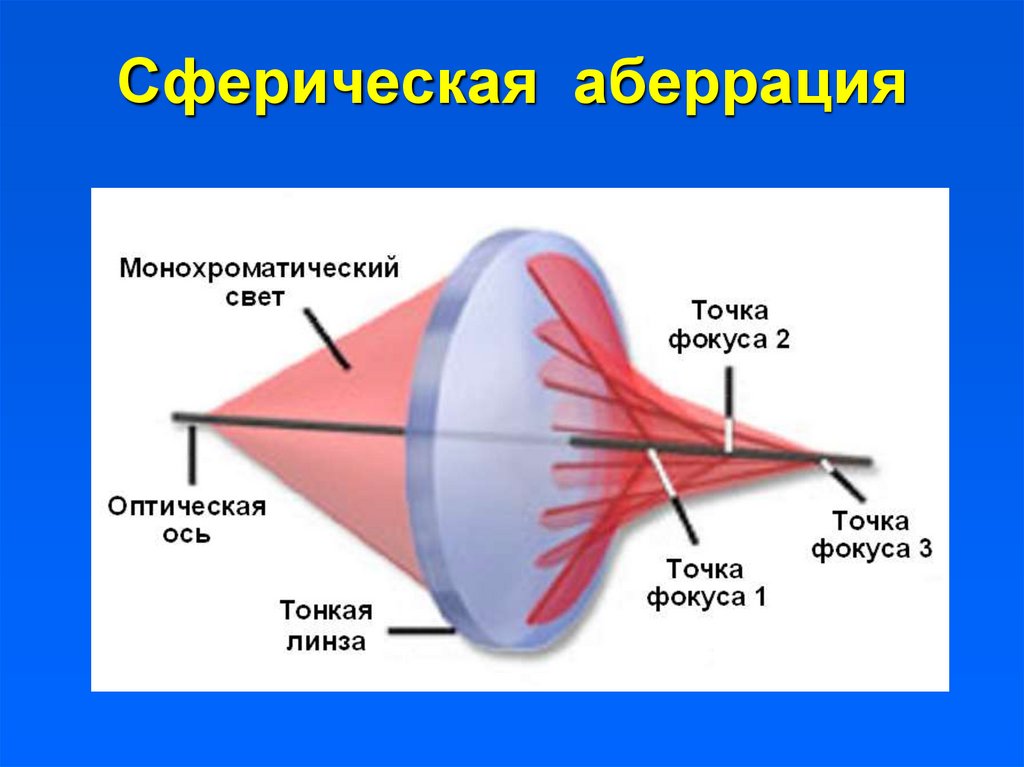 Использование уравнения линзы также предполагает идеальную линзу, и это уравнение практически верно только для лучей, близких к оптической оси, так называемых параксиальных лучей. Для объектива со сферической аберрацией наилучшее приближение фокусного расстояния — это расстояние, на котором разница между параксиальным и краевым лучами наименьшая. Это не идеально, но отклонение от идеального фокуса образует то, что называется «кругом наименьшего беспорядка». Сферическая аберрация — одна из причин, по которой меньшая апертура (большее число f) объектива камеры дает более четкое изображение и большую глубину резкости, поскольку разница между параксиальными и маргинальными лучами меньше.
Использование уравнения линзы также предполагает идеальную линзу, и это уравнение практически верно только для лучей, близких к оптической оси, так называемых параксиальных лучей. Для объектива со сферической аберрацией наилучшее приближение фокусного расстояния — это расстояние, на котором разница между параксиальным и краевым лучами наименьшая. Это не идеально, но отклонение от идеального фокуса образует то, что называется «кругом наименьшего беспорядка». Сферическая аберрация — одна из причин, по которой меньшая апертура (большее число f) объектива камеры дает более четкое изображение и большую глубину резкости, поскольку разница между параксиальными и маргинальными лучами меньше. Изгиб линзы также может дать частичную коррекцию аберрации комы.
Изгиб линзы также может дать частичную коррекцию аберрации комы.