Что такое полная, активная и реактивная мощность?
Power Solutions / Блог / Полезная информация / Что такое полная, активная и реактивная мощность?
В повседневной жизни практически каждый сталкивается с понятием “электрическая мощность”, “потребляемая мощность” или “сколько эта штука “кушает” электричества”. В данной подборке мы раскроем понятие электрической мощности переменного тока для технически подкованных специалистов и покажем на картинке электрическую мощность в виде “сколько эта штука кушает электричества” для людей с гуманитарным складом ума :-). Мы раскрываем наиболее практичное и применимое понятие электрической мощности и намеренно уходим от описания дифференциальных выражений электрической мощности.
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для практических расчётов бесполезна. Прямой расчёт среднего значения мощности требует интегрирования по времени.
Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.
Активная мощность (Real Power)
Единица измерения — ватт (русское обозначение: Вт, киловатт – кВт; международное: ватт -W, киловатт – kW).
Среднее за период Τ значение мгновенной мощности называется активной мощностью, и
выражается формулой:
В цепях однофазного синусоидального тока , где υ и Ι это среднеквадратичные значения напряжения и тока, а φ — угол сдвига фаз между ними.
Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S, активная связана соотношением .
В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.
Реактивная мощность (Reactive Power)
Единица измерения — вольт-ампер реактивный (русское обозначение: вар, кВАР; международное: var).
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними:
(если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью P соотношением: .
Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной.
Величина sin φ для значений φ от 0 до минус 90° является отрицательной величиной. В соответствии с формулой
реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.
Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети.
Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения
Полная мощность (Apparent Power)
Единица полной электрической мощности — вольт-ампер (русское обозначение: В·А, ВА, кВА-кило-вольт-ампер; международное: V·A, kVA).
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: ; соотношение полной мощности с активной и реактивной мощностями выражается в следующем виде: где P — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q›0, а при ёмкостной Q‹0).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии.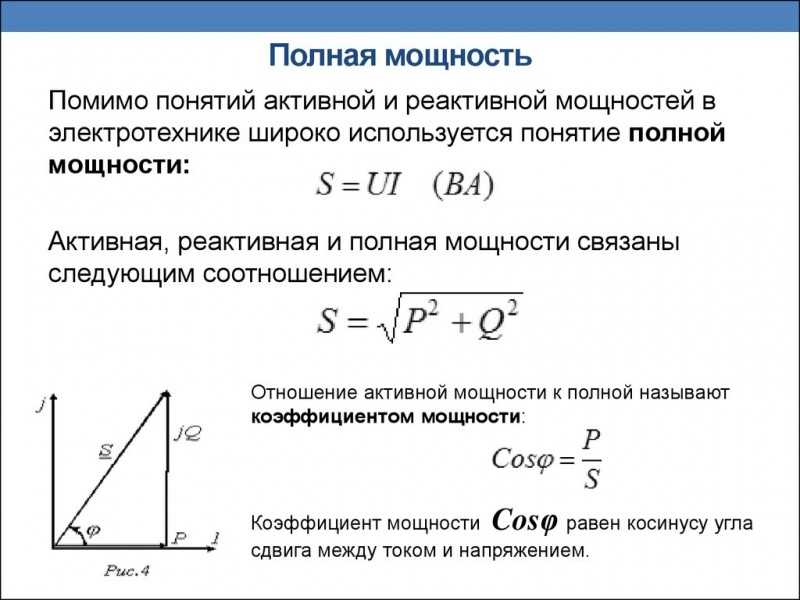
Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Визуально и интуитивно-понятно все вышеперечисленные формульные и текстовые описания полной, реактивной и активной мощностей передает следующий рисунок 🙂
Специалисты компании НТС-групп (ТМ PowerSol) имеют огромный опыт подбора специализированного оборудования для построения систем обеспечения жизненно важных объектов бесперебойным электропитанием. Мы умеем максимально качественно учитывать большое количество электрических и эксплуатационных параметров, которые влияют на выбор оборудования. Производители ИБП и электрогенераторов в документации обязательно указывают полную и активную мощность. Производители стабилизаторов напряжения обычно указывают коэффициент 1(кВт=кВА). Специалисты компании НТС-ГРУПП помогут Вам разобраться в технических характеристиках и максимально комфортно купить ИБП. Несмотря на то что у нас большой выбор стабилизатор напряжения для дома или офиса- мы поможем Вам найти именно тот, который Вам нужен.
© Материал подготовлен специалистами компании НТС-групп (ТМ PowerSol) с использованием информации из открытых источников, в т.ч. из свободной энциклопедии ВикипедиЯ https://ru.wikipedia.org
Что такое реактивная энергия или реактивная мощность?
Когда речь идет об электрических приборах, чаще всего интересуются их электрической мощностью. При этом считается, что чем больше эта мощность, обычно указываемая в документации, приложенной к электроизделию, тем большую полезную работу можно получить от этого изделия.
Электроприборы представляют собой нагрузку, которая для переменного тока имеет разную величину. Так все нагревательные приборы: лампы накаливания, ТЭНы в утюгах, электрических плитах, электрочайниках, стиральных машинах, электрообогревателях и т. п., это активные нагрузки. Все виды трансформаторов, стабилизаторов, электродвигателей – в стиральных машинах, кондиционерах, вентиляторах, отопительных приборах, электроинструменте, насосах для полива и для отопления, газонокосилках, измельчителях веток (шредерах ) и мн.
др. – это нагрузки активно-индуктивные. Люминесцентные лампы и светильники, энергосберегающие компактные лампы (КЛЛ) и пр. – это активно-емкостные нагрузки.
Реактивной называется энергия возникающая при прохождении переменного электрического тока через катушку индуктивности (образуется магнитное поле) или через конденсатор (образуется электрическое поле). Она может увеличиваться или уменьшаться. При увеличении она потребляет мощность из сети, при уменьшении – отдает обратно в сеть.
В домашней электрической сети действует переменное напряжение, величина которого 220 В, а частота 50 Гц. По форме это синусоида, которая 100 раз в секунду переходит через «0». В этот момент происходит смена направления движения тока. При подключении этого напряжения к нагрузке, которая имеет только активную составляющую, ток в цепи по фазе (по моменту действия) полностью совпадает с напряжением. Т. е. при нарастании тока идет нарастание напряжения, при спаде напряжения спадает и ток, при переходе напряжения через «0» ток в это же мгновение тоже переходит через «0».
В случае емкостной нагрузки процесс тот же, но только ток опережает напряжение.
Происходят эти процессы потому, что в первом случае ток, протекающий по катушке индуктивности (обмотке двигателя или трансформатора) создает каждым витком катушки магнитное поле. А т. к. ток изменяется – нарастает или спадает, то суммарное поле тоже увеличивается или уменьшается. Изменяющееся магнитное поле по закону электромагнитной индукции (закону Майкла Фарадея) наводит в соседних витках той же катушки или соседней с ней, например вторичной катушке трансформатора э.
Таким образом, работы нет, а потери присутствуют.
Те же процессы происходят и при включении нагрузки. Но на фоне больших рабочих токов, протекающих при этом, реактивные токи мало заметны.
Уменьшить эти токи можно подключением к индуктивным цепям конденсаторов, а к емкостным, соответственно, индуктивностей. Это называется компенсированием реактивных составляющих.
Оценить реактивную составляющую можно по Км – коэффициенту мощности или по cos φ. При этом cos φ = Р/S, где:
- Р – активная мощность, обеспечивающая рабочие характеристики;
- S – полная мощность, потребляемая устройством.
При cos φ = 1 – вся мощность устройства активная, при меньших значениях – появляется реактивная составляющая. Мощность потребляемая растет, а работа остается та же.
Например, если на дрели и вентиляторе написано, что его мощность 600 Вт, а cos φ = 0,75, то их реальная мощность, потребляемая из сети будет равна 800 Вт, а работу они сделают на 600 Вт.
Правильная компенсация реактивной мощности дает возможность уменьшить мощность, передаваемую по кабельным и проводным сетям предприятия. Это позволяет снизить расход до 10-20 %, а в тех случаях, когда cos φ = 0,5 и даже менее его, результат может быть до 1/3.Предприятия с большим количеством мощных недогруженных электродвигателей должны компенсировать их реактивную мощность.
Небольшие организации, офисы, торговые предприятия могут иметь большую реактивную составляющую за счет люминесцентных источников освещения, двигателей вентиляции приточной и вытяжной, кондиционеров, приводов теплоснабжения и водоснабжения и другой нелинейной нагрузки. К такой нагрузке могут относиться тиристорные и симисторные регуляторы систем освещения, импульсные блоки питания и мн. др. Все эти виды потребителей электроэнергии используют в своей работе импульсный режим, при этом этот режим часто сопровождается крутыми передними и задними фронтами импульсов (нарастанием и спаданием тока и напряжения).
Поэтому передовые производители современных компактных люминесцентных ламп (КЛЛ) заботятся об энергетической эффективности не только самой лампы, но и всей электрической сети, используемой для их питания. Для этого они, незначительно усложнив схему их питания, получают коэффициент мощности, равный 0,92 – 0,97. В то же время простые КЛЛ имеют его значительно меньшей величины, а обычные традиционные люминесцентные «трубки» с электромагнитным пуско-регулирующим аппаратом имеют коэффициент мощности вообще равный 0,5.
Поэтому, выбирая для своей квартиры или офиса малогабаритные энергосберегающие высокоэффективные источники света в виде КЛЛ, обязательно интересуйтесь таким их параметром, как коэффициент мощности. И если он не указан в параметрах продаваемой лампы, то лучше отказаться от такой покупки.
Предлагаем приобрести качественные энергосберегающие лампы:
A60 10W PA LS-V10 E27 4000
Наименование: Лампа светодиодная стандартная LS-V10 10W E27 4000K алюмопл. корп. A-LS-1520
Мощность: 10
Световой поток: 900
Тип лампы: Стандартная
Напряжение (V): 220
Цветовая температура К: 4000
Тип цоколя: E27
Группа: Лампы
Подгруппа: Лампы светодиодные (LED)
Модель: ls-V10
Тип колбы: Стандартная
Цвет стекла: Опаловый
Тип светодиода: SMD
Угол рассеивания, (C): 270
Ресурс часов: 25000
A mm: 110
B mm: 60
Штрих код упаковки: 4895127217815
Количество в упаковке шт.: 50
Производитель: Electrum
(Код: A-LS-1520)
82.49 грн
Наименование: Лампа светодиодная стандартная LS-V10 10W E27 4000K алюмопл. корп. A-LS-1520
Артикул: A-LS-1520
Тип цоколя: E27
Купить
B60 10W PA10L E27 3000 3 шт.
Наименование: Комплект ламп светодиодных стандартных B60 PA10L 10W E27 3000K алюмопл. корп. 3шт. 18-0120
Артикул: 18-0120
Мощность: 10
Световой поток: 750
Тип лампы: Стандартная
Напряжение (V): 220
Цветовая температура К: 3000
Тип цоколя: E27
Группа: Лампы
Подгруппа: Лампы светодиодные (LED)
Модель: PA10L
Тип колбы: Стандартная
Цвет стекла: Опаловый
Тип светодиода: SMD
Ресурс часов: 20000
A mm: 109
B mm: 60
Штрих код упаковки: 4895127203382
Количество в упаковке шт.: 40/120
Производитель: ELM
(Код: 18-0120)
215.98 грн
Наименование: Комплект ламп светодиодных стандартных B60 PA10L 10W E27 3000K алюмопл. корп. 3шт. 18-0120
Артикул: 18-0120
Мощность: 10
Тип цоколя: E27
Купить
B60 10W PA10 E27 4000 3 шт.
Наименование: Комплект ламп светодиодных стандартных B60 PA10L 10W E27 4000K алюмопл. корп. 3шт. 18-0150
Артикул: 18-0150
Мощность: 10
Световой поток: 806
Тип лампы: Стандартная
Напряжение (V): 220
Цветовая температура К: 4000
Тип цоколя: E27
Группа: Лампы
Подгруппа: Лампы светодиодные (LED)
Модель: PA10L
Тип колбы: Стандартная
Цвет стекла: Опаловый
Тип светодиода: SMD
Угол рассеивания, (C): 250
Ресурс часов: 20000
A mm: 109
B mm: 60
Штрих код упаковки: 4895127200930
Количество в упаковке шт.: 50
Производитель: ELM
(Код: 18-0150)
168.50 грн
Наименование: Комплект ламп светодиодных стандартных B60 PA10L 10W E27 4000K алюмопл. корп. 3шт. 18-0150
Артикул: 18-0150
Мощность: 10
Тип цоколя: E27
Купить
A60 10W PA LS-33 Elegant Е27 Ra90 4000
Наименование: Лампа светодиодная стандартная A60 LS-33 Elegant 10W E27 Ra90 4000K алюмопл.
корп. A-LS-1912
Артикул: A-LS-1912
Мощность: 10
Световой поток: 850
Цветовая температура: 4000
Тип лампы: Стандартная
Тип цоколя: E27
Напряжение (V): 220
Ресурс часов: 25000
A mm: 111
B mm: 60
Модель: LS-33 Elegant
Тип светодиода: SMD Samsung
Количество в ящике (шт): 50
Угол рассеивания, (C): 270
Производитель: Electrum
(Код: A-LS-1912)
91.15 грн
Наименование: Лампа светодиодная стандартная A60 LS-33 Elegant 10W E27 Ra90 4000K алюмопл. корп. A-LS-1912
Артикул: A-LS-1912
Мощность: 10
Световой поток: 850
Купить
Мощность в цепи переменного тока – активная мощность, реактивная мощность, полная мощность
В электрических и электронных схемах мощность является одной из наиболее важных величин, используемых для анализа цепей для практических приложений. Электрическая мощность определяется как скорость расширения или поглощения энергии в цепи во времени, т.
е.
$$\mathrm{Power,P=\frac{Energy \;expanded\; или\; поглощенный (𝑊)}{Time(𝑡)}}…..(1)$$
Эта статья предназначена для объяснения отношения мощности в цепях переменного тока . Где цепь переменного тока — это цепь, которая возбуждается от источника переменного напряжения.
Мгновенная мощность в цепи переменного тока
Значение электрической мощности в цепи переменного тока, измеренное в определенный момент времени, называется мгновенная мощность . Обычно обозначается строчной буквой $p$. В целом, мгновенная мощность в цепи переменного тока получается путем умножения мгновенного напряжения на мгновенный ток, т. е.
$$\mathrm{Мгновенная \;мощность, 𝑝 = \upsilon. i\;\;}….(2)$$
Рассмотрим любую цепь переменного тока, если мгновенные значения напряжения и тока в цепи заданы формулой
$$\mathrm{\upsilon=V_{m}\ sin\left({wt}\right)}….(3)$$
$$\mathrm{i=I_{m}\sin\left({wt-\phi}\right)}.. ..(4)$$
Где $\mathrm{\phi}$ — фазовый угол между напряжением и током в любой момент времени.
Где $\mathrm{\phi}$ имеет отрицательное значение, когда ток отстает от напряжения, положительное значение, когда ток опережает напряжение, и ноль, когда ток и напряжение находятся в одной фазе.
Следовательно, по определению мгновенная мощность определяется выражением
$$\mathrm{p=vi=V_{m}\sin(wt).I_{m}\sin(wt-\phi)}$ $
$$\mathrm{\Rightarrow\; p=\frac{1}{2}\times2\times\; V_{m}I_{m}\sin wt \sin (wt-\phi)}$$
$$\mathrm{\Rightarrow\; p=\frac{V_{m}I_{m}}{2}[\cos\phi-\cos(2wt-\phi)]}$$
$$\mathrm{\следовательно\; p=\frac{V_{m}I_{m}}{2}\cos\phi-\frac{V_{m}I_{m}}{2}\cos(2wt-\phi)}…. ..(5)$$
Здесь второе слагаемое в правой части уравнения (5) содержит удвоенный частотный член, а модуль среднего значения этого члена равен нулю, поскольку среднее значение синусоидальной величины по полному цикл нулевой. Таким образом, мгновенная мощность состоит только из первого члена уравнения (5), т. е.
$$\mathrm{P=\frac{1}{2}\;V_{m}I_{m}\cos\phi..
….(6)}$$
Этот термин равен средняя мощность в цепи переменного тока. Кроме того, средняя мощность в цепи переменного тока может быть выражена через среднеквадратичные значения напряжения и тока следующим образом:
$$\mathrm{P=\frac{V_{m}}{\sqrt{2}}\frac{I_ {m}}{\sqrt{2}}\cos\phi}$$
$$\mathrm{\следовательно \;P=VI\cos\phi…..(7)}$$
Где , $\mathrm{\cos\phi}$ известен как коэффициент мощности схемы.
В электрической цепи переменного тока различают следующие три вида электроэнергии −
- Активная мощность
- Реактивная мощность
- Полная мощность
Активная мощность
Активная мощность – это количество полной электроэнергии в электрической цепи переменного тока, которая фактически потребляется или используется. Его также называют реальной мощностью или реальной мощностью . Активная мощность измеряется в ваттах (Вт). Более крупными единицами активной мощности являются киловатт (кВт), мегаватт (МВт), гигаватт (ГВт) и так далее.
Технически, когда в электрической цепи переменного тока угол сдвига фаз становится равным нулю, т.е. коэффициент мощности становится равным единице, то мощность, потребляемая в цепи, называется 9{\circ}}$$
$$\mathrm{\следовательно, Active\;Power,P=VI}$$
На практике активная мощность используется для определения номинальных характеристик электрических нагрузок, таких как двигатели, лампочки, утюги, и т.д.
Реактивная мощность
Реактивная мощность — это количество общей электрической мощности, которая остается неиспользованной в электрической цепи переменного тока и течет туда и обратно в электрической системе от нагрузки к источнику и наоборот . Обозначается буквой Q и измеряется в Вольт-ампер реактивный (ВАР) .
Реактивная мощность в цепи переменного тока также может быть определена как произведение среднеквадратичных значений напряжения и тока на синус фазового угла, т. е.
$$\mathrm{Q=VI\sin\phi}$$
Реактивная мощность также известна как мощность Вт или квадратурная мощность .
Для индуктивной нагрузки потребляемая реактивная мощность равна отстающей реактивной мощности , а потребляемая конденсатором — опережающей реактивной мощности . Следовательно, есть два элемента цепи переменного тока, а именно индуктор и конденсатор, которые отвечают за поток реактивной мощности в цепи.
Реактивная мощность отвечает за работу всех электромагнитных машин, таких как двигатели, генераторы и т. д., поскольку она создает в этих машинах необходимое магнитное возбуждение.
Полная мощность
Полная мощность, производимая источником переменного тока, равна полной мощности . Он измеряется как произведение среднеквадратичных значений напряжения и тока. Полная мощность обозначается буквой S и измеряется в Вольт-ампер (ВА) .
$$\mathrm{Полная\;мощность,\;S=VI}$$
Полная мощность также определяется суммой векторов активной и реактивной мощностей, т.е.
$$\mathrm{S=P +jQ}$$
На практике полная мощность используется для определения номинальных характеристик электрических устройств, которые действуют как источники и передатчики энергии, таких как генераторы, генераторы переменного тока, трансформаторы и т.
д.
Числовой пример
Если значения RMS тока и напряжения в цепи переменного тока составляют 220 В и 5 А. Если между напряжением и током имеется разность фаз 60°. Определить активную мощность, реактивную мощность и полную мощность в цепи.
Решение
Данные,
Следовательно, активная мощность в данной цепи равна,
$$\mathrm{P=VI\cos\phi}$$
$$\mathrm\Rightarrow{P=220 \times5\times\cos60}$$
$$\mathrm{\следовательно\;P=550W}$$
Реактивная мощность, протекающая по цепи, равна,
$$\mathrm{Q=VI\sin\ phi}$$
$$\mathrm{Q=220\times5\times\sin60}$$
$$\mathrm{\следовательно Q = 952,63 \;VAR}$$
Полная мощность, подводимая к схема,
$$\mathrm{S = VI = 220\times5}$$
$$\mathrm{\следовательно S = 1100 \;VA}$$
Заключение
В этой статье мы обсудили три основных типа электрических мощностей, а именно активной мощности, реактивной мощности и полной мощности в цепи переменного тока.
Основная причина такой классификации мощностей заключается в том, что в цепи переменного тока электрическая мощность зависит от коэффициента мощности.
Активная и реактивная мощность – x-engineer.org
Содержание
- Введение
- Активная мощность
- Реактивная мощность
- Резюме
- Ссылки
Введение
В цепях переменного тока передачу электрической энергии и поведение электрических машин часто легче понять, работая с мощностью вместо того, чтобы иметь дело с напряжениями и токами. Мощность может быть определена различными способами, применимость определения зависит от типа цепи.
Наиболее распространенное определение мощности: энергия, затрачиваемая в единицу времени [Дж/с] .
P [Вт] = E [Дж] / время [с]
В цепях переменного тока понятие мощности немного отличается в том смысле, что существует три типа мощности:
- активная мощность
- реактивная мощность
- Полная мощность
Активная мощность
Для лучшего понимания концепции активной мощности мы будем использовать простую цепь переменного тока, состоящую из источника синусоидального напряжения и резистора.
Изображение: Источник переменного напряжения с резисторной цепью
В этой простой схеме мы видим, что ток протекает через резистор R = 2 Ом, меняя свое направление. Если предположить, что напряжение переменного тока равно E [В], а ток равен I [А], мощность через резистор будет P [Вт] = EI.
Когда резистор включен в цепь переменного тока, он не изменит фазу (θ) между проходящим через него напряжением (E) и током (I). Другими словами, напряжение и ток, проходящий через резистор, находятся в фазе друг с другом . Если представить напряжение и ток, проходящие через резистор, в виде векторов (фазоров), они будут перекрываться.
Изображение: векторная диаграмма — резистор
Для лучшей визуализации этой концепции давайте создадим простую имитационную модель приведенной выше схемы с помощью Simetrix.
Изображение: Активная мощность – схема Simetrix
В этой имитационной модели у нас есть источник напряжения с амплитудой 162 В и частотой 60 Гц.
Электрический ток будет течь через резистор сопротивлением 2 Ом. Измеряются напряжение, ток и мощность на резисторе, и результаты отображаются на изображении ниже.
Изображение: Активная мощность – график Simetrix
Как видно на верхнем графике, напряжение и ток совпадают по фазе, задержки между сигналами нет. Кроме того, мощность всегда положительна, будучи произведением напряжения и тока, которые имеют один и тот же знак, положительный или отрицательный. Мощность, которую мы измеряем на резисторе, равна 90 186 активной мощности 90 187, потому что она всегда течет от источника (напряжения) к нагрузке (резистор). В чисто резистивной цепи вся мощность в цепи является активной мощностью.
В этом случае мощность преобразуется из одной формы в другую, например: из электричества в тепло, из механической в электрическую и т. д. Это определение мощности обычно используется в физике и также известно как активная мощность или реальная мощность или реальная мощность .
В заключение, активная мощность P , также известная как истинная/реальная мощность , представляет собой мощность, которая преобразуется из одной формы в другую (например, электричество в тепло) и измеряется в Вт [Вт] . Мощность в чисто резистивной электрической цепи представляет собой полностью активную мощность.
Пример расчета активной мощности
Рассчитайте активную мощность, рассеиваемую на резисторе R = 2 Ом в цепи переменного тока при пиковом напряжении E пик = 162 В и частоте f = 60 Гц. Визуализируйте функцию напряжения, тока и мощности от времени t [с] на графике вместе с их пиковыми и среднеквадратичными значениями.
Шаг 1 . Рассчитать E среднеквадратичное значение = E пик / √2 = 162 / √2 = 114,55 В
Шаг 2 . Рассчитать I пик = E пик / R = 162 / 2 = 81 A
Шаг 3 .
Вычислите I скз = I пик / √2 = 81 / √2 = 57,28 А
Шаг 4 . Рассчитайте активную мощность P = E СКЗ ⋅ I СКЗ = 114,55 ⋅ 57,28 = 6,56 кВт
Шаг 5 . Визуализируйте функцию напряжения, тока и мощности от времени t [с] на графике.
Изображение: график напряжения, тока и активной мощности
Реактивная мощность
Когда электрическая цепь переменного тока содержит катушку индуктивности или конденсатор в дополнение к резистору, мощность, содержащаяся в этой цепи, не является полностью активной/истинной/реальной. Это связано с тем, что катушка индуктивности и конденсатор могут накапливать энергию в виде магнитных или электрических полей и возвращать ее обратно в цепь в виде электрической энергии.
В схеме ниже мы последовательно соединяем источник переменного напряжения, резистор и катушку индуктивности.
Изображение: источник переменного напряжения с цепью резистор-индуктор
Ток все еще проходит через компоненты, меняя свое направление, но в этом случае между напряжением и током имеется фазовая задержка 90º.
Эта фазовая задержка возникает из-за индуктора, который преобразует энергию из электрической формы в магнитную и обратно. Если мы представим вектор напряжения и тока для приведенной выше схемы, мы получим следующее:
Изображение: векторная диаграмма — индуктор
Напряжение 0186 опережает ток с фазовой задержкой 90º.
Чтобы объяснить понятие реактивной мощности, мы будем использовать простую электрическую цепь переменного тока, которая содержит источник переменного напряжения с амплитудой 120 В и частотой 60 Гц, резистор 1 мкОм и катушку индуктивности 5 мГн (см. ниже). Сопротивление установлено очень низким, чтобы иметь «чисто» индуктивную цепь.
Изображение: Реактивная мощность — схема Simetrix
Мощность измеряется на выводе катушки индуктивности и напряжение на ней. Измерение тока выполняется перед резистором, но одинаково для обоих компонентов, соединенных последовательно. Эта схема смоделирована в Simetrix, и результаты показаны ниже.
Изображение: Реактивная мощность – график Simetrix
По результатам моделирования мало что можно заметить.
Во-первых, мы видим, что ток отстает от напряжения с фазовой задержкой 90º. Кроме того, мощность на катушке индуктивности меняет знак, будучи либо положительной, либо отрицательной. Изменение знака означает, что мощность течет от источника напряжения к индуктору (положительная мощность) и от индуктора к источнику напряжения (отрицательная мощность). Мощность, отображаемая на графике, равна чисто 9.0186 реактивный , что означает, что он вообще не рассеивается в виде тепла. Реактивная мощность также известна как мнимая мощность .
Это изменение знака мощности связано с поведением индуктора, который заряжается энергией из цепи, а затем разряжает ту же энергию обратно в цепь. Можно сказать, что энергия «перерабатывается» и не используется для производства тепла или механической работы.
Изображение: источник переменного напряжения со схемой резистор-индуктор-переключатель
Схема выше помогает объяснить, как ведет себя индуктор и как мощность преобразуется из электрической формы в магнитную и обратно.
Схема разделена на две части: цепь зарядки (слева) и цепь разряда (справа). Активация/деактивация каждой цепи осуществляется с помощью переключателя S. Действие зарядки/разрядки связано с катушкой индуктивности. При зарядке катушки индуктивности мощность от источника напряжения (12 В) разделяется на две части: активная/активная мощность, рассеиваемая резистором R 1 = 140 Ом и реактивная/мнимая мощность, запасенная в катушке индуктивности L = 3H.
Когда переключатель S размыкает цепь зарядки, он также замыкает цепь разрядки. В этом состоянии запасенная в индукторе энергия разряжается через резистор R 2 = 140 Ом. В фазе разряда вся электрическая мощность в цепи разряда представляет собой активную мощность из-за того, что она проходит через резистор, а катушка индуктивности теряет накопленную энергию.
Мощность, которая течет туда и обратно между источником и нагрузкой, называется реактивной или мнимой мощностью . Символ реактивной мощности — Q , и он также рассчитывается как произведение напряжения на ток, но единицей измерения является Вольт-ампер реактивный [ВАР] .
Из-за увеличения и уменьшения магнитного поля (катушка индуктивности) или электрического поля (конденсатор) реактивная мощность (Q) забирает мощность из цепи переменного тока, что затрудняет прямую подачу активной мощности (P) к цепи или нагрузке.
Пример расчета реактивной мощности
Рассчитайте реактивную мощность в катушке индуктивности L = 5 мГн в цепи переменного тока с пиковым напряжением E пик = 162 В и частотой f = 60 Гц.
Шаг 1 . Вычислить E rms = E пик / √2 = 162 / √2 = 114,55 В
Шаг 2 . Рассчитайте индуктивное сопротивление X L = 2 ⋅ π ⋅ f ⋅ L = 2 ⋅ π ⋅ 60 ⋅ 5⋅10 -3 = 1,885 Ом
Шаг 3 . Вычислите I пик = E пик / X L = 162 / 1,885 = 85,994 A
Шаг 4 . Вычислите I скз = I пик / √2 = 85,994 / √2 = 60,771 А
Шаг 5 .
Расчет реактивной мощности Q = E действ. ⋅ I действ. = 114,55 ⋅ 60,771 = 6,9614 ВАр
Резюме
Основные различия между активной и реактивной мощностью приведены в таблице ниже.
| Активная мощность | Реактивная мощность |
| Реальная мощность, используемая/потребляемая/рассеиваемая цепью/нагрузкой | работа |
| Всегда положительный, не меняет направление | Может быть положительным или отрицательным, периодически меняет направление |
| Поток только от источника к нагрузке/контуру | Потоки от источника к нагрузке или обратно, от нагрузки к источнику |
| Обозначается буквой P и измеряется в ваттах, P [Вт] | Обозначается буквой Q и измеряется в вольт-ампер-реактивных, Q [ VAR] |
| Измерено в реальной цепи с помощью ваттметра | Измерено в реальной цепи с помощью варметра |
| Вырабатывает полезную работу, например, механическую энергию, тепло или свет | Не производит полезную работу, только колеблется в обратную сторону и далее между источником и нагрузкой/контуром |
| Зависит от рассеивающих элементов цепи (сопротивление) | Зависит от индуктивных или емкостных элементов цепи (реактивное сопротивление) |
| Максимум в чисто резистивной цепи емкостная цепь |
Ссылки
[1] Теодор Вилди, Электрические машины, приводы и энергосистемы, 6-е издание, Pearson, 2005.
