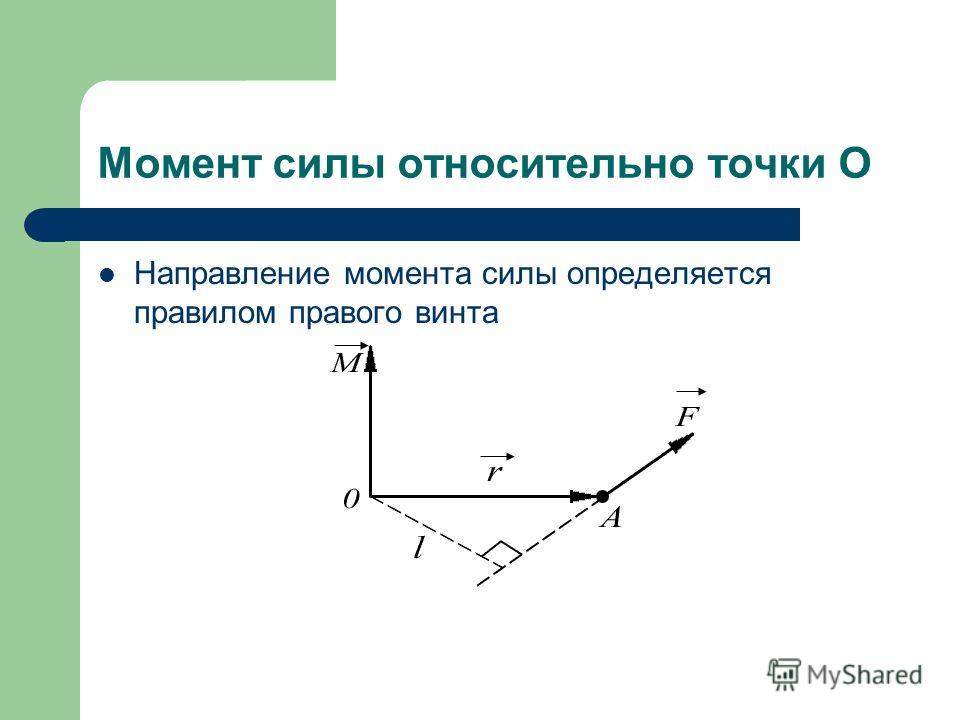
Что такое плечо силы относительно точки: Плечо силы. Определение и примеры расчета — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Формула плеча силы в физике

Определение и формула плеча силы

Рассмотрим рычаг с осью вращения находящийся в точке О. (рис.1). Силы ${\overline{F}}_1$ и ${\overline{F}}_2$, действующие на рычаг направлены в одну сторону.

Минимальное расстояние между точкой опоры (точка О) и прямой, вдоль которой действует на рычаг сила, называют плечом силы.

Для нахождения плеча силы следует из точки опоры опустить перпендикуляр к линии действия силы. Длинна данного перпендикуляра и станет плечом рассматриваемой силы. Так, на рис.1 расстояние $\left|OA\right|=d_1$- плечо силы $F_1$; $\left|OA\right|=d_2$- плечо силы $F_2$.

Рычаг находится в состоянии равновесия, если выполняется равенство:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1\right).\]

Предположим, что материальная точка движется по окружности (рис.2) под действием силы $\overline{F}$ (сила действует в плоскости движения точки). В таком случае угловое ускорение ($\varepsilon $) точки определяется тангенциальной составляющей ($F_{\tau }$) силы $\overline{F}$:

\[mR\varepsilon =F_{\tau }\left(2\right),\]

где $m$ — масса материальной точки; $R$ — радиус траектории движения точки; $F_{\tau }$ — проекция силы на направление скорости движения точки.

Если угол $\alpha $ — это угол между вектором силы $\overline{F}$ и радиус — вектором $\overline{R}$, определяющим положение рассматриваемой материальной точки (Этот радиус- вектор проведен из точки О в точку А на рис.2), тогда:

\[F_{\tau }=F{\sin \alpha \ \left(3\right).\ }\]

Расстояние $d$ между центром O и линией действия силы $\overline{F}$ называют плечом силы. Из рис.2 следует, что:

\[d=R{\sin \alpha \ \left(4\right).\ }\]

Если на точку будет действовать сила ($\overline{F}$), направленная по касательной к траектории ее движения, то плечо силы будет равно $d=R$, так как угол $\alpha $ станет равен $\frac{\pi }{2}$.

Момент силы и плечо

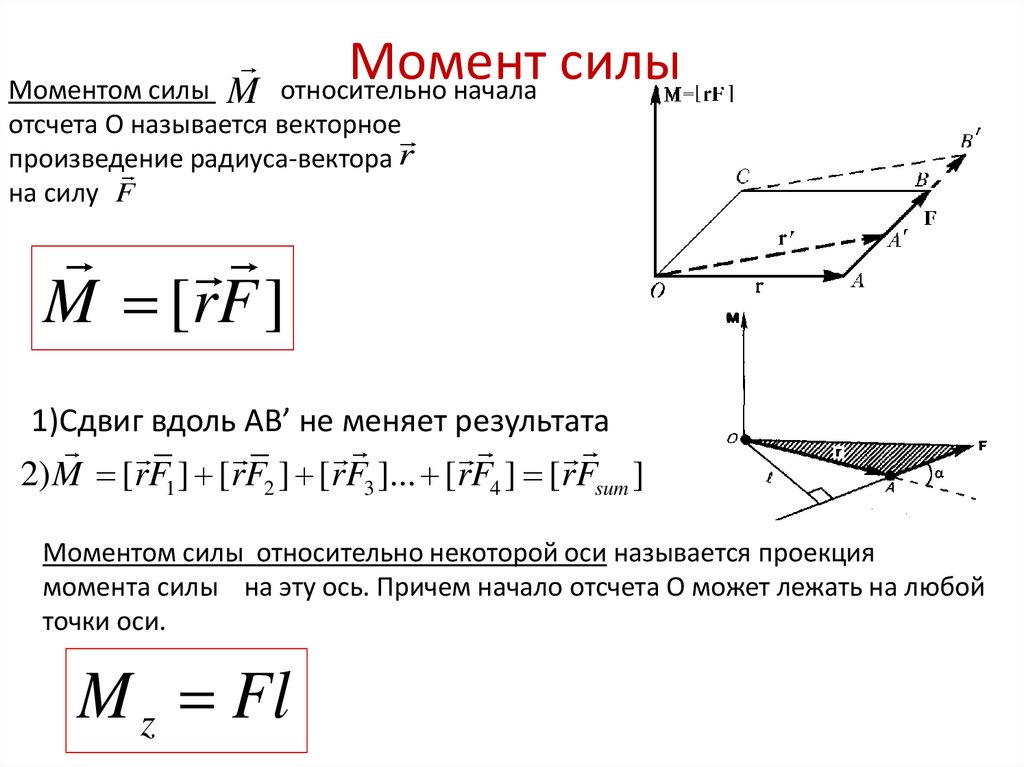
Понятие плечо силы иногда используют, для записи величины момента силы ($\overline{M}$), который равен:

\[\overline{M}=\left[\overline{r}\overline{F}\right]\left(5\right),\]

где $\overline{r}$ — радиус — вектор проведенный к точке продолжения силы$\ \overline{F}$.

Модуль вектора момента силы равен:

\[M=F{r\sin \alpha =\ }Fd\ \left(6\right).\]

Построение плеча силы

И так, плечом силы называют длину перпендикуляра, который проводят из некоторой выбранной точки, иногда ее называют полюсом (выбираемой произвольно, но при рассмотрении одной задачи один раз). При рассмотрении задач точку О выбирают обычно на пересечении нескольких сил) к силе (рис.3 (а)). Если точка О будет лежать на одной прямой с силами или на самой силе, то плечи сил будут равны нулю.

Если перпендикуляр не получается построить, то вектор силы продлевают в нужном направлении, после этого строят перпендикуляр (рис.3 (б)).

Примеры задач с решением

Пример 1

Задание. Какова масса меньшего тела ($m_1$), если его уравновешивает тело массой $m_2={\rm 2\ }$кг? Тела находятся на невесомом рычаге (рис.3) отношение плеч рычага 1:4?

Решение.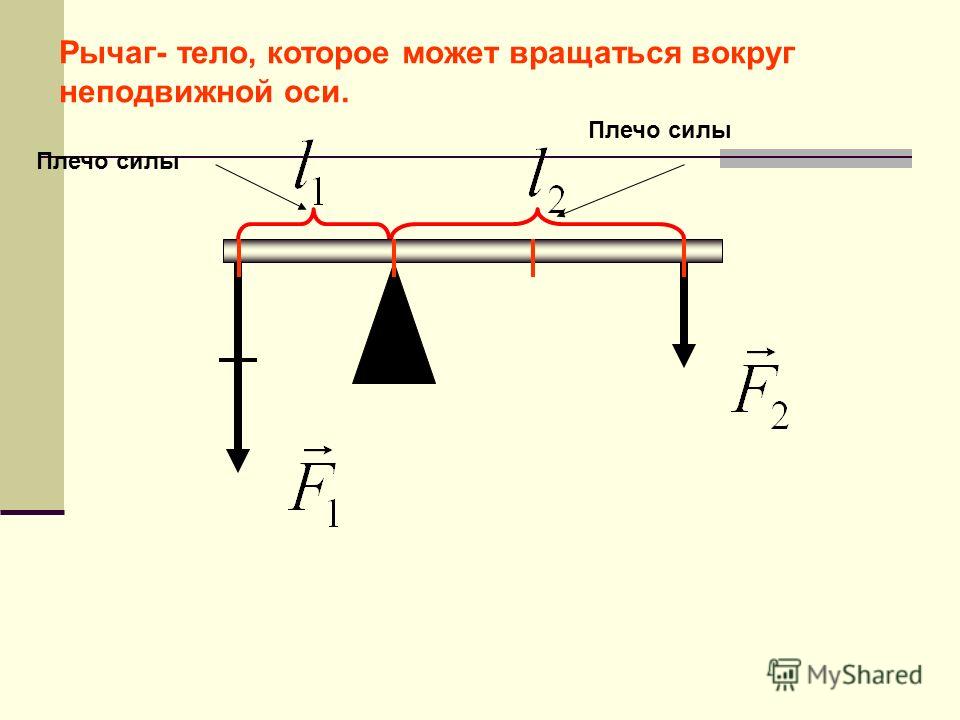 Основой решения задачи является правило равновесия рычага:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1.1\right),\]

где силы, действующие на концы рычага равны по модулю силам тяжести, которые действуют на тела, следовательно, формулу (1.1) перепишем в виде:

\[\frac{m_1g}{m_2g}=\frac{d_2}{d_1}\to \frac{m_1}{m_2}=\frac{d_2}{d_1}\left(1.2\right).\]

Из выражения (1.2) получим искомую массу $m_1$:

\[m_1=\frac{m_2d_2}{d_1}.\]

Вычислим искомую массу:

\[m_1=2\cdot \frac{1}{4}=0,5\ (кг).\]

Ответ. $m_1=0,5\ кг$

Пример 2

Задание. Однородный стержень длинной $l\ $и массой $M$ расположен горизонтально. Один конец стержня в точке А закреплён так, что может вращаться вокруг этой точки, другой конец опирается на наклонную плоскость, угол наклона которой к горизонту равен $\alpha $.

На стержне на расстоянии $b\ $от точки А лежит небольшой груз. Каковы плечи сил, действующих на стержень?

Решение. Изобразим на рис.4 силы, действующие на стержень. Это: сила тяжести: $M\overline{g}$, вес груза, расположенного на нем $\overline{P}=m_1\overline{g}$, сила реакции наклонной плоскости: $\overline{N}$; сила реакции опоры в точке A: $\overline{N}’$.

Плечи сил будем искать относительно точки A. Плечо силы $\overline{N’}$ будет равно нулю, так как сила приложена к стержню в точке А:

\[d_{N’}=0\ \left(2.1\right).\]

Плечо другой силы реакции опоры ($\overline{N}$) равно длине перпендикуляра AC:

\[d_N=l{\sin (90-\alpha )\ }=l{\cos \alpha \ \left(2.2\right).\ }\]

Плечо силы $M\overline{g}$ из рис.4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:

\[d_{Mg}=\frac{l}{2}\left(2.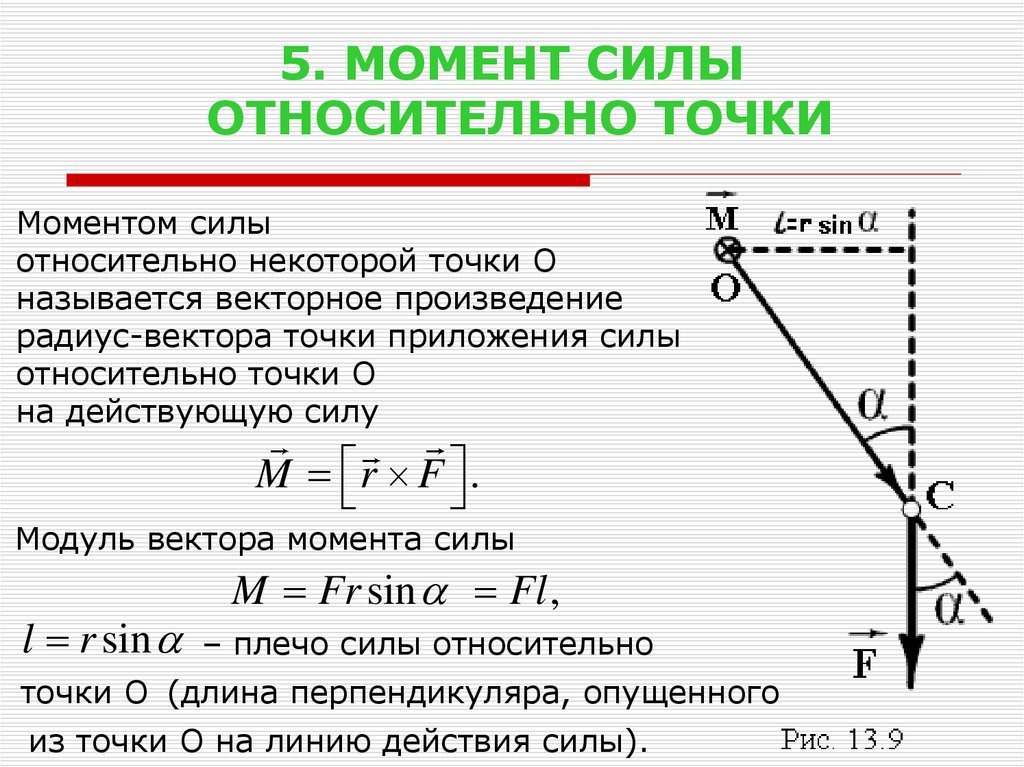 3\right).\]

Плечо силы $m_1\overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:

\[d_{m_1g}=b.\]

Ответ. $d_{N’}=0;;\ d_N=l{sin (90-\alpha )\ }=l{cos \alpha \ \left(м\right),\ }d_{Mg}=\frac{l}{2},\ d_{m_1g}=b$

Читать дальше: формула полезной мощности.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Как найти плечо силы. Плечо силы

ПЛЕЧО СИЛЫ

Кратчайшее расстояние от данной точки (центра) до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы (см. МОМЕНТ СИЛЫ).

— ́ — наиболее проксимальный сегмент руки, прикрепляющийся к туловищу посредством плечевого сустава. располагается между плечевым суставом и локтевым суставом.. .
Атлас анатомии человека
— Единица мер Древнего Востока = 1367 кв.м. …
Словарь мер
— ближайший к туловищу отдел передней конечности наземных позвоночных. Расположено между плечевым и локтевым суставами. Плечевая кость в суставах соединяется вверху с плечевым поясом, внизу — с костями предплечья…
Биологический энциклопедический словарь
— кратчайшее расстояние от данной точки до линии действия силы. См. Момент силы….
Естествознание. Энциклопедический словарь
— I ́ проксимальный сегмент верхней конечности…
Медицинская энциклопедия
— проксимальная часть верхней конечности, ограниченная сверху линией, соединяющей нижние края большой грудной мышцы и широчайшей мышцы спины, а снизу — линией, проходящей на два поперечных пальца выше надмыщелков…
Большой медицинский словарь
— см. Момент силы….
Большой энциклопедический политехнический словарь
— 1. На судне П. называется закругление наружной обшивки борта. 2. Плечом яра называется место, где изогнутый берег переходит в прямолинейный…
Морской словарь
— человека, ближайший к туловищу сегмент верхней конечности. Сверху П. ограничено плечевым суставом, снизу — локтевым суставом…
— относительно точки, кратчайшее расстояние от данной точки до линии действия силы, т. е. длина перпендикуляра, опущенного из этой точки на линию действия силы…
Большая Советская энциклопедия
— кратчайшее росстояние от данной точки до линии действия силы. См. Момент…
Большой энциклопедический словарь
— Общеславянское слово, образованное от ныне исчезнувшего плето – …
Этимологический словарь русского языка Крылова
— Древнерусское – плече…
Этимологический словарь русского языка Семенова
— см.: А через?…
Словарь русского арго
— плече ср. рамо; вообще, место соединенья плечевой кости, лопатки и ключицы; о человеке часть тела от шеи до локтя, или до половины, трети раменной кости. | Плечо представитель силы, могуты, власти…
Толковый словарь Даля
— ́, -а, мн. плечи, плеч, плечам, ср. 1. Часть туловища от шеи до руки. Нести узел на плече. Закинуть рюкзак за плечи и за плечи. Расправить плечи. Взвалить на плечи и на плечи что-н. . На плечах что-н. у кого-н. …
Толковый словарь Ожегова

«ПЛЕЧО СИЛЫ» в книгах

Плечо друга

Из книги Хроника рядового разведчика. Фронтовая разведка в годы Великой Отечественной войны. 1943–1945 гг. автора Фокин Евгений Иванович

Плечо друга

Из книги Хроника рядового разведчика автора Фокин Евгений Иванович

Плечо друга — Вперед! Не отставать! — простуженным голосом кричит лейтенант, и мы, разведчики, с ходу минуем только что отбитые окопчики противника и устремляемся за убегающими автоматчиками. Стало как-то неестественно тихо. Мгновение назад немцы вели по нас

Кредитное плечо

Из книги Секреты профессионалов трейдинга.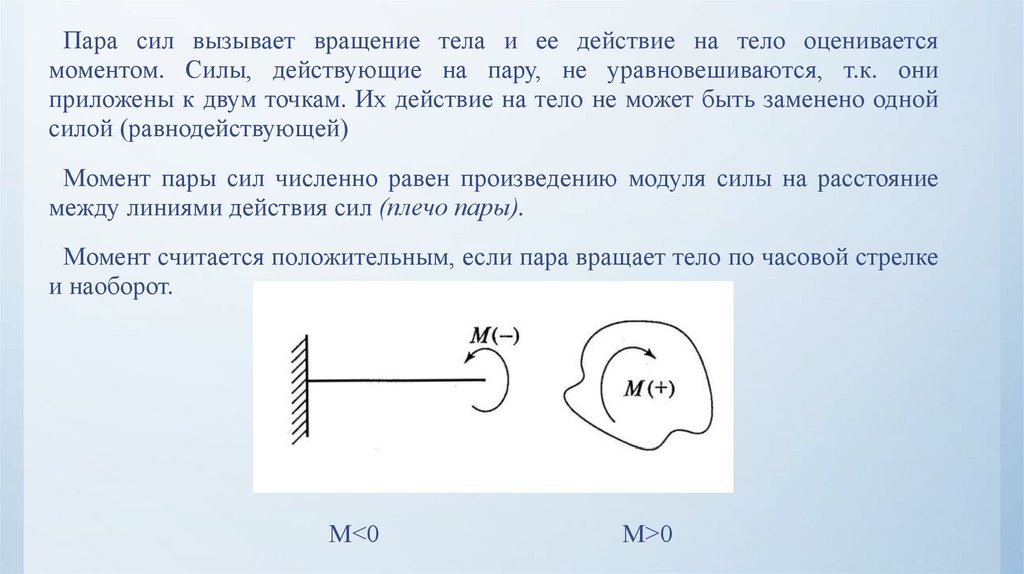

Методы, используемые профессионалами для успешной игры на финансовых рынках автора Буруджян Джек

Кредитное плечо Многие инвесторы и трейдеры не имеют четкого представления о кредитном плече – как следствие, оно их пугает. Многие говорили мне о том, что прекрасно понимают принцип работы кредитного плеча и благодарны фьючерсам за то, что они предоставляют самый

И друга крепкое плечо…

Из книги Эскадрилья ведет бой автора Сухов Константин Васильевич

И друга крепкое плечо… …Морозное утро. Механик Николай Годулянов проводил своего боевого друга, командира звена старшего лейтенанта Викентия Карповича в ответственный полет — на разведку.Истребитель МиГ-3 взял курс на Горловку, затем повернул на Макеевку. Летчик зорко

Shoulder Arms На плечо!

Из книги Авторская энциклопедия фильмов. Том II автора Лурселль Жак

Плечо

БСЭ

Плечо силы

Из книги Большая Советская Энциклопедия (ПЛ) автора БСЭ

ПЛЕЧО (БОЛЬ)

Из книги Твое тело говорит «Люби себя!» автора Бурбо Лиз

ПЛЕЧО (БОЛЬ) Физическая блокировкаПлечо соединяет руку с туловищем и является сложным и очень подвижным суставным комплексом, который позволяет совершать движения во всех направлениях, одновременно широкие и точные. Приведенное ниже описание касается только боли в

brachium, i n – плечо

Из книги автора

Из книги Стартап-гайд. Как начать… и не закрыть свой интернет-бизнес автора Зобнина М. Р.

Посчитайте плечо метрики В каждой конкретной ситуации метрики будут влиять на прибыль по-разному. Оцените, как изменение конверсии, стоимости привлечения, дохода с платящего и числа пользователей влияет на прибыль, и вы увидите, над какой метрикой сейчас нужно работать в

Синдром «плечо-кисть»

Из книги Точка боли. Уникальный массаж пусковых точек боли автора Ситель Анатолий Болеславович

Синдром «плечо-кисть» Синонимами названия синдрома «плечо-кисть» являются рефлекторная нейроваскулярная дистрофия конечности, или синдром Стейнброккера.Механизм возникновения синдрома «плечо-кисть», как и плечелопаточного периартроза, считается рефлекторным. У

Плечо

Из книги Целительство. Том 2. Введение в анатомию: структурный массаж автора Подводный Авессалом

Плечо Разгрузка плеч Горилла. а) Клиент сидит, согнув руку в локте под углом около 90 0, кисть сжата в массажный кулак, тыльная сторона ладони направлена вниз (рис. 4.31). Клиент пытается согнуть руку в локте, а массажист противостоит этому усилию; кроме того, клиент медленно

Плечо товарища

Из книги Дорога домой (Публицистика) автора Астафьев Виктор Петрович

Плечо товарища С Петром Борисковым мы познакомились и близко сошлись на Высших литературных курсах. Как-то разговорились, и оказалось, что в сорок втором году осенью служили в одном запасном полку, в пехотном, и, зная, какое плохое зрение у Пети, я, естественно,

Мужское плечо

Из книги Небесная канцелярия [сборник] автора Векшин Николай Л.

Мужское плечо Нежнейшая строка идёт от сердца. Мозги тут вроде как бы ни причем. Но есть закон: плечо мужское крепче, Коль чувством юмора мужик не

«Плечо» успеха

Из книги 10 шагов к финансовой свободе.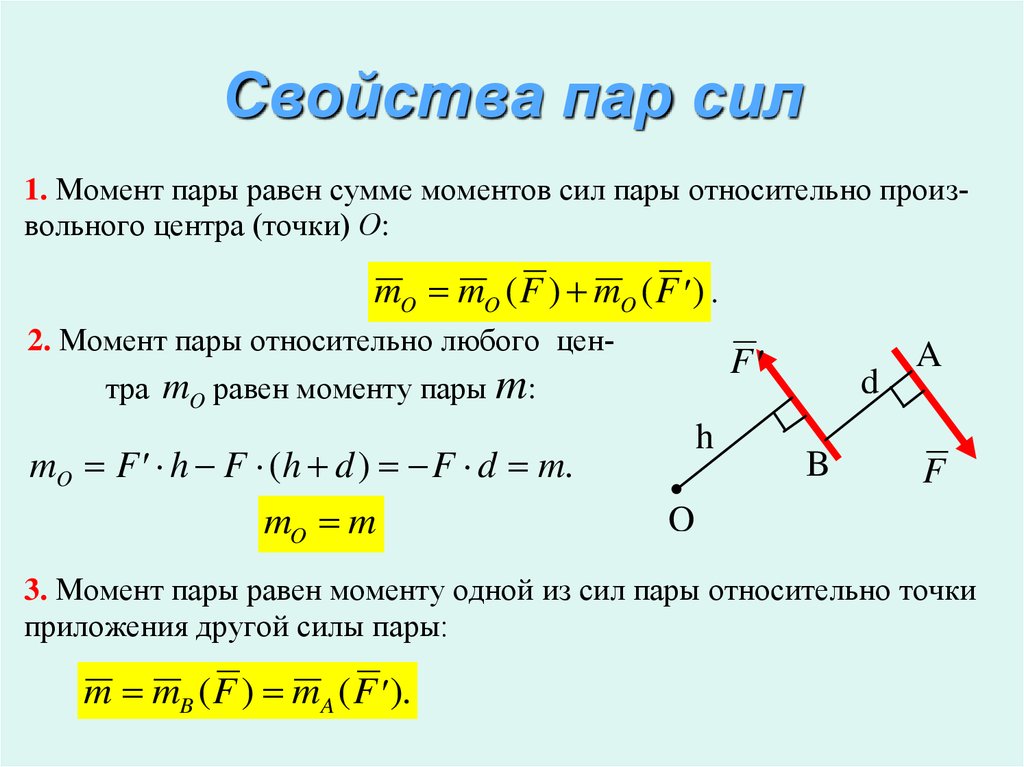 Мой путь автора Парабеллум Андрей Алексеевич

«Плечо» успеха Далее мы поговорим о такой важной и интересной вещи, как рычаг, путь к успеху. Рычаг, или «плечо» – то, что позволяет вам, затрачивая те же усилия, получить в десятки раз больший эффект. Люди изобрели его давно. Например, можно вспомнить Архимеда и его

Плечо силы — это длина перпендикуляра из некоторой вымышленной точки О к силе. Вымышленный центр, точку О, будем выбирать произвольно, моменты каждой силы определяем относительно этой точки. Нельзя для определения моментов одних сил выбрать одну точку О, а для нахождения моментов других сил выбрать ее в другом месте!

На камень действуют сила тяжести, сила трения, сила реакции опоры, две дополнительные внешние силы F 1 и F 2

Выбираем точку О в произвольном месте, больше ее местоположение не изменяем. Тогда плечо силы тяжести — это длина перпендикуляра (отрезок d) на рисунке

Плечо силы реакции опоры определяется аналогично

Если перпендикуляр нет возможности построить, то вектор силы продлевается в необходимом направлении, после чего строим перпендикуляр к этой линии. Плечо силы F 2

Плечо силы F 1

Осталась сила трения! Если точка О и сила лежат на одной линии, то плечо этой силы равно нулю. Плечо силы трения равно нулю.

При решении задач выгодно точку О выбирать в точке пересечения нескольких сил. Тогда плечи всех этих сил будут нулевыми. Например, если точку О в предыдущем примере выбрать иначе, то плечи сил будут иными.

Плечи сил F 1 , F 2 и силы тяжести равны нулю, так как точка О лежит с ними на одной прямой (или на самой силе). Плечо силы реакции опоры — это длина d 1 . Плечо силы трения — это длина d 2 .

Момент силы

Это векторная величина , определяется по формуле

Направление вектора момента силы определяется следующим образом. Представляем в какую сторону сила пытается повернуть (тащить) тело относительно точки О, если тело с точкой О закреплены осью. Если по часовой стрелки, то вектор имеет знак «+», если против часовой, тогда знак «-«.

Момент силы реакции опоры отрицательный, так как сила реакции опоры «поворачивает» тело против часовой стрелки

Момент силы тяжести положительный, так как сила тяжести «поворачивает» тело по часовой стрелки

Если точка О выбрана на теле

Момент силы реакции опоры и силы трения положительные, так как силы «поворачивают» тело по часовой стрелки

Рычаг находится в состоянии равновесия, если выполняется равенство:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1\right).\]

Расстояние $d$ между центром O и линией действия силы $\overline{F}$ называют плечом силы. Из рис.2 следует, что:

Момент силы и плечо

Понятие плечо силы иногда используют, для записи величины момента силы ($\overline{M}$), который равен:

\[\overline{M}=\left[\overline{r}\overline{F}\right]\left(5\right),\]

где $\overline{r}$ — радиус — вектор проведенный к точке продолжения силы$\ \overline{F}$. Модуль вектора момента силы равен:

Построение плеча силы

Примеры задач с решением

Пример 1

Решение. Основой решения задачи является правило равновесия рычага:

\[\frac{F_1}{F_2}=\frac{d_2}{d_1}\left(1.1\right),\]

\[\frac{m_1g}{m_2g}=\frac{d_2}{d_1}\to \frac{m_1}{m_2}=\frac{d_2}{d_1}\left(1.2\right).\]

Из выражения (1. 2) получим искомую массу $m_1$:

Вычислим искомую массу:

Ответ. $m_1=0,5\ кг$

Пример 2

Плечи сил будем искать относительно точки A. Плечо силы $\overline{N»}$ будет равно нулю, так как сила приложена к стержню в точке А:

Плечо другой силы реакции опоры ($\overline{N}$) равно длине перпендикуляра AC:

Плечо силы $M\overline{g}$ из рис. 4 , так как сила тяжести приложена к центру масс стержня, который для однородного стержня находится на его середине:

Плечо силы $m_1\overline{g},$ учитывая, что груз маленький и принимая его за материальную точку, равно:

Ответ. $d_{N»}=0;;\ d_N=l{sin (90-\alpha)\ }=l{cos \alpha \ \left(м\right),\ }d_{Mg}=\frac{l}{2},\ d_{m_1g}=b$

Которая равна произведению силы на ее плечо.

Момент силы вычисляют при помощи формулы:

где F — сила, l — плечо силы.

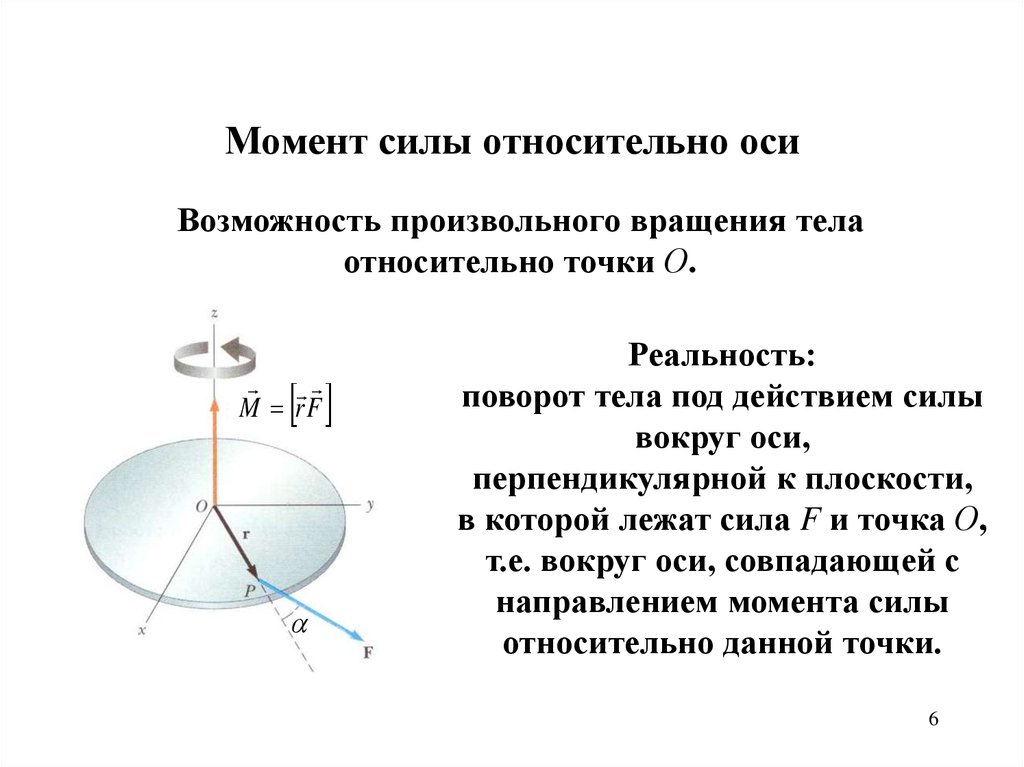
Плечо силы — это самое короткое расстояние от линии действия силы до оси вращения тела. На рисунке ниже изображено твердое тело, которое может вращаться вокруг оси. Ось вращения этого тела является перпендикулярной к плоскости рисунка и проходит через точку, которая обозначена как буква О. Пле-чом силы F t здесь оказывается расстояние l , от оси вращения до линии действия силы. Определяют его таким образом. Первым шагом проводят линию действия силы, далее из т. О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра оказывается плечом данной силы.

Момент силы характеризует вращающее действие силы . Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу необходимо приложить, чтобы получить желаемый результат, то есть один и тот же момент силы (см. рис. выше). Именно поэтому открыть дверь, толкая ее возле петель, намного сложнее, чем берясь за ручку, а гайку отвернуть намного легче длинным, чем коротким гаечным ключом.

За единицу момента силы в СИ принимается момент силы в 1 Н , плечо которой равно 1м — ньютон-метр (Н · м).

Правило моментов.

Твердое тело, которое может вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М 1 вращающей его по часовой стрелке, равняется моменту силы М 2 , которая вращает его против часовой стрелки:

Правило моментов есть следствие одной из теорем механики , которая была сформулирована французским ученым П. Вариньоном в 1687 г.

Пара сил.

Если на тело действуют 2 равные и противоположно направленные силы, которые не лежат на одной прямой, то такое тело не находится в равновесии, так как результирующий момент этих сил относительно любой оси не равняется нулю, так как обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил . Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена «свободному телу, то оно будет вращаться вокруг оси. проходящей через центр тяжести тела, рисунке б .

Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние l между силами, которое называется плечом пары , независимо от того, на какие отрезки l , и разделяет положение оси плечо пары:

Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относи-тельно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме нить действием одной пары сил с тем же моментом.

Рычагом называют твердое тело, которое может вращаться вокруг неподвижной точки. Неподвижную точку называют точкой опоры . Расстояние от точки опоры до линии действия силы называют плечом этой силы.

Условие равновесия рычага : рычаг находится в равновесии, если приложенные к рычагу силы F 1 и F 2 стремятся вращать его в противоположных направлениях, причем модули сил обратно пропорциональны плечам этих сил: F 1 /F 2 = l 2 /l 1 Это правило было установлено Архимедом. По легенде он воскликнул: Дайте мне точку опоры и я подниму Землю .

Для рычага выполняется «золотое правило» механики (если можно пренебречь трением и массой рычага).

Прикладывая к длинному рычагу некоторую силу, можно другим концом рычага поднимать груз, вес которого намного превышает эту силу. Это означает, что, используя рычаг, можно получить выигрыш в силе. При использовании рычага выигрыш в силе обязательно сопровождается таким же проигрышем в пути.

Все типы рычагов:

Момент силы. Правило моментов

Произведение модуля силы на ее плечо называют моментом силы . M = Fl , где М — момент силы, F — сила, l — плечо силы.

Правило моментов : рычаг находится в равновесии, если сумма моментов сил, стремящихся вращать рычаг в одном направлении, равна сумме моментов сил, стремящихся вращать его в противоположном направлении. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси.

Момент силы характеризует вращающее действие силы . Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается. Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т.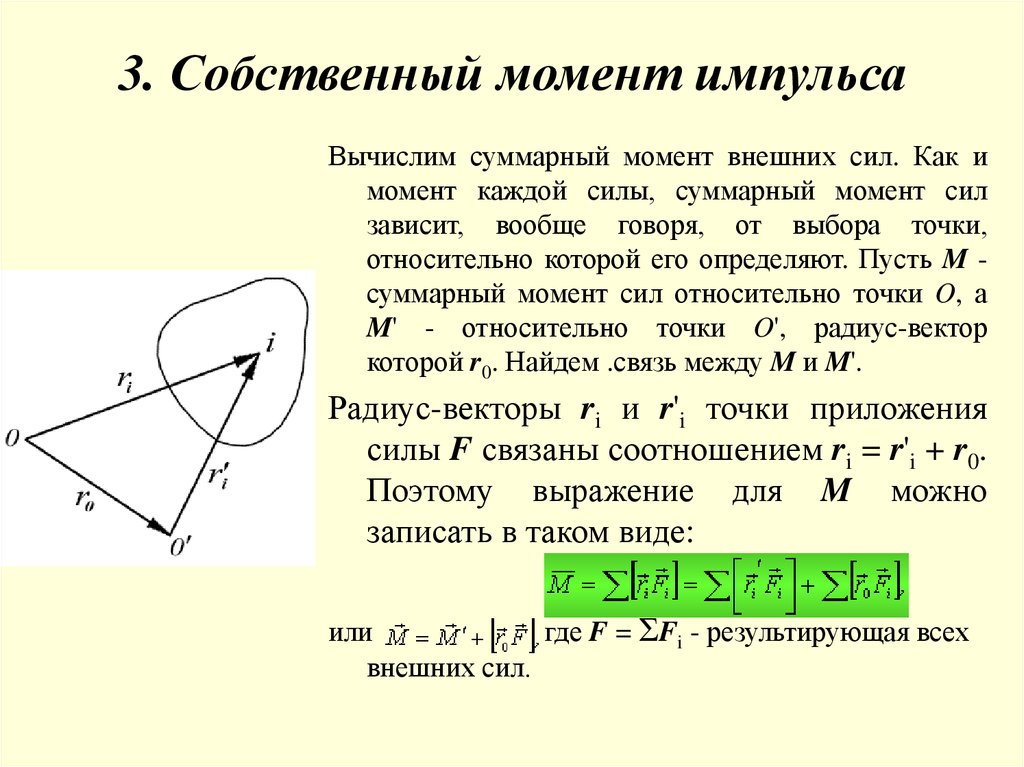 д.

Единицей момента силы в СИ является ньютон-метр (1 Н*м). Это момент силы 1 Н, имеющей плечо 1 м.

Простые механизмы — Рычаги | Поговорим о науке

AB 4 Наука 1-6 (1996) Тема B. Колеса и рычаги

BC 5 Наука 5 класс (июнь 2016 г.) Большая идея: Машины — это устройства, передающие силу и энергию.

МБ 5 Наука 5 класс (2000) Кластер 3: Силы и простые машины

NB 5 Наука 5: Живые и технологические системы (октябрь 2019 г.) Простые машины

NL 5 Наука 5 класс (2017) Модуль 2: Силы и простые машины

NS 5 Наука 5 (2019) Физические науки: силы и простые машины

NU 6 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: Движение

NU К Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: машины вокруг нас

NU 2 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: Механизм

NU 3 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.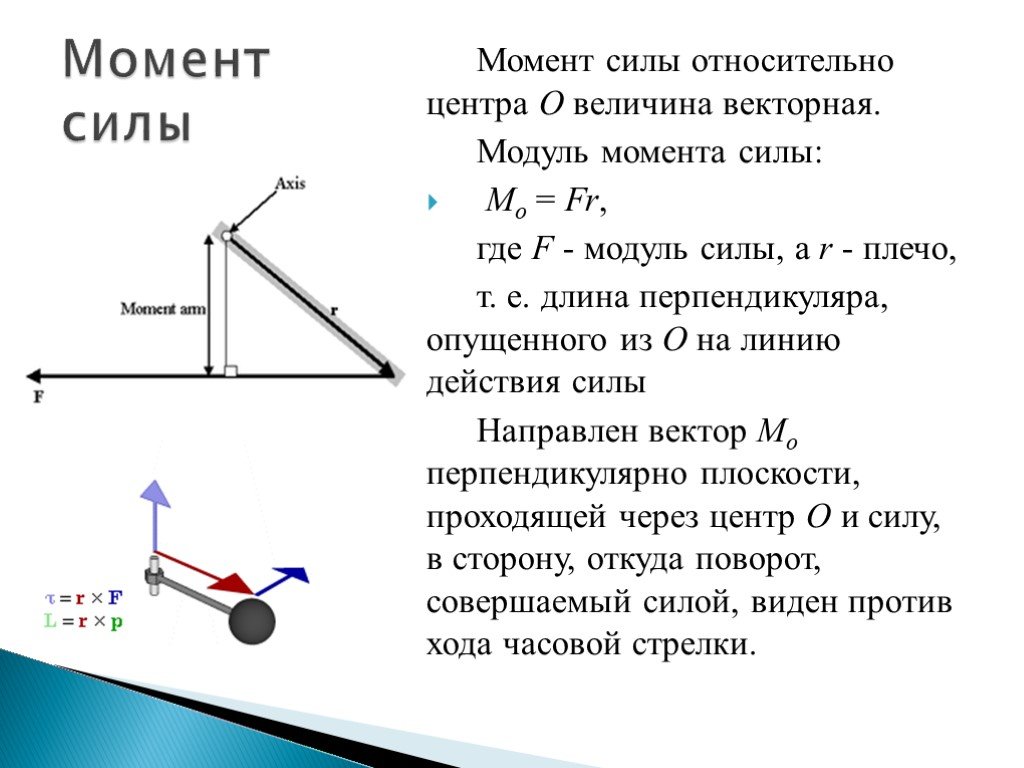 ) Конструкции и механизмы: Стабильность

NU 5 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: Силы, действующие на конструкции и механизмы

КК Элементарный цикл 2 Наука и техника, элементарный Материальный мир

YT 5 Science Grade 5 (Британская Колумбия, июнь 2016 г.) Большая идея: Машины — это устройства, передающие силу и энергию.

СК 5 Наука 5 класс (2011) Физические науки – Силы и простые машины (FM)

ON 2 Наука и техника, 2 класс (2022) Стрэнд Д. Структуры и механизмы; Простые машины и движение

ON 4 Наука и техника, 4 класс (2022) Направление D: Машины и их механизмы

НТ 6 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: Движение

NT К Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: машины вокруг нас

NT 2 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: Механизм

NT 3 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г. ) Конструкции и механизмы: Стабильность

NT 5 Учебная программа K-6 по науке и технологиям (СЗТ, 2004 г.) Конструкции и механизмы: Силы, действующие на конструкции и механизмы

АВ 8 Наука о знаниях и трудоустройстве 8, 9 (пересмотрено в 2009 г.) Блок D: Механические системы

AB 11 Наука о знаниях и трудоустройстве 20–4 (2006 г.) Модуль B: Общие сведения о системах преобразования энергии

AB 8 Наука 7-8-9 (2003 г., обновлено в 2014 г.) Блок D: Механические системы

BC 11 Физика 11 (июнь 2018 г.) Большая идея: Энергия существует в различных формах, сохраняется и способна выполнять работу.

Обратите внимание 11 Физика 11 (2003) Импульс и энергия

н.с. 11 Физика 11 (2021) Импульс и энергия

NU 8 Наука о знаниях и трудоустройстве 8 (Альберта, редакция 2009 г.) Блок D: Механические системы

NU 8 Наука 8 (Альберта, 2003 г., обновлено в 2014 г.) Блок D: Механические системы

NU 11 Наука о знаниях и трудоустройстве 20–4 (Альберта, 2006 г. ) Модуль B: Общие сведения о системах преобразования энергии

PE 10 Наука 421А (2019) Знание содержания: CK 3.2

PE 11 Физика 521А (2009) Импульс и энергия

контроль качества Раздел III Наука и технология Технологический мир

КК Раздел IV Прикладная наука и технологии Технологический мир

КК Раздел IV Наука и технология Технологический мир

КК Раздел V Физика Преобразование энергии

КК Раздел I Наука и технология Технологический мир: Силы и движение

КК Раздел III Прикладная наука и технологии Технологический мир

NT 8 Наука о знаниях и трудоустройстве 8 (Альберта, редакция 2009 г.) Раздел D: Механические системы

НТ 8 Наука 8 (Альберта, 2003 г., обновлено в 2014 г.) Блок D: Механические системы

NT 11 Наука о знаниях и трудоустройстве 20–4 (Альберта, 2006 г.) Модуль B: Общие сведения о системах преобразования энергии

ON 8 Наука и техника, 8 класс (2022) Направление D: Системы в действии

Рычаги и крутящий момент

Цели

Исследовать рычаги
Рассчитать крутящий момент
Рассчитать механическое преимущество

Настройка

Метровый стержень
Пружинные весы
Строка
Масса.

Теория

Рычаги используют крутящий момент, чтобы помочь нам поднимать или перемещать предметы. Крутящий момент крестовина Произведение силы на расстояние силы от точки опоры (центральная точка вокруг которого вращается система). Перекрестное произведение принимает только компонент сила, действующая перпендикулярно расстоянию. С помощью тригонометрии определяется крутящий момент как:

Крутящий момент = сила × расстояние до точки опоры × грех (θ)

Помните, что работа была также силой, умноженной на расстояние, но это была точка произведения и использовали косинус угла между силой и расстоянием: сила × расстояние × соз (θ).

В этой лаборатории сила будет перпендикулярна (90°) расстоянию. синус 90° равен единице, поэтому крутящий момент будет:

Крутящий момент = Сила × Расстояние до точки опоры × sin (θ)
Крутящий момент = Сила × Расстояние до точки опоры × sin (90°)
Крутящий момент = Сила × Расстояние до точки опоры × 1
Крутящий момент = Сила × Расстояние до точки опоры

Процедура, сбор данных и расчеты

Рычаги класса I пробные один: d

_e = d _r

В рычаге первого класса точка опоры находится между силой сопротивления (F _r ) и сила усилия (F _e ). В классе один рычаг сила усилие (F _e ), умноженное на расстояние усилия от точки опоры (d _и ) равна силе сопротивления (F _r ), умноженной на расстояние сопротивление от точки опоры (d _r ). Усилие и сопротивление включены противоположные стороны точки опоры. Плоскогубцы являются примером рычага первого класса.

На схеме масса обеспечивает сопротивление, пружинная шкала измеряет наше усилия. Пружинная шкала откалибрована в граммах. грамм не является единицей сила сама по себе, но в этой лаборатории мы будем использовать термин «грамм-сила» как сила, действующая на один грамм на поверхности Земли за счет ускорения свободного падения. Один «грамм-сила» будет эквивалентна 980 см/сек ² (дин).

для диаграммы: F _E × D _E = F _R × D _R
Mechanical Advantage = F _R /F _E

_{/F _E 9000 34444444444444444444444444444444444444444444444444444444444444444444444444449ня см, повесьте пружинную шкалу на отметке 90
см, подвесьте метровую рейку к отметке 50 см. Найдите F _e , d _e , F _r , d _r в граммах силы. К
определить грамм-силу массы (F _r ) используйте весы балансира. д _д и
d _r должны быть 40 см при правильной установке. F _e можно прочитать из
весенняя граммовая шкала напрямую.
Рассчитать F _e × d _e и F _r × d _r .
Укажите, является ли F _e × d _e = F _r × d _r .
Рассчитайте механическое преимущество F _r /F _e .
Ф _и д _д F _e × d _e Ф _р д _р F _R × D _R F _e d _e = F _r d _r ? М. А.
________ ________ ________ ________ ________ ________ Да | № ________
Класс I Рычаги пробные два: d
_e > d _r For the diagram: F _e × d _e = F _r × d _r
Mechanical advantage = F _r /F _e
Switch masses to a 500 gram mass or две гири по 200 грамм связаны
вместе.
Поместите груз массой 500 грамм на отметку 10 см, а пружинные весы на отметку 9.отметка 0 см, подвеска
метровая палочка от отметки 30 см.
Найдите F _e , d _e , F _r , d _r в граммах силы.
Рассчитать F _e × d _e и F _r × d _r .
Укажите, является ли F _e × d _e = F _r × d _r .
Рассчитайте механическое преимущество F _r /F _e .
Ф _е д _д F _e × d _e Ф _р д _р F _R × D _R F _e d _e = F _r d _r ? М.А.
________ ________ ________ ________ ________ ________ Да | № ________
Рычаги класса II
В рычаге второго класса сопротивление находится между силой усилия и
точка опоры. В рычаге второго класса сила усилия, умноженная на расстояние
усилие от точки опоры противоположно и равно силе сопротивления
умножается на расстояние сопротивления от точки опоры. Усилия и
сопротивления находятся по одну сторону от точки опоры, но направлены в противоположные стороны.
Расстояние усилия (также иногда называемое «плечом усилия») на длиннее чем расстояние сопротивления.
Тачки и гигантские шесты для копания таро (когда мы нажимаем на шест) являются примерами
рычаги второго класса.
Обратите внимание, что наш выбор дауна как положительного в первой части лаборатории означает, что
up теперь отрицателен в этом разделе. Итак, F _e — отрицательная сила.
Запишите F _e как отрицательное в таблице, а затем -F _e × d _е будет
будь позитивным.
Для диаграммы: -F _e × d _e = F _r × d _r
Механическое преимущество = |F _r /F _e | где | означает «абсолютный
значение.» Механическое преимущество всегда положительно.
Переместите груз 500 грамм (или два груза по 200 грамм) примерно на 30 см
отметку и пружинную шкалу на отметке 90 см, подвешивают измерительную рейку к отметке 10 см. Возможно, вам придется отрегулировать положение груза в соответствии со способностями вашего тела.
пружинная шкала для обеспечения точных показаний. Вы хотите избежать необходимости читать либо
очень маленькое усилие в грамме или усилие в грамме слишком велико для вашей весовой шкалы. Если вы отрегулируете
позиции, не забудьте измерить фактический d _e и d _r вы используете!
Найдите F _e , d _e , F _r , d _r в граммах силы.
Рассчитать F _e × d _e и F _r × d _r .
Укажите, является ли -F _e × d _e = F _r × d _r .
Рассчитайте механическое преимущество F _r /F _e .
F _и д _д -F _e × d _e Ф _р д _р F _R × D _R -F _e d _e = F _r d _r ? М. А.
________ ________ ________ ________ ________ ________ Да | № ________
Рычаги класса III
В рычаге третьего класса сопротивление находится между силой усилия и
точка опоры. В рычаге третьего класса сила усилия, умноженная на расстояние
усилие от точки опоры противоположно и равно силе сопротивления
умножается на расстояние сопротивления от точки опоры. Усилия и
сопротивления находятся по одну сторону от точки опоры, но направлены в противоположные стороны.
Расстояние усилия (также иногда называемое «плечом усилия») на короче чем расстояние сопротивления.
Для диаграммы: -F _e × d _e = F _r × d _r
Механическое преимущество = |F _r /F _e | где | означает «абсолютный
значение.» Механическое преимущество всегда положительно.
Переключиться на массу 100 грамм.
Переместите 100-граммовую массу на отметку 90 см, а пружинную шкалу — примерно на 65 см.
см до отметки 70 см, держа измерительную рейку подвешенной к отметке 10 см. Снова
при необходимости отрегулируйте шкалу пружины и положения массы, чтобы получить точные показания
Весенняя шкала.
Найдите F _e , d _e , F _r , d _r в граммах силы.
Рассчитать F _e × d _e и F _r × d _r .
Укажите, является ли -F _e × d _e = F _r × d _r .
Рассчитайте механическое преимущество F _r /F _e .
Ф _и д _д -F _e × d _e Ф _р д _р F _R × D _R -F _e d _e = F _r d _r ? М. А.
________ ________ ________ ________ ________ ________ Да | № ________
В рычаге класса III механическое преимущество можно назвать механическим
недостаток. Почему? (Предложение: рассмотрите силу усилия,
меньше силы сопротивления или больше силы сопротивления?)
Обратите внимание, что нижняя часть руки человека представляет собой рычаг третьего класса: бицепс, прикрепленный чуть ниже
локоть, может использоваться для подъема веса, удерживаемого рукой в конце нижнего
рука.
Непрерывные рычаги: отвертки
Отвертка на самом деле представляет собой форму рычага, в котором рукоятка с большим радиусом обеспечивает
механическое преимущество при повороте лезвия с меньшим радиусом. Все виды циркулярки.
устройства используют эту форму механического преимущества. Круглые ручки водяного клапана, шина
утюги, торцевые ключи, гаечные ключи и многие другие предметы используют это время
круговой рычаг.}