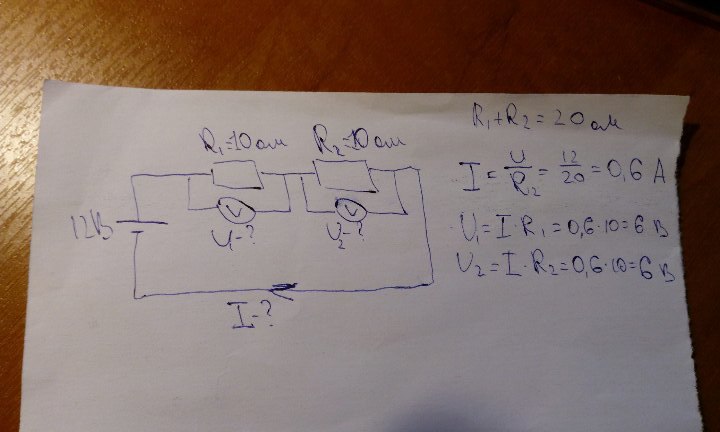
Напряжение, ток и сопротивление в электротехнике
Электрическое напряжение равна разности потенциалов между двумя точками. U=f1-f2. С точки зрения логики, напряжение может быть как положительным, так и отрицательным значением. Единицей измерения является вольт (В).
Содержание
Закон Ома и взаимосвязь между R, I и U
Сначала мы рассмотрим определения основных электрических величин, а затем изучим законы, связывающие эти величины друг с другом с помощью формул и графических зависимостей. Таким образом, эта статья будет развиваться от простого к сложному.
Первое, что следует отметить, это то, что существуют цепи постоянного и переменного тока. Разница между ними заключается в характере протекания электрических величин – в цепях переменного тока ток и напряжение изменяются во времени по определенному закону (например, по синусоиде). В цепях постоянного тока, с другой стороны, значение остается постоянным с течением времени.
В обеих схемах основными величинами являются ток, напряжение и сопротивление.
Электрический ток – Упорядоченное движение заряженных частиц (электронов) по проводнику (проводящей среде) от точки с более высоким потенциалом к точке с более низким потенциалом. Обычно говорят, что в цепях постоянного тока ток течет от плюса к минусу. Измеряется в амперах и обозначается символом “i”.
Электрическое сопротивление Характеризует способность ограничивать величину электрического тока. Оно измеряется в омах и обозначается r. Обратной величиной сопротивления является проводимость. В зависимости от величины сопротивления материалы делятся на: проводники, диэлектрики и изоляторы.
Электрическое напряжение равна разности потенциалов между двумя точками. U=f1-f2. С точки зрения логики, напряжение может быть как положительным, так и отрицательным значением. Единицей измерения является вольт (В).
Связь между этими величинами описывается законом Ома:
Величина тока в электрической цепи прямо пропорциональна величине напряжения и обратно пропорциональна сопротивлению. I=U/R – эта формула применима к цепи постоянного тока. Зная две величины, мы всегда найдем третью.
I=U/R – эта формула применима к цепи постоянного тока. Зная две величины, мы всегда найдем третью.
Для переменного тока формула будет иметь вид I=U/Z, где Z – полное сопротивление цепи, которое состоит из активной, емкостной и индуктивной составляющих:
- R – активное (омическое) сопротивление
- XL – индуктивное сопротивление (характерно для катушек, обмоток, статора TH) – препятствует протеканию тока
- XC – Емкость (емкость, встречается в кабелях) – препятствует прохождению напряжения
- Z – Реактивное сопротивление (импеданс, импеданс) состоит из двух элементов: активного сопротивления (R) и реактивного сопротивления (X). Реактивное сопротивление (X) уже состоит из индуктивного сопротивления (XL) и емкостного сопротивления (XC).
Взаимосвязь между сопротивлениями можно представить графически в виде правильного треугольника (векторное представление).
В цепях переменного тока значения тока и напряжения изменяются во времени по определенному закону. Например, в соответствии с синусоидой:
Например, в соответствии с синусоидой:
В этой формуле I – мгновенное значение тока, Im – амплитудное значение.
Значение амплитуды – это максимальное значение, амплитудное значение, которое принимает величина за данный период. В приведенных выше формулах это значение с подстрочным индексом “m” – максимальный тип.
Немедленно – это значение величины в определенный момент времени. Максимальное из мгновенных значений является амплитудным значением.
Эффективная стоимость – это значение переменного тока, при котором за один период в резисторе выделяется столько же тепла, сколько в цепи постоянного тока. Это те значения, которые показывают наши вольтметры и амперметры. Для синусоидальной волны эффективное значение составляет 0,707 от амплитудного значения. 1/корень(2)=0,707.
В зависимости от преобладания данной характеристики сопротивления, векторы тока и напряжения будут смещены друг относительно друга:
Чисто активное сопротивление – ток и напряжение совпадают по фазе.
Индуктивная составляющая преобладает – поэтому, как написано выше, ток протекает труднее и отстает от напряжения.
Преобладает емкостная составляющая – ток исчезает, напряжение подавляется емкостью.
Цепи переменного тока могут быть однофазными и трехфазными. В трехфазных цепях используются обозначения фаз: фаза А (желтая, U), фаза В (зеленая, V) и фаза С (красная, W). Как недавно сообщил один из железнодорожных порталов: фаза А идет до Минска.
Фазы могут быть соединены друг с другом в различных вариантах: звезда, треугольник, зигзаг и другие более редкие.
Электрическое напряжение:
Основные электрические формулы. Мощность. Сопротивление. Текущий. Напряжение. Закон Ома.
Ниже приведены некоторые формулировки закона Ома для участка цепи:
Электрическое напряжение:
- U = R * I – закон Ома для участка цепи
- U = P / I
- U = (P*R) 1/2
Электрическая энергия:
- P= U* I
- P= R* I 2
- P = U 2 / R
Электрический ток:
- I = U / R
- I = P / E
- I = (P / R) 1/2
Электрическое сопротивление:
- R = U / I
- R = U 2 / P
- R = P / I 2
НЕ ЗАБЫВАЙТЕ: Законы Кирхгофа и правила Кирхгофа для тока и напряжения.
Цепь синусоидально переменного тока с частотой ω.
Применимость формул: Мы игнорируем зависимость сопротивления от тока и частоты.Напомним, что любой сигнал можно с любой точностью разложить в ряд Фурье, т.е. предполагая, что параметры сети не зависят от частоты – эта формулировка применима ко всем гармоникам любого сигнала.
Закон Ома для цепей переменного тока:
U=I*Z
Конечно, в случае цепей переменного тока можно говорить и об активной/реактивной мощности.
X_C=-j<1/<C>>.” />
Теоретические основы электротехники – TE. Пособия для студентов.
. ” /> или
Уравнения расположены в соответствии со вторым законом Кирхгофа для контурных токов.
Токи ветвей выражаются в терминах циркулирующих токов в соответствии с первым законом Кирхгофа.
Количество выбираемых контуров и количество решаемых уравнений равно количеству уравнений по второму закону Кирхгофа: .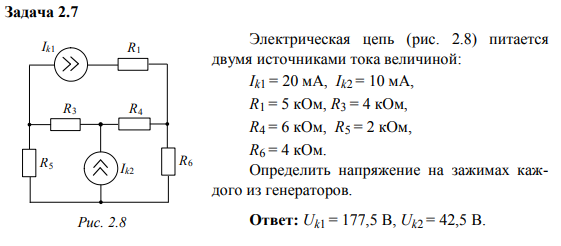
Сумма сопротивлений всех резистивных элементов каждой цепи со знаком плюс – коэффициент при токе цепи имеет следующие показатели: или
Активная мощность:
Реактивная мощность:
=0;” />
где – резонансная частота напряжения, определяемая из условия
Затем
.
Для противотока:
.
Для мгновенных значений:
Где
При расчетах всегда приводите все значения в одних единицах, например, если вы рассчитываете мощность в ваттах, то соответственно напряжение в вольтах, сопротивление в омах. и т.д.
Сложная мощность обозначается буквой S со знаком многоточия (тильда) над ней.
- А теперь электротехнические формулы, которые часто используются для расчетов (дома, на работе), В порядке от простого к очень простому, Для студенческого сообщества я размещу отдельно сложные и очень сложные, а по TEC напишу целую лекцию.

ФОРМЫ ДС
Закон Ома для участка цепи и всей цепи постоянного тока:
Пример расчета сопротивления проводника (Подробнее об удельном сопротивлении проводников см. на стр. 18 и 19.. Концепции и определения):
Мощность в цепи постоянного тока, здесь нет ничего сложного, как и все в постоянном токе, я просто отмечу, что значения тока и напряжения постоянны и равны мгновенным значениям в каждый момент времени, единица мощности (Р) составляет -1 кВт = 1000 ватт:
- В качестве напоминания, длядля любознательных,вы можете например, электрическая энергия может быть, например, преобразована из электрической энергии в механическую энергию и наоборот: 1 кВт/ч = 367000 кгс*м; 1 кВт = 102 кгс*м/с, т.е. на 1 кВт/ч. То есть, вы можете поднять массу 367 кг на высоту 1 км или 102 кг за 1 секунду на расстояние в один метр.

ФОРМУЛЫ ПЕРЕМЕННОГО ТОКА
В отличие от постоянного тока, особенностью переменного тока является то, что электрический ток изменяет свою величину и направление с течением времени. Элементы этой электрической цепи влияют на амплитуду тока и его фазу. Символ переменного тока в электрооборудовании ̴ ( eng. попеременно текущий и обозначается латинскими буквами AC):
Электромагнитные процессы, происходящие в электрических устройствах, обычно довольно сложны, поэтому приведенные ниже формулы будут скорее учебными, чем практическими, т.е. для студентов и любознательных.Преобразование (конвертация) мощности (P в W), тока (I в A), сопротивления (R в Ом) и напряжения (U в V) может быть выполнено, как показано ниже, на простом примере (см. рисунок ниже):
Обратите внимание, что если в цепи 220 В есть электродвигатели, трансформаторы и т.д. Обратите внимание, что если в цепи 220 В есть электродвигатели, трансформаторы и т.
 д. (индуктивные или емкостные нагрузки – реактивные компоненты), то необходимо учитывать следующее cos φ , например:
д. (индуктивные или емкостные нагрузки – реактивные компоненты), то необходимо учитывать следующее cos φ , например:В цепи 380 В необходимо добавить U √3 (корень из трех равен – 1,73), напр:
для тока: I = P/(√3*U*cos φ), или I = P/(1,73*U*cos φ), для мощности: P = √3*U*I*cos φ.
Продолжение формулы пальцев ног:См. также продолжение формулы ниже:
перейти на: формула палец ноги 1 краткое содержание страницы – электрический ток (I, ампер), электродвижущая сила (ЭДС, E=A/q=J/Q=V, вольт), электрическое напряжение (U, вольт), электрическая энергия и мощность (Eq, J, джоуль) и ватты (P, W, ватт)…. перейти на: Формула пальцев 2 краткое описание страницы — Пассивные элементы цепи (резистор, индуктор и конденсатор), их основные характеристики и параметры….Автор этой страницы надеется, что вы найдете полезную информацию, как простую, так и более глубокую, в других разделах сайта.
 Не забудьте проверить рекламу google, реклама бесплатна для вас и для меня, чтобы развивать сайт, удачи.
Не забудьте проверить рекламу google, реклама бесплатна для вас и для меня, чтобы развивать сайт, удачи.Напряжение в параллельной цепи будет везде одинаковым и может быть рассчитано по закону Ома: V = IR (где I – ток, а R – сопротивление).
Полное сопротивление в цепи переменного тока Обычно цепь переменного тока содержит активное сопротивление, емкость и индуктивность. Общее сопротивление (Z) – это векторная сумма всех сопротивлений: активного, емкостного и индуктивного. … – индуктивное сопротивление.
Согласно закону Ома, ток (I) пропорционален напряжению (U) и обратно пропорционален сопротивлению (R), а мощность (P) рассчитывается как произведение напряжения и тока. Из этого рассчитывается ток в сечении проводника: I = P/U.
Значение полезной мощности может быть рассчитано по трем формулам: P = I 2R, P = U2 / r, P = IU, где I – сила тока на данном участке цепи; U – напряжение на клеммной части (зажимах) источника тока, а R – сопротивление нагрузки или внешней цепи.

Формулы для постоянного тока
Постоянный электрический ток не меняет своей величины или направления. Он используется для расчета замкнутого контура, однородной цепи, мощности и других параметров. Поэтому важно знать его формулы и основные законы, связанные с ним.
Основной список формул
Закон Ома для участка однородной цепи
Для того чтобы существовал электрический ток, необходимо поле. Чтобы создать его, нужны потенциалы или разность потенциалов, выраженная в виде напряжения. Ток будет направлен к более низким потенциалам, а электроны начнут свое движение в обратном направлении. В 1826 году Г. Ом провел испытания и пришел к выводу, что чем выше напряжение, тем больше тока проходит через поле.
Внимание! Соседние проводники проводят электричество по-разному. Это означает, что каждый элемент имеет разную проводимость, или электрическое сопротивление.
Следовательно, согласно теореме Ома, ток через участок однородной цепи будет прямо пропорционален напряжению на нем и обратно пропорционален сопротивлению проводника.

закон Ома
Используя формулу I = U / R, где I считается силой тока, U – напряжение, а R – электрическое сопротивление, последнее значение можно найти, если p * l / S, где p – сопротивление проводника, l – длина проводника, а S – площадь поперечного сечения проводника.
Закон Ома для замкнутой цепи с источником тока
Закон Ома также дает формулу для замкнутой цепи. Согласно ему, ток на этом участке от источника тока с внутренним и внешним сопротивлением нагрузки равен делению электродвижущей силы источника на сумму внутреннего и внешнего сопротивлений. Это выглядит следующим образом: I = e / R + r, где I – сила тока, e – ЭДС, R – сопротивление и r – внутреннее сопротивление источника напряжения.
Примечание. В физическом смысле, согласно этому закону, чем выше ЭДС, тем выше источник энергии, тем выше скорость заряда. Чем выше удельное сопротивление, тем меньше величина тока.
Закон Ома для замкнутой цепи
Работа с постоянным током
Энергия, проходя через проводник, упорядоченно перемещается к носителю.
 Во время движения он совершает работу. Следовательно, работа постоянного тока – это действие поля по перемещению электрических зарядов по проводнику. Она равна произведению I и работы, совершенной напряжением и временем.
Во время движения он совершает работу. Следовательно, работа постоянного тока – это действие поля по перемещению электрических зарядов по проводнику. Она равна произведению I и работы, совершенной напряжением и временем.Закон Джоуля-Ленца
Когда электрический ток проходит через проводник с сопротивлением, всегда выделяется тепло. Количество тепла, которое выделяется за определенное время, определяется законом Джоуля-Ленца. Согласно формуле, тепловая мощность равна плотности электрической энергии, умноженной на напряжение – w = j * E = oE(2).
Примечание. На практике этот закон влияет на снижение потерь электроэнергии, выбор проводника для электрической цепи, выбор электронагревателя и использование предохранителя для защиты электрической сети.
Закон Джоуля-Ленца
Полная мощность, развиваемая источником тока
Мощность – это работа, выполняемая за одну секунду времени. Электрическая мощность – это физическая величина, характеризующая скорость передачи электрической энергии с преобразованием.

Работа, совершаемая источником электрической энергии в цепи, является полной мощностью. Его можно определить по формуле P = El, где E – ЭДС, а I – значение токовой характеристики.
Обратите внимание! Если нагрузка линейна, то полная мощность равна квадратному корню из квадратов активной и реактивной работы источника. Если нагрузка нелинейная, то она равна квадратному корню из квадратов активной и неактивной работы источника.
Общая мощность
В практических измерениях эта работа выражается в киловаттах в час. Он используется для измерения потребления электроэнергии в бытовых и промышленных условиях и для определения электроэнергии, вырабатываемой электроприборами.
Полезная мощность
Максимальная или полезная мощность – это мощность, которая рассеивается во внешнем разрыве цепи, т.е. когда резистор нагружен. Его можно применить к любой задаче. Аналогичная концепция может быть использована для расчета работы электродвигателя или трансформатора, который может потреблять активные и реактивные компоненты.

Полезная мощность
Полезная мощность может быть рассчитана по трем формулам: P = I 2R, P = U2 / r, P = IU, где I – сила тока на данном участке цепи; U – напряжение на клеммной части (зажимах) источника тока, а R – сопротивление нагрузки или внешней цепи.
Эффективность источника тока
КПД источника тока – это отношение полезной мощности, отдаваемой источником, к полной мощности. Если внутреннее сопротивление источника равно внешнему сопротивлению, то половина результатов всей работы будет теряться в источнике, а другая половина будет выделяться на нагрузку. В этой ситуации КПД составит 50%.
В наиболее понятной форме, когда электрические заряды движутся в замкнутой цепи, источник тока совершает некоторую полезную и общую работу. Выполняя первое из этих действий, он перемещает заряды во внешний контур. Совершая вторую работу, он перемещает заряженные частицы по контуру.
Эффективность источника питания
Обратите внимание! Полезная работа достигается, когда сопротивление внешней цепи будет иметь определенное значение, зависящее от источника и нагрузки.
 Отношение полезной работы к общей работе выражается формулой: η = A полезно / Apoln = P полезно / Apoln = U/ε = R / (R + r).
Отношение полезной работы к общей работе выражается формулой: η = A полезно / Apoln = P полезно / Apoln = U/ε = R / (R + r).Первый закон Кирхгофа
Первый закон Кирхгофа гласит, что сумма токов в любой части цепи равна нулю. Направленный заряд к узлу положителен, а от узла – отрицателен. Алгебраическая сумма токов зарядов, направленных к узлу, равна сумме токов зарядов, направленных от него. Если перевести это правило, то получится следующее определение: сколько тока втекает в узел, столько же вытекает из него. Это правило вытекает из закона сохранения заряженных частиц.
Решая линейные уравнения на основе правила Кирхгофа, можно найти все токи и напряжения для постоянного, переменного и квазистационарного электрических токов.
Обратите внимание! В электротехнике правило Кирхгофа имеет особое значение, поскольку оно повсеместно используется для решения многих задач теории электрических цепей. Его можно использовать для расчета сложных электрических цепей.
 Используя его, можно получить систему линейных уравнений для токов или напряжений во всех соединенных ветвях цепи.
Используя его, можно получить систему линейных уравнений для токов или напряжений во всех соединенных ветвях цепи.Первое правило Кирхгофа
Второй закон Кирхгофа
Второе правило Кирхгофа следует из первого и третьего уравнений Максвелла. Согласно ему, алгебраическая сумма напряжений на резистивных элементах замкнутой цепи равна сумме ЭДС, содержащихся в ней. Если на участке нет ЭДС, то сумма падений напряжения равна нулю. Проще говоря, когда цепь полностью шунтирована, потенциал цепи изменяется. Он возвращается к своему первоначальному значению.
Обычным случаем для одного участка цепи является закон Ома. При составлении уравнений напряжения для цепи требуется положительное шунтирование. Для этого следует знать, что при выборе байпаса падение напряжения в ответвлении будет положительным, если направление байпаса в ответвлении совпадает с ранее выбранным. Если они не совпадают, падение напряжения на ответвлении будет отрицательным.
Важно! Второе правило Кирхгофа может быть применено к линейной или нелинейной линеаризованной цепи для любого изменения токов и напряжений.

Второй закон Кирхгофа
В результате, чтобы понять основы физики явлений, электричества, электродинамики и успешно применять знания в жизни, необходимо знать выведенные теоремы, законы, формулы и принципы в области электричества, изложенные выше. Например, представив, как выглядит та или иная формула, можно решить любую задачу из учебника физики или из жизни.
- В качестве напоминания, длядля любознательных,вы можете например, электрическая энергия может быть, например, преобразована из электрической энергии в механическую энергию и наоборот: 1 кВт/ч = 367000 кгс*м; 1 кВт = 102 кгс*м/с, т.е. на 1 кВт/ч. То есть, вы можете поднять массу 367 кг на высоту 1 км или 102 кг за 1 секунду на расстояние в один метр.
Читайте далее:
- Лекции по ТЭ – #27 Явление резонанса в электрических цепях.
- Полное сопротивление цепи переменного тока – Основы электроники.
- Разветвленные цепи. Правило обхода цепи – Электричество и магнетизм – Киберфорум.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Законы Кирхгофа таковы. Что такое законы Кирхгофа?.
- Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
- Что такое реактивная мощность и как с ней бороться; Сайт для электриков – статьи, советы, примеры, диаграммы.

Напряжение, сила тока, сопротивление, мощность.
Пусть имеется один пустой бак, который стоит на земле и один полный бак с водой, установленный на некоторой высоте. Между баками есть разность давлений. Если соединить баки шлангом, то по нему потечет вода в бак с меньшим давлением. При этом крыльчатка будет вращаться, совершая работу и создавая некоторое сопротивление движущейся воде. Аналогично соединив проводником две клеммы с напряжением U между ними, потечет электрический ток I. Лампа будет нагреваться от протекающего тока, совершая работу и создавая сопротивление R движущемуся току. Чем больше сопротивление лампы, тем меньше сила протекающего тока.
Мощность, выделяемая в электроприемнике при протекании через него тока: .
Для примера, определим протекающий ток и выделяемую мощность в лампе с сопротивлением 484Ом, подключенную к напряжению 220В:
Протекающий ток , выделяемая мощность
Задание 2.
 Электроприемники в однофазной сети.
Электроприемники в однофазной сети.Электроприемники – лампы освещения, нагревательные элементы, электродвигатели и т.д. При включении в сеть они потребляют электрический ток и совершают определенную работу.
Мощность, которая расходуется на совершение полезной работы, например, нагрев спирали, вращение вала, излучение света и т.п. называется активной мощностью P и измеряется в ваттах (Вт).
Н оминальная активная мощность P и напряжение U указывается в паспорте электроприемника. Например, на лампе указано: , т.е. лампа предназначена для подключения к напряжению 220В и при этом выделяется мощность 100Вт в виде нагрева и излучения света.
При этом лампа накаливания при включении ее на 220В потребляет ток:
Ваттметр предназначен для измерения активной мощности нагрузки в ваттах, и в данном случае покажет 100Вт.
Следует отметить,
что при включении лампы на другое
напряжение, отличное от номинального
220В, потребляемый ток будет другой, и
выделяемая на лампе мощность будет
другой, отличной от 100Вт.
По паспортным данным сопротивление лампы: . Потребляемый ток: . Мощность лампы при этом: . Лампа будет гореть очень тускло при включении ее на напряжение 127В.
Активно-реактивные электроприемники. Электродвигатели, некоторые светильники потребляют как активную P, так и «бесполезную» реактивную мощность Q в ВАр – вольт амперах реактивных, которая тратится только на образование магнитного поля в обмотках этих электроприемников.
Треугольник мощностей электроприемника P=100Вт, cosφ=0,8 |
Полная потребляемая мощность S, в ВА, складывается из активной и реактивной мощности согласно треугольнику мощностей следующим образом:
Полная мощность S несколько больше P,
что видно из треугольника мощностей.
Соотношение S и P показывает коэффициент активной мощности , и указывается в паспорте электроприемников, например, для светильника: . О пределим полную мощность и потребляемый ток данным светильником:
Видно, что потребляемый ток данным светильником больше, чем ток потребляемый лампой накаливания той же активной мощности 100Вт. При полной мощности в 125ВА ваттметр покажет 100Вт, как и в предыдущем случае.
В ряде задач приведен потребляемый ток и нужно определить полную мощность, которая равна произведению показания амперметра на напряжение сети
Все параметры в треугольнике мощностей связаны законами тригонометрии, например реактивная мощность равна:
Для электродвигателей
вместо активной мощности P
приводится механическая мощность на
валу P2 и КПД, например: 500Вт,
КПД 0,9. Разделив мощность на валу на КПД, получим
активную электрическую мощность
двигателя 500Вт/0,9=555Вт, причем потери на
трение и нагрев обмоток составят
555Вт-500Вт=55Вт.
Разделив мощность на валу на КПД, получим
активную электрическую мощность
двигателя 500Вт/0,9=555Вт, причем потери на
трение и нагрев обмоток составят
555Вт-500Вт=55Вт.
Параллельное включение электроприемников. На практике электроприемники включаются и работают в сети параллельно.
На примере определим суммарный ток, который будет потреблять из сети нагрузка из нескольких электроприемников, а также активную мощность всей нагрузки. Пусть, к однофазной сети 220В подключены: лампа накаливания, нагревательная спираль, светильник с люминесцентной лампой и однофазный электродвигатель (см. рис. 2.2 а). Для измерения параметров имеется ваттметр W и амперметр А.
Построим треугольник мощностей нагрузки. По горизонтали отложим в масштабе все активные мощности электроприемников (рис. 2.2 б). Сумма активных мощностей электроприемников 1255Вт и будут показаниями ваттметра.
Далее по вертикали откладываются
реактивные мощности всех электроприемников,
которые определяются дополнительно —
светильника 75ВАр, электродвигателя
416ВАр. Лампа накаливания и нагревательная
спираль — не потребляют реактивной
мощности.
Лампа накаливания и нагревательная
спираль — не потребляют реактивной
мощности.
а) б) |
Рис. 2.2 – Электрическая схема (а) и треугольник мощностей (б) |
В результате длина вектора полной мощности S составит 1350ВА.
Потребляемый ток нагрузкой от сети:
Итак, в примере показания амперметра РА равны 6,1А.
Можно определить коэффициент активной мощности cosφ нагрузки как отношение прилежащего катета к гипотенузе, т.е. активной (1255Вт) мощности к полной (1350ВА). В приведенном примере cosφ=1255Вт/1350ВА=0,93.
Компенсация реактивной мощности.
Нежелательную реактивную мощность
нагрузки можно скомпенсировать при
помощи конденсаторов и таким образом
уменьшить потребляемый нагрузкой ток. Конденсатор, включенный в сеть, потребляет
реактивную мощность «другого знака»,
направленную в противоположную сторону.
Подключим параллельно нагрузке
конденсатор C емкостью, например 12,5мкФ
(см. рис. 2.3 а). Определим его реактивную
мощность QС по формуле:
Конденсатор, включенный в сеть, потребляет
реактивную мощность «другого знака»,
направленную в противоположную сторону.
Подключим параллельно нагрузке
конденсатор C емкостью, например 12,5мкФ
(см. рис. 2.3 а). Определим его реактивную
мощность QС по формуле:
(при частоте f=50Гц)
На треугольнике емкостная реактивная мощность откладывается в обратную сторону реактивных мощностей нагрузки (см рис. 2.3 б).
б) а) |
Рис. 2.3 – Электрическая схема (а) и треугольник мощностей (б) при компенсации реактивной мощности конденсатором |
В результате видно, что полная мощность
S уменьшилась (стала 1295ВА, была 1350ВА),
снизился и потребляемый от сети ток
(стал 5,9А, был 6,1А) при неизменной полезной
активной мощности. Также увеличился
коэффициент активной мощности cos
до 0,97 (был 0,93).
Также увеличился
коэффициент активной мощности cos
до 0,97 (был 0,93).
Таким образом, конденсатор позволяет компенсировать реактивную мощность нагрузки, в результате чего уменьшается полная мощность S и потребляемый нагрузкой ток. При этом коэффициент мощности нагрузки cos увеличивается.
Из треугольника мощностей видно, чтобы полностью скомпенсировать реактивную мощность нагрузки необходимо подобрать такую емкость конденсатора, чтобы QC=Q. В примере, для полной компенсации реактивной мощности в 491ВАр необходима емкость конденсатора:
После полной компенсации мощность полная мощность S совпадает с активной P, и потребляемый ток равен I=S/U=P/U, а cos=P/S нагрузки равен единице.
Потребляемый ток нагрузкой после компенсации:
На практике компенсация реактивной
мощности осуществляется включением
специальных батарей конденсаторов
нужной емкости параллельно нагрузке и
имеет экономическое значение, т. к.
снижается протекающий ток и соответственно
потери в сетях.
к.
снижается протекающий ток и соответственно
потери в сетях.
Основы электротехники – формулы и уравнения
Область техники, которая занимается изучением проектирования и реализации различных электрических устройств и систем, используемых в нашей повседневной жизни, а также производством, передачей и распределением электроэнергии, широко известна как Электротехника .
Электротехника в основном занимается изучением электрических цепей, энергетических систем, электрических машин, силовой электроники, систем управления и многого другого. Электротехника использует формулы и математические уравнения для объяснения и доказательства правильности концепций. Эти формулы и уравнения очень полезны для понимания поведения электрических систем и помогают выполнять различные расчеты на практике.
Эта статья предназначена для описания всех важных формул и уравнений электротехники, которые необходимо знать каждому студенту-электрику и профессионалу.
Электрический заряд
Субатомное свойство веществ, благодаря которому вещества проявляют электрические свойства, называется электрическим зарядом .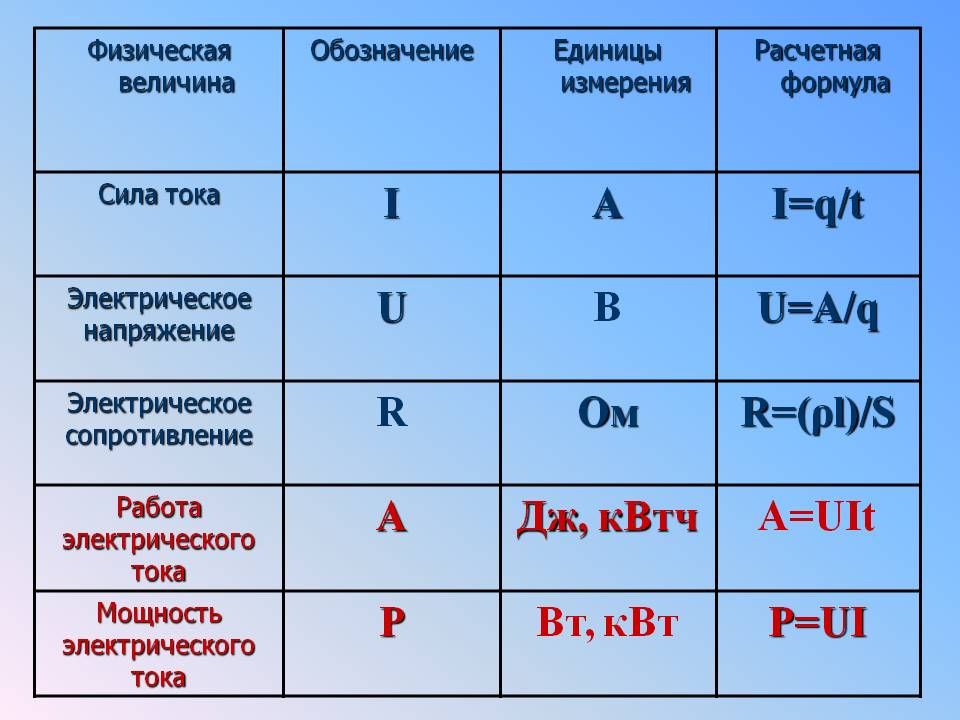 Электрический заряд обозначается как Q (или q) и измеряется в кулонов (Кл) . Электрический заряд переносится двумя элементарными атомными частицами, а именно электронами и протонами, где электрон несет отрицательный заряд, а протон несет положительный заряд. 9{-19} C}$$
Электрический заряд обозначается как Q (или q) и измеряется в кулонов (Кл) . Электрический заряд переносится двумя элементарными атомными частицами, а именно электронами и протонами, где электрон несет отрицательный заряд, а протон несет положительный заряд. 9{-19} C}$$
Электрический заряд является квантованной величиной, а это означает, что электрический заряд всегда существует как целое кратное элементарного заряда (e), т. е.
$$\mathrm{Q = ne;\ :\:\: где, n = 0,\, 1,\, 2,\, 3,\, \cdot \cdot \cdot}$$
Напряжение
Напряжение, также называемое разностью потенциалов , определяется как разность электрических потенциалов двух точек электрической цепи. Измеряется в Вольт (В) . Его также можно определить как количество работы, необходимой для перемещения единицы заряда из одной точки в другую в электрической цепи, т. е.
$$\mathrm{Напряжение, \: V\, =\, \frac{Работа\: выполнена\: \влево ( W \вправо )}{Заряд\: \влево ( Q \вправо )}}$$
Электрический ток
Направленный поток электрического заряда, в частности электронов, через проводник известен как электрический ток .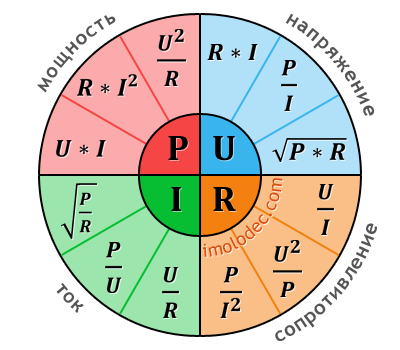 Электрический ток обозначается буквой I (или i) и измеряется в Ампер (А) . Электрический ток можно также определить как скорость изменения заряда во времени, т.е.
Электрический ток обозначается буквой I (или i) и измеряется в Ампер (А) . Электрический ток можно также определить как скорость изменения заряда во времени, т.е.
$$\mathrm{I\, =\, \frac{Q}{t}}$$
В дифференциальной форме,
$$\mathrm{i\, =\, \frac{dq}{dt}}$$
Электрическое сопротивление
Электрическое сопротивление является мерой сопротивления, оказываемого веществом в потоке электрического тока. Обозначается R и измеряется в Ом (Ом) .
$$\mathrm{R\, =\, \frac{\rho l}{a}}$$
Где ρ – это константа, называемая удельным сопротивлением или удельным сопротивлением материала. Удельное сопротивление определяется как свойство материала, благодаря которому он препятствует протеканию через него тока.
Закон Ома
Закон Ома — это основной закон, относящийся к электрической цепи. В нем говорится, что напряжение на проводнике прямо пропорционально току, протекающему по нему, при условии, что физические условия остаются постоянными. Он дает взаимосвязь между напряжением, током и сопротивлением проводника в виде называется проводимостью и определяется как величина, обратная электрическому сопротивлению, т. е.
Он дает взаимосвязь между напряжением, током и сопротивлением проводника в виде называется проводимостью и определяется как величина, обратная электрическому сопротивлению, т. е.
$$\mathrm{Проводимость,\, G \, =\, \frac{I}{R}\, =\, \frac{a}{\rho l}\, =\,\frac{\sigma a}{l}}$$
Где σ — проводимость материала и определяется как:
$$\mathrm{Conductivity,\, \sigma \, =\, \frac{1}{\ rho }}$$
Электроэнергия
Скорость выполнения работы в электрической цепи называется электроэнергией. Обозначается P и измеряется в ватт (Вт) .
$$\mathrm{P\, \sigma \, =\, \frac{dW}{dt }}$$ 9{2}}{R}}$$
В однофазных цепях переменного тока,
$$\mathrm{Активная\: мощность, P = VI\: cos\, \phi }$$
$$\mathrm {Реактивная\: мощность, Q = VI\: sin\, \phi}$$
$$\mathrm{Полная\: мощность, S = VI}$$
Где активная мощность измеряется в ваттах (Вт) , реактивная мощность в реактивных вольт-амперах (ВАр) и полная мощность в вольт-амперах (ВА).
В трехфазных цепях переменного тока,
$$\mathrm{Активная\: мощность,P\, =\, 3V_{p}I_{p}\, cos\, \phi \, = \, \, = \, \sqrt{3}V_{L}I_{L}\, cos\, \phi }$$
$$\mathrm{Реактивная\: мощность,Q\, =\, 3V_{p}I_{p}\, sin\, \phi \, = \, \, =\, \sqrt{3}V_{ L}I_{L}\, sin\, \phi }$$
$$\mathrm{Кажущаяся\: мощность,S\, =\, 3V_{p}I_{p}\, = \, \, = \, \sqrt{3}V_{L}I_{L}}$$
Коэффициент мощности
Коэффициент мощности является мерой использования электроэнергии в электрической цепи переменного тока. Он предоставляет информацию о части общей мощности, используемой нагрузкой в электрической системе. Он определяется отношением активной мощности к полной мощности, т. е.
$$\mathrm{Мощность\: коэффициент, cos\, \phi \, =\, \frac{Активная\: мощность (P)}{Кажущаяся\: мощность (S)}}$$
Коэффициент мощности электрической нагрузки изменяется от -1 до 1. Для резистивной нагрузки она равна единице (1), для индуктивной — отстающая, а для емкостной — опережающая.
Частота и период времени
Количество циклов, которые переменная величина совершает за одну секунду, называется частотой величины. Обозначается буквой f и составляет в герцах (Гц) .
$$\mathrm{f \, =\, \frac{No.\: of\: cycles}{time}}$$
Время, необходимое переменной величине для завершения одного цикла, называется его периодом времени . Обозначается Т, и измеряется в секундах (с) .
Частота переменной величины обратно пропорциональна ее периоду времени, т. е.
$$\mathrm{f \propto \frac{1}{T}}$$
Длина волны расстояние между двумя последовательными гребнями в соседних циклах волны называется
длина волны сигнала. Обозначается греческой буквой , лямбда (λ) . $$\mathrm{\lambda \, =\, \frac{
u }{f}}$$
Где v скорость волны и f частота
Емкость
Свойство вещества запасать электрический заряд в виде электростатического поля называется емкостью вещества.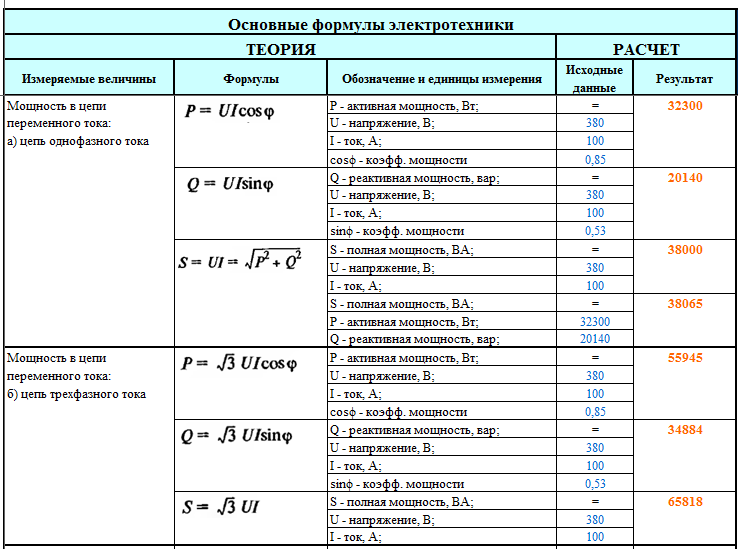 Элемент цепи, используемый для введения емкостного эффекта в электрическую цепь, называется 9.0003 конденсатор . Емкость конденсатора обозначается Кл, и измеряется в фарад (Ф) .
Элемент цепи, используемый для введения емкостного эффекта в электрическую цепь, называется 9.0003 конденсатор . Емкость конденсатора обозначается Кл, и измеряется в фарад (Ф) .
Емкость конденсатора определяется выражением,
$$\mathrm{C \, =\, \frac{Q }{V}}$$
Где, Q — электрический заряд, накопленный на каждой пластине конденсатора, а В — напряжение на обкладках конденсатора.
Мы также можем выразить емкость конденсатора через его физические размеры следующим образом:
$$\mathrm{C \, =\, \frac{\epsilon A }{d}}$$
Где, ε – диэлектрическая проницаемость среды между пластинами, A – площадь пересечения сечение пластины конденсатора, а d — расстояние между пластинами конденсатора.
Индуктивность
Индуктивность – это свойство материалов сохранять электрическую энергию в виде магнитного поля. Элемент известен как индуктор. Индуктивность обозначается как л и измеряется в Генри (Гн) . {2 }}}$$ 9{2}} }$$
{2 }}}$$ 9{2}} }$$
Где Q 1 и Q 2 — статические заряды, а d — расстояния между этими зарядами
Закон Гаусса для электрического потока
Закон электростатики Гаусса дает
$$\mathrm{\phi _{e}\, =\, \frac{Q}{\epsilon } }$$
Уравнение ЭДС генератора постоянного тока генератором постоянного тока:
$$\mathrm{E_{g}\, =\, \frac{NP\phi Z}{60A } }$$
Где Н — скорость вращения якоря, P — число полюсов поля, ϕ — магнитный поток на полюс, Z — число проводников якоря и А — нет. параллельных путей.
Противо-ЭДС двигателя постоянного тока
ЭДС, индуцированная в двигателе постоянного тока из-за электромагнитной индукции, называется противо-ЭДС или противо-ЭДС. Это определяется как,
$$\mathrm{E_{b}\, =\, \frac{NP\phi Z}{60A } }$$
Уравнение ЭДС трансформатора
Выражение, которое дает значение ЭДС, индуцированной в обмотках трансформатора, называется уравнением ЭДС.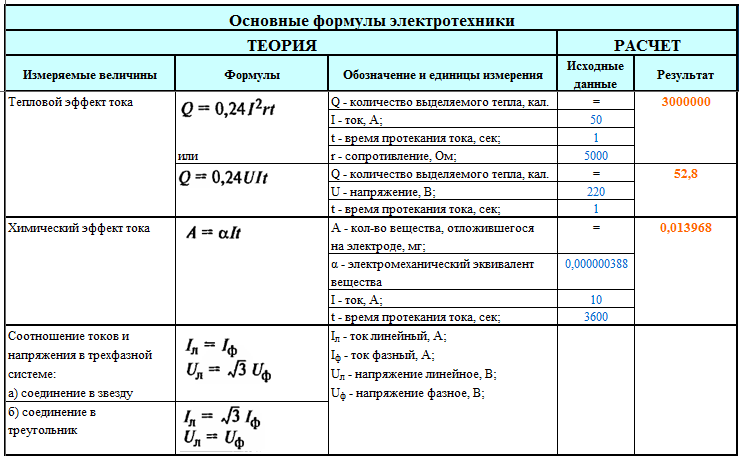 Это определяется как,
Это определяется как,
$$\mathrm{E\, =\,4,44\, f\phi _{m}N }$$
Где, f — частота переменного тока, ϕ м — максимальный поток, а N — количество витков в обмотке.
Гистерезисные потери
Потери мощности в железных сердечниках электрических машин (двигатель, генератор, трансформатор и т. д.) из-за перемагничивания называются гистерезисными потерями и рассчитываются по формуле 9{2}\, V }$$
Где k e — константа, а t — толщина каждого слоя сердечника.
Коэффициент трансформации трансформатора и коэффициент трансформации
Коэффициент трансформации трансформатора определяется как отношение числа витков первичной обмотки к числу витков вторичной обмотки, т.е. \, =\,\frac{N_{1}}{N_{2}}\,=\,\frac{E_{1}}{E_{2}}\,=\,\frac{V_{1} }{V_{2}}\,=\,\frac{I_{2}}{I_{1}}}$$
Коэффициент трансформации трансформатора определяется как отношение выходного напряжения к входному, т. е.
е.
$$\mathrm{Преобразование \: коэффициент\, =\,\frac{V_{2}}{V_{1 }}\,=\,\frac{E_{2}}{E_{1}}\,=\,\frac{N_{2}}{N_{1}}\,=\,\frac{I_{ 1}}{I_{2}}\,=\,\frac{1}{a}}$$
Синхронная скорость
Во вращающихся электрических машинах, таких как двигатели и генераторы, магнитное поле вращается с постоянной скоростью, которая называется синхронной скоростью.
$$\mathrm{N_{s}\, =\, \frac{120\, f}{P}}$$
Где f — частота питания, а P — полюса возбуждения в машине.
КПД
Для электрической машины отношение выходной мощности к подводимой мощности известно как КПД машины, т. е.
$$\mathrm{КПД,\eta \, =\, \frac{Выход\ : power\left ( P_{o} \right )}{Input\: power\left ( P_{i} \right )}}$$
Уравнение ЭДС трехфазного генератора
Уравнение ЭДС трехфазного генератора фазный генератор дает величину генерируемой ЭДС. Генерируемая ЭДС на фазу,
$$\mathrm{E_{ph} \, =\,2.22k_{p}k_{d}f\phi Z\, =\, 4.44k_{p}k_{d}f\phi T }$$
Где, k p и k d — шаговой коэффициент и коэффициент распределения обмотки якоря соответственно, Z — число проводников на фазу, а T — число витков на фазу .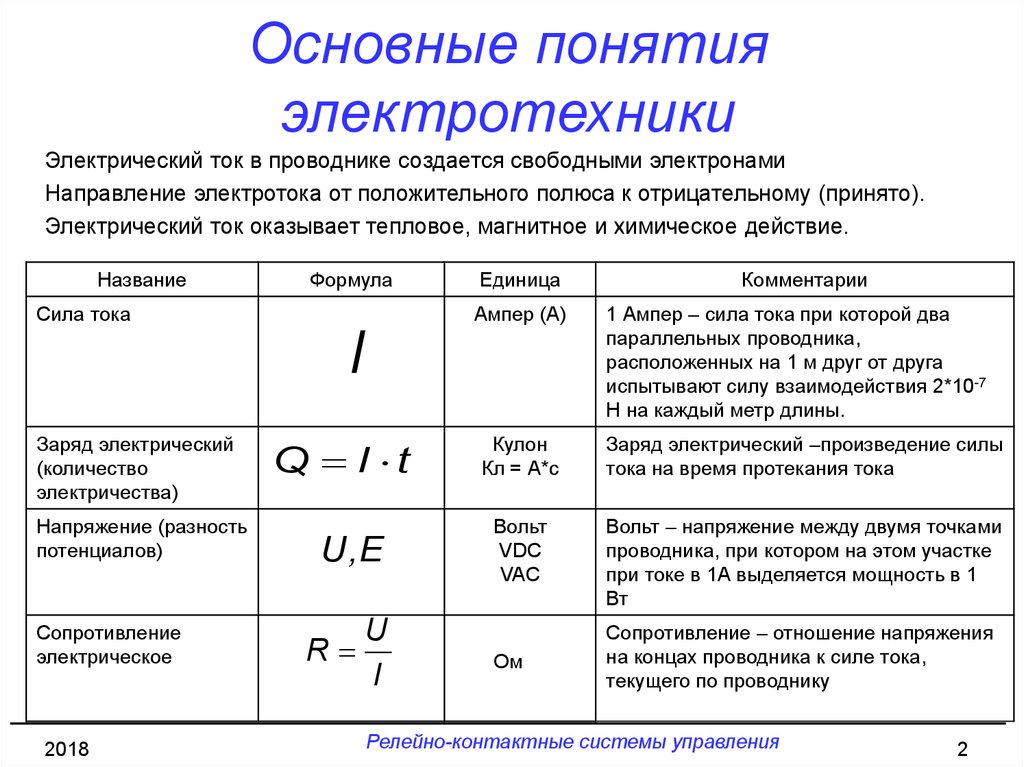
Электрический импеданс
В цепях переменного тока комбинированное сопротивление, создаваемое сопротивлением, индуктивностью и (или) емкостью при протекании тока, называется импедансом. Обозначается цифрой Z и измеряется в Ом (Ом) .
$$\mathrm{Z \, =\,R+jX}$$
Где X — реактивное сопротивление, создаваемое катушкой индуктивности или конденсатором.
Для дросселя,
$$\mathrm{Индуктивность\: реактивное сопротивление,\, X_{L} \, =\,\omega L\, =\, 2\pi fL}$$
Для конденсатора,
$$\mathrm{Емкостный\: реактивное сопротивление,\, X_{C} \, =\,\frac{1}{\omega C}\, =\, \frac{1}{2\pi fC}}$$
Заключение
В этой статье мы перечислили все важные формулы и уравнения основ электротехники. Кроме того, мы определили каждое количество для вашей справки. Все эти формулы должен знать каждый инженер-электрик, потому что они часто используются в различных расчетах.
ЭЛЕКТРОТЕХНИКА ДЛЯ ПРАКТИКИ EN
EE P 502 Аналитические методы в электротехнике (4)
Применение аналитических и математических методов в электротехнике, включая: MATLAB, непрерывные сигналы и линейные системы, ряды Фурье и преобразование Фурье , сигналы с дискретным временем и линейные системы, линейная алгебра, вероятностные и случайные процессы.
Подробнее о курсе в MyPlan: EE P 502
EE P 520 Программная инженерия для встраиваемых приложений (4)
Основы языков программирования и разработки программного обеспечения, общие для всех уровней программирования встроенных систем. Обзоры C++ и подобных языков, обычно используемых для встраиваемых систем, а также способы использования инструментов сборки, контроля версий и расширенных редакторов. Будут изучены структуры данных и алгоритмы, общие для встроенных систем, такие как планировщики, циклы событий, конечные автоматы, модели датчиков, ограничения в реальном времени и управление питанием.
Просмотр сведений о курсе в MyPlan: EE P 520
EE P 522 Встроенные системы и системы реального времени (4)
Определение характеристик встроенного аппаратного и программного обеспечения посредством практических исследований. Охватывает конкретную аппаратную платформу, системное программное обеспечение, пределы вычислений, анализ архитектуры и взаимодействие с физическим миром. Вводит управление питанием, надежностью, системами, критически важными для безопасности, и моделированием.
Вводит управление питанием, надежностью, системами, критически важными для безопасности, и моделированием.
Подробнее о курсе в MyPlan: EE P 522
EE P 527 Микропроизводство (4)
Принципы и методы изготовления микроэлектронных устройств и интегральных схем. Включает лабораторные практики в чистых помещениях и химическую безопасность, фотолитографию, влажное и сухое травление, окисление и диффузию, металлизацию и диэлектрическое осаждение, системы сжатого газа, вакуумные системы, системы термической обработки, плазменные системы и метрологию. Обширная лаборатория с ограниченным набором. Рекомендовано: Не может быть принято в качестве кредита, если кредит получен за E E 527.
Подробнее о курсе в MyPlan: EE P 527
EE P 545 Беспилотный автомобиль: введение в ИИ для мобильных роботов (4)
Оценка состояния (фильтры частиц, модели движения, модели датчиков), планирование/управление (поиск планировщики на основе решеток, методы отслеживания траектории), а также восприятие и обучение (обнаружение объектов, обучение на демонстрациях) для мобильных роботов.


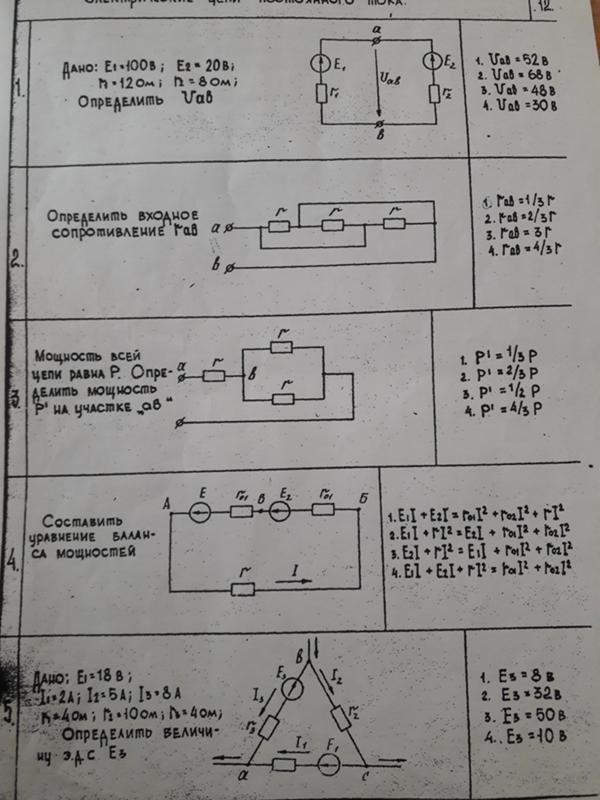

 д. (индуктивные или емкостные нагрузки – реактивные компоненты), то необходимо учитывать следующее cos φ , например:
д. (индуктивные или емкостные нагрузки – реактивные компоненты), то необходимо учитывать следующее cos φ , например: Не забудьте проверить рекламу google, реклама бесплатна для вас и для меня, чтобы развивать сайт, удачи.
Не забудьте проверить рекламу google, реклама бесплатна для вас и для меня, чтобы развивать сайт, удачи.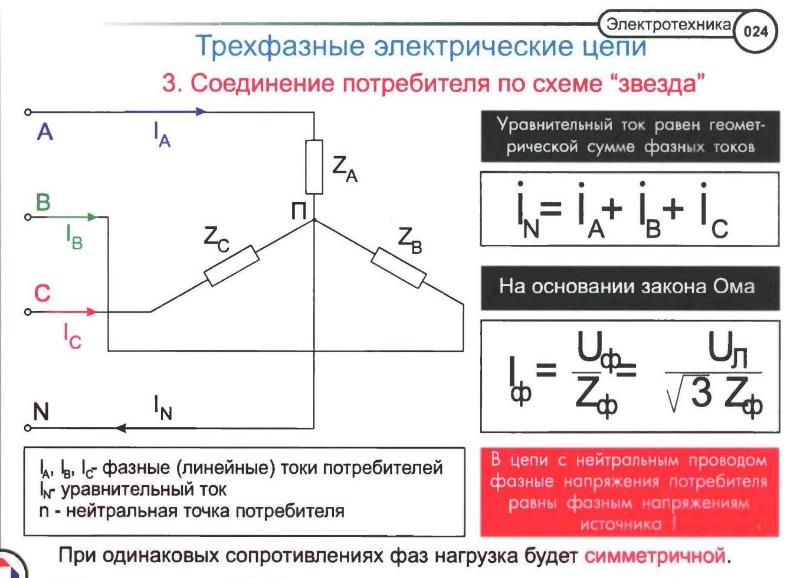

 Во время движения он совершает работу. Следовательно, работа постоянного тока – это действие поля по перемещению электрических зарядов по проводнику. Она равна произведению I и работы, совершенной напряжением и временем.
Во время движения он совершает работу. Следовательно, работа постоянного тока – это действие поля по перемещению электрических зарядов по проводнику. Она равна произведению I и работы, совершенной напряжением и временем.

 Отношение полезной работы к общей работе выражается формулой: η = A полезно / Apoln = P полезно / Apoln = U/ε = R / (R + r).
Отношение полезной работы к общей работе выражается формулой: η = A полезно / Apoln = P полезно / Apoln = U/ε = R / (R + r). Используя его, можно получить систему линейных уравнений для токов или напряжений во всех соединенных ветвях цепи.
Используя его, можно получить систему линейных уравнений для токов или напряжений во всех соединенных ветвях цепи.