Момент инерции | это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Содержание
|
Осевой момент инерции
Осевые моменты инерции некоторых тел.
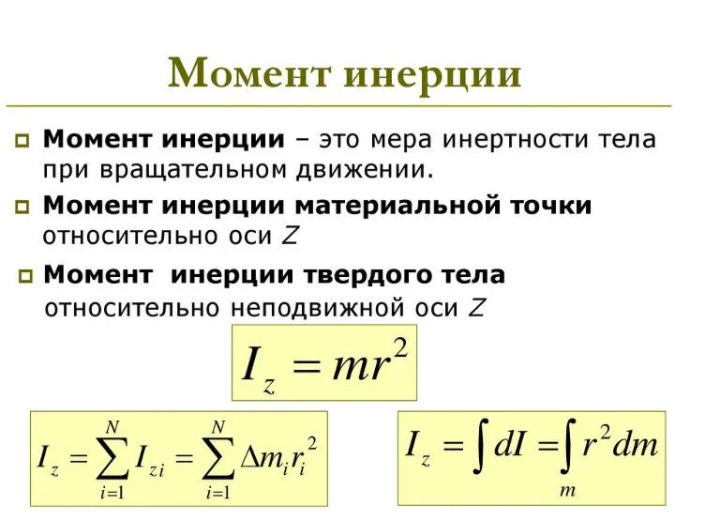
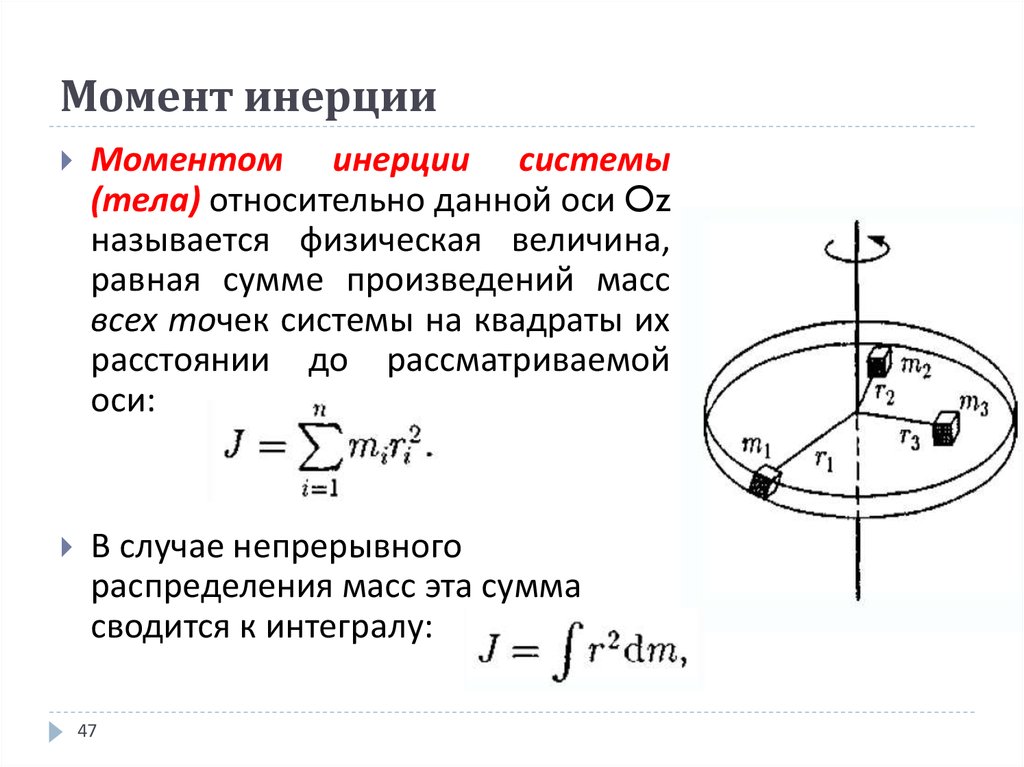
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Основная статья: Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
| Тело | Описание | Положение оси a | Момент инерции Ja |
|---|---|---|---|
| Материальная точка массы m | |||
| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | ||
| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | ||
| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | ||
| Сплошной цилиндр длины l, радиуса r и массы | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | ||
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | ||
| Шар радиуса r и массы m | Ось проходит через центр шара | ||
| Конус радиуса r и массы m | Ось конуса | ||
| Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину | ||
| Правильный треугольник со стороной | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
| Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс |
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[1][2]
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.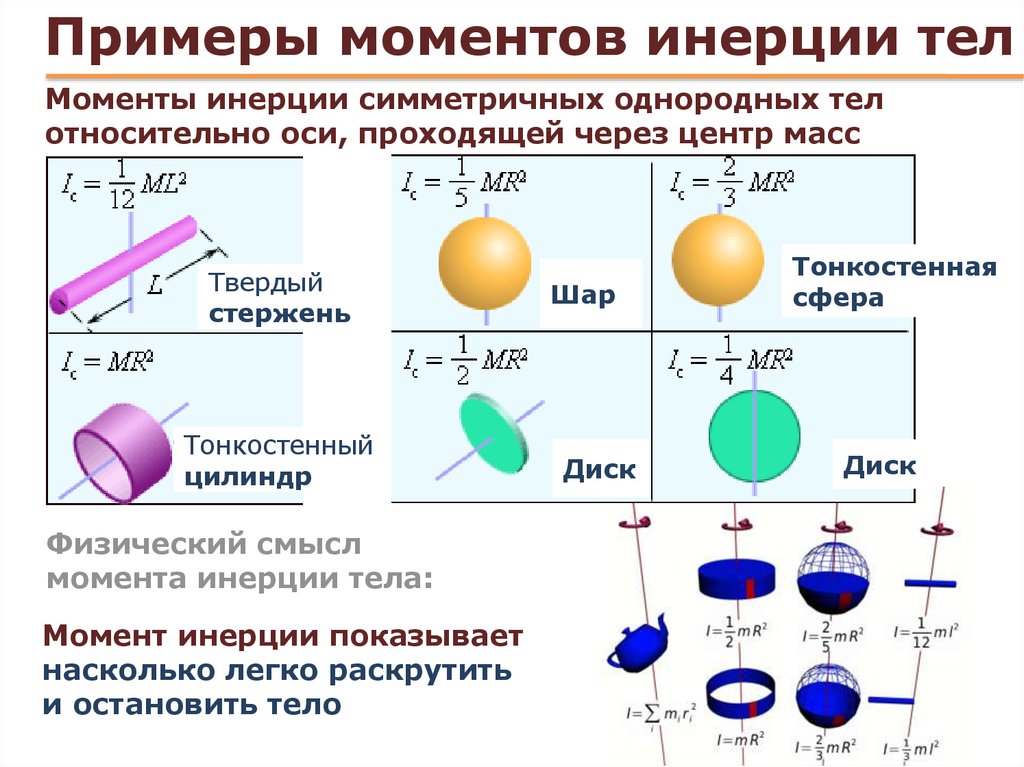
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м
Из него выражается момент сопротивления сечения:
- .
| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром | |
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
- Движение твёрдого тела
- Метод главных компонент
- Сопротивление материалов
- Теорема Штейнера
- Механические приложения тройного интеграла
- Механические приложения двойного интеграла
- Полярный момент инерции
- Список моментов инерции
Примечания
- ↑ Planetary Fact Sheet
- ↑ Showman, Adam P.; Malhotra, Renu (1999). «The Galilean Satellites» (PDF). Science 286 (5437): 77–84. DOI:10.1126/science.286.5437.77. PMID 10506564.
- ↑ Галкин И.Н. Внеземная сейсмология.
 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X - ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д.
 В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm - Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
- Определение момента инерции тел простой формы
- Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур
- Online Калькулятор осевых моментов инерции, моментов сопротивления и радиусов инерции плоских фигур
Момент инерции | это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Содержание
|
Осевой момент инерции
Осевые моменты инерции некоторых тел.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Основная статья: Теорема Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
| Тело | Описание | Положение оси a | Момент инерции Ja |
|---|---|---|---|
| Материальная точка массы m | На расстоянии r от точки, неподвижная | ||
| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | ||
| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | ||
| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | ||
| Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | ||
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | ||
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | ||
| Шар радиуса r и массы m | Ось проходит через центр шара | ||
| Конус радиуса r и массы m | Ось конуса | ||
| Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину | ||
| Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
| Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс |
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr.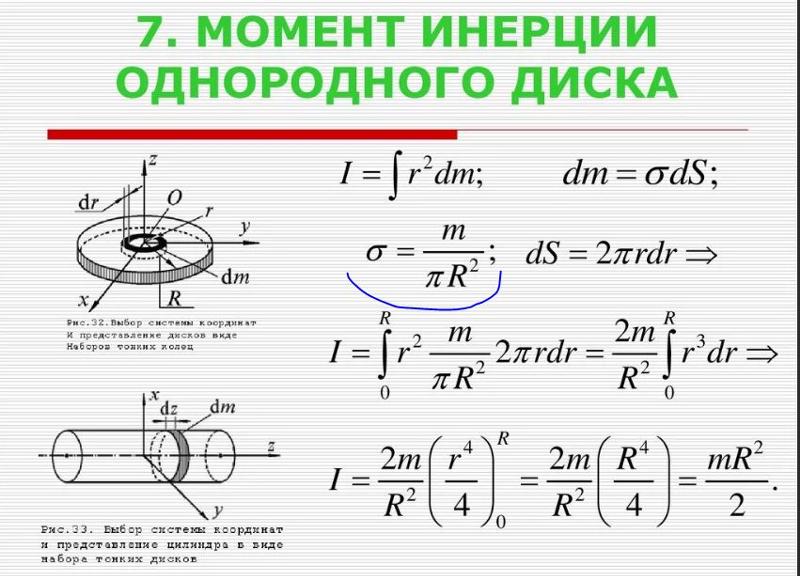 Масса и момент инерции такого фрагмента равна
Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[1][2]
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине.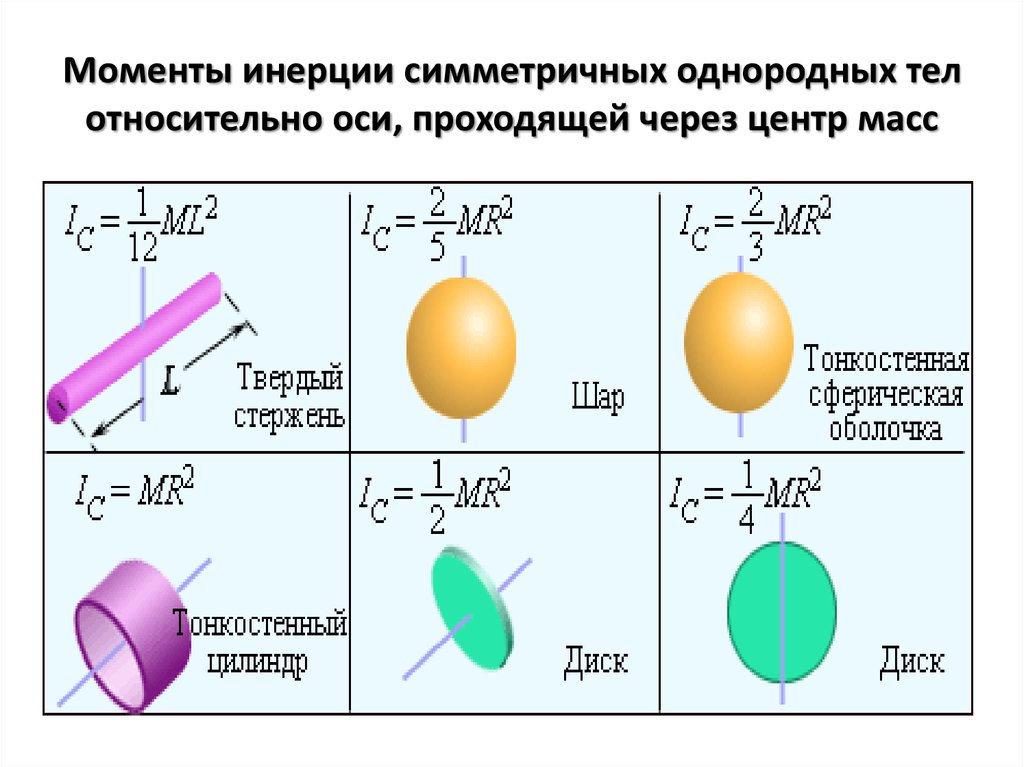 Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
| Геометрические моменты инерции некоторых фигур | |
|---|---|
| Прямоугольника высотой и шириной : | |
| Прямоугольного коробчатого сечения высотой и шириной по внешним контурам и , а по внутренним и соответственно | |
| Круга диаметром | |
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
- — масса малого элемента объёма тела ,
- — плотность,
- — расстояние от элемента до точки O.

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах.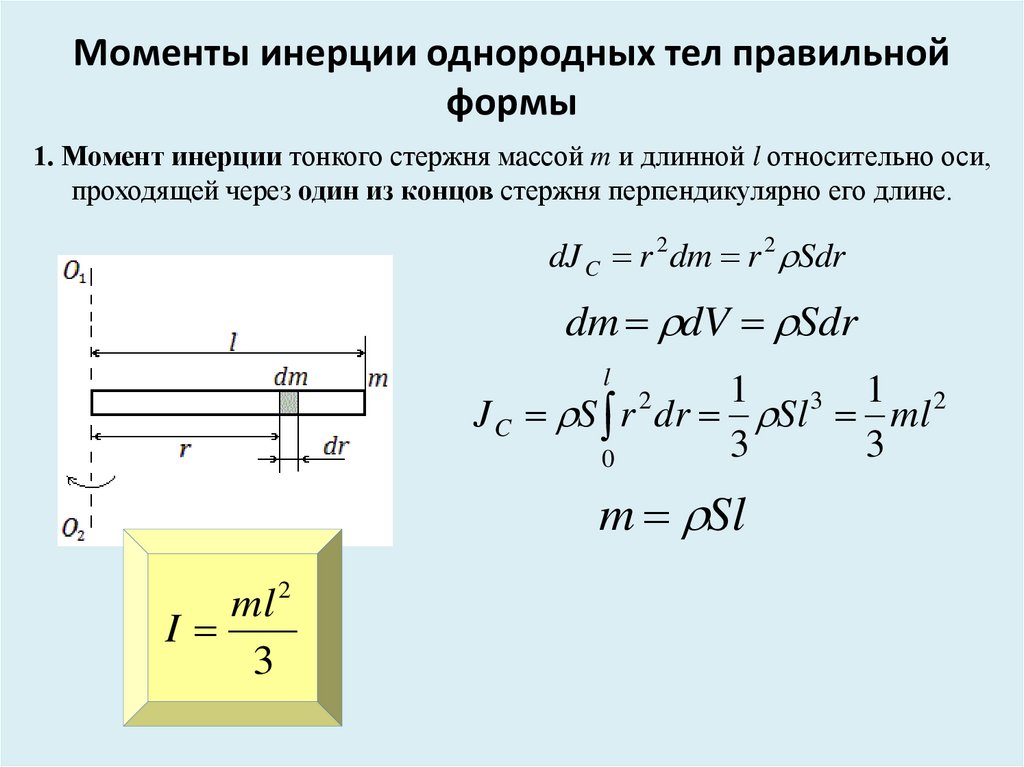 Разделив обе части уравнения на
Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
- Движение твёрдого тела
- Метод главных компонент
- Сопротивление материалов
- Теорема Штейнера
- Механические приложения тройного интеграла
- Механические приложения двойного интеграла
- Полярный момент инерции
- Список моментов инерции
Примечания
- ↑ Planetary Fact Sheet
- ↑ Showman, Adam P.; Malhotra, Renu (1999). «The Galilean Satellites» (PDF). Science 286 (5437): 77–84. DOI:10.1126/science.286.5437.77. PMID 10506564.
- ↑ Галкин И.Н. Внеземная сейсмология.
 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X - ↑ Пантелеев В. Л. Физика Земли и планет. Гл. 3.4 — Гравитационное поле планеты
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д.
 В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm - Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
- Определение момента инерции тел простой формы
- Осевые моменты инерции, моменты сопротивления и радиусы инерции плоских фигур
- Online Калькулятор осевых моментов инерции, моментов сопротивления и радиусов инерции плоских фигур
Момент инерции | Определение, уравнение, единица измерения и факты
момент инерции
Просмотреть все СМИ
- Похожие темы:
- инерция вращения радиус вращения
См. все связанное содержимое →
момент инерции , в физике, количественная мера инерции вращения тела, т. е. противодействие, которое тело проявляет при изменении скорости вращения вокруг оси при приложении крутящего момента (сила поворота). Ось может быть внутренней или внешней и может быть фиксированной или нефиксированной. Момент инерции ( I ), однако, всегда указывается относительно этой оси и определяется как сумма произведений, полученных путем умножения массы каждой частицы материи в данном теле на квадрат ее расстояния от оси. При расчете углового момента твердого тела момент инерции аналогичен массе в линейном импульсе. Для линейного импульса импульс p равен массе m , умноженной на скорость v ; тогда как для углового момента угловой момент L равно моменту инерции I , умноженному на угловую скорость ω.
Ось может быть внутренней или внешней и может быть фиксированной или нефиксированной. Момент инерции ( I ), однако, всегда указывается относительно этой оси и определяется как сумма произведений, полученных путем умножения массы каждой частицы материи в данном теле на квадрат ее расстояния от оси. При расчете углового момента твердого тела момент инерции аналогичен массе в линейном импульсе. Для линейного импульса импульс p равен массе m , умноженной на скорость v ; тогда как для углового момента угловой момент L равно моменту инерции I , умноженному на угловую скорость ω.
На рисунке показаны два стальных шарика, приваренных к стержню AB , прикрепленному к стержню OQ на C . Если пренебречь массой AB и предположить, что все частицы массой m каждого шара сосредоточены на расстоянии r от OQ , момент инерции будет равен I = 2 mr 2 .
Викторина «Британника»
Физика и естественное право
Единица момента инерции является составной единицей измерения. В Международной системе (СИ) m выражается в килограммах, а r — в метрах, при этом I (момент инерции) имеет размерность килограмм-метр в квадрате. В обычной системе США м выражено в слаговых единицах (1 слаг = 32,2 фунта) и r в футах, причем I выражено в единицах слаг-футовой площади.
Момент инерции любого тела, форма которого может быть описана математической формулой, обычно рассчитывается с помощью интегрального исчисления. Момент инерции диска на фигуре около OQ можно аппроксимировать, разрезав его на ряд тонких концентрических колец, найдя их массы, умножив массы на квадраты их расстояний от OQ и сложив эти продукты. При использовании интегрального исчисления процесс суммирования осуществляется автоматически; ответ I = ( мР 2 )/2.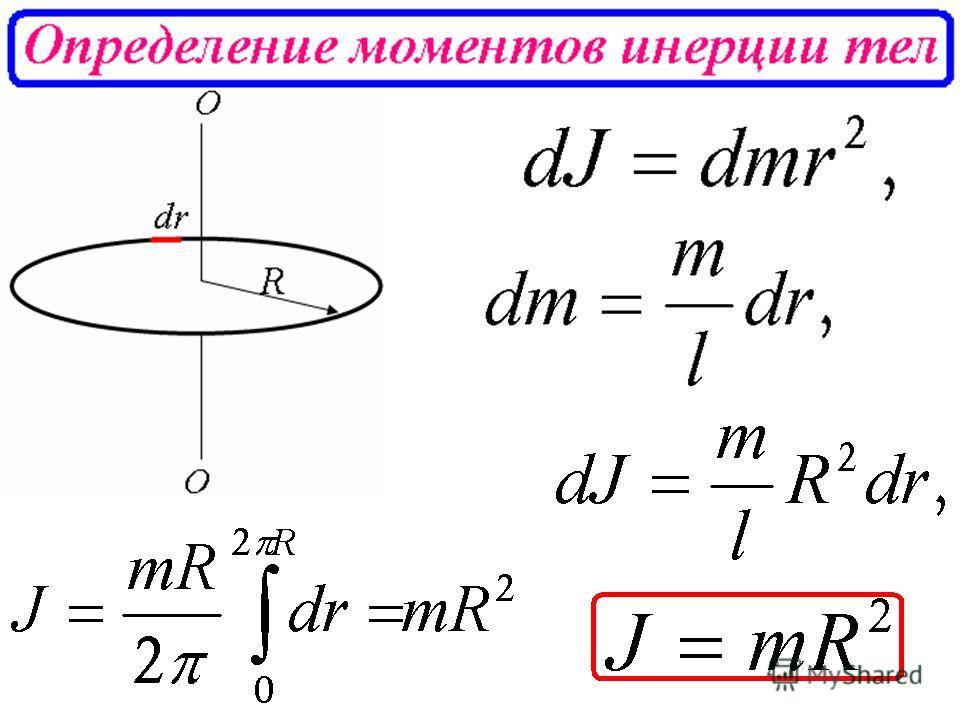 (См. механику; крутящий момент.)
(См. механику; крутящий момент.)
Для тела математически не поддающейся описанию формы момент инерции можно определить экспериментальным путем. В одной из экспериментальных методик используется связь между периодом (временем) колебаний крутильного маятника и моментом инерции подвешенной массы. Если бы диск на рисунке был подвешен на проволоке OC , закрепленной в точке O , он бы колебался примерно OC , если его скрутить и отпустить. Время одного полного колебания будет зависеть от жесткости проволоки и момента инерции диска; чем больше инерция, тем больше время.
Редакторы Британской энциклопедии Эта статья была недавно отредактирована и дополнена Эриком Грегерсеном.
Момент инерции — Формулы, MOI объектов [Примеры решения]
Момент инерции является важной темой и задается в большинстве физических задач, связанных с массой во вращательном движении. Обычно MOI используется для расчета углового момента.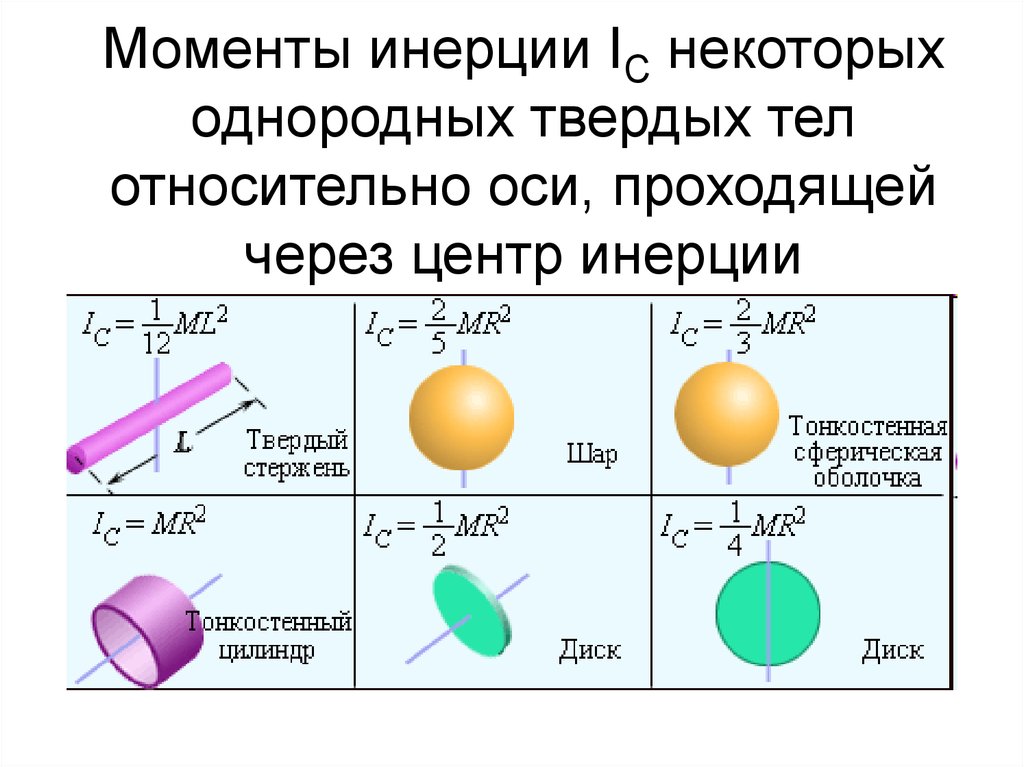 Мы узнаем об этой теме больше в следующих параграфах.
Мы узнаем об этой теме больше в следующих параграфах.
JEE Main 2021 LIVE Physics Paper Solutions 24 февраля Shift-1 На основе памяти
Что такое момент инерции?
Момент инерции определяется как величина, выражаемая телом, сопротивляющимся угловому ускорению, которое представляет собой сумму произведения массы каждой частицы на квадрат ее расстояния от оси вращения. Или, проще говоря, его можно описать как величину, которая определяет величину крутящего момента, необходимого для определенного углового ускорения по оси вращения. Момент инерции также известен как угловая масса или инерция вращения. Единицей момента инерции в системе СИ является кг·м·9.0049 2 .
Момент инерции обычно указывается относительно выбранной оси вращения. В основном это зависит от распределения массы вокруг оси вращения. MOI варьируется в зависимости от выбранной оси.
Содержание
- Формула
- Факторы, влияющие на МВД
- Момент инерции системы частиц
- Для жестких тел
- Расчет
- Момент инерции для различных объектов
- Теорема о параллельных осях
- Радиус вращения
- Решенные примеры
- Момент инерции различных форм и объектов
Формула момента инерции
В общем виде момент инерции выражается как I = m × r 2
где,
м = Сумма произведения массы.
r = Расстояние от оси вращения.
и, Интегральная форма: I = ∫dI = ∫ 0 M r 2 дм
⇒ Размерная формула момента инерции определяется как M 1 L 2 T 0 .
Роль момента инерции такая же, как роль массы в линейном движении. Это измерение сопротивления тела изменению его вращательного движения. Она постоянна для конкретной жесткой рамы и определенной оси вращения.
Момент инерции, I = ∑m i r i 2 . . . . . . . (1)
Кинетическая энергия, К = ½ I ω 2 . . . . . . . . . (2)
От каких факторов зависит момент инерции?
Момент инерции зависит от следующих факторов,
- Плотность материала
- Форма и размер корпуса
- Ось вращения (распределение массы относительно оси)
Системы с вращающимся корпусом можно разделить на следующие категории:
- Дискретный (Система частиц)
- Непрерывный (жесткий корпус)
Читайте также:
- Площадь момента инерции
- Полярный момент инерции
- Массовый момент инерции
Момент инерции системы частиц
Момент инерции системы частиц определяется выражением
I = ∑ m i r i 2 [из уравнения (1)]
где r i — перпендикулярное расстояние от оси до i-й частицы, имеющей массу m и .
Пример:
Момент инерции твердых тел
Момент инерции непрерывного распределения масс находится методом интегрирования. Если система разделена на бесконечно малый элемент массы «dm» и если «x» — это расстояние от элемента массы до оси вращения, момент инерции равен:
I = ∫ r 2 дм . . . . . . (3)
Расчет момента инерции
Ниже приведено пошаговое руководство по расчету момента инерции:
Момент инерции однородного стержня относительно биссектрисы
Рассмотрим однородный стержень массой M и длиной L, и момент инерции следует вычислить относительно биссектрисы AB. Исходная точка находится по адресу 0.
.Рассматриваемый элемент массы «dm» находится между x и x + dx от начала координат.
Поскольку стержень однороден, масса на единицу длины (линейная массовая плотность) остается постоянной.
∴ М/л = дм/дх
дм = (М/л)дх
Момент инерции дм ,
dI = дм x 2
dI = (M/L) x 2 .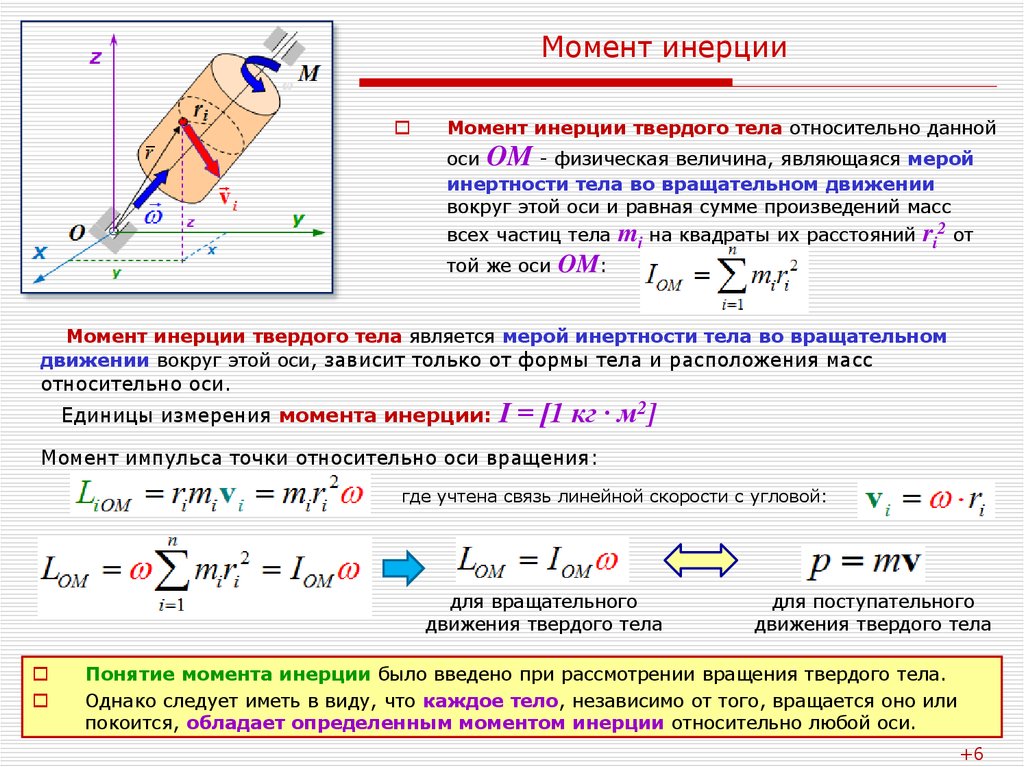 dx
dx
I = -L/2 ∫ +L/2 dI = M/L × -L/2 ∫ +L/2 x 2 dx
Здесь x = -L/2 — левый конец стержня, а x изменяется от –L/2 до +L/2, элемент покрывает весь стержень.
I = M/L × [x 3 /3] +L/2 -L/2
I = ML 2 /12.
Следовательно, момент инерции однородного стержня относительно серединного перпендикуляра (I) = ML 2 /12.
Момент инерции кругового кольца относительно его оси
Рассмотрим прямую, перпендикулярную плоскости кольца, проходящую через его центр. Радиус кольца принимается за R, а его масса за M. Все элементы находятся на одинаковом расстоянии от оси вращения, R.
Линейная массовая плотность постоянна.
∴ М/2π = дм/dθ
дм = M/2π × dθ
I = ∫ R 2 dm = R 2 0 ∫ 2π [M/2π] dθ
Пределы: θ = от 0 до 2π включает всю массу кольца
∴ I = R 2 [M/2π] × [θ] 2π 0
Следовательно, момент инерции круглого кольца относительно его оси (I) = MR 2 .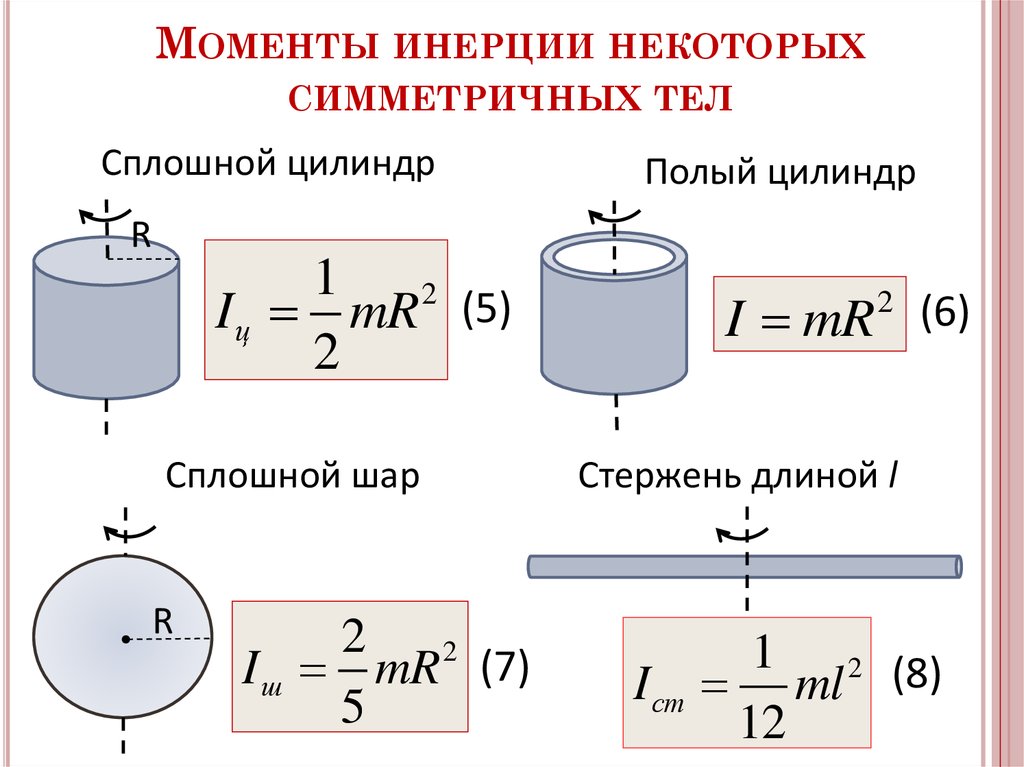
⇒ Обратите внимание, что в одномерных телах, если они однородны, их линейная массовая плотность (M/L) остается постоянной. Точно так же для 2D и 3D M/A (поверхностная плотность) и M/V (объемная плотность) остаются постоянными соответственно.
⇒ Узнайте соотношение между крутящим моментом и моментом инерции здесь
Момент инерции прямоугольной пластины относительно линии, параллельной краю и проходящей через центр
Элемент массы можно взять между x и x + dx от оси AB.
Поскольку пластина однородна, M/A постоянна.
М/А = дм/да
M/[l×b] = dm/dx.b
дм = (М/фунт) × b × dx = (М/л) dx
I = ∫ x 2 дм = (М/л) × -l/2 ∫ +l/2 [x 2 ] dx
Пределы: левый конец прямоугольной пластины находится в точке x = -1/2, и вся пластина покрывается взятием x от x = -1/2 до x = +1/2.
I = (M/l) [x 3 /3] -l/2 +l/2 = Ml 2 /12
Следовательно, момент инерции прямоугольной пластины относительно линии, параллельной ребру и проходящей через центр (I) = Ml 2 /12.
⇒ Примечание: 9.0016 Если элемент массы выбран параллельно длине пластины, то момент инерции будет I = Mb 2 /12.
Момент инерции однородной круглой пластины относительно ее оси
Пусть масса пластины равна M, а радиус равен R. Центр находится в точке O, а ось перпендикулярна плоскости пластины. Рассматриваемый элемент массы представляет собой тонкое кольцо между x и x+dx толщиной dx и массой dm.
Поскольку плоскость однородна, поверхностная плотность массы постоянна.
М/А = дм/да
M/πR 2 = dm/[2π.x.dx]
I = ∫ x 2 dm = 2M/R 2 × 0 ∫ R x 3 . дх
Ограничения: Поскольку мы берем площадь всех элементов массы от x=0 до x=R, мы покрываем всю пластину.
I = (2M/R 2 )[x 4 /4] R 0 = (2M/R 2 ) × R 4 /4 = MR 0 3 2 Следовательно, момент инерции однородной круглой пластины относительно своей оси (I) = MR 2 /2. Пусть M и R — масса и радиус сферы, O — ее центр, а OY — заданная ось. Масса распределена по поверхности сферы, а внутри она полая. Рассмотрим радиусы сферы под углом θ и под углом θ+dθ с осью OY и возьмем элемент (тонкое кольцо) массы dm радиуса Rsinθ при вращении этих радиусов вокруг OY. Ширина этого кольца равна Rdθ, а его периферия — 2πRsinθ. Поскольку полая сфера однородна, поверхностная массовая плотность (M/A) постоянна. М/А = дм/да (M/4πR 2 ) = dm/[2π × Rsinθ. Rdθ] дм = [М/4πR 2 ] × 2πR 2 . sinθ dθ = [M/2] × sinθ dθ I = ∫ x 2 dm = 0 ∫ π (R sin θ) 2 × [M/2] sinθ dθ Ограничения: при увеличении θ от 0 до π кольца элементов покрывают всю сферическую поверхность. I = [МР 2 /2] × 0 ∫ π SIN 3 θ Dθ = MR 2 /2 × 0 ∫ π [SIN 2 θ. = [MR 2 /2] 0 ∫ π (1 – cos 2 θ) sin θ × dθ Теперь, интегрируя приведенное выше уравнение методом подстановки, мы получаем Возьмем u = cos θ dθ Тогда du = – sin θ dθ Изменение пределов, когда θ = 0, u = 1 Когда θ = π, u = -1 I = [MR 2 /2] × 1 ∫ -1 (1 – u 2 ) (-du) = [MR 2 /2] × 1 ∫ -1 (u 2 – 1) (du) = [MR 2 /2] × [u 3 /3 – u] 1 -1 = [MR 2 /2] [-2/3 + 2] = [MR 2 /2 ]× [4/3] = 2MR 2 /3 Следовательно, момент инерции тонкой сферической оболочки и однородной полой сферы (I) = 2MR 2 /3. Рассмотрим шар радиуса R и массы M. В качестве элемента массы принимается тонкая сферическая оболочка радиуса x, массы dm и толщины dx. М/В = дм/дВ M/[4/3 × πR 3 ] = dm/[4πx 2 .dx] dm = [M/(4/3 × πR 3 ) ] × 4πx 2 dx = [3M/R 3 ] x 2 дх I = ∫ dI = (2/3) × ∫ dm . х 2 = (2/3) × ∫ [3M/R 3 dx] x 4 =( 2M/R 3 )× 0 ∫ R x 4 dx Ограничения: При увеличении x от 0 до R элементарная оболочка покрывает всю сферическую поверхность. I = (2M/R 3 )[x 5 /5] R 0 = (2M/R 3 )× R 5 /5 Следовательно, момент инерции однородного твердого шара (I) = 2MR 2 /5. Как видно из таблицы выше, момент инерции зависит от оси вращения. Что бы мы ни рассчитали до сих пор, это момент инерции этих объектов, когда ось проходит через их центр масс (I см ). Момент инерции объекта относительно оси, проходящей через его центр масс, является минимальным моментом инерции для оси в этом направлении в пространстве. Момент инерции относительно оси, параллельной этой оси, проходящей через центр масс, равен I = I см + Md 2 Где d — расстояние между двумя осями. ⇒ Подробнее о теореме о параллельных и перпендикулярных осях Если момент инерции (I) тела массы m относительно оси записать в виде: I = Мк 2 Здесь k называется радиусом вращения тела вокруг данной оси. Радиус вращения твердого шара вокруг своей оси: Mk 2 = 2MR 2 /5, или k = √[2/5] × R. 1. Из однородного круглого диска радиусом R и массой 9 M отделяют небольшой диск радиусом R/3, как показано на рисунке. Вычислите момент инерции оставшегося диска относительно оси, перпендикулярной плоскости диска и проходящей через центр диска. Решение: Момент инерции снятой детали упирается в ось, проходящую через центр масс и перпендикулярную плоскости диска = I см + md 2 = [м × (R/3) 2 ]/2 + m × [4R 2 /9] = мР 2 /2 Следовательно, момент инерции оставшейся части = момент инерции всего диска – момент инерции удаленной части = 9 мР 2 /2 – мР 2 /2 = 8 мР 2 /2 Следовательно, момент инерции оставшейся части (I оставшихся ) = 4mR 2 . 2. Момент Два шара, соединенные стержнем, как показано на рисунке ниже (массу стержня не учитывать). Масса шара X 700 грамм, масса шара Y 500 грамм. Каков момент инерции системы относительно AB? Дано Ось вращения АВ м X = 700 грамм = 0,7 кг м Y = 500 г = 0,5 кг r X = 10 см = 0,1 м r Y = 40 см = 0,4 м Решение: I = m X r X 2 + m Y r Y 2 I = (0,7)× (0,1) 2 + (0,5)× (0,4) 2 I = (0,7) х (0,01) + (0,5) х (0,16) I = 0,007 + о,08 I = 0,087 кг·м 2 Момент инерции системы 0,087 кг·м 2 3. Два шара, соединенные стержнем, как показано на рисунке ниже (без учета массы стержня). Дано м X = 300 грамм = 0,3 кг м Y = 500 г = 0,5 кг r X = 0 см = 0 м r Y = 30 см = 0,3 м Решение: I = m X r X 2 + m Y r Y 2 I = (0,3)× (0) 2 + (0,5)× (0,3) 2 I = 0 + 0,045 I = 0,045 кг·м 2 Момент инерции системы 0,045 кг·м 2 4. Масса каждого шара 200 грамм, соединенного шнуром. Длина шнура 80 см, ширина шнура 40 см. Чему равен момент инерции шариков относительно оси вращения (без учета массы шнура)? Дано Масса мяча = m 1 = m 2 = m 3 = m 4 = 200 грамм = 0,2 кг Расстояние между шаром и осью вращения (r 1 ) = 40 см = 0,4 м Расстояние между шаром 2 и осью вращения (r 2 ) = 40 см = 0,4 м Расстояние между шаром 3 и осью вращения (r 2 ) = 40 см = 0,4 м Расстояние между шаром 4 и осью вращения (r 2 ) = 40 см = 0,4 м Решение: I = m 1 r 1 2 + m 2 r 2 2 + m 3 r 3 2 + m 4 r 4 2 I = (0,2) × (0,4) 2 + (0,2) × (0,4) 2 + (0,2) × (0,4) 2 + (0,2) × (0,4) 2 I = 0,032 + 0,032 + 0,032 + 0,032 I = 0,128 кг м 2 Момент инерции шаров относительно оси o,128 кг·м 2 Вот список МВД различных форм и объектов.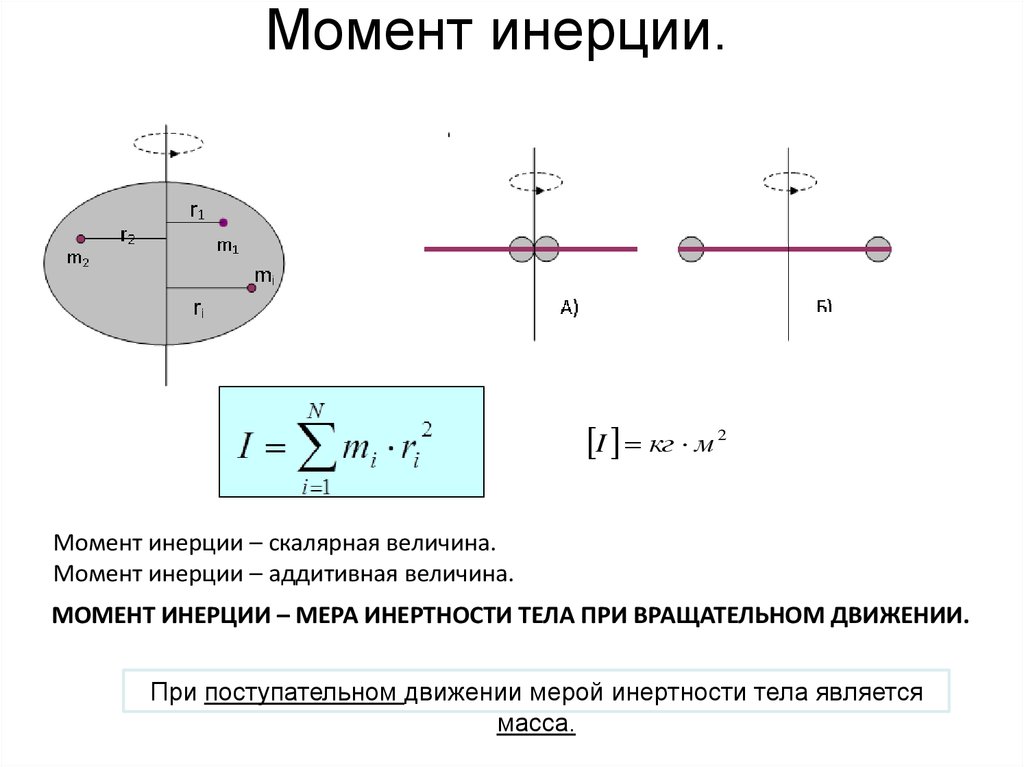
Момент инерции тонкой сферической оболочки или однородной полой сферы
 sin θ] × dθ
sin θ] × dθ Момент инерции однородного твердого шара
 Объемная плотность (M/V) остается постоянной, поскольку твердая сфера однородна.
Объемная плотность (M/V) остается постоянной, поскольку твердая сфера однородна. Момент инерции для различных объектов
 Выбрав две разные оси, вы заметите, что объект по-разному сопротивляется изменению вращения. Следовательно, чтобы найти момент инерции относительно любой заданной оси, полезны следующие теоремы.
Выбрав две разные оси, вы заметите, что объект по-разному сопротивляется изменению вращения. Следовательно, чтобы найти момент инерции относительно любой заданной оси, полезны следующие теоремы. Теорема о параллельных осях
Радиус вращения
 Он представляет собой радиальное расстояние от данной оси вращения, на котором можно предположить, что вся масса тела сосредоточена так, что его инерция вращения остается неизменной.
Он представляет собой радиальное расстояние от данной оси вращения, на котором можно предположить, что вся масса тела сосредоточена так, что его инерция вращения остается неизменной. Решенный пример

 Чему равен момент инерции системы?
Чему равен момент инерции системы?
Момент инерции различных форм и объектов



 также
также
 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm

 — М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X
— М.: Наука, 1988. — С. 42-73. — 195 с. — (Планета Земля и Вселенная). — 15 000 экз. — ISBN 502005951X В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm