Что такое момент инерции: определение, законы, формулы для чайников – Список моментов инерции — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Момент инерции — Википедия. Что такое Момент инерции

Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции

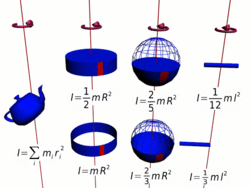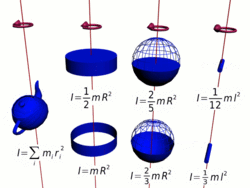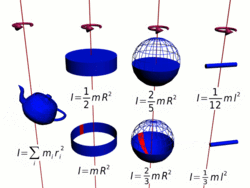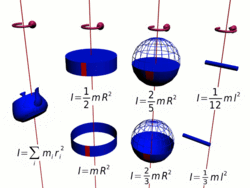Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J

a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси^[1]:

Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}

где:

m_i — масса i-й точки,
r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}

где:

dm = ρ dV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

Ja=ρ∫(V)r2dV.{\displaystyle J_{a}=\rho \int \limits _{(V)}r^{2}dV.}

Теорема Гюйгенса — Штейнера

Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела J_c относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями^[1]:

J=Jc+md2,{\displaystyle J=J_{c}+md^{2},}

где m — полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

J=Jc+md2=112ml2+m(l2)2=13ml2.{\displaystyle J=J_{c}+md^{2}={\frac {1}{12}}ml^{2}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{3}}ml^{2}.}

Осевые моменты инерции некоторых тел

Вывод формул

Тонкостенный цилиндр (кольцо, обруч)

Вывод формулы

Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJ_i. Тогда

J=∑dJi=∑Ri2dm.(1).{\displaystyle J=\sum dJ_{i}=\sum R_{i}^{2}dm.\qquad (1).}

Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду

J=∑R2dm=R2∑dm=mR2.{\displaystyle J=\sum R^{2}dm=R^{2}\sum dm=mR^{2}.}

Толстостенный цилиндр (кольцо, обруч)

Вывод формулы

Однородный диск (сплошной цилиндр)

Вывод формулы

Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R₁ = 0), получим формулу для момента инерции цилиндра (диска):

J=12mR2.{\displaystyle J={\frac {1}{2}}mR^{2}.}

Сплошной конус

Вывод формулы

Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен

r=RhH,{\displaystyle r={\frac {Rh}{H}},}

где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят

dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}

dJ=12r2dm=12πρr4dh=12πρ(RhH)4dh;{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {Rh}{H}}\right)^{4}dh;}

Интегрируя, получим

J=∫0HdJ=12πρ(RH)4∫0Hh5dh=12πρ(RH)4h55|0H==110πρR4H=(ρ⋅13πR2H)310R2=310mR2.{\displaystyle {\begin{aligned}J=\int _{0}^{H}dJ={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\int _{0}^{H}h^{4}dh={\frac {1}{2}}\pi \rho \left({\frac {R}{H}}\right)^{4}\left.{\frac {h^{5}}{5}}\right|_{0}^{H}=={\frac {1}{10}}\pi \rho R^{4}H=\left(\rho \cdot {\frac {1}{3}}\pi R^{2}H\right){\frac {3}{10}}R^{2}={\frac {3}{10}}mR^{2}.\end{aligned}}}

Сплошной однородный шар

Вывод формулы

Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле

r=R2−h3.{\displaystyle r={\sqrt {R^{2}-h^{2}}}.}

Масса и момент инерции такого диска составят

dm=ρdV=ρ⋅πr2dh;{\displaystyle dm=\rho dV=\rho \cdot \pi r^{2}dh;}

dJ=12r2dm=12πρr4dh=12πρ(R2−h3)2dh=12πρ(R4−2R2h3+h5)dh.{\displaystyle dJ={\frac {1}{2}}r^{2}dm={\frac {1}{2}}\pi \rho r^{4}dh={\frac {1}{2}}\pi \rho \left(R^{2}-h^{2}\right)^{2}dh={\frac {1}{2}}\pi \rho \left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh.}

Момент инерции шара найдём интегрированием:

J=∫−RRdJ=2∫0RdJ=πρ∫0R(R4−2R2h3+h5)dh==πρ(R4h−23R2h4+15h5)|0R=πρ(R5−23R5+15R5)=815πρR5==(43πR3ρ)⋅25R2=25mR2.{\displaystyle {\begin{aligned}J&=\int _{-R}^{R}dJ=2\int _{0}^{R}dJ=\pi \rho \int _{0}^{R}\left(R^{4}-2R^{2}h^{2}+h^{4}\right)dh=\\&=\pi \rho \left.\left(R^{4}h-{\frac {2}{3}}R^{2}h^{3}+{\frac {1}{5}}h^{5}\right)\right|_{0}^{R}=\pi \rho \left(R^{5}-{\frac {2}{3}}R^{5}+{\frac {1}{5}}R^{5}\right)={\frac {8}{15}}\pi \rho R^{5}=\\&=\left({\frac {4}{3}}\pi R^{3}\rho \right)\cdot {\frac {2}{5}}R^{2}={\frac {2}{5}}mR^{2}.\end{aligned}}}

Тонкостенная сфера

Вывод формулы

Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:

J0=25MR2=815πρR5.{\displaystyle J_{0}={\frac {2}{5}}MR^{2}={\frac {8}{15}}\pi \rho R^{5}.}

Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.

J=dJ0dRdR=ddR(815πρR5)dR==83πρR4dR=(ρ⋅4πR2dR)23R2=23mR2.{\displaystyle {\begin{aligned}J&={\frac {dJ_{0}}{dR}}dR={\frac {d}{dR}}\left({\frac {8}{15}}\pi \rho R^{5}\right)dR=\\&={\frac {8}{3}}\pi \rho R^{4}dR=\left(\rho \cdot 4\pi R^{2}dR\right){\frac {2}{3}}R^{2}={\frac {2}{3}}mR^{2}.\end{aligned}}}

Тонкий стержень (ось проходит через центр)

Вывод формулы

Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна

dm=mdrl;dJ=r2dm=mr2drl.{\displaystyle dm={\frac {mdr}{l}};\qquad dJ=r^{2}dm={\frac {mr^{2}dr}{l}}.}

Интегрируя, получим

J=∫−l/2l/2dJ=2∫0l/2dJ=2ml∫0l/2r2dr=2mlr33|0l/2=2mll324=112ml2.{\displaystyle J=\int _{-l/2}^{l/2}dJ=2\int _{0}^{l/2}dJ={\frac {2m}{l}}\int _{0}^{l/2}r^{2}dr={\frac {2m}{l}}\left.{\frac {r^{3}}{3}}\right|_{0}^{l/2}={\frac {2m}{l}}{\frac {l^{3}}{24}}={\frac {1}{12}}ml^{2}.}

Тонкий стержень (ось проходит через конец)

Вывод формулы

При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние ^l⁄₂. По теореме Штейнера новый момент инерции будет равен

J=J0+mr2=J0+m(l2)2=112ml2+14ml2=13ml2.{\displaystyle J=J_{0}+mr^{2}=J_{0}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{12}}ml^{2}+{\frac {1}{4}}ml^{2}={\frac {1}{3}}ml^{2}.}

Безразмерные моменты инерции планет и их спутников^[2]^[3]^[4] $J=J_{0}+mr^{2}=J_{0}+m\left({\frac {l}{2}}\right)^{2}={\frac {1}{12}}ml^{2}+{\frac {1}{4}}ml^{2}={\frac {1}{3}}ml^{2}.$

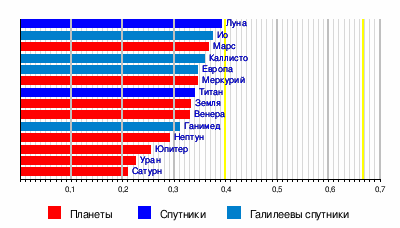
Безразмерные моменты инерции планет и спутников

Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr²). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра^[5]^[6].

Центробежный момент инерции

Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины^[1]^[7]:

Jxy=∫(m)xydm=∫(V)xyρdV,{\displaystyle J_{xy}=\int \limits _{(m)}xydm=\int \limits _{(V)}xy\rho dV,}

Jxz=∫(m)xzdm=∫(V)xzρdV,{\displaystyle J_{xz}=\int \limits _{(m)}xzdm=\int \limits _{(V)}xz\rho dV,}

Jyz=∫(m)yzdm=∫(V)yzρdV,{\displaystyle J_{yz}=\int \limits _{(m)}yzdm=\int \limits _{(V)}yz\rho dV,}

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.

Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу.

Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела^[7].

Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции^[7].

Геометрические моменты инерции

Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой

[8]:

JVa=∫(V)r2dV,{\displaystyle J_{Va}=\int \limits _{(V)}r^{2}dV,}

где, как и ранее r — расстояние от элемента dV до оси a.

Размерность J_Va — длина в пятой степени (dimJVa=L5{\displaystyle \mathrm {dim} J_{Va}=\mathrm {L^{5}} }), соответственно единица измерения СИ — м⁵.

Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой^[8]:

JSa=∫(S)r2dS,{\displaystyle J_{Sa}=\int \limits _{(S)}r^{2}dS,}

где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.

Размерность J_Sa — длина в четвёртой степени (dimJSa=L4{\displaystyle \mathrm {dim} J_{Sa}=\mathrm {L^{4}} }), соответственно единица измерения СИ — м⁴. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см⁴.

Через геометрический момент инерции площади выражается момент сопротивления сечения:

W=JSarmax.{\displaystyle W={\frac {J_{Sa}}{r_{max}}}.}

Здесь r_max — максимальное расстояние от поверхности до оси.

Момент инерции относительно плоскости

Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости^[9].

Если через произвольную точку O{\displaystyle O} провести координатные оси x,y,z{\displaystyle x,y,z}, то моменты инерции относительно координатных плоскостей xOy{\displaystyle xOy}, yOz{\displaystyle yOz} и zOx{\displaystyle zOx} будут выражаться формулами:

JxOy=∑i=1nmizi2 ,{\displaystyle J_{xOy}=\sum _{i=1}^{n}m_{i}z_{i}^{2}\ ,}

JyOz=∑i=1nmixi2 ,{\displaystyle J_{yOz}=\sum _{i=1}^{n}m_{i}x_{i}^{2}\ ,}

JzOx=∑i=1nmiyi2 .{\displaystyle J_{zOx}=\sum _{i=1}^{n}m_{i}y_{i}^{2}\ .}

В случае сплошного тела суммирование заменяется интегрированием.

Центральный момент инерции

Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) JO{\displaystyle J_{O}} — это величина, определяемая выражением^[9]:

Ja=∫(m)r2dm=∫(V)ρr2dV,{\displaystyle J_{a}=\int \limits _{(m)}r^{2}dm=\int \limits _{(V)}\rho r^{2}dV,}

где:

Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей^[9]:

JO=12(Jx+Jy+Jz),{\displaystyle J_{O}={\frac {1}{2}}\left(J_{x}+J_{y}+J_{z}\right),}

JO=JxOy+JyOz+JxOz.{\displaystyle J_{O}=J_{xOy}+J_{yOz}+J_{xOz}.}

Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором s→=‖sx,sy,sz‖T,|s→|=1{\displaystyle {\vec {s}}=\left\Vert s_{x},s_{y},s_{z}\right\Vert ^{T},\left\vert {\vec {s}}\right\vert =1}, можно представить в виде квадратичной (билинейной) формы:

Is=s→T⋅J^⋅s→,{\displaystyle I_{s}={\vec {s}}^{T}\cdot {\hat {J}}\cdot {\vec {s}},\qquad } (1)

где J^{\displaystyle {\hat {J}}} — тензор инерции. Матрица тензора инерции симметрична, имеет размеры 3×3{\displaystyle 3\times 3} и состоит из компонент центробежных моментов:

J^=‖Jxx−Jxy−Jxz−JyxJyy−Jyz−Jzx−JzyJzz‖,{\displaystyle {\hat {J}}=\left\Vert {\begin{array}{ccc}J_{xx}&-J_{xy}&-J_{xz}\\-J_{yx}&J_{yy}&-J_{yz}\\-J_{zx}&-J_{zy}&J_{zz}\end{array}}\right\Vert ,}

Jxy=Jyx,Jxz=Jzx,Jzy=Jyz,{\displaystyle J_{xy}=J_{yx},\quad J_{xz}=J_{zx},\quad J_{zy}=J_{yz},\quad }Jxx=∫(m)(y2+z2)dm,Jyy=∫(m)(x2+z2)dm,Jzz=∫(m)(x2+y2)dm.{\displaystyle J_{xx}=\int \limits _{(m)}(y^{2}+z^{2})dm,\quad J_{yy}=\int \limits _{(m)}(x^{2}+z^{2})dm,\quad J_{zz}=\int \limits _{(m)}(x^{2}+y^{2})dm.}

Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора J^{\displaystyle {\hat {J}}}:

J^d=Q^T⋅J^⋅Q^,{\displaystyle {\hat {J}}_{d}={\hat {Q}}^{T}\cdot {\hat {J}}\cdot {\hat {Q}},}

J^d=‖JX000JY000JZ‖,{\displaystyle {\hat {J}}_{d}=\left\Vert {\begin{array}{ccc}J_{X}&0&0\\0&J_{Y}&0\\0&0&J_{Z}\end{array}}\right\Vert ,}

где Q^{\displaystyle {\hat {Q}}} — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины JX,JY,JZ{\displaystyle J_{X},J_{Y},J_{Z}} — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:

Is=JX⋅sx2+JY⋅sy2+JZ⋅sz2,{\displaystyle I_{s}=J_{X}\cdot s_{x}^{2}+J_{Y}\cdot s_{y}^{2}+J_{Z}\cdot s_{z}^{2},}

откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на Is{\displaystyle I_{s}}

(sxIs)2⋅JX+(syIs)2⋅JY+(szIs)2⋅JZ=1{\displaystyle \left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{X}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Y}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}\cdot J_{Z}=1}

и произведя замены:

ξ=sxIs,η=syIs,ζ=szIs,{\displaystyle \xi ={s_{x} \over {\sqrt {I_{s}}}},\eta ={s_{y} \over {\sqrt {I_{s}}}},\zeta ={s_{z} \over {\sqrt {I_{s}}}},}

получаем канонический вид уравнения эллипсоида в координатах ξηζ{\displaystyle \xi \eta \zeta }:

ξ2⋅JX+η2⋅JY+ζ2⋅JZ=1.{\displaystyle \xi ^{2}\cdot J_{X}+\eta ^{2}\cdot J_{Y}+\zeta ^{2}\cdot J_{Z}=1.}

Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:

r2=ξ2+η2+ζ2=(sxIs)2+(syIs)2+(szIs)2=1Is.{\displaystyle r^{2}=\xi ^{2}+\eta ^{2}+\zeta ^{2}=\left({s_{x} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{y} \over {\sqrt {I_{s}}}}\right)^{2}+\left({s_{z} \over {\sqrt {I_{s}}}}\right)^{2}={1 \over I_{s}}.}

См. также

↑ В правильности использования знака «+» в этой формуле можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r₁ к r₂ формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».

Примечания

Литература

Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.

Ссылки

Момент инерции — Большая советская энциклопедия

Моме́нт ине́рции

Величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z называется величина, определяемая равенством:

где m_i — массы точек тела, h_i — их расстояния от оси z, ρ — массовая плотность, V — объём тела. Величина I_z является мерой инертности тела при его вращении вокруг оси (см. Вращательное движение). Осевой М. и. можно также выразить через линейную величину k, называемую радиусом инерции, по формуле I_z = Mk², где М — масса тела. Размерность М. и. — L²M; единицы измерения — кг․м² или г․см².

Центробежным М. и. относительно системы прямоугольных осей х, у, z, проведённых в точке О, называют величины, определяемые равенствами:

или же соответствующими объёмными интегралами. Эти величины являются характеристиками динамической неуравновешенности масс. Например, при вращении тела вокруг оси z от значений I_xz и I_yz зависят силы давления на подшипники, в которых закреплена ось.

М. и. относительно параллельных осей z и z’ связаны соотношением

I_z = I_z_‘ + М d² (3)

где z’ — ось, проходящая через центр масс тела, a d — расстояние между осями (теорема Гюйгенса).

М. и. относительно любой, проходящей через начало координат О оси Ol с направляющими косинусами α, β, γ находится по формуле:

l_ol = I_x α² + I_y β

2 + I_z γ² — 2I_xy αβ — 2I_yz βγ — 2I_zxγα. (4)

Зная шесть величин I_x, I_y, I_z, I_xy, I_yх, I_zx, можно последовательно, используя формулы (4) и (3), вычислить всю совокупность М. и. тела относительно любых осей. Эти шесть величин определяют т. н. тензор инерции тела. Через каждую точку тела можно провести 3 такие взаимно-перпендикулярные оси, называемые главными осями инерции, для которых I_xy = I_yz = I_zx = 0. Тогда М. и. тела относительно любой оси можно определить, зная главные оси инерции и М. и. относительно этих осей.

М. и. тел сложной конфигурации обычно определяют экспериментально. Понятием о М. и. широко пользуются при решении многих задач механики и техники.

Лит.: Краткий физико-технический справочник, под общ. ред. К. П. Яковлева, т. 2, М., 1960, с. 94—101; Фаворин М. В., Моменты инерции тел. Справочник, М., 1970; Гернет М. М., Ратобыльский В. Ф., Определение моментов инерции, М., 1969; см. также лит. при ст. Механика.

С. М. Тарг.

Источник: Большая советская энциклопедия на Gufo.me

Значения в других словарях

Момент инерции — (Moment d’inertie, Trägheitsmoment, Moment of inertia) — понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий. Энциклопедический словарь Брокгауза и Ефрона
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Большой энциклопедический словарь

МОМЕНТ ИНЕРЦИИ — Величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. Физический энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ (обозначение I), для вращающегося тела — сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы привести тело во вращение. Научно-технический словарь

Значение словосочетания МОМЕНТ ИНЕРЦИИ. Что такое МОМЕНТ ИНЕРЦИИ?

Моме́нт ине́рции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Источник: Википедия

момент инерции
1. физ. скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, характеризующаяся распределением масс в теле и равная сумме произведений элементарных масс на квадрат их расстояний до базового множества

Источник: Викисловарь

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова бережливость (существительное):

Кристально
понятно

Понятно
в общих чертах

Могу только
догадываться

Понятия не имею,
что это

Другое
Пропустить

момент инерции — это… Что такое момент инерции?

момент инерции

1) Av. Massenträgheitsmoment

2) eng. Beharrungsmoment

3) auto. Drehmasse

4) artil. Beschleunigungsmoment

6) aerodyn. Massenmoment

Универсальный русско-немецкий словарь. Академик.ру. 2011.

момент импульсной характеристики
момент инерции Земли

Смотреть что такое «момент инерции» в других словарях:

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь
Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь
Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов
момент инерции — 3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси. Источник: ГОСТ Р 52776 2007: Машины электрические вращающиеся. Номинальные… … Словарь-справочник терминов нормативно-технической документации
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь

Книги

Механика и молекулярная физика. Учебное пособие, Ландау Лев Давидович, Ахиезер Александр Ильич, Лифшиц Евгений Михайлович. Трудно писать о книге Л. Д. Ландау, А. И. Ахиезера, Е. М. Лифшица, потому что это как раз тот случай, когда ни книга, ни, тем более, её авторы, как принято говорить,`в рекламене нуждаются`.… Подробнее Купить за 1849 грн (только Украина)
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга

Другие книги по запросу «момент инерции» >>

момент инерции — это… Что такое момент инерции?

момент инерции

1) Sports: angular momentum, swing weight

2) Engineering: second moment of area

3) Construction: inertia couple, moment of gyration

4) Mathematics: second moment

6) Astronautics: momentum of inertia, product of inertia, products of inertia, spin inertia

7) Metrology: rotational inertia

8) Automation: mass moment of inertia

9) Robots: inertia

10) Makarov: product of inertia

Универсальный русско-английский словарь. Академик.ру. 2011.

момент импульса движения
момент инерции (приводимой) нагрузки

Смотреть что такое «момент инерции» в других словарях:

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь
Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь
Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов
момент инерции — 3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси. Источник: ГОСТ Р 52776 2007: Машины электрические вращающиеся. Номинальные… … Словарь-справочник терминов нормативно-технической документации
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь

Книги

Механика и молекулярная физика. Учебное пособие, Ландау Лев Давидович, Ахиезер Александр Ильич, Лифшиц Евгений Михайлович. Трудно писать о книге Л. Д. Ландау, А. И. Ахиезера, Е. М. Лифшица, потому что это как раз тот случай, когда ни книга, ни, тем более, её авторы, как принято говорить,`в рекламене нуждаются`.… Подробнее Купить за 1849 грн (только Украина)
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга

Другие книги по запросу «момент инерции» >>

собственный момент инерции — это… Что такое собственный момент инерции?

собственный момент инерции: adj
shipb. Eigenträgheitsmoment

собственный материал
собственный нагрев

Смотреть что такое «собственный момент инерции» в других словарях:

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
Центробежный момент инерции — Момент инерции скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м².… … Википедия
Момент вращения — Момент инерции скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м².… … Википедия
Момент иннерции — Момент инерции скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости). Единица измерения СИ: кг·м².… … Википедия
МОМЕНТ КОЛИЧЕСТВА ДВИЖЕНИЯ — (кинетический момент, угловой момент), одна из мер механич. движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращат. движения. Как и для момента силы, различают М. к. д. относительно центра (точки) и… … Физическая энциклопедия
собственный кинетический момент гироскопа — Составляющая вектора кинетического момента ротора, направленная по оси собственного вращения. Примечание Вектор собственного кинетического момента традиционно обозначается через H: H = CΩ В этом уравнении С момент инерции ротора… … Справочник технического переводчика
Момент количества движения — кинетический момент, одна из мер механического движения материальной точки или системы. Особенно важную роль М. к. д. играет при изучении вращательного движения (См. Вращательное движение). Как и для момента силы (См. Момент силы),… … Большая советская энциклопедия
Момент — (от лат. momentum, movere двигать) 1) миг, мгновение; время, когда наступает, осуществляется, проявляется что либо; 2) существенное обстоятельство, составная часть; отдельная сторона чего либо, какого либо явления, события; 3) (в физике)… … Начала современного естествознания
Тензор инерции — Тензор инерции в механике абсолютно твёрдого тела тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью: где тензор инерции, угловая скорость, момент… … Википедия
гироскопический момент — Момент сил, приложенных со стороны ротора к подшипникам оси собственного вращения ротора, возникающий при изменении направления оси и определяемый уравнением: М=–М = H×ω (2) В этом уравнении Н собственный кинетический момент… … Справочник технического переводчика
Сопротивление материалов* — Когда, при составлении проекта сооружения или машины, форма, главные размеры частей и силы, которым они будут подвержены, уже определены на основании требований задания, данных механики и технологии, приходится еще определять остальные размеры… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

момент инерции — это… Что такое момент инерции?

момент инерции

1) Sports: angular momentum, swing weight

2) Engineering: second moment of area

3) Construction: inertia couple, moment of gyration

4) Mathematics: second moment

6) Astronautics: momentum of inertia, product of inertia, products of inertia, spin inertia

7) Metrology: rotational inertia

8) Automation: mass moment of inertia

9) Robots: inertia

10) Makarov: product of inertia

Универсальный русско-английский словарь. Академик.ру. 2011.

момент импульса движения
момент инерции (приводимой) нагрузки

Смотреть что такое «момент инерции» в других словарях:

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь
Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь
Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов
момент инерции — 3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси. Источник: ГОСТ Р 52776 2007: Машины электрические вращающиеся. Номинальные… … Словарь-справочник терминов нормативно-технической документации
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь

Книги

Механика и молекулярная физика. Учебное пособие, Ландау Лев Давидович, Ахиезер Александр Ильич, Лифшиц Евгений Михайлович. Трудно писать о книге Л. Д. Ландау, А. И. Ахиезера, Е. М. Лифшица, потому что это как раз тот случай, когда ни книга, ни, тем более, её авторы, как принято говорить,`в рекламене нуждаются`.… Подробнее Купить за 1849 грн (только Украина)
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга

Другие книги по запросу «момент инерции» >>

Момент инерции — Википедия. Что такое Момент инерции

Осевой момент инерции

Теорема Гюйгенса — Штейнера

Осевые моменты инерции некоторых тел

Вывод формул

Безразмерные моменты инерции планет и спутников

Центробежный момент инерции

Геометрические моменты инерции

Момент инерции относительно плоскости

Центральный момент инерции

См. также

Комментарии

Примечания

Литература

Ссылки

Момент инерции — Большая советская энциклопедия

Значения в других словарях

Значение словосочетания МОМЕНТ ИНЕРЦИИ. Что такое МОМЕНТ ИНЕРЦИИ?

момент инерции

Делаем Карту слов лучше вместе

момент инерции — это… Что такое момент инерции?

Смотреть что такое «момент инерции» в других словарях:

Книги

момент инерции — это… Что такое момент инерции?

Смотреть что такое «момент инерции» в других словарях:

Книги

собственный момент инерции — это… Что такое собственный момент инерции?

Смотреть что такое «собственный момент инерции» в других словарях:

момент инерции — это… Что такое момент инерции?

Смотреть что такое «момент инерции» в других словарях:

Книги

alexxlab

Добавить комментарий Отменить ответ

Рубрики