Определение коэффициента трения

Введение

Трение играет большую роль в природе и технике. Благодаря трению движется транспорт, удерживается забитый в стену гвоздь и т.д.

Силы трения могут быть различной природы, но в результате их действия механическая энергия всегда превращается во внутреннюю энергию соприкасающихся тел.

В некоторых случаях силы трения оказывают вредное воздействие и поэтому их нужно уменьшать. Для этого на трущиеся поверхности наносят смазку, которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что  поверхности  как  бы  перестают  касаться  одна  другой.  В  этом случае отдельные слои жидкости скользят один относительно другого. Сила трения при этом уменьшается примерно в 10 раз. Радикальным способом уменьшения величины силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники).

Основные понятия

Различают два основных типа трения – внутреннее и внешнее.

Внутренним трением или вязкостью называется явление возникновения касательных сил,  препятствующих перемещению частей жидкости или газа по отношению друг к другу.

Внешним трением называется взаимодействие между телами, возникающее в месте их соприкосновения и препятствующее их относительному перемещению,

В зависимости от характера относительного движения тел различают:

•        трение            скольжения,   возникающее при      поступательном

перемещении одного тела по поверхности другого;

•        трение качения, возникающее тогда, когда одно тело катится по поверхности другого.

В чистом виде трение качения имеет место только в том случае, если линия или точка соприкосновения трущихся тел совпадает с мгновенной осью вращения катящегося тела. Во всех остальных случаях трение качения сопровождается трением скольжения.

Внешнее трение, происходящее между движущимися относительно друг друга телами, называется кинематическим. Внешнее трение между взаимно неподвижными телами называется трением  покоя.   Оно  проявляется  в  том,  что  для  возникновения

относительного перемещения двух соприкасающихся тел к одному из

r

них  нужно приложить внешнюю силу  F ,  величина которой больше

величины  максимальной  силы  трения  покоя

r           r

Fòð.ï î ê.max .  Отсутствие

взаимного перемещения тел при

F < Fòð.ï î ê.max

называется явлением

застоя. Оно широко используется в технике для передачи усилий от одних деталей машин к другим (ременные передачи, фрикционные муфты и т. д.).

Трение скольжения между телами, поверхности которых не подвергаются смазке, называется сухим трением, а трение между обильно и непрерывно смазываемыми телами – жидкостным трением.

В  зависимости  от  толщины  слоя  смазки  между  трущимися телами и степени шероховатости их поверхностей различают несколько переходных видов трения скольжения: полусухое, граничное, полужидкостное.

Сила трения скольжения в случае сухого трения в основном вызывается механическим зацеплением между неровностями поверхностей тел и сцеплением между молекулами обоих тел в областях непосредственного соприкосновения.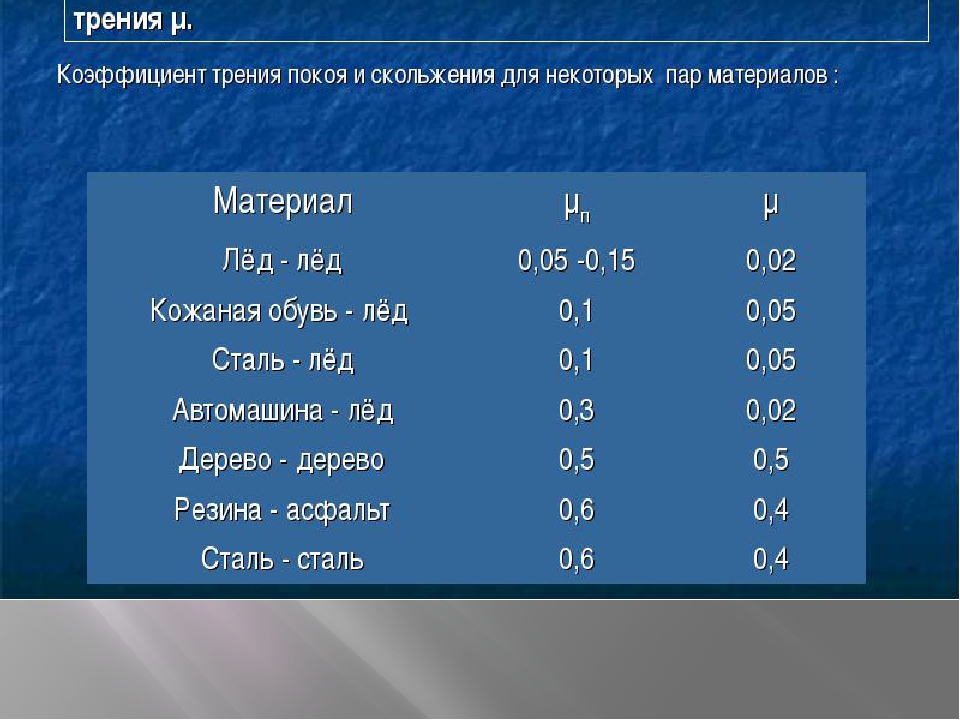

В приближенных расчетах можно считать, что сила трения скольжения прямо пропорциональна силе нормального давления между поверхностями трущихся  тел.  В  этом  случае  величина  силы  трения  может  быть

вычислена с помощью закона Амонтона4

4 Гийом Амонтон (1663 – 1703 гг.) – французский физик.

r

Fòð

= Fòð

=μ ⋅ N ,

где       μ

–          безразмерный            кинематический        коэффициент трения

скольжения, зависящий от свойств материалов, из которых изготовлены контактирующие тела. В действительности коэффициент трения зависит от множества других факторов: качества обработки поверхностей трущихся тел, наличия на них загрязнений, скорости скольжения одной поверхности относительно другой и т. д. Поэтому его определяют на основе экспериментальных данных.

Величину       максимальной           силы   трения            покоя  чаще    всего

определяют по формуле

Fòð.ï î ê.max

= μ⋅ N.

Практически  коэффициент

μ0 ,    соответствующий     предельной

(максимальной) силе  трения  покоя,  обычно  больше  коэффициента кинематического трения.

Часто вместо коэффициента трения μ пользуются углом трения

tgϕ0 , связанным с коэффициентом трения

tgϕ0  =μ .

μ соотношением

Угол

ϕ0  = arctgμ0

равен  тому    наименьшему            углу    наклона

плоскости к горизонту, при котором лежащее на ней тело начинает скользить вниз под действием силы тяжести.

Более  точным           является          двучленный   закон   трения,

установленный         на        основе            учета   влияния          сил      притяжения   между молекулами трущихся тел

r

Fòð

= Fòð

=μ ⋅ (N + S ⋅ P0 ) ,

где

μ –  истинный  коэффициент трения;  P0

добавочное  давление,

вызванное силами молекулярного притяжения; S – общая площадь всех областей непосредственного контакта между телами.

При     качении          по        плоской          поверхности  тел,      имеющих       форму круглых цилиндров или шаров, возникают не  только упругие, но  и

пластические деформации.   Поэтому         линия  действия         реакции          R

r

плоскости  не  совпадает  с  линией  действия  силы       N         нормального

r

давления (рис. 1). Нормальная к плоскости составляющая Rn

r силы R r

численно равна модулю силы N , а горизонтальная составляющая F

представляет собой силу трения качения.

В первом приближении можно считать, что

r

F = F = k ⋅ N

r

– закон Кулона5.

Здесь г радиус катящегося тела; k – коэффициент трения качения,

имеющий       размерность   длины и          зависящий      от        материала       тел,

r

состояния их поверхностей и целого ряда других факторов; N = N  –

модуль силы нормальной реакции опоры.

Сила   трения,           приложенная к          катящемуся    телу,    создает

вращающий   момент           трения

Mòð

относительно точки  О,        равный

r

векторному произведению векторов r

и F .

r           r r

Mòð

= ⎡r,F⎤ .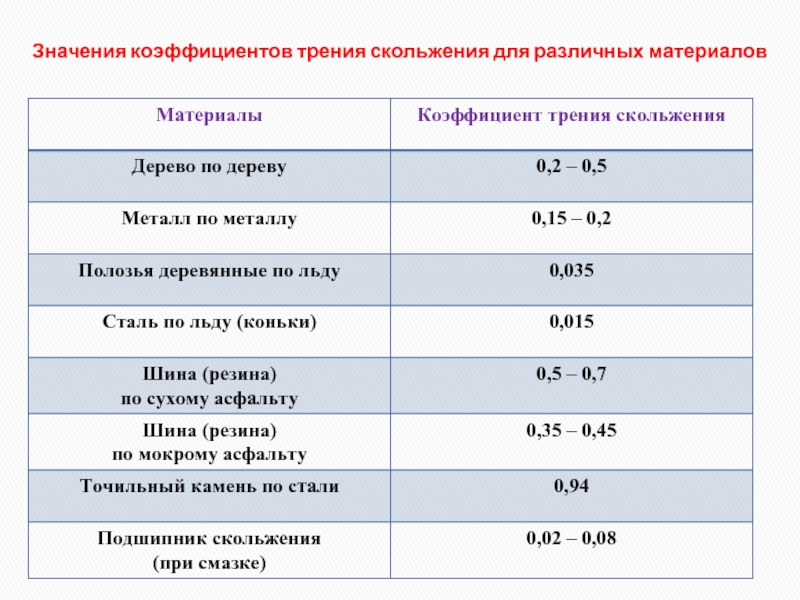

Описание лабораторной установки

Существуют различные методы определения коэффициента трения  по  экспериментальным  данным.  Во  всех  методах используются: трибометр и брусок, коэффициент трения которого о поверхность трибометра требуется определить.

Метод 1. На брусок, лежащий на горизонтальной поверхности,

r

действуют две силы: сила тяжести  mg

r

и сила нормальной реакции

опоры

N . Если к бруску прикрепить пружину (динамометр) так, как это

показано на рис 2, и потянуть, то пружина деформируется, возникает сила упругости. На тело начинает действовать сила упругости. Возникает сила трения покоя. По третьему закону Ньютона величина силы упругости равна величине силы, с которой растягивают пружину

и они обе равны модулю силы, с которой пружина действует на брусок

r           r           ∗        r

Fóï ð

= Fóï ð

= F ⇒ F = Fóï ð .

5 Шарль Огюстен Кулон (1736 – 1806 гг.) – французский инженер и физик, один из основателей электростатики.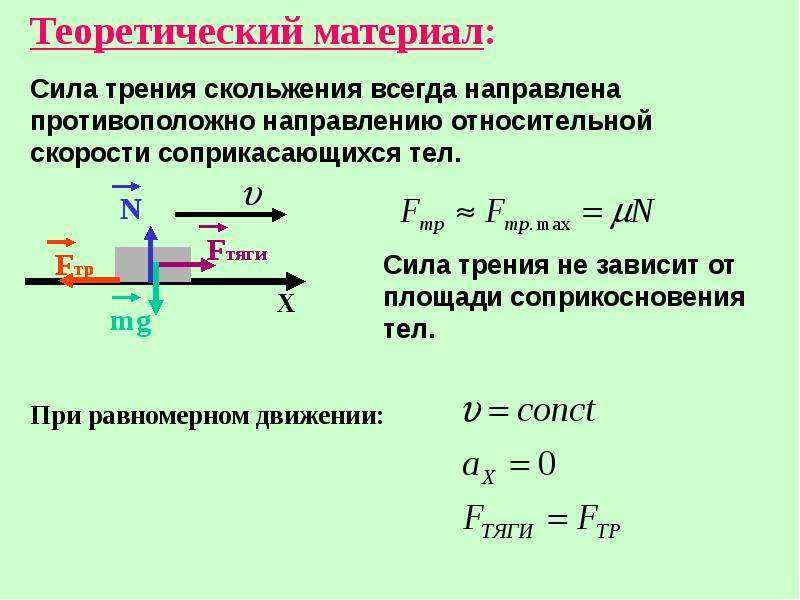

Исследовал деформацию кручения нитей, установил ее законы. Изобрел (1784 г.) крутильные весы и открыл (1785 г.) закон, названный его именем. Установил законы сухого трения.

X

Рис.1   Рис.2

Когда величина силы, с которой мы растягиваем пружину (а, следовательно, и величина силы упругости), становится чуть больше, чем максимальная сила трения покоя – тело начинает двигаться. Сила трения, действующая при этом на брусок, является силой трения скольжения. Величину силы трения скольжения можно определить по

формуле

Если величина силы упругости, действующей на брусок со стороны пружины, будет равна величине силы трения скольжения, то брусок будет двигаться равномерно (с постоянной по величине скоростью, т. е. ускорение бруска будет равно нулю). Этим условием можно воспользоваться для определения коэффициента трения.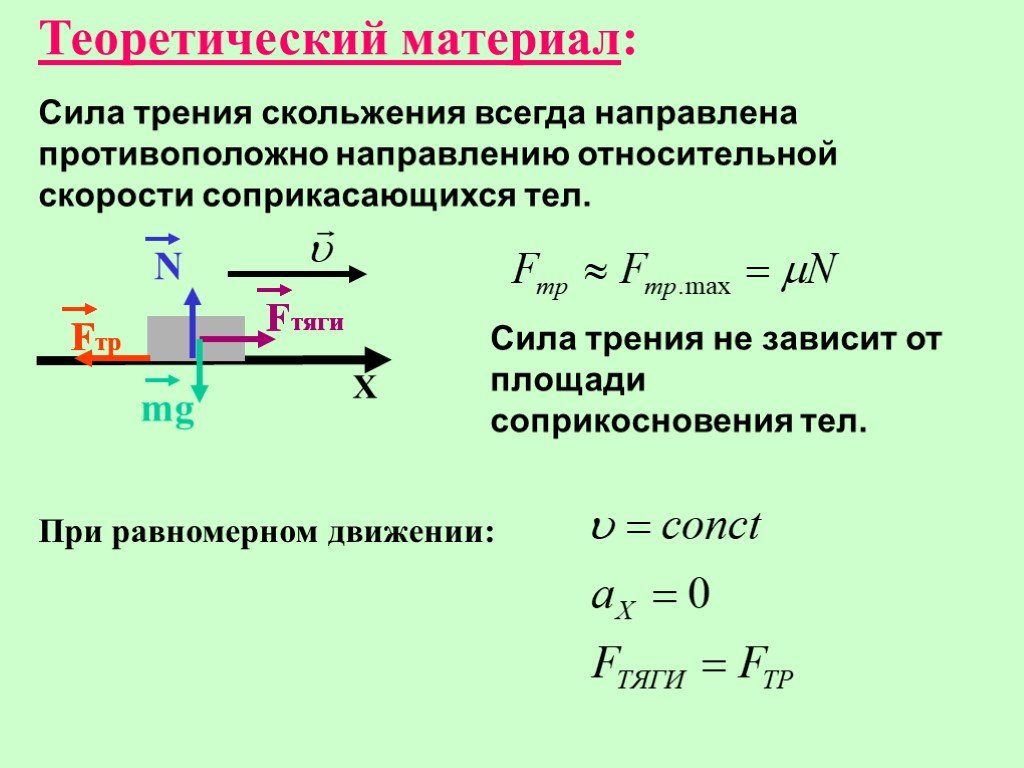

Запишем  уравнение  второго  закона  Ньютона  для  равномерно

движущегося бруска (см. рис.2)

r           r           r           r

Fóï ð + mg + Fòð + N = 0 .

Распишем это уравнение в проекциях на оси ОХ и OY

⎧⎪OX :        Fóï ð − Fòð  = 0 ⇒ Fóï ð = Fòð

⎨

⎪⎩OY :        N − mg = 0 ⇒ N = mg.

(1)

Так как по определению Fòð

следует, что N = mg , то

= μ⋅ N , а из второго уравнения системы (1)

Fòð

=μ ⋅ mg .     (2)

Величину силы упругости можно измерять с помощью динамометра.

Из  первого  уравнения  системы  (1)  следует,  что

учетом уравнения (2)

Fóï ð = Fòð .  Тогда  с

Fóï ð

Fóï ð

=μ ⋅ mg ⇒ μ =      .           (3)

mg

Метод  2.  Положим  брусок  на  наклонную  плоскость.  Брусок  (в зависимости от величины угла наклона плоскости к горизонту) либо:

1) покоится на поверхности наклонной плоскости;

2) начинает соскальзывать вниз.

В первом случае брусок удерживается на наклонной плоскости силой трения покоя.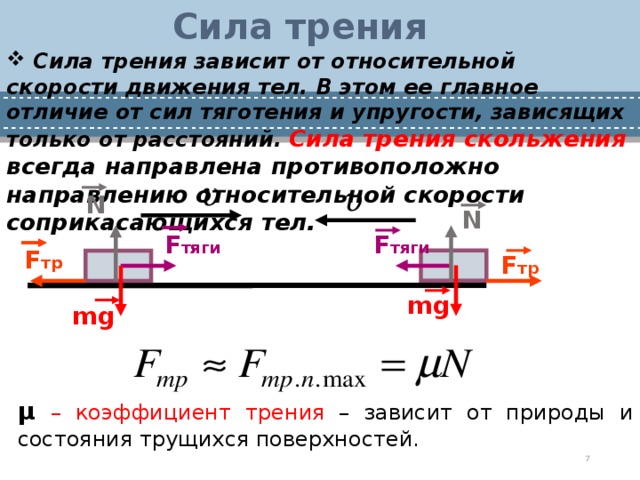 Во втором случае сила, которая «тянет» брусок вниз вдоль наклонной плоскости, больше или равна максимальной силе трения покоя.

Рассмотрим  подробно  второй  случай.  Силы,  действующие  на

брусок: сила тяжести

r

трения скольжения Fòð

r

mg ; сила нормальной реакции опоры

Если ускорение бруска равно нулю (брусок покоится или движется с постоянной скоростью), то

μ0 = tgα0 .   (7)

Метод 3. Для того чтобы равномерно перемещать брусок вверх вдоль наклонной плоскости, нужно приложить силу, направленную параллельно наклонной плоскости (рис. 4), например, с помощью динамометра.

Если известна величина минимальной силы F , необходимой для равномерного перемещения бруска вверх вдоль наклонной плоскости,

и масса бруска, то можно определить коэффициент трения.

1. Трибометр.

2. Брусок.

3. Секундомер.

4. Линейка.

Оборудование

5. Транспортир.

6. Динамометр.

7. Весы

8. Штатив с лапкой

Порядок выполнения измерений

Внесите технические данные измерительных приборов в табл. 1.

Таблица 1

Измерительный прибор	Предел измерения	Цена деления	Приборная погрешность
Секундомер
Линейка
Транспортир
Весы
Динамометр

Задание 1 (метод 1).

На горизонтальную поверхность трибометра положите брусок. С помощью динамометра перемещайте брусок равномерно по горизонтальной поверхности трибометра (динамометр должен быть

r

параллелен     поверхности).            Определите    величину        силы

Fóï ð ,

необходимой для того, чтобы движение бруска было равномерным.

Результат запишите в табл. 2.

Массу  бруска  mi   определите  методом  двойного  взвешивания

(один раз брусок на правой чашке весов, а гири на левой; второй раз наоборот).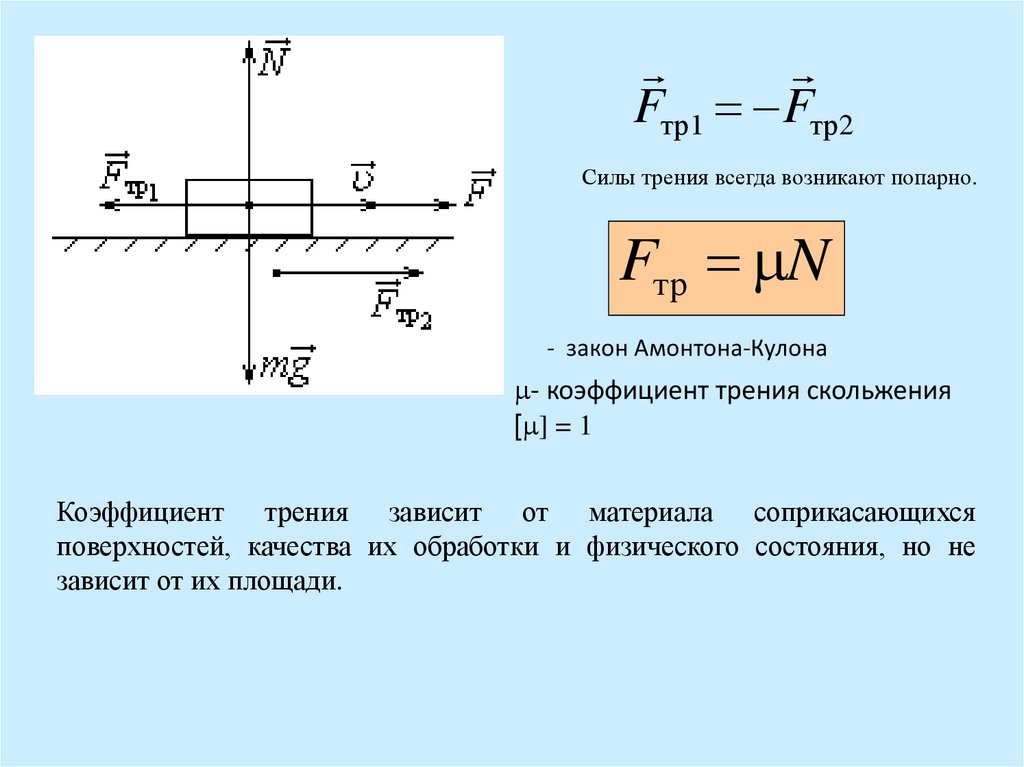 Результаты запишите в табл. 2.

Таблица 2

Fóï ð , Н	mi, кг	mñð  = m1 ⋅ m2 , кг	μ

Задание 2 (метод 2).

Положите брусок на горизонтальную поверхность трибометра. Поднимайте трибометр до тех пор, пока брусок не начнет соскальзывать. Измерьте транспортиром величину этого угла. Повторите измерения 5 раз. Результаты запишите в табл. 3.

Таблица 3

№ п/п	αi	Δαi	(Δα )2 i
1
2
3
4
5
Среднее значение угла соскальзывания			N         2 ∑(Δαi )        = i=1

Задание 3 (метод 3).

Закрепите трибометр под некоторым углом αi

к горизонту таким

образом, чтобы брусок с него соскальзывал. При этом величина угла

αi       должна быть больше самого большего угла из  αi

в табл. 3. С

помощью динамометра определите величину силы, необходимой для равномерного перемещения бруска вверх вдоль наклонной плоскости

(динамометр должен быть параллелен поверхности трибометра).

Измерения повторите 5 раз при различных значениях угла  αi

(величина угла αi

каждый раз должна быть больше самого большего

угла αi

из табл. 3). Результаты запишите в табл. 4.

Таблица 4

№ п/п	αi	Fi , Н	μi
1
2
3
4
5
			μñð =

Задание 4 (метод 2).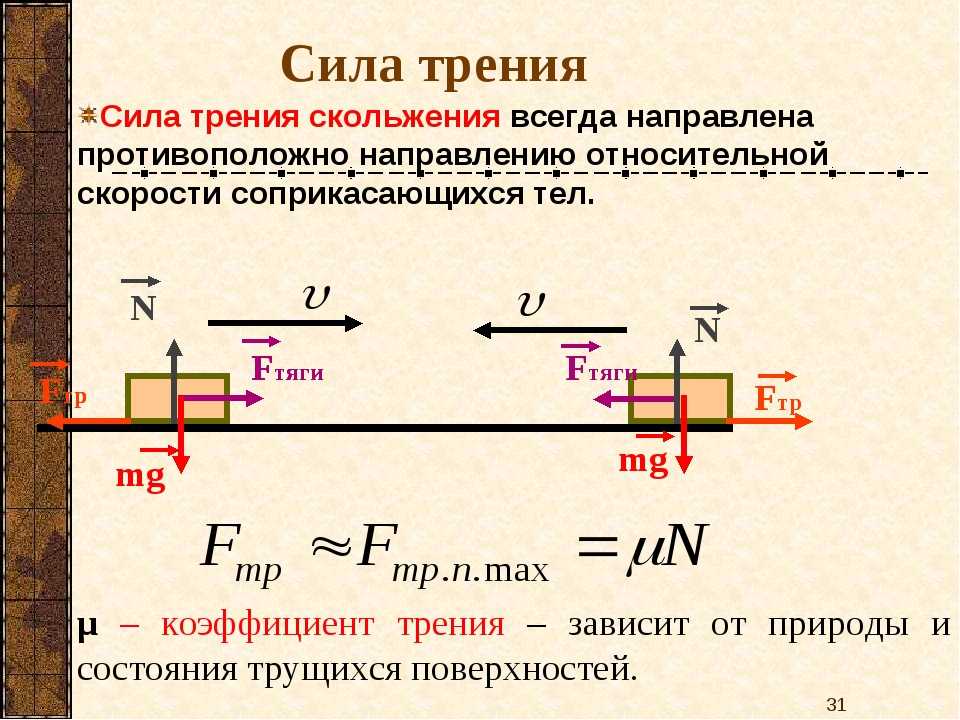

Закрепите трибометр под некоторым углом αi

к горизонту таким

образом, чтобы брусок с него соскальзывал. При этом величина угла

αi       должна  быть  больше  самого  большего  угла  из           αi

в  табл.  3.

Предоставьте бруску возможность скользить вдоль поверхности трибометра (без начальной скорости). Измерьте расстояние, проходимое бруском и время, за которое это расстояние пройдено.

Измерения повторите 5 раз при различных значениях угла  αi

(величина угла αi

каждый раз должна быть больше самого большего

угла αi

из табл. 3). Результаты запишите в табл. 5.

Таблица 5

№ п/п	αi	ti , с	S , м	ai , м/с2	μi
1
2
3
4
5
				μñð =

Задание 1.

Обработка результатов измерений

Рассчитайте   среднее           значение         массы  бруска по        формуле

mñð  =

m1 ⋅ m2 . Рассчитайте среднее значение коэффициента трения

по формуле (3)

μ=      Fóï ð

mñð ⋅ g

. Результаты запишите в табл. 2.

Рассчитайте   относительную          и                      абсолютную   погрешности измерения      коэффициента            трения                        по                    следующим                формулам:

ε        = ΔF +

Δm + Δg ,

Δμ = εμ ⋅ μñð

.           Ускорение      свободного    падения

F          mñð     g

считайте равным 9,81 м/с2,

Δg = 0,01 м/с2.

Задание 2.

Рассчитайте среднее значение угла наклона

αñð , при котором

брусок начинает соскальзывать с наклонной плоскости. Рассчитайте абсолютную   погрешность  каждого            измерения      по        формуле

Δαi = αñð − αi . Результаты запишите в табл. 3.

Рассчитайте   абсолютную               и                      относительную          погрешности измерения      угла       наклона          α                    по        следующим                формулам:

Рассчитайте   относительную          и          абсолютную   погрешности измерения коэффициента трения для данного метода по следующим

Δα

формулам:

Задание 3.

Для каждого значения угла рассчитайте величину коэффициента

F

трения по формуле (8)

μi =   i           − tgαi . Массу бруска возьмите

mñð ⋅ g ⋅ cos αi

из табл. 2. Рассчитайте среднее значение коэффициента трения.

Задание 4.

По результатам измерения времени ti прохождения расстояния S

рассчитайте ускорения бруска для всех значений угла αi

2S

по формуле

(6)

ai =

2  .       По       результатам    вычисления   ускорений      рассчитайте

i

a

значения  коэффициента  трения  по  формуле  (5)

μi = tgαi −              i 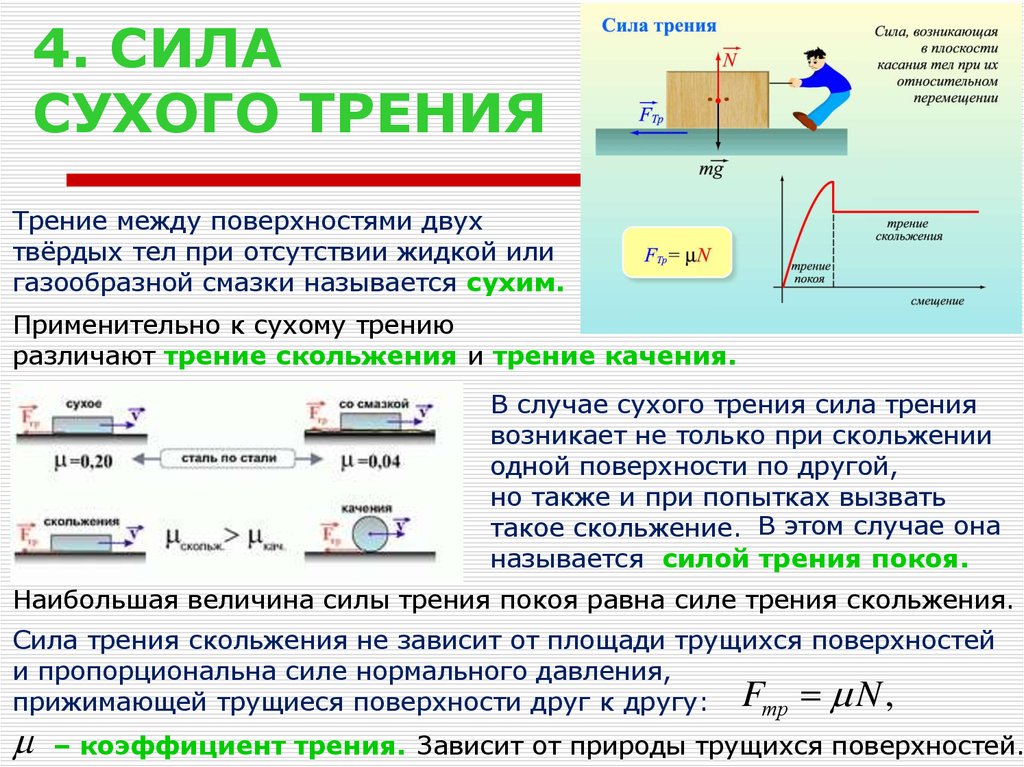          . g ⋅ cos αi

Результаты     запишите        в          табл.    5.         Рассчитайте   среднее           значение

коэффициента трения.

Запись результатов

Задание 2.

Задание 1.

μ= μñð ± Δμ

μ = μñð ± Δμ

εμ =

α= 0, 9 .

Задание 3. μ= μñð .

Задание 4. μ= μñð .

Вопросы и задачи для защиты лабораторной работы № 5

1.         Что называется внутренним трением?

2.         Что      называется     внешним        трением?        Какие  разновидности внутреннего трения существуют?

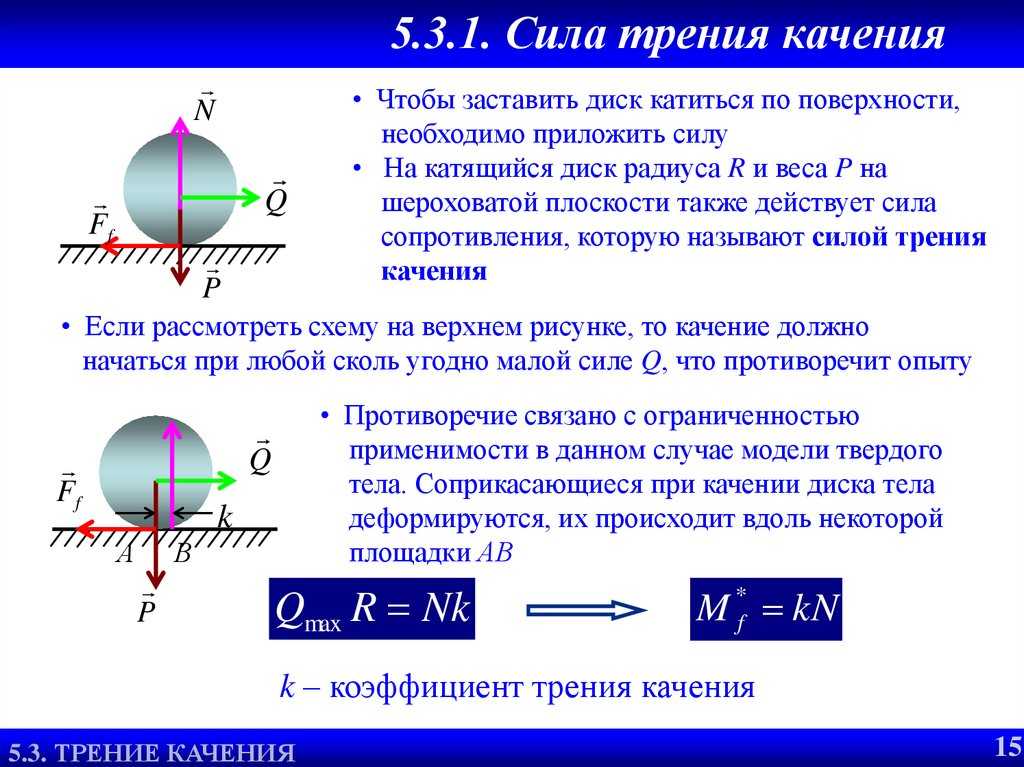
3.         При каких условиях возникает сила трения качения и от чего она зависит? Объясните механизм возникновения силы трения качения.

4.         Какое трение называется кинематическим?

5.         Когда трение называется трением покоя? Какой может быть его величина?

6.         Напишите      формулу,        по        которой          определяется  величина максимальной силы трения покоя.

7.         Что называется явлением застоя? Где оно используется?

8.          Запишите закон трения в форме, учитывающей силы притяжения между молекулами.

9.         Расскажите    о          силе    сухого трения.           Объясните      механизм        ее возникновения.

10.       Что такое коэффициент трения, и от чего он зависит?

11.    Что называется углом трения? Как он определяется?

12.       Дайте определение понятия «сила трения качения». Напишите закон Кулона для величины силы трения качения.

13.       Почему           при      движении       одного            тела     по        поверхности  другого возникает сила трения?

14.    Когда трение вредно, и когда оно полезно? Приведите примеры.

15.    Как возникло представление о существовании силы трения?

16.    Укажите способы уменьшения величины силы трения.

17.    От чего зависит величина силы трения?

18.       В         чем      состоит           метод  двойного        взвешивания?            Зачем  он применяется?

19.       Что  такое  трибометр?  Как  с  его  помощью  можно  определить коэффициент трения?

20.   Можно   ли   использовать   трибометр   для   определения коэффициента трения между заданными материалами, например, резиной и сталью?

21.       Какие превращения энергии происходят в результате действия сил трения любой природы?

22.       Сформулируйте        второй            закон   Ньютона.        Запишите       формулу второго закона Ньютона для следующих объектов:

a. равномерно движущегося по горизонтальной поверхности автомобиля;

b. автомобиля, движущегося по горизонтальной поверхности с постоянным ускорением;

c. бруска покоящегося на наклонной плоскости;

d. бруска, который соскальзывает по наклонной плоскости с постоянной скоростью;

e. бруска, который соскальзывает по наклонной плоскости с постоянным ускорением;

f.          бруска,            движущегося равномерно    вверх  по        наклонной плоскости;

g. бруска,        движущегося вверх  по        наклонной     плоскости      с постоянным ускорением.

23.    На тело массой 200 г, лежащее на горизонтальной поверхности,

начинает   действовать   горизонтальная   сила   80   Н.    Коэффициент трения скольжения тела о поверхность равен 0,4. Определите ускорение, с которым движется тело.

24.    На наклонной плоскости длиной 5 м и высотой 3 м находится груз   массой   40   кг.   Определите   величину   силы,   которую   надо приложить вдоль плоскости, чтобы удержать этот груз? Коэффициент трения груза о плоскость 0,3.

25.   Тело массой 5 кг равномерно перемещают по горизонтальной поверхности. Какую горизонтальную силу при этом прилагают, если коэффициент трения равен 0,1?

26.    За какое время тело соскользнёт с наклонной плоскости высотой

0,1 м, наклонённой под углом 60о  к горизонту, если при угле наклона

30о оно движется по этой плоскости равномерно.

27.   На тело массой 1 кг, лежащее на горизонтальной поверхности, действуют силы 20 Н и 5 Н, направленные, соответственно, горизонтально и вертикально вверх. Коэффициент трения равен 0,1. Определите   ускорение,   с   которым   движется   тело.   Определите скорость тела через 3 мин после начала движения и путь, пройденный телом к этому моменту времени.

28.   Вагонетка массой 400 кг движется по горизонтальному пути с ускорением 0,1 м/с2. Определите значение коэффициента трения скольжения, если горизонтальная сила тяги 50 Н.

29.    Определите коэффициент трения, если известно, что тело, имея скорость 7 м/с и двигаясь вверх по наклонной плоскости, до полной остановки проходит путь 2 м. Угол наклона плоскости равен 45о.

30. Найдите силу тяги, развиваемую мотором автомобиля, движущегося в гору с ускорением 2 м/с2. Масса автомобиля 800 кг. Угол наклона горы 30о. Коэффициент трения 0,1.

31.    Чтобы удержать тележку на наклонной плоскости с углом 45о,

надо  приложить  силу  5  Н,  направленную  вверх  параллельно наклонной плоскости. А чтобы перемещать её равномерно вверх, требуется сила равная 20 Н. Определите коэффициент трения скольжения тела о плоскость.

32.    Шайба, пущенная по поверхности льда с начальной скоростью

20        м/с,  остановилась  через  40  с.  Найдите  коэффициент  трения скольжения шайбы о лёд.

33. Санки, скатившись с горы, проехали по горизонтальной поверхности 10 м за 5 с. Определите коэффициент трения скольжения полозьев о снег.

34.  Какой путь пройдёт ранее покоящееся тело массой 1кг по горизонтальной поверхности за 2 с под действием силы 10 Н, направленной вверх под углом 30о  к горизонту? Коэффициент трения скольжения равен 0,1.

35. Определите тормозной путь автомобиля массой 1000 кг, движущегося  по  горизонтальной  дороге,  если  при  горизонтальной силе торможения 4000 Н время торможения равно 4 с.

36.   Человек тянет сани массой 105 кг за верёвку с силой 500 Н. Верёвка составляет с горизонтом угол 45о. Определите коэффициент трения, если известно, что сани движутся с ускорением 1 м/с2.

37.    Паровоз   тянет   вверх   по   уклону   поезд   массой   1000   кг   с постоянной скоростью 8 м/с. Определите развиваемую паровозом мощность, если коэффициент трения скольжения равен 0,1. Угол уклона равен 5о.

38.    Автомобиль массой 1000 кг движется под гору при выключенном моторе с постоянной скоростью 15 м/с. Уклон горы 4 м на каждые

100 м пути. Какую мощность должен развивать двигатель автомобиля,

чтобы он двигался с той же скоростью в гору с тем же уклоном?

39.    Лента транспортера для подъема грузов наклонена к горизонту под углом 30о. Коэффициент трения между грузами и лентой 0,6. С каким максимальным ускорением лента транспортера может передвигать грузы?

40.    Вверх  по  наклонной  плоскости  с  углом  наклона  45о   пущена

шайба. Через некоторое время она останавливается и соскальзывает вниз.  Определите  коэффициент  трения  шайбы  о  плоскость,  если время спуска в 2 раза больше времени подъема

41.    Конькобежец пересек финишную прямую со скоростью 15 м/с и покатился  по  льду,  не  прилагая  никаких  усилий.  Найдите коэффициент трения скольжения коньков о лед, если он остановился

через 40 с.

42.       Тележка  массой  200  кг  движется  по  горизонтальному  пути  с ускорением 1 м/с2 под действием горизонтальной силы 300 Н. Определите коэффициент трения скольжения.

43.    Тело  движется  по  горизонтальной  поверхности  со  скоростью

10 м/с  и  останавливается  при  торможении  через  2  с.  Определите коэффициент трения. Движение считайте равнозамедленным.

44.  Удлинение буксирного троса с жесткостью 50000 Н/м при буксировке с постоянной скоростью по горизонтальной дороге саней массой 1500 кг равно 0,06 м. Определите коэффициент трения саней о дорогу.

45.    Человек,  толкая  ящик  массой  30  кг  сзади  под  углом  30о   к

горизонту, равномерно перемещал его по полу, прикладывая силу 200

Н. Какую силу он должен был приложить для равномерного перемещения этого ящика, если бы тянул его за веревку под тем же по величине углом?

46.    Определите силу тяги локомотива, сообщающего составу массой

200 т ускорение 0,04 м/с2. Коэффициент трения скольжения равен 0,4.

47.       Определите  тормозной  путь  движущегося  по  горизонтальной дороге  автомобиля,  если  его  скорость  перед  началом  торможения

40 м/с. Коэффициент трения между шинами и дорогой 0,8.

Редактор Е.К.Евстратова

Технический редактор Е.К.Евстратова

Тем. план 2006 г., п.81
Подписано в печать Печать офсетная	Усл. печ.л. 2,4	Формат 60х84/16 Уч.-изд.л. 1,9
Тираж 500 экз.	Заказ	Цена 15 р.

Ротапринт МАДИ(ГТУ). 125319, Москва, Ленинградский проспект, 64

Материал взят из книги Концепции современного естествознания (В.М. Жураковский)

Коэффициент трения и ситуации, в которых он возникает :: SYL.ru

Что такое коэффициент трения в физике и с чем он связан? Как вычисляют эту величину? Чему численно равен коэффициент трения? На эти и некоторые другие вопросы, которые затрагивает основная тема, мы дадим ответы в ходе статьи. Конечно же, разберем и конкретные примеры, где мы сталкиваемся с явлением, в котором фигурирует коэффициент трения.

Что такое трение?

Трение – один из видов взаимодействий, происходящих между материальными телами. Возникает процесс трения между двумя телами при их соприкосновении той или иной площадью поверхности. Как и многие прочие виды взаимодействия, трение существует исключительно с оглядкой на третий закон Ньютона. Как это получается на практике? Возьмем два абсолютно любых тела. Пускай это будут два деревянных бруска средних размеров.

Начнем проводить их друг мимо друга, осуществляя соприкосновении по площадям. Вы заметите, что перемещать их относительно друг друга станет заметно сложнее, чем просто перемещать их в воздухе. Здесь как раз свою роль начинает играть коэффициент трения. В данном случае мы абсолютно спокойно можем говорить о том, что сила трения может быть описана третьим законом Ньютона: она, приложенная к первому телу, будет равна численно (по модулю, как любят говорить в физике) такой же силе трения, приложенной ко второму телу. Но не будем забывать, что в третьем законе Ньютона есть минус, говорящий о том, что силы хоть и равны между собой по модулю, но направлены в разные стороны. Таким образом, сила трения – векторная.

Природа силы трения

Как и упругие силы, сила трения имеет электромагнитную природу. Вследствие чего же она возникает? Все дело в том, что атомы и молекулы тел, которые претерпевают соприкосновение, начинают взаимодействовать друг с другом.

Сила сухого трения

Это сила, которая возникает при контакте двух или более твердых тел. При этом обязательным условием будет отсутствие между этими телами газообразной и жидкой прослойки. Сила сухого трения во всех случаях направлена по касательной линии, проведенной к соприкасающимся площадям.

Одна из разновидностей такого процесса – трение покоя. Оно возникает даже в том случае, если тела покоятся друг относительно друга. Определяется такое трение как величина силы, приложенной извне. В данном случае сила должна быть направлена в противоположную сторону.

Ограничение силы трения покоя

Соответствующая сила всегда имеет некоторое максимальное (граничное) значение. Если внешняя сила становится по модулю еще больше и, в конце концов, превосходит это максимальное значение, между телами мы сможем наблюдать проскальзывание. То есть тело придет в движение. Это явление также можно связать со вторым законом Ньютона, который рассказывает о сумме сил, их компенсации и, как о результате всего этого, равноускоренном движении тела.

Сила трения скольжения

Раньше было сказано о том, что если внешняя сила превосходит определенное максимальное значение, допустимое для соответствующей системы, то тела, входящие в такую систему, придут в движение относительно друг друга. Будет ли двигаться одно тело или два, или больше – все это неважно. Важно то, что в этом случае возникает сила трения скольжения. Если говорить о ее направлении, то направлена она в сторону, которая противоположна направлению скольжения (или движения). Зависит она от того, какую относительную скорость имеют тела. Но это если вдаваться в разного рода физические нюансы.

Необходимо заметить, что в большинстве случаев принято считать силу трения скольжения независимой от скорости одного тела относительно другого. Она также никак не связана с максимальным значением силы трения покоя. Огромное количество физических задач решаются именно при помощи применения аналогичной модели поведения, что позволяет существенно облегчить процесс решения.

Что такое коэффициент трения скольжения?

Это есть не что иное, как коэффициент пропорциональности, который присутствует в формуле, описывающей процесс приложения силы трения к тому или иному телу. Коэффициент – это безразмерная величина. Иными словами, он выражается исключительно числами. Он не измеряется в килограммах, метрах или еще чем-то. Практически во всех случаях коэффициент трения численно меньше единицы.

От чего он зависит?

Зависит коэффициент трения скольжения от двух факторов: от того, из какого материала изготовлены тела, которые претерпевают соприкосновение, а также от того, как обработана их поверхность. Она может быть рельефной, гладкой, а также на нее может быть нанесено какое-то специальное вещество, которое будет или снижать, или повышать трение.

Как направлена сила трения?

Она направлена в сторону, которая противоположна направлению движения двух или более соприкасающихся тел. Вектор направления прикладывается по касательной линии.

Если контакт происходит между твердым телом и жидкостью

В том случае, если происходит соприкосновение твердого тела с жидкостью (или некоторым объемом газа), мы можем говорить о возникновении силы так называемого вязкого трения. Она, конечно же, численно будет значительно меньше, чем сила сухого трения. Но направление ее (вектор действия) сохраняется тем же. В случае вязкого трения о покое говорить не приходится.

Связана соответствующая сила со скоростью тела. Если скорость маленькая, то сила будет пропорциональна скорости. Если высокая, то она будет пропорциональна уже квадрату скорости. Коэффициент пропорциональности будет неразрывно связан с тем, какую форму имеют тела, между которыми происходит соприкосновение.

Другие случаи возникновения силы трения

Имеет место данный процесс и при качении какого-либо тела. Но обычно им в задачах пренебрегают, так как сила трения качения весьма и весьма мала. Это, на самом деле, упрощает процесс решения соответствующих задач, хотя при этом сохраняется достаточная степень точности итогового ответа.

Внутреннее трение

Этот процесс также называется в физике альтернативным словом “вязкость”. На самом деле он представляет собой ответвление явлений переноса. Свойственен этот процесс текучим телам. Причем речь идет не только о жидкостях, но и о газообразных веществах. Свойство вязкости заключается в оказании сопротивления при переносе одной части вещества относительно другой. При этом логично совершается работа, необходимая на перемещение частиц. Но она рассеивается в окружающем пространстве в виде тепла.

Закон, определяющий силу вязкого трения, был предложен еще Исааком Ньютоном. Произошло это в 1687 году. Закон и по сегодняшний день носит имя великого ученого. Но все это было только в теории, а экспериментальное подтверждение удалось получить только в начале 19-го века. Соответствующие опыты ставились Кулоном, Хагеном и Пуазейлем.

Итак, сила вязкого трения, которая оказывает на жидкость воздействие, пропорциональна относительной скорости слоев, а также площади. В то же время она обратно пропорциональна тому расстоянию, на котором располагаются слои относительно друг друга. Коэффициент внутреннего трения — это коэффициент пропорциональности, который в данном случае определяется сортом газа или жидкого вещества.

Аналогичным образом будет определяться и другой коэффициент, который имеет место в ситуациях с относительным движением двух течений. Это, соответственно, коэффициент гидравлического трения.

сопротивление — Какие факторы определяют коэффициент трения?

Коэффициент трения между двумя материалами. Таким образом, резина будет иметь другой коэффициент трения на асфальте, чем на стекле. Тем не менее, некоторые материалы, такие как резина, имеют более высокий коэффициент трения со многими другими материалами. Другие материалы, такие как ПТФЭ и лед, имеют низкий коэффициент трения со многими другими материалами. В качестве примера материала с низким коэффициентом трения часто приводят лед. Ниже приводится краткое объяснение некоторых эффектов, влияющих на коэффициент трения. Более подробно эта тема относится к категории трибологии.

Шероховатость поверхности +

Если оба материала очень шероховатые (например, наждачная бумага с зернистостью <200), то части, выступающие на одной поверхности (неровности), часто попадают в углубления на другой поверхности, как зубья шестерни. Это взаимодействие помогает предотвратить скольжение поверхностей друг относительно друга. Таким образом, материалы с более высокой шероховатостью часто будут иметь более высокие коэффициенты трения.

Смазка —

Часто между двумя поверхностями находится некоторая легко деформируемая среда. Масло в вашем двигателе так хорошо разделяет стальные детали, что сталь вообще не соприкасается. В этом случае сила трения фактически возникает из-за вязкостных эффектов деформации масла и сильно зависит от скорости. Мокрая дорога имеет более низкий коэффициент трения с резиной, чем сухая, из-за того, что вода действует как смазка. Лед будет смазываться при таянии, образуя слой воды, отделяющий кристаллы льда от другой поверхности. Другие твердые тела, такие как графит, будут самосмазываться, отламывая от себя крошечные кусочки, которые затем будут действовать как смазка.

Межмолекулярные силы +

Когда молекулы сближаются очень близко друг к другу, они начинают взаимодействовать. Часто они хотят держаться друг за друга с помощью силы Ван-дер-Ваальса или иным образом. Это приводит к увеличению трения. ПТФЭ (торговое название тефлон) имеет очень низкие межмолекулярные силы и, как следствие, низкое трение.

Жесткость ?

В приведенных выше абзацах есть много «склонен к» и «часто» из-за того, как эти (и другие) эффекты взаимодействуют. Например, увеличение шероховатости поверхности может фактически уменьшить трение, если позволяет смазке лучше заполнить зазоры между поверхностями. Это также может уменьшить трение, просто отделив большую часть молекул от другой поверхности, чтобы уменьшить межмолекулярные силы. Жесткость поверхностей вступает в игру, когда одна поверхность деформирует другую. Например, каучук очень легко деформируется, что позволяет ему соответствовать шероховатости поверхности другого материала, сцепляясь с ним и уменьшая межмолекулярные расстояния для увеличения межмолекулярных сил. Это одна из причин, по которой резина имеет высокое трение. Латунь на руке, хотя она также легко деформируется, имеет тенденцию деформироваться таким образом, что отрываются шероховатости, которые затем образуют смазывающие частицы. Таким образом, мягкость латуни фактически снижает трение.

Кинетическое трение: определение, взаимосвязь и формулы

Вы когда-нибудь задумывались, почему во время дождя дороги становятся скользкими, что затрудняет остановку автомобиля? Оказывается, это прямое следствие кинетической силы трения, так как сухой асфальт обеспечивает лучшее сцепление шины с дорогой, чем мокрый асфальт, что сокращает время остановки автомобиля.

Кинетическое трение — это сила трения, которая почти неизбежна в нашей повседневной жизни. Иногда это остановка, а иногда необходимость. Он присутствует, когда мы играем в футбол, пользуемся смартфонами, гуляем, пишем и занимаемся многими другими обычными делами. В сценариях реальной жизни, когда бы мы ни рассматривали движение, ему всегда будет сопутствовать кинетическое трение. В этой статье мы лучше поймем, что такое кинетическое трение, и применим эти знания к различным примерам задач.

Кинетическое трение Определение

Когда вы пытаетесь толкнуть коробку, вам нужно будет приложить определенное усилие. Как только коробка начинает двигаться, легче поддерживать движение. По опыту, чем легче ящик, тем легче его передвигать.

Представим себе тело, лежащее на плоской поверхности. Если одна контактная сила \(\vec{F}\) приложена к телу горизонтально, мы можем определить четыре составляющие силы, перпендикулярные и параллельные поверхности, как показано на рисунке ниже.

Рис. 1 — Если объект положить на горизонтальную поверхность и приложить к нему горизонтальную силу, то кинетическая сила трения возникнет в направлении, противоположном движению, и будет пропорциональна нормальной силе.

Нормальная сила, \(\vec{F_\mathrm{N}}\), перпендикулярна поверхности, а сила трения, \(\vec{F_\mathrm{f}}\),

равна параллельно поверхности. Сила трения направлена ​​против движения.

Кинетическое трение — это тип силы трения, которая действует на движущиеся объекты.

Обозначается \(\vec{F_{\mathrm{f, k}}}\), а его величина пропорциональна величине нормальной силы.

Это отношение пропорциональности интуитивно понятно, как мы знаем из опыта: чем тяжелее объект, тем труднее заставить его двигаться. На микроскопическом уровне большая масса равна большему гравитационному притяжению; поэтому объект будет ближе к поверхности, увеличивая трение между ними.

Формула кинетического трения

Величина кинетической силы трения зависит от безразмерного коэффициента кинетического трения \(\mu_{\mathrm{k}}\) и нормальной силы \(\vec{F_\mathrm{N}} \) измеряется в ньютонах (\(\mathrm{N}\)). Эту связь можно показать математически

$$ \vec{F}_{\mathrm{f,k}}=\mu_{\mathrm{k}} \vec{F_\mathrm{N}}.$$

Кинетический коэффициент трения

Отношение кинетической силы трения контактирующих поверхностей к нормальной силе известно как коэффициент кинетического трения . Обозначается \(\mu_{\mathrm{k}}\). Его величина зависит от того, насколько скользкой является поверхность. Поскольку это отношение двух сил, коэффициент кинетического трения безразмерен. В таблице ниже мы можем видеть приблизительные коэффициенты кинетического трения для некоторых распространенных комбинаций материалов.

Материалы	Коэффициент кинетического трения, \(\mu_{\mathrm{k}}\)
Сталь по стали	\(0.57\)
Aluminum on steel	\(0.47\)
Copper on steel	\(0.36\)
Glass on glass	\(0.40\)
Copper on glass	\(0. 53\)
Teflon on Teflon	\(0.04\)
Teflon on steel	\(0.04\)
Rubber on concrete (dry )	\(0,80\)
Резина на бетоне (мокром)	\(0,25\)

Теперь, когда мы знаем уравнение для расчета кинетической силы трения и познакомились с коэффициентом кинетического трения, давайте применим это знание к некоторым примерным задачам. !

Примеры кинетического трения

Для начала давайте рассмотрим простой случай непосредственного применения уравнения кинетического трения!

Автомобиль движется с постоянной скоростью с нормальной силой \(2000 \, \mathrm{N}\). Если кинетическое трение, приложенное к этому автомобилю, равно \(400 \, \mathrm{N}\). Тогда вычислите коэффициент кинетического трения, связанного с этим?

Решение

В примере даны величины нормальной силы и кинетической силы трения. Итак, \(\vec{F}_{\mathrm{f,k}}=400 \, \mathrm{N}\) и \(F_\mathrm{N}= 2000 \, \mathrm{N}\) . Если мы подставим эти значения в формулу кинетического трения

$$ \vec{F}_{\mathrm{f,k}}=\mu_{\mathrm{k}} \vec{F_\mathrm{N}}, $$

получаем следующее выражение

$$400 \, \mathrm{N} =\mu_{\mathrm{k}} \cdot 2000 \, \mathrm{N}, $$

которое можно преобразовать в найти коэффициент трения 9{\circ}\) к горизонтальной поверхности. Кинетическая сила трения направлена ​​противоположно силе.

Решение

В примере сказано, что мы хотим поддерживать постоянную скорость. Постоянная скорость означает, что объект находится в состоянии равновесия (т.е. силы уравновешивают друг друга). Давайте нарисуем диаграмму свободного тела, чтобы лучше понять силы, и посмотрим на горизонтальную и вертикальную составляющие.

Рис. 3 — Свободная схема коробки. Силы действуют как в горизонтальном, так и в вертикальном направлении.

Когда мы смотрим на перпендикулярные компоненты силы, направленные вверх силы должны быть равны по величине направленным вниз силам. {\ circ} = F _ {\ mathrm {f, k}} = \ mu _ {\ mathrm {k}} F_ \ mathrm {N}. $ $ 9{\circ}} \\ T &= \frac{0,5000 \cdot 200,0 \, \mathrm{N}}{0,87 + 0,5000 \cdot 0,5} \\ T &= 89,29 \, \mathrm{N}. \end{align}$$

Наконец, давайте рассмотрим аналогичный пример, только на этот раз ящик расположен на наклонной плоскости.

Коробка скользит вниз с постоянной скоростью с наклонной плоскости, составляющей угол \(\alpha\) с горизонтом. Поверхность имеет коэффициент кинетического трения \(\mu_{\mathrm{k}}\). Если вес коробки равен \(w\), найдите угол \(\alpha\).

Рис. 4. Коробка, скользящая по наклонной плоскости. Он движется с постоянной скоростью.

Давайте посмотрим на силы, действующие на коробку на рисунке ниже.

Рис. 5 — Все силы, действующие на коробку, скользящую по наклонной плоскости. Мы можем применить новую систему координат, чтобы написать соответствующие уравнения.

Если мы получим новые координаты (\(x\) и \(y\)), то увидим, что в направлении \(x\) действуют кинетическая сила трения и горизонтальная составляющая веса. В направлении \(y\) действуют нормальная сила и вертикальная составляющая веса. Поскольку ящик движется с постоянной скоростью, он находится в равновесии.

1. Для направления \(x\): \(w\cdot\sin\alpha=F_\mathrm{f,k} = \mu_{\mathrm{k}}F_\mathrm{N}\)
2. Для \(y\)-направления: \(F_\mathrm{N}=w\cdot\cos\alpha\)

Мы можем вставить второе уравнение в первое уравнение:

$$ \begin{align} w \cdot \sin\alpha & =\mu_\mathrm{k}w \cdot \cos\alpha \\ \cancel{w}\cdot\sin\alpha & =\mu_\mathrm{k} \cancel{w} \cdot \cos\alpha \\ \mu_\mathrm{k} & = \tan\alpha \end{align}$$

Тогда угол \(\alpha\) равен

$$ \alpha = \arctan\mu_\mathrm{k}.$$

Статическое трение и кинетическое трение

В целом коэффициент трения может принимать две формы, одной из которых является кинетическое трение. Другой тип известен как статическое трение . Как мы уже установили, кинетическая сила трения является разновидностью силы трения, действующей на движущиеся объекты. Итак, в чем же разница между статическим трением и кинетическим трением?

Статическое трение — это сила, обеспечивающая неподвижность объектов, покоящихся друг относительно друга.

Другими словами, кинетическое трение относится к движущимся объектам, тогда как статическое трение относится к неподвижным объектам.

Разницу между двумя типами можно запомнить прямо из словаря. В то время как статика означает отсутствие движения, кинетика означает отношение к движению или его следствие!

Математически статическое трение \(F_\mathrm{f,s}\) очень похоже на кинетическое трение,

$$ F_\mathrm{f,s} = \mu_\mathrm{s}F_\mathrm{N}$$

, где единственным отличием является использование другого коэффициента \(\mu_\mathrm{s} \), который является коэффициентом статического трения.

Давайте рассмотрим пример, когда объект испытывает оба типа трения.

Тяжелая коробка лежит на столе и остается неподвижной до тех пор, пока не будет приложена некоторая сила в горизонтальном направлении, чтобы сдвинуть ее по столу. Поскольку поверхность стола довольно неровная, изначально коробка не движется, несмотря на приложенную силу. В результате коробку толкают еще сильнее, пока, в конце концов, она не начнет двигаться по столу. Объясните различные этапы сил, действующих на коробку, и постройте график зависимости трения от приложенной силы.

Решение

• Сначала к ящику не приложены никакие силы, поэтому он испытывает только гравитационное притяжение вниз и нормальную силу стола, толкающую его вверх.
• Затем к коробке горизонтально прикладывается некоторая толкающая сила \(F_\mathrm{p}\). В результате возникнет сопротивление в противоположном направлении, известное как трение \(F_\mathrm{f}\).
• Учитывая, что коробка тяжелая, а поверхность стола неровная, коробка не будет легко скользить, так как обе эти характеристики влияют на трение.

нормальная сила и шероховатость/гладкость задействованных поверхностей являются основными факторами, влияющими на трение.

• Итак, в зависимости от величины приложенной силы коробка будет оставаться неподвижной за счет трения покоя \(F_\mathrm{f,s}\).
• С увеличением приложенной силы, в конце концов, \(F_\mathrm{p}\) и \(F_\mathrm{f,s}\) будут иметь одинаковую величину. Эта точка известна как порог движения, 9После достижения 0040 и коробка начнет двигаться.
• Как только коробка начнет двигаться, сила трения, влияющая на движение, будет равна кинетическому трению \(F_\mathrm{f,k}\). Поддерживать его движение станет легче, так как коэффициент трения у движущихся объектов обычно меньше, чем у неподвижных.

Графически все эти наблюдения можно увидеть на рисунке ниже.

Рис. 6 – График зависимости трения от приложенной силы.

Кинетическое трение — основные выводы

• Кинетическая сила трения — это тип силы трения, действующей на движущиеся объекты.
• Величина кинетической силы трения зависит от коэффициента кинетического трения и нормальной силы.