Что называют индуктивностью проводника

При самоиндукции, как и при всяком процессе индукции, индуцированная в катушке э. Магнитный же поток пропорционален силе тока в цепи. В, то индуктивность подобной катушки принимают за единицу для измерения индуктивности. Эта единица получила название генри Гн в честь американского физика Джозефа Генри Таким образом, если измерять индуктивность катушки в генри, ток в амперах, а время в секундах, то э. Если, например, индуктивность катушки равна 5 Гн и ток в ней изменяется на 1 А за 0,02 с, то средняя индуцированная э.

Поиск данных по Вашему запросу:

Схемы, справочники, даташиты:

Прайс-листы, цены:

Обсуждения, статьи, мануалы:

Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.

Содержание:

• Физика. 11 класс
• КАТУШКА ИНДУКТИВНОСТИ
• Единица измерения индуктивности
• Индуктивность
• Что называется индуктивностью проводника
• Научный форум dxdy
• ИНДУКТИВНОСТЬ

ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Урок 288. Явление самоиндукции (окончание). Задачи на индуктивность

Физика. 11 класс

Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток. Индуктивность является электрической инерцией, подобной механической инерции тел. А вот мерой этой электрической инерции как свойства проводника может служить ЭДС самоиндукции.

Характеризуется свойством проводника противодействовать появлению, прекращению и всякому изменению электрического тока в нём. Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока [4] :.

При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током [4] :. Практически участки цепи со значительной индуктивностью выполняют в виде катушек индуктивности [4]. Элементами малой индуктивности применяемыми для больших рабочих частот могут быть одиночные в том числе и неполные витки или даже прямые проводники; при высоких рабочих частотах необходимо учитывать индуктивность всех проводников [5].

Для имитации индуктивности, то есть ЭДС на элементе, пропорциональной и противоположной по знаку скорости изменения тока через этот элемент, в электронике используются [6] и устройства, не основанные на электромагнитной индукции см. Гиратор ; такому элементу можно приписать определённую эффективную индуктивность, используемую в расчётах полностью хотя вообще говоря с определёнными ограничивающими условиями аналогично тому, как используется обычная индуктивность.

Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Символ L , используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца [9] [10]. Единица измерения индуктивности названа в честь Джозефа Генри [11]. Сам термин индуктивность был предложен Оливером Хевисайдом в феврале года [12].

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле [4]. Будем вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля достаточно слабы либо меняются достаточно медленно, чтобы можно было пренебречь порождаемыми ими магнитными полями. Ток считаем одинаковым по всей длине контура пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину.

Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле вектор магнитной индукции , создаваемое всем проводником, также пропорционально порождающему току.

Рассуждение выше верно для вакуума. В случае присутствия магнитной среды [13] магнетика с заметной или даже большой магнитной восприимчивостью, вектор магнитной индукции который и входит в выражение для магнитного потока будет заметно или даже во много раз отличаться от того, каким бы он был в отсутствие магнетика в вакууме.

Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший или уменьшившийся в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже.

Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует ведь свойство пропорциональности току сохраняется для любой.

В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур.

Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур. Но это действительно так: возьмём две такие поверхности.

Вместе они будут составлять одну замкнутую поверхность. А мы знаем из закона Гаусса для магнитного поля , что магнитный поток через любую замкнутую поверхность равен нулю. Что доказывает корректность определения. Величина магнитного потока , пронизывающего одновитковый контур, связана с величиной тока следующим образом [4] :. В случае катушки , состоящей из N витков предыдущее выражение модифицируется к виду:.

Но в реальных катушках магнитные поля в центре и на краях отличаются, поэтому используются более сложные формулы. Отсюда следует формула для индуктивности соленоида без сердечника :. Для тороидальной катушки, намотанной на сердечнике из материала с большой магнитной проницаемостью, можно приближённо пользоваться формулой для бесконечного прямого соленоида см.

Лучшее приближение дает формула. Для длинного прямого или квазилинейного провода кругового сечения индуктивность выражается приближённой формулой [19] :.

В высокочастотном случае ток течёт в поверхности проводников скин-эффект и в зависимости от вида проводников иногда нужно различать индуктивность высокой и низкои частоты. В случае скин-эффекта нужно учитывать, что при маленьких расстояниях между проводниками в поверхностях текут дополнительные вихревые токи эффект экранирования , и выражения, содержащие Y , становятся неточными. Материал из Википедии — свободной энциклопедии. Электрическая цепь. Ковариантная формулировка. Известные учёные.

Основы электротехники. Теоретические основы электротехники. Электрические цепи. Национальная энциклопедия. Общий курс физики. The expression given is the inductance of a cylinder with a current around its surface. Электронные компоненты.

Резистор Переменный резистор Подстроечный резистор Варистор Фоторезистор Конденсатор Переменный конденсатор Подстроечный конденсатор Катушка индуктивности Кварцевый резонатор Предохранитель Самовосстанавливающийся предохранитель Трансформатор Мемристор Бареттер.

Электронно-лучевая трубка ЖК-дисплей Светодиод Газоразрядный индикатор Вакуумно-люминесцентный индикатор Блинкерное табло Семисегментный индикатор Матричный индикатор Кинескоп. Терморезистор Термопара Элемент Пельтье. Категории : Физические величины по алфавиту Магнетизм Физические величины. Скрытые категории: Статьи с ссылкой на БСЭ, без указания издания Википедия:Статьи с некорректным использованием шаблонов:Cite web не указан язык Википедия:Статьи с некорректным использованием шаблонов:Cite web указан неверный параметр Страницы, использующие волшебные ссылки ISBN Википедия:Статьи с переопределением значения из Викиданных.

Пространства имён Статья Обсуждение. Просмотры Читать Править Править код История. Эта страница в последний раз была отредактирована 2 октября в Текст доступен по лицензии Creative Commons Attribution-ShareAlike ; в отдельных случаях могут действовать дополнительные условия.

Подробнее см. Условия использования. Политика конфиденциальности Описание Википедии Отказ от ответственности Свяжитесь с нами Разработчики Заявление о куки Мобильная версия. Классическая электродинамика. Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток.

КАТУШКА ИНДУКТИВНОСТИ

Явление самоиндукции. Явление возникновения э. Согласно явлению электромагнитной индукции, это изменение магнитного потока и приводит к появлению э. Найдём э. Пусть по проводнику с индуктивностью L течёт электрический ток. В момент времени t1 сила этого тока равна I1, а к моменту времени t2 она стала равной I2.

Мы уже изучили, что около проводника с током возникает магнитное поле. А также а ток, возникающий при этом, называется током самоиндукции.

Единица измерения индуктивности

Индуктивность проводников Ь зависит от их формы и размеров. Индуктивность проводника в данной среде определяется исключительно его размерами и формой. Индуктивность прямолинейного провода невелика. Индуктивность того же провода в форме витка значительно больше. При одинаковых размерах катушек длин и диаметров их индуктивность пропорциональна квадрату числа витков. Индуктивность катушки прямо пропорциональна магнитной проницаемости ia сердечника. Индуктивность проводника зависит от его формы, размеров, а также от свойств окружающей среды. Если сила тока изменяется со временем, то изменяется и магнитный поток, сцепленный с контуром. Изменение магнитного потока, в свою очередь, вызывает появление в проводнике индукционного тока. Так как индукционный ток вызван изменением силы тока в самом проводнике, то данное явление возникновения индукционного тока называется самоиндукцией, а возникающая эдс — эдс самоиндукции.

Индуктивность

Последний раз редактировалось jast Доброго дня. Объясните пожалуйста, почему индуктивность прямого отрезка проводника уменьшается с увеличением его диаметра? Именно проводника а не катушки. Индуктивность равна отношению магнитного потока к силе тока.

Этим термином называют коэффициент, определяющий пропорциональное отношение между суммарным магнитным потоком Фс и электрическим током I в определенном контуре. Данная публикация поможет разобраться с тематическими вычислениями и применением теоретических знаний для расчета катушек, других специальных изделий.

Что называется индуктивностью проводника

Явление самоиндукции. Основные понятия. Энергия магнитного поля. Мы уже изучили, что около проводника с током возникает магнитное поле. А также изучили, что переменное магнитное поле порождает ток явление электромагнитной индукции. Рассмотрим электрическую цепь.

Научный форум dxdy

Одним из основных и важных элементов, используемых в радиотехнике, является катушка индуктивности. Эта наиболее распространенная деталь радиоаппаратуры характеризуется рядом специфических и неповторимых физических свойств, без понимания которых невозможно полноценно осознавать процессы, происходящие в цепях. В году датским ученым Хансом Эрстедом была найдена зависимость магнитного поля от тока: при протекании электрического тока по проводу вокруг него образовывается магнитное поле. С целью охарактеризовать магнитное поле был введен некий критерий — это магнитная индукция. Поскольку магнитная индукция имеет свою ориентацию, то она является векторной величиной и описывает силу поля в конкретной точке пространства и объясняет влияние поля на контур катушку или элементарные заряженные частицы. Используя закон правого винта, находится ориентация трасс поля В.

Поэтому в том же самом проводнике, по которому идет переменный ток, возникает ЭДС индукции. Это явление называют самоиндукцией.

ИНДУКТИВНОСТЬ

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами катушки колебательных контуров, трансформаторы, дроссели, реакторы.

Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток. Индуктивность является электрической инерцией, подобной механической инерции тел. А вот мерой этой электрической инерции как свойства проводника может служить ЭДС самоиндукции. Характеризуется свойством проводника противодействовать появлению, прекращению и всякому изменению электрического тока в нём.

Регистрация Вход.

Отметим, что определение строгим не является, но оно позволит нам определить единицы измерения индуктивности. Иногда проводят аналогию между индуктивностью и массой тела. При этом говорят, что масса тела не позволяет мгновенно изменять телу его скорость соответственно кинетическую энергию , также как индуктивность не дает возможность магнитному полю изменять мгновенно свою энергию. При этом сравнивают выражение для кинетической энергии тела, вида:. В Международной системе единиц СИ генри — единица измерения индуктивности.

Без катушек индуктивности — свернутых в спираль проводников, запасающих магнитную энергию в виде магнитного поля, — невозможно построить ни радиопередатчик , ни радиоприемник , ни телевизор , ни аппаратуру проводной электрической связи. Используются и как катушка к пускателям втягивающего типа. Основа катушки — проводник.

Индуктивность проводника. Явление самоиндукции. Индуктивность соленоида. План: индуктивность проводника

Download 34.31 Kb. Sana 01.04.2022 Hajmi 34.31 Kb. #622231

Bog’liq
44. Индуктивность проводника. Явление самоиндукции. Индуктивность соленоида.
17, 17, 1 sho’rtan gaz kimyo majmuasi ishlash texnologik jarayoni bayoni, 62- dars, mis, Ibn Sino, топшириқ(1-u)(6), Lotin, Namuna, Namuna, HELLADOS Nodar Dumbadze, boshlangich sinf matematika darslarida pedagogik texnologiyalardan foydalanish metodikasi, Tushunchalar jadvali, 10-мавзу, 1. Sinf rahbari-WPS Office

Bu sahifa navigatsiya:

• ИНДУКТИВНОСТЬ СОЛЕНОИДА
• ЭДС самоиндукции
• Кату́шка индукти́вности

ИНДУКТИВНОСТЬ ПРОВОДНИКА. ЯВЛЕНИЕ САМОИНДУКЦИИ. ИНДУКТИВНОСТЬ СОЛЕНОИДА. ПЛАН: ИНДУКТИВНОСТЬ ПРОВОДНИКА ЯВЛЕНИЕ САМОИНДУКЦИИ ИНДУКТИВНОСТЬ СОЛЕНОИДА При любом изменении тока в проводнике его собственное магнитное поле также изменяется. Вместе с ним изменяется и поток магнитной индукции, пронизывающий поверхность, охваченную контуром проводника. В результате в этом контуре индуцируется ЭДС. Это явление называется явлением самоиндукции. В соответствии с законом Био-Савара-Лапласа индукция магнитного поля В пропорциональна силе тока I в проводнике. Отсюда следует, что поток магнитной индукции  и сила тока I также пропорциональны друг другу:  Коэффициент пропорциональности L называютиндуктивностью проводника. За единицу индуктивности в СИ принимают индуктивность такого проводника, у которого при силе тока 1А создается поток магнитной индукции, равный 1Вб. Эту единицу называют Генри, Гн. Индуктивность проводника зависит от его формы и размеров, а также от магнитных свойств окружающей его среды (магнитной проницаемости μ). Заметим при этом, что линейная зависимость между  и I остается справедливой и в том случае, когда μ зависит от напряженности магнитного поля Н, а значит, от I (например, ферромагнитная среда). В этом случае индуктивность L также зависит от I. Согласно основному закону электромагнитной индукции, ЭДС самоиндукции, возникающая при изменении силы тока в проводнике, есть: Скрыть рекламу:Не интересуюсьУже купилСпамМешаетСпасибо, объявление скрыто. Скрыть рекламу:Не интересуюсьУже купилСпамМешаетСпасибо, объявление скрыто. . Или, записав  , будем иметь:  . В том случае, когда среда не является ферромагнитной L=const, тогда:  Последняя формула дает возможность определить индуктивность L как коэффициент пропорциональности между скоростью изменения силы тока в проводнике и возникающей вследствие этого ЭДС самоиндукции. 12345678910Следующая ⇒ Катушка индуктивности ( дроссель) на материнской плате компьютера Обозначение на электрических принципиальных схемах Кату́шка индукти́вности (иногда дроссель  ) — винтовая, спиральная или винтоспиральная катушка из свёрнутого изолированного проводника, обладающая значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении. Как следствие, при протекании через катушку переменного электрического тока наблюдается её значительная инерционность. Применяются для подавления помех, сглаживания биений, накопления энергии, ограничения переменного тока, в резонансных ( колебательный контур) и частотно-избирательных цепях, в качестве элементов индуктивности искусственных линий задержки с сосредоточенными параметрами, создания магнитных полей, датчиков перемещений и так далее. Литература Основная: Q.P.Abduraxmanov, V.S.Xamidov, N.A.Axmedova. FIZIKA. Toshkent. 2018 К.П.Абдурахманов, Ў.Эгамов “Физика курси”. Тошкент. 2010 й. 3. Абдурахманов К.П., Тигай О.Э., Хамидов В.С. Комплекс мультимедийных лекций. Pdf + диск + СНМ. Дополнительная: 4.Савельев И. В. Курс физики. М.: Наука 2005 5.Аҳмаджонов О. Физика курси. Т.: «Ўқитувчи», 1987. т. 1,2,3- қисмлар 6.Исмоилов М., Хабибуллаев П.К., Халиуллин М. Физика курси, Т.; Ўзбекистон», 2000. Т.1. Download 34.31 Kb. Do’stlaringiz bilan baham:

---

Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©fayllar.org 2022
ma’muriyatiga murojaat qiling

Индуктивность — Физическая энциклопедия

ИНДУКТИВНОСТЬ в электродинамике (коэффициент самоиндукции) (от лат. inductio — наведение, побуждение) — параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним — катушка самоиндукции). И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновению вихревого электрич. поля E(r, t)с отличной от нуля циркуляцией

по замкнутым контурам l_i; пронизываемым магн. потоком Ф_i. Внутри проводника вихревое поле Е взаимодействует с порождающим его током и оказывает противодействие изменению магн. потока (Ленца правило ).Циркуляция E_i и магн. ) — циркуляция вектора E вдоль этой линии тока, j_n — нормальная к S_np составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должна удовлетворять энергетич. соотношению: =E_сиI (Р — суммарная мощность взаимодействия поля с током). Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:

Ф=L.I (в СИ), Ф=¹/_c(LI) (в системе СГС). (1)

Коэф. L и L наз. И. Величина L измеряется в генри, L — в см. Для эдс самоиндукции справедливо соотношение

E_си=-d/dt(LI) (в СИ), E_cи⁼-(1/с²)(d/dt)(LI) (2) (в системе СГС).

Производная по времени от И. определяет ту часть E_си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. В известном смысле И. характеризует инерционность цепи по отношению к изменению в ней тока и является электродинамич. аналогом массы тела в механике (при этом I сопоставляется со скоростью тела). В частности, для цепей пост. тока энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.

W^m=¹/₂LI² (в СИ), W^m=¹/₂c²LI² (в системе СГС). (3)

Соотношение (3) позволяет различать И. внутреннюю L_i, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю L_e, связанную с внеш. магн. полем (L=L_i+L_e, L=L_i+L_e). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусами их изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения L_i=(m₀/8p)m_il (l — длина провода, m_i — магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l₁) совпадает с осевой линией проводника, а другая (l₂) совмещена с его поверхностью:

где r₁, r₂ — радиус-векторы точек на контурах l_l,<sub>l2, mе — магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L»(m0/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:

где l и а — длина и радиус провода. Это выражение обладает логарифмич. точностью — его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.

Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m0R(ln(8R/r)-2+¹/4mi), Гн, r<<R.</sub>

Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой — соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеального соленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j_пов=Ik (I — ток в соленоиде, k — число витков на единице длины).

Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл—магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока I_wи эдс самоиндукции E_w связаны соотношением:

И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление R_L(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса — Кронига соотношением:

где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением R_L(w) можно пренебречь, тогда E_w и I_w сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:

где W^m_w — усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения). Если в цепи действует гармонич. сторонняя эдс , то во втором законе Кирхгофа величина E_w может быть перенесена (со сменой знака) в правую часть равенства:

где С — ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину Z_L=iwL как индуктивную часть импеданса цепи (при атом Z_C=-i/wС — ёмкостная, a Z_R=R — активная части полного импеданса Z=Z_L+Z_C+Z_R). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён в среду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:

Величина L_Д(I)=dФ/dI наз. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:

B линейном приближении (при I»0) L_Д»L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е. , Основы теории электричества 9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин

      Предметный указатель      >>   

Что такое индуктивность простыми словами

Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф

B), индукция пропорциональна силе тока в проводнике
(B

I), следовательно магнитный поток пропорционален силе тока (Ф

ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.

Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность – физ.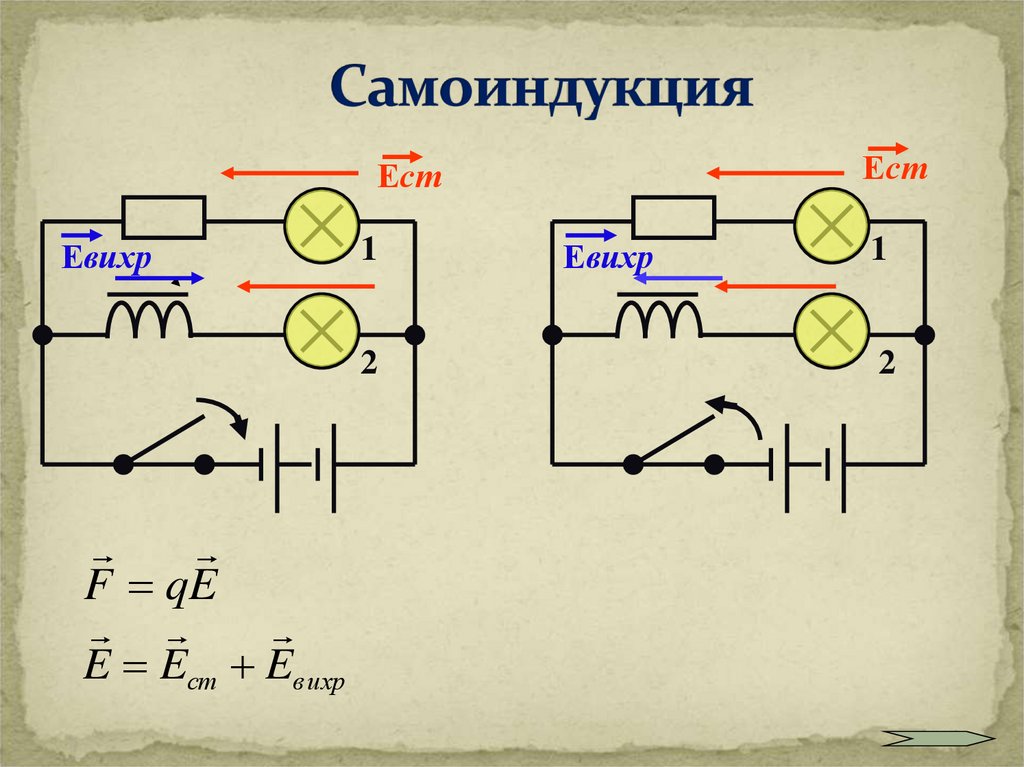 величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.

Также индуктивность можно рассчитать по формуле:

где Ф – магнитный поток через контур, I – сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды

Индуктивность взаимная – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).

Магнитный поток Ф₁₂ через контур 2, созданный током I₁ в контуре 1, прямо пропорционален току:

Коэффициент пропорциональности M₁₂ зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.

Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.

Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E₁ и с действующим значением напряжения U₁. На вторичной обмотке ЭДС E₂ и напряжение U₂.

Из законов Ома следует, что напряжение на обмотке равно

(1)

где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r₁ делают очень малым, поэтому часто им можно пренебречь. Тогда

Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e₁, как и ЭДС индукции e₂ в каждом витке первичной обмотки, т.е. e₁ = e₂. Следовательно, отношение ЭДС в первичной E₁ и вторичной E₂ обмотках равно отношению числа витков в них:

(2)

Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I₁/I₂ приблиз = w₁/w₂ = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.

Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником

часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Ф_р (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен

.

(1.14)

На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:

.

Так как , то .То есть поток рассеяния , в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).

Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9226 – | 7356 – или читать все.

78.85.5.182 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Слово состоит из 13 букв: первая и, вторая н, третья д, четвёртая у, пятая к, шестая т, седьмая и, восьмая в, девятая н, десятая о, одиннадцатая с, двенадцатая т, последняя ь,

Слово индуктивность английскими буквами(транслитом) – induktivnost

• Буква с встречается 1 раз. Слова с 1 буквой с
• Буква у встречается 1 раз. Слова с 1 буквой у
• Буква т встречается 2 раза. Слова с 2 буквами т
• Буква ь встречается 1 раз. Слова с 1 буквой ь
• Буква в встречается 1 раз. Слова с 1 буквой в
• Буква д встречается 1 раз. Слова с 1 буквой д
• Буква и встречается 2 раза. Слова с 2 буквами и
• Буква к встречается 1 раз. Слова с 1 буквой к
• Буква н встречается 2 раза. Слова с 2 буквами н
• Буква о встречается 1 раз. Слова с 1 буквой о

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность, краем которой является этот контур.

ИНДУКТИВНОСТЬ — в электродинамике (коэффициент самоиндукции) (от лат. inductio – наведение, побуждение) – параметр электрич. цепи, определяющий величину эдс самоиндукции…

Индуктивность (от лат. inductio — наведение, побуждение), физическая величина, характеризующая магнитные свойства электрической цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пространстве магнитное поле, причём магнитный поток Ф…

ИНДУКТИВНОСТЬ ВЗАИМНАЯ величина, характеризующая магн. связь двух или более электрич. цепей (контуров). Магн. поток через контур 1 с током I1 (рис.) частично пронизывает площадь, ограниченную контуром 2…

Индуктивность взаимная, величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура (1 и 2, см. рис.), то часть линий магнитной индукции, создаваемых током в первом контуре…

ВЗАИМНАЯ ИНДУКТИВНОСТЬ — количеств. хар-ка M 21 связи между полным магнитным потоком Ф 21 через нек-рую электрич. цепь 2, создаваемым электрич. током, текущим в др. цепи 1, и силой этого тока I 1 : М 21 = Ф 21/I 1.

Большой энциклопедический политехнический словарь

Индуктивности измерители, приборы для измерения индуктивности контуров с сосредоточенными параметрами, обмоток трансформаторов и дросселей, катушек индуктивности и пр.

ИНДУКТИВНОСТИ ИЗМЕРИТЕЛЬ (генриметр), прибор для измерения индуктивности элементов электрич. цепей. Действие И. и. основано на тех же методах измерений, что и действие ёмкости измерителя.

ИНДУКТИВНОСТИ ИЗМЕРИТЕЛЬ (генриметр), прибор для измерения индуктивности элементов электрич. цепей. Действие И. и. основано на тех же методах измерений, что и действие ёмкости измерителя.

Индуктивности мера, катушка индуктивности, применяемая при электрических измерениях и в качестве образцовых индуктивностей для проверки и градуировки измерительных устройств.

Кату́шка индукти́вности катушка из одножильного (реже многожильного) изолированного провода, намотанного обычно на каркас из диэлектрика цилиндрической, тороидальной или прямоугольной формы…

Кату́шка индукти́вности — катушка из одножильного (реже многожильного) изолированного провода, намотанного обычно на каркас из диэлектрика цилиндрической, тороидальной или прямоугольной формы…

Индуктивности катушка, свёрнутый в спираль изолированный проводник, обладающий значительной индуктивностью при относительно малой ёмкости и малом активном сопротивлении.

Морфемно-орфографический словарь. — 2002

Физический энциклопедический словарь. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1983 .

в электродинамике (коэффициент самоиндукции) (от лат. inductio – наведение, побуждение) – параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним – катушка самоиндукции).И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновениювихревого электрич. поля E(r, t )с отличной от нуля циркуляцией

по замкнутым контурам l_i;пронизываемым магн. ) – циркуляция вектора E вдоль этой линии тока, j_n – нормальная к S_np составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должнаудовлетворять энергетич. соотношению: =E _сиI ( Р– суммарная мощность взаимодействия поля с током).Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:

Ф=L.I (в СИ), Ф= 1 /_c(LI)(в системе СГС). (1)

Коэф. L и Lназ. И. Величина L измеряется в генри, L – в см.

E _си=-d/dt(LI) (в СИ), E_cи = -(1/с 2 )(d/dt)(LI)(2) (в системе СГС).

Производная по времени от И. определяет ту часть E _си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.

W m = 1 /₂LI 2 (в СИ), W m = 1 /₂c 2 LI 2 (в системе СГС). (3)

Соотношение (3) позволяет различать И. внутреннюю L_i, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю L_e, связанную с внеш. магн. полем (L=L_i+L_e, L=L_i+L_e). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусамиих изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения L_i=(m_{/8p)mil (l – длина провода, mi – магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l1) совпадает с осевой линией проводника, а другая (l2) совмещена с его поверхностью:}

где r₁, r₂ – радиус-векторы точек на контурах l_l, l₂,m _е – магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L «(m_{/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:}

где l и а – длина и радиус провода. Это выражение обладает логарифмич. точностью – его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.

Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m_{R(ln(8R/r)-2+ 1 /4mi), Гн, r}

Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой – соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеальногосоленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j _пов=Ik (I – ток в соленоиде, k – число витков на единице длины).

Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока I_w и эдс самоиндукции E_w связаны соотношением:

И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление R_L(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса – Кронига соотношением:

где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением R_L(w) можно пренебречь, тогда E_w и I_w сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:

где W m _w– усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения).Если в цепи действует гармонич. сторонняя эдс , то во втором законе Кирхгофа величина E_w может быть перенесена (со сменой знака) в правую часть равенства:

где С –ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину Z_L=iwLкак индуктивную часть импеданса цепи (при атом Z_C=-i/w С –ёмкостная, a Z_R=R– активная части полного импеданса Z=Z_L+Z_C+Z_R). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён всреду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:

Величина L _Д(I)=d Ф /dIназ. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:

B линейном приближении (при I «0) L _Д «L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Явление электромагнитной индукции — FINDOUT.SU

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности

Состоит в том, что в проводнике находящимся в магнитном поле при определенных условиях может возникать (индуктироваться. наводиться, появляться) ЭДС. При этом на концах проводника появляется разность потенциалов: «плюс» и «минус».

Явление электромагнитной индукции это одно из основополагающих явлений в электротехнике. На использовании этого явления работает множество электрических и электронных устройств.

    Для упрощения, рассмотрим явление электромагнитной индукции в двух вариантах. Это явление едино, с точки зрения физики, но так нам проще.

    Первый вариант явления электромагнитной индукции: проводник перемещается в магнитном поле, пересекая его силовые линии, как показано на рис. 32. (Заметим, что проводник не перемещается самостоятельно, его нужно перемещать руками или с помощью какого-то устройства.)

 

Рис. 32. Проводник перемещают в магнитном поле. В нём наводится ЭДС

 

    Величина ЭДС, возникающей в проводнике, определяется по формуле:

, где:

Е — величина ЭДС,

l — длина части проводника, находящейся в магнитном поле,

V — скорость перемещения проводника.

     Анализируя формулу, заметим, что величина ЭДС будет возрастать при увеличении силы магнитного поля (индукции В), длины проводника и скорости его движения.

    На величину ЭДС влияет также угол α, под которым проводник пересекает силовые линии. Наибольшая ЭДС возникает в случае, когда проводник пересекает их под прямым углом (α=90 градусов). Если жн проводник перемещать параллельно силовым линиям (α=0 градусов), ЭДС равна нулю, т.к. sin угла в ноль градусов равен нулю.

    Направление ЭДС, возникающей в проводнике определяется правилом правой руки: силовые линии входят в ладонь, отогнутый большой палец показывает направление движения проводника, четыре пальца ладони покажут направление ЭДС.

    На рис. 32 проводник перемещается, а магнитное поле неподвижно. Но, возможен обратный случай, когда проводник неподвижен, а перемещается магнитное поле. Так, на рис. 33, показано, что постоянный магнит перемещают вверх-вниз в катушке. При этом силовые линии магнитного поля пересекают проводник катушки и в ней наводится ЭДС. Появление ЭДС регистрирует измерительный прибор – гальванометр.

 

Рис. 33. Магнитное поле перемещается относительно неподвижного проводника

        

    Таким образом главное условие появления (наведения) ЭДС в проводнике состоит в том, чтобы проводник пересекался силовыми линиями магнитного поля.    При этом неважно, что именно движется, а что неподвижно.

    Рассмотренный вариант явления используется в генераторах, вырабатывающих для нас электрическую энергию. Так, в гидроэлектростанциях, поток падающей воды вращает генератор электроэнергии, заставляя магнитное поле перемещаться относительно проводника.

        

Второй вариант явления электромагнитной индукции: проводник неподвижен, но находится в переменном магнитном поле (рис. 34). На рисунке показано, что проводник находится в переменном магнитном поле.                      

Рис. 34. Неподвижный проводник находится в переменном магнитном поле

 

Переменным называется магнитное поле, величина которого изменяется во времени.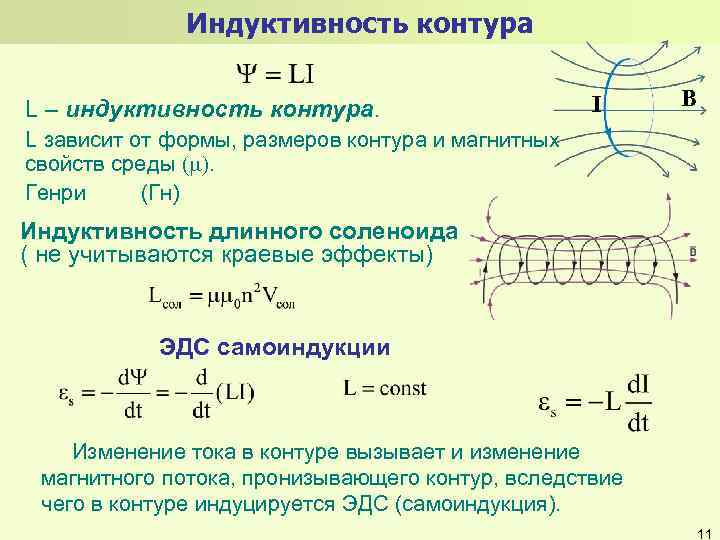 Его сила то возрастает, то убывает. Это означает, что магнитное поле расширяется и сужается. При этом силовые линии пересекают проводник и наводят в нем ЭДС.

Величину ЭДС найдём по формуле:

 

 

Буквой ∆ (дельта) в формулах обозначают изменение (увеличение или уменьшение) какой-то величины.

В числителе формулы видим изменение магнитного потока Ф. В знаменателе – изменение времени. Например, если магнитный поток Ф изменился на 100 Вб за время t, длительностью 5 секунд, то в проводнике возникает ЭДС 20 В:

Этот вариант явления электромагнитной индукции используется в трансформаторах. Проводники их обмоток неподвижны. В обмотках трансформаторов наводится ЭДС, т.к. на обмотки воздействует переменное магнитное поле, существующее в сердечнике трансформатора.

 

Правило Ленца

 

Правило Ленца (закон Ленца) гласит: ток, вызванный индуктированной ЭДС, порождает эффекты, препятствующие появлению этой ЭДС.

Действие правила Ленца проявляется по разному в разных вариантах явления электромагнитной индукции, но действует оно всегда.

Рассмотрим, как проявляется действие правила Ленца в первом из рассмотренных вариантов явления электромагнитной индукции.

Прежде всего, отметим, что если ЭДС наводится, но ток в цепи не протекает, то правило Ленца не действует (рис. 32).

Если же цепь замкнута и по ней протекает ток, вызванный индуктированной ЭДС, правило Ленца действует. Рис.35 отличается от рис. 32 тем, что к концам проводника, в котором наводится ЭДС, подключён резистор R. По проводу, в котором наводится ЭДС, через резистор R и по проводам протекает ток I.

Рис. 35. В следствии проявления правила Ленца возникает сила, препятствующая появлению ЭДС в проводнике

 

    Известно, что на проводник с током, помещённый в магнитное поле, действует сила F. Определив направление этой силы по правилу левой руки, видим, что эта сила препятствует движению проводника, тормозит его. Тем самым действие этой силы препятствует наведению ЭДС в проводнике.

 

Явление самоиндукции

    Явление самоиндукции состоит в том, проводник, собственным магнитным полем наводит в себе ЭДС. Если по проводнику протекает ток, меняющийся по величине (переменный ток), вокруг проводника возникает магнитное поле. Это магнитное поле тоже будет меняться по величине (будет переменным). Переменное магнитное поле проводника, как бы «окутывает» его.

Рис. 36. Явление электромагнитной индукции. Проводник наводит сам в себе ЭДС

    Известно, что в проводнике, находящимся в переменном магнитном поле, наводится ЭДС самоиндукции. В данном случае проводник сам создаёт переменное магнитное поле, которое в нём самом наводит ЭДС.

Величина ЭДС самоиндукции определяется по формуле:

, где:

∆I — изменение силы тока в проводнике,

∆t — изменение времени

L — индуктивность проводника.

    Таким образом, величина ЭДС самоиндукции зависит от скорости изменения тока в цепи и коэффициента, называемого индуктивностью проводника. Измеряется индуктивность проводника в Генри [Гн].

    Явление самоиндукции может проявляться также и в цепях постоянного тока. В них оно проявляется в моменты включения и выключения цепи. При включении цепи ток нарастает от нуля до номинального значения, а при выключении цепи – спадает от номинального значения до нуля. Изменение величины тока вызывает изменение магнитного поля вокруг проводника. В эти короткие периоды времени и проявляется явление самоиндукции. В установившемся режиме, когда ток не меняется по величине, явление самоиндукции не проявляется.

    Индуктивность характеризует свойства проводника в отношении величины возникающей в нём ЭДС самоиндукции.

    У прямолинейных проводников индуктивность мала. Следовательно, возникающая в них ЭДС самоиндукции незначительна. Обычно ею просто можно пренебречь.

Если же проводник выполнен в виде катушки, имеющей большое число витков, то в нём возникает значительная по величине ЭДС самоиндукции, пренебрегать которой нельзя. Особенно велика ЭДС самоиндукции в катушках, снабженных ферромагнитным сердечником.

Влияние явления самоиндукции на работу цепей переменного тока будет рассмотрено позднее.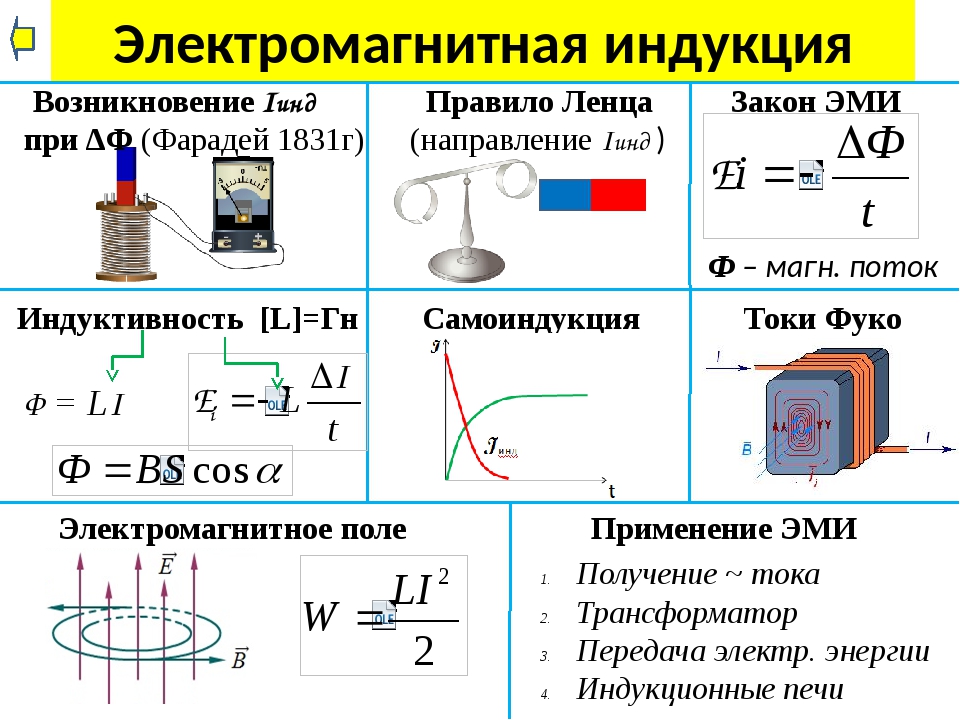

Явление взаимоиндукции

 

Взаимоиндукция – это частный случай общего явления электромагнитной индукции. Состоит в том, что один проводник своим магнитным полем наводит ЭДС в соседнем проводнике.

На рис. 37 показаны два проводника, расположенные рядом. По первому проводнику проходит переменный ток. Вокруг него возникает переменное магнитное поле. Во втором проводнике, находящимся в переменном магнитном поле первого проводника, наводится ЭДС взаимоиндукции.

Рис. 37. Явление взаимоиндукции. Силовые линии магнитного поля, созданного проводником 1, пронизывают проводник 2

 

Величина ЭДС взаимоиндукции в проводнике определяется по формуле:

, где:

М — коэффициент взаимоиндукции; измеряется в Генри.

    Видно, что эта формула очень похожа на предыдущую. Разница только в наименовании коэффициента. Взаимная индуктивность М характеризует систему из двух проводников в отношении величины ЭДС взаимоиндукции.

    Величина ЭДС взаимоиндукции зависит от скорости изменения тока в соседнем проводнике и от взаимной индуктивности M (Гн).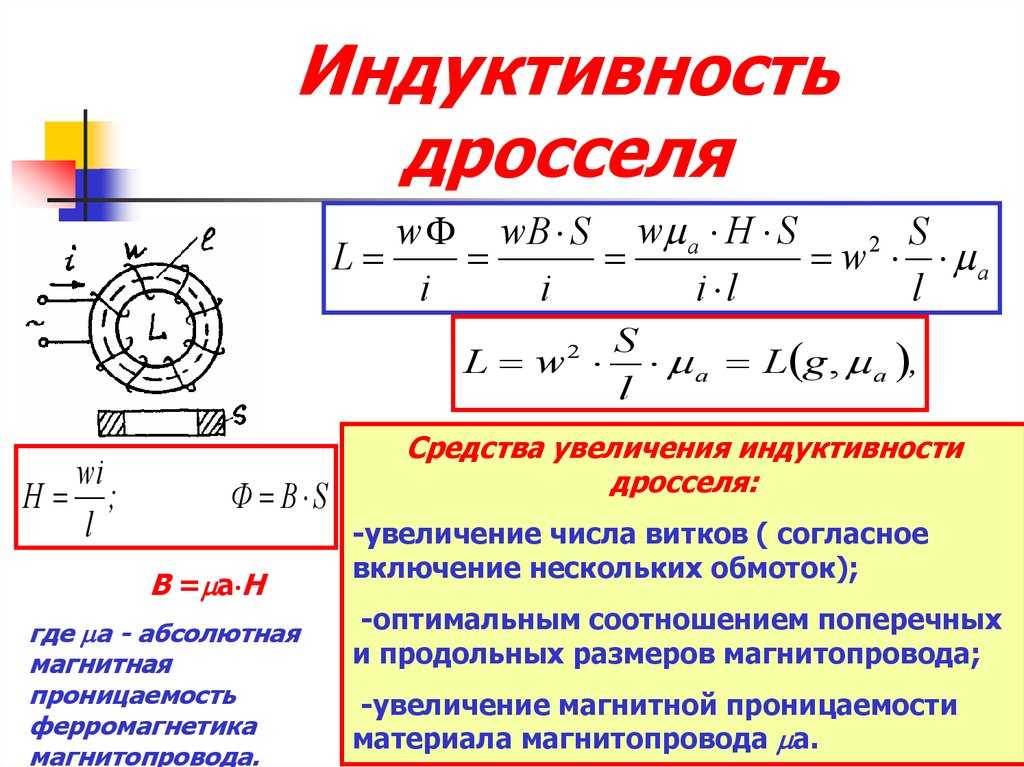

Взаимная индуктивность М зависит от формы и размеров проводников. Для прямолинейных проводников взаимная индуктивность незначительна и явление взаимоиндукции проявляется слабо.

Взаимная индуктивность будет больше, если проводники выполнены в виде катушек. Еще лучше, если они расположены на общем ферромагнитном сердечнике (рис. 38).

Как и в случае явления самоиндукции, взаимоиндукция может проявляться в цепях постоянного тока в моменты включения и ли выключения цепи.

Рис. 38. Проявление явления взаимоиндукции

    На рис. 38 показаны две катушки, размещённые на общем ферромагнитном сердечнике. На одну из обмоток подаётся постоянное напряжение от аккумулятора. Аккумулятор обеспечивает постоянное напряжение на своих зажимах и, соответственно, постоянный ток в цепи правой катушки (если замкнут выключатель). Ко второй катушки источник тока на подключён, но подключён  гальванометр (измерительный прибор). Гальванометр отмечает появление ЭДС на зажимах левой катушки а момент включения и в момент выключения тока в цепи.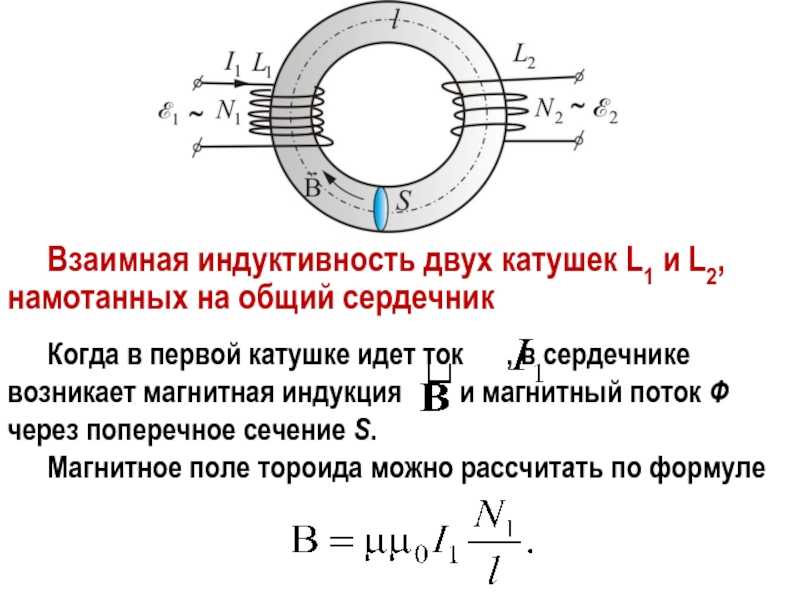 Это объясняется тем, что в момент замыкания или размыкания контактов выключателя меняется сила тока в цепи и, соответственно, магнитное поле, созданное правой катушкой. При этом во второй катушке наводится ЭДС взаимоиндукции, что и отмечает гальванометр – его стрелка отклоняется.

 

Вихревые токи

Многие электротехнические устройства, например трансформатор или электродвигатель, снабжены железным сердечником. В сердечнике, при работе этих устройств, существует переменное магнитное поле.

В соответствии с явлением электромагнитной индукции (второй вариант) в проводнике, помещенном в магнитное поле, наводится ЭДС. В данном случае проводником является стальной сердечник трансформатора или электродвигателя.

По сердечнику потекут токи. Они замыкаются по кругу и поэтому называются вихревыми токами.

Рис. 39. В сердечнике, который пронизывает переменный магнитный поток,

возникают вихревые токи. Они протекают во всём объёме сердечника, а не только в верхней части, как показано на рисунке

 

На образование вихревых токов тратится энергия, хотя для работы трансформатора вихревые токи не нужны. Следовательно, часть энергии, вместо совершения полезной работы трансформатором, затрачена на образование ненужных и даже вредных вихревых токов. Эта энергия называется потерями на вихревые токи и её желательно свести к минимуму.

Кроме того, в соответствии с законом Ленца, вихревые токи порождают собственное магнитное поле, которое направлено встречно магнитному полю, порождающему их. А это недопустимо, т.к. порождающее их поле необходимо для работы устройства и ослаблять его нельзя.

Для ослабления вихревых токов сердечник трансформаторов и других устройств набирается из тонких стальных пластин. Толщина пластин 0,2 – 0,5 мм. Пластины изолируют друг от друга путем окрашивания. Изоляция пластин друг от друга не позволяет вихревым токам протекать по всей площади поперечного сечения сердечника, как это показано на рис. 39. При этом возникновение вихревых токов и их вредное влияние будут ослаблены.

Конец первой части

 

 

Список рекомендованной литературы:

1. Электротехника и основы электроники: Иванов И. И., Соловьев Г. И., Фролов В. Я. Учебник. 7-е изд., перераб. и доп. — СПб.: Издательство «Лань», 2012. — 736 с

2. Электротехника (4-е изд.) Год: 2004 Автор: Шихин А.Я. (Под ред.) Издательство: М.: Высшая школа

 

ОГЛАВЛЕНИЕ

электромагнитная индукция — Что означает индуктивность?

Индуктивность — это свойство замкнутой цепи (цепь означает петлю проводника) сопротивляться изменениям тока, особенно из-за магнитного потока через петлю. Чтобы понять индуктивность, мы сначала рассмотрим , когда применяется индуктивность . Можно начать с уравнений Максвелла, и это действительно самый практичный способ, учитывая, что учащийся с ними знаком. Предполагая, что это не так, для общности обучения мы сосредоточимся только на интересующих количествах и на том, как они соотносятся друг с другом.

История вопроса

Центральными величинами в электромагнетизме являются электрическое поле (представление электрической силы) и магнитное поле (вектор, который перпендикулярен «плоскости действия» магнитной силы). Глядя на некоторую двумерную область в пространстве, где электрическое поле $\mathbf{E}$ и магнитное поле $\mathbf{B}$ существуют и являются постоянными, мы можем вычислить потока полей в (или » через») поверхность, взяв только компонент $\mathbf{E}$ или $\mathbf{B}$ (или любого векторного поля), который является нормальным к поверхности, на поверхности, и умножив это значение поля на площадь поверхности. Например, электрический поток через прямоугольник $2\text{m}\times 2$m в квадрате в пространстве, когда электрическое поле имеет постоянное значение прямо через поверхность $3$ N/C (ньютонов на кулон), составляет $3 *(2*2) = 12 = \Phi_E$, где $\Phi_E$ — поток электрического поля на поверхности. Чтобы обобщить эту концепцию потока за пределы прямоугольных поверхностей и постоянных полей, мы на самом деле берем поверхностный интеграл векторного поля по поверхности.

На практике поверхность — это область в середине контура цепи. Мы находим, что по закону электромагнитной индукции Фарадея, если у нас есть замкнутая проволочная петля и переменное магнитное поле $\mathbf{B}$, то в проволочной петле возникает ток, пропорциональный магнитному потоку (произведение магнитного поля на площадь петли). Обратите внимание, что мы говорим не о катушках или резисторах, а о всей площади цепи .

Индуктивность

Индуктивность легко определить. По закону Фарадея для контура с магнитным потоком $\Phi_M$ существует индуцированное напряжение $V$, $$V(t) = -\frac{\partial \Phi_M}{\partial t}$$ Теперь стоит отметить, что замкнутый контур провода, подверженный изменению магнитного потока, имеет определяемый потенциал (напряжение) , а не , точно так же, как цепь с, например, батарея. Контур замкнут, но ток течет — электрическое поле есть, но напряжение не определено. Вы не можете выбрать две точки и рассчитать теоретическое падение напряжения между ними.

Тем не менее, из-за тока присутствует падение напряжения, напр. резисторов, и это напряжение является наведенным напряжением в цепи.

Теперь рассмотрим схему, которая подчиняется соотношению $$V(t) = L \frac{dI}{dt}$$ Где $V(t)$ — индуцированное напряжение, $I$ — ток, протекающий в контуре, а $L$ — константа пропорциональности. Мы видим, что: $$L\frac{dI}{dt} = \frac{d \Phi_M}{d t}$$ Где частная производная была заменена производной с одной переменной для простоты, а правая часть положительна, потому что рассматриваемая ЭДС является обратной ЭДС. Следовательно, константа пропорциональности $L$ равна: $ $ L = \ frac {\ frac {d \ Phi_M} {d t}} {\ frac {dI} {dt}} = \ frac {\ Phi_M} {I} $ $ То есть отношение магнитного потока к току в контуре. Эта константа пропорциональности существует для замкнутых цепей и называется индуктивность цепи.

Важно понимать, что для того, чтобы цепь имела индуктивность, она должна быть замкнутой (течет ток). Не менее важно понимать, что компонентов в цепи не имеют индуктивности, но они вносят вклад в индуктивность цепи, и этот вклад называется индуктивностью этого компонента.

Ток в цепи создает магнитное поле вокруг проводников. Магнитное поле, в свою очередь, отвечает за магнитный поток, определяющий индуктивность цепи. Другим влияющим фактором является размер петли: если петлю сделать больше, увеличивается поток и увеличивается индуктивность цепи. Точно так же, если рядом находится другая цепь (не связанная электрически), ее магнитное поле вносит вклад в магнитный поток в цепи, и это увеличивает индуктивность (взаимную индуктивность).

Для цепи с током $I$, если ток останется прежним, магнитное поле вокруг цепи также останется практически постоянным по амплитуде. Однако перемещение проводов, использование более коротких или длинных проводов, наматывание проводов друг на друга, чтобы их магнитные поля складывались, — все это влияет на общий магнитный поток через цепь и, следовательно, на индуктивность. Следовательно, индуктор представляет собой компонент, геометрия которого при протекании через него определенного количества тока имеет известную величину магнитного потока через его площадь, внося известную величину индуктивности.

Тонкости и замечания

Свойством индуктивности является тенденция замкнутой цепи воздействовать на себя током, протекающим внутри нее. Это следует очень простым линейным соотношениям, но включает производные по времени, которые придают индуктивности качество, препятствующее току. Независимо от того, насколько запутанной является геометрия цепи, все, что имеет значение для индуктивности, это (а) площадь, окруженная цепью, (б) ток, протекающий по цепи, и (в) близость токоведущих проводов друг к другу. . Расчет индуктивности не тривиален, но наблюдение за причинами индуктивности может помочь в разработке простых катушек индуктивности и уменьшении эффектов индукции.

Причина возникновения индуктивности заключается в том, что индуцированное напряжение в цепи пропорционально изменениям магнитного потока, а изменения магнитного потока зависят от тока, протекающего через цепь. Логика не круговая, как может показаться, а прямое следствие закона Фарадея. В своей общей интегральной форме закон Фарадея гласит, что: $$\oint_C \mathbf{E} \cdot d\mathbf{l} = -\frac{\partial}{\partial t} \int_S \mathbf{B} \cdot d\mathbf{s}$$ Где $C$ — путь контура, а $S$ — поверхность с границей $C$. Определив магнитный поток $\Phi_M$ как: $$\Phi_M = \int_S \mathbf{B} \cdot d\mathbf{s}$$ А электрический потенциал (или напряжение ) вокруг контура $C$ как: $$V = \int_C \mathbf{E} \cdot d\mathbf{l}$$ Закон Фарадея сводится к: $$V(t) = -\frac{\partial \Phi_M}{\partial t}$$ Это то же самое уравнение, что и раньше, предполагая, что $V(t)$ представляет собой потенциал замкнутой цепи (ноль в отсутствие изменяющихся магнитных полей).

Единственная связь, которую мы желаем для схемы, имеет форму: $$V(t) = L \frac{dI}{dt}$$ То есть линейная зависимость между изменением тока и наведенного напряжения. Как мы уже показали, именно так мы приходим к величине индуктивности. Таким образом, индуктивность представляет собой константу пропорциональности между напряжением и изменениями тока и описывает тенденцию изменений тока в цепи изменять магнитный поток через эту цепь. Это, посредством своего рода процесса обратной связи, ограничивает скорость изменения тока. 93$). Следовательно, вклад магнитного поля конкретного отрезка провода наиболее силен сразу за поверхностью проводника и очень быстро падает. Это означает, что большая часть вклада в индуктивность всего контура происходит в непосредственной близости от поверхности проводника.

Используя подобные линии, мы можем написать выражение для частичной индуктивности компонента без обратной связи (например, прямого провода или катушки), даже если мы не можем строго определить индуктивность без замкнутой петли. Как правило, когда эффекты магнитного поля ограничены небольшой областью в большей цепи, расчет индуктивности этой области (даже если это не замкнутый контур) дает очень хорошее приближение и дает представление о влиянии этой области. на общую индуктивность контура.

Закон Био-Савара также помогает продемонстрировать, почему форма и размер проводника являются определяющими факторами при расчете индуктивности. При анализе конфигурации проводника мы часто рассматриваем линейный ток (иногда называемый нитью накала), центр которого находится внутри провода, как источник магнитного поля. Затем, хотя закон Био-Савара, кажется, подразумевает бесконечно сильное магнитное поле по мере приближения к центру, мы фактически интегрируем поле только снаружи проводника. Разница между проводами калибра 30 и 22 внезапно становится важной, потому что чем меньше провод, тем ближе к бесконечной напряженности поля вы можете получить. На самом деле токи, конечно, не нити, а ток плотностью как источник магнитного поля, с некоторым распределением внутри проводника. Поля внутри проводника еще больше усложняют ситуацию.

На самом деле, на низких частотах (в частности, когда скин-эффектом можно пренебречь) мы должны учитывать не только магнитное поле вокруг провода с током для расчета индуктивности, но и магнитное поле внутри этого провода. В отличие от электрического поля, которое обязательно должно быть равно нулю в идеальном проводнике, магнитное поле может существовать внутри проводника и (как можно было ожидать из вышеизложенного) может иметь значительное влияние. Но взаимодействие плотности тока и магнитного поля внутри проводника не так просто связать с индуктивностью цепи цикл . По этой причине эти два понятия часто делятся на внутреннюю и внешнюю индуктивность для индуктивности внутри проводника и индуктивности снаружи проводника соответственно.

Наконец, расчеты индуктивности часто усложняются при передаче переменного тока из-за скин-эффекта и эффекта близости, оба из которых могут значительно изменить результат. Эти эффекты часто обсуждаются при проектировании ВЧ и СВЧ, а также при проектировании систем распределения электроэнергии и энергетики. Хороший справочник (например, Grover’s Inductance Calculations ) должны помочь вам с различными исправлениями и вторичными эффектами, если вы хотите пойти дальше.

Вычисление индуктивности прямого провода

Время от времени возникает вопрос, можно ли вычислить индуктивность одиночного прямого провода. Этот, казалось бы, простой вопрос на самом деле не имеет ответа, и дает нам возможность поговорить об очень интересном моменте при решении уравнений Максвелла. Любой, кто работает в области вычислительной электромагнетизма, должен иметь представление об этой ключевой концепции, поскольку она поможет вам правильно настроить и интерпретировать модели, связанные с магнитными полями.

Какова индуктивность одиночного прямого провода?

Прежде чем мы перейдем к этой концепции, давайте еще раз посмотрим на вопрос: какова индуктивность одиночного прямого провода? Для начала рассмотрим определение индуктивности на основе энергии: , плотность магнитной энергии пропорциональна B ² . Магнитное поле B существует внутри и снаружи провода. Внутри проволоки она увеличивается линейно наружу от осевой линии, а вне проволоки падает как 1/ r , где r — радиус. Итак, для расчета магнитного поля и распределения магнитной энергии мы строим модель, основанную на уравнениях Максвелла, в данном случае на законе Ампера. К одному концу провода прикладывается источник тока, а другой конец заземлен. Тангенциальная плотность магнитного потока ограничена нулем на внешних границах модели.

Эту модель можно построить в COMSOL Multiphysics, используя физический интерфейс Магнитные и электрические поля модуля AC/DC, который будет определять электрические поля и токи в проводах, а также магнитные поля в проводниках. провода и окружающий воздух. Граничное условие Terminal возбудит структуру и автоматически вычислит индуктивность, используя приведенную выше формулу. Граничное условие Ground на другом конце провода обеспечивает сток тока, а Граничное условие 0003 Magnetic Insulation устанавливает плотность тангенциального магнитного потока равной нулю.

Теперь поля простираются бесконечно вокруг провода, но плотность магнитной энергии падает как 1/ r ² , поэтому мы можем подумать, что достаточно изучить увеличивающиеся радиусы нашей моделируемой области, и что индуктивность сойдутся. Однако если мы попробуем это сделать, индуктивность как функция радиуса будет выглядеть так:

По мере увеличения радиуса увеличивается и индуктивность. Как бы мы ни делали область моделирования, индуктивность для этой модели прямого провода не сходится!

Не только решение для индуктивности

Все выглядит довольно мрачно, если мы даже не можем правильно вычислить этот простой случай, верно? Ну, на самом деле, мы не просто решаем индуктивность провода в этой модели. Вы всегда решаете для индуктивности системы, и это должно включать в себя текущий обратный путь. Основные уравнения Максвелла сформулированы в предположении, что тока (электронов) не могут быть ни созданы, ни уничтожены . На самом деле Магнитная изоляция граничные условия обеспечивают этот обратный путь тока. Мы можем увидеть это, построив ток в объемах, а также поверхностные токи:

Красные стрелки на рисунке выше показывают, что ток течет по проводу, а также течет по граничным условиям Магнитная изоляция как поверхностное течение. Граничное условие Magnetic Insulation можно рассматривать как представление материала с бесконечной проводимостью, по которому ток может течь беспрепятственно. Текущий путь на приведенном выше рисунке равен 9.0003 соленоидный , что означает, что ток течет по замкнутому пути. Существует токопроводящий путь не только от клеммы до наземных граничных условий, по проводу, но и от наземного граничного условия обратно к клеммам, по границам.

Соленоидальный тракт

Эта концепция соленоидального тракта для тока является ключевым моментом здесь. Всякий раз, когда вы настраиваете любую модель магнитных полей, вы должны убедиться, что ток может протекать по замкнутому контуру. У вас нет выбора: этого требуют уравнения Максвелла. Вы также должны знать, что этот текущий путь возврата повлияет на результаты. В приведенной выше модели мы не только вычисляем индуктивность из-за тока, протекающего по проводу, мы также рассматриваем влияние тока, протекающего обратно по граничным условиям магнитной изоляции.

При настройке любой модели магнитных полей вы должны смоделировать полный соленоидальный путь тока, а индуктивность, которую вы вычисляете на основе такой модели, относится ко всей токовой петле.

Так вот почему вы не можете вычислить индуктивность одного прямого провода!

Конечно, пока система, которую вы анализируете, является соленоидальной, с током, протекающим по контуру, вы можете правильно вычислить индуктивность.

Дополнительная литература

Чтобы увидеть примеры, в которых вычисляется взаимная индуктивность между круглыми проволочными витками и сравниваются аналитические решения, см.:

• Взаимная индуктивность и наведенные токи между одновитковыми катушками
• Взаимная индуктивность и наведенные токи в группе катушек
• Взаимная индуктивность и индуктивные токи в многовитковой катушке

9.

2: Индуктивность и катушки индуктивности — технические библиотеки LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

25148

• Джеймс М. Фиоре
• Муниципальный колледж Mohawk Valley

Для начала нам нужно рассмотреть взаимосвязь между электрическим током и магнитными полями в проводнике. Когда ток проходит через проводник, например провод, вокруг проводника создается магнитное поле, пропорциональное силе тока. Это показано на рисунке 9..2.1 .

Рисунок 9.2.1 : Магнитное поле вокруг проводника.

Магнитное поле можно представить в виде набора концентрических колец вокруг проводника, хотя для ясности на рисунке показаны только отдельные петли. Количество магнитных линий в данной области известно как магнитный поток и обозначается символом \(\Phi\) (греческая буква phi). Единицей магнитного потока является вебер, Вб, названный в честь Вильгельма Вебера, немецкого физика XIX века.

\[\text{Магнитный поток } \equiv \text{ количество магнитных линий, заключенных в данной области.} \label{9.1} \]

Обратите внимание, что магнитное поле проходит по всей длине проводника. Направление силовых линий соответствует правилу правой руки: если вы берете провод правой рукой так, что ваш большой палец указывает в направлении обычного тока, то ваши пальцы скручиваются в направлении магнитного поля. Это правило показано на рис. 9.2.2. .

Рисунок 9.2.2 : Правило правой руки. Источник изображения (измененный)

Если мы сформируем из проводника петлю, силовые линии соберутся в центр петли. Это показано на рисунке 9..2.3 . На этой диаграмме видно, что линии эффектно собираются в центре, уходя вглубь страницы.

Рисунок 9.2.3 : Магнитное поле вокруг петли.

Эффект улучшения можно усилить, добавив больше циклов в тандеме. Это называется соленоидом и показано на рис. 9.2.4. . Это самая основная форма индуктора.

Рисунок 9.2.4 : Соленоид.

Концентрирующее действие магнитного поля показано на рисунке 9..2.5 . На этом рисунке катушка показана сбоку, как сечение отдельных петель. Точки внутри проводников указывают на то, что ток течет к вам, из страницы; в то время как кресты указывают на то, что ток течет на страницу. Линии потока выходят справа, зацикливаются и снова входят слева. Из-за ограниченного места вся петля для каждой линии не рисуется, и важно помнить, что линии магнитного потока не заканчиваются, а всегда создают петлю. Кроме того, хотя здесь оно показано в виде плоскости, это поле трехмерно, с линиями, петляющими как вглубь страницы, так и перед ней.

Рисунок 9.2.5 : Магнитное поле в соленоиде. Источник изображения

Так можно создавать электромагниты ¹ . Северный полюс — это выходной конец (правая сторона) рисунка 9.2.5. в то время как южный полюс является входящим концом (левая сторона).

Если ток изменится, произойдет соответствующее изменение магнитного поля. Кроме того, это изменение поля индуцирует ток в проводнике, который создает магнитное поле, противодействующее первоначальному изменению поля. Это известно как закон Ленца. В качестве альтернативы можно сказать, что индуцированный ток, вызванный изменяющимся магнитным полем, будет противодействовать изменению исходного тока, вызвавшему это изменение исходного магнитного поля.

Здесь мы можем предложить правильное определение вебера:

\[1 \text{ weber } \equiv \text{ магнитный поток, который, действуя на одну петлю проводника, создает потенциал 1 вольт, если поток уменьшается до нуля с равномерной скоростью в течение 1 секунды.} \метка{9.2} \]

В магнитных цепях нас также интересует плотность магнитного потока, которая представляет собой магнитный поток на единицу площади. Символ плотности потока \(B\) в единицах тесла (T), названный в честь Николы Теслы, сербско-хорватско-американского инженера и изобретателя. Один тесла определяется как один вебер на квадратный метр. 92 \метка{9.3} \]

Для справки: плотность магнитного потока Земли вблизи экватора составляет примерно 31 \(\мк\)Тл, а значение зазора звуковой катушки в громкоговорителе составляет примерно от 1 до 2 Тл, а медицинские МРТ-сканеры еще немного выше.

Наконец, мы подошли к определению индуктивности и ее единицы, генри:

\[\text{Индуктивность — это мера тенденции проводника сопротивляться изменению тока, протекающего по нему.} \label{9.4} \] 92 \метка{9.6} \]

Где

\(Вт\) — энергия в джоулях,

\(L\) — индуктивность в генри,

\(I\) — сила тока в амперах.

Рисунок 9.2.6 : Простые размеры индуктора с воздушным сердечником.

Катушка индуктивности в простейшей форме состоит из ряда проволочных петель. Они могут быть намотаны на железный сердечник, хотя также может использоваться сердечник из цветного металла.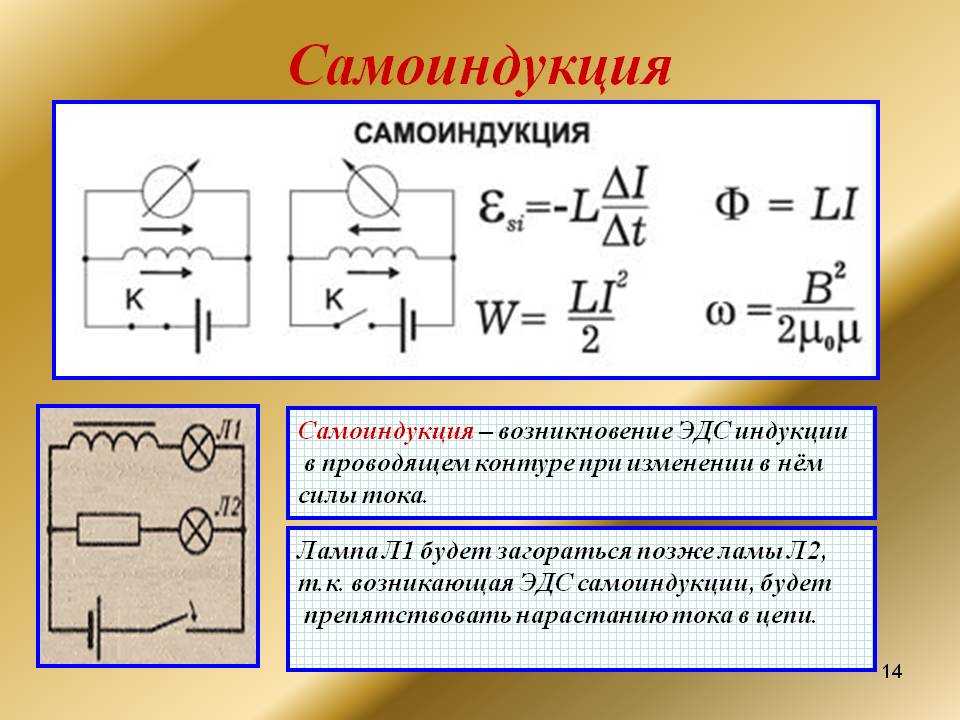 Для простого однослойного индуктора, такого как изображенный на рис. 9.2.6. , индуктивность описывается следующей формулой: 92}{l} \метка{9.7} \]

Где

\(L\) — индуктивность в генри,

\(\mu\) — проницаемость материала заполнителя,

\(A\) — площадь поперечного сечения катушки,

\(N\) — количество витков или витков,

\(l\) — длина катушки.

Катушки индуктивности

также могут быть намотаны с использованием нескольких слоев или вокруг тороидального сердечника, и в этих конструкциях используются альтернативные формулы.

Типы индукторов и упаковка

Уравнение \ref{9.7} показывает, что для достижения высокой индуктивности нам нужен сердечник с высокой проницаемостью, причем проницаемость является мерой того, насколько легко установить магнитный поток в указанном материале. Вещества, такие как железо или феррит, обладают гораздо большей проницаемостью, чем воздух, и обычно используются для сердечников. У них есть недостаток в том, что они насыщаются раньше, чем воздушное ядро, и это может привести к искажению.

Рисунок 9.2.7 : Звукосниматель для электробас-гитары.

Другой подход состоит в том, чтобы упаковать как можно больше витков в пределах заданной длины. Один из способов сделать это — минимизировать толщину изоляции вокруг провода ² . Этого можно добиться, используя тонкое эмалевое покрытие вместо обычной пластиковой изоляции. Второй метод заключается в использовании очень тонкой проволоки. Это приводит к двум проблемам, а именно к нежелательному увеличению эквивалентного последовательного сопротивления (известного в просторечии как сопротивление катушки или \(R_{катушка}\)) и ограниченной пропускной способности по току. Все эти эффекты должны быть сбалансированы для достижения наилучшей производительности для данного приложения.

Стоимость промышленных катушек индуктивности варьируется от долей наногенри для небольших «чиповых» катушек индуктивности для поверхностного монтажа до нескольких генри. Некоторые устройства имеют большую внутреннюю индуктивность, даже если они специально не используются в качестве катушек индуктивности. Одним из распространенных примеров является трансформатор. Другим примером является звукосниматель для электрогитары или баса, такой как показанный на рис. 9.2.7. со снятой крышкой. Такие устройства могут состоять из нескольких тысяч витков очень тонкой проволоки (обычно AWG 41–44) и достигать индуктивности более одного генри.

Различные катушки индуктивности показаны на рис. 9.2.9. , все из которых относятся к типу сквозных отверстий (индукторы для поверхностного монтажа не сильно отличаются от своих родственников резисторов и конденсаторов для поверхностного монтажа).

Рисунок 9.2.9 : Коллекция катушек индуктивности.

Два блока слева представляют собой литые катушки индуктивности и имеют стандартную цветовую маркировку, аналогичную той, что используется для резисторов и конденсаторов. Блок вверху (желтый) представляет собой сильноточный индуктор с низким \(R_{катушка}\). В трех катушках индуктивности в центре используются очевидные ферритовые сердечники, две из которых намотаны на прямые сердечники, а третья намотана на тороидальный сердечник. Блок справа использует материал с высокой проницаемостью в самом верху и обернут в пластиковую оболочку для защиты. Также возможны переменные катушки индуктивности, которые можно изготовить с использованием ферритового сердечника, который можно перемещать внутри катушек, эффективно изменяя проницаемость сердечника (частично ферритовый, частично воздушный).

Рисунок 9.2.10 : Схематические обозначения индуктора (сверху вниз): стандартный, регулируемый, железный/ферритовый сердечник.

Схематические обозначения катушек индуктивности показаны на рис. 9.2.10. . Стандартный символ находится вверху. Символ переменной катушки индуктивности находится посередине и представляет собой устройство с двумя выводами, чем-то напоминающее символ реостата. Внизу находится символ катушки индуктивности с железным, ферритовым или аналогичным сердечником с высокой магнитной проницаемостью. В общем, как и резисторы, одиночные катушки индуктивности не поляризованы и не могут быть вставлены в цепь задом наперед. Однако существуют специальные приложения, в которых несколько катушек могут быть намотаны на общий сердечник, и для них может иметь значение полярность их соединения.

Лист данных индуктора

Часть листа данных индуктора показана на рис. 9.2.12. . На этой странице перечислены доступные размеры этой конкретной модели с соответствующими количествами. Мы видим, что эта модель доступна со значениями индуктивности в диапазоне от 1 \(\ мкГн) до 100 мГн. Допустимое отклонение меньших значений составляет \(\pm\)10%, а значений при 33 \(\mu\)H и выше составляет \(\pm\)5%. \(Q\) — это коэффициент качества, который особенно важен в цепях переменного тока (чем выше, тем лучше), наряду с соответствующей частотой \(f_Q\). Продолжая движение, мы находим \(I_R\). Это максимальный номинальный ток. Мы обнаружили, что для меньших значений они могут выдерживать более 2 ампер, в то время как более крупные устройства могут выдерживать только десятки миллиампер.

Рисунок 9.2. 12 : Лист данных индуктора. Предоставлено TDK

Наконец, мы приходим к \(R_{max}\). Это также известно как \(R_{катушка}\). Он представляет собой эквивалентное последовательное сопротивление катушки индуктивности. В общем, чем меньше, тем лучше. Для этой модели он колеблется от долей ома до нескольких сотен ом. Эта тенденция типична для индукторов; При прочих равных, чем больше индуктивность, тем больше значение соответствующего последовательного сопротивления. Во многих схемах нельзя игнорировать значение \(R_{coil}\). 92\) увеличивается в четыре раза, а длина уменьшается вдвое. Следовательно, катушки индуктивности добавляют значения так же, как последовательно соединенные резисторы. В более широком смысле, параллельные катушки индуктивности ведут себя как параллельные резисторы. Эквивалент параллельных катушек индуктивности можно найти, используя либо правило произведения суммы, либо взяв обратную величину суммы их обратных величин.

Пример 9.2.1

Найдите эквивалентную индуктивность сети, показанной на рис. 9.2.11. .

Рисунок 9.2.11 : Схема для примера 9.2.1 .

Катушки индуктивности 6 мГн и 12 мГн включены параллельно. Эквивалентное значение пары:

\[L_{параллельно} = \frac{L_2 L_3}{L_2+L_3} \номер\]

\[L_{параллельный} = \frac{6 mh22 mH}{6 mH+12 mH} \nonumber \]

\[L_{параллельно} = 4 мГн \номер\]

Эта комбинация включена последовательно с катушкой индуктивности 5 мГн. Таким образом, общая эквивалентная индуктивность составляет 4 мГн + 5 мГн или 9 мГн.

Зависимость тока от напряжения

Основное отношение тока к напряжению катушки индуктивности является зеркальным отражением зависимости конденсатора:

\[\mathcal{v} = L \frac{di}{dt} \label{9.8} \]

утверждает, что напряжение на катушке индуктивности зависит от того, насколько быстро изменяется ток. Если ток не меняется (т. Е. В установившемся режиме), то напряжение на катушке индуктивности равно нулю. В этом случае индуктор ведет себя как короткое замыкание или, точнее, как его значение \(R_{катушка}\). Напротив, при быстром начальном изменении тока напряжение катушки индуктивности может быть большим, и поэтому катушка индуктивности ведет себя как разомкнутая.

Если мы изменим уравнение \ref{9.8} и найдем скорость изменения тока, мы найдем, что:

\[\frac{di}{dt} = \frac{\mathcal{v}}{L} \label{9.9} \]

Таким образом, если индуктор питается от источника постоянного напряжения, ток будет возрастать с постоянной скоростью, равной \(\mathcal{v}/L\). Например, рассматривая схему на рис. 9.2.11. , мы видим источник напряжения, питающий один индуктор. Если бы мы построили график зависимости тока катушки индуктивности от времени, мы бы увидели график, подобный рисунку 9..2.12 .

Рисунок 9.2.11 : Индуктор с источником напряжения.

Рисунок 9.2.12 : Ток индуктора в зависимости от времени.

С течением времени ток через индуктор увеличивается, протекая сверху вниз. С теоретически идеальными катушкой индуктивности и источником это будет продолжаться до тех пор, пока цепь находится под напряжением. В действительности эта линия либо начала бы отклоняться горизонтально, когда источник достиг своих пределов, либо катушка индуктивности вышла бы из строя, как только был бы достигнут максимальный допустимый ток или мощность. Наклон этой линии определяется размером приложенного источника напряжения и индуктивностью.

Пример 9.2.2

Определить скорость изменения тока через дроссель в цепи рис. 9.2.13 . Также определите ток катушки индуктивности через 10 мкс после включения питания.

Рисунок 9.2.13 : Схема для примера 9.2.2 .

Из уравнения \ref{9.9} скорость изменения тока составляет:

\[\frac{di}{dt} = \frac{\mathcal{v}}{L} \nonumber \]

\[\frac{di}{dt} = \frac{10V}{50 мГн} \nonumber \]

\[\frac{di}{dt} = 200 А \text{ в секунду} \nonumber \]

Другими словами, каждую секунду ток увеличивается еще на 200 ампер. Таким образом, всего через 10 микросекунд он возрастет до 200 А/с, умноженных на 10 \(\мк\)с, или 2 мА.

Уравнение \ref{9.8} является ключом к пониманию поведения катушек индуктивности. Как отмечалось ранее, если катушка индуктивности управляется источником фиксированного напряжения и игнорирует \(R_{катушка}\), ток через нее возрастает с постоянной скоростью \(\mathcal{v}/L\). Это изменение тока через индуктор не безгранично. Мгновенное изменение требует, чтобы \(di/dt\) было бесконечным, и, следовательно, напряжение, управляющее катушкой индуктивности, также должно быть бесконечным, что совершенно невозможно. Поэтому мы можем указать особенно важную характеристику конденсаторов:

\[\text{Ток через индуктор не может измениться мгновенно.} \label{9.10} \]

Это наблюдение будет центральным при анализе работы индукторов в цепях постоянного тока.

Каталожные номера

¹ Одно из самых крутых изобретений всех времен: магнит с выключателем.

² Обмотанная проволока должна быть изолирована, иначе каждая петля закоротится на соседние с ней петли, и у нас останется трубка вместо ряда петель.

---

Эта страница под названием 9.2: Индуктивность и катушки индуктивности распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Джеймсом М. Фиоре посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   Джеймс М. Фиоре

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. source@http://www. dissidents.com/resources/DCElectricalCircuitAnalysis.pdf

Разница между проводником и индуктором [обновлено в 2022 г.]

Одно из фундаментальных отличий между проводником и индуктором заключается в том, что проводник идет против регулировки напряжения, а индуктор — против регулировки тока.

Кроме того, индуктор хранит энергию в виде поля притяжения, а проводник хранит энергию в виде электрического поля.

Проводник и индуктор

Основное различие между проводником и индуктором заключается в том, что последний непроницаем для свободного прохождения теплой или электрической энергии. В отличие от этого, первый, опять же, реагирует на прогрессию тепла или силы.

Проводник изображается как материал, который позволяет электронам беспрепятственно и эффективно течь, начиная с одного конкретного, а затем к следующему, по крайней мере, в одном подшипнике.

Такое свободное движение электронов позволяет энергии в виде тепла или электрического заряда беспрепятственно проходить через соответствующий материал.

Катушка индуктивности — это материал, который не позволяет электронам течь беспрепятственно.

Несмотря на то, что обычно ожидается, он прочно удерживает электроны внутри молекул материала и, таким образом, препятствует свободному распространению энергии в виде тепла или электрического тока, проходящего через материал.

Таблица сравнения проводника и индуктора

Параметры сравнения	Проводник	Индуктор
Work
.	Противостоит изменениям тока.
Частота	Напряжение в проводнике не меняется мгновенно.	Ток в катушке индуктивности не меняется быстро
Единица измерения	Единицей проводимости является Фарад.	Единицей индуктивности является Генри.
Формула	Напряжение меньше тока на π/2	Ток меньше напряжения на π/2
Типы тока для постоянного тока

Что такое проводник?

Это относится к любому из различных веществ, которые позволяют развивать электрический поток или ядерную энергию. Они обладают высокой проводимостью и беспомощной защитой от распространения электрической или ядерной энергии.

Это происходит из-за наличия «свободных электронов в ядерной конструкции проводника».

«Свободные электроны» относятся к тем электронам, которые можно без проблем обменять на электроны других йот. Это их связь с молекулой, частью которой они являются, нуждающейся в прочности.

Это отсутствие солидарности позволяет свободному продвижению энергии, начиная с одной йоты и заканчивая следующей.

Степень, в которой материал или вещество позволяет зарядам или теплу проходить через него, зависит от количества «свободных электронов», которые он имеет в самых дальних кругах своих йот.

Вещество или материал можно считать хорошим проводником в том случае, если оно имеет обильное количество «свободных электронов» в самых дальних или краевых оболочках своих молекул.

Кроме того, между зоной проводимости и валентной зоной (известной как незаконная энергетическая дыра) не должно быть пространства, чтобы электроны могли без особых усилий перемещаться в разные йоты.

Предмет, сделанный из материала с ведущими характеристиками, будет получать заряды, о которых говорят «нет», благодаря ему от другого объекта, и позволит этим зарядам распространяться по всей его поверхности, за исключением случаев, когда ужасные силы, существующие между избыточными электронами, уменьшатся до наибольшей мыслимой степени.

Что такое индуктор?

Свет представляет собой резистор (преграда создает тепло, чтобы волокно в лампочке искрилось — для тонкостей узнайте, как работает свет).

Провод в петле имеет много нижних препятствий (это просто провод), поэтому мы ожидаем, что при включении выключателя лампочка слабо вспыхнет.

Большая часть потока должна следовать по кругу с низкими препятствиями. Вместо этого происходит то, что когда вы замыкаете выключатель, лампочка ярко горит, а затем тускнеет.

В тот момент, когда вы открываете контроллер, лампочка ярко горит, а затем быстро гаснет.

Причиной этого странного поведения является индуктор. Когда нынешние первоначальные зачатки текли по петле, завиток должен был развить притягательное поле. Пока область строится, петля препятствует прохождению тока.

Когда участок построен, ветер обычно может дуть через проволоку. Когда переключатель размыкается, привлекательное поле вокруг контура удерживает ток в витке до тех пор, пока поле не разрушится.

Этот ток заставляет лампочку светиться некоторое время, даже если выключатель разомкнут. Катушка индуктивности может накапливать энергию в своем поле притяжения, и в общем случае индуктор будет сопротивляться любой корректировке меры тока, проходящего через нее.

Основные различия между проводником и индуктором

1. Проводник хранит энергию в виде электрического поля, а индуктор хранит энергию в виде поля притяжения.
2. Энергия, отводимая в Проводнике, определяется напряжением, например, ½ CV2. Отводимая мощность определяется по току, например, ½ LI2 
3. Ток не проходит через пластины проводника, но в индукторе ток проходит через петлю.
4. Проводники служат защитой для цепи постоянного тока, а индуктор используется в качестве проводника для цепи постоянного тока.
5. В схеме кондиционера для проводника ток опережает напряжение на 90 градусов, а в случае индуктора ток опережает напряжение на 90 градусов.

Заключение

Так как проводник хорошо направляет на высоких частотах, они обычно используются в высоковольтных источниках питания, где они могут просеять шум.

Как правило, они использовались в обстоятельствах, когда требовались огромные уровни емкости и силы, например, в радарах.

Они также используются для устройств, таких как радиоприемники, которые используют сигналы колебания, в которых одна пластина конденсатора может освобождаться, а другая может заряжаться за доли секунды.

Проводники дополнительно регулярно располагаются рядом с микропроцессорами, чтобы препятствовать импедансу от сигналов постоянного тока; для этой ситуации они развязывают проводник.

Индукторы известны широким ассортиментом современных гаджетов и устройств. Телевизоры, радиоприемники и свечи зажигания в целом обычно используются для катушек индуктивности.

В обстоятельствах, когда частоты или реверберация являются значительными, катушки индуктивности могут быть соединены с проводниками и резисторами для усиления или ограничения движений в цепи.

Обычные катушки индуктивности обычно слишком велики, чтобы их можно было использовать с современными центральными процессорами; однако катушки индуктивности для поверхностного монтажа производятся в недостаточном количестве для существующего оборудования.

Другие типы катушек индуктивности имеют дополнительную мощность, аналогичную использованию связанных катушек индуктивности в трансформаторах.

Ссылки

1. https://ieeexplore. ieee.org/abstract/document/1211182/
2. https://ieeexplore.ieee.org/abstract/document/1516170/
Разница» в Google. Оцените этот пост!

[Всего: 0]

Один запрос?

Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы быть полезным для вас. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/семьей. SHARING IS ♥️

Содержание

сообщить об объявлении

Как читать данные каталога — индуктивность

Индуктивность электрического кабеля обычно не указывается в паспорте или каталог. Причина в том, что индуктивность не является проблемой в обычных электрических схема. Но есть еще редкие случаи, когда это значение необходимо. Здесь мы объясняем, как оценить это значение по данным каталога. (Примечание 1)

1. Значение индуктивности

Индуктивность цепи определяет запасенную в ней магнитную энергию. 92 / 2 (1) куда Wl = магнитная энергия, поступающая в цепь (Дж) L = индуктивность цепи (Гн) I = ток, протекающий через индуктивность (А) Обратите внимание, что магнитная энергия не существует, если нет тока. Эта причина становится ясной, когда мы изучаем специальную теорию относительности.

В случае электрического кабеля у нас есть четкое понимание, разделив полная индуктивность к двум парциальным индуктивностям. Один связан с электромагнитным полем. энергия существует внутри проводника, другая из-за проводника внешнее пространство.

  Л = Ли + Ле
  куда
L = общая индуктивность провода (Гн)
Li = внутренняя индуктивность провода (Гн)
Le = внешняя индуктивность провода (Гн)
 

В случае постоянного (постоянного) тока через всю сечение проводника. Но частота тока становится выше, ток концентрируется на поверхности проводника за счет скин-эффекта. В результате внутренняя индуктивность уменьшается, а общая индуктивность кабеля близка к внешней индуктивности кабеля.

То есть разделение внешней и внутренней индуктивности есть отражение явления скин-эффекта.

Кроме того, отмечается, что индуктивность определена для закрытой контурная петля. (Заметка 2)

2. Расчет индуктивности кабеля

Таким образом, мы знаем, что индуктивность зависит от частоты и имеет максимальное значение индуктивность постоянного тока (постоянный ток). А суммарная индуктивность уменьшается с увеличением частоты, приближаясь к Le.

Обычно при частоте около 10 МГц или выше индуктивность электрического кабеля становится почти Ле. И нет существенной разницы в стоимости индуктивность по постоянному току и ВЧ (высокочастотная) индуктивность.

2.1. Индуктивность на высокой частоте

Для нормального электрического кабеля на частоте 10 МГц и более: отношения устанавливаются.

 Z0 ≈ sqrt(L/C) (2)
  v ≈ 1 / sqrt(L * C) (3)
  Vr = v / c
     ≈ 1 / sqrt(εs) (4)
  куда
Z0 = волновое сопротивление кабеля (Ом)
v = фазовая скорость электромагнитной волны, распространяющейся по кабелю (м/с)
Vr = коэффициент скорости троса (0
Поскольку электрический кабель нельзя использовать на высокой частоте,
если Vr или Z0 не является постоянным значением, эти два важных свойства всегда
указано в каталоге или техпаспорте. 
 

Следующие соотношения получаются с помощью (1) и (2) на высокой частоте.
 
 
  L = Z0 / (с * Vr) (5)
  С = 1 / (с * Vr * Z0) (6)
 
 2.2 Индуктивность при постоянном токе 
 Внутренняя индуктивность электрического кабеля зависит от частоты.
Максимальная внутренняя индуктивность достигается при постоянном токе.
Для немагнитного цилиндрического проводника,
это максимальное значение следующее.
  Li = 0,05e-6 (Гн/м) (7)
 
Для кабеля с двумя параллельными проводами мы можем оценить значение индуктивности постоянного тока.
путем добавления (5) и дважды (7).
 Аналитическое решение легко получить в случае цилиндрического проводника.
Но в другой форме это довольно громоздкая процедура.
Пожалуйста, посмотрите на следующий текст, если вы заинтересованы.
  Фредерик В. Гровер, - Расчеты индуктивности
  (Dover Publications, Inc.) ISDN 0-486-49577-9
 
Это классика, но она доступна и сейчас.
 В наше время целесообразно использовать численный метод, такой как конечный
элементный метод. Рекомендуется прочитать следующую книгу.
 92 (9) 

Для большинства электрических цепей избегают большого тока, чтобы уменьшить потери тепла (джоулево тепло). Таким образом, устанавливается следующее соотношение,

  я
это, как правило, уменьшает влияние индуктивности по сравнению с емкостью.
 

Если большой ток протекает как электрический нагреватель, электрическое сопротивление равно
больше, чем индуктивность, также влияние индуктивности невелико.
 
 

Кроме того, следующее соотношение, полученное из (1) и (8), содержит
проблема достойная внимания.
 92 (10)
 

3.2. Определение индуктивности

Важно отметить, что индуктивность определяется только для замкнутого контурная петля. Другими словами, индуктивность подводящего провода (разомкнутая петля) не имеет значения. Есть много недоразумений по этому поводу, мы можем видеть даже в стандарт ИЭЭЭ.

Индуктивность электрического кабеля определяется индуктаном на единицу длины. (ч/м). Это значение на обоих концах короткозамкнутого кабеля достаточной длины, чтобы можно было пренебречь конечный эффект обоих концов.

А индуктивность или емкость электрического кабеля определяется только для нормальный режим . Емкость и индуктивность синфазного сигнала невозможно предсказать во время отгрузки кабеля. Эти параметры зависят от способа проводки на месте.

Индуктивность линии передачи | bartleby

Что такое индуктивность?

Индуктивность — это электрический термин, относящийся к проводнику или индуктору. Индуктивность — это свойство или способность проводника противостоять изменению тока через конкретную цепь. Термин индуктивность происходит от индуктора. Символ L обозначает индуктивность, а единицей индуктивности является Генри (Гн). Индуктивность обычно представляет собой отношение напряжения к скорости изменения тока (ампер). На практике каждый проводник обладает свойством индуктивности.

Что такое линия передачи?

Линии передачи — это линии, используемые для передачи чего-то вроде сигналов. С точки зрения основных электрических линий, линии передачи — это кабели или специальные кабели, используемые для передачи энергии высокого напряжения из одной точки в другую (например, из точки P в точку Q). Линии электропередач используются для передачи большой мощности на большие расстояния.

CC-Зеро| https://commons.wikimedia.org | Эдуардо Санчес

Какова индуктивность линии передачи?

Когда энергия передается по линии передачи, ее прерывают многие параметры, такие как емкость, индуктивность, сопротивление и т. д. Одним из них является индуктивность. Согласно закону Фарадея, магнитный поток начинает генерироваться, когда ток проходит через проводник. Поскольку ток изменяется, генерируемый поток также изменяется, что приводит к индуцированной ЭДС (напряжению или потенциалу). Эта ЭДС, которая индуцируется во время этого процесса, возникает из-за индуктивности.

Части связующего потока внутри проводника:

• Внутренний поток
• Внешний поток

Внутренний поток

Внутренний поток обычно индуцируется из-за протекания тока через проводник.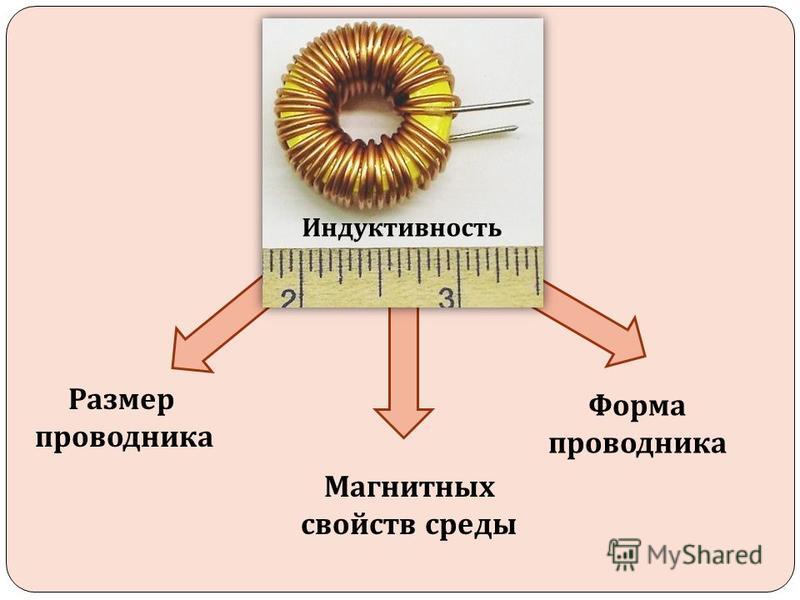

Внешний поток

Внешний поток создается двумя токами, одним из которых является ток, а другим является проводник, расположенный рядом с ним. Внешний поток создается вокруг проводника.

Причина индуктивности в линии передачи

Линии электропередачи передают большую мощность или высокое напряжение и большой ток, которые носят переменный характер. Сильный переменный магнитный поток будет генерироваться, когда через проводник проходит переменный ток высокого напряжения. Этот поток образует связь с другим потоком, генерируемым другим проводником, параллельным ему. Потокосцепление бывает как внутренним, так и внешним. Соотношение потокосцепления и тока вызывают индуктивность в этом положении.

Выражение для индуктивности:

L=ϕI

Здесь L — индуктивность, ϕ — потокосцепление, I — ток.

Если катушка имеет N число витков, то:

Индуктивность=NϕI

В линии передачи количество катушек равно 1. Потокосцепление обозначается λ.

Существует два типа флюса: внутренний флюс и внешний флюс. Здесь индуктивность запрашивается только для одного проводника, поэтому он приобретает только внутренний магнитный поток, создаваемый током проводника.

Предположим, размеры проводника следующие:

Длина проводника L , сила тока I , радиус R , внутренний переменный радиус r .

Отношение площадей к внутреннему переменному радиусу и исходному радиусу равно:

IrI=πr2πR2

Переставив приведенные выше члены, получим:

Ir=πr2πR2I

Выражение для магнитного потока: B=µ0Hr ……. (1)

H  является намагничивающей силой.

Выражение для потокосцепления имеет вид:

dλ=IrIdϕdλ=πr2πR2dϕ

Для исходной длины имеем: =λILinternal=μ08π

Типы кабелей передачи

Различные типы кабелей передачи:

• Сбалансированный двухжильный кабель
• Коаксиальный кабель
• Волновод
• Микрополосковый
• Волоконная оптика

Тип провода, используемый при передаче

Мы используем различные типы провода при передаче большой мощности. Но в основном в открытых длинных линиях передачи используется многожильный провод или многожильный провод передачи.

Многожильный провод определяется как провод, образованный двумя или более типами материала, в котором материалы обладают различными типами свойств, такими как стабильность, прочность, проводимость и т. д.

Типы передачи на основе фазы и линии

Виды передачи по фазно-проводной основе:

• Однофазная двухпроводная линия
• Симметричная трехфазная трехпроводная линия
• Несимметричная трехфазная трехпроводная линия

Двухпроводная одиночная -фазная линия

Получает два провода в одной фазе с размерами провода. Оба провода имеют свои потокосцепления. Предположим, что имеются два проводника A и B.

Потокосцепление проводника A:

λA=2×10-7IA ln 1Daa+IB1DABλA=2×10-7I ln Dr

Потокосцепление проводника B:

λB=2×10-7I ln Dr

Индуктивность ( L ) = индуктивность проводника A = индуктивность проводника B .

L=LA=LB=λB=2×10-7lnDr

Однофазная линия

Симметричные трехфазные трехпроводные линии

При таком расположении провод или проводник расположены под углом 60 градусов к друг друга с одинаковым расстоянием между ними. Его образуют три провода.

Индуктивность всех трех проводов одинакова, т. е.

L=LA=LB=LC=2×10-7lnDr

Здесь L индуктивность симметричной трехфазной трехпроводной системы такая же, как и однофазной двухпроводной системы.

Несимметричные трехфазные трехпроводные линии

В этом типе расположения три проводника или провода не находятся в симметричном положении, что означает, что угол между ними не составляет точно 60 градусов друг от друга и имеет неравное расстояние между ними . Он используется в эксплуатации, потому что такая схема дешевле и проще в конструкции.

Индуктивность проводника A относительно проводника B и проводника C:

LA=2×10-7lnD12D23D3113r=LB=LC

Здесь D представляет собой расстояние между проводниками.

Трехпроводные линии

Роль индуктивности в линии передачи

Индуктивность, наведенная в линии передачи, снижает эффект Ферранти.

Когда линии передачи работают без нагрузки или имеют очень низкую нагрузку, в этом состоянии напряжение на принимающей стороне немного превышает напряжение на передающей стороне. Этот эффект известен как эффект Ферранти. Чтобы избавиться от этого эффекта, индуктивность, наведенная в линии передачи, помогает уменьшить эффект Ферранти.

Распространенные ошибки

Необходимо знать разницу между линиями передачи и кабелями передачи.

Контекст и приложения

Это очень интересная и важная тема, которая будет полезна в

• Бакалавр технологии в области электротехники и электроники
• Магистр технологии в области электротехники
• Изоляторы 70977
• в линии передачи

Практические задачи

Q1. Какой параметр не является параметром линии передачи?

1. емкость
2. Индуктивность
3. Сопротивление
4. Импеданс

Правильный вариант: (D)

Explanation: Ampedance Ampedance IS All All.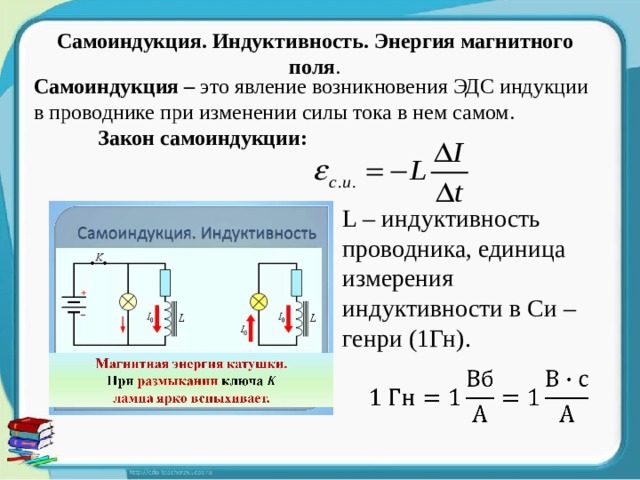

Q2. Какое условие отвечает за эффект Ферранти?

1. Без нагрузки
2. Тяжелый груз
3. Оба
4. Ни один из вышеперечисленных

Правильный вариант: (a)

Объяснение: Никакая нагрузка не отвечает за эффект Ферранти.

Q3. Какой параметр требуется для симметричной схемы передачи?

1. Сопротивление
2. Масса провода
3. Расстояние между проводами или фазами
4. Материал

Правильный вариант: (c)

Объяснение: Для симметричного расположения важно иметь одинаковое расстояние между всеми фазами.