11.Что такое главный вектор и главный момент?

Момент, равный геометрической сумме моментов всех сил системы относительно точки О, называется главным моментом системы сил относительно этой точки

Геометрическая сумма всех сил системы называется главным вектором системы сил и в отличие от равнодействующей R обозначается R*.

R^*=главный вектор

M₀=момент

R^*=Р₁+Р₂+Р₃= F₁+F₂+F₃

M= M₁₀+M₂₀+M₃₀=M₀

12.Чем схожи и различны главный вектор и равнодействующая?

R*≠0, M₀=0 – в этом случае система сил приводится к равнодействующей R равной главному вектору системы сил R=R*

R*≠0, M₀≠0, R*перпендикулярно M₀ т.к. R* — M₀ =0 – в этом случае систему сил можно приводить к равнодействующей.

Равной главному вектору этой системы, но приложенной не в центре приведения O, а стоящему от него на расстоянии OC. OC=IM₀I/IR*I

13.Зависимость главного момента от центра приведения.

При изменении центра приведения изменяется только главный момент, а главный вектор не изменяется. Влияет на направление главного момента.

14.Инварианты статики.

Инвариант – такие величины которые не зависят от выбора центра приведения.

1)Векторный инвариант I₁=R^*

2)Скалярный инвариант I₂=R^*×M

15.Частные случаи приведения произвольной пространственной системы сил.

1)R*=0, M₀=0 — в этом случае исходная система является уравновешенной, а тело находится в состоянии покоя.

2) R*=0, M₀≠0 – в этом случае исходная система или приводится к чему то или …. .

3) R*≠0, M₀=0 – в этом случае система сил приводится к равнодействующей R равной главному вектору системы сил R=R*

4) R*≠0, M₀≠0, R*перпендикулярно M₀ т.к. R* — M₀ =0 – в этом случае систему сил можно приводить к равнодействующей. Равной главному вектору этой системы, но приложенной не в центре приведения O, а стоящему от него на расстоянии OC. OC=IM

0I/IR*I

5) R*≠0, R*×M₀≠0 – в этом случае силу можно привести к динамическому винту(динаме) или к двум скрещивающимися силам.

По правилу параллелограмма, метод силового треугольника

17.Какие задачи являются статически определёнными и статически неопределёнными?

Стат. Опред. Называются задачи которые можно решать методом статики твёрдого тела, число неизвестных не превышает число уровней. Стат. Неопред. Задачи где число не известных превышает число уравнений, которые нельзя решать методом статики, для решения которых нужно учитывать деформацию тела.

18.Как направлены реакции при скольжении тела по шероховатой поверхности.

При скольжении тела по шероховатой поверхности к нему приложена сила трения скольжения. Направление этой силы, противодействующей скольжению,

противоположно направлению скорости тела

Модуль силы трения скольжения пропорционален нормальному давлению N:

F = fN.

Коэффициент пропорциональности f называется коэффициентом трения скольжения и определяется опытным путем.

19.Как находится угол трения. Дать понятие конуса трения.

Угол tg которого равен коэф. трения называется углом трения. Tg(альфа) = Fтр./Nа=fNа/Nа=f

Y=arctgf

Геометрическое место всех возможных направлений предельной реакции Ra образует коническую поверхность – конус трения.

20.Сформулировать условие, при котором возможно и не возможно скольжение тела по шероховатой поверхности в зависимости от угла наклона силы к нормали поверхности скольжения.

@>Y таким образом чтобы тело скользило по поверхности необходимо что бы угол образованной силы с нормалью поверхности был больше угла трения, т.е. сила должна быть приложена вне конуса трения. Если @<Y то скольжение не возможно, если @=Y то имеет случай предельного равновесия.

21.Какие реакции возникают при качении тела по шероховатой поверхности без скольжения.

22.Размерность коэф.трения качения и скольжения.

Безразмерный коэффициент f называется коэф. трения скольжения.

23.Как находится центр параллельных сил?

X_c=

Y_c=

Z_c=

24.Можно ли найти равнодействующую 2 параллельных неравных по модулю сил, направленных в одну сторону? Если да, то чему равна равнодействующая, и где она приложена?

Любую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, прило­женной в какой-либо точке тела (центре приведения) и равной глав­ному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.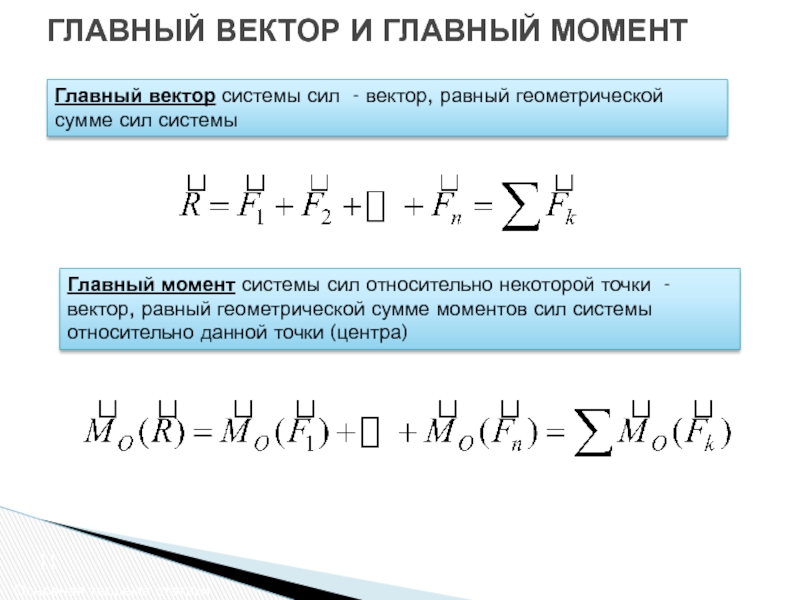 Поскольку вы имеете дело с двумя параллельными силами, направленными в одну сторону, то на отрезке, соединяющем точки их приложения, найдется точка, относительно которой главный момент этих сил равен нулю. Если в этой точке приложить силу, равную векторной сумме этих двух сил (то есть главный вектор), то она заменит их действие на тело. Таким образом, вы можете найти равнодействующую и точку ее приложения так, что при этом не понадобится дополнительная пара сил.

Краткий курс теоретической механики

Краткий курс теоретической механики

Тарг С. М. Краткий курс теоретической механики: Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с. В книге изложены основы механики материальной точки, системы материальных точек и твердого тела в объеме, соответствующем программам технических вузов. Приведено много примеров и задач, решения которых сопровождаются соответствующими методическими указаниями. В 10-м издании (9-е — 1974 г.) значительно изменены и более компактно изложены вопросы статики; в разделе «Динамика» дополнительно рассмотрены приложения общих теорем к изучению движения жидкости, малые колебания системы и некоторые другие вопросы. Для студентов очных и заочных технических вузов. Оглавление ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ ВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V. ПЛОСКАЯ СИСТЕМА СИЛ § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50. РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Раздел третий. ДИНАМИКА ТОЧКИ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА

Векторы силы – технология проектирования

Векторы силы, основные измерения величины, направления и точки приложения

Описание

Лист с заметками

Примеры

Интерактивная диаграмма

Зная, что величины силы могут действовать как точечные нагрузки, линейные нагрузки или поверхностные нагрузки, становится важным думать о них как о распределениях векторов.

Мы будем использовать термин «Вектор» для описания некоторых атрибутов сил, полезных для нашего понимания структур. Точечные нагрузки, например, имеют Величина или значение, равное величине силы, измеренной в фунтах, тысячах фунтов или ньютонах.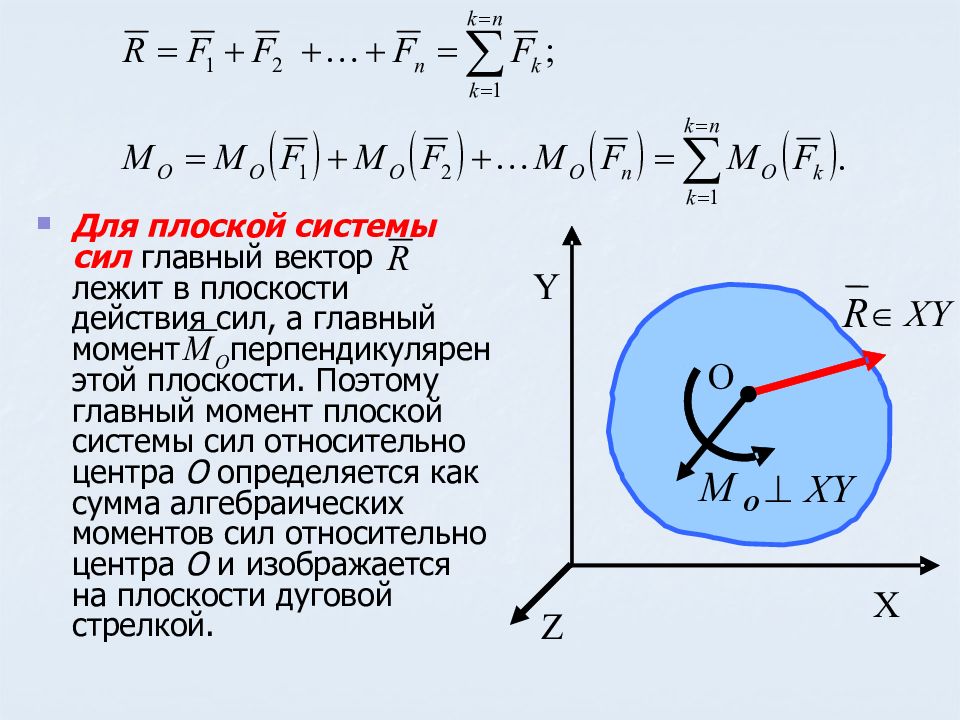 Точечная нагрузка также имеет Направление , которое описывает угол ориентации или направление, в котором она действует. Третий атрибут — это Точка приложения , которая описывает, как сила вступает в контакт со структурой, на которую она действует. на. Проще всего думать о векторах силы как о стрелках с начальной и конечной точками и определенным углом в двумерной плоскости X-Y.

Например, если точечная нагрузка представляет собой груз весом 50 фунтов, стоящий на полу, его величина будет равна 50 фунтам, а направление направлено прямо вниз (направление силы тяжести!), а его точка приложения будет сверху. пола. Теперь, если бы вместо этого тот же груз был подвешен этажом выше, Величина и Направление были бы такими же, но точка приложения была бы совсем другой. Вместо того, чтобы давить на пол, вес сопротивляется натяжению сверху — другое структурное устройство.

Величина вектора силы либо задана, либо легко вычисляется, тогда как его направление требует некоторого размышления. Нам нужно определить систему координат, чтобы мы могли описывать векторы в двумерном пространстве. Наиболее распространена декартова система координат, в которой расстояние по горизонтали соответствует оси X, а расстояние по вертикали — оси Y. Мы будем часто рисовать маленькую диаграмму с X и Y, показанную ниже, просто чтобы напомнить себе. Стрелки на оси также указывают в положительном направлении, поэтому мы можем использовать положительное и отрицательное, чтобы описать, указывает ли вектор влево или вправо. С помощью этой системы координат мы можем описать направление вектора силы с помощью горизонтальной и вертикальной меры расстояния в направлениях X и Y. Мы называем их компонентами вектора.

Мы также можем описать Направление вектора с помощью измерения угла (либо от горизонтальной плоскости, либо от вертикальной плоскости) и длины вектора. Этот угол может быть задан в градусах, где окружность состоит из 360 градусов. Или радианы, где круг состоит из 2? радианы. Преобразование между ними не слишком сложно, но очень важно знать, как вы измеряете углы. Указание угла и длины часто называют полярной системой координат.

Конечно, декартовы и полярные координаты связаны через геометрию и тригонометрию. Возможно, вспоминая предыдущую курсовую работу, это хорошее время, чтобы вспомнить фундаментальные отношения между расстояниями и углами и то, как мы вычисляем одно из другого. Синус, косинус и тангенс являются основными функциями углов, которые мы будем использовать, связывая смежные, противоположные и гипотенузные стороны полученного прямоугольного треугольника. Прямоугольный треугольник — это тот, у которого 9Угол 0 градусов внутри. Смежная сторона — это сторона, ближайшая к углу, а Противоположная сторона — это сторона, расположенная прямо напротив угла. Гипотенуза — самая длинная сторона, диагональная линия между концами двух других сторон. Аббревиатура SOH CAH TOA может быть знакома, и полезно запомнить следующее:

SIN θ = ПРОТИВОПОЛОЖНАЯ / ГИПОТЕНУЗА
COS θ = СМЕЖНАЯ / ГИПОТЕНУЗА
TAN θ = ПРОТИВОПОЛОЖНАЯ / СМЕЖНАЯ

Мы также использовать пифагорейское соотношение:

X ² + Y ² = ГИПОТЕНУЗА ²

Мы будем использовать эти соотношения для решения задач. В некоторых случаях у нас может быть только несколько фрагментов информации, и нам нужно вычислить другие. Например, уклон или угол крыши может определяться водоотводом, а ширина дома размерами комнат. Это значит, что мы можем рассчитать необходимую высоту крыши.

Связанный файл представляет собой загружаемый отдельный лист для справки.

Лист с заметками по вектору силы

Геометрия структур опирается на эти отношения.

Пример 1

Рассмотрим изображение справа. Сила в 10 килофунтов тянет веревку так, что веревка образует угол 60 градусов с горизонтом, как показано на рисунке. Чему равны горизонтальная (x) и вертикальная (y) составляющие силы?

Если мы визуализируем силу как вектор, образующий треугольник с горизонтальными и вертикальными сторонами, мы можем использовать тригонометрию (SOH, CAH, TOA) для определения смежных и противоположных сторон треугольника.

При показанном угле компонент X (горизонтальный) СМЕЖЕН с углом 60 градусов. Таким образом, это означает, что компонент Y (вертикальный) ПРОТИВОПОЛОЖНО. Сам вектор является ГИПОТЕНУЗОЙ.

Решение для компонента x Сначала мы знаем:
cos θ = прилегающий/ гипотенуза

, поэтому, если мы переставляем:

Прилегающий = cos θ * Гипотенуза

ПЛИЗИВА = COS (60 градусов) * 10 тысяч фунтов = (0,5) * 10 тысяч фунтов = 5 тысяч фунтов

Это компонент X вектора, 5 тысяч фунтов! Однако в правильных обозначениях мы должны объявить это ОТРИЦАТЕЛЬНОЙ силой, потому что она должна указывать в отрицательном направлении на основании нашего соглашения о знаках:

X = -5 тысяч фунтов

Решение для компонента Y почти идентично, за исключением использования SOH:

SIN θ = ПРОТИВОПОЛОЖНОСТЬ/ ГИПОТЕНУЗА

поэтому, если мы переставим:

ПРОТИВОПОЛОЖНОСТЬ = SIN θ * ГИПОТЕНУЗА

Подставляя, мы получаем:

ПРОТИВОПОЛОЖНОЕ = SIN (60 градусов) * 10 тысяч фунтов = (0,866) * 10 тысяч фунтов = 8,66 тысяч фунтов

Опять же, принимая во внимание отрицательное:

Y = -8,66 тысяч фунтов

Диаграмма ниже свойства векторов. Перетащите ползунки, чтобы изменить величину силы и угол силы. Выпадающее меню меняет отображение с декартовых на полярные координаты.

Определение, формула, количество I StudySmarter

Силы имеют как величину, так и направление и поэтому считаются векторов . Величина силы определяет, какая сила воздействует на объект.

Как действует сила

Сила действует на объекты, когда они взаимодействуют друг с другом. Сила перестает существовать, когда прекращается взаимодействие. Направление движения объекта также является направлением, в котором движется сила. Объекты в покое или в равновесии имеют противодействующие силы, удерживающие их на месте.

Итак, силы могут вызывать движение объектов и заставлять объекты оставаться в покое. Ваша интуиция подсказывает вам, что если вы хотите, чтобы объект сдвинулся влево, вы толкаете его влево.

В этом разделе мы познакомимся с понятием равнодействующей силы. Когда на частицу объекта действует ряд сил, результирующая сила представляет собой сумму всех сил, действующих на объект.

Примеры векторов

Вот несколько примеров того, как силы могут быть выражены в виде векторных величин.

Если вы возьмете две силы и приложите их к объекту, какова результирующая сила?

Ответ:

Сначала нанесите свои силы на график, чтобы увидеть их направление.

Рисунок 1. Пример равнодействующей силы

Если частица в точке 0 притягивается силами 1 и 2, можно предположить, что результирующая сила будет находиться где-то около пунктирной линии посередине двух сил на диаграмме выше. Однако вопрос подразумевает, что мы должны найти точную результирующую силу. Кроме того, другие вопросы могут быть не такими простыми, как этот.

Результирующий вектор =

Это означает, что сила будет притягиваться к точке , как показано ниже.

Рисунок 2. Результирующая сила

Силы могут тянуть частицу со всех сторон с одинаковой величиной, а результирующая сила равна 0. Это означает, что частица будет находиться в равновесии.

Рисунок 3. Результирующая сила

Рисунок 3. Результирующая сила

Как показано ниже, вычислите величину и направление результирующего вектора, который образуется при суммировании двух векторов.

Рис. 4. Результирующая сила

Ответ:

Мы разбиваем каждый вектор на составные части и складываем компоненты вместе, чтобы получить результирующий вектор в компонентной форме. Затем мы найдем величину и направление этого вектора.

Итак, мы определяем компоненты x и y каждого вектора силы.

Пусть x компонент .

И компонент y .

Теперь давайте проделаем то же самое с компонентом y.

Теперь у нас есть компоненты x и y

, а j используется для обозначения единичных векторов. для векторов по оси x и j для векторов по оси y.

Повторим процесс для .

[45° — опорный угол, но нам нужен угол относительно положительной оси x, который равен 135°].

И сделайте то же самое для компонента y:

Теперь, когда у нас есть обе силы в компонентной форме, мы можем сложить их, чтобы получить результирующую силу.

Мы сложим компоненты x, а затем компоненты y.

Нанесите это на график

Это относительно больше, чем длина оси X. Гипотенуза образованного треугольника будет величиной, и она была помечена c. Воспользуемся теоремой Пифагора, чтобы найти c.

Здесь написано

Итак,

Поскольку c здесь то же самое, что и ,

Это величина результирующего вектора.

Чтобы найти направление, нам нужно вернуться к графику и обозначить угол, обозначенный как .

= 82,9 °

Если вам нужен угол, который положителен к оси x, вы вычтите 𝜃R из 180, поскольку все они лежат на прямой.

𝜃 + 82,9 = 180

𝜃 = 180 — 82,9

𝜃 = 97,1°

Теперь у нас есть величина и направление равнодействующей силы.

Сила как вектор – ключевые выводы

• Сила обладает как величиной, так и направлением.
• Объекты движутся в направлении чистой силы.
• Результирующая сила — это единственная сила, которая оказывает на частицу такое же воздействие, как если бы к ней было приложено много сил.
• При нахождении равнодействующей силы вы складываете все силы, действующие на частицу.

Часто задаваемые вопросы о силе как векторе

Числовое значение силы показывает ее величину, а знак перед ним указывает ее направление.

 Это диаграмма свободного тела, изображающая величину и направление сил, действующих на объект.

Их можно изобразить на графике. Его величина представлена ​​длиной стрелки, а его направление представлено направлением стрелки.

Вектор силы представляет собой представление силы, которая имеет как величину, так и направление. Однако векторы не имеют сил.

Тест Final Force as a Vector

Вопрос

Что такое вектор силы?

Показать ответ

Ответ

Вектор силы представляет собой представление силы, которая имеет величину и направление

Показать вопрос

Вопрос

Является ли крутящий момент вектором?

Показать ответ

Ответ

Крутящий момент является векторной величиной. Его направление зависит от направления силы на оси вращения.

Показать вопрос

Вопрос

Как найти направление вектора силы?

Показать ответ

Ответ

По функции арктангенса. Он равен углу, образованному с осью x или с осью y, в зависимости от приложения.

Показать вопрос

Вопрос

Может ли величина быть отрицательной?

Показать ответ

Ответ

 Величина всегда имеет положительное значение.

Показать вопрос

Вопрос

Что такое диаграмма вектора силы?

Показать ответ

Ответ

 Это диаграмма свободного тела, изображающая величину и направление сил, действующих на тело.

Показать вопрос

Вопрос

Что такое диаграмма вектора результирующей силы?

Показать ответ

Ответ

Диаграмма, представляющая сумму векторных сил, действующих на объект.

Показать вопрос

Вопрос

Что вызывает движение объектов и может заставить объекты оставаться в покое?

Показать ответ

Ответ

Показать вопрос

Вопрос

Когда силы притягивают частицу со всех сторон с одинаковой величиной, значение вашей равнодействующей силы будет …

Показать ответ

Ответ

Показать вопрос

Вопрос

Объекты всегда движутся в направлении чистой силы

Показать ответ

Ответ

Показать вопрос

Вопрос

Какова величина силы?

Показать ответ

Ответ

Величина силы определяет, какая сила воздействует на объект.