Где возникает эдс индукции — Вместе мастерим

Возникновение в проводнике ЭДС индукции

Если поместить в магнитное поле проводник и перемещать его так, чтобы он при своем движении пересекал силовые линии поля, то в проводнике возникнет электродвижущая сила , называемая ЭДС индукции .

ЭДС индукции возникнет в проводнике и в том случае, если сам проводник останется неподвижным, а перемещаться будет магнитное поле, пересекая проводник своими силовыми линиями.

Если проводник, в котором наводится ЭДС индукции, замкнуть на какую-либо внешнюю цепь, то под действием этой ЭДС по цепи потечет ток, называемый индукционным током.

Явление индуктирования ЭДС в проводнике при пересечении его силовыми линиями магнитного поля называется электромагнитной индукцией .

Электромагнитная индукция — это обратный процесс, т. е. превращение механической энергии в электрическую.

Явление электромагнитной индукции нашло широчайшее применение в электротехнике. На использовании его основано устройство различных электрических машин.

Величина и направление ЭДС индукции

Рассмотрим теперь, каковы будут величина и направление индуктированной в проводнике ЭДС.

Величина ЭДС индукции зависит от количества силовых линий поля, пересекающих проводник в единицу времени, т. е. от скорости движения проводника в поле.

Величина индуктированной ЭДС находится в прямой зависимости от скорости движения проводника в магнитном поле.

Величина индуктированной ЭДС зависит также и от длины той части проводника, которая пересекается силовыми линиями поля. Чем большая часть проводника пересекается силовыми линиями поля, тем большая ЭДС индуктируется в проводнике. И, наконец, чем сильнее магнитное поле, т. е. чем больше его индукция, тем большая ЭДС возникает в проводнике, пересекающем это поле.

Итак, величина ЭДС индукции, возникающей в проводнике при его движении в магнитном поле, прямо пропорциональна индукции магнитного поля, длине проводника и скорости его перемещения.

Зависимость эта выражается формулой Е = Blv,

где Е — ЭДС индукции; В — магнитная индукция; I — длина проводника; v — скорость движения проводника.

Следует твердо помнить, что в проводнике, перемещающемся в магнитном поле, ЭДС индукции возникает только в том случае, если этот проводник пересекается магнитными силовыми линиями поля. Если же проводник перемещается вдоль силовых линий поля, т. е. не пересекает, а как бы скользит по ним, то никакой ЭДС в нем не индуктируется. Поэтому приведенная выше формула справедлива только в том случае, когда проводник перемещается перпендикулярно магнитным силовым линиям поля.

Направление индуктированной ЭДС (а также и тока в проводнике) зависит от того, в какую сторону движется проводник. Для определения направления индуктированной ЭДС существует правило правой руки.

Если держать ладонь правой руки так, чтобы в нее входили магнитные силовые линии поля, а отогнутый большой палец указывал бы направление движения проводника, то вытянутые четыре пальца укажут направление действия индуктированной ЭДС и направление тока в проводнике.

Правило правой руки

ЭДС индукции в катушке

Мы уже говорили, что для создания в проводнике ЭДС индукции необходимо перемещать в магнитном поле или сам проводник, или магнитное поле. В том и другом случае проводник должен пересекаться магнитными силовыми линиями поля, иначе ЭДС индуктироваться не будет. Индуктированную ЭДС, а следовательно, и индукционный ток можно получить не только в прямолинейном проводнике, но и в проводнике, свитом в катушку.

При движении внутри катушки постоянного магнита в ней индуктируется ЭДС за счет того, что магнитный поток магнита пересекает витки катушки, т. е. точно так же, как это было при движении прямолинейного проводника в поле магнита.

Если магнит опускать в катушку медленно, то возникающая в ней ЭДС будет настолько мала, что стрелка прибора может даже не отклониться. Если же, наоборот, магнит быстро ввести в катушку, то отклонение стрелки будет большим. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от скорости движения магнита, т. е. от того, насколько быстро силовые линии поля пересекают витки катушки. Если теперь поочередно вводить в катушку с одинаковой скоростью сначала сильный магнит, а затем слабый, то можно заметить, что при сильном магните стрелка прибора будет отклоняться на больший угол.

Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от величины магнитного потока магнита.

И, наконец, если вводить с одинаковой скоростью один и тот же магнит сначала в катушку с большим числом витков, а затем со значительно меньшим, то в первом случае стрелка прибора отклонится на больший угол, чем во втором. Значит, величина индуктируемой ЭДС, а следовательно, и сила тока в катушке зависят от числа ее витков. Те же результаты можно получить, если вместо постоянного магнита применять электромагнит.

Направление ЭДС индукции в катушке зависит от направления перемещения магнита. О том, как определять направление ЭДС индукции, говорит закон, установленный Э. X. Ленцем.

Закон Ленца для электромагнитной индукции

Всякое изменение магнитного потока внутри катушки сопровождается возникновением в ней ЭДС индукции, причем чем быстрее изменяется магнитный поток, пронизывающий катушку, тем большая ЭДС в ней индуктируется.

Если катушка, в которой создана ЭДС индукции, замкнута на внешнюю цепь, то по виткам ее идет индукционный ток, создающий вокруг проводника магнитное поле, в силу чего катушка превращается в соленоид.

Получается таким образом, что изменяющееся внешнее магнитное поле вызывает в катушке индукционный ток, которой, в свою очередь, создает вокруг катушки свое магнитное поле — поле тока.

Изучая это явление, Э. X. Ленц установил закон, определяющий направление индукционного тока в катушке, а следовательно, и направление ЭДС индукции. ЭДС индукции, возникающая в катушке при изменении в ней магнитного потока, создает в катушке ток такого направления, при котором магнитный поток катушки, созданный этим током, препятствует изменению постороннего магнитного потока.

Закон Ленца справедлив для всех случаев индуктирования тока в проводниках, независимо от формы проводников и от того, каким способом достигается изменение внешнего магнитного поля.

При движении постоянного магнита относительно проволочной катушки, присоединенной к клеммам гальванометра, или при движении катушки относительно магнита возникает индукционный ток.

Индукционные токи в массивных проводниках

Изменяющийся магнитный поток способен индуктировать ЭДС не только в витках катушки, но и в массивных металлических проводниках. Пронизывая толщу массивного проводника, магнитный поток индуктирует в нем ЭДС, создающую индукционные токи. Эти так называемые вихревые токи распространяются по массивному проводнику и накоротко замыкаются в нем.

Сердечники трансформаторов, магнитопроводы различных электрических машин и аппаратов представляют собой как раз те массивные проводники, которые нагреваются возникающими в них индукционными токами. Явление это нежелательно, поэтому для уменьшения величины индукционных токов части электрических машин и сердечники трансформаторов делают не массивными, а состоящими из тонких листов, изолированных один от другого бумагой или слоем изоляционного лака. Благодаря этому преграждается путь распространения вихревых токов по массе проводника.

Но иногда на практике вихревые токи используются и как токи полезные. На использовании этих токов основана, например, работа индукционных нагревательных печей, счетчиков электрической энергии и так называемых магнитных успокоителей подвижных частей электроизмерительных приборов.

Электромагнитная индукция (индукция значит наведение) это явление, при котором в замкнутом контуре возникает электрический ток при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было обнаружено в 1831 г.

М. Фарадеем. Ток, возникающий при электромагнитной индукции называют индукционным.

Закон электромагнитной индукции

ЭДС индукции в контуре равна скорости изменения магнитного поля сквозь поверхность, ограниченную контуром.

Электромагнитная индукция
1831 г. – М. Фарадей обнаружил, что в замкнутом проводящем контуре при изменении магнитного поля возникает так называемый индукционный ток. (Индукция, в данном случае, – появление, возникновение).
Индукционный ток в катушке возникает при перемещении постоянного магнита относительно катушки; при перемещении электромагнита относительно катушки; при перемещении сердечника относительно электромагнита, вставленного в катушку; при регулировании тока в цепи электромагнита; при замыкании и размыкании цепи
Появление тока в замкнутом контуре при изменении магнит­ного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил (или о возникно­вении ЭДС индукции). Явление возникновения ЭДС в замкнутом проводящем контуре при изменении магнитного поля (потока), пронизывающего контур, назы­вается электромагнитной индукцией. Или:явление возникновения электрического поля при изменении магнитного поля (потока), называется электромагнитной индукцией.
Закон электромагнитной индукции При всяком изменении магнитного потока через проводящий замкнутый контур в этом контуре возникает электрический ток. I зависит от свойств контура (сопротивление): . e не зависит от свойств контура: . ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
Основные применения электромагнитной индукции: генерирование тока (индукционные генераторы на всех электростанциях, динамомашины), трансформаторы.

Правило Ленца Возникновение индукционного тока – следствие закона сохранения энергии! В случае 1: При приближении магнита, увеличении тока, замыкании цепи: ; Магнитный поток Ф­ → ΔФ>0. Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону, противоположную внешнему полю: , где – т.н. индукционное магнитное поле. В случае 2: при удалении магнита, уменьшении тока, размыкании цепи: . Магнитный поток Ф → ΔФ 0). Ток в контуре имеет положительное направление ( ), если совпа­дает с , (т.е. ΔΦ

Не нашли то, что искали? Воспользуйтесь поиском:

Электрические токи порождают вокруг себя магнитные поля. Данная связь дала толчок к многочисленным попыткам создать электрический ток в контуре при помощи магнитного поля.

Данную задачу решил М. Фарадей в 1831 году. Ученый открыл явление электромагнитной индукции.

Электромагнитная индукция

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре, если изменяется поток магнитной индукции, который рассматриваемый контур охватывает, появляется электрический ток. Возникающий электрический ток называют током индукции.

Анализируя свои множественные эксперименты, М. Фарадей пришел к выводу о том, что:

1. Индукционный ток появляется всегда при изменении магнитного потока, который охватывает проводящий контур. Так, если в однородном магнитном поле проводящий замкнутый контур повернуть, то в момент разворота в нем будет течь ток индукции. В этом случае индукция магнитного поля постоянна около проводящего контура, переменным является только поток магнитной индукции, который изменяется за счет изменения площади контура.
2. Величина тока индукции не связана со способом изменения магнитного потока. Она определена только скоростью его изменения. Сила тока индукции тем больше, чем больше скорость перемещения магнита, или быстрота изменения силы тока, или скорость перемещения катушек.

Попробуй обратиться за помощью к преподавателям

Электромагнитная индукция подтверждает связь между электрическими и магнитными явлениями.

Закон Фарадея

Анализируя данные своих экспериментов, М. Фарадей предложил количественный закон, описывающий электромагнитную индукцию. Ученый доказал, что каждый раз при изменении потока магнитной индукции, который сцеплен с проводящим контуром, в проводнике появляется ток индукции. Наличие индукционного тока означает то, что в цепи присутствует электродвижущая сила (ЭДС), которую в данном случае называют электродвижущей силой электромагнитной индукции ($Ɛ_i$).

Величина тока индукции, а значит, и величина $Ɛ_i$ зависит от скорости изменения магнитного потока:

$left|Ɛ_
ight|=frac

left( 1
ight)$.

Ф>

где $Ф$ – поток магнитной индукции.

Определимся со знаком ЭДС индукции. Знак потока магнитной индукции связан с выбором положительной нормали к рассматриваемому проводящему контуру. А направление силы тока и направление нормали связывает правило правого буравчика (винта). Получается, что фиксируя направление нормали, мы устанавливаем знак магнитного потока, направление тока и $Ɛ_i$ в контуре.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Сформулируем закон электромагнитной индукции Фарадея в окончательном виде:

Не зависимо от причины изменения магнитного потока, который охватывает замкнутый проводящий контур, электродвижущая сила индукции, появляющаяся в этом контуре равна:

где под $frac

$ понимают полную скорость изменения потока магнитной индукции, охватываемого проводником.

Ф>

Минус в формуле (2) указывает на то, что:

• При росте потока магнитной индукции (скорость изменения магнитного потока больше нуля) ($frac
  >0)$, ЭДС индукции меньше нуля ($Ɛ_i
  Ф>
• При уменьшении потока магнитной индукции (скорость изменения магнитного потока меньше нуля), ЭДС индукции больше нуля ($Ɛ_i>0$). Что значит, направление потока и направление поля тока индукции совпадают.

Знак минус в формуле (2) – это математическое отображение правила Ленца, которое используют для того, чтобы найти направление тока индукции.

Закон Фарадея справедлив при:

1. произвольных перемещениях замкнутого проводящего контура;
2. при любых его деформациях;
3. изменениях магнитного поля.

ЭДС индукции измеряется с Международной системе единиц (СИ) в вольтах (В).

Значение закона Фарадея

Закон Фарадея выражает новое физическое явление, в котором переменное магнитное поле порождает электрическое поле. Отсюда делается вывод о том, что электрическое поле может порождаться не только электрическими зарядами, но и изменяющимся магнитным полем.

Электромагнитная индукция – это всеобщий фундаментальный закон природы, реализующий связь между электрическими и магнитными полями.

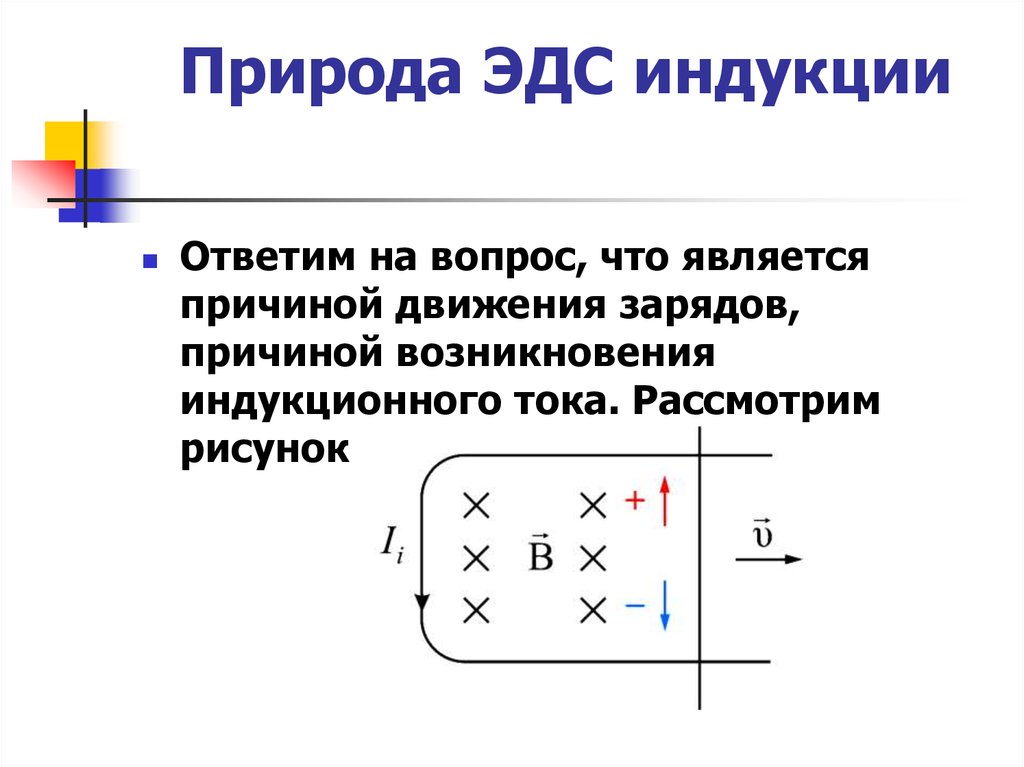
Природа электродвижущей силы индукции

Если проводник перемещается в магнитном поле, то на свободные электроны его вещества действуют силы Лоренца. Эти электроны под воздействием названной силы приходят в движение относительно проводника, что означает: в проводнике появляется ток.

Рисунок 1. Проводники. Автор24 — интернет-биржа студенческих работ

Рассмотрим прямой участок $DG$ проводника на рис.1. Этот участок перемещается со скоростью $vec v$ по проводникам $CK$ и $AL$, как по направляющим. При этом контур $AGDCA$ постоянно замкнут. Вектор индукции внешнего магнитного поля нормален плоскости рассматриваемого контура. Магнитное поле будем считать однородным. На заряды, которые перемещаются вместе с проводником, действует сила Лоренца, равная:

$vec_=qleft( vec imes vec
ight)left( 3
ight)$.

где$ vec$– индукция внешнего магнитного поля. Под воздействием силы Лоренца свободные электроны проводника приходят в движение и образуют электрический ток. Направление этого тока принимают за положительный обход контура, положительная нормаль ($vec n$) к площади контура указана на рис.1.

Наличие силы Лоренца эквивалентно тому, что в проводнике на заряды действует электрическое поле напряженность которого равна:

Поэтому ЭДС индукции между точками 1 и 2 проводника найдем как:

$left( Ɛ_
ight)_<21>=intlimits_1^2 vec dvec=intlimits_1^2left( vec imes vec
ight) dvecleft( 5
ight)$.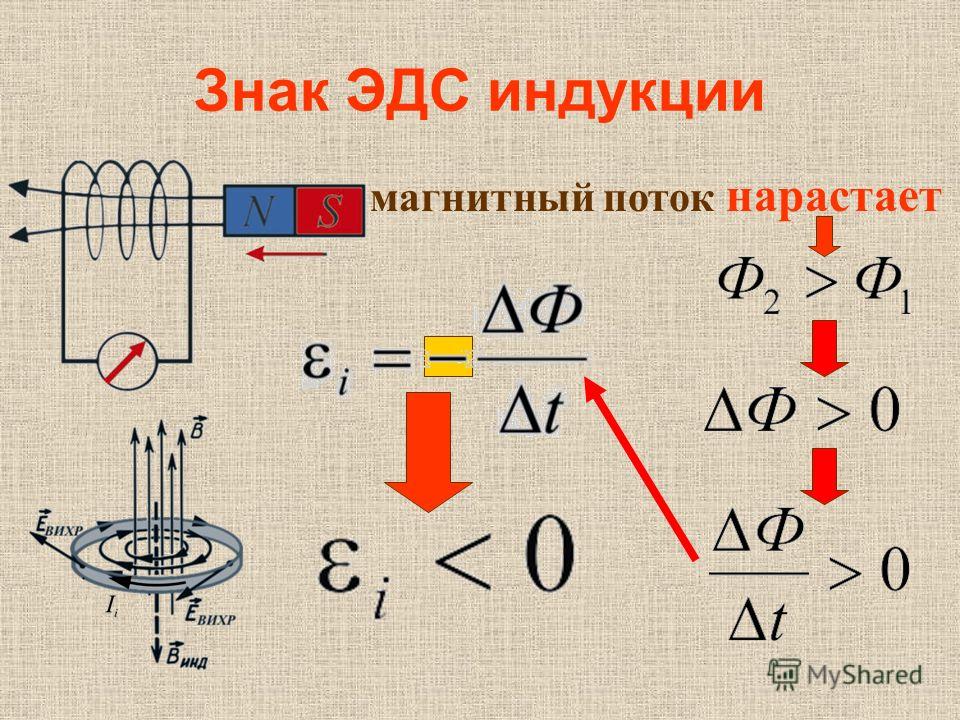

В случае, который мы рассматриваем на рис.1 точки 1 и 2 соответствуют точкам $D$ и $G$:

На не движущихся участках замкнутого контура, который мы рассматриваем, ЭДС не возникает. Следовательно, ЭДС контура равна ЭДС подвижного проводника $DG$, перемещающейся в магнитном поле.

Скорость перемещения проводника выразим как:

где $x$ – координата контактов проводника в точках $D$ и $G$ направляющими проводниками:

где $Ф$ – поток магнитной индукции через поверхность, которую ограничивает контур $AGDCA$. Знак минус указывает на то, что направления векторов $vec B$ и $ dvec S$ противоположны,

Выражение (11) мы получили, рассматривая движение части проводника. При перемещении нескольких участков проводника, ЭДС индукции находят как алгебраическую сумму ЭДС индукции, появляющихся на каждом участке.

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Электромагнитная индукция (характеристика) – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Закон электромагнитной индукции формулируется именно для ЭДС, а не для силы индукционного тока, т.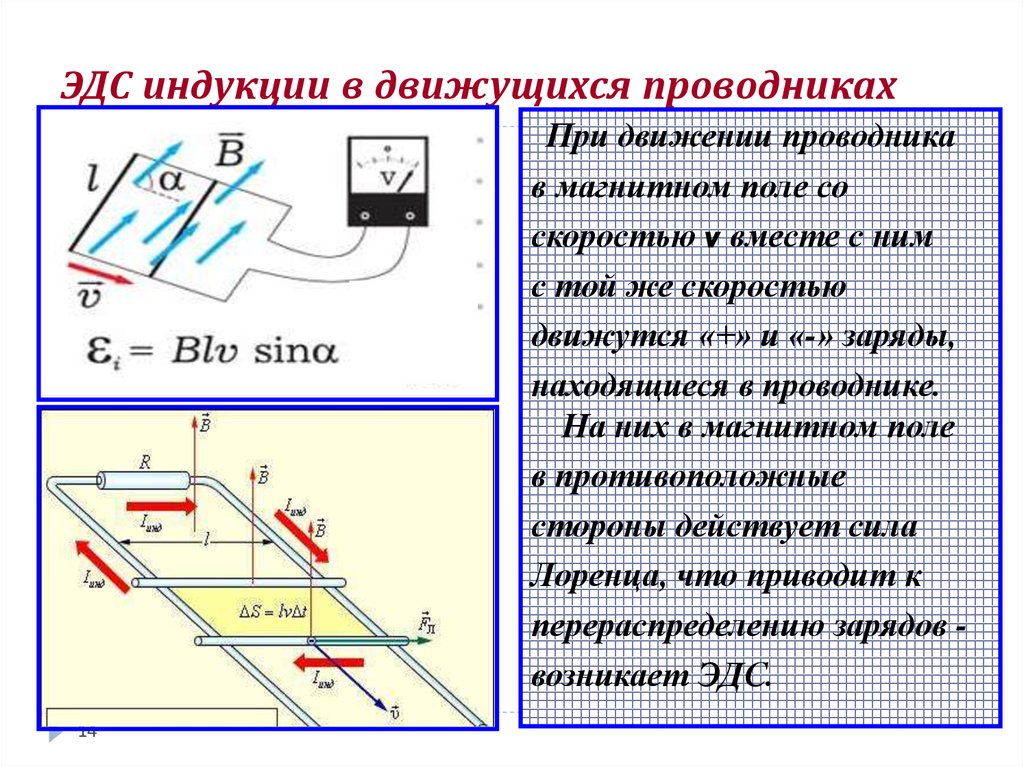 к. сила тока зависит и от свойств проводника, для ЭДС определяется только изменением магнитного потока. Согласно закону электромагнитной индукции, ЭДС индукции в замкнутом контуре равна по модулю, скорости изменения магнитного потока через поверхность, ограниченную контуром:

\(\varepsilon_i = \left | \frac {\Delta \Phi}{\Delta t} \right |\).

Известно, что в цепи появляется электрический ток в том случае, когда на свободные заряды проводника действуют сторонние силы. Величину, численно равную работе этих сил при перемещении единичного положительного заряда вдоль замкнутого контура, называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в контуре появляются сторонние силы, действие которых характеризует ЭДС, называемая ЭДС индукции. Обозначают ее буквой \(\varepsilon\).

Согласно закону Ома для замкнутой цепи, \(I_i = \frac {\varepsilon_i}R\). Сопротивление проводника не зависит от изменения магнитного потока. Следовательно, соотношение это справедливо только потому, что ЭДС индукции пропорциональна \(\frac {\Delta\Phi}{\Delta t}.\)

Другими словами, можно сказать, что электромагнитная индукция – явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока – изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током. Закон электромагнитной индукции Фарадея = ПРАВИЛО ЛЕНЦА

\(\varepsilon = — \frac {d\Phi_B}{dt}\).

Знак «минус» в формуле отражает правило Ленца, названное так по имени русского физика Э. {\circ} \) с вектором индукции магнитного поля. Индукция магнитного поля, пронизывающего рамку, изменяется по закону \(B=0,1\) t (Тл). Определите ЭДС индукции, возникающая в рамке, по истечении \(3\) с.

В магнитном поле, индукция которого увеличивается от \(1\) до \(5\) Тл в течение \(0,05\) с, находится замкнутая накоротко катушка диаметром \(16\) см, имеющая \(10\) витков. Определите среднее значение ЭДС индукции катушки, если плоскость витков перпендикулярна силовым линиям поля.

Определите модуль ЭДС индукции в проводящем контуре, который находится в переменном магнитном поле, поток которого изменяется со скоростью 8 Вб/с?

Как называется явление, когда при выдвигании из катушки постоянного магнита в ней возникает электрический ток?

Чему равна индукция магнитного поля прямого проводника длиной \(25\) см, движущегося в однородном магнитном поле со скоростью \(2\) м/с перпендикулярно линиям магнитной индукции, если ЭДС индукции на концах проводника – \(0,5\) В?

Катушка индуктивностью \(0,1\) Гн и сопротивлением \(6\) Ом была отключена от цепи постоянного тока, при этом выделилось \(0,45\) Дж энергии.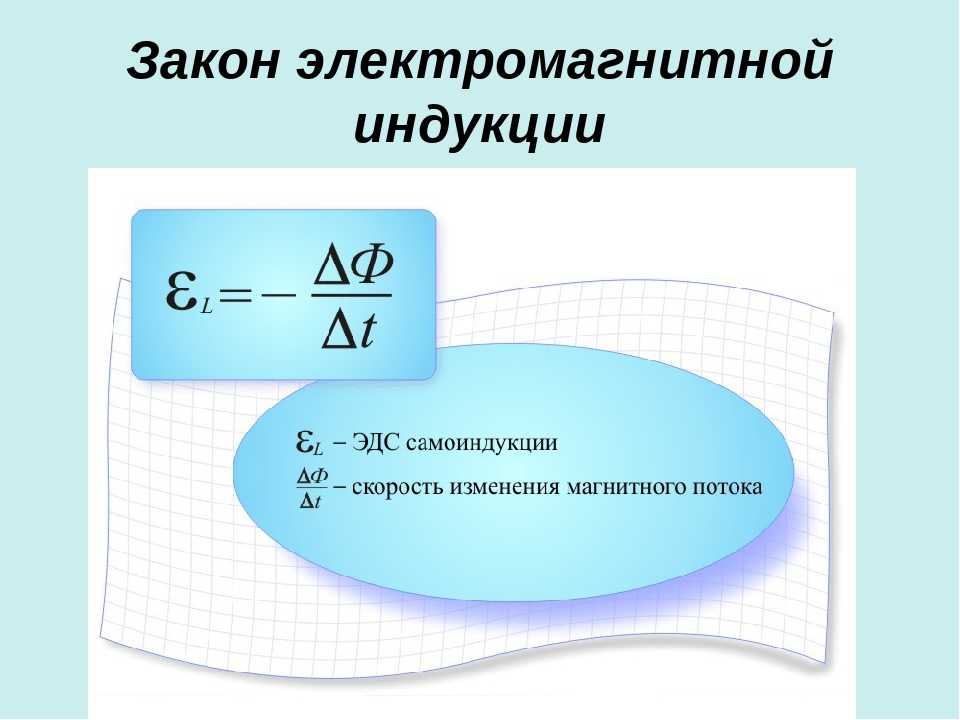 Чему было равно напряжение на концах этой катушки?

Сообщить об ошибке

Явление электромагнитной индукции — Студопедия

Поделись  

Тема: Явление электромагнитной индукции

На рисунке показана зависимость силы тока от времени в электрической цепи с индуктивностью 1 мГн:

Модуль среднего значения ЭДС самоиндукции в интервале от 0 до 5 с (в мкВ) равен …

Решение:
В соответствии с законом Фарадея модуль среднего значения электродвижущей силы самоиндукции равен: . Изменение тока в интервале от 0 до 5 с находится из графика.

___________________________________________________________________

Тема: Явление электромагнитной индукции

Сила тока в проводящем круговом контуре индуктивностью 100 мГн изменяется с течением временипо закону (в единицах СИ):

Абсолютная величина ЭДС самоиндукции в момент времени 2 с равна ____ ; при этом индукционный ток направлен …

			0,12 В; против часовой стрелки

Решение:
ЭДС самоиндукции, возникающая в контуре при изменении в нем силы тока I, определяется по формуле: , где L – индуктивность контура. Знак минус в формуле соответствует правилу Ленца: индукционный ток направлен так, что противодействует изменению тока в цепи: замедляет его возрастание или убывание.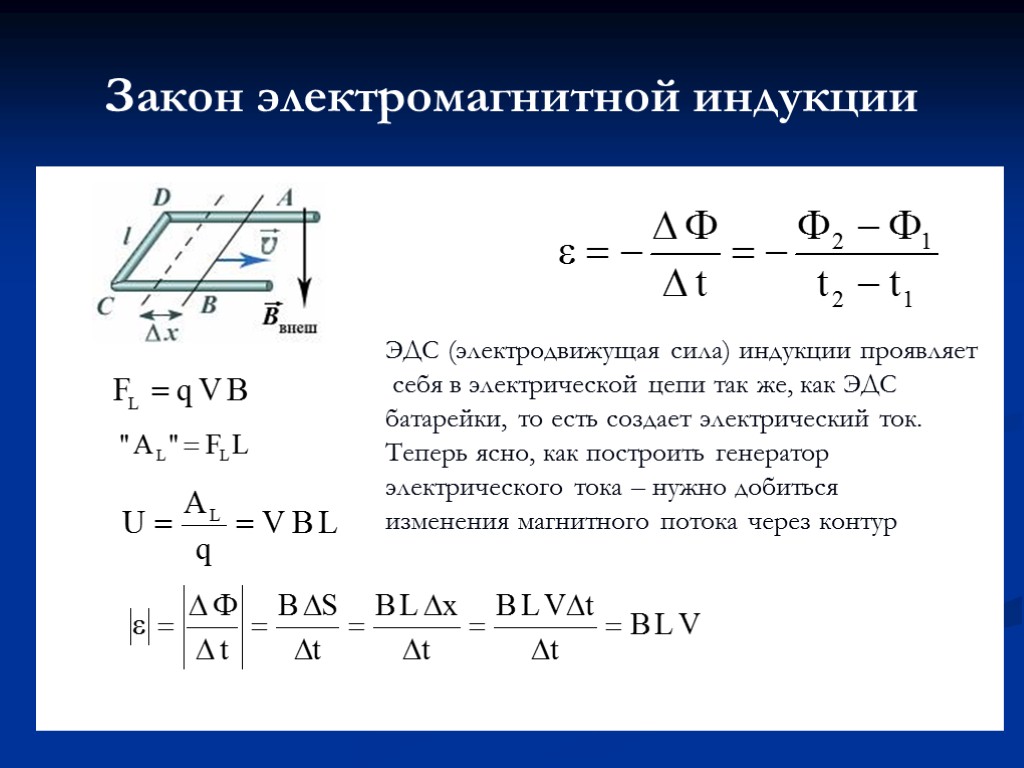 Таким образом, ЭДС самоиндукции равна . Абсолютная величина ЭДС самоиндукции равна , индукционный ток направлен против часовой стрелки. При этом учтено направление тока в контуре и его возрастание со временем (что следует из заданного закона изменения силы тока).

_______________________________________________________________

1. На рисунке представлена зависимость магнитного потока, пронизывающего некоторый контур, от времени:

График зависимости ЭДС индукции в контуре от времени представлен на рисунке …

2. По параллельным металлическим проводникам, расположенным в однородном магнитном поле, с постоянной скоростью перемещается проводящая перемычка, длиной (см. рис.). Если сопротивлением перемычки и направляющих можно пренебречь, то зависимость индукционного тока от времени можно представить графиком …

Решение:
При движении проводящей перемычки в магнитном поле в ней возникает ЭДС индукции и индукционный ток. Согласно закону Ома для замкнутой цепи, , а ЭДС индукции определяется из закона Фарадея: , где – магнитный поток сквозь поверхность, прочерчиваемую перемычкой при ее движении за промежуток времени . Учитывая, что (поскольку индукция магнитного поля перпендикулярна плоскости, в которой происходит движение проводника), а , где – длина перемычки, получаем: . Тогда , а величина индукционного тока . Поскольку то и индукционный ток не изменяется со временем.

3. По параллельным металлическим проводникам, расположенным в однородном магнитном поле, с постоянным ускорением перемещается проводящая перемычка, длиной (см. рис.). Если сопротивлением перемычки и направляющих можно пренебречь, то зависимость индукционного тока от времени можно представить графиком …

Решение:
При движении проводящей перемычки в магнитном поле в ней возникает ЭДС индукции и индукционный ток. Согласно закону Ома для замкнутой цепи, , а ЭДС индукции определяется из закона Фарадея: , где – магнитный поток сквозь поверхность, прочерчиваемую перемычкой при ее движении за промежуток времени . Учитывая, что (поскольку индукция магнитного поля перпендикулярна плоскости, в которой происходит движение проводника), а , где – длина перемычки, получаем: . Тогда , а величина индукционного тока . Поскольку , где а – ускорение перемычки, то индукционный ток возрастает со временем по линейному закону.
—————————————————————————————————-

4. Проводящая рамка вращается с постоянной угловой скоростью в однородном магнитном поле вокруг оси, лежащей в плоскости рамки и перпендикулярной вектору индукции (см. рис.). На рисунке также представлен график зависимости от времени потока вектора магнитной индукции, пронизывающего рамку.

Если максимальное значение магнитного потока мВб, сопротивление рамки Ом, а время измерялось в секундах, то закон изменения со временем силы индукционного тока имеет вид …

Решение:
Сила индукционного тока , где – ЭДС индукции, R – сопротивление рамки. В соответствии с законом Фарадея для электромагнитной индукции . Чтобы найти закон изменения ЭДС индукции со временем, необходимо знать зависимость от времени магнитного потока, пронизывающего рамку. Из приведенного графика следует, что , поскольку Тогда , а

5. Контур площадью м² расположен перпендикулярно к линиям магнитной индукции. Магнитная индукция изменяется по закону . ЭДС индукции, возникающая в контуре, изменяется по закону …

Решение:
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Поскольку плоскость контура перпендикулярна линиям магнитной индукции, где S – площадь контура. Таким образом, .

6. На рисунке представлена зависимость ЭДС индукции в контуре от времени.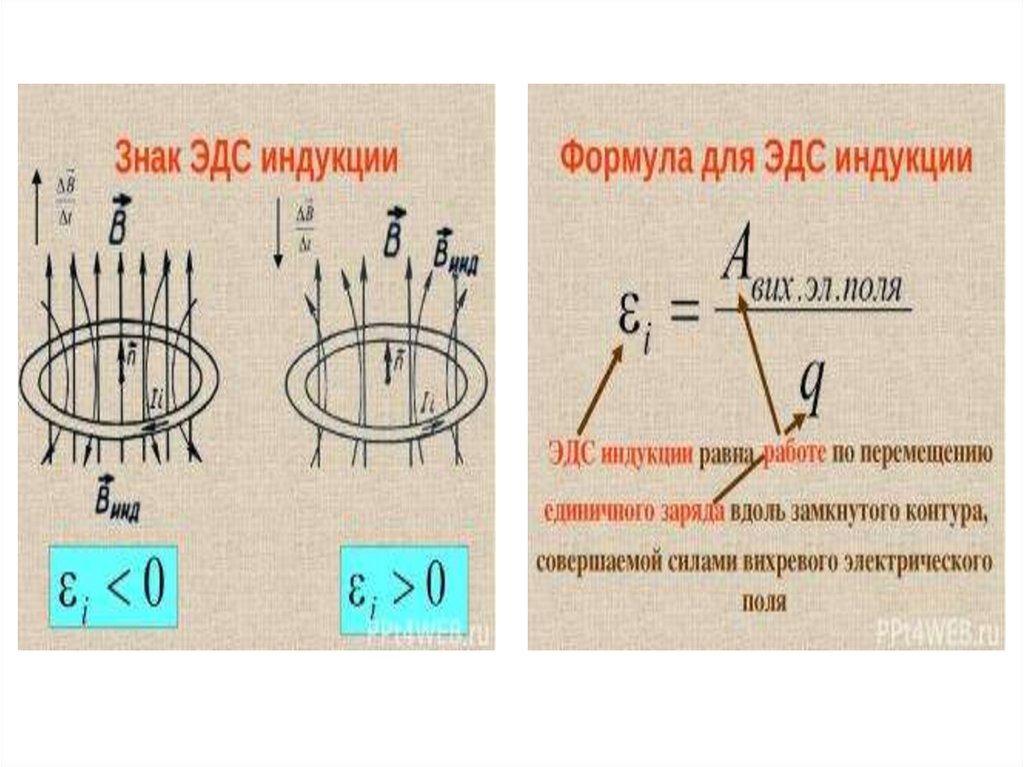 Магнитный поток сквозь площадку, ограниченную контуром, увеличивается со временем по линейному закону в интервале …

Е

Решение:
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Следовательно, если магнитный поток увеличивается со временем по линейному закону, то ЭДС индукции будет равна отрицательной постоянной величине, что имеет место в интервале Е.

7. На рисунке представлена зависимость ЭДС индукции в контуре от времени. Магнитный поток сквозь площадку, ограниченную контуром, увеличивается со временем по закону (а, b, c – постоянные) в интервале …

В

Решение:
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Следовательно, если магнитный поток увеличивается со временем по закону , то ЭДС индукции будет убывать со временем по линейному закону, что имеет место в интервале В.

8. Прямоугольная проволочная рамка расположена в одной плоскости с прямолинейным длинным проводником, по которому течет ток I. Индукционный ток в рамке будет направлен по часовой стрелке при ее …

поступательном перемещении в положительном направлении оси OX

Решение:
При изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в нем возникает индукционный ток, направление которого можно найти по правилу Ленца, согласно которому индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока. В данном случае в прямоугольной проволочной рамке индукционный ток будет протекать по часовой стрелке при ее поступательном перемещении в положительном направлении оси OX.

9. Прямоугольная проволочная рамка расположена в одной плоскости с прямолинейным длинным проводником, по которому течет ток I. Индукционный ток в рамке будет направлен по часовой стрелке при ее …

поступательном перемещении в отрицательном направлении оси OX

Решение:
При изменении магнитного потока сквозь поверхность, ограниченную замкнутым проводящим контуром, в нем возникает индукционный ток, направление которого можно найти по правилу Ленца, согласно которому индукционный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного потока. В данном случае в прямоугольной проволочной рамке индукционный ток будет протекать по часовой стрелке при ее поступательном перемещении в отрицательном направлении оси OX.

10. Проводящий плоский контур площадью 75 см² расположен в магнитном поле перпендикулярно линиям магнитной индукции. Если магнитная индукция изменяется по закону мТл, то ЭДС индукции, возникающая в контуре в момент времени (в мВ), равна …

0,18

Решение:
В соответствии с законом Фарадея для электромагнитной индукции электродвижущая сила индукции в замкнутом проводящем контуре численно равна и противоположна по знаку скорости изменения магнитного потока сквозь поверхность, ограниченную этим контуром: . Поскольку плоскость контура перпендикулярна линиям магнитной индукции, где S – площадь контура. Таким образом,

12. Проводящая рамка вращается с постоянной угловой скоростью в однородном магнитном поле вокруг оси, лежащей в плоскости рамки и перпендикулярной вектору индукции (см. рис.). На рисунке также представлен график зависимости от времени потока вектора магнитной индукции, пронизывающего рамку.

Если максимальное значение магнитного потока мВб, а время измерялось в секундах, то закон изменения со временем ЭДС индукции имеет вид …



ЭДС индукции и магнитный поток | Физика |

Цели обучения

К концу этого раздела вы сможете:

• Рассчитать поток однородного магнитного поля через петлю произвольной ориентации.
• Описать методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.

Устройство, использованное Фарадеем для демонстрации того, что магнитные поля могут создавать токи, показано на рисунке 1. Когда переключатель замкнут, в катушке в верхней части железного кольца создается магнитное поле, которое передается на катушку в верхней части железного кольца. нижняя часть кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке на дне. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр регистрирует ток в одном направлении в катушке на дне. (Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель размыкается, гальванометр обнаруживает ток в противоположном направлении. Интересно, что если переключатель остается замкнутым или разомкнутым какое-то время, ток через гальванометр отсутствует. Замыкание и размыкание переключателя индуцирует ток. Именно изменение в магнитном поле создает ток. Более важным, чем текущий ток, является ЭДС, которая его вызывает. Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.

Рис. 1. Аппарат Фарадея для демонстрации того, что магнитное поле может производить ток. Изменение поля, создаваемого верхней катушкой, индуцирует ЭДС и, следовательно, ток в нижней катушке. Когда переключатель размыкается и замыкается, гальванометр регистрирует токи в противоположных направлениях. Через гальванометр не протекает ток, когда переключатель остается замкнутым или разомкнутым.

Эксперимент, который легко выполнить и часто проводят в физических лабораториях, показан на рис. 2. ЭДС индуцируется в катушке, когда стержневой магнит вталкивается в нее и из нее. ЭДС разных знаков создаются движением в противоположных направлениях, а также изменением полярности ЭДС на противоположное. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.

Рис. 2. Движение магнита относительно катушки создает ЭДС, как показано на рисунке. Такие же ЭДС возникают, если катушку перемещать относительно магнита. Чем больше скорость, тем больше величина ЭДС, а ЭДС равна нулю, когда нет движения.

Метод индукции ЭДС, используемый в большинстве электрических генераторов, показан на рисунке 3. Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут исследованы в последующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (еще одна симметрия).

Рис. 3. Вращение катушки в магнитном поле создает ЭДС. Это основная конструкция генератора, в котором работа по вращению катушки преобразуется в электрическую энергию. Обратите внимание, генератор очень похож по конструкции на двигатель.

Итак, мы видим, что изменение величины или направления магнитного поля создает ЭДС. Эксперименты показали, что существует решающая величина, называемая магнитным потоком , Φ , определяемая как

Φ  =  BA  cos θ ,

где B — напряженность магнитного поля на площади A под углом θ к перпендикуляру к площади, как показано на рисунке 5. Любое изменение магнитного потока Φ индуцирует ЭДС . Этот процесс определяется как электромагнитная индукция . Единицами магнитного потока Φ являются Т ⋅ м ² . Как видно на рис. 4, B cos θ = B _⊥ , которая является компонентой B , перпендикулярной площади A . Таким образом, магнитный поток равен Φ = B _⊥ A , произведение площади и составляющей магнитного поля, перпендикулярной ей.

Рис. 4. Магнитный поток Φ связан с магнитным полем и площадью, над которой оно существует. Поток Φ = BA cos θ относится к индукции; любое изменение Φ индуцирует ЭДС.

Вся индукция, включая примеры, приведенные до сих пор, возникает из-за некоторого изменения магнитного потока Φ . Например, Фарадей менял B и, следовательно, Φ при размыкании и замыкании переключателя в своем аппарате (показанном на рис. 1). Это также верно для стержневого магнита и катушки, показанных на рисунке 2. При вращении катушки генератора угол θ и, следовательно, Φ изменяется. То, насколько велика ЭДС и какое направление она принимает, зависит от изменения Φ и от того, как быстро это изменение происходит, как будет рассмотрено в следующем разделе.

Резюме раздела

• Решающей величиной индукции является магнитный поток Φ , определяемый как Φ = BA cos θ , где B — напряженность магнитного поля на площади A под углом перпендикуляр к площади.
• Единицами магнитного потока Φ являются Тл⋅м ² .
• Любое изменение магнитного потока Φ индуцирует ЭДС — процесс определяется как электромагнитная индукция.

Концептуальные вопросы

1. Как многоконтурные катушки и железное кольцо в варианте аппарата Фарадея, показанном на рисунке 1, улучшают наблюдение ЭДС индукции?

2. Когда магнит втягивается в катушку, как показано на рис. 2(а), как направлена ​​сила, действующая на магнит со стороны катушки? Нарисуйте диаграмму, показывающую направление тока, индуцируемого в катушке, и создаваемое им магнитное поле, чтобы обосновать свой ответ.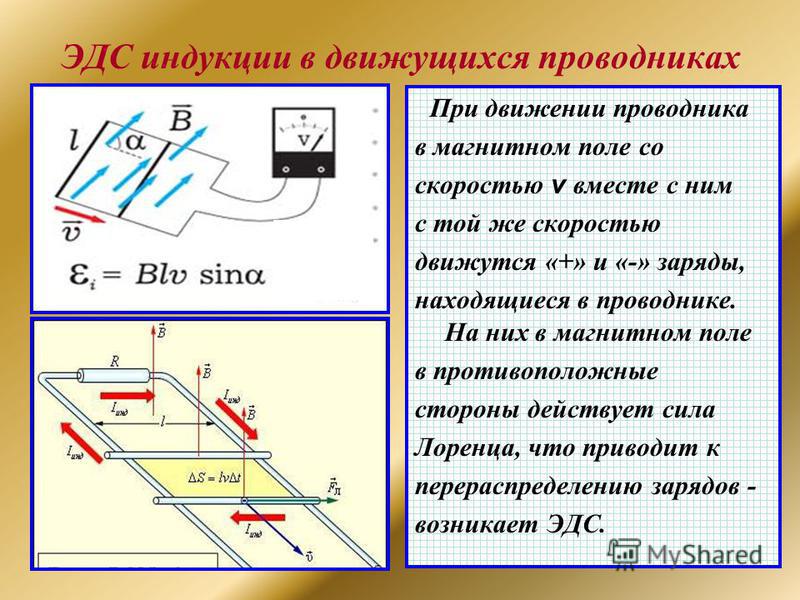 Как величина силы зависит от сопротивления гальванометра?

3. Объясните, как магнитный поток может быть равен нулю, если магнитное поле не равно нулю.

4. Наводится ли ЭДС в катушке на рисунке 5, когда она растягивается? Если да, укажите почему и укажите направление индукционного тока.

Рис. 5. Круглая катушка проволоки натянута в магнитном поле.

Задачи и упражнения

1. Каково значение магнитного потока в катушке 2 на рисунке 6 из-за катушки 1?

Рис. 6. (а) Плоскости двух катушек перпендикулярны. б) провод перпендикулярен плоскости катушки.

2. Какова величина магнитного потока через катушку на рисунке 6(b) из-за провода?

Глоссарий

магнитный поток:

величина магнитного поля, проходящего через определенную площадь, рассчитанная по формуле Φ = B A cos θ , где B   – напряженность магнитного поля на площади 90 0138 A угол θ с перпендикуляром к площади

электромагнитная индукция:

процесс наведения ЭДС (напряжения) при изменении магнитного потока

Упражнения

1. Ноль

Лицензии и ссылки

Контент по лицензии CC, совместно используемый ранее

• College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Атрибуция . Условия лицензии : Находится в Лицензии

23.1 ЭДС индукции и магнитный поток — College Physics

Сводка

• Рассчитайте поток однородного магнитного поля через петлю произвольной ориентации.
• Описать методы создания электродвижущей силы (ЭДС) с помощью магнитного поля или магнита и проволочной петли.

Устройство, использованное Фарадеем для демонстрации того, что магнитные поля могут создавать токи, показано на рисунке 1. Когда переключатель замкнут, магнитное поле создается в катушке в верхней части железного кольца и передается на катушку в нижней части. часть кольца. Гальванометр используется для обнаружения любого тока, наведенного в катушке на дне. Было обнаружено, что каждый раз, когда переключатель замыкается, гальванометр регистрирует ток в одном направлении в катушке на дне. (Вы также можете наблюдать это в физической лаборатории.) Каждый раз, когда переключатель размыкается, гальванометр обнаруживает ток в противоположном направлении. Интересно, что если переключатель остается замкнутым или разомкнутым какое-то время, ток через гальванометр отсутствует. Замыкание и размыкание переключателя индуцирует ток. Это изменение магнитного поля создает ток. Более важным, чем текущий ток, является ЭДС , которая его вызывает. Ток является результатом ЭДС , индуцированной изменяющимся магнитным полем , независимо от того, есть ли путь для протекания тока.

Рис. 1. Аппарат Фарадея для демонстрации того, что магнитное поле может создавать ток. Изменение поля, создаваемого верхней катушкой, индуцирует ЭДС и, следовательно, ток в нижней катушке. Когда переключатель размыкается и замыкается, гальванометр регистрирует токи в противоположных направлениях. Через гальванометр не протекает ток, когда переключатель остается замкнутым или разомкнутым.

Эксперимент, который легко провести и который часто проводят в физических лабораториях, показан на рисунке 2. ЭДС индуцируется в катушке, когда стержневой магнит вдвигается и выталкивается из нее. ЭДС разных знаков создаются движением в противоположных направлениях, а также изменением полярности ЭДС на противоположное. Те же результаты получаются, если перемещать катушку, а не магнит — важно относительное движение. Чем быстрее движение, тем больше ЭДС, а когда магнит неподвижен относительно катушки, ЭДС отсутствует.

Рис. 2. Движение магнита относительно катушки создает ЭДС, как показано на рисунке. Такие же ЭДС возникают, если катушку перемещать относительно магнита. Чем больше скорость, тем больше величина ЭДС, а ЭДС равна нулю, когда нет движения.

Метод индукции ЭДС, используемый в большинстве электрических генераторов, показан на рисунке 3.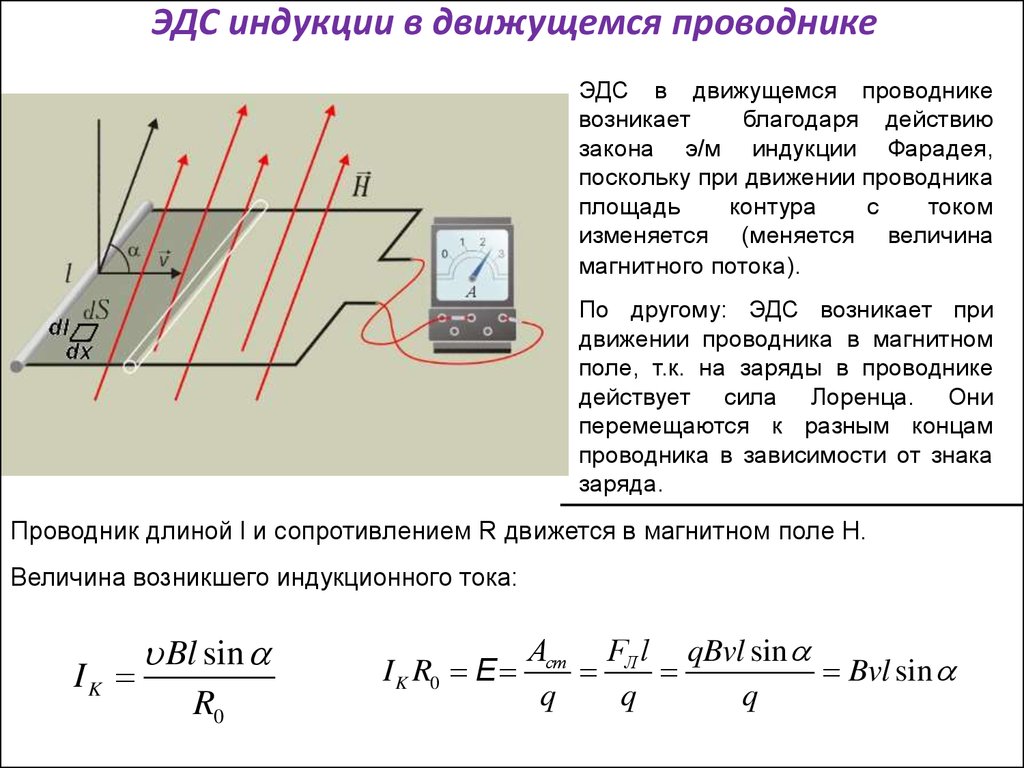 Катушка вращается в магнитном поле, создавая ЭДС переменного тока, которая зависит от скорости вращения и других факторов, которые будут исследованы в последующих разделах. Обратите внимание, что генератор очень похож по конструкции на двигатель (еще одна симметрия).

Рис. 3. Вращение катушки в магнитном поле создает ЭДС. Это основная конструкция генератора, в котором работа по вращению катушки преобразуется в электрическую энергию. Обратите внимание, генератор очень похож по конструкции на двигатель.

Итак, мы видим, что изменение величины или направления магнитного поля создает ЭДС. Эксперименты показали, что существует решающая величина, называемая магнитным потоком, [латекс]\жирныйсимвол{\фи}[/латекс] , определяемая как

[латекс]\boldsymbol{\phi = BA \;\textbf{cos} \;\theta},[/latex] 92}[/латекс]. Как видно на рисунке 4, [latex]\boldsymbol{B \;\textbf{cos} \;\theta = B_{\perp}}[/latex], который является компонентом [latex]\boldsymbol{B}[ /latex] перпендикулярно области [latex]\boldsymbol{A}[/latex]. Таким образом, магнитный поток представляет собой [латекс]\boldsymbol{\phi = B_{\perp} A}[/латекс], произведение площади и перпендикулярной к ней составляющей магнитного поля.

Рис. 4. Магнитный поток Φ связан с магнитным полем и площадью, над которой оно существует. поток Φ = BA cos θ относится к индукции; любое изменение Φ индуцирует ЭДС.

Вся индукция, включая примеры, приведенные до сих пор, возникает из-за некоторого изменения магнитного потока [латекс]\boldsymbol{\phi}[/латекс]. Например, Фарадей менял [латекс]\жирныйсимвол{B}[/латекс] и, следовательно, [латекс]\жирныйсимвол{\фи}[/латекс] при размыкании и замыкании переключателя в своем устройстве (показанном на рисунке 1). Это также верно для стержневого магнита и катушки, показанных на рис. 2. При вращении катушки генератора угол [латекс]\жирныйсимвол{\тета}[/латекс] и, следовательно, [латекс]\жирныйсимвол{\фи }[/latex] изменен. То, насколько велика ЭДС и какое направление она принимает, зависит от изменения [латекс]\жирныйсимвол{\фи}[/латекс] и от того, насколько быстро происходит это изменение, как будет рассмотрено в следующем разделе. 92}[/латекс].

Любое изменение магнитного потока [латекс]\boldsymbol{\phi}[/латекс] индуцирует ЭДС — процесс определяется как электромагнитная индукция.

магнитный поток

количество магнитного поля, проходящего через определенную область, рассчитанное с помощью [латекс]\boldsymbol{\phi = BA \;\textbf{cos} \; \theta}[/latex], где [latex]\boldsymbol{B}[/latex] – напряженность магнитного поля на площади [латекс]\boldsymbol{A}[/latex] под углом [латекс]\boldsymbol{\ theta}[/latex] с перпендикуляром к площади

электромагнитная индукция

процесс наведения ЭДС (напряжения) при изменении магнитного потока

Физическая модель низкочастотной электромагнитной индукции в ближнем поле, основанная на прямом взаимодействии электронов передатчика и приемника

Proc Math Phys Eng Sci. 2016 июль; 472(2191): 20160338.

doi: 10.1098/rspa.2016.0338

, ¹ , ¹ , ² , ^{0 1 и 0 10069 1}

Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности

Разработана физическая модель электромагнитной индукции, которая напрямую связывает силы между электронами в обмотках передатчика и приемника концентрических коаксиальных конечных катушек в ближней зоне. Применяя принцип суперпозиции, вклады от ускоряющих электронов в последовательных петлях тока суммируются, что позволяет точно предсказать пиковое индуцированное напряжение в приемнике. Результаты показывают хорошее соответствие между теорией и экспериментом для различных приемников с разным радиусом, в пять раз превышающим радиус передатчика. Обсуждаются ограничения линейной теории электромагнитной индукции с точки зрения неравномерного распределения тока, вызванного скин-эффектом. В частности, объяснение с точки зрения электромагнитной энергии и теоремы Пойнтинга противопоставляется более прямому объяснению, основанному на переменной индукции нити накала по поперечному сечению проводника. Поскольку прямая физическая модель, разработанная здесь, имеет дело только с силами между дискретными элементами тока, ее можно легко адаптировать для соответствия различным геометриям катушки и широко применять в различных областях исследований, таких как связь ближнего поля, проектирование антенн, беспроводная передача энергии, датчики. приложений и не только.

Ключевые слова: катушки , электромагнитная индукция, распространение, беспроводная передача энергии, соленоиды, трансформаторы. [2,3] и беспроводной передачи энергии [4]. Они все чаще используются в беспроводных подземных сенсорных сетях [5,6] для таких приложений, как мониторинг окружающей среды (в почве [7] и воде [8]), обследование оползней [9].] и наблюдения за подземным трубопроводом [10]. Традиционные подходы с использованием беспроводных датчиков сдерживаются сложными средами распространения (например, почвой, камнем, водой). Однако при использовании низкочастотных магнитных полей ближнего поля трудности, связанные с задержкой распространения, замираниями и многолучевым распространением, становятся менее заметными. Термин ближнее поле относится к безызлучательному распространению на короткие расстояния магнитных или электрических полей вследствие индуктивной или емкостной связи соответственно. Напротив, дальнее поле относится к электромагнитным полям излучения на больших расстояниях от источника, которые получили широкое распространение [11–14].

Было предпринято несколько ценных исследовательских инициатив по моделированию электромагнитных полей в ближней зоне, которые обычно включают точные представления и/или интенсивные вычисления [15–23], которые, согласно Микки и Антару [24], «не могут привести к значительным результатам». понимание общих вопросов, таких как природа электромагнитного излучения или внутренняя структура антенны ближнего поля». Тем не менее, моделирование ближнего магнитного поля является важной задачей, например, при проектировании сложных схем для определения соответствия стандартам ЭМС [25].

В этой статье мы развиваем метод для случая многовитковой конечной пары катушек передатчика и приемника круговой геометрии, расположенных концентрически.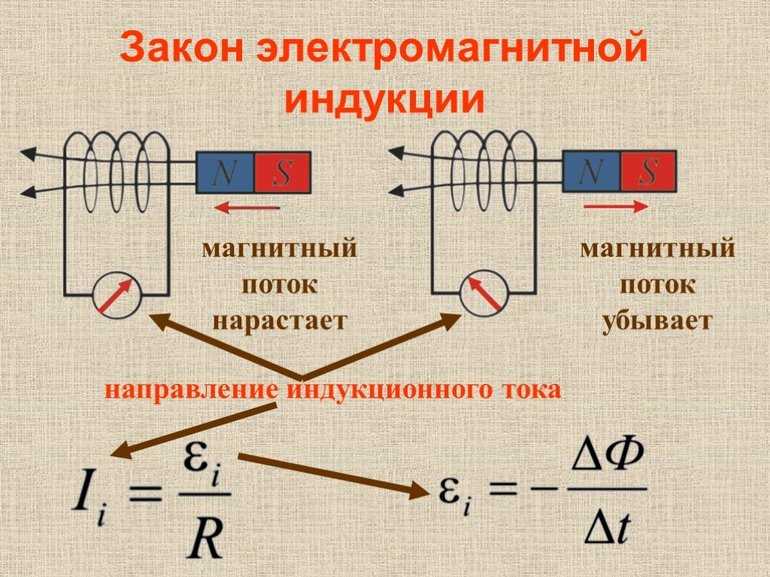 В основе этого метода, адаптированного для расчета ЭДС индукции в приемнике на некотором расстоянии от источника, лежит формула силы Вебера, которую можно рассматривать как модификацию закона Кулона для зарядов, находящихся в относительном движении [26–32] . Эта сила напрямую связана с силой между движущимися зарядами с точки зрения их смещения, относительной радиальной скорости и относительного радиального ускорения в дискретной системе.

Определение границ области ближнего поля является неоднозначной задачей, так как это зависит от геометрии и возбуждения рассматриваемого передатчика. Микки и Антар справедливо подчеркивают в своем подробном и всестороннем обзоре теории антенн в ближнем поле «необходимость продолжительного, всестороннего и строгого рассмотрения темы ближнего поля, рассмотрения, учитывающего специфический характер антенны». электромагнитное поведение в этой зоне [24]». Принято считать, что «ближнее поле» включает, по крайней мере, окружающее пространство до расстояния в одну длину волны и вполне может простираться дальше. Мы также представляем предварительные результаты того, как индуцированное напряжение изменяется как с расстоянием, так и с частотой на основе взаимодействий между частицами в этой зоне.

Во-первых, мы исследуем теоретические основы низкочастотной электромагнитной индукции. При этом мы разрабатываем модель прямого действия, которая напрямую связана с распределением тока в конечных катушках передатчика и приемника. Модель подтверждается экспериментальными измерениями путем расчета отклика приемника при увеличении расстояния от источника. Наконец, мы обсуждаем преимущества и ограничения модели и даем предложения для дальнейших исследований.

Рассматриваемый случай электромагнитной индукции иногда называют трансформаторной индукцией. Устройство состоит из коаксиальных катушек, расположенных концентрически, при этом передатчик (T) определяется внутренней катушкой, а приемник (R) — внешней, как показано на рис.

Открыть в отдельном окне

Конфигурация коаксиальных конечных катушек с воздушным сердечником. Передатчик (T) длиной, L _T , радиусом, r _T с N _T плотно навитых витков расположен внутри приемника (R) длиной, L _{R , радиус, r R и N R плотно намотанные витки. (Онлайн-версия в цвете.)}

(a) Закон индукции Фарадея

Закон Фарадея связывает ЭДС индукции e в замкнутой цепи со скоростью изменения магнитного потока в этой цепи. Обычно это дается

e=−d∅dt,

2,1

где ∅ — магнитный поток (примечание: уравнение (2.1) строго справедливо только для провода бесконечно малого сечения). Для устройства катушка передатчика питается переменным током, I =  I ₀ sin⁡ ω t , где I ₀ — пиковый ток, а ω — радиальная частота, определяемая выражением ω  = 2 πf . Магнитный поток через приемник следует за током так, что ∅=∅ ₀ sin 2 πft , а ЭДС индукции в приемнике определяется выражением

eR=−d∅dt=−∅02πf cos⁡(2πft).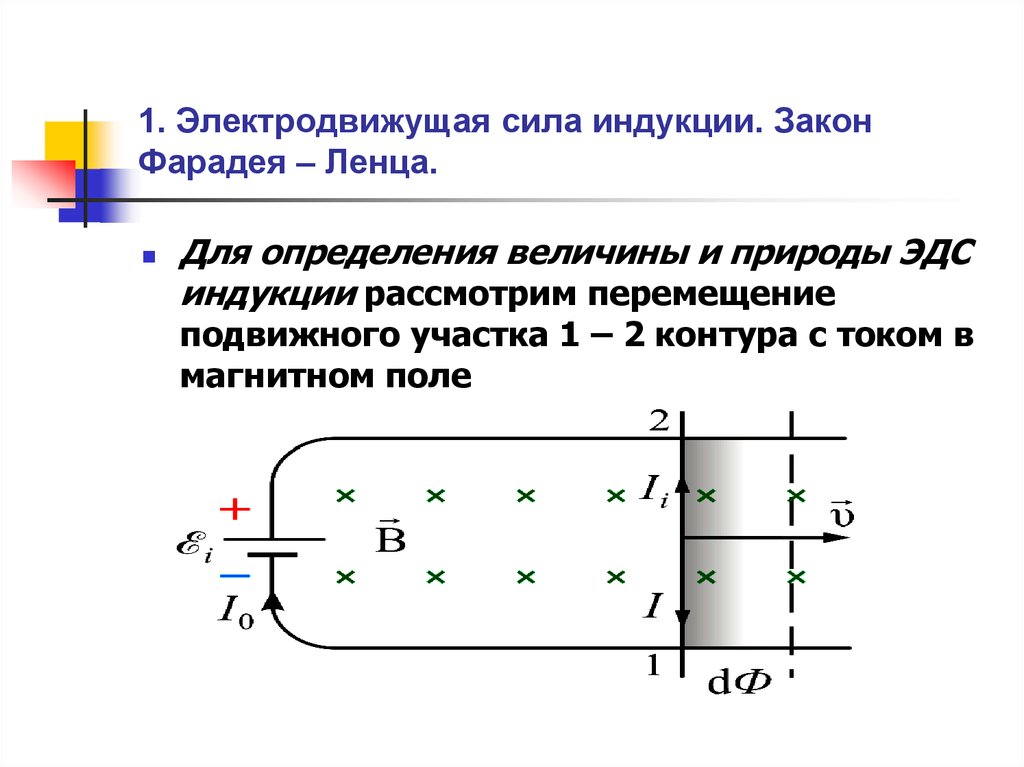

2,2

Для случая бесконечной многовитковой катушки плотность магнитного потока в центральной области равна B = μ ₀ NI ₀ , где μ ₀ — это проницаемость свободного пространства, а N — плотность обмотки (= N / L . Пиковый магнитный поток на виток, соединяющий передатчик и приемник, определяется как произведение плотности потока на площадь поперечного сечения одного витка ( Bπr ² _T ). Предполагая, что приемник намотан близко к передатчику, так что r _R − r _T ≅0, то пиковая ЭДС наведения в приемнике определяется выражением

(ER) 0 = −2π2rt2ntnRi0fε0C2,

2,3

, где ε ₀ = проницаемость свободного пространства, C = скорость света и N _{T .}

(b) Формула взаимной индуктивности Неймана

Более общий метод расчета ЭДС между замкнутыми цепями можно получить из формулы Неймана. Предполагая, что плотность магнитного потока пропорциональна току (закон Био–Савара) и выражая поток через векторный потенциал ( A ), then for closed loops T and R with elements d l _T , d l _R at a distance r apart где

AT=μ0I04π∮dlTr

Так что

∅R=μ0IT4π∮∮dlTr⋅dlR

Потому что ∅ _R = M _RT I _T , где M _RT = M _TR , что является взаимной индуктивностью двух контуров, тогда по формуле Неймана

MRT=μ04π∮∮1rdlT⋅dlR.

2.4

Взаимная индуктивность между двумя замкнутыми цепями является геометрической величиной, относящейся к размеру, форме и взаимному расположению двух цепей, и не зависит от того, какая цепь действует как передатчик или приемник. Переписав закон Фарадея с учетом взаимной индуктивности ( M ), переменный ток передатчика I и связанный с ним изменяющийся магнитный поток, ЭДС индукции в приемнике определяется выражением

eR=−d∅dt=−MdIdt.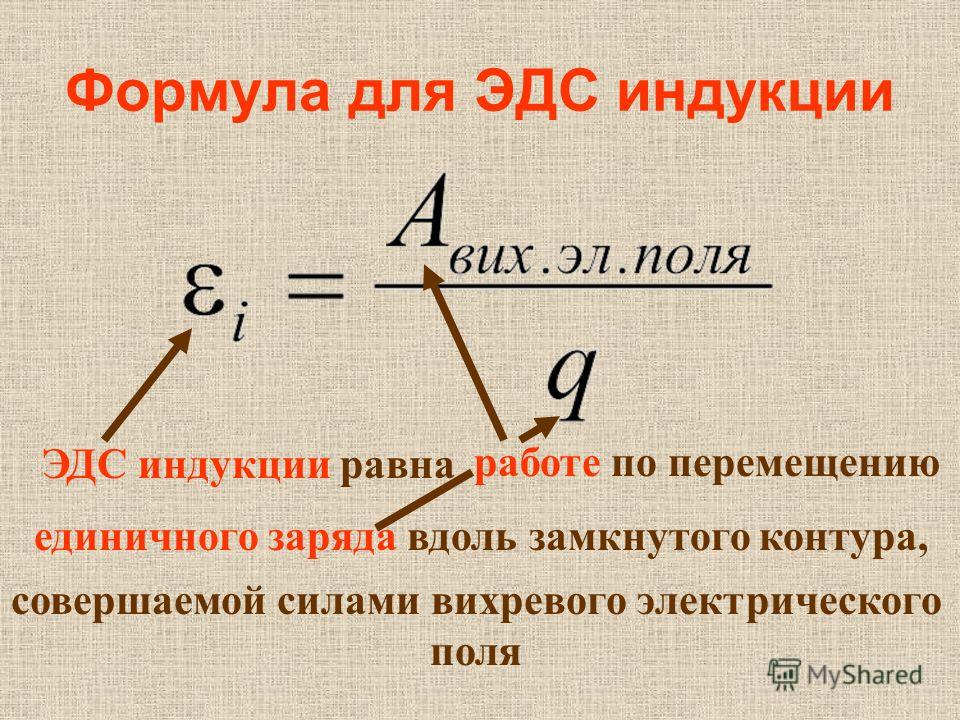

Предполагая, как и ранее, что приемник намотан близко к передатчику, так что r _R − r _T ≅0. Тогда, учитывая, что M = μ ₀ πr ² _T ( N _T / l _T ) и I = I ₀  sin⁡ ω t

(eR)0=−2π2rT2nTNRI0fε0c2

, что совпадает с (2.3).

(c) Решение Гровера, когда

r _T ≠ r _R

Конкретное решение для концентрических коаксиальных катушек различных радиусов приведено в [33] по формуле

M=0,004π2rT2nTNR(B1r1−B2r2),

где r1=rR2+(1/4)(lT+lR)2 и r2=rR2+(1/4)(lT−lR)2

Функции B ₁ и B ₂ зависят от параметров, p12 = RR2/R12, P22 = RR2/R22, α = R _T / R _{RAIN BAINDINGED TA} / R _{777 RAINDINED TA} / R _{777777 RANIDENDAIND TA} / R 777777777 7.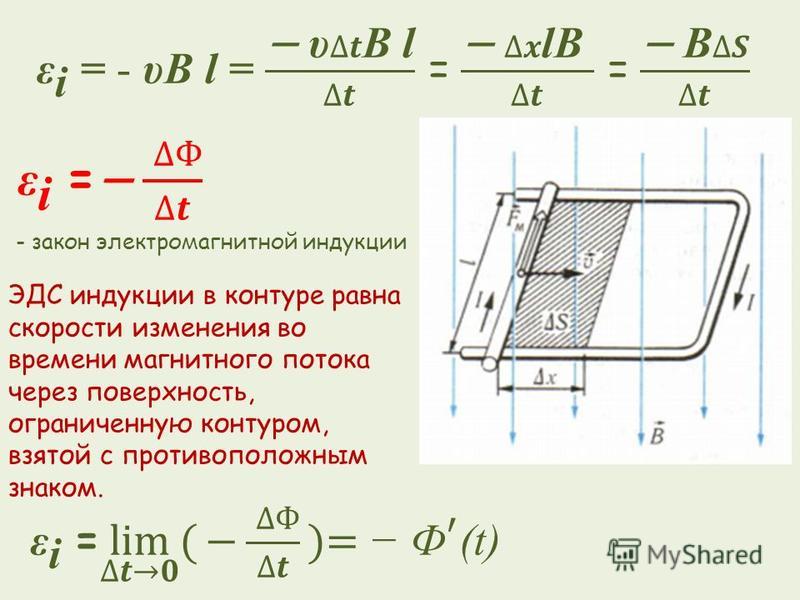 таблицы в ссылке [33]. Например, используя данные конкретной катушки в настоящем эксперименте, значения для M были рассчитаны как 9,22  мГн ( r _T / r _R =1) и 8,66 мГн ( r _T / r _{R 8 = 0.0), когда приемник дает приблизительно 7% увеличения от} =0. быть тесно намотан.

(d) Векторный потенциал

Векторный потенциал вне длинного соленоида определяется как A =∅/2 πr , где ∅ — общий магнитный поток внутри катушки передатчика. Тогда электрическое поле снаружи передатчика равно E =-∂ A /∂ t =-(1/2 πr )(d∅/ dt ). Приравнивая ∅= LI = μ ₀ nIπr ² _T , где L — это индуктивность на единицу длины n витков1 бесконечной многовитковой катушки1 единица длины, затем для одной петли радиусом r _R , окружающей передатчик

E = −½( μ ₀ n r _T 2 π f ) I ₀ cos⁡ ω t .

Интегрирование по одному контуру и включение множителя для учета N _R оборотов приемника

(eR)0=∮E.dl=2πrTE=−2π2rT2nTNRI0fε0c2

, что опять равно (2.3).

Рассмотрим два отдельных круговых контура передатчика (T) и приемника (R). Петля передатчика имеет радиус r _T и возбуждается переменным током заданной частоты f , а окружающий контур приемника имеет радиус r _R , по которому индуцируется ЭДС ( r _{R > r T ), как показано на .}

Открыть в отдельном окне

Геометрия одиночных круговых петель, составляющих часть катушек передатчика и приемника. На вставке показана геометрия, спроецированная на двумерную плоскость ( x – и ).

Используя декартову систему координат, мы определяем центр контура приемника как начало координат. При применении закона силы Вебера к этому случаю сила определяется между линейным элементом заряда (= r _T δθ ) в передатчике, расположенном в точке M , и единицей заряда, расположенной в приемнике в точке N , где расстояние между этими точками равно MN = r .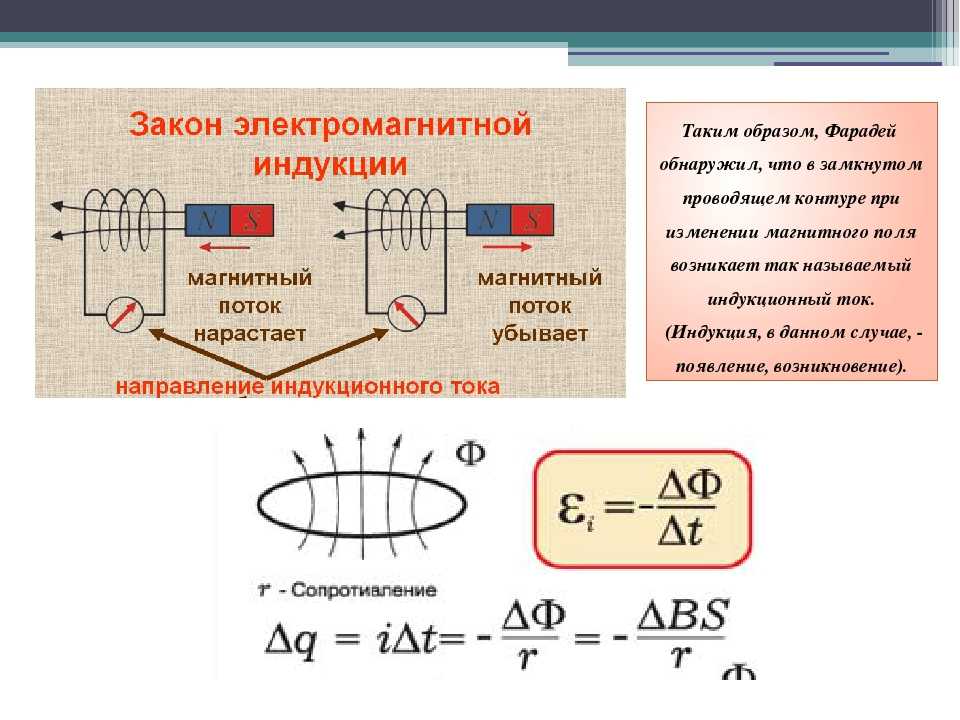 Используя формулу силы Вебера, адаптированную в терминах относительной скорости [32], сила, разрешенная вдоль 9— единичный вектор вдоль r , u _r — относительная скорость вдоль r и u — относительная скорость между M и N . В этом случае, когда в приемнике нет чистого потока тока, относительная скорость между M и N определяется скоростью дрейфа электронов, v , на M в контуре передатчика. Отсюда в (3.1) u ² = v ² . The relative velocity along r is given as u _r = d r /d t =  v  cos⁡ β =  v b  sin⁡ θ / р . Оба члена u ² и ur2, которые появляются в (3.1), включают члены v ² , которыми можно пренебречь для малых токов, оставив только член ускорения, r (d ² R /D T ) = R (D U _R /D T ), а R определяется по тригонометрии, R2 = RT2+RR2O 2ORR. я2. Дифференцируя U _R и отмечая, что V = R _T (D θ /D T ), игнорируя V ), игнорируя V 013 013 013 013 013 013 013 . u _r /d t = r _R  sin⁡ θ (d v /d t ). Поскольку I = n ′ Ave , то v˙=I˙/n′Ae и, следовательно,

Fr=rTrR sin⁡θ4πε0c2r2I˙.

3,2

Разрешение вдоль касательной к петле приемника дает силу на единицу заряда, E _T = F _R COS⁡ γ , где COS⁡ γ = — γ , где COS⁡ γ = — γ , где COS⁡ γ = — γ , где COS⁡ γ = — γ , где COS⁡ γ = — γ , где COS⁡ γ = γ , где COS⁡ γ = γ . _T  sin⁡ θ / r и, следовательно,

ET=-rT2rRI˙4πε0c2sin2θr3δθ.

3,3

ЭДС индукции в приемнике определяется путем интегрирования по замкнутому контуру так, что

er=∮E.dl=2πrRET=−2πrT2rR2I˙4πε0c2sin2θr3δθ.

3,4

Дифференцируя ток передатчика, мы получаем пиковую ЭДС в одном контуре приемника как

(eR)0=πrT2rR2I0ε0c2f∫02πsin2θr3dθ.

3,5

Для расчета ЭДС индукции в конечной многовитковой катушке принцип суперпозиции применяется к вкладам тока от каждого отдельного витка катушки. Подынтегральная функция из (3.5) вычисляется для диапазона z -значения с каждого хода. Значения z относятся к вертикальному расстоянию между витками, выраженному в единицах диаметра провода, d . Тогда с помощью стандартного численного интегрирования (правило трапеций с интервалами 5 ^°) получаем где +z2. Коэффициент 2 учитывает вклад обоих слоев передатчика (т. е. катушка передатчика имеет двойную обмотку). Матрица имеет 20 ( N _R ) строк по 650 ( N _T /2) столбцов, представляющих все вклады отдельных витков, где z -значение равно нулю для случая, когда отдельные излучающая и приемная катушки повороты прямо совмещены. Суммирование в (3.6) производится для всех отдельных членов матрицы. Например, суммирование первой строки матрицы дает индуцированное напряжение в первом витке приемника из всех 650 отдельных витков передатчика (см. приложение А).

Для проверки вышеупомянутого подхода были проведены следующие экспериментальные измерения. Экспериментальная установка состоит из конечной коаксиальной внутренней катушки передатчика и внешней катушки приемника, как показано на рис. Передающая (внутренняя) катушка длиной L _T =0,5 м состоит из 1300 витков, дважды намотанных одножильным эмалированным медным проводом диаметром 0,7 мм и плотностью намотки =2600 витков на метр на каркасе из радиус, r _T примерно 0,0292 м. Были использованы три приемные катушки с одинаковой плотностью витков и числом витков ( N _R = 20), но с разными радиусами r _R 0,0375, 0,075 и 0,15 м.

Катушка передатчика была подключена к цифровому генератору сигналов (Lascells, Великобритания), обеспечивающему синусоидальный ток передатчика 3 мА (среднеквадратичное значение), измеренный 5,5-разрядным мультиметром Keithley в диапазоне частот 0–14 кГц. Одновременно измерялось напряжение на приемнике с помощью цифрового осциллографа (Tektronix, США). Принципиальная принципиальная схема показана на . Для улучшения отношения сигнал-шум катушка приемника была экранирована от внешних помех по всей ее окружности с помощью экрана из мю-металла (полностью термообработанный, толщиной 0,35 мм, ASTM A753 Alloy 4, Magnetic Shields, Великобритания). Все расчеты выполнены с использованием программы Matlab 2014a (MathWorks, США).

Открыть в отдельном окне

Принципиальная схема экспериментальной установки для измерения ЭДС индукции в приемной катушке.

Результаты экспериментов суммированы в –. показывает ЭДС приемника (от пика до пика) в зависимости от частоты для двух разных радиусов катушки приемника 3,75 и 15  см. Меньшая приемная катушка находится на расстоянии менее примерно 1 см от внешней поверхности передающей катушки, тогда как большая приемная катушка находится на расстоянии примерно 12 см от передающей катушки, а ее диаметр примерно в пять раз больше диаметра передающей катушки. Обе катушки следуют одной и той же тенденции: ЭДС индукции больше для катушки с меньшим радиусом (т.е. ближе к передатчику), чем для большей для каждого измерения. Первоначально тренд ЭДС индукции в зависимости от частоты соответствует линейной характеристике. Это хорошо видно в том числе и смоделированные данные, рассчитанные по (3.6) с эквивалентными параметрами модели. На графике рассчитанный модельный тренд в зависимости от радиусов приемника сравнивается с результатами измерений для трех различных экспериментальных радиусов катушки приемника ( r _R =0,0375, 0,075, 0,15 м) на разных частотах.

Открыть в отдельном окне

ЭДС индукции ( пик – пик , мВ) отклик от частоты для радиусов приемника 3,75 и 15 см. (Онлайн-версия в цвете.)

Открыть в отдельном окне

ЭДС индукции ( пик – пик , мВ) в зависимости от частоты в диапазоне 1–8  кГц по сравнению с расчетными данными для радиусов приемника 3,75 и 15 см. (Онлайн-версия в цвете.)

Открыть в отдельном окне

Расчетная ЭДС индукции ( пк – пк , мВ) в зависимости от радиуса приемника для диапазона частот, дополненная измерениями для радиусов приемника 3,75, 7 и 15 см для f ≤ 5 кГц. (Онлайн-версия в цвете.)

Преимущество формулировки, основанной на Вебере, заключается в том, что она может легко работать с различными радиусами приемника и передатчика. Сравнение между экспериментом и теорией показано в и , где смоделированные данные находятся в пределах погрешности эксперимента, в линейном режиме ( f < приблизительно .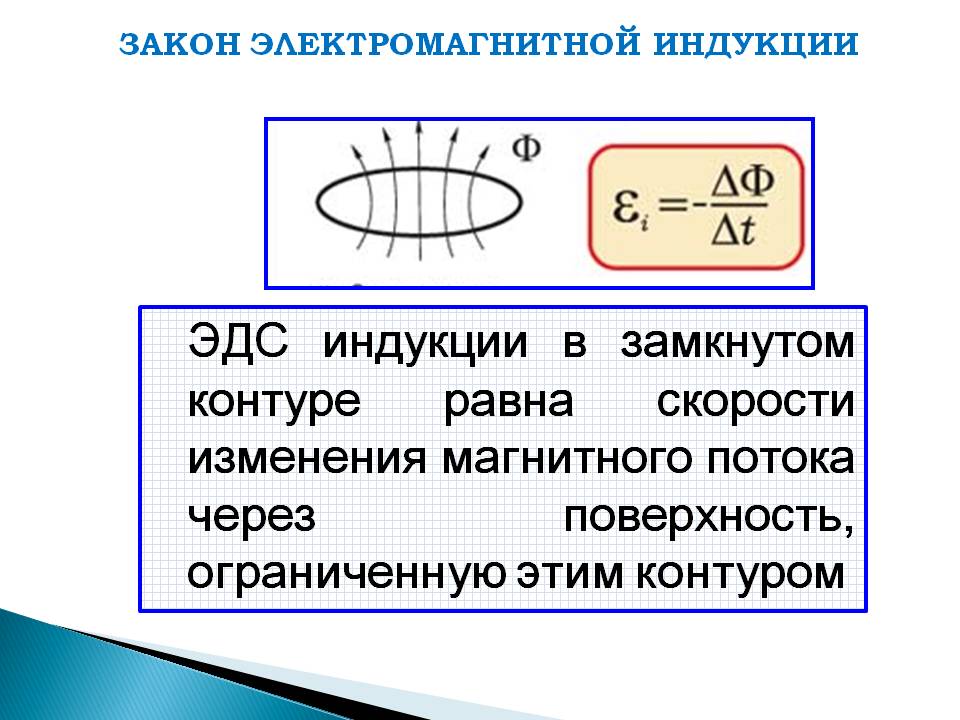 5 кГц). Согласно модели, ЭДС уменьшается с увеличением радиуса приемника из-за уменьшения межэлектронных сил, так как связь между катушками уменьшается с расстоянием.

Нелинейность, связанная с ЭДС индукции на более высоких частотах, проявляется в . Приблизительно выше 5 кГц характеристика отличается от линейной. Из (3.5) видно, что модель прямого действия линейно зависит от частоты, как и в случае с законом Фарадея, приведенным в (2.3). По закону Фарадея ЭДС индукции зависит от скорости изменения тока, отсюда линейная зависимость от ф . Точно так же для подхода прямого действия относительные ускорения электронов также линейно зависят от частоты. Насколько известно авторам, не существует какой-либо удовлетворительной теории, которая могла бы иметь дело со случаем электромагнитной индукции переменной частоты. Фейнман [34] обсуждает попытки модифицировать уравнения Максвелла, все из которых сталкиваются с трудностями, связанными с допущением точечных зарядов, самовоздействием заряда на самого себя (реакцией излучения) и ролью ЭМ массы по сравнению с механической массой.

Для модели прямого действия предполагается, что ток равномерно распределяется по поперечному сечению провода и что принцип суперпозиции применяется к последовательным участкам катушки. С увеличением частоты любая модель линейной индукции выйдет из строя, поскольку распределение тока станет неравномерным, что приведет к появлению хорошо известных скин-эффектов и эффектов близости. Явление, получившее название скин-эффекта, было открыто Максвеллом, выдвинувшим гипотезу о неравномерном распределении тока [35]. Высокочастотное сопротивление можно представить как сопротивление постоянному току эквивалентной «кожи» с определенной глубиной проникновения. Эффект близости связан с интерференцией токов между отдельными соседними контурами, поскольку геометрическая форма поля не постоянна, а изменяется с частотой. Это представляет серьезную проблему для любой модели электромагнитной индукции. Однако подход прямого действия имеет внутреннее преимущество, заключающееся в том, что он может учитывать условия ускорения более высокого порядка. На более высоких частотах теория может быть адаптирована для моделирования тонких трубок с током, а не для предположения об однородной плотности тока.

Для определения скин-эффекта в различных условиях были разработаны различные концепции и решения [36–42]. Более прямое и физическое объяснение скин-эффекта заключается в большей индуктивности (инерции электронов) нитей вблизи центра проводника по сравнению с нитями на поверхности. То есть инверсии тока на центральных нитях испытывают более высокое сопротивление/реактивное сопротивление по сравнению с инверсиями на поверхности. Следовательно, по мере увеличения частоты ток становится более ограниченным внешними областями проводника. Возможная физическая основа скин-эффекта была предложена в терминах электромагнитной массы ( М _и ). Калвик [43] предположил, что эффективный заряд электронов проводимости не равен заряду всех имеющихся электронов проводимости и что ток переносится небольшим числом электронов, движущихся с высокой скоростью. Следуя этим рассуждениям, индуктивность можно рассматривать как аналог электромагнитной массы. Гровер [33], напротив, описывает скин-эффект в следующих терминах: «Электромагнитная энергия входит в поверхность провода и все больше и больше ослабляется и отстает по фазе по мере приближения к центру. На очень высоких частотах затухание настолько велико, что амплитуда тока становится незаметной после того, как волна проникнет в провод всего на долю миллиметра». По сути это объяснение, основанное на теореме Пойнтинга, согласно которой энергия, подводимая к проводнику с током, течет не по проводу, а через окружающее ЭМ поле [44].

Поскольку в настоящее время не существует удовлетворительной общей нелинейной теории электромагнитной индукции, полезно подгонять данные о частоте ЭДС индуцирования с помощью некоторой формы эмпирического закона. Существует линейное изменение примерно до 5 кГц в соответствии с законом Вебера. Приблизительно выше 5 кГц, когда скин-эффект становится все более значительным, задействованы частотные составляющие более высокого порядка.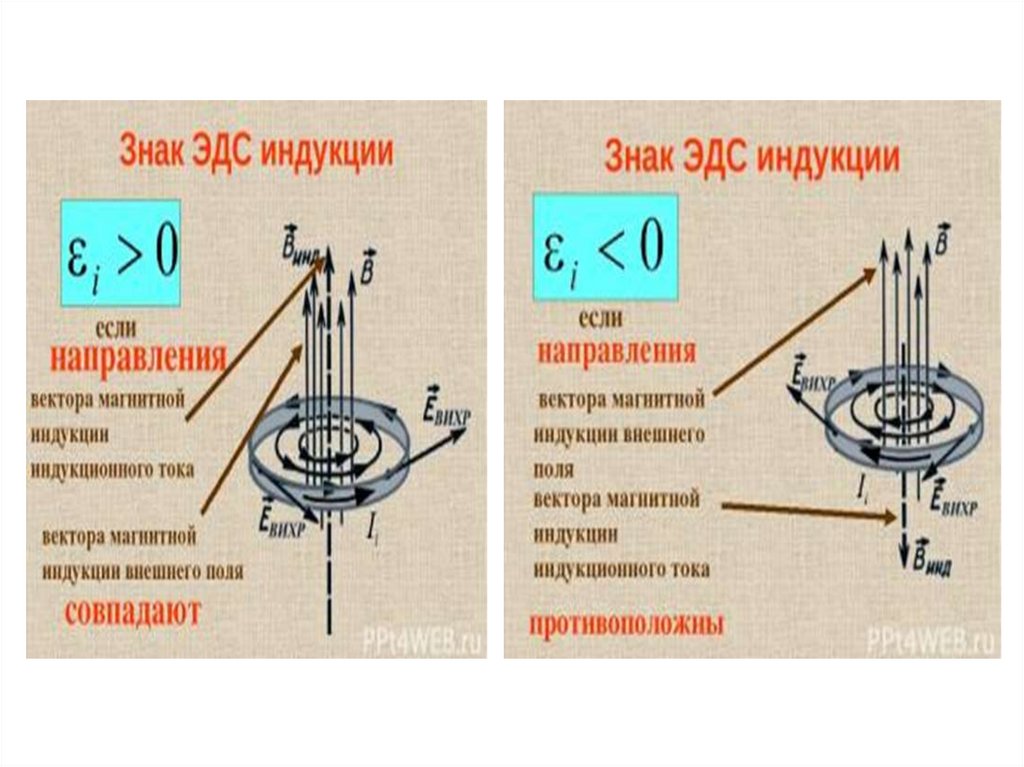 С помощью инструмента подгонки кривой Matlab получаются следующие выражения для значений выше 5 кГц (),

( e _R ) _{p k − p k} ⟨ r _R = 0.0375⟩ = 2.3 f ²  − 22.4 f + 127.5

6.1

и

( e _R ) _{p k − p k} ⟨ r _R = 0.15⟩ = 2.2 f ²  − 23.1 f + 124 , 

6,2

, где ЭДС индукции выражена в мВ, а частота в кГц. Квадратичный отклик получается с коэффициентом детерминации ( R ² ), рассчитанным как 0,9983 и 0,9986 для уравнений (6.1) и (6.2) соответственно. Такие эмпирические подгонки для данной геометрии могут оказаться полезными в качестве основы для сравнения взаимной индуктивности в диапазоне частот.

Наконец, стоит прокомментировать, почему любая нелинейная теория индукции оказывается трудной. Электрон проводимости, на который действует переменная сила, приходит в вынужденное колебание, при котором на него действуют как восстанавливающая, так и демпфирующая силы. По мере увеличения частоты воздействия и ограничения потока электронов внешними областями проводника тот же ток через уменьшенную площадь вызовет увеличение скорости дрейфа электронов и, следовательно, увеличение амплитуды колебаний. Затем это приводит к нелинейной восстанавливающей силе (т. е. не слишком отличающейся от пружины, которая может становиться «жестче» или «мягче» в механической системе). Следствием этого является то, что гармоническое движение при малых амплитудах может стать гармоникой при больших амплитудах и, таким образом, привести к частотным членам более высокого порядка, которые затем необходимы для описания изменения напряжения вторичной обмотки.

Для изученной конструкции коаксиальной катушки подход прямого действия показывает хорошее согласие с экспериментальными измерениями для прогнозирования ЭДС индукции в приемной катушке на различных расстояниях от передатчика в ближней зоне (до пятикратного диаметра передающей катушки). Модель представляет интерес за пределами изучаемой здесь конструкции, поскольку ее вполне можно адаптировать для использования с катушками другой геометрии. Модель учитывает радиус каждой катушки, применяемую частоту, амплитуду тока возбуждения и вклад отдельных витков катушки, как указано в (3.6).

Показано, что линейность между ЭДС индукции и частотой сохраняется до частот приблизительно 5 кГц. Кроме того, постепенное ограничение тока внешними областями проводника (скин-эффект) приводит к нелинейной зависимости индуцированного напряжения от частоты. Было обнаружено, что данные соответствуют квадратичной зависимости от частоты, как указано в (6.1) и (6.2). Что касается скин-эффекта, стандартное объяснение, основанное на поле, заключается в том, что он включает в себя поток электромагнитной энергии сбоку в проводник в соответствии с теоремой Пойнтинга. Модель, разработанная в этом исследовании, предполагает, что альтернативное объяснение связано с изменением инерции/индуктивности электронов в проводнике. В последнее время возобновился интерес к гидродинамическим аналогам потока электронов в конкретных материалах с некоторыми свидетельствами того, что электронная вязкость играет важную роль в определении электрического сопротивления [45]. В связи с этим интересно отметить, что существует также гидродинамическая аналогия с электрической толщиной скин-слоя, связанная с акустическим течением в заполненной воздухом трубе, в которой низкочастотный пульсирующий поток накладывается на существующий установившийся поток [46]. Показано, что скорость частиц достигает максимального значения на расстоянии от стенки трубы, равном dw≈υ/πf, где υ – кинематическая вязкость. Это контрастирует с электрической глубиной скин-слоя, δ=1/πfμ0σ. Поскольку μ ₀ постоянно и ρ = 1/ σ , то δ≈ρ/πf обеспечивает аналогию с электронной вязкостью и электрическим сопротивлением.

Будущая работа будет включать в себя разработку этой модели для других случаев, в том числе конкретных приложений, таких как визуализация ИМ, а также изучение возможности расширения модели для включения частотных членов более высокого порядка. Этот подход представляет интерес помимо того, что изучается здесь, поскольку он обеспечивает альтернативные и, возможно, более эффективные средства моделирования электромагнитной индукции в ближнем поле, которые могут быть полезны в смежных областях, таких как связь ближнего поля, радиочастотная идентификация и совместимость с электромагнитными помехами. Точность предсказания модели на значительном расстоянии от передатчика означает, что такое расположение может быть адаптировано в качестве эталонного стандарта для калибровки измерителей напряженности поля для приемных рамочных антенн. Кроме того, этот метод может иметь значение для изучения влияния электромагнитных взаимодействий ближнего поля с биологическими телами. Поскольку формулировка силы Вебера описывает движущиеся заряды, и это не обязательно должны быть электроны в медной проволоке, теория вполне может быть распространена на движущиеся заряженные частицы [47–51] или ионные частицы в биомедицинских системах [52–54]. в частности, предоставление информации о влиянии электромагнитной индукции на конкретные биологические процессы.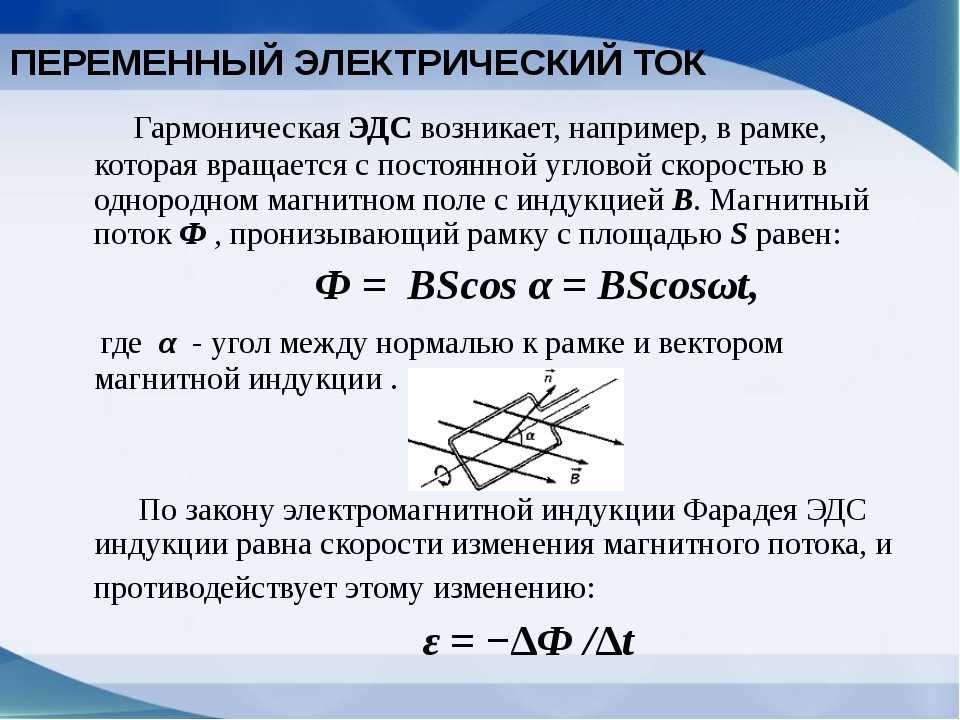

Авторы признают положения Департамента электротехники и электроники Ливерпульского университета.

показывает отдельные обороты передатчика-приемника, используемые при суммировании уравнения (3.6).

Рис. 7.

Открыть в отдельном окне

( a ) На схеме показано положение отдельных витков в схеме приемо-передающей катушки. ( b ) Разложение матрицы из уравнения (3.6) для иллюстрации процедуры суммирования. (Онлайн-версия в цвете.)

Р.Т.С. и С.М. разработал и инициировал проект. Эксперименты проводились RTS при поддержке S.M., F.P.M.J. и И.С.Ю. Рукопись и рисунки были подготовлены R.T.S. и С.М. Все авторы рассмотрели рукопись.

У авторов нет конфликта интересов, о котором следует заявить.

Это исследование не получило специального грантового финансирования.

1. Бансал Р. 2004. Магнитная связь в ближнем поле. Распространение антенн IEEE. Маг. 46, 114–115. (дои: 10.1109/MAP.2004.1305555) [Google Scholar]

2.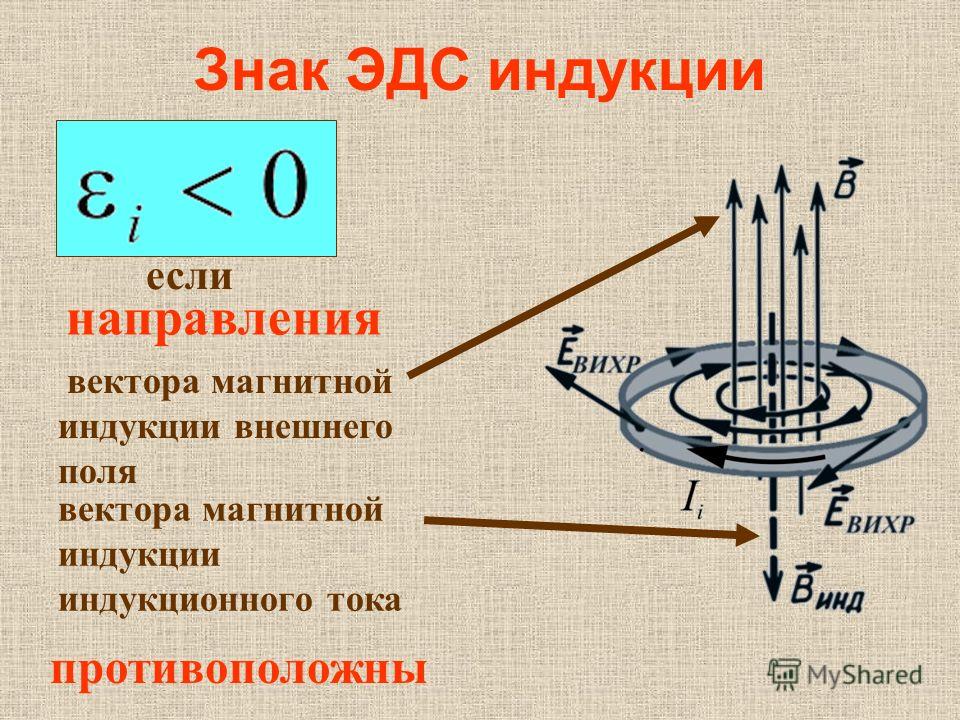 Griffiths H. 2001. Магнитно-индукционная томография. Изм. науч. Технол. 12, 1126 (doi:10.1088/0957-0233/12/8/319) [Google Scholar]

3. Darrer BJ, Watson JC, Bartlett P, Renzoni F. 2015. Магнитное изображение: новый инструмент национальной ядерной безопасности Великобритании. Науч. Респ. 5, 7944 (doi:10.1038/srep07944) [бесплатная статья PMC] [PubMed] [Google Scholar]

4. Курс А., Каралис А., Моффатт Р., Джоаннопулос Дж. Д., Фишер П., Солячич М. 2007. Беспроводная передача энергии через сильно связанные магнитные резонансы. Наука 317, 83–86. (doi:10.1126/science.1143254) [PubMed] [Google Scholar]

5. Акылдиз И.Ф., Стунтебек Э.П. 2006. Беспроводные подземные сенсорные сети: проблемы исследования. Специальная сеть. 4, 669–686. (doi:10.1016/j.adhoc.2006.04.003) [Google Scholar]

6. Sun Z, Akyildiz IF. 2010. Магнитно-индукционная связь для беспроводных подземных сенсорных сетей. IEEE Trans. Антенны Распространение. 58, 2426–2435. (doi:10.1109/TAP.2010.2048858) [Google Scholar]

7. Ma J, Zhang X, Huang Q, Cheng L, Lu M. Экспериментальное исследование влияния проводимости грунта на подземный магнитоиндукционный канал. Антенны IEEE и беспроводное распространение. лат. 14, 1782–1785 гг. (doi:10.1109/LAWP.2015.2423687).

8. Доминго МЦ. 2012. Магнитная индукция для подводных сетей беспроводной связи. IEEE Trans. Антенны Распространение. 60, 2929–2939. (doi:10.1109/TAP.2012.2194670) [Google Scholar]

9. Shentu N, Zhang H, Li Q, Zhou H. 2011. Исследование датчика глубинных перемещений на основе электромагнитной индукции. Датчики IEEE J. 11, 1504–1515. (doi:10.1109/JSEN.2010.2086056) [Google Scholar]

10. Sun Z, Wang P, Vuran MC, Al-Rodhaan MA, Al-Dhelaan AM, Akyildiz IF. 2011. MISE-PIPE: беспроводные сенсорные сети на основе магнитной индукции для мониторинга подземных трубопроводов. Специальная сеть. 9, 218–227. (doi:10.1016/j. adhoc.2010.10.006) [Google Scholar]

11. Huang Y, Boyle K. 2008. Антенны: от теории к практике . Чичестер, Великобритания: John Wiley & Sons. [Академия Google]

12. Коллин Р., Ротшильд С. 1964. Оценка антенны Q. IEEE Trans. Антенны Распространение. 12, 23–27. (doi:10.1109/TAP.1964.1138151) [Google Scholar]

13. Фанте Р.Л. 1969. Добротность общих идеальных антенн. IEEE Trans. Антенны Распространение. 17, 151–155. (doi:10.1109/TAP.1969.1139411) [Google Scholar]

14. Yaghjian AD, Best SR. 2005. Импеданс, полоса пропускания и добротность антенн. IEEE Trans. Антенны Распространение. 53, 1298–1324. (дои: 10.1109/TAP.2005.844443) [Google Scholar]

15. Werner DH. 1998. Метод моментов для эффективного и точного моделирования цилиндрических проволочных антенн средней толщины. IEEE Trans. Антенны Распространение. 46, 373–382. (doi:10.1109/8.662656) [Google Scholar]

16. Overfelt P. 1996. Ближние поля постоянного тока тонкой круглой рамочной антенны произвольного радиуса.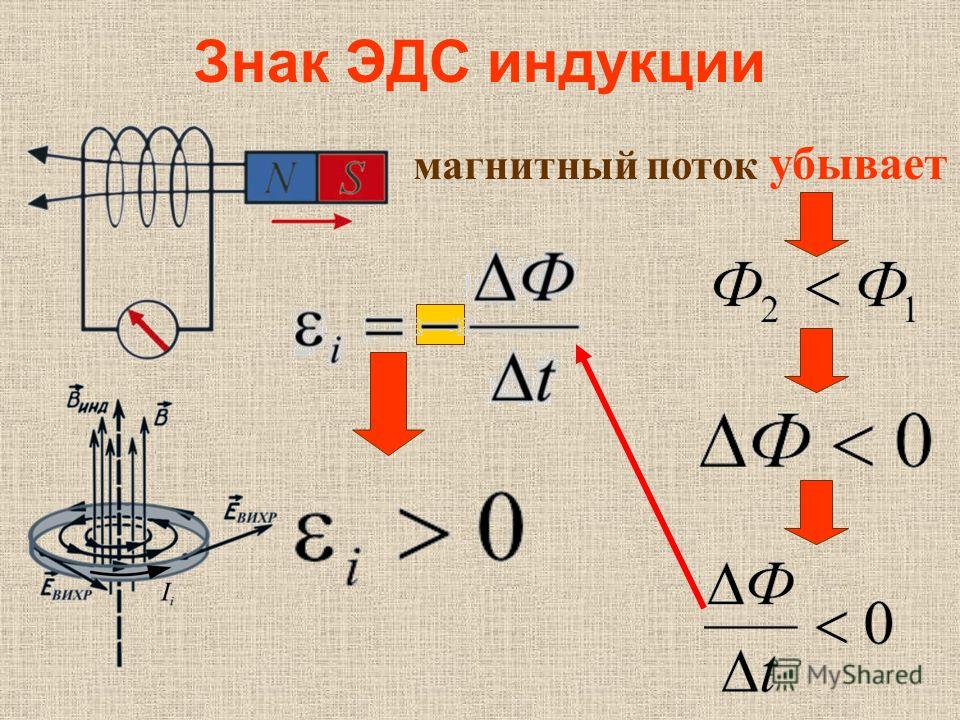 IEEE Trans. Антенны Распространение. 44, 166–171. (doi:10.1109/8.481643) [Google Scholar]

17. Конвей Дж.Т. 2005. Новая процедура точного решения для ближних полей обычной тонкой круглой рамочной антенны. IEEE Trans. Антенны Распространение. 53, 509–517. (doi:10.1109/TAP.2004.838804) [Google Scholar]

18. Werner DH, Colegrove TW. 1999. О новом цилиндрическом гармоническом представлении для сферических волн. IEEE Trans. Антенны Распространение. 47, 97–100. (doi:10.1109/8.752999) [Google Scholar]

19. Fikioris G, Papakanellos PJ, Anastassiu HT. 2008. Об использовании несингулярных ядер в некоторых интегральных уравнениях тонкопроволочных рамочных антенн. IEEE Trans. Антенны Распространение. 56, 151–157. (doi:10.1109/TAP.2007.

6) [Google Scholar]

20. Андрианезис П., Фикиорис Г. 2012. Ближние поля сверхдирективного типа в методе вспомогательных источников. IEEE Trans. Антенны Распространение. 60, 3056–3060. (doi:10.1109/TAP.2012.2194671) [Google Scholar]

21. Микки С.М., Антар Ю.М. 2015. Физические и вычислительные аспекты ближнего поля антенны: скалярная теория. Прог. Электромагн. Рез. Б 63, 67–78. (дои: 10.2528/PIERB15021209) [Google Scholar]

22. Микки С.М., Антар Ю.М.М. 2011. О пространственной структуре антенны электромагнитного ближнего поля . Генеральная ассамблея и научный симпозиум , XXXth URSI 2011, Стамбул, Турция, 13–20 августа . стр. 1–4.

23. Микки С.М., Антар Ю.М. 2015. Анализ общих взаимодействий ближнего поля с использованием функции Грина тока антенны. Прог. Электромагн. Рез. С 59, 1–9. (doi:10.2528/PIERC15060304) [Google Scholar]

24. Mikki SM, Antar YMM. 2011. Теория антенного электромагнитного ближнего поля — часть I. IEEE Trans. Антенны Распространение. 59, 4691–4705. (doi:10.1109/tap.2011.2165499) [Google Scholar]

25. Эме Дж., Руде Дж., Клавель Э., Ауин О., Лабарр С., Коста Ф. , Экрабе Дж. 2007. Прогнозирование и измерение ближнего магнитного поля статического преобразователя . In Industrial Electronics, 2007. ISIE 2007. IEEE Int. Symp ., Виго, Испания, 4–7 июня , стр. 2550–2555. Пискатауэй, Нью-Джерси: IEEE.

26. Уэсли Дж.П. 1990. Электродинамика Вебера, часть I. Общая теория, эффекты установившегося тока. Найдено. физ. лат. 3, 443–469. (doi:10.1007/BF00665929) [Google Scholar]

27. Уэсли Дж. 1990. Электродинамика Вебера, часть II, униполярная индукция, Z-антенна. Найдено. физ. лат. 3, 471–490. (doi:10.1007/BF00665930) [Google Scholar]

28. Уэсли Дж. 1990. Электродинамика Вебера: часть III. механика, гравитация. Найдено. физ. лат. 3, 581–605. (doi:10.1007/BF00666027) [Google Scholar]

29. Kinzer E, Fukai J. 1996. Сила Вебера и уравнения Максвелла. Найдено. физ. лат. 9, 457–461. (doi:10.1007/BF021) [Google Scholar]

30. Ассис АКТ, Фукаи Дж., Карвальо Х. 2000. Веберовская индукция. Физ. лат. А 268, 274–278. (doi:10.1016/S0375-9601(00)00212-7) [Google Scholar]

31. Assis AKT, Hernandes J. 2005. Уравнение телеграфии из электродинамики Вебера. IEEE Trans. Цепи Сист. Часть 2: Экспресс. Трусы 52, 289–292. (doi:10.1109/TCSII.2005.848958) [Google Scholar]

32. Smith RT, Jjunju FP, Maher S. 2015. Оценка отклонения электронного пучка поперек соленоида с помощью электродинамики Вебера-Ритца и Максвелла-Лоренца. Прогр. Электромагн. Рез. 151, 83–93. (doi:10.2528/PIER15021106) [Google Scholar]

33. Гровер Ф.В. 2004. Расчет индуктивности . Минеола, Нью-Йорк: Dover Publications. [Google Scholar]

34. Фейнман Р.П., Лейтон Р.Б., Сэндс М. 1963 год. Фейнмановские лекции по физике, в основном по электромагнетизму и материи , vol. II Редвуд-Сити: Эддисон Уэсли. [Google Scholar]

35. Максвелл Дж.К. 1954. Трактат об электричестве и магнетизме , том. 2 Нью-Йорк, штат Нью-Йорк: Довер. [Академия Google]

36. Де Зуттер Д., Нокарт Л. 2005. Моделирование скин-эффекта на основе оператора дифференциальной проводимости поверхности. IEEE Trans. Теория микроволнового излучения. 53, 2526–2538. (doi:10.1109/TMTT.2005.852766) [Google Scholar]

37. Mei S, Ismail YI. 2004. Моделирование скин-эффектов и эффектов близости с уменьшенными реализуемыми схемами RL. IEEE Trans. Интеграл очень большого масштаба. (СБИС) Сист. 12, 437–447. (doi:10.1109/TVLSI.2004.825863) [Google Scholar]

38. О, К.С. 2000. Точное моделирование переходных процессов в линиях электропередачи с использованием скин-эффекта. IEEE Trans. Компьютерный Des. интегр. Цирк. Сист. 19, 389–396. (doi:10.1109/43.833207) [Google Scholar]

39. Бир О., Бом П., Прейс К., Вачутка Г. 2000. Краевой конечно-элементный анализ нестационарных задач скин-эффекта. IEEE Trans. Магн. 36, 835–839. (doi:10.1109/20.877574) [Google Scholar]

40. Berleze SL, Robert R. 2003. Скин-эффекты и эффекты близости в немагнитных проводниках. IEEE Trans. Образовательный 46, 368–372. (doi:10.1109/TE.2003.814591) [Google Scholar]

41. Айелло Г., Альфонцетти С., Борзи Г., Салерно Н. 2001. Улучшенная схема решения задач скин-эффекта с открытой границей. IEEE Trans. Магн. 37, 3474–3477. (doi:10.1109/20.952640) [Google Scholar]

42. Джафари-Шапурабади Р., Конрад А., Синклер А. 2002. Сравнение трех формулировок для задач вихревых токов и скин-эффекта. IEEE Trans. Магн. 38, 617–620. (doi:10.1109/20.996161) [Google Scholar]

43. Калвик Э.Г. 1949. Основы электромагнетизма . Кембридж, Великобритания: Издательство Кембриджского университета.

44. Чубыкало А., Эспиноза А., Цончев Р. 2004. Экспериментальная проверка совместимости определений плотности электромагнитной энергии и вектора Пойнтинга. евро. физ. Дж. Д. 31, 113–120. (doi:10.1140/epjd/e2004-00135-x) [Google Scholar]

45.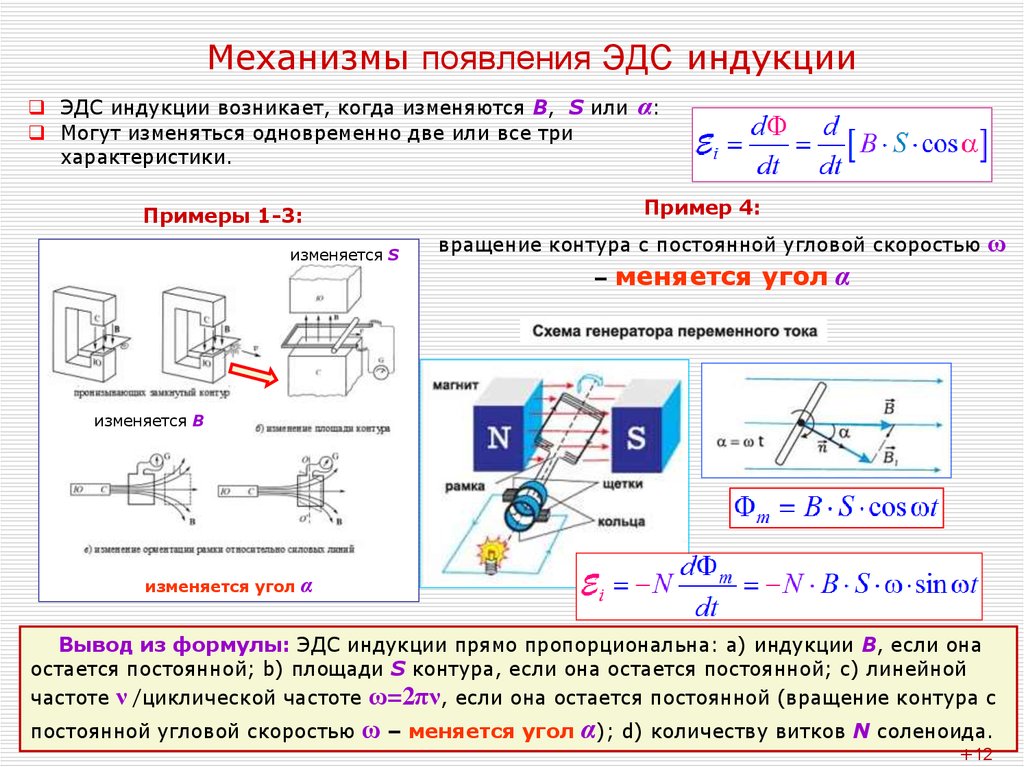 Moll PJW, Kushwaha P, Nandi N, Schmidt B, Mackenzie AP. 2016. Доказательства гидродинамического потока электронов в PdCoO ₂ . Наука 351, 1061–1064. (doi:10.1126/science.aac8385) [PubMed] [Google Scholar]

46. Ричардсон Э.Г. 1961. Динамика реальных жидкостей . Лондон, Великобритания: Эдвард Арнольд. [Google Scholar]

47. Maher S, Jjunju FP, Taylor S. 2015. Коллоквиум: 100 лет масс-спектрометрии: перспективы и будущие тенденции. Ред. Мод. физ. 87, 113 (doi:10.1103/RevModPhys.87.113) [Google Scholar]

48. Syed S, Maher S, Taylor S. 2013. Работа квадрупольного фильтра масс под действием магнитного поля. Дж. Масс-спектр. 48, 1325–1339. (doi:10.1002/jms.3293) [PubMed] [Google Scholar]

49. Syed SU, Maher S, Eijkel GB, Ellis SR, Jjunju F, Taylor S, Heeren RM. 2015. Метод прямой визуализации ионов для исследования динамики ионов в мультипольных ионопроводах. Анал. хим. 87, 3714–3720. (doi:10.1021/ac5041764) [PubMed] [Google Scholar]

50. Maher S, Syed SU, Hughes DM, Gibson JR, Taylor S. 2013. Отображение диаграммы устойчивости квадрупольного масс-спектрометра при приложении статического поперечного магнитного поля. Дж. Ам. соц. Масс-спектр. 24, 1307–1314. (doi:10.1007/s13361-013-0654-5) [PubMed] [Google Scholar]

51. Шрикумар Дж., Хоган Т.Дж., Тейлор С. 2012. Моделирование СМК с учетом влияния давления в ионном источнике электронного удара. IEEE Trans. Инструм. Изм. 61, 3024–3030. (doi:10.1109/TIM.2012.2202166) [Google Scholar]

52. Chafai DE, Mehle A, Tilmatine A, Maouche B, Miklavčič D. 2015. Оценка электрохимических эффектов импульсных электрических полей в суспензии биологических клеток. Биоэлектрохимия 106, 249–257. (doi:10.1016/j.bioelechem.2015.08.002) [PubMed] [Google Scholar]

53. Liu C, Duan W, Xu S, Chen C, He M, Zhang L, Yu Z, Zhou Z. 2013. Воздействие радиочастотного электромагнитного излучения с частотой 1800 МГц вызывает окислительное повреждение оснований ДНК в клеточной линии, полученной из сперматоцитов мыши.