формула, задачи, примеры и факты —
Как найти частоту волны? Процесс прост; количество оборотов, которое требуется для завершения конкретной вещи, называется частотой.
Когда объект движется, мы обычно определяем движение, силу и многие другие факторы. Но нам также нужно знать, с какой частотой он будет двигаться в данный момент времени. Таким образом, обратное время дается как частота в стандартных терминах.
В подробном случае мы также могли бы определить частоту данной волны, частицы в краткосрочной перспективе, а также более широкий контекст. частота является широко используемым фактором с точки зрения волны. Скажем, например, волна распространяется с определенной скоростью, и мы должны найти частоту волны.
Обычно мы погружаемся в математическую часть решения, но, говоря простым языком, мы также можем быстро определить волны. То частота сколько циклов он делает за одну секунду. Таким образом, если волна завершает один цикл, частота составляет половину от него.
Частота — это то, что появляется постоянно или в определенный момент времени. Подобно соленоиду, он имеет несколько витков при намотке на проводник и производит электричество. Точно так же частота — это количество циклов, которые волна совершает за одну секунду, и она обычно равна 2 герцам.
Компания количество циклов световой волны сделанное за одну секунду, также оценивается с точки зрения длины волны и скорость световой волны. Звуковая волна является наиболее распространенной областью, где часто рассматривается частотный термин.
Существует также научная вещь: собаки и птицы слышат звук за пределами определенного уровня, который даже люди не способны слышать. Мы созданы таким образом, что только определенное количество частота звука мы могли вынести услышать.
«Файл:Amfm3-en-de.gif» by Берсеркерус под лицензиейЧастота волновой формулыЧастота имеет общую формулу, которую можно применять во всех контекстах. Период времени является основной причиной, которая помогает в формуле частоты.
Период времени является основной причиной, которая помогает в формуле частоты.
Количество циклов, которые волна делает за один, рассматривается как частота этой конкретной волны. Следовательно, формула частоты в повседневном исчислении такова: f=1/T. Здесь Т — период времени, за который волны совершают число циклов.
Чтобы рассчитать частоту, нам нужно знать характеристики волны. Волна — это совокупность вибраций, называемых энергиями. Они достигли пика на обоих концах. Верхний узел называется впадина, а нижний узел называется гребень.
Высота волны обычно считается амплитудой волны. Высота волны будет определять, будет ли амплитуда больше или меньше. Поэтому, когда они изменяются, циклы, сделанные в секунду, также будут изменены.
Таким образом, когда волна завершает один цикл, то есть если волна имеет и гребень, и впадину в одной и той же фазе, тогда получаемая частота равна половине.
Волна совершает определенное количество циклов за одну секунду, что в основном известно как частота волны. И это дается формулой f=1/Т. Тип волны может зависеть от среды, через которую она проходит.
И это дается формулой f=1/Т. Тип волны может зависеть от среды, через которую она проходит.
Теперь давайте посмотрим, как найти частоту волны на графике. Во-первых, частота — это количество циклов, которые волна пытается совершить, чтобы совершить один полный круг в данный конкретный момент времени.
Когда волна сделает один цикл, на это потребуется некоторое время. На графике мы называем это единицами. По сути, на графике есть несколько единиц, по которым мы можем быстро определить, как найти частоту волны в данном конкретном случае.
Скажем, например, волна движется с определенной скоростью, и мы также должны знать, сколько секунд это занимает. Скажи, что есть 12 секунд отмечены на графике, поэтому этой волне требуется 4 секунды, чтобы завершить один полный цикл. Итак, по формуле f=1/Т, частота волны 0.25Гц.
«синусоидальная форма волны» by Творчество103 под лицензией CC BY-SA 2.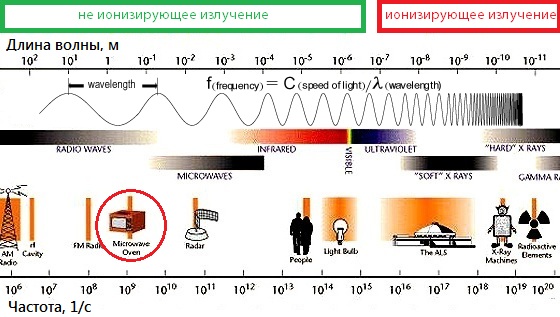 0
0Давайте рассмотрим несколько задач по расчету частоты.
Проблема:Типичная волна совершает два цикла за 30 секунд, и какова будет частота волны, если она будет распространяться в той же среде?
Решение:f=1/Т
f=2/30
f=0.0667 Гц
Всегда возникает путаница между частота волны и скорость волны. Есть амплитуда волны, которая в основном является высотой волны. Таким образом, скорость рассчитывается, чтобы найти скалярную часть скорости, которая является скоростью.
Когда мы обнаруживаем, что волна является световой, звуковой или электромагнитной волной, нам нужно найти частоту волна, завершающая циклы. Период времени между циклами, совершаемыми волной, обычно определяется формулой как обратную частоту.
Как найти частоту волны по длине и амплитуде?Как найти частоту волны по длине и амплитуде? Когда мы рассматриваем волну как свет, мы должны знать все факторы, влияющие на частоту волны.
Во-первых, необходимо учитывать длину волны. Как найти частоту волны с длиной волны? Формула очень проста, и нам нужно найти формулу скорости света.
Будет формула, называемая скоростью света, с = fλ. Здесь c — скорость света, f — определяемая частота, λ — длина волны света. Из этой формулы мы можем найти частоту волны через длину волны, переставив члены, данные в формуле.
Если говорят, что волна движется с определенной скоростью и временем, нам также нужно найти частота с которым распространяется световая волна. Таким образом, формула, упомянутая выше, будет использоваться для расчета частоты в заданный период времени.
Найдем частоту волны и посмотрим, как частота определяется по формуле.
Проблема:Световая волна распространяется со скоростью 3×108 РС. Данную длину волны световой волны называют равной 2000 Å. Какова частота?
Решение:с = fλ
f = с / λ
ф = 3×108 / 2000 Å
f= 1.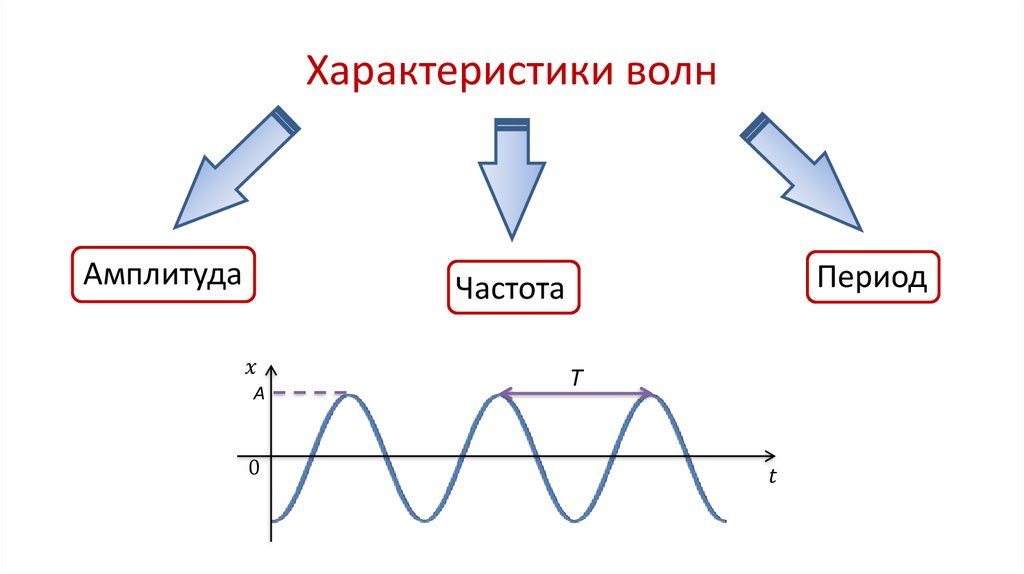 5 х 1018 герц
5 х 1018 герц
Итак, из вышеприведенной задачи видно, что частоту можно найти, используя длину волны.
Теперь нам нужно знать, как найти частоту волны через амплитуду. Для этого рассмотрим теперь общую формулу частоты, т. е. f=1/Т. Здесь f также можно записать как f = ω / 2 π.
Здесь формула для T дается как 2 π/ω. Отсюда легко найти значение амплитуды, если упомянут период времени. А частоту можно найти по приведенной выше формуле, если в конкретной задаче задана амплитуда.
Как найти частоту волны, зная только длину волны?Нам нужно знать, как длина волны влияет на волну, когда она распространяется с определенной скоростью и в заданном направлении. Это то, как далеко волна сможет пройти в среде.
Мы все знаем, что скорость света является стандартом для большинства формул, и мы также знаем, как переставить детали данной формулы, чтобы найти частоту данной волны. Как правило, когда световая волна распространяется в определенном направлении со скоростью 3×108, он также будет собирать информацию о частоте волны.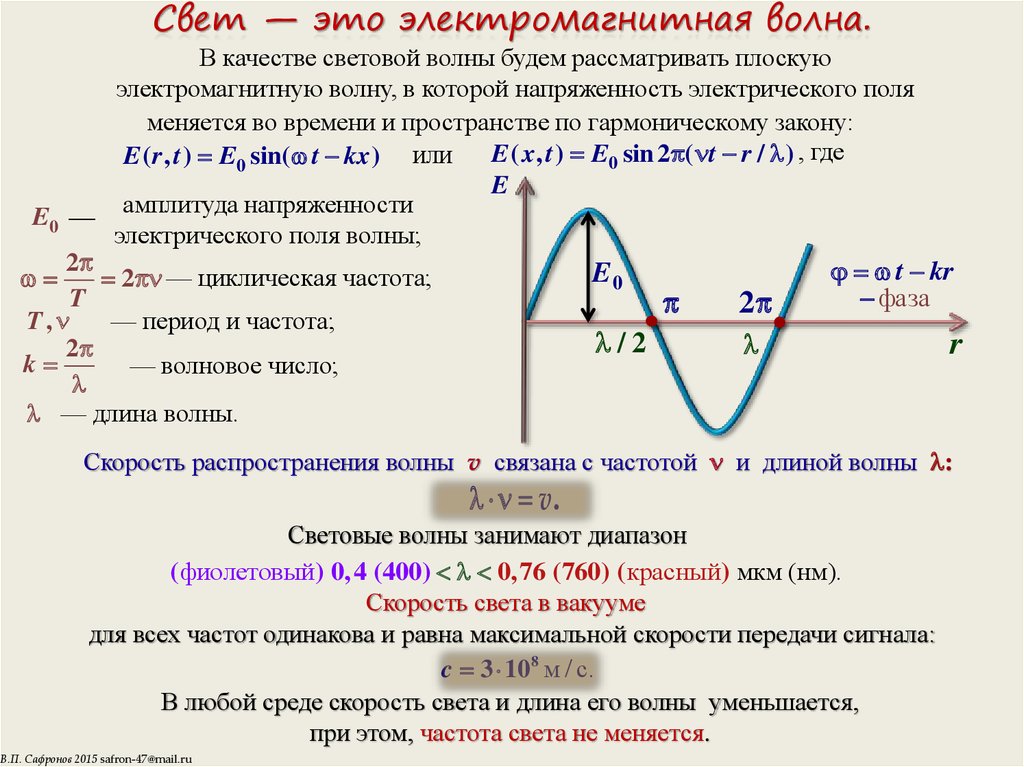
Формула скорости света является основой для определения длины волны или частоты распространяющейся световой волны. Скорость формулы света определяется выражением с = fλ. Отсюда мы получаем частоту волны через длину волны, соответствующим образом изменяя формулу.
Окончательная формула f = с / λ. Давайте посмотрим на проблему, как работает формула для электромагнитной волны.
Проблема:Вычислите частоту электромагнитной волны, которая распространяется со скоростью 2×106м/с с длиной волны 1000 Å. С заданными деталями используйте формулу частота по длине волны.
Решение:с = fλ
f = с / λ
f = 0.002 х 106 герц
f = 2 х 106/ 1000 Å
Таким образом, мы можем быстро определить частоту волны, используя значение скорости и, главным образом, значение длины волны.
Длина волны волны — это в основном пространство между гребнями или впадинами волны, которые следуют друг за другом. В основном концы одной и той же волны, которая была передана с точки зрения звука или электромагнитная волна.
В основном концы одной и той же волны, которая была передана с точки зрения звука или электромагнитная волна.
Когда гребни и впадины волны, находящиеся в одной и той же фазе, встречаются в одном и том же месте, обычно считается, что это длина волны.
Как найти частоту волны по заданному периоду?Как найти частоту волны через период времени? Ответ на этот вопрос прост, так как это общая формула для определения частоты волны.
Мы должны знать, что период времени в волне — это расстояние между гребнем и впадиной в одной и той же фазе. Поэтому, когда волна в основном распространяется с определенной частотой в заданный промежуток времени, нам нужна формула для расчета частоты.
Вот формула для частота с точки зрения периода времени, f=1/Т. Период времени обычно является еще одним термином для амплитуды волны. Т можно также записать как 2 π/ω, Где ω является мерой амплитуды.
Компания амплитуда — это в основном высота волны в зависимости от чего нам нужно сделать вывод, что амплитуда большая или малая. Если высота волны велика, то амплитуда называется значительной, а если высота волны мала, то говорят, что амплитуда волны мала.
Амплитуда имеет два конца, называемые гребень и впадина. Впадина — это верхний узел амплитуды, а гребень — нижний узел амплитуды.
Когда расстояние между двумя волнами называется длиной волны, а количество циклов, которое совершает одна волна, называется частота, когда период времени равен единице единица на графике, что в стандартном выражении составляет одну секунду.
Как найти частоту волны без скорости?Из формулы скорости света мы могли бы заметить, что длина волны обратно пропорциональна частоте волны, то есть циклам, совершаемым волной за период времени.
Мы также знаем, что частота не прямо пропорциональна периоду времени; следовательно, длина волны и период времени пропорциональны друг другу.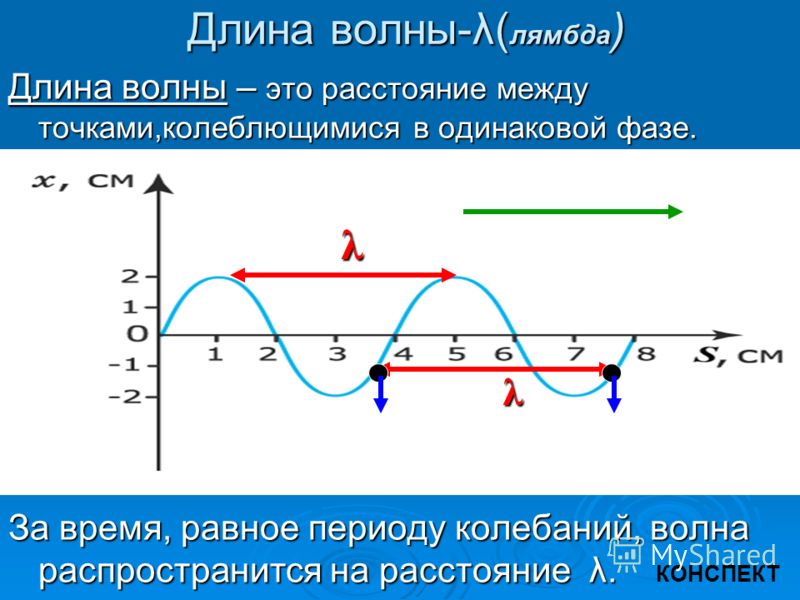 Длина волны связана с энергией, поэтому, когда длина волны увеличивается, энергия уменьшается. Формула основана на энергии фотона.
Длина волны связана с энергией, поэтому, когда длина волны увеличивается, энергия уменьшается. Формула основана на энергии фотона.
Мы предполагаем, что длина волны и период времени пропорциональны, а частота и энергия быть пропорциональным. Частота волны без скорости была бы формулой энергии, где E=hf, где E — энергия, h — постоянная Планка, f — частота.
Итак, зная конкретную базовую формулу света и энергии, мы можем соответствующим образом переставить термины и узнать, как найти частоту волны во всех возможных терминах. Кроме того, все эти факторы влияют на волну и ее количество, способствуя ее собственному распространению.
чем отличается рентген от света
Радиоволны, свет от лампочки в потолке, невидимые лучи в кабинете рентгенолога и таинственная смертельная радиация в зонах отчуждения — все это лишь разные проявления одного и того же физического явления: электромагнитного излучения. Разобраться, где что, не так уж сложно. Достаточно лишь связать свойства излучения с длиной волны.
Почти в каждом школьном кабинете физики висела разноцветная диаграмма с картинками, которая гордо называлась «Спектр электромагнитного излучения». Условная синусоида начиналась слева, с радиоволн. Расстояние между соседними «горбами» в этой части было наибольшим. Частота колебаний является обратной длине волны величиной. Если длина волны есть расстояние между двумя «горбами» волны, то время, за которое она проходит это расстояние, определяется как расстояние, деленное на скорость. Время же есть единица, деленная на частоту. К правому концу диаграммы волна «сжималась», подобно пружине: длина волны уменьшалась, а частота увеличивалась. В левой части диаграммы располагались некие «гамма-лучи».
Не занимайтесь самолечением! В наших статьях мы собираем последние научные данные и мнения авторитетных экспертов в области здоровья. Но помните: поставить диагноз и назначить лечение может только врач.
Почему одни волны короче или длиннее других? Причина в источнике этих волн — колеблющемся электрическом заряде. Чем быстрее колеблется заряд, тем меньше длина электромагнитного излучения. Если бы электромагнитное поле было водой в озере, а заряд — рыболовным поплавком, то круги на воде условно изобразили бы электромагнитные волны. Чем быстрее дергается поплавок, тем чаще отходят от него водные круги — колебания, и меньше расстояние между ними — длина волны.
Чем быстрее колеблется заряд, тем меньше длина электромагнитного излучения. Если бы электромагнитное поле было водой в озере, а заряд — рыболовным поплавком, то круги на воде условно изобразили бы электромагнитные волны. Чем быстрее дергается поплавок, тем чаще отходят от него водные круги — колебания, и меньше расстояние между ними — длина волны.
Радиоволны порождаются колебаниями в проводниках с током, видимый свет — переходами электронов внутри атома, рентгеновские и гамма-лучи возникают, когда заряды движутся в электрическом поле атомного ядра, либо из-за процессов в самом ядре. Если говорить грубо, то, чем меньше «масштаб» взаимодействия, тем короче электромагнитная волна.
РЕКЛАМА – ПРОДОЛЖЕНИЕ НИЖЕ
Волны или фотоны?
Физики называют фотоны переносчиками электромагнитного взаимодействия. Частицами. Стоит только свыкнуться с этой мыслью и нарисовать в воображении чрезвычайно быстрые «шарики», как те же физики начинают утверждать, что взаимодействие между зарядами осуществляется через колебания электромагнитного поля — волны.
Какую «личность» примерит на себя фотон зависит от объектов, с которыми он взаимодействует. Длина волны радиосигнала измеряется километрами. На его пути возникают дома, фонарные столбы, люди — объекты, намного меньшие, чем длина волны. Значит, излучение будет огибать их или отклоняться от первоначального направления при «встрече», то есть проявлять волновые свойства, подобно великану, который огромным шагом переступает целый город. Видимый свет имеет длину волны такую, что может «врезаться» в атомный электрон лоб-в-лоб и вытолкнуть его из атома. В этом случае он ведет себя как частица или бильярдный шар, ударившийся о другой шар.
Чем меньше длина волны излучения, тем меньше в мире остается препятствий, которые волна может «обойти», а значит, хочешь-не хочешь, взаимодействовать придется. Рентгеновское и гамма-излучение настолько коротковолновые, что все в мире, даже крошечные электроны — серьезное препятствие для них, как забор для мухи.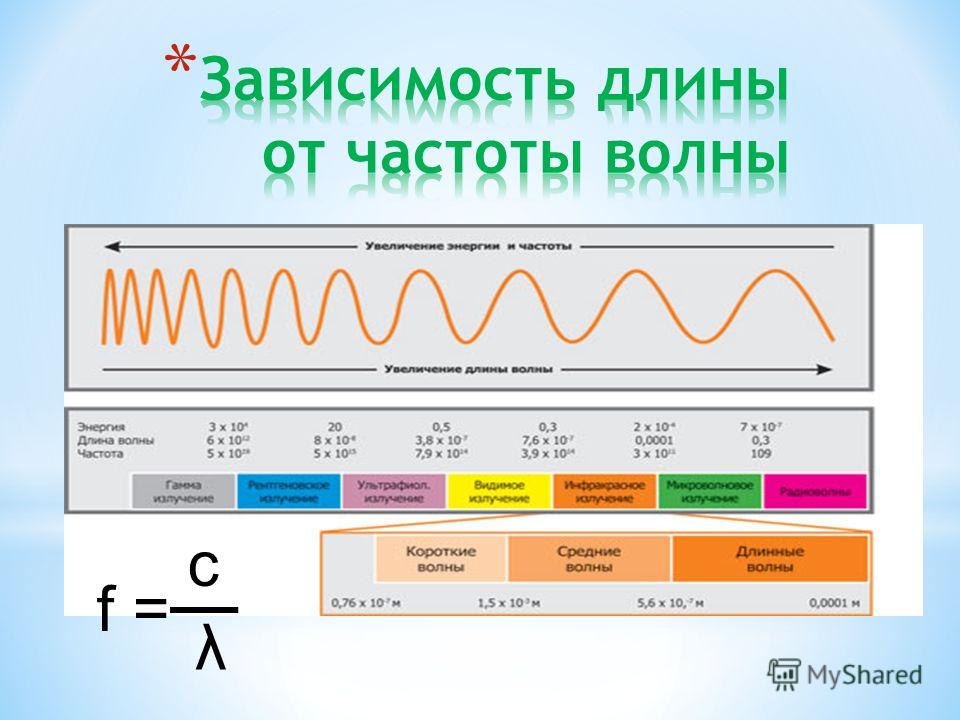
Преобладающая часть атома — это пустота. Огромная равнина с редкими заборами: по одному на каждый гектар. Когда длина волны излучения меньше расстояния между электронами и ядром, фотон словно «протискивается» сквозь атом. Чем меньше при этом плотность вещества, тем меньше вероятность попадания волны/фотона в атом. По этому принципу работает рентгеновская диагностика: более плотные кости задерживают рентгеновские лучи сильнее. Но часть фотонов пролетает все тело и рисует знакомые снимки.
Коротковолновое излучение опасно не только из-за того, что проникает куда угодно, в том числе, в человеческие ткани. Дело в том, что частота излучения прямо пропорциональна его энергии. Эта связь выводится в квантовой теории. Энергией определяется количество взаимодействий с атомами вещества — сколько из них фотон может «испортить» или ионизировать на своем пути, пока обессиленный не упадет после столкновения с последним «забором».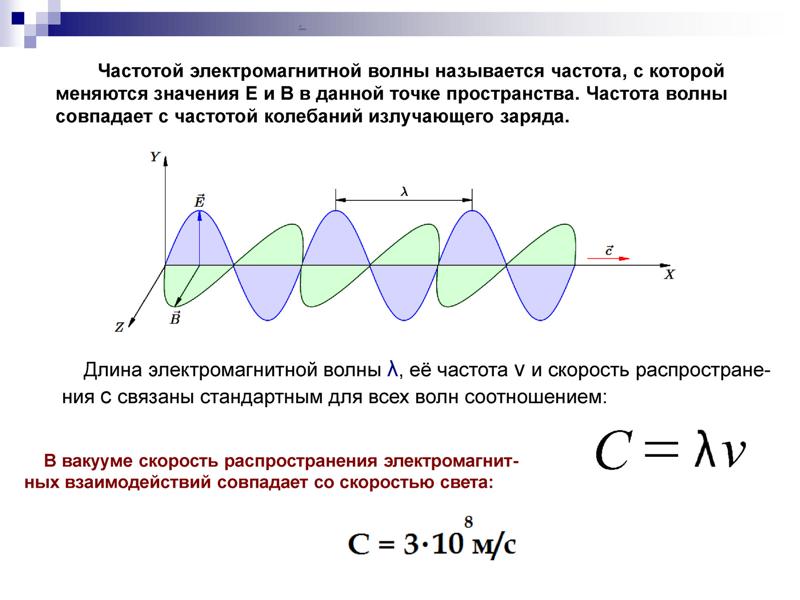
Ионизация вещества означает его уничтожение. Рушатся атомы, затем молекулы, а вслед за ними и клетки. «Радиация» в знакомом смысле этого слова буквально сжигает тело изнутри. К тому же излучение может проникнуть внутрь клеток и повредить молекулы ДНК. В этом случае потомство облученного человека будет под угрозой мутаций.
Когда энергия излучения достигает той, что нарабатывается в ускорителях, фотоны, проникая в ткани тела, множатся в геометрической прогрессии. В электрическом поле ядра они превращаются в пары частиц электрон-позитрон, которые сразу же аннигилируют — исчезают, оставляя после себя пару фотонов. Энергии новорожденных фотонов хватает, чтобы снова создать электрон-позитронные пары. Начинается лавинообразный процесс.
Резюме
Свет, радиоволны, рентген, инфракрасное и ультрафиолетовое излучение — одно и то же с точки зрения физики. Чем меньше длина волны, тем большая проникающая способность у волн/фотонов. Энергия излучения увеличивается с уменьшением длины волны, а значит, коротковолновое излучение вредит людям больше, чем длинноволновое.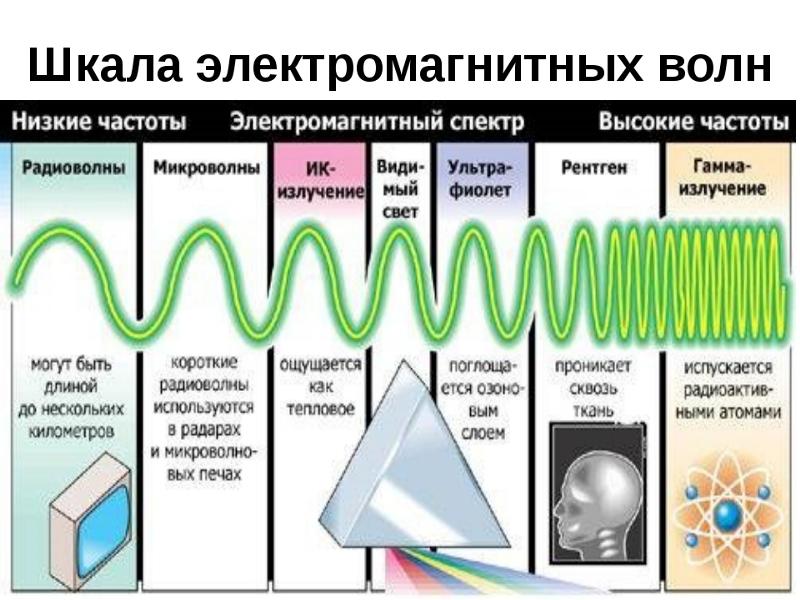
13.2 Свойства волны: скорость, амплитуда, частота и период
Цели обучения Волновые переменные Связь между частотой волны, периодом, длиной волны и скоростьюРешение волновых задачПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее: период, длина волны и скорость волны
| длина волны | скорость волны |
Волновые переменные
В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:
- Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
- Частота — количество событий в единицу времени
- Период — время, необходимое для совершения одного колебания
Для волн эти переменные имеют одинаковое основное значение.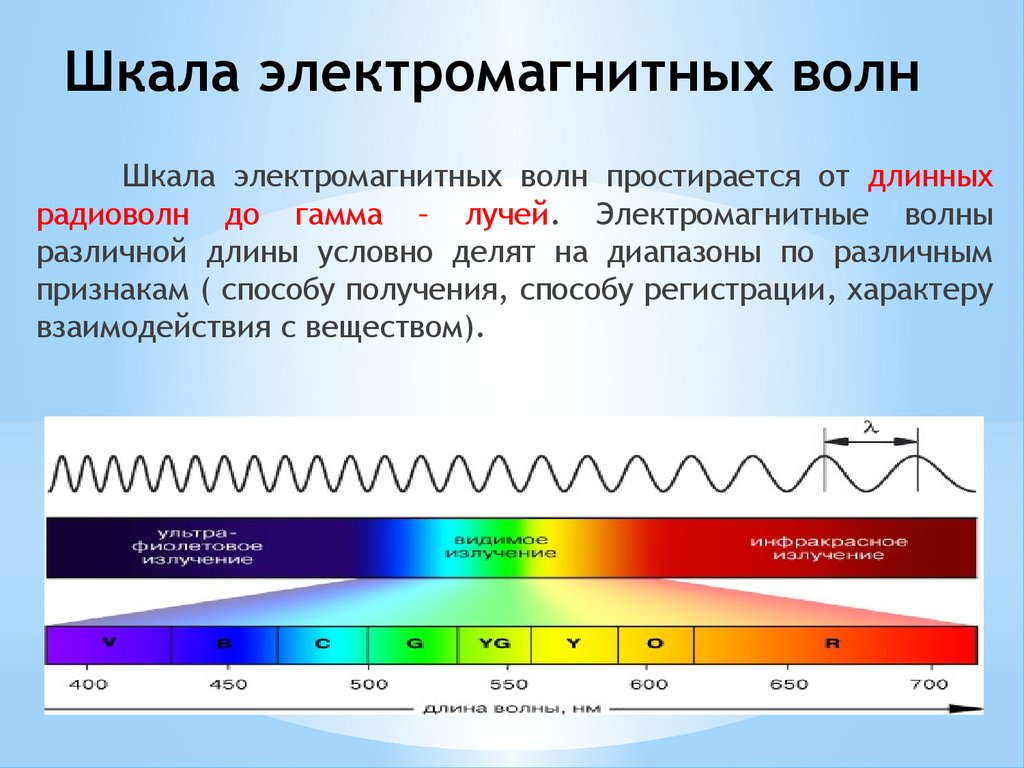 Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:
- Амплитуда — расстояние между положением покоя и максимальным смещением волны
- Частота — количество волн, проходящих через определенную точку в секунду
- Период — время, необходимое для завершения одного цикла волны
Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны. Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.
Советы по достижению успеха
Скорость волны иногда также называют скоростью распространения или скоростью распространения , потому что возмущение распространяется из одного места в другое.
Рассмотрим периодическую волну воды на рис.
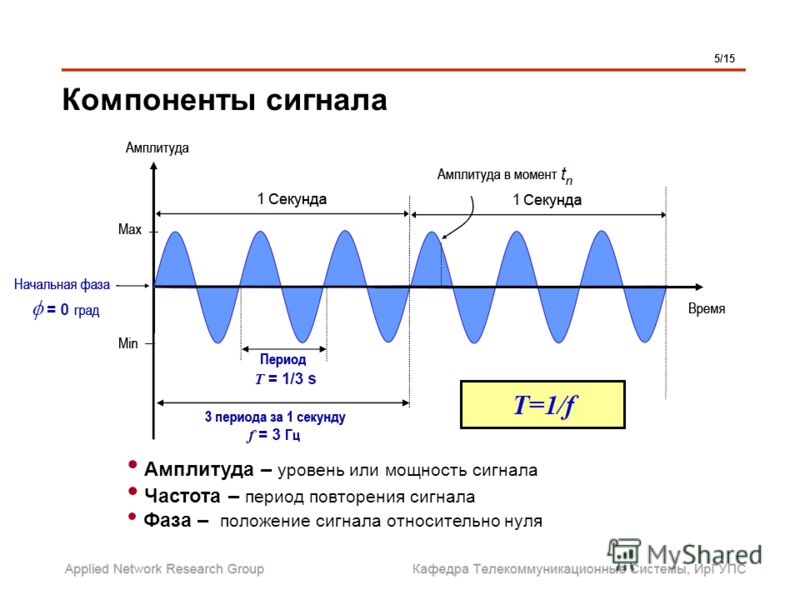
Рисунок 13.7 Волна имеет длину волны λ , что является расстоянием между соседними идентичными частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v в .
Смотреть физику
Амплитуда, период, частота и длина волны периодических волн
Это видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.
Щелкните для просмотра содержимого
Советы для достижения успеха
Гребень волны иногда также называют вершиной .
Проверка захвата
Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1 м, какова высота волны с вашего местоположения?
- 1м
- 2 м
- 4 м
- 8м
Связь между частотой волны, периодом, длиной волны и скоростью
Поскольку частота волны — это количество волн в секунду, а период — это, по существу, количество секунд на волну, соотношение между частотой и периодом составляет
13.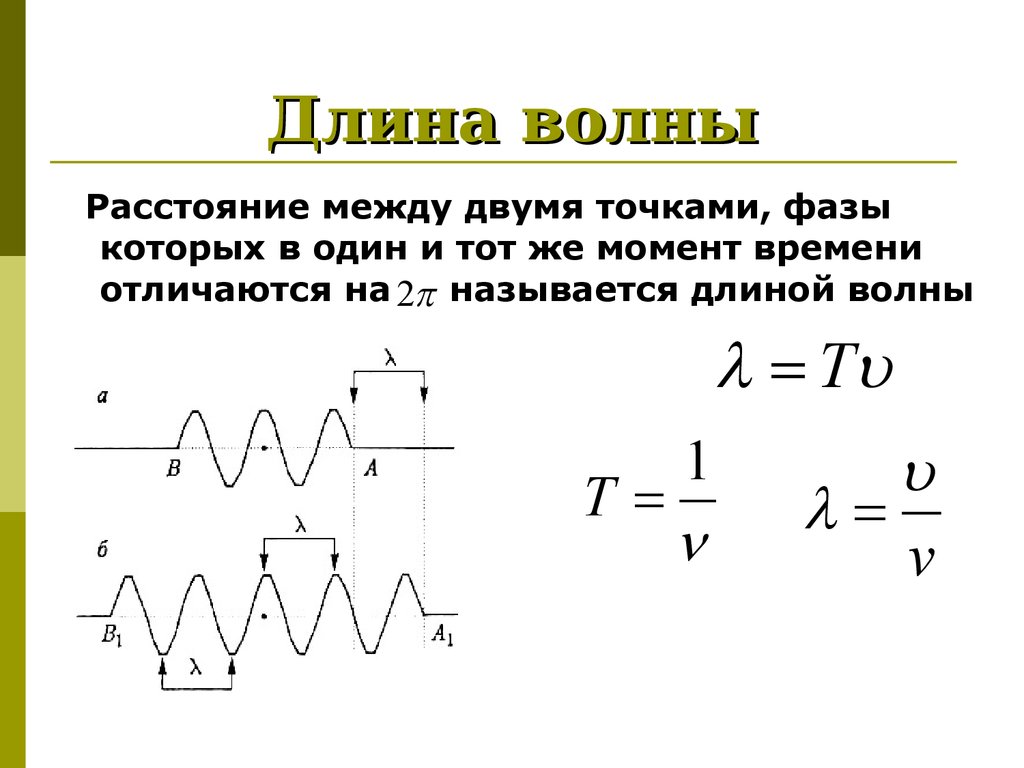 1f=1Tf=1T
1f=1Tf=1T
или
13.2T=1f,T=1f,
так же, как и в случае гармонического движения объекта. Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.
Скорость распространения v w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как
13.3vw=λTvw=λT
или
13.4vw=fλ.vw=fλ.
Из этого соотношения мы видим, что в среде, где v w постоянно, чем выше частота, тем меньше длина волны. См. рисунок 13.8.
Рисунок 13.8. Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.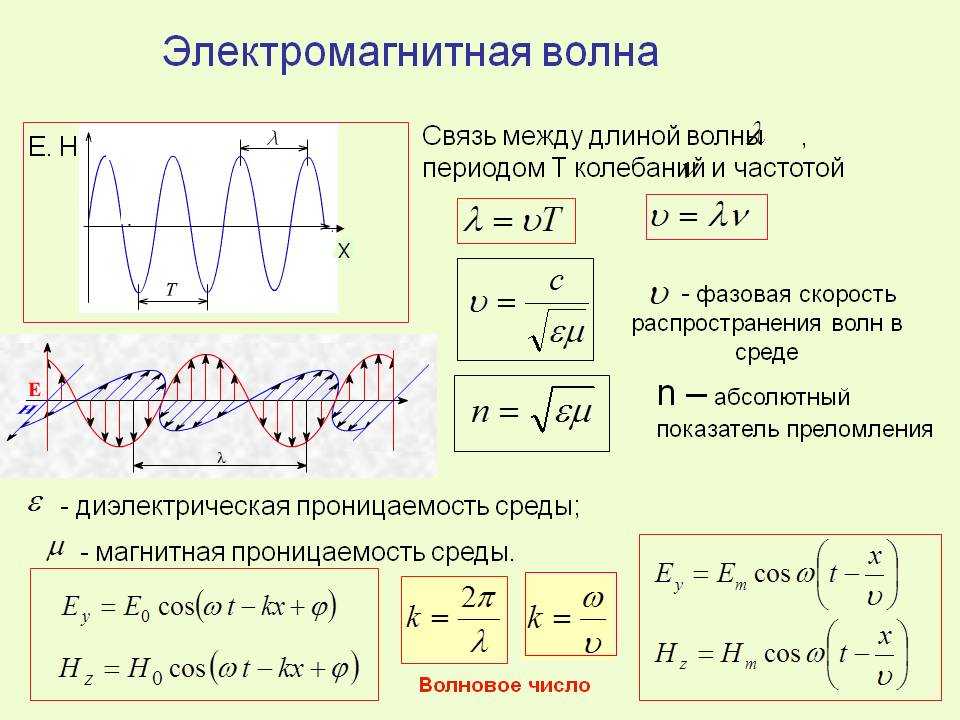
Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v w — это скорость поверхностной волны; для звука v w — скорость звука; а для видимого света v w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v w и зависит только от количества энергии в волне.
Лаборатория Snap
Волны в чаше
В этой лаборатории вы проведете измерения, чтобы определить, как на амплитуду и период волн влияет передача энергии от пробки, брошенной в воду. Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.
Материалы
- Большая миска или таз
- Вода
- Пробка (или мячик для пинг-понга)
- Секундомер
- Рулетка
Инструкции
Процедура
- Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
- Аккуратно бросьте пробку в середину чаши.
- Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
- Выньте пробку из миски и подождите, пока вода снова не осядет.
- Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
- Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, опуская пробку с разной высоты и записывая полученные длины волн и периоды.

- Интерпретируйте свои результаты.
Проверка захвата
Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?
- Нет, влияет только на амплитуду.
- Да, длина волны затронута.
Виртуальная физика
Волна на струне
Рисунок 13.10 Щелкните здесь для моделирования волны на струне.
В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.
Проверка захвата
Какая из настроек — амплитуда, частота, демпфирование или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?
- Частота; он уменьшает амплитуду волны по мере ее распространения.

- Частота; он увеличивает амплитуду волны по мере ее распространения.
- Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
- Демпфирование; он увеличивает амплитуду волны по мере ее распространения.
Решение волновых задач
Рабочий пример
Рассчитайте скорость распространения волн: чайка в океане
Рассчитайте скорость распространения океанской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10,0 м и время, за которое чайка качается вверх и вниз составляет 5,00 с.
СТРАТЕГИЯ
Заданы значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем используйте vw=λTvw=λT, чтобы найти скорость волны.
Решение
Введите известные значения в vw=λTvw=λT
13,5vw=10,0 м5,00 с=2,00 м/с.vw=10,0 м5,00 с=2,00 м/с.
Обсуждение
Такая низкая скорость кажется приемлемой для океанской волны.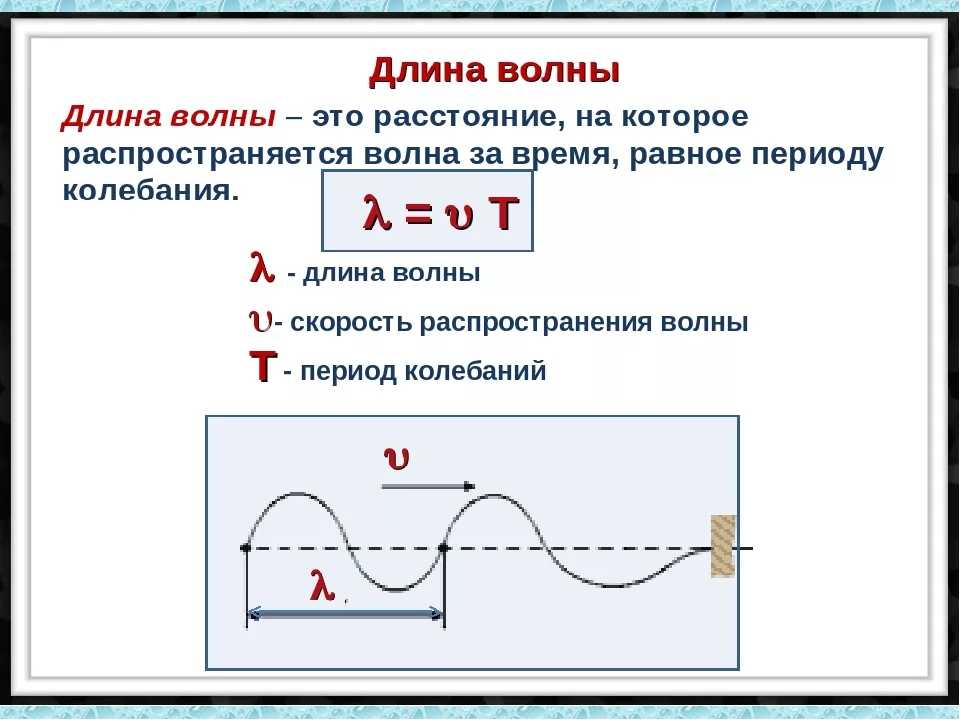 Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.
Рабочий пример
Расчет периода и скорости волны игрушечной пружины
Женщина на рис. 13.3 каждую секунду создает две волны, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (б) Если каждая волна проходит 0,9метров после одного полного волнового цикла, какова скорость распространения волны?
СТРАТЕГИЯ ДЛЯ (A)
Чтобы найти период, мы решаем для T=1fT=1f, учитывая значение частоты (f=2s−1).(f=2s−1).
Решение для (a)
Введите известное значение в T=1fT=1f
13,6T=12 с-1=0,5 с.T=12 с-1=0,5 с.
СТРАТЕГИЯ ДЛЯ (B)
Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, значения длины волны (λ = 0,9м)(λ=0,9 м), а также частота. Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.
Решение для (b)
Введите известные значения в vw=fλvw=fλ
vw=fλ=(2 с−1)(0,9 м) = 1,8 м/с.vw=fλ=(2 с-1 )(0,9 м) = 1,8 м/с.
Обсуждение
Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части ( а), и мы бы пришли к тому же ответу.
Практические задачи
Частота волны 10 Гц. Каков его период?
- Период волны 100 с.
- Период волны 10 с.
- Период волны 0,01 с.
- Период волны 0,1 с.
Какова скорость волны с длиной волны 2 м и частотой 5 Гц?
- 20 м/с
- 2,5 м/с
- 0,4 м/с
- 10 м/с
Проверьте свое понимание
Упражнение 7
Какова амплитуда волны?
- Четверть общей высоты волны
- Половина общей высоты волны
- Удвоенная общая высота волны
- Четырехкратная общая высота волны
Упражнение 8
Что понимают под длиной волны?
- Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.

- Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
- Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
- Длина волны — это расстояние между гребнем и прилегающей впадиной волны, перпендикулярное направлению распространения.
Упражнение 9
Как можно математически выразить частоту волны через период волны?
- f=1T
- ф=(1Т)2
- ф=Т
- ф=(Т)2
Упражнение 10
Когда длина волны прямо пропорциональна периоду волны?
- Когда скорость волны уменьшается вдвое
- Когда скорость волны постоянна
- Когда скорость волны удваивается
- Когда скорость волны утроится
- Печать
- Поделиться
Меры оптических волн Гигагерц-Оптик
Как и все другие волны (волны в струне, волны на воде, звук, волны землетрясений .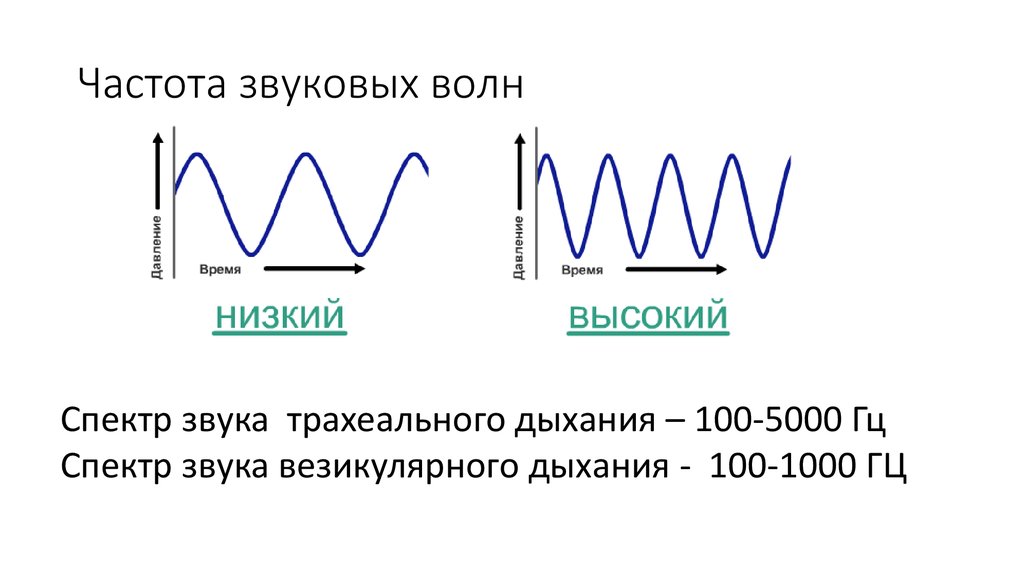 ..), свет и электромагнитное излучение в целом можно описать как вибрацию (в более общем виде: периодическое изменение некоторой физической величины), которое распространяется в пространстве. Распространение вызвано тем, что вибрация в определенном месте влияет на область рядом с этим местом. Например, в случае со звуком попеременное разрежение и сжатие молекул воздуха в определенном месте приводит к периодическим изменениям местного давления, что, в свою очередь, вызывает движение соседних молекул воздуха к этому месту или от него.
..), свет и электромагнитное излучение в целом можно описать как вибрацию (в более общем виде: периодическое изменение некоторой физической величины), которое распространяется в пространстве. Распространение вызвано тем, что вибрация в определенном месте влияет на область рядом с этим местом. Например, в случае со звуком попеременное разрежение и сжатие молекул воздуха в определенном месте приводит к периодическим изменениям местного давления, что, в свою очередь, вызывает движение соседних молекул воздуха к этому месту или от него.
Рис. 1: Формирование и распространение волны в струне
Распространение вызвано тем, что вибрация в определенном месте влияет на область рядом с этим местом. Например, в случае со звуком попеременное разрежение и сжатие молекул воздуха в определенном месте приводит к периодическим изменениям местного давления, что, в свою очередь, вызывает движение соседних молекул воздуха к этому месту или от него.
Рис.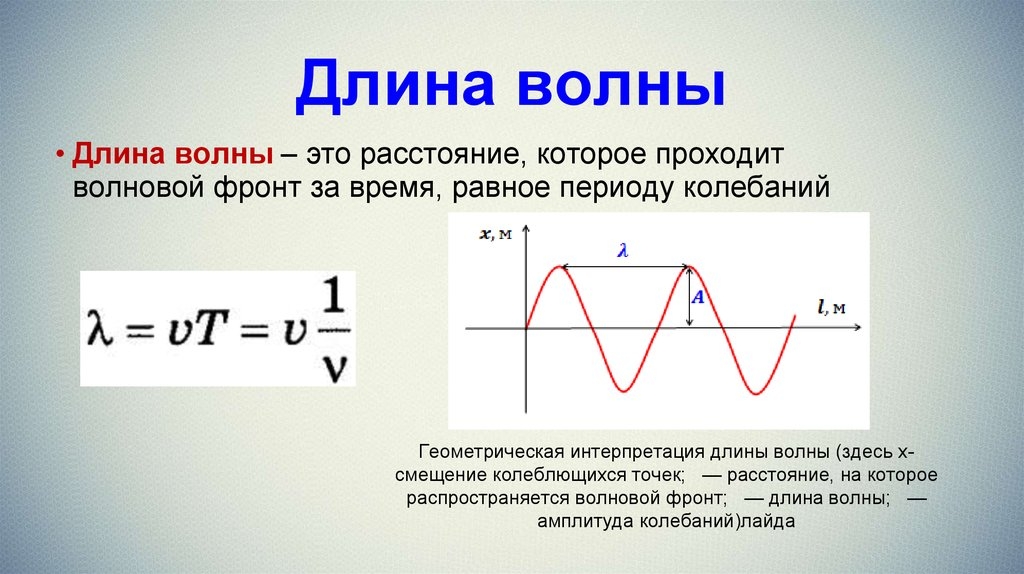 2: Формирование и распространение волны сжатия в воздухе, явление, в просторечии называемое звуком
2: Формирование и распространение волны сжатия в воздухе, явление, в просторечии называемое звуком
В случае электромагнитной волны механизм распространения включает взаимную генерацию периодически гораздо труднее понять, чем звук. Тем не менее, результат все еще может быть описан как периодическое изменение физической величины (напряженность электрического и магнитного поля), распространяющееся в пространстве. Скорость этого распространения обычно обозначается буквой c (единица измерения: метры в секунду, м / с) и зависит от среды и характера волны (см. Таблицу 1 ниже).
| Sound | Optical (electromagnetic) radiation | |||
| at λ = 434 nm | at λ = 589 nm | AT λ = 656 NM | ||
| в вакууме | — | 299921 04040404040404040404040404040404.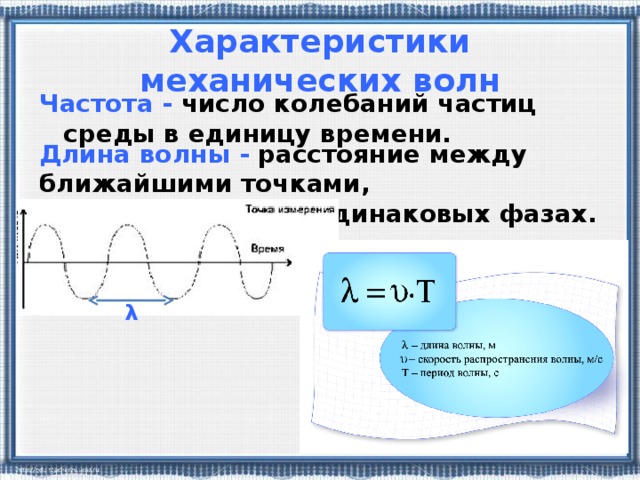 0404040404040404040404040404040404040404040404040н.0405 / s 0404040404040404040404040404040404040404040404040н.0405 / s (n = 1) | 299792 km / s (n = 1) | 299792 km / s (n = 1) |
| in air | 340 m / s | 299708 km / s (n = 1.000280) | 299709 km / s (n = 1.000277) | 299710 km / s (n = 1. 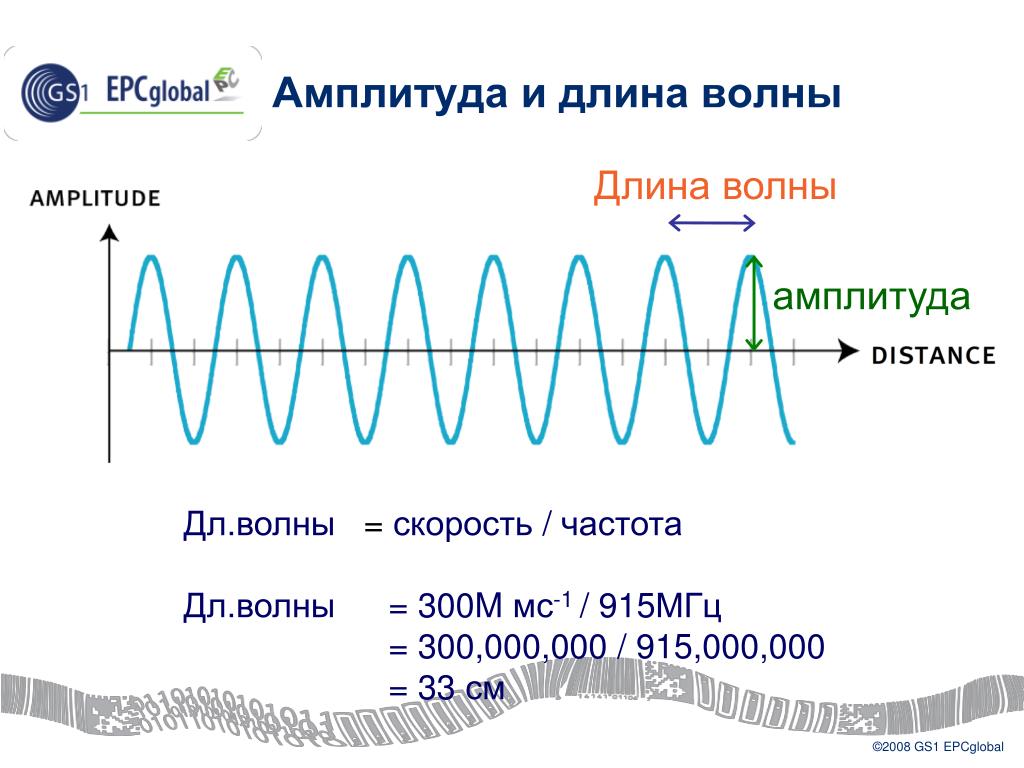 000275) 000275) |
| in water | 1500 m / s | 223725 km / s (n = 1.340) | 224900 km / s (n = 1.333) | 225238 km / s (n = 1.331) |
Tab. 1: Скорости звука и света в воздухе и в воде. Для оптического излучения в скобках указан соответствующий показатель преломления
Для описания основных свойств волны были определены следующие величины для всех видов волн:
Амплитуда является максимальным нарушением равновесия среды. В случае волны в горизонтальной струне это значение равно половине расстояния по вертикали между гребнем волны и ее впадиной.

Длина волны λ – это расстояние между двумя соседними гребнями (или впадинами), которое указывается в метрах.
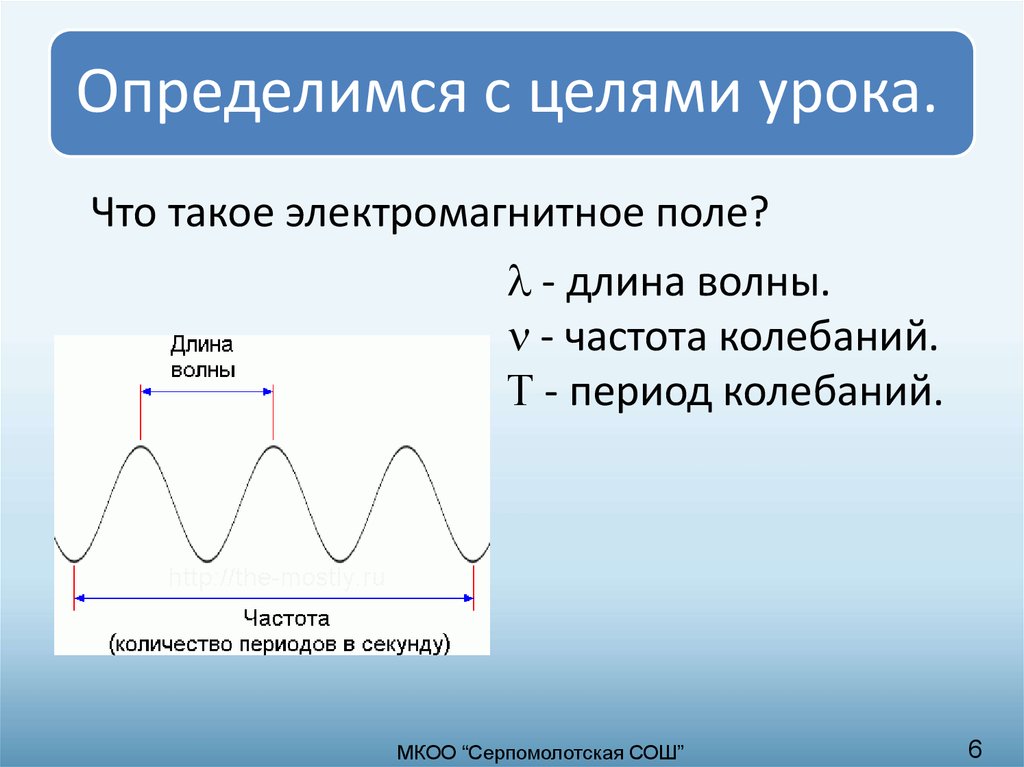
период T волны — это время, которое проходит между приходом двух последовательных гребней (или впадин) в определенном месте X. Это определение идентично утверждению, что период – это время, за которое вибрация в точке X совершает полный цикл от гребня до впадины и до гребня. Период волны указан в секундах.
Частота f волны – это количество циклов вибрации в секунду в определенном месте X. Единица измерения – герц (Гц), а 1 Гц – величина, обратная 1 секунде. Например, волна с периодом T = 0,25 с занимает ¼ секунды, чтобы завершить полный цикл вибрации (максимум – – впадина – максимум) в определенном месте и, таким образом, совершает четыре колебания в секунду.
 Следовательно, его частота равна f = 4 Гц. Из этого примера видно, что период волны полностью определяет ее частоту и наоборот. Отношение между этими величинами определяется выражением f = 1 / T.
Следовательно, его частота равна f = 4 Гц. Из этого примера видно, что период волны полностью определяет ее частоту и наоборот. Отношение между этими величинами определяется выражением f = 1 / T.
Если мы рассматриваем волну как периодический в пространстве и во времени процесс, мы можем рассматривать длину волны λ как расстояние между двумя повторениями процесса в пространстве, а период T как «расстояние» между два повторения процесса во времени.
Основное соотношение между длиной волны, частотой и скоростью следует из следующего соображения:
За время гребень должен пройти расстояние, равное одной длине волны λ от точки X до точки Y. Этот промежуток времени идентичен периоду волны T. amounts to
| c = | λ | = λ f |
| T |
When a wave passes from one medium to another, its frequency remains the same .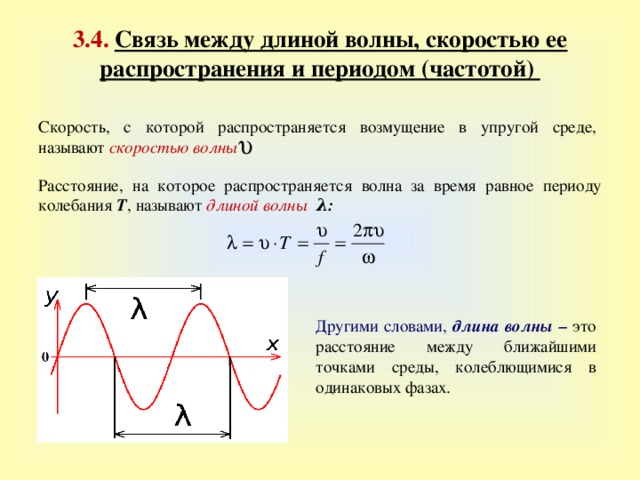 Если скорости волны в двух средах различаются, длины волн в двух средах также различаются, как следствие. Поскольку частота волны не зависит от среды, через которую проходит волна, для характеристики волны удобнее использовать частоту, а не длину волны. В акустике это обычная практика — в большинстве случаев высота звука характеризуется его частотой, а не длиной волны в определенной среде (например, в воздухе).
Если скорости волны в двух средах различаются, длины волн в двух средах также различаются, как следствие. Поскольку частота волны не зависит от среды, через которую проходит волна, для характеристики волны удобнее использовать частоту, а не длину волны. В акустике это обычная практика — в большинстве случаев высота звука характеризуется его частотой, а не длиной волны в определенной среде (например, в воздухе).
В оптике ситуация иная: в большинстве случаев вместо частоты используется длина волны, хотя это и приводит к определенному усложнению: например, зеленый свет имеет длину волны 520 нм в вакууме, но в воде его скорость равна меньше в 1,33 раза и, таким образом, в воде тот же зеленый свет имеет длину волны всего 520 / 1,33 = 391,0 нм. Следовательно, если мы хотим охарактеризовать волну ее длиной волны, мы также должны указать среду, для которой дано фактическое значение длины волны.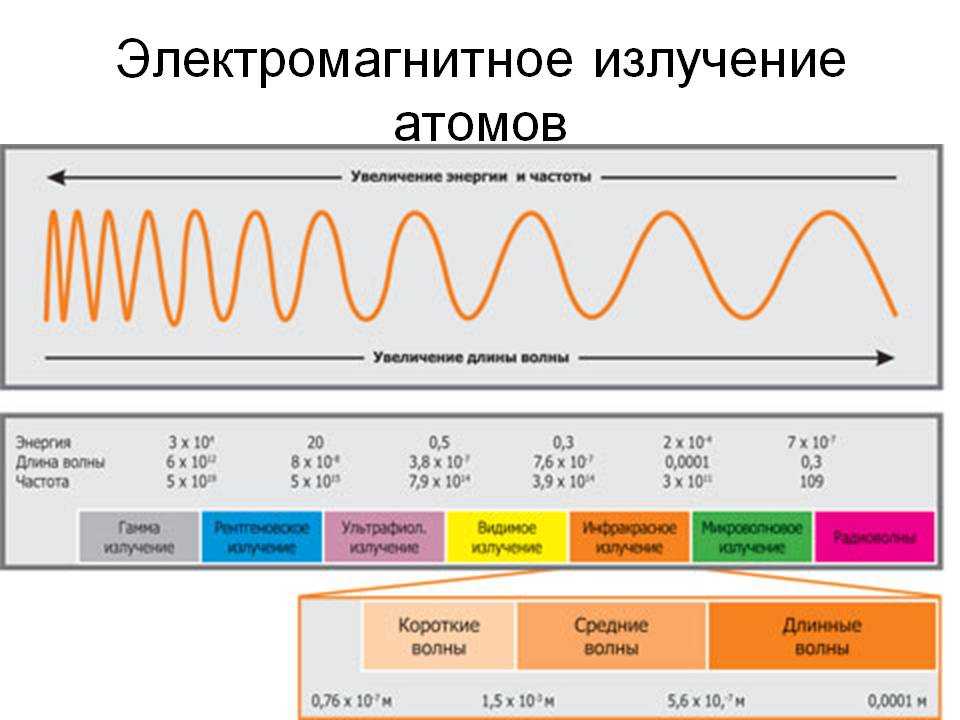 Согласно правилам CIE, которые применяются в этом руководстве, термин «длина волны» относится к «длине волны в воздухе», если не указано иное. Однако, применяя данные длины волны к свету, проходящему через среду, отличную от вакуума, следует иметь в виду, что длина волны света изменяется согласно следующему соотношению
Согласно правилам CIE, которые применяются в этом руководстве, термин «длина волны» относится к «длине волны в воздухе», если не указано иное. Однако, применяя данные длины волны к свету, проходящему через среду, отличную от вакуума, следует иметь в виду, что длина волны света изменяется согласно следующему соотношению
| λ Medium = | λ Vacuum | = | λ Air × n Air |
| n Medium | N Среда |
с
| N AIR = | 9CI 6 = | CO 6666669 | CO 666 = | CI . |





 Следовательно, его частота равна f = 4 Гц. Из этого примера видно, что период волны полностью определяет ее частоту и наоборот. Отношение между этими величинами определяется выражением f = 1 / T.
Следовательно, его частота равна f = 4 Гц. Из этого примера видно, что период волны полностью определяет ее частоту и наоборот. Отношение между этими величинами определяется выражением f = 1 / T.