Алгебра логики — Умскул Учебник
На этой странице вы узнаете- Что такое алгебра логики и зачем здесь котики?
- Как вычислить истинность логического выражения?
- Для чего нужны законы логики?
Как часто поведение котов вам кажется странным? А если кот в галстуке или вооружен? Сейчас будем разбираться в логике с помощью этих пушистых созданий.
Понятие алгебры логикиОбратите внимание на этого персонажа:
Я скажу про него две вещи:
- Этот кот в галстуке.
- Этот кот белого цвета.
Очевидно, что с первым высказыванием и поспорить нельзя, а вот второе — наглая ложь. А если я захочу вас запутать: «Этот кот в галстуке или он белого цвета, из чего следует, что он белого цвета и в галстуке или не белый». Что это в итоге — правда или ложь?
Чтобы это определить, в математике есть отдельный раздел.
Алгебра логики — это раздел математики, который занимается логическими операциями над высказываниями.
Любое высказывание может быть либо истинным, либо ложным. Цель алгебры логики — определять истинность логических выражений на основании отдельных высказываний. Алгебра логики действительно может, например, складывать и умножать высказывания друг с другом, и чтобы в записи это выглядело адекватно, истину принято обозначать как 1, а ложь — как 0.
| Что такое алгебра логики и зачем здесь котики? В примере с котиком высказывание А было истинно, а высказывание В — ложно. |
Как вычислить истинность логического выражения?
Термин высказывание, мы теперь знаем. Но что такое логическое выражение? Выражение — это уравнение из высказываний, как математическое уравнение из чисел.
«Этот кот вооружен и его глаза зеленого цвета», — в одном выражении мы использовали два высказывания.
Истинность выражения определяется истинностью логических высказываний, а также логическими операторами, которые стоят между ними.
Например, я скажу про того же самого кота: «Этот кот вооружен и его глаза голубые». Это будет наглая ложь, так как я употребил союз И, то есть подразумеваю, что оба высказывания истинны — что неправда. Но если бы я сказал: «Этот кот вооружен или его глаза голубые», союз ИЛИ защитил бы меня от клейма лжеца. Я делаю акцент на истинности только одного высказывания из двух.
Так и работают логические операторы — в зависимости от них все выражение и принимает значение истины или лжи.
Основные логические операторы алгебры логики:
- Конъюнкция: логическое умножение или логическое И. В записи обозначается как ∧. А ∧ В дает истину только в том случае, если оба высказывания А и В истинны.
Называется логическим умножением, потому что имеет схожий принцип работы: если хоть один из множителей будет равен 0, все выражение будет равно 0.

В примере про кота выше выражение «Этот кот вооружен ∧ его глаза голубые» будет ложным. Он вооружен, но глаза у него не голубые. Одно из высказываний не выполнилось, так что конъюнкция равна 0.
- Дизъюнкция: логическое сложение или логическое ИЛИ. В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.
Называется логическим сложением за схожесть: если складывать только 0 и 1, чем мы и занимаемся, то достаточно одному слагаемому быть 1, чтобы все выражение не было равно 0.
Важно сразу понять — если применить логическое сложение к двум единицам (1 ∨ 1), мы получим не 2, а все еще 1. Все-таки единица здесь означает не число, а истину, и сложив две, мы не получим одну сверх-истину.
Тогда выражение «Этот кот вооружен ∨ его глаза голубые» будет уже истинным: глаза его не голубые, но он все-таки вооружен. Дизъюнкция вернет нам 1.

- Инверсия: логическое отрицание или логическое НЕ. Превращает истину в ложь и наоборот.
Ложное высказывание «Его глаза голубые» можно легко превратить в истину, если сказать «Его глаза НЕ голубые». В записи обозначается чертой над выражением или знаком ¬, например, ¬А.
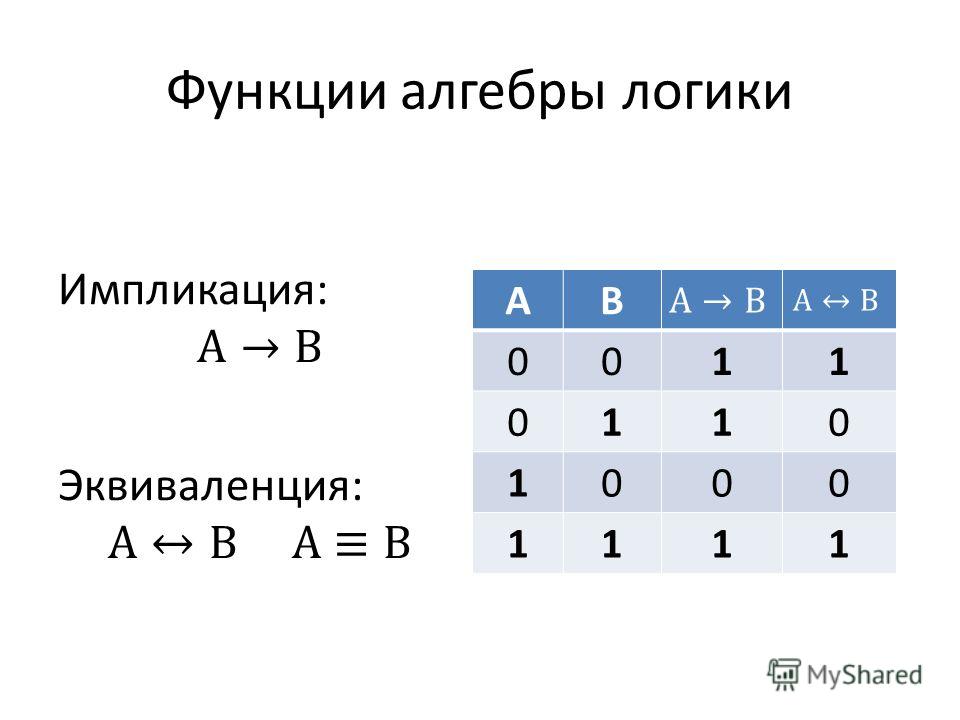
- Эквиваленция, если проще — равенство. Если оба высказывания равны (оба 0 или оба 1), то получим истину, иначе — ложь. Обозначается как ≡.
Истинным будет выражение «У кота нет оружия так же, как его глаза голубые». И то, и другое — ложь, но мы их сравнили, сказав, что они одинаковы по истинности, что уже правда.
- Импликация, иначе говоря, следование. Обозначается стрелочкой, например А ⇒ В. Если из истины следует ложь, то это автоматически ложь, все остальное — истина.
Например, вас никто не просил кормить кота. Если вы этого не сделаете, ничего плохого и не случится. А если сделаете — тоже хорошо, кот будет рад.
 А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.
А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.
Приоритет этих операторов:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквиваленция.
Как и везде в математике, приоритет можно менять с помощью скобок — что в них, то выполняется в первую очередь.
Таблицы истинностиВ логических уравнениях высказывания используются в виде переменных, а главная проблема, которую рассматривает алгебра логики — когда точно неизвестна истинность каждого высказывания. Назовем эту ситуацию “кот в мешке”. Сказать про кота можно что угодно, но будет ли это правдой — мы не узнаем, пока не заглянем в мешок. В таких ситуациях нам может помочь таблица истинности.
Таблица истинности — это таблица, которая показывает истинность всего логического уравнения в зависимости от истинности отдельных переменных.
В этой таблице содержатся все возможные наборы переменных. Количество наборов N зависит от количества различных переменных i как N = 2i.
Чтобы удобно записать наборы, нумеруем их по порядку начиная с 0, переводим их номер в двоичную систему счисления (2сс) и записываем набор цифр.
Давайте запишем таблицы истинности для известных нам логических операторов:
- инверсия берет только 1 переменную и сразу меняет ее значение:
- конъюнкция берет две переменные и возвращает 1 только в том случае, если обе равны 1:
- дизъюнкция вернет 1, если хотя бы одна из переменных равна 1:
- эквиваленция вернет 1, если переменные равны, и 0 в противном случае:
- импликация вернет 0, если из истины будет следовать ложь, и 1 во всех остальных случаях:
| Импликацию можно выразить через дизъюнкцию: А ⇒ В = ¬А ∨ В |
Зная таблицы истинности отдельных операторов, давайте попробуем составить таблицу истинности для полного выражения.
Например, для выражения: А ∧ (В ∨ С) ≡ В ⇒ ¬А.
Важно правильно расставить порядок операций. Как и всегда, в первую очередь выполняется действие в скобках, а дальше — в порядке приоритета.
Здесь порядок операций будет следующим:
Создадим таблицу, в которой сразу пропишем все наборы 0 и 1 для переменных А и В и добавим столбцы для каждого шага вычисления.
Чтобы удобно записать наборы, пронумеруем их по порядку начиная с 0. Переведем их номер в 2сс и запишем набор цифр. У нас 3 различные переменные, поэтому должно быть 8 наборов.
- Первое действие — сложение В и С. Для каждого набора запишем результат сложения в соответствующий столбец.
- Второе действие — инверсия переменной А.
- Третье действие — умножение значения А на результат первого действия:
- Четвертое — импликация значения В и результата второго действия:
- И последнее действие — эквиваленция результатов 3 и 4 действий:
Последний столбец — и есть результат таблицы истинности. По нему можно сказать, что при А = 1, В = 0 и С = 1 все исходное выражение равно 1, а во всех остальных случаях — 0.
По нему можно сказать, что при А = 1, В = 0 и С = 1 все исходное выражение равно 1, а во всех остальных случаях — 0.
| Для чего нужны законы логики? Законы логики позволяют упрощать логические уравнения, делая их не такими большими и более решаемыми. |
Их не так уж и мало: от самых простых и очевидных до достаточно хитрых; от тех, которые встречаются очень часто до довольно редких.
Не обязательно знать все наизусть — часть из них действительно проста и похожа на правила математики начальной школы. Про остальные стоит помнить: если увидите очень большое логическое уравнение, высока вероятность того, что эти законы помогут его сократить.
Попробуем упростить исходное выражение ¬(¬А ∧ ¬В) ∨ В ∧ С:
- Первым можно увидеть закон де Моргана, где у нас идет отрицание целой скобки:
¬(¬А ∧ ¬В) ∨ В ∧ С = ¬(¬А) ∨ ¬(¬В) ∨ В ∧ С
- Здесь же появляются переменные А и В, к которым можно применить закон двойного отрицания:
¬(¬А) ∨ ¬(¬В) ∨ В ∧ С = А ∨ В ∨ В ∧ С
- Можно заметить закон поглощения — В складывается с умножением В на С:
А ∨ В ∨ В ∧ С = А ∨ В
Итого, уравнение с 3 переменными и множеством отрицаний мы смогли превратить в максимально простую запись, где осталось всего 2 переменные:
¬(¬А ∧ ¬В) ∨ В ∧ С = А ∨ В
Фактчек- Алгебра логики — это математика, которая пользуется не числами, а высказываниями, являющимися истинными или ложными.
 Истина обозначается как 1, а ложь — как 0.
Истина обозначается как 1, а ложь — как 0. - Основными логическими операторами являются инверсия, конъюнкция, дизъюнкция, импликация и эквиваленция.
- Для расчета истинности логического уравнения используется таблица истинности.
- Законы логики помогают сокращать логические уравнения.
Задание 1.
Выберите правильный порядок приоритета логических операторов:
- Импликация, эквиваленция, конъюнкция, дизъюнкция, инверсия.
- Инверсия, конъюнкция, дизъюнкция, импликация, эквиваленция.
- Инверсия, конъюнкция, дизъюнкция, эквиваленция, импликация.
- Инверсия, дизъюнкция, конъюнкция, эквиваленция, импликация.
Задание 2.
Сопоставьте название логического оператора с упрощенным:
| Инверсия | А. Умножение |
| Эквиваленция | Б. Отрицание |
| Импликация | В. Следование Следование |
| Дизъюнкция | Г. Равенство |
| Конъюнкция | Д. Сложение |
Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения: А ∨ В ⇒ ¬С?
- 11101010
- 11101111
- 11111110
- 11000100
Задание 4.
Сократите логическое выражение: ¬(А ∨ В) ∧ (¬А ∨ С)
- ¬(А ∧ В)
- ¬А ∨ ¬В ∨ С
- ¬А ∧ ¬В ∧ С
- ¬А ∧ ¬В
Ответы: 1. — 2; 2. — 1Б, 2Г, 3В, 4Д, 5А; 3. — 1; 4. — 4.
Элементы алгебры логики (8 класс, информатика)
4.4
Средняя оценка: 4.4
Всего получено оценок: 436.
4.4
Средняя оценка: 4.4
Всего получено оценок: 436.
Одним из направлений теоретической информатики является алгебра логики. Основы алгебры логики изучаются в школьном курсе информатики в 8 классе. Кратко об элементах алгебры логики можно прочитать в данной статье.
Элементы алгебры логики
Одним из разделов теоретической информатики является алгебра логики. Некоторые элементы алгебры логики доступны для понимания уже на школьном уровне.
Первые элементы алгебры логики были описаны в 19 веке в работах английского математика Джорджа Буля. Он первый высказал мысль о связи логики с математикой.
Высказывания
Объектом изучения алгебры логики являются высказывания, которые представляют собой повествовательные предложения, которые могут быть однозначно оценены как истинные или ложные. Истинность высказывания обозначают единицей, ложность – нулем. Примером высказывания может быть предложение «Москва столица Российской федерации».
Не все предложения, несущие ту или иную информацию можно назвать высказываниями. Например, вопросительные или побудительные предложения – это не высказывания. Также не являются высказываниями математические выражения с переменными.
Например, не являются высказываниями следующие предложения:
- Сколько весит слон?
- Летайте самолетами Аэрофлота!
- 5*х + 8*y = 24
- Этот фильм самый лучший.

Алгебра логики изучает методы работы с высказываниями.
Действия над высказываниями
Высказывания как объекты могут быть операндами следующих логических действий
- Пересечение.
- Объединение.
- Инверсия.
Наглядно логические операции поясняют круги Эйлера или диаграммы Венна.
Пересечение
Пересечение – это действие над высказываниями, в результате которого будет получено новое высказывание истинное только в том случае, когда и исходные высказывания одновременно истинны.
Например, для высказываний «На каникулах я поеду в Волгоград» и «Выходные я проведу у бабушки» результатом операции пересечения будет новое высказывание «На каникулах я поеду в Волгоград и выходные я проведу у бабушки», которое является истиной только в том случае, когда истины оба исходных утверждения одновременно
Пересечение также называют логическим умножением, конъюнкцией или логическим И.
Обозначают знаками И, & или ∩.
На диаграмме операция пересечения выглядит как закрашенная область – представляющая собой общую для каждого операнда часть.
Объединение
Объединение – представляет собой действие над двумя высказываниями, в результате которого будет получено новое высказывание, ложное в том случае, когда одно из двух исходных операндов ложно.
Например, для исходных высказываний «На каникулах я поеду в Волгоград» и «На каникулах я поеду в Питер» результатом операции объединения будет высказывание «На каникулах я поеду в Волгоград или на каникулах я поеду в Питер», которое ложно только в том случае, когда ложны оба исходных высказывания. Если хотя бы одно из первоначальных высказываний является правдой, то и результат будет иметь значение «Истина».
Объединение также называют логическим сложением, дизъюнкцией, логическим ИЛИ.
Для ее обозначения используются знаки: ИЛИ, +, U.
Рис. 2. Диаграмма Венна для операции объединенияНа диаграмме Венна операция объединения представляет собой всю область, относящуюся и к первому и ко второму операнду.
Инверсия
Инверсия – унарная логическая операция, заключающаяся в изменении на противоположное значение.
Например, высказывание «На каникулах я поеду в Волгоград» в инверсной форме будет выглядеть так «На каникулах я не поеду в Волгоград».
Инверсию обозначают знаками НЕ, ¬, ¯.
Инверсия на диаграмме Венна выглядит как область, не относящаяся к операнду.
Рис. 3. Диаграмма Венна для операции инвертированияАксиомы алгебры логики
В математике есть понятие аксиома – постулат, не требующий доказательств.
В математической логике также есть бездоказательные утверждения, касающиеся логических операций над высказываниями.
Для объединения справедливы аксиомы:
- А + 0 = А
- А + 1 = 1
- А + А = А
- А + НЕ(А) = 1
Для пересечения характерны такие аксиомы:
- А & 0 = 0
- А & 1 = А
- А & А = А
- А & НЕ(А) = О
Для операции инверсии применима аксиома двойного отрицания НЕ (НЕ (А)), когда дважды проинвертировав операнд получают в итоге само исходное значение.
Что мы узнали?
Алгебра логики стоит на стыке математики и информатики и составляет теоретическую базу, на основе которой строятся методы работы с информацией. Объектом изучения этого направления является высказывания. Основными логическими операциями являются пересечение, объединение и инверсия. В алгебре логики действуют ряд аксиом.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Некит Розводовский
9/10
Алиса Волк
6/10
Оценка статьи
4.4
Средняя оценка: 4.4
Всего получено оценок: 436.
А какая ваша оценка?
Почему логика важна для информатики и математики
Шведский перевод этой страницы доступен по адресу
Научный блог: https://www. expertoautorecambios.es/science/?p=998 .
expertoautorecambios.es/science/?p=998 .
Эстонский перевод этой страницы доступен по адресу:
https://www.espertoautoricambi.it/science/2017/11/03/miks-loogika-on-oluline-et-arvuti-teadust-ja-matemaatika/
4
7 A Португальский перевод этой страницы доступен по адресу:
https://www.homeyou.com/~edu/ciencia-da-computacao-e-matematica
Логика связана с формами рассуждений. С
рассуждение участвует в большинстве интеллектуальных действий, логика имеет отношение к
широкий круг занятий. Изучение логики необходимо для школьников.
Информатика. Это также очень ценно для студентов, изучающих математику, и других
которые используют математические доказательства, например, студенты-лингвисты. в
процесс рассуждения делает выводы. В выводе используется
совокупность утверждений, предпосылок, чтобы оправдать другое утверждение,
вывод.
Большинство наших курсов логики включают точный анализ характеристик
дедуктивный вывод. Эти курсы вводят некоторые специальные символы в то, что
называется «формальными языками», но логика не является операцией с символами. Курсы
обучать общим понятиям и методам, которые полезны независимо от формальных
языки. Студенты узнают, как строить доказательства на английском языке, а также на
формальный язык, так что понятия и методы, которые изучены, могут быть использованы в
разнообразие контекстов. Учатся даже доказывать теоремы о формальных
языки; это особенно важно для информатики, лингвистики и
некоторые разделы математики.
Идея компьютера общего назначения, машины Тьюринга, была изобретена в
курс исследований по логике. Программы для ЭВМ пишутся на специальных,
символьные языки, например, Fortran, C++, Lisp, Prolog.
Эти языки содержат черты логического символизма, а Лисп и Пролог
производные от формальных языков для логики. Благодаря таким связям изучение
логика может помочь в разработке программ. Другие математические методы
описанные в PHL 313K, например рекурсивные определения, широко используются в программах.
Теория множеств, описанная в PHL 313K, используется в современных проектах баз данных. Но
информатика — это не только программирование. включает в себя логические и
математический анализ программ. С помощью таких анализов можно доказать
корректность процедур и оценить количество шагов, необходимых для выполнения
заданную программу. В такой работе используется современная логика, и она заложена
в программы, которые помогают построить доказательства таких результатов. Логика тоже играет роль
в разработке новых языков программирования, и это необходимо для работы в
искусственный интеллект и когнитивная наука.
Понимание предметов, преподаваемых в PHL 313K, требуется для успешная специальность по информатике: 1. Так же, как исчисление используется в инженерных курсах, основы логики и теории множеств используются во многих курсы информатики. 2. Курсы CS для старших классов не являются программированием. сверла; эти курсы охватывают общие принципы и требуют математических доказательств об этих принципах. PHL 313K обучает основным принципам и методам построение и оценка доказательств.
Математики рассуждают об абстрактных понятиях, например, непрерывных
функции, алгебраические системы, такие как «кольца», и топологические пространства. Большинство
студенты-математики учатся писать доказательства таких вещей, следуя примерам в
их классы. Это часть изучения математики, но она медленная и часто приводит к
к путаницам. Специалисты по математике, изучающие логику, обнаруживают, что она помогает им в их учебе.
математическое мышление. Это помогает избежать путаницы и помогает в
построение ясных, убедительных доказательств. Изучение логики необходимо для работы
в основаниях математики, которая в значительной степени связана с природой
математической истины и с обосновывающими доказательствами математических объектов,
такие как целые числа, комплексные числа и бесконечные множества. Математические специальности в UT не
необходимо пройти курс логики, но те, кто это делает, почти всегда сообщают, что это
интересно и полезно.
Это помогает избежать путаницы и помогает в
построение ясных, убедительных доказательств. Изучение логики необходимо для работы
в основаниях математики, которая в значительной степени связана с природой
математической истины и с обосновывающими доказательствами математических объектов,
такие как целые числа, комплексные числа и бесконечные множества. Математические специальности в UT не
необходимо пройти курс логики, но те, кто это делает, почти всегда сообщают, что это
интересно и полезно.
PHL 313K — введение в логику, элементарную теорию множеств, основы теории чисел и использования индукции и рекурсии. Это требует серьезного изучения, но он охватывает интересный и полезный материал. Хорошие курсы повышения квалификации, для студентов, заинтересованных в более продвинутой логике, есть PHL 344K (= M 344K) и PHL. 358.
Robert L. Causey
Обновление RLC: 22.09.17
логика — Применение теории моделей и алгебры в информатике
Задавать вопрос
спросил
Изменено 6 лет, 4 месяца назад
Просмотрено 1к раз
$\begingroup$
, как следует из названия, я ищу приложения двух первых к последнему.
Есть некоторые приложения, алгебраическая теория чисел в ИТ-безопасности, теория конечных моделей может рассматриваться как поле на пересечении математики. логика. и теор. CS с описательной теорией сложности, безусловно, очень интересны.
Но я ищу что-то немного другое, скоро мне нужно будет написать диссертацию по CS, а так как у меня также есть знания по математике, я хотел бы это использовать. По алгебре я прослушал два вводных курса, так что сейчас я на уровне Атьи-Макдональда и достаточно продвинулся в теории моделей. Я только начал с учебника Markers по теории моделей и довольно быстро продвигаюсь, благодаря своему опыту в области алгебры и Чанга-Кейслера.
Итак, мой вопрос в основном таков: каковы хорошие рекомендации для дальнейшего обучения в CS, где я могу полностью использовать ресурсы MT и алгебры и их тесную связь? Мне было бы очень интересно, есть ли такие приложения в криптографии и смежных областях.
Большое спасибо!
- логика
- коммутативная алгебра
- информатика
- теория моделей
$\endgroup$
$\begingroup$
Вопрос «Применение логики и алгебры в компьютерных науках» похож на ваш, но на самом деле он совершенно другой.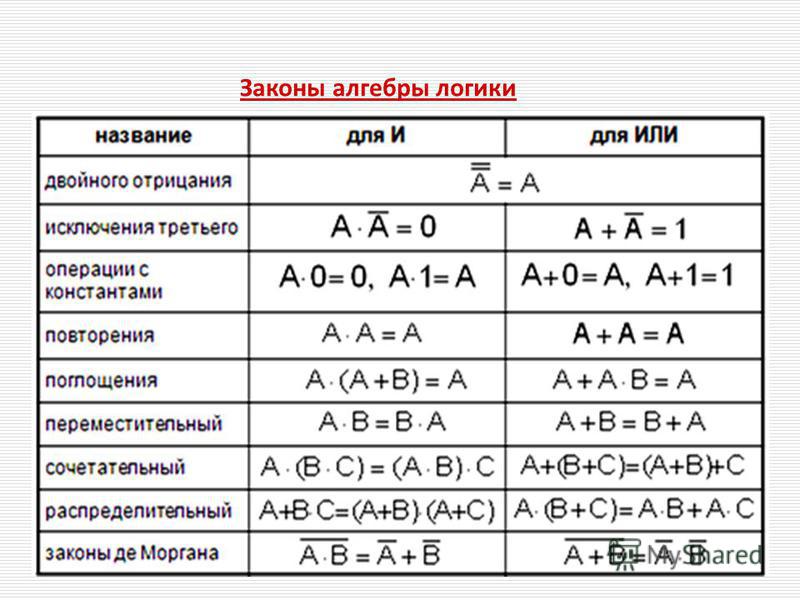 Тем не менее, некоторые ответы могут быть интересны.
Тем не менее, некоторые ответы могут быть интересны.
Кроме того, подобные вопросы задавались по cstheory, и некоторые ответы могут дать вам хорошие рекомендации для дальнейшего изучения CS. Вот мой выбор:
Алгебра
Вам следует взглянуть на вопрос Использование алгебраических структур в теоретической информатике, на принятый ответ и, возможно, также на другие ответы.
Возможно, вас также заинтересует вопрос «Алгебра-ориентированная отрасль теоретической информатики».
Теория моделей
Позвольте мне упомянуть Указатели для приложений CS логики. В частности, вот цитата, извлеченная из ответа Виджая Д.
.Теория конечных моделей
Простейшее ограничение классической теории моделей с точки зрения информатики заключается в изучении структур в конечной вселенной. Эти структуры встречаются в виде реляционных баз данных, графов, и другие комбинаторные объекты, возникающие повсюду в компьютере наука.
Ответ Дай Ле на этот вопрос также дает некоторые другие соответствующие ссылки.
$\endgroup$
$\begingroup$
Еще одна область теории сложности, которая в значительной степени опирается на методы теории моделей, — это сложность доказательства. Эта область имеет то преимущество, что она использует стандартные методы из (бесконечной) теории моделей. Теория конечных моделей имеет то же название, что и теория бесконечных моделей, но в основном использует разные методы.
Сложность доказательства можно изучать с точки зрения теории доказательств или модели. Хорошим введением в сложность доказательства с точки зрения теории моделей является книга Яна Крайчека «Ограниченная арифметика, логика высказываний и теория сложности». Подход Крайчека обычно также использует довольно много алгебры. Поэтому я думаю, что эта книга может быть полезной. ищу тебя
$\endgroup$
$\begingroup$
Ну, у вас есть богатое пересечение теории моделей и CS в вещах, связанных с вычислимостью, таких как соответствие Карри-Ховарда и интерпретация вычислимости теоремы Лёба и других классических результатов.



 А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.
А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.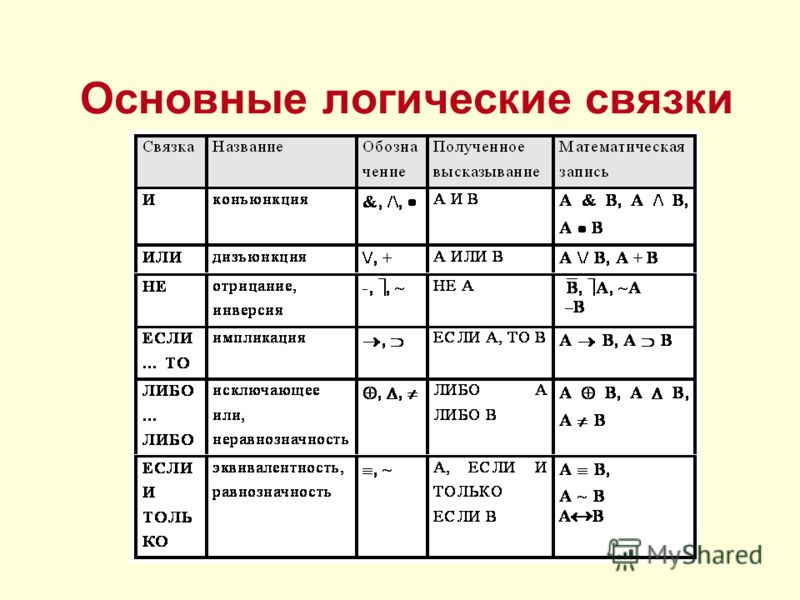 Истина обозначается как 1, а ложь — как 0.
Истина обозначается как 1, а ложь — как 0.
