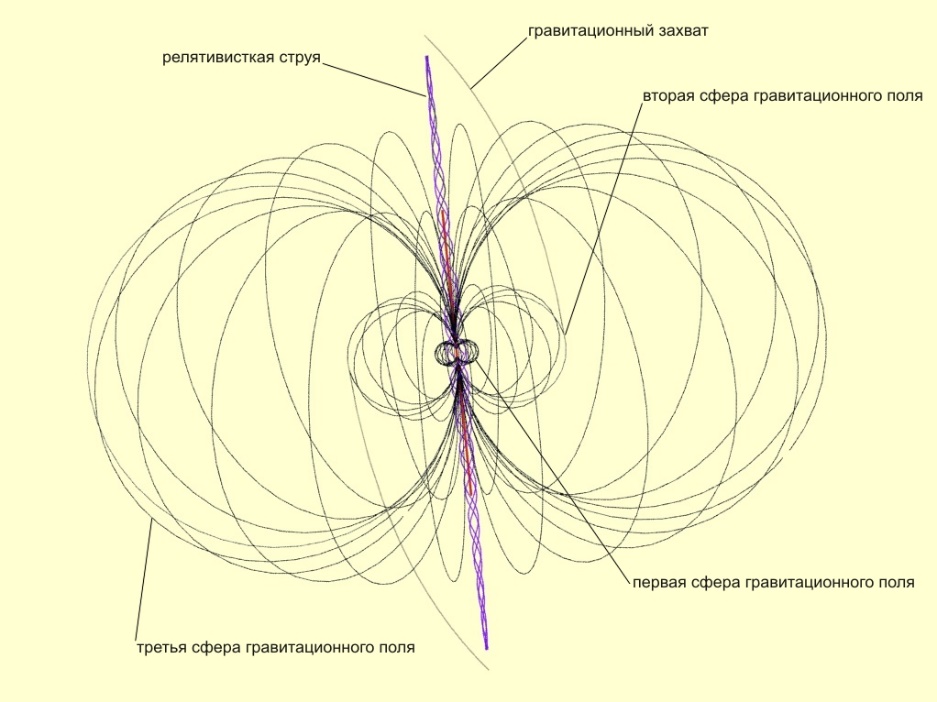
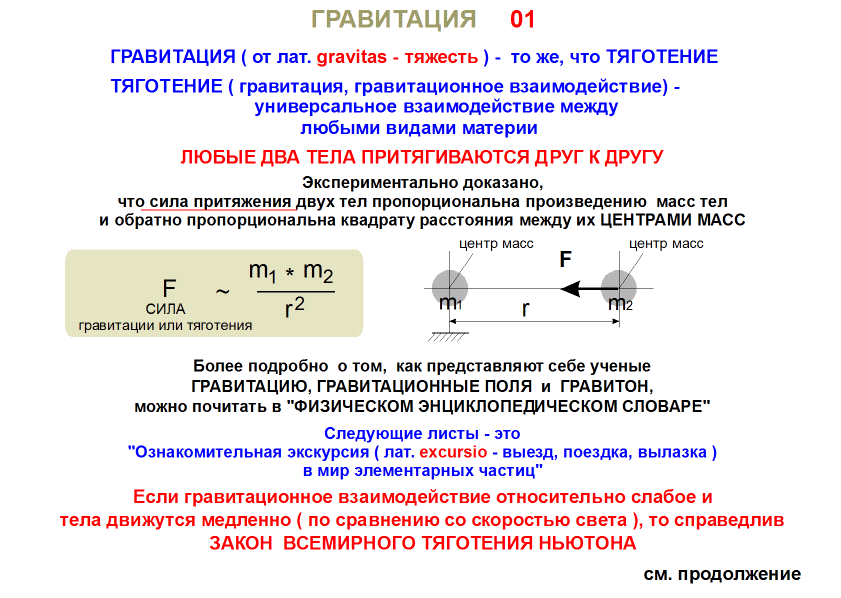
§3 Гравитационное поле

Гравитационное поле— материальная среда, посредством которой осуществляется гравитационное взаимодействие между телами. Отличительная особенность гравитационного поля состоит в том, что на помещенную в него материальную точку действует сила, пропорциональная массе этой точки. Силовой характеристикой гравитационного поля является его напряженность— векторная величина , равная .

Напряженность гравитационного поля не зависит от массы материальной точки, а является функцией координат точек рассматриваемого поля. В случае нестационарного поля зависит также от времени. Напряженность стационарного гравитационного поля неподвижной материальной точки массой М, находящейся в начале координат определяется по формуле , где — радиус-вектор рассматриваемой точки поля.

Гравитационное поле потенциально, так как сила, действующая на внесенную в него материальную точку массы m – центральная сила.

Потенциальная энергия материальной точки в стационарном гравитационном поле равна W_п==.

В силу потенциальности гравитационного поля вводится его энергетическая характеристика- потенциал φ. Потенциал в какой-либо точке гравитационного поля численно равен работе, совершаемой силами поля при перемещении материальной точки единичной массы из этой точки поля в ту точку, где потенциал поля принят равным 0. Для гравитационного поля материальной точки или тела шарообразной формы φ =.

Гравитационные поля удовлетворяет принципу суперпозиции ; φ=.

Рассмотренная классическая теория гравитационного поля достаточно полно описывает только сравнительно слабые гравитационные поля, потенциалы которых |φ| <<с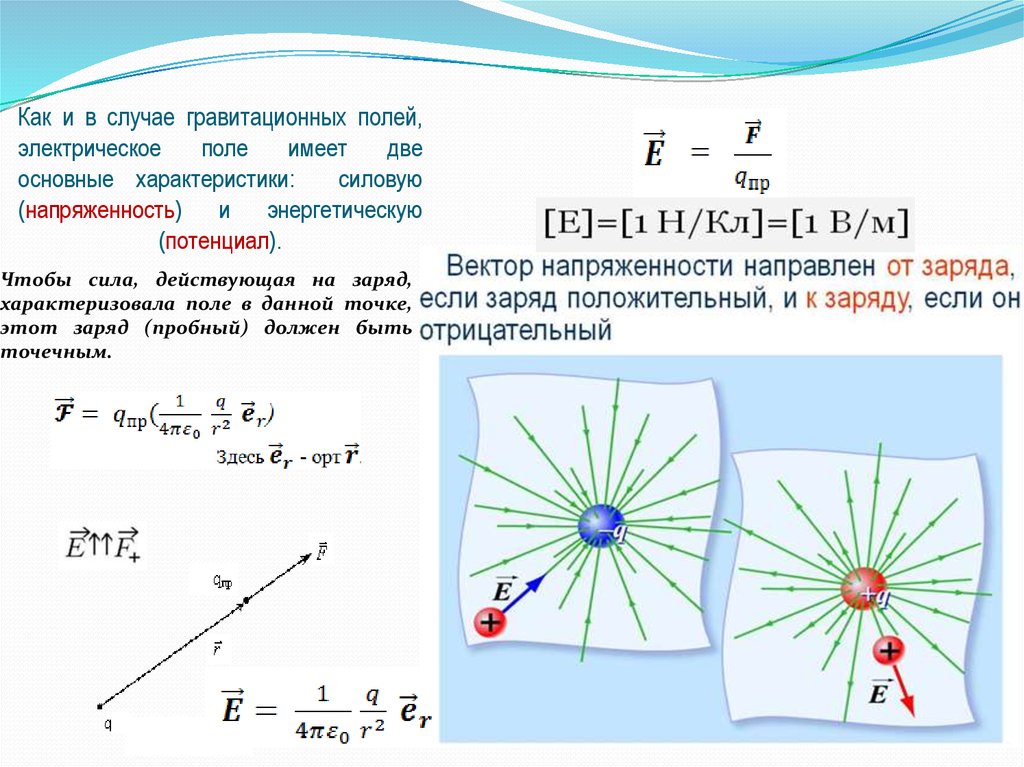

2, где с- скорость света в вакууме. Современная (релятивистская) теория тяготения, представляющая единую теорию пространства, времени и тяготения- общая теория относительности, в соответствии с которой геометрические свойства пространства-времени зависят от распределения в пространстве тяготеющих тел и их движения.

Тела, создающие гравитационное поле, искажают реальное трехмерное пространство и по разному изменяют ход времени в различных его точках. В релятивистской теории тяготения было показано, что для произвольных гравитационных полей принцип суперпозиции не выполняется.

С микроскопической точки зрения гравитационное поле состоит из элементарных частиц- квантов поля (гравитонов).

Вопросы для самоконтроля:

1.Что понимают под гравитационным полем?

2.Какую физическую величину называют напряженностью гравитационного поля, и по какой формуле определяется напряженность гравитационного поля материальной точки?

3.Какую физическую величину называют потенциалом гравитационного поля, и по какой формуле определяется потенциал гравитационного поля материальной точки?

4.По какой формуле определяется потенциальная энергия гравитационного взаимодействия двух материальных точек?

5. С каких частиц с микроскопической точки зрения состоит гравитационное поле?

Взаимодействие между электрически заряженными частицами или телами, движущимися произвольным образом относительно инерциальной системы отсчета, осуществляется посредством электромагнитного поля, которое представляет собой совокупность двух взаимосвязанных полей – электрического поля и магнитного

поля. Это поле характеризуется напряженностью электрического поля () и магнитной индукцией (). Деление электромагнитного поля на электрическое и магнитное поле условно. В различных инерциальных системах отсчета, движущихся одна относительно другой, векторы и в электромагнитном поле в одной и той же точке пространства различны.

Характерная особенность электрического поля, отличающая его от других полей, состоит в том, что оно действует на движущийся электрический заряд (заряженную частицу или тело) с силой, которая не зависит от скорости движения заряда. Видами электрического поля являются электростатическое, стационарное электрическое и вихревое электрическое

поле.

В отличие от электрического поля магнитное поле действует на движущиеся электрические заряды (заряженные частицы или тела) с силой, пропорциональной скорости заряда и направленной перпендикулярно этой скорости.

Вектор напряженности — силовая характеристика электрического поля: ; где q₀ –пробный точечный заряд, помещенный в рассматриваемую точку поля; — сила, с которой поле действует на пробный точечный заряд.

Характеристикой электрического поля в среде является вектор электрической индукции . =ε_о, =ε_оχ, ε_оε, ε=1+χ ,где ε_о-электрическая постоянная, -вектор поляризации, χ- относительная диэлектрическая восприимчивость вещества, ε- относительная диэлектрическая проницаемость среды.

Для описания электрического поля вводится понятие потока напряженности. Элементарным потоком напряженности электрического поля сквозь малый участок площадью поверхности, проведенной в поле, называется физическая величина ,

где — вектор напряженности электрического поля в точках площадки , — единичный вектор, нормальный к площадке dS, — вектор площади, — проекция вектора на направление вектора , — площадь проекции элемента

dS поверхности на плоскость, перпендикулярную вектору (рис.5).

Поток напряженности электрического поля сквозь поверхность S равен алгебраической сумме потоков сквозь все малые участки этой поверхности.

.

При этом все векторы нормалей к площадкам dS должны быть направлены в одну и ту же сторону относительно поверхности S.

Для расчета электростатических полей в вакууме применяется теорема Остроградского-Гаусса: поток напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность, проведенную в поле, пропорционален алгебраической сумме электрических зарядов, охватываемых этой поверхностью.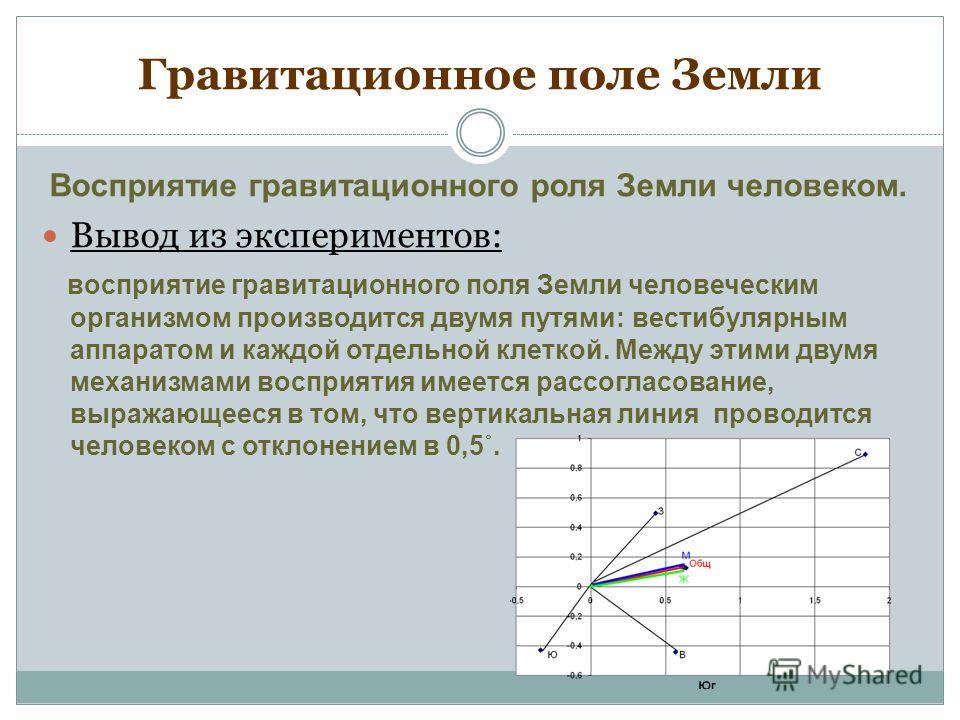

.

Использование теоремы Остроградского-Гаусса особенно удобно в случае полей, которые обладают заранее неизвестной симметрией, обусловленной симметрией в конфигурации зарядов.

Графическое изображение стационарного, т.е. не изменяющегося со временем электрического поля проводится методом линий напряженности. Линиями напряженности (силовыми линиями электрического поля) называются линии, проведенные в электрическом поле так, что в каждой точке поля касательная к линии напряженности совпадает с направлением вектора напряженности в этой точке поля.

Электрическое поле называется однородным, если во всех его точках вектор напряженности имеет одно и то же значение. В противном случае электрическое поле называется неоднородным. Для электрического поля справедлив принцип суперпозиции: , где -вектор напряженности электрического поля, созданного i-тым зарядом.

Энергетической характеристикой электростатического поля является его потенциал.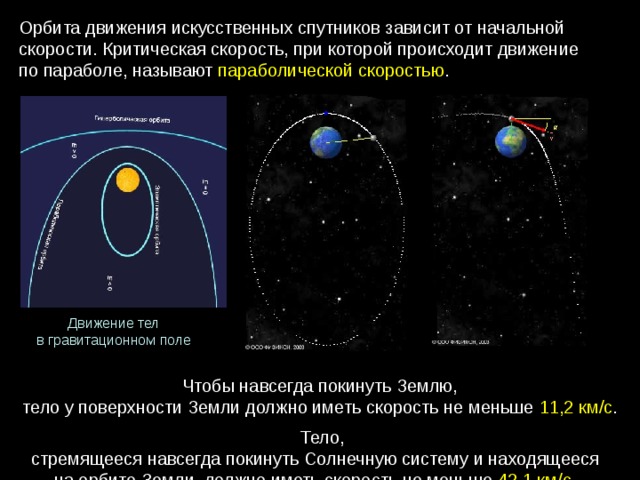 Потенциалом электростатического поля называется физическая величина , равная отношению потенциальной энергии пробного точечного электрического заряда, помещенного в рассматриваемую точку поля, к величине этого заряда: . В соответствии с принципом суперпозиции электрических полей , где — потенциал электростатического поля в рассматриваемой точке, созданного

i-тым зарядом. При этом предполагается одинаковый для всех накладывающихся полей выбор точки, в которой потенциал считается равным нулю. Например, потенциал электростатического поля, созданного точечным зарядом, равен 0 в бесконечности.

Если заряды распределены в пространстве непрерывно, то потенциал их поля в вакууме (при выборе точки, где , в бесконечности) равен: , где интегрирование проводится по всем зарядам, образующим рассматриваемую систему. При перемещении точечного заряда

q из точки 1 поля (потенциал ) в точку 2 (потенциал ) силами электростатического поля совершается работа, равная: . Если , то .

Геометрическое место точек электростатического поля, в которых значения потенциала одинаковы, называется эквипотенциальной поверхностью.

Работа сил поля при перемещении d заряда q в электростатическом поле равна: . С другой стороны .Из соотношения этих выражений для , где — проекция вектора напряженности на направление вектора перемещения.

Если вектор направлен по касательной к эквипотенциальной поверхности, то и , т.к. . Следовательно, эквипотенциальные поверхности ортогональны к силовым линиям. Работа, совершаемая силами электростатического поля при перемещении электрического заряда по одной и той же эквипотенциальной поверхности, равна нулю.

Электростатическое поле графически изображается не только с помощью силовых линий, но и эквипотенциальных поверхностей. Эквипотенциальные поверхности обычно строят так, чтобы разности потенциалов между любыми двумя соседними поверхностями были одинаковы. Зная расположение этих поверхностей, можно построить силовые линии и найти значения напряженности поля. Наоборот, по известному расположению силовых линий электростатического поля можно построить эквипотенциальные поверхности.

Вектор магнитной индукции можно ввести одним из трех взаимосвязанных способов:

— исходя из силового действия магнитного поля на движущуюся в нем заряженную частицу – точечный электрический заряд;

— основываясь на силовом действии магнитного поля на малый элемент проводника с током;

— исходя из силового действия магнитного поля на небольшую рамку с током.

Пусть для исследования магнитного поля используют пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров (рис. 6). Магнитный момент такого пробного контура равен: ,где S – площадь, ограниченная контуром. Здесь — положительная нормаль, определяемая по правилу буравчика. Оказывается, что магнитное поле оказывает ориентирующее действие на этот контур

На пробные контуры, отличающиеся значением , действуют в данной точке поля разные по величине вращательные моменты . Однако отношение будет для всех контуров одно и то же для одной и той же точки магнитного поля и может быть принято для количественной характеристики поля.

Физическую величину В, пропорциональную этому отношению, называют магнитной индукцией:; (Тесла). Магнитная индукция – векторная физическая величина. Условились считать, что вектор магнитной индукции совпадает по направлению с .

Для графического изображения стационарного магнитного поля пользуются методом линий магнитной индукции. Линиями магнитной индукции (силовыми линиями магнитного поля) называются линии, проведенные в магнитном поле так, что в каждой точке поля касательная к линии магнитной индукции совпадает с направлением вектора магнитной индукции в этой точке поля.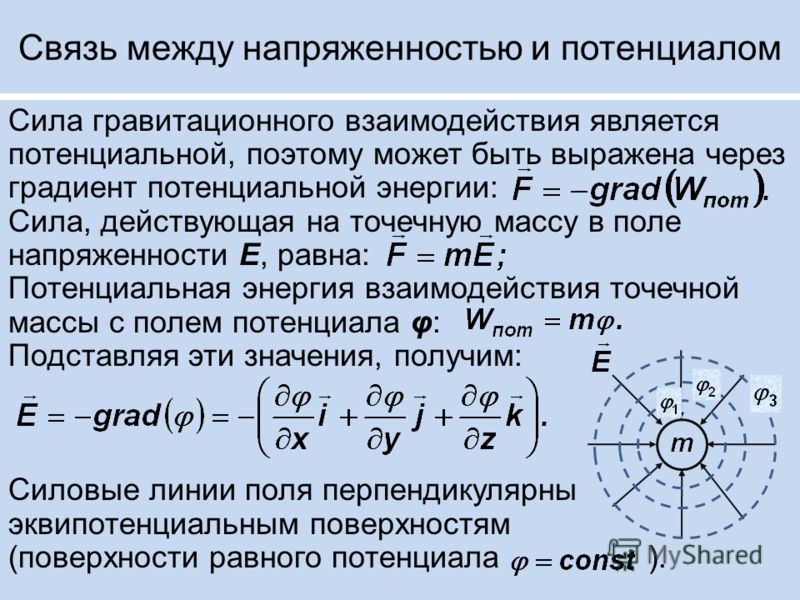 Линии магнитной индукции нигде не обрываются, т.е. не начинаются и не заканчиваются. Они либо замкнуты, либо идут из бесконечности в бесконечность, либо бесконечно навиваются на некоторую поверхность, всюду плотно заполняя ее.

Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение. В противном случае магнитное поле называется неоднородным. Для магнитного поля, справедлив принцип суперпозиции:

Магнитная индукция поля в вакууме малого элемента проводника длиной , по которому идет постоянный электрический ток силой I, определяется по закону Био-Савара-Лапласа: , где , — вектор плотности тока, — радиус-вектор, проведенный из элемента проводника в рассматриваемую точку поля, k – коэффициент пропорциональности, зависящий от выбора системы единиц. В СИ , где — магнитная постоянная. Тогда .

Направление вектора определяется по правилу Максвелла (правилу правого буравчика).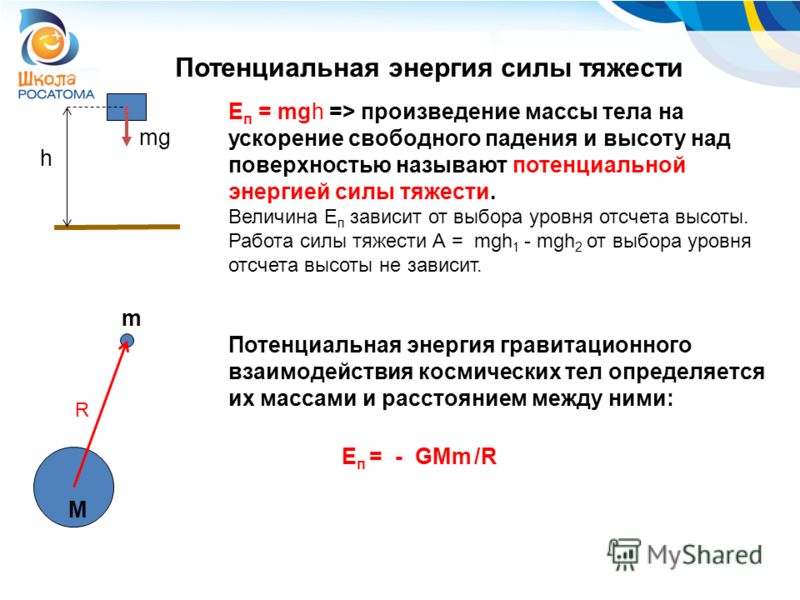

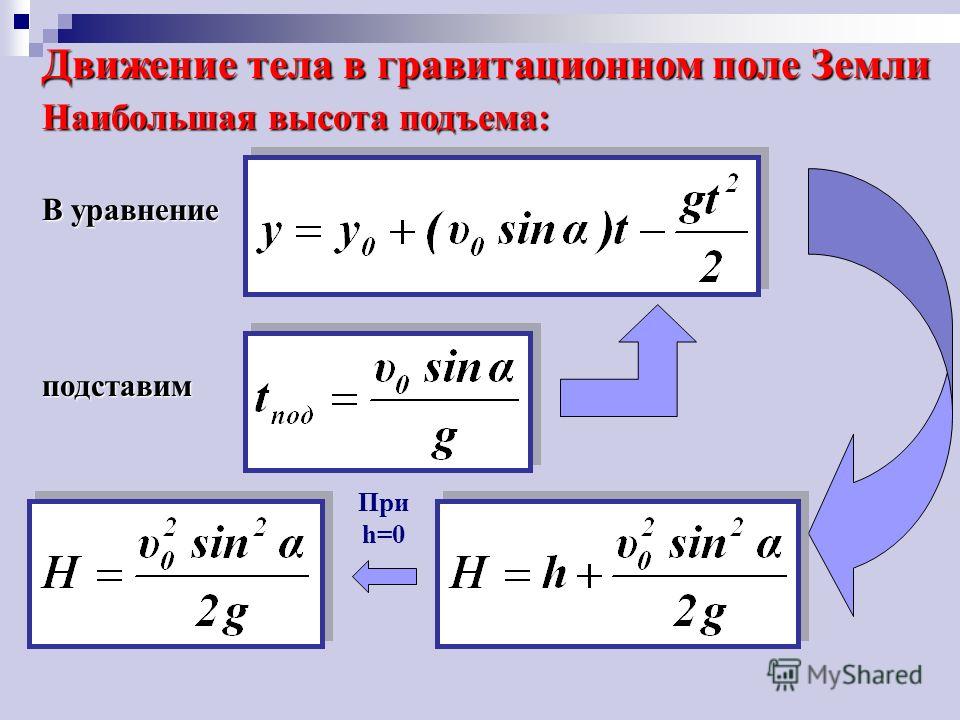
Из закона Био-Савара-Лапласа следует, что , где — угол, под которым виден из рассматриваемой точки поля элемент проводника с током. ,где интегрирование проводится по всей длине l проводника.

Индукция магнитного поля, возбуждаемого в вакууме движущейся с постоянной скоростью (<<с) заряженной частицей, равна ; , где q – заряд частицы, а — радиус-вектор, проведенный от движущейся частицы в рассматриваемую точку поля. Вектор направлен перпендикулярно плоскости, проведенной через вектора и с учетом знака заряда движущейся частицы. Магнитное поле движущегося заряда переменно, так как даже при радиус-вектор изменяется и по модулю и по направлению.

Для описания магнитного поля в веществе рассматривается вектор напряженности магнитного поля . , где — вектор намагниченности вещества, χ- магнитная восприимчивость вещества, μ- магнитная проницаемость вещества. Взаимосвязь между магнитной проницаемостью и магнитной восприимчивостью вещества выражается формулой μ = 1+ χ.

Для описания магнитного поля вводится понятие потока вектора магнитной индукции. Элементарным потоком вектора магнитной индукции магнитного поля сквозь малый участок площадью поверхности, проведенной в поле, называется физическая величии , где — вектор магнитной индукции магнитного поля в точках площадки , — единичный вектор, нормальный к площадке dS, — вектор площади, — проекция вектора на направление вектора , — площадь проекции элемента dS поверхности на плоскость, перпендикулярную вектору .

Поток вектора магнитной индукции сквозь поверхность S равен алгебраической сумме потоков сквозь все малые участки этой поверхности.

.

При этом все векторы нормалей к площадкам dS должны быть направлены в одну и ту же сторону относительно поверхности S.

С переменным магнитным полем неразрывно связано вихревое индукционное электрическое поле, что подтверждается явлением электромагнитной индукции и явлением самоиндукции.

Электромагнитной индукцией называют возникновение электродвижущей силы в проводнике при его перемещении в магнитном поле, либо в замкнутом проводящем контуре вследствие его движения в магнитном поле или изменения самого поля. Эта электродвижущая сила называется электродвижущей силой электромагнитной индукции. В соответствии с законом электромагнитной индукции (законом Фарадея-Максвелла) . При этом несущественно, чем именно вызвано изменение магнитного потока – деформацией контура, его перемещением в магнитном поле или изменением самого поля с течением времени. Направление обхода контура при вычислении и направление нормали при вычислении Ф_В должны быть согласованы по правилу правого винта.

Знак «минус» в правой части закона электромагнитной индукции соответствует правилу Ленца: при всяком изменении потока сквозь поверхность, “натянутую” на замкнутый проводящий контур, в контуре возникает индукционный ток такого направления, что его собственное магнитное поле противодействует изменению магнитного поля, вызвавшему индукционный ток.

Возникновение ЭДС электромагнитной индукции в электрической цепи вследствие изменения в ней электрического тока называют самоиндукцией, а соответствующее ЭДС – электродвижущей силой самоиндукции. Из закона электромагнитной индукции следует, что , где — потокосцепление самоиндукции рассматриваемого контура с током. , где — индуктивность контура. Индуктивность контура зависит только от его формы и размеров, а также от магнитной проницаемости μ среды. Выражение для ЭДС самоиндукции имеет вид .

Если контур не деформируется и находится в неферромагнитной среде, то при изменении электрического тока I индуктивность контура не изменяется. Поэтому . Изменяющееся (вихревое) электрическое поле порождает вихревое магнитное поле.

Обобщающей теорией единого электромагнитного поля в вакууме является макроскопическая феноменологическая теория Максвелла, представленная системой уравнений. Первое уравнение Максвелла является обобщением закона электромагнитной индукции. Его можно записать в виде: , где , — единичный вектор нормали к малому элементу поверхности S, натянутой на замкнутый контур L (из конца вектора обход контура L виден происходящим против часовой стрелки).

Максвелл обобщил закон полного тока, предположив, что переменное электрическое поле, так же как и электрический ток, является источником магнитного поля. Количественной мерой магнитного действия переменного электрического поля является ток смещения:, где — поток вектора электрического смещения сквозь поверхность S. Максвелл добавил в правую часть закона полного тока ток смещения и записал закон полного тока в форме . Это и есть второе уравнение Максвелла.

Максвелл обобщил теорему Остроградского-Гаусса для электростатического поля. Он предположил, что она справедлива для любого электрического поля. Соответственно, третье уравнение Максвелла имеет вид:. Он также предположил, что теорема Остроградского-Гаусса справедлива для любого магнитного поля. Поэтому четвертое уравнение Максвелла имеет вид: .

Приведенную систему уравнений необходимо дополнить уравнениями, характеризующими электрические и магнитные свойства среды. В случае изотропных сред и макротоков эти уравнения имеет вид: ,. Важным свойством уравнений Максвелла явилась их инвариантность относительно преобразований Лоренца.

С макроскопической точки зрения свободное поле проявляется прежде как поток энергии и импульса, распределяемых в пространстве. Объемная плотность энергии и импульс электромагнитного поля в линейной изотропной среде определяется по формулам , .

С микроскопической точки зрения электромагнитное поле состоит из элементарных частиц- квантов поля (фотонов). Существование фотонов подтверждается огромным экспериментальным материалом. Подтверждается формула взаимосвязи энергии и импульса фотона Е= рс.

Фотон, как и всякая другая элементарная частица, обладает строго определенными значениями импульса и энергии.

Вопросы для самоконтроля:

1.Что понимают под электромагнитным полем?

2. Какие выделяют виды электрического поля?

3.Какую физическую величину называют напряженностью электрического поля, по какой формуле определяется напряженность электрического поля точечного заряда?

4.Какую физическую величину называют электрической индукцией электрического поля?

5.Какую физическую величину называют потенциалом электрического поля?

6.Как формулируется теорема Остроградского-Гаусса?

7.Как вводят вектор магнитной индукции по действию магнитного поля на пробный контур с током?

8.Какую физическую величину называют напряженностью магнитного поля?

9.Какое явление называют явлением электромагнитной индукции?

10.Какое уравнение Максвелла является обобщением закона электромагнитной индукции?

11. Какое уравнение Максвелла является обобщением закона полного тока?

12.Какое уравнение Максвелла является обобщением теоремы Остроградского-Гаусса?

Гравитационное взаимодействие и гравитационное поле

Попытки объяснения наблюдаемой картины мира, и прежде всего строения Солнечной системы, занимали умы многих великих людей. Что связывает планеты и Солнце в единую систему? Каким законам подчиняется их движение?

Во II в. н. э. древнегреческим ученым Клавдием Птолемеем была разработана геоцентрическая система мира, согласно которой все наблюдаемые перемещения небесных светил объяснялись их движением вокруг неподвижной Земли. «Что я смертен, я знаю, и что дни мои сочтены, но когда я в мыслях неустанно и жадно выслеживаю орбиты созвездий,— писал Птолемей,— тогда я больше не касаюсь ногами Земли: за столом Зевса наслаждаюсь я пищей богов».

В XVI в. польский астроном Николай Коперник «изгнал» Землю из центра мироздания, «поместил» на ее место Солнце, а все планеты «заставил» обращаться вокруг него. Геоцентрическая система мира была заменена гелиоцентрической. Система мира, предложенная Коперником, была прекрасна. «В середине всех этих орбит,— писал восхищенный Коперник,— находится Солнце; ибо может ли прекрасный этот светоч быть помещен в столь великолепной храмине в другом, лучшем месте, откуда он мог бы все освещать собой?»

Что же удерживает планеты, в частности Землю, в их движении вокруг Солнца?

Если придерживаться воззрений Аристотеля и связывать силу со скоростью, а не с ускорением, то причину этого приходится искать именно в направлении скорости. Однако смотреть в направлении скорости Земли бесполезно. Ничего, кроме какой-нибудь одинокой незначительной звезды, там не увидишь.

Ньютон связал силу с ускорением. Если же посмотреть в сторону ускорения Земли, то там окажется само Солнце. И именно Солнце поэтому естественно считать причиной обращения вокруг него Земли и планет.

Но не только планеты притягиваются к Солнцу. Солнце также притягивается планетами.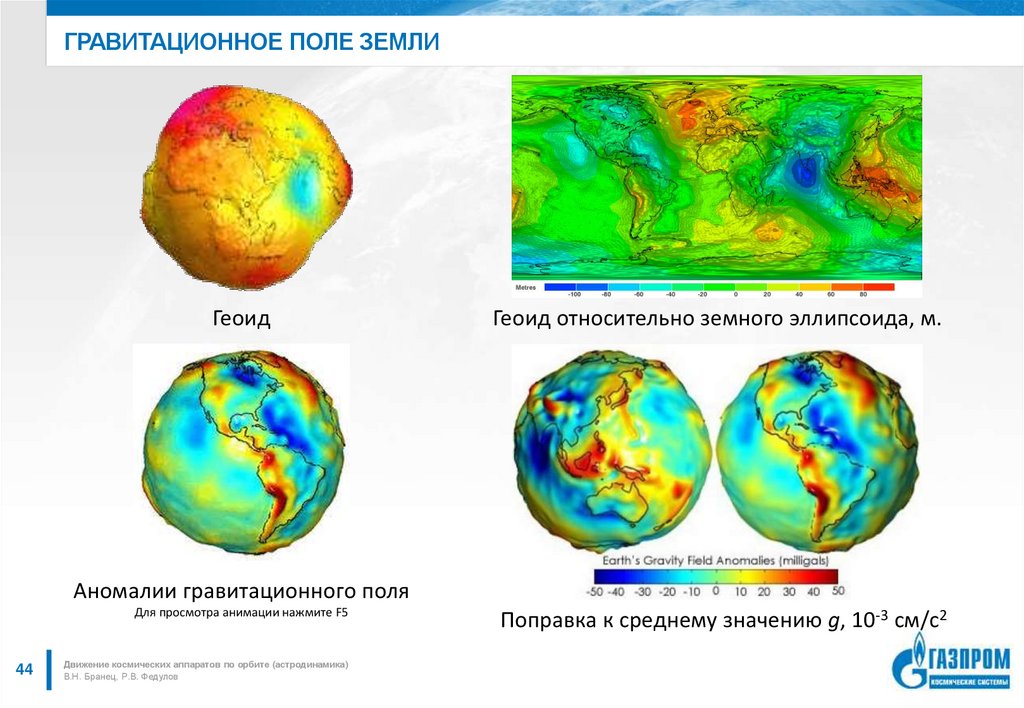 Да и сами планеты взаимодействуют между собой. Одним из первых, кто это понял, был английский ученый Роберт Гук. Так, в 1674 г. он писал: «Все небесные тела имеют притяжение, или силу тяготения к своему центру, вследствие чего они не только притягивают собственные части и препятствуют им разлетаться, как наблюдаем на Земле, но притягивают также все другие небесные тела, находящиеся в сфере их действия. Поэтому не только Солнце и Луна имеют влияние на движение Земли, но и Меркурий, и Венера, и Марс, и Юпитер, и Сатурн также своим притяжением имеют значительное влияние на ее движение. Подобным образом и Земля соответственным притяжением влияет на движение каждого из этих тел».

Окончательное завершение эти идеи получили в работах Ньютона. В своих знаменитых «Математических началах», в которых были сформулированы три его закона, вопрос о тяготении Ньютон излагает последовательно и доказательно. Все тела Вселенной, как небесные, так и находящиеся на Земле, утверждает Ньютон, подвержены взаимному тяготению, причем силы, с которыми притягиваются все эти тела, имеют одинаковую природу и подчиняются одному и тому же закону.

Итак, все тела Вселенной, как небесные, так и находящиеся на Земле, подвержены взаимному притяжению. Если же мы и не наблюдаем его между обычными предметами, окружающими нас в повседневной жизни (например, между книгами, тетрадями, мебелью и т. д.), то лишь потому, что оно в этих случаях слишком слабое.

Взаимодействие, свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу, называют гравитационным, а само явление всемирного тяготения — гравитацией (от лат. gravitas — тяжесть).

Гравитационное взаимодействие осуществляется посредством особого вида материи, называемого гравитационным полем. Такое поле существует вокруг любого тела, будь то планета, камень, человек или лист бумаги. При этом тело, создающее гравитационное поле, действует им на любое другое тело так, что у того появляется ускорение, всегда направленное к источнику поля. Появление такого ускорения и означает, что между телами возникает притяжение.

Гравитационное поле не следует путать с электромагнитными полями, которые существуют вокруг наэлектризованных тел, проводников с током и магнитов.

Интересной особенностью гравитационного поля, которой не обладают электромагнитные поля, является его всепроникающая способность. Если от электрических и магнитных полей можно защититься с помощью специальных металлических экранов, то от гравитационного поля защититься ничем нельзя: оно проникает сквозь любые материалы.

Для обнаружения гравитационного экранирования проводились специальные эксперименты, но они дали отрицательный результат: если между двумя телами поместить в виде экрана третье тело, то притяжение между двумя первыми телами нисколько не ослабляется. Во всяком случае, если экранирование гравитации и существует, то оно настолько слабое, что лежит за пределами той точности, которая достигнута в современных экспериментах. Поэтому с большой уверенностью можно сказать, что никакого «кейворита», который, по словам одного из героев романа Г. Уэллса «Первые люди на Луне», «не подчиняется силе тяготения и преграждает взаимное притяжение между телами», в природе не существует.

Взаимодействие тел с гравитационным полем характеризуют особой физической величиной, называемой гравитационным зарядом. Поскольку всемирному тяготению подвержены все тела Вселенной, то, значит, и все они обладают тем или иным гравитационным зарядом. При этом, чем больше гравитационный заряд тела, тем сильнее на него действует гравитационное поле окружающих тел и тем более сильное поле создает вокруг себя само это тело.

В отличие от электрического заряда гравитационный заряд любого тела совпадает с его массой. Они всегда оказываются равными. В 1971 г. российские физики В. Б. Брагинский и В. И. Панов с помощью очень чувствительной аппаратуры подтвердили это равенство с точностью до одной триллионной. (Данная точность означает тоже самое, как если бы вы взвесили корабль водоизмещением в десять тысяч тонн вместе с грузом с точностью до одной сотой грамма!) По этой причине сегодня уже никто не сомневается в их равенстве и гравитационный заряд любого тела обозначают той же буквой, что и массу, т. е. m.

??? 1. Какое взаимодействие называют гравитационным? 2. Посредством чего осуществляется гравитационное взаимодействие? 3. Какими свойствами обладает гравитационное поле? 4. Чем отличается гравитационный заряд от электрического? 5. Чему равен гравитационный заряд, которым вы обладаете?

Что такое гравитационное поле | Упражнения по физике

 

Гравитационное поле Гравитация или гравитация — это природное явление, при котором физические тела притягиваются с силой, пропорциональной их массам.

Гравитационное взаимодействие между двумя телами может быть выражено центральной силой, которая пропорциональна массе тел и обратно пропорциональна квадрату расстояния, разделяющего их.

Биопрофе |Что такое гравитационное поле | 01

 

Гравитационное поле — это физическое свойство, сообщаемое пространству массой M. Это поле характеризуется:

• Чтобы быть консервативным
• Быть устойчивым.

 

Поля как гравитационное поле, определяемые в каждой точке пространства векторной величиной, называются векторными полями . Эти поля могут быть представлены силовыми линиями . Силовая линия имеет свойство касаться во всех своих точках направления поля в этой точке, и ее значение такое же, как и у поля.

 

Принцип суперпозиции.

В случае поля, созданного несколькими телами, мы используем принцип суперпозиции, чтобы узнать совокупное поле в данной точке. Принцип суперпозиции говорит нам, что гравитационное поле, создаваемое телом в точке, не зависит от гравитационных полей, создаваемых другими телами. Мы будем работать, находя поле, создаваемое каждым телом в рассматриваемой точке, и мы будем добавлять их все (векторную сумму) для общего поля.

Биопрофе |Что такое гравитационное поле | 02

 

Скорость убегания — это минимальная скорость, с которой должно быть брошено тело, чтобы вырваться из-под гравитационного притяжения Земли или другого небесного тела. Это означает, что тело или снаряд не упадет на Землю или не стартует в астро, оставив в состоянии покоя на достаточно большом (в принципе бесконечном) расстоянии от Земли или звезды.

 

Эта скорость объясняет, почему у одних планет есть атмосфера, а у других нет. Согласно кинетической теории газов молекулы газа движутся со скоростью:

Биопрофе |Что такое гравитационное поле | 03

 

Черная дыра — это конечная область пространства, внутри которой существует концентрация массы, достаточно высокая для создания гравитационного поля, из которого не может вырваться никакая материальная частица, даже свет.
Гравитация черной дыры, или «кривизна пространства-времени», вызывает сингулярность, окруженную замкнутой поверхностью, называемой горизонтом событий.

 

ОБЗОР ФОРМУЛЫ:

Закон всемирного тяготения Ньютона

(G = универсальная гравитационная постоянная)

Bioprofe |Что такое гравитационное поле | 04

 

Знак минус означает, что гравитационное поле направлено в направлении, противоположном единичному вектору, указывающему направление от Земли к рассматриваемой точке.

Третий закон Кеплера

(T = период обращения каждой планеты; R = большая полуось орбиты)

Биопрофе |Что такое гравитационное поле | 05

Период обращения планеты

(M = масса Солнца; R = расстояние между центром Солнца и центром планеты)

Bioprofe |Что такое гравитационное поле | 06

Гравитационное ускорение

Биопрофе |Что такое гравитационное поле | 07

Ускорение свободного падения в зависимости от высоты

Биопрофе |Что такое гравитационное поле | 08

Гравитационная потенциальная энергия

Биопрофе |Что такое гравитационное поле | 09

Орбитальная скорость снаряда

Биопрофе |Что такое гравитационное поле | 10

Убегающая скорость снаряда

Биопрофе |Что такое гравитационное поле | 11

Эквипотенциальные поверхности

Эквипотенциальная поверхность образована точками, все из которых имеют одинаковый гравитационный потенциал. Так как все точки находятся на одной высоте от земли, все обладают одинаковым гравитационным потенциалом, то можно считать, что гравитационные эквипотенциальные поверхности параллельны поверхности земных плоскостей. Поверхность, образованная всеми этими точками, называется эквипотенциальной поверхностью.

 

 

 

 

 

 

Пожертвовать BioProfe

Пожертвовать здесь

Напряженность гравитационного поля: уравнение, Земля, единицы

Современная физика определяется в основном в терминах полей, которые являются физическими объектами, простирающимися в пространстве и времени. Эти объекты являются обычными источниками неконтактных сил и позволяют нам описать динамику почти каждой известной нам системы.

Ученый британского происхождения Исаак Ньютон уже вычислил, что гравитация — это поле , которое существует из-за наличие массы . Более того, он понял, что это всегда была сила притяжения . Давайте посмотрим на определение напряженности гравитационного поля:

Напряженность гравитационного поля является мерой интенсивности гравитационного поля, которое имеет массу в качестве источника и притягивает другие массы.

Сила гравитационного поля создается массами и порождает силу притяжения, которая ослабевает с расстоянием.

Уравнение напряженности гравитационного поля

Исторически не существовало однозначного описания гравитации. Благодаря экспериментам мы знаем, что выражение Ньютона работает с планетами, звездами (и т. д.) и их окружением.

При рассмотрении более сложных явлений, таких как черные дыры, галактики, отклонение света, нам нужны более фундаментальные теории, такие как общая теория относительности, разработанная Альбертом Эйнштейном.

Вспомним закон всемирного тяготения Ньютона . Его формула

где вектор Z — напряженность поля, создаваемого массой M, G — универсальная постоянная гравитации, r — радиальное расстояние, измеренное от центра массы тела-источника, а вектор e _r — радиальный единичный вектор, идущий к ней. Если мы хотим получить силу, которую тело с массой m испытывает под действием поля Z, мы можем просто рассчитать ее как измеряется в ньютонах [N = кг⋅м/с ² ]. В результате напряжённость поля измеряется в м/с ² , т.е. это ускорение. Массу обычно измеряют в килограммах, а расстояние в метрах. Это дает нам единицы универсальной гравитационной постоянной G: Нм ² /кг ² = м ³ /с ² ⋅кг. Значение G составляет 6,674 ⋅ 10 ^-11 м ³ /с ² ⋅кг.

Гравитационная потенциальная энергия, с другой стороны, измеряется в джоулях.

Напряженность гравитационного поля Земли

Важно знать! Значение напряженности гравитационного поля на Земле варьируется по высоте, однако вблизи поверхности Земли оно составляет 9,81 м/с ² или Н/кг.

Каковы основные характеристики напряженности гравитационного поля?

К основным характеристикам гравитационного поля относятся

• Симметрия из описания любого из двух тел.
• Радиальная симметрия.
• Конкретное значение, которое принимает универсальная постоянная гравитации.

Понимание этих характеристик важно даже для современных ученых для разработки более совершенных моделей гравитации, воспроизводящих основные аспекты гравитации Ньютона.

Взаимность тел

Одним из важнейших следствий выражения Ньютона для напряженности гравитационного поля является взаимность масс . Это согласуется с третьим законом Ньютона о движении , который гласит: если одно тело действует с силой на другое тело, то последнее действует на первое с такой же силой в противоположном направлении.

Взаимность глубже, чем кажется, поскольку она утверждает, что фундаментальная особенность напряженности гравитационного поля заключается в том, что она эквивалентна описанию гравитационных взаимодействий с точки зрения того или иного тела. Это кажется тривиальным, но имеет глубокие последствия, касающиеся, например, общей теории относительности.

Радиальная зависимость и ориентация

Одной из основных особенностей ньютоновского выражения для напряженности гравитационного поля является радиальная квадратичная зависимость . Оказывается, в трехмерном пространстве это правильная зависимость для достижения бесконечного диапазона напряженности поля, достигающего любой части пространства. Любая другая зависимость не позволила бы ему иметь бесконечный диапазон или вызвать физические несоответствия.

Кроме того, к этой сферической зависимости добавляется сферическая радиальная симметрия в направлении напряженности поля. Это не только обеспечивает привлекательный характер, но и согласуется с изотропией : в трехмерном пространстве нет особого направления. Способ уравнять все направления состоит в наложении сферической симметрии, что приводит к радиальной зависимости и радиальному вектору.

Значение универсальной постоянной гравитации

Универсальная постоянная гравитации или постоянная Кавендиша измеряет напряженность гравитационного поля. Конечно, интенсивность поля будет зависеть от характеристик для каждого случая, но это мера в следующем смысле: если мы установим все переменные в единицу (с соответствующими единицами), какое число мы получим?

Например, если мы возьмем два заряда в 1 кулон, разделенные расстоянием в 1 метр, мы получим определенную электростатическую силу. Если мы проделаем то же самое с двумя телами по 1 кг каждое, мы получим другое число для гравитационной силы. Значение, по сути, является значением константы перед каждой из формул. Получается, что постоянная для гравитации G меньше константы электромагнетизма k (8,988 ⋅ 10 ⁹ Н⋅м ² /C ² ), поэтому гравитация является более слабой силой.

Фактически, из четырех фундаментальных взаимодействий (гравитация, электромагнетизм, сильное взаимодействие и слабое взаимодействие) напряженность гравитационного поля является самой слабой. Кроме того, он единственный, который действует в межпланетных масштабах.

Четыре основных взаимодействия: гравитация, электромагнетизм, сильное взаимодействие и слабое взаимодействие.

Примеры напряженности гравитационного поля

Вот несколько примеров расчетов напряженности гравитационного поля, чтобы лучше понять, как оно работает в различных астрономических объектах.

• Земля. Радиус Земли составляет примерно 6371 км. Его масса составляет около 5,972 ⋅ 10 ²⁴ кг. Применение уравнения дает нам поверхностную напряженность гравитационного поля 9,81 м/с ² .
• Луна. Радиус Луны составляет примерно 1737 км. Его масса составляет около 7,348 ⋅ 10 ²² кг. Применение уравнения дает напряженность поверхностного гравитационного поля 1,62 м/с ² .
• Марс. Радиус Марса составляет около 3390 км. Его масса составляет примерно 6,39 ⋅ 10 ²³ кг. Применение уравнения дает нам поверхностную напряженность гравитационного поля 3,72 м/с ² .
• Юпитер. Радиус Юпитера составляет около 69,911 км, а его масса составляет около 1,898 ⋅ 10 ²⁷ кг. Применение уравнения дает напряженность поверхностного гравитационного поля 24,79.м/с ² .
• Вс. Радиус Солнца составляет примерно 696,340 км, а его масса составляет примерно 1,989 ⋅ 10 ³⁰ кг. Применение уравнения дает нам поверхностную напряженность гравитационного поля 273,60 м/с ² .

Напряженность гравитационного поля — основные выводы

• Гравитация — это поле, и его напряженность в классической модели может быть измерена и смоделирована с помощью математической теории, разработанной Исааком Ньютоном.
• Хотя существуют более фундаментальные теории, Ньютон сформулировал первый строгий подход к пониманию напряженности гравитационного поля. Он действителен только для определенных обстоятельств (не считая очень массивных объектов, небольших расстояний или очень высоких скоростей).