Действующие значения силы тока и напряжения.

Презентация по физике

Переменный электрический ток. Активное сопротивление. Действующие значения силы тока и напряжения.

Выполняли ученицы 11 «А» класса Радукан Яна, Иванова Алина.

Переменный электрический ток

• Как известно, ток (электрический) бывает переменным и постоянным.Переме́нный ток (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.В настоящее время очень широко используется переменный электрический ток. Его можно получить с помощью электрогенераторов переменного тока с применением эффекта электромагнитной индукции. На рисунке изображена примитивная установка для выработки переменного тока.

• Принцип действия установки прост. Проволочная рамка вращается в однородном магнитном поле с постоянной скоростью. Своими концами рамка закреплена на кольцах, вращающихся вместе с ней. К кольцам плотно прилегают пружины, выполняющие роль контактов. Через поверхность рамки непрерывно будет протекать изменяющийся магнитный поток, но поток, создаваемый электромагнитом, останется постоянным. В связи с этим в рамке возникнет ЭДС индукции.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

Ф = BScoswt «

Переменный ток в осветительной сети квартиры, применяемый па заводах и фабриках и т. д., представляет собой не что иное, как вынужденные электромагнитные колебания. Данные колебания напряжения легко обнаружить с помощью осциллографа.(рис. 4.8)

Стандартная частота промышленного переменного тока равна 50 Гц. Это означает, что на протяжении 1 с ток 50 раз идет в одну сторону и 50 раз — в противоположную. Частота 50 Гц принята для промышленного тока во многих странах мира.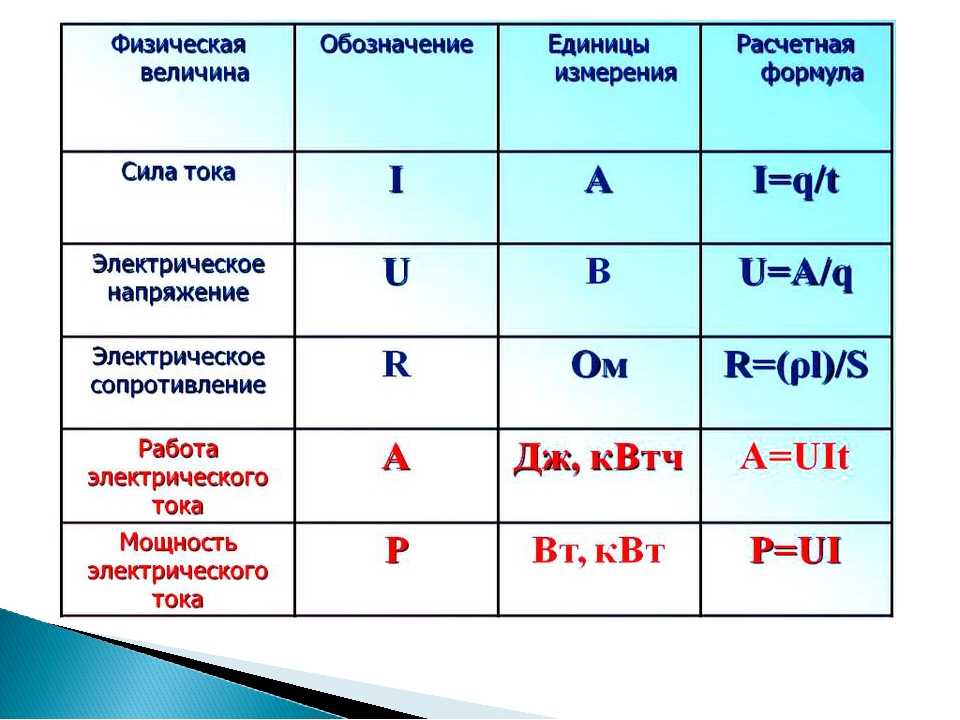 В США принята частота 60 Гц. Если напряжение на концах цепи меняется по гармоническому закону, то и напряженность электрического поля внутри проводников будет также меняться гармонически.

Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока. Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла а между нормалью к рамке и вектором магнитной индукции (рис. 4.9):

Ф = BScos а

При равномерном вращении рамки угол а увеличивается прямо пропорционально времени: а=2Пnt , где n – частота вращения.Поэтому поток магнитной индукции меняется гармонически :

Ф = BS cos 2Пnt , Здесь 2Пn число колебаний магнитного потока за 2П с. Это ЦИКЛИЧЕСКАЯ ЧАСТОТА колебаний w=2Пn = Ф = BScoswt

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «-» скорости изменения потока магнитной индукции, т. е. производной потока магнитной индукции по времени:

Если к рамке подключить колебательный контур,  то угловая скорость w вращения рамки определит  частоту w колебаний значений ЭДС, напряжения на paзличныx участках цепи и силы тока.

Если напряжение меняется с циклической частотой , то и сила тока в цепи будет меняться с той же частотой. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока і в любой момент времени (мгновенное значение силы тока) определяется по формуле

Здесь I m — амплитуда силы тока, т. е. максимальное по модулю значение силы тока, а — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Активное сопротивление .

Действующие значения силы тока и напряжения.

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от  генератора. Эта энергия превращается во внутреннюю энергию проводников — они  нагреваются.   Будем  считать, что напряжение на зажимах цепи меняется по гармоническому закону:

u = U m cos w t

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома :

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найти среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой :

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения (рис. 4.17), а амплитуда силы тока определяется равенством

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.

19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой :

P = i 2 R. (4.19)  

Средняя мощность

равна первому члену в формуле (4.20)

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем закон Ома для участка цепи переменного тока с резистором

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Конденсатор в цепи переменного тока

Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком.

Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА’) лампа не светится.

Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ’) лампа загорается, если емкость конденсатора достаточно велика.

Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.

Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Сила тока, представляющая собой производную заряда по времени , равна:

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14).

Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на

(рис. 4.15).

Напряжение на конденсаторе

Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.

Амплитуда силы тока равна:

I m = U m C

(4.29)

Если ввести обозначение :

В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение X c . С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим :

C

Величину X c , обратную произведению

циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением .

Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания  напряжения на

Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.

КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта.

Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока.

Соберем цепь из катушки с большой индуктивностью и электрической лампы накаливания (рис. 4.16). С помощью переключателя можно подключить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны.

Объясняется это различие явлением самоиндукции.

Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.

Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (рис. 4.17). Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.

i

k

=

—

Из равенства

следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции е і ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: е і = -u.

Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля

При изменении силы тока по гармоническому закону :

t

i =  I m   sin

ЭДС самоиндукции равна:

порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля

e і = — L i ‘ = — L

l m cos

t.

Так как u = -е і , то напряжение на концах катушки оказывается равным

создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на

Индуктивное сопротивление зависит от частоты

что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на (рис. 4.18)

Постоянный ток вообще «не замечает» индуктивности катушки. При = 0

индуктивное сопротивление равно нулю (X L = 0).

Амплитуда силы тока в катушке равна:

Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.

Катушка индуктивности оказывает сопротивление переменному току.

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим:

Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.

Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на

Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Согласно формуле (4.35) действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Спасибо за внимание!

Источники:https://vk.com/away.php?to=http%3A%2F%2Fselectelement.ru%2Fbasic-concepts%2Felectric-ac.php&cc_key= https://vk.com/away.php?to=https%3A%2F%2Fsites.google.com%2Fsite%2Fopatpofizike%2Fteoria%2Fteoria-11-klass%2Feds-zakon-oma-dla-polnoj-cepi%2Fperemennyj-elektriceskij-tok-aktivnoe-induktivnoe-eemkostnoe-soprotivlenia&cc_

Что называют действующим значением силы тока напряжения — Dudom

Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток. <2>dt>>.>

Содержание

Действующее значение в типичных случаях [ править | править код ]

Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.

Синусоида [ править | править код ]

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , <displaystyle I=<frac <1><sqrt <2>>>cdot I_approx 0<,>707cdot I_,>

Прямоугольная форма [ править | править код ]

Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:

I = I m D , <displaystyle I=I_<sqrt >,>

В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):

I = I m 0 , 5 ≈ 0 , 707 ⋅ I m . <displaystyle I=I_<sqrt <0,5>>approx 0,707cdot I_.>

Для тока, имеющего форму двухполярного меандра:

I = I m . <displaystyle I=I_.>

Треугольная форма [ править | править код ]

Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . <displaystyle I=<frac <1><sqrt <3>>>cdot I_approx 0<,>577cdot I_.>

Трапециевидная форма [ править | править код ]

Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:

I = I m t 1 + 3 t 2 + t 3 3 T , <displaystyle I=I_<sqrt <frac +3t_<2>+t_<3>><3T>>>,> 1>

Дугообразная форма [ править | править код ]

Для тока имеющего форму дуги (половины окружности):

I = I m 2 3 ≈ 0,816 ⋅ I m . <displaystyle I=I_<sqrt <frac <2><3>>>approx 0<,>816cdot I_.>

Дополнительные сведения [ править | править код ]

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение). <2>dt>>.>

Содержание

Действующее значение в типичных случаях [ править | править код ]

Приведены формулы для электрического тока. Аналогичным образом определяются действующие значения ЭДС и напряжения.

Синусоида [ править | править код ]

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , <displaystyle I=<frac <1><sqrt <2>>>cdot I_approx 0<,>707cdot I_,>

Прямоугольная форма [ править | править код ]

Для тока, имеющего форму однополярного прямоугольного импульса, действующее значение тока зависит от скважности:

I = I m D , <displaystyle I=I_<sqrt >,>

В частности, для тока, имеющего форму однополярного меандра (коэффициент заполнения 0,5):

I = I m 0 , 5 ≈ 0 , 707 ⋅ I m . <displaystyle I=I_<sqrt <0,5>>approx 0,707cdot I_.>

Для тока, имеющего форму двухполярного меандра:

I = I m . <displaystyle I=I_.>

Треугольная форма [ править | править код ]

Для тока треугольной и пилообразной формы (независимо от того, меняется ли направление тока):

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . <displaystyle I=<frac <1><sqrt <3>>>cdot I_approx 0<,>577cdot I_.>

Трапециевидная форма [ править | править код ]

Для тока трапециевидной формы действующее значение можно определить разбив период на отрезки положительного фронта, действия максимального значения и отрицательного фронта:

I = I m t 1 + 3 t 2 + t 3 3 T , <displaystyle I=I_<sqrt <frac +3t_<2>+t_<3>><3T>>>,> 1>

Дугообразная форма [ править | править код ]

Для тока имеющего форму дуги (половины окружности):

I = I m 2 3 ≈ 0,816 ⋅ I m . <displaystyle I=I_<sqrt <frac <2><3>>>approx 0<,>816cdot I_.>

Дополнительные сведения [ править | править код ]

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS или rms — root mean square — среднеквадратичное (значение).

Электроизмерительные приборы (амперметры, вольтметры) для измерения в цепях переменного тока обычно градуируются так, чтобы их показания соответствовали действующему значению синусоидального тока или напряжения. При измерении несинусоидальных токов и напряжений приборы различных систем могут давать разные показания [1] .

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока. Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения. В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока — это значение постоянного тока, при котором за период переменного тока в

проводнике выделяется столько же теплоты, сколько и при переменном токе.

Исходя из определения, установим соотношение между действующим и амплитудным значениями.

Пусть при постоянном токе I (и равном ему действующем значении переменного тока) в некотором активном сопротивлении R за период Т переменного тока выделится теплота Q:

Теплота dQ, выделяемая переменным током в том же сопротивлении R за бесконечно малый промежуток dt в любой момент цикла, может быть выражена через мгновенное значение тока к

Примем далее, что ток изменяется по закону синуса:

и за период Т выделится теплота

после некоторых преобразований —

Легко видеть, что второй интеграл равен нулю, тогда остается

Приравняв (1.5) и (1 6), найдем действующее значение переменного тока:

Выражения для действующих значений ЭДС и напряжения аналогичны выражению (1.7)

В соответствии с ГОСТом действующие значения силы тока, ЭДС и напряжения обозначают соответственно прописными латинскими буквами без индексов

Электроизмерительные приборы переменного тока градуируют в действующих значениях измеряемых величин

Integrated Publishing — ваш источник военных спецификаций и образовательных публикаций

Администрация — Навыки, процедуры, обязанности и т. д. военного персонала

Продвижение — Военный карьерный рост книги и т. д.

Аэрограф/метеорология — Метеорология основы, физика атмосферы, атмосферные явления и др.
Руководства по аэрографии и метеорологии военно-морского флота

Автомобилестроение/Механика — Руководства по техническому обслуживанию автомобилей, механика дизельных и бензиновых двигателей, руководства по автомобильным деталям, руководства по деталям дизельных двигателей, руководства по деталям бензиновых двигателей и т. д.
Автомобильные аксессуары | Перевозчик, персонал | Дизельные генераторы | Механика двигателя | Фильтры | Пожарные машины и оборудование | Топливные насосы и хранение | Газотурбинные генераторы | Генераторы | Обогреватели | HMMWV (Хаммер/Хамви) | и т.д…

Авиация — Принципы полетов, авиастроение, авиационная техника, авиационные силовые установки, справочники по авиационным частям, справочники по авиационным частям и т. д.
Руководства по авиации ВМФ | Авиационные аксессуары | Общее техническое обслуживание авиации | Руководства по эксплуатации вертолетов AH-Apache | Руководства по эксплуатации вертолетов серии CH | Руководства по эксплуатации вертолетов Chinook | и т.д…

Боевой — Служебная винтовка, пистолет меткая стрельба, боевые маневры, органическое вспомогательное вооружение и т. д.
Химико-биологические, маски и оборудование | Одежда и индивидуальное снаряжение | Боевая инженерная машина | и т.д…

Строительство — Техническое администрирование, планирование, оценка, планирование, планирование проекта, бетон, кирпичная кладка, тяжелый строительство и др.
Руководства по строительству военно-морского флота | Совокупность | Асфальт | Битумный корпус распределителя | Мосты | Ведро, Раскладушка | Бульдозеры | Компрессоры | Обработчик контейнеров | дробилка | Самосвалы | Землеройные машины | Экскаваторы | и т. д…

Дайвинг — Руководства по водолазным работам и спасению различного снаряжения.

Чертежник — Основы, методы, составление проекций, эскизов и т. д.

Электроника — Руководства по обслуживанию электроники для базового ремонта и основ. Руководства по компьютерным компонентам, руководства по электронным компонентам, руководства по электрическим компонентам и т. д.
Кондиционер | Усилители | Антенны и мачты | Аудио | Батареи | Компьютерное оборудование | Электротехника (NEETS) (самая популярная) | техник по электронике | Электрооборудование | Электронное общее испытательное оборудование | Электронные счетчики | и т.д…

Машиностроение — Основы и методы черчения, составление проекций и эскизов, деревянное и легкокаркасное строительство и т. д.
Военно-морское машиностроение | Армейская программа исследований прибрежных бухт | и т. д…

Еда и кулинария — Руководства по рецептам и оборудованию для приготовления пищи.

Логистика — Логистические данные для миллионов различных деталей.

Математика — Арифметика, элементарная алгебра, предварительное исчисление, введение в вероятность и т. д.

Медицинские книги — Анатомия, физиология, пациент уход, оборудование для оказания первой помощи, фармация, токсикология и т. д.
Медицинские руководства военно-морского флота | Агентство регистрации токсичных веществ и заболеваний

Военные спецификации — Государственные спецификации MIL и другие сопутствующие материалы

Музыка — Мажор и минор масштабные действия, диатонические и недиатонические мелодии, паттерны такта, и т.д.

Основы ядра — Теории ядерной энергии, химия, физика и т.
Справочники Министерства энергетики США

Фотография и журналистика — Теория света, оптические принципы, светочувствительные материалы, фотофильтры, копирование редактирование, написание публикаций и т. д.
Руководства по фотографии и журналистике военно-морского флота | Руководство по армейской фотографии, печати и журналистике

Религия — Основные религии мира, функции поддержки богослужений, свадьбы в часовне и т. д.

Определите фактическое значение. Действующие значения тока и напряжения

переменного тока долгое время не находили практического применения. Это было связано с тем, что первые генераторы электрической энергии производили постоянный ток, что полностью удовлетворяло технологическим процессам электрохимии, а двигатели постоянного тока имели хорошие характеристики управления. Однако по мере развития производства постоянный ток все меньше стал удовлетворять возрастающим требованиям экономичного источника питания. Переменный ток позволял эффективно дробить электрическую энергию и изменять напряжение с помощью трансформаторов. Появилась возможность производить электроэнергию на крупных электростанциях с последующей ее экономичной раздачей потребителям, увеличился радиус энергоснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с переменным — переменным — током по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимоиндукции, оказывающие наиболее существенное влияние на процессы, происходящие в цепях, усложняя их анализ.

Переменный ток (напряжение, ЭДС и т. д.) — это ток (напряжение, ЭДС и т. д.), который изменяется во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, и наименьший интервал времени, через который наблюдаются эти повторения, равен периода Т.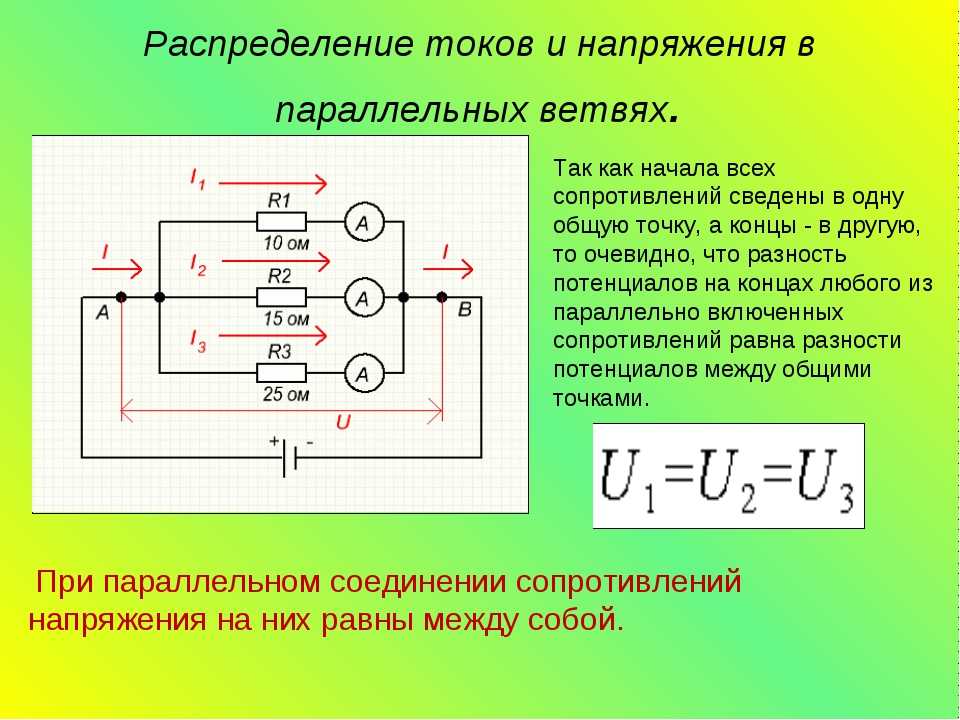   Для периодического тока имеем

Диапазон частот используются в технике: от сверхнизких частот (0,01¸10 Гц — в системах автоматического управления, в аналоговых вычислительных машинах) — до сверхвысоких (3000 300000 МГц — миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f  = 50 Гц .

Мгновенное значение переменной является функцией времени. Обозначается обычно строчной буквой:

i  — мгновенное значение тока;

и — мгновенное значение напряжения;

и — мгновенное значение ЭДС;

r — мгновенное значение мощности.

Наибольшее мгновенное значение переменной за период называется амплитудой (обычно обозначается прописной буквой с индексом м ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное значению постоянного тока, который в течение одного периода будет производить такой же тепловой или электродинамический эффект, как и периодический ток, называется эффективное значение периодический ток:

определяются значения ЭДС и напряжения.

Синусоидальный ток

Из всех возможных форм периодических токов наиболее распространенным является синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично производить, передавать, распределять и использовать электрическую энергию. Только при использовании синусоидального тока можно сохранить неизменной форму кривых напряжения и тока на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальной ЭДС, напряжения и тока на плоскости декартовых координат

Синусоидальные токи и напряжения могут быть изображены графически, записаны с помощью уравнений с тригонометрическими функциями, представленными в виде векторов на декартовой плоскости или с помощью комплексных чисел.

Приведенные на рис. 1, 2 графики двух синусоидальных ЭДС и 1   и e 2    соответствуют уравнениям:

 Значения аргументов синусоидальных функций называются фазы синусоиды, а значение фазы в начальный момент времени ( t =0): и — начальная фаза ( ).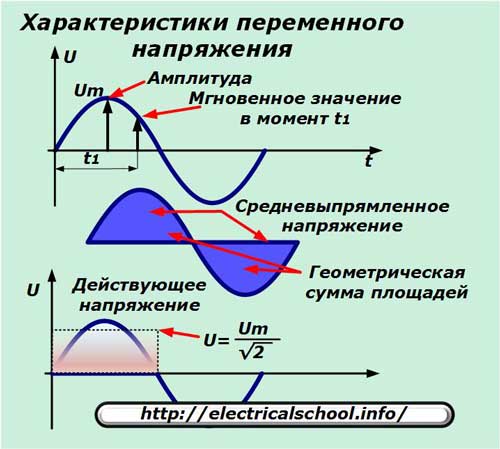

Величина, характеризующая скорость изменения фазового угла, называемая угловой частотой. Так как фазовый угол синусоиды за один период T   изменяется на рад., то угловая частота равна где f– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равная разнице между начальными фазами, называется фазовый угол .

Для синусоидальной ЭДС e 1   и e 2 Фазовый угол:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости от начала координат берут векторы, равные по величине амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки ( в ТОЭ это направление принимается положительным ) с угловой частотой равной в . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции векторов вращения на ось у равны мгновенным значениям ЭДС e 1   и e 2    (рис. 3). Набор векторов, представляющих синусоидально изменяющиеся ЭДС, напряжения и токи, называется векторной диаграммой . При построении векторных диаграмм удобно располагать векторы на начальный момент времени. ( т =0), , что следует из равенства угловых частот синусоидальных величин и эквивалентно тому, что сама система декартовых координат вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы зафиксированы (рис. 4). Векторные диаграммы широко используются при анализе цепей синусоидального тока. Их использование делает расчет схемы более интуитивным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) полный ток равен сумме токов двух ветвей:

Каждый из этих токов синусоидальный и может быть представлен уравнение

Результирующий ток также будет синусоидальным:

Определение амплитуды и начальной фазы этого тока с помощью соответствующих тригонометрических преобразований довольно громоздко и не очень наглядно, особенно если суммируется большое количество синусоидальных величин. Гораздо проще это сделать с помощью векторной диаграммы. На рис. 6 показаны начальные положения векторов токов, проекции которых на ось y дают мгновенные токи за т =0. При вращении этих векторов с одинаковой угловой скоростью w их относительное положение не меняется, а фазовый угол между ними остается равным.

Поскольку алгебраическая сумма проекций векторов на ось Y равна мгновенному значению полного тока, вектор полного тока равен геометрической сумме векторов тока:

.

Построение векторной диаграммы в масштабе позволяет определить значения диаграмм, после чего можно записать решение для мгновенного значения с формальным учетом угловой частоты:.

Физический смысл этих понятий примерно такой же, как физический смысл средней скорости или других величин, усредненных по времени. В разные моменты времени мощность переменного тока и его напряжение принимают разные значения, поэтому говорить о мощности переменного тока вообще можно лишь условно.

В то же время совершенно очевидно, что разные токи имеют разные энергетические характеристики — они производят разную работу за один и тот же промежуток времени. Производимая работа тока принимается за основу для определения действующего значения силы тока. Они задаются определенным периодом времени и рассчитывают работу, совершаемую переменным током за этот промежуток времени. Затем, зная эту работу, производят обратный расчет: узнают силу постоянного тока, которая совершила бы аналогичную работу за тот же промежуток времени. То есть производить усреднение по мощности. Расчетная сила, предположительно протекающая через тот же проводник постоянного тока, производящая ту же работу, является действующим значением начального переменного тока. Проделайте то же самое с напряжением. Этот расчет сводится к определению значения такого интеграла:

Откуда взялась эта формула? Из известной формулы мощности тока, выраженной через квадрат его силы.

Действующие значения периодических и синусоидальных токов

Расчет действующих значений для произвольных токов является непроизводительным занятием. А вот для периодического сигнала этот параметр может быть очень полезен. Известно, что любой периодический сигнал можно разложить на спектр. То есть представлен в виде конечной или бесконечной суммы синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам необходимо знать, как рассчитать действующее значение простого синусоидального тока. В результате, складывая действующие значения нескольких первых гармоник с максимальной амплитудой, получаем приближенное значение действующего значения тока для произвольного периодического сигнала. Подставив выражение для гармонического колебания в приведенную выше формулу, получим вот такую ​​приближенную формулу.

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно задаться вопросом, какое значение тока будет измерять включенный в цепь амперметр?

При расчете цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом действии периодически изменяющегося тока (количество выделяемого тепла, совершенная работа и т. д.) нельзя судить по амплитуде этого тока.

Введение понятий так называемых текущих значений тока и напряжения . Эти представления основаны на тепловом (или механическом) действии тока независимо от его направления.

Величина переменного тока   — это величина постоянного тока, при которой за время действия переменного тока в проводнике выделяется такое же тепло, как и при переменном токе.

Для оценки действия переменного тока сравним его действия с тепловым действием постоянного тока.

Мощность P постоянного тока I, проходящего через сопротивление r, будет равна P = P 2 r.

Мощность переменного тока выражается как среднее мгновенное воздействие мощности I 2 r за весь период или среднее значение из (Im x sinωt) 2 x r за то же время.

Пусть среднее значение t2 за период равно M. Приравнивая мощность постоянного тока и мощность переменного тока, имеем: I 2 r = Mr, откуда I = √M,

Значение I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определяется следующим образом.

Построить синусоидальную кривую тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Значение тока Ac

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода при возведении в квадрат дают положительные значения.

Постройте прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, рассчитанное с помощью высшей математики, будет равно 1/2I 2 м. Следовательно, М = 1/2I 2 м

Поскольку действующее значение переменного тока I равно I = √M, то, наконец, I = Im / √2

Аналогично соотношение между значениями тока и амплитуды для напряжения U и E равно:

U = Um/√2, E = Em/√2

Допустимые значения переменных обозначаются прописными буквами без индексов (I, U, E).