Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости.  § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры.  § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии.  Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. ГЛАВА III.  ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей.  Общие уравнения прямой. Общие уравнения прямой.§ 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка.  Конструкции В. Г. Шухова. Конструкции В. Г. Шухова.Упражнения Ответы |
Вся элементарная математика — Средняя математическая интернет-школа
Вектор – это направленный отрезок, соединяющий две точки в пространстве или в плоскости. Векторы обычно обозначаются либо маленькими буквами, либо начальной и конечной точками. Сверху обычно ставят чёрточку.
Например, вектор, направленный из точки
__
Нулевой вектор 0 или
0 — это вектор,
у которого начальная и конечная точки совпадают, т.
e
. A = B . Отсюда, 0 = – 0 .
Отсюда, 0 = – 0 .
Длина (модуль) вектора
Векторы называются коллинеарными , если их направленные отрезки лежат на параллельных прямых. Коллинеарные векторы a и b обозначаются a || b .
Три и более векторов называются компланарными
Сложение векторов. Так как
векторы — это направленные отрезки, то их сложение может быть
выполнено геометрически . (Алгебраическое сложение
векторов изложено
ниже, в пункте «Единичные ортогональные векторы»).
Предположим
,
что
(Алгебраическое сложение
векторов изложено
ниже, в пункте «Единичные ортогональные векторы»).
Предположим
,
что
__ __
a = AB and b = CD ,
тогда вектор __ __
a + b = AB + CD
есть результат выполнения двух операций:
a ) параллельного переноса одногоиз векторов таким образом, чтобы его начальная точка совпала с конечной точкой второго вектора;
б ) геометрического сложения ,
т.е. построения результирующего вектора, идущего от начальной точки
неподвижного вектора к конечной точке
перенесённого вектора
.
Вычитание векторов. Эта операция сводится к предыдущей путём замены вычитаемого вектора на противоположный: a – b = a + ( – b ) .
Законы сложения .
I . a + b = b + a ( П е р е м е с т и т е л ь н ы й закон ).
II
. ( a + b ) + c = a + ( b + c ) ( С о ч е т а т е л ь н ы й закон
).
III . a + 0 = a .
IV. a + ( – a ) = 0 .
Законы умножения вектора на число.
I. 1
· a = a , 0
· a = 0 , m · 0 = 0 , ( – 1 )
· a = – a .
II. m a = a m , | m a | = | m | · | a | .
III . m ( n a ) = ( m n ) a . ( С о ч е т а т е л ь н ы й
закон умножения на число ).
IV . ( m + n ) a = m a + n a , ( Р а с п р е д е л и т е л ь н ы й
m ( a + b ) = m a +
m b . закон
умножения на число ).
закон
умножения на число ).
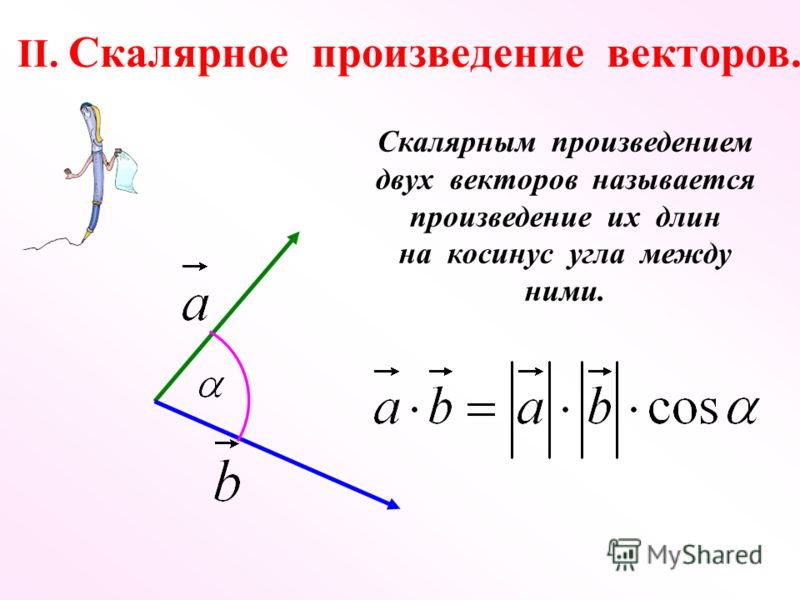
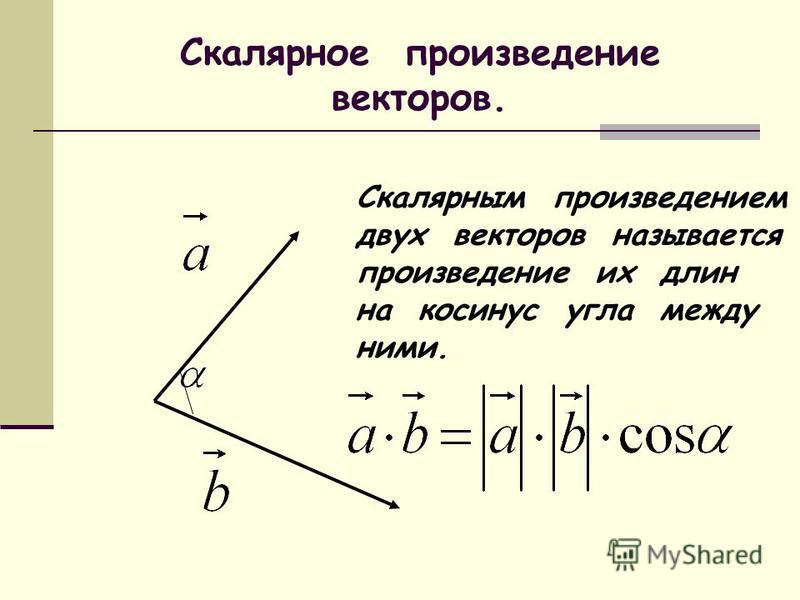
Скалярное произведение векторов . __ __
Угол между ненулевыми векторами AB и CD – это угол, образованный векторами при их параллельном переносе до совмещения точек A и C . Скалярным произведением векторов a и b называется число, равное произведению их длин на косинус угла между ними:
Если один из векторов нулевой, то их скалярное произведение в соответствии с определением равно нулю:
( a
, 0 ) = ( 0 , b ) = 0 .
Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле :
Скалярное произведение ( a , a ), равное | a | 2 , называется скалярным квадратом. Длина вектора a и его скалярный квадрат связаны соотно шением:
Скалярное произведение двух векторов:
— положительно , если угол между векторами острый ;
— отрицательно, если угол между векторами тупой .
Скалярное произведение двух
ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, т.е. когда эти векторы
перпендикулярны (ортогональны):
когда эти векторы
перпендикулярны (ортогональны):
Свойства скалярного произведения. Для любых векторов a , b , c и любого числа m справедливы следующие соотношения:
I . ( a , b ) = ( b , a ) . ( П е р е м е с т и т е л ь н ы й закон )
II
. ( m a
, b ) = m ( a
, b ) .
III . ( a + b , c ) = ( a , c ) + ( b , c ) . ( Р а с п р е д е л и т е л ь н ы й закон )
Единичные ортогональные векторы. В любой прямоугольной
системе координат можно ввести единичные попарно ортогональные векторы i , j и k ,
связанные с координатными осями: i – с осью Х , j – с осью
Y
и k – с осью Z . В соответствии с этим определением:
В соответствии с этим определением:
( i , j ) = ( i , k ) = ( j , k ) = 0,
| i | = | j | = | k | = 1.
Любой вектор a может быть выражен
через эти векторы единственным образом: a = x i
+ y j
+ z k . Другая форма записи
: a = ( x,
y, z ).
Здесь x , y , z
— координаты вектора a в этой системе координат. В
соответствии с последним соотношением и свойствами единичных ортогональных
векторов i
,
j
,
k скалярное произведение двух векторов
можно выразить иначе.
Другая форма записи
: a = ( x,
y, z ).
Здесь x , y , z
— координаты вектора a в этой системе координат. В
соответствии с последним соотношением и свойствами единичных ортогональных
векторов i
,
j
,
k скалярное произведение двух векторов
можно выразить иначе.
Пусть a =
( x
,
y
,
z )
; b =
( u
,
v
,
w )
. Тогда
( a , b ) = xu
+
yv
+
zw .
Тогда
( a , b ) = xu
+
yv
+
zw .
Скалярное произведение двух векторов равно сумме произведений соответствующих координат.
Длина (модуль) вектора a = ( x , y , z ) равна:
Кроме того, теперь мы получаем возможность проведения алгебраических операций над векторами, а именно, сложение и вычитание векторов может выполняться по координатам :
a + b = ( x + u , y + v , z + w ) ;
a – b = ( x – u , y – v , z – w ) .
Векторное произведение векторов. Векторным произведением [ a ,
b ] векторов a и b ( в указанном порядке ) называется вектор:
Существует другая формула длины вектора
[ a, b ]
:
/\
| [ a, b ] | = | a | | b | sin ( a, b ) ,
т.
e
. длина (
модуль
) векторного произведения
векторов a и b равна
произведению длин ( модулей )
этих векторов на синус угла между ними. Иначе говоря: длина (
модуль ) вектора [ a
,
b ] численно равна площади параллелограмма, построенного на векторах a и b .
длина (
модуль
) векторного произведения
векторов a и b равна
произведению длин ( модулей )
этих векторов на синус угла между ними. Иначе говоря: длина (
модуль ) вектора [ a
,
b ] численно равна площади параллелограмма, построенного на векторах a и b .
Свойства векторного произведения
.
I . Вектор [ a , b ] перпендикулярен (ортогонален) обоим векторам a и b .
( Докажите это , пожалуйста ! ) .
II. [ a , b ] = – [ b , a ] .
III. [ m a , b ]
= m [ a , b ]
.
IV. [ a + b , c ] = [ a , c ] + [ b , c ] .
V. [ a , [ b , c ] ] = b ( a , c ) – c ( a , b ) .
VI. [ [ a , b ] , c ]
= b ( a
, c ) – a ( b
, c ) .
[ [ a , b ] , c ]
= b ( a
, c ) – a ( b
, c ) .
Необходимое и достаточное условие коллинеарности векторов
a = ( x , y , z ) и b = ( u, v, w ) :
Необходимое и достаточное условие компланарности векторов a = ( x, y, z ), b = ( u, v, w ) и c = ( p, q, r ) :
П р и м е р
. Даны векторы: a = ( 1, 2, 3 ) и b = ( – 2 , 0 ,4 ).
Даны векторы: a = ( 1, 2, 3 ) и b = ( – 2 , 0 ,4 ).
Вычислить их скалярное и векторное произведения и угол
между этими векторами.
Р е ш е н и е . Используя соответствующие формулы (см. выше), получим:
a ). скалярное произведение:
( a , b ) = 1 · ( – 2 ) + 2 · 0 + 3 · 4 = 10 ;
б). векторное произведение:
Назад
Скалярные и векторные произведения — Скалярное и векторное произведение двух векторов и примеров
Основные понятия физики имеют математическую основу. Все измеряемые величины являются физическими величинами. Движение объектов можно описать двумя математическими величинами: скаляром и вектором.
Движение объектов можно описать двумя математическими величинами: скаляром и вектором.
Скалярная величина полностью описывается величиной или числами. Примерами скалярных величин являются длина, масса, расстояние, энергия, объем и т. д.
Векторная величина нуждается в величине, а также в направлении, чтобы описать ее полностью. Примерами векторных величин являются смещение, скорость, вес, дипольный момент и т. д. обсудим скалярные и векторные произведения и решим несколько примеров, где мы найдем скалярное и векторное произведение двух векторов.
Определение скалярного произведения двух векторов
Скалярное произведение двух векторов дает число или скаляр. Скалярные произведения полезны для определения отношений энергии и работы. Одним из примеров скалярного произведения является работа, выполняемая Силой (которая является вектором) при смещении (векторе) объекта, задаваемая скалярным произведением векторов Силы и Смещения.
 Скалярное произведение обозначается точкой (.), а формула скалярного произведения приведена ниже:
Скалярное произведение обозначается точкой (.), а формула скалярного произведения приведена ниже:\[\widehat{X}\] . \[\widehat{Y}\] = XY Cos ፀ, где ፀ — угол между векторами.
Скалярное произведение также называется скалярным произведением из-за используемого в нем точечного представления.
Свойства скалярного произведения двух векторов
Направление угла ፀ не имеет значения в скалярном произведении двух векторов. Угол ፀ можно измерить от любого из векторов к другому, поскольку Cos ፀ = Cos (-ፀ) = Cos (2ℼ — ፀ)
Если ፀ больше 90 градусов и меньше или равно 180 градусам, то скалярный продукт является отрицательным значением, т.е. 900 < ፀ <= 1800
Если ፀ больше 0 градусов и меньше или равно 90 градусам, то скалярное произведение является положительным значением.
 т. е. 00 < ፀ <= 900
т. е. 00 < ፀ <= 900Скалярное произведение двух векторов, параллельных друг другу, равно \[\widehat{X}\] . \[\widehat{Y}\]= XY, потому что 0 = XY.
Скалярное произведение двух антипараллельных векторов равно \[\widehat{X}\] . \[\widehat{Y}\] = XY Cos 180 = -XY.
Скалярное произведение вектора, умноженного на самого себя, равно квадрату его величины. \[\широкая шляпа{X}\] . \[\widehat{X}\] = XX, потому что 0 = X2
Скалярное произведение двух ортогональных векторов равно 0, т.е. \[\widehat{X}\] . \[\widehat{Y}\]= XY Cos 90 = 0
(изображение скоро будет загружено)
Скалярное произведение коммутативно, т.
 е. не важно. Итак, \[\widehat{X}\] . \[\widehat{Y}\] = \[\widehat{Y}\]. \[\widehat{X}\]
е. не важно. Итак, \[\widehat{X}\] . \[\widehat{Y}\] = \[\widehat{Y}\]. \[\widehat{X}\]Скалярное произведение является дистрибутивным, что означает \[\widehat{X}\] (\[\widehat{Y}\]+ \[\widehat{Z}\]) = \[\широкая шляпа{X}\] . \[\широкая шляпа{Y}\] + \[\широкая шляпа{X}\] . \[\широкая шляпа{Z}\]
Определение векторного произведения двух векторов
Когда мы берем векторное произведение двух векторов, мы получаем вектор. Векторное произведение также называется перекрестным произведением, поскольку знак векторного произведения — это крест (X)
\[\widehat{X}\] X \[\widehat{Y}\]
Направление векторное произведение двух векторов перпендикулярно обоим векторам. Это означает, что векторное произведение двух векторов \[\widehat{X}\] и \[\widehat{Y}\] лежит в плоскости, перпендикулярной плоскости, содержащей X и Y. Формула для определения величины векторный продукт:
| \[\widehat{X}\] x \[\widehat{Y}\] | = XY *Sin θ.
 Здесь угол θ между векторами измеряется от первого вектора в формуле (здесь вектор X) до второго вектора (вектор Y) в формуле.
Здесь угол θ между векторами измеряется от первого вектора в формуле (здесь вектор X) до второго вектора (вектор Y) в формуле.(Изображение будет загружено в ближайшее время)
Свойства векторного произведения двух векторов
Угол между векторами θ лежит в пределах от 0 до 180 градусов.
Векторное произведение векторов, которые параллельны друг другу (где θ = 0) или антипараллельны друг другу (где θ = 180), равно 0, поскольку Sin 0 = Sin 180 = 0
Результирующий вектор векторного произведения двух векторов может лежать либо в восходящей, либо в нисходящей плоскости.
Векторы \[\widehat{X}\] X \[\widehat{Y}\] и \[\widehat{Y}\] X \[\widehat{X}\] антипараллельны друг другу следовательно, векторное произведение не коммутативно.

При изменении порядка умножения результирующий вектор меняет знак, т.е. \[\widehat{X}\] X \[\widehat{Y}\]= — \[\widehat{Y}\] X \[\широкая шляпа{X}\].
Обычная мнемоника, используемая для определения направления векторного произведения векторов, — это правило правой руки штопора. Направление вектора задается поворотом ручки штопора от первого ко второму вектору.
(изображение будет загружено в ближайшее время)
(изображение будет загружено в ближайшее время)
. Поперечный продукт двух векторов распределяется, то есть, т.е. \ [\ Widehat {x} \] X (\[\widehat{Y}\]+ \[\widehat{Z}\] ) = \[\widehat{X}\] X \[\widehat{Y}\] + \[\widehat{X} \] X \[\widehat{Z}\].

Умножение на скаляр удовлетворяет (k * \[\widehat{X}\]) X \[\widehat{Y}\] = k * ( \[\widehat{X}\] X \[\ widehat{Y}\]) = \[\widehat{X}\] X (k * \[\widehat{Y}\])
Решенные примеры скалярного и векторного произведения двух векторов
Пусть Найдем скалярное и векторное произведение двух векторов с помощью нескольких примеров:
Решение. Если два вектора перпендикулярны друг другу, то их скалярное произведение равно 0. Таким образом, мы получаем: 92)}\] = \[\sqrt{9 + 16}\] = \[\sqrt{25}\] = 5
Векторное произведение A X B = AB Sin θ = 5 * \[\sqrt{13}\ ] * Sin 60 = 5*\[\sqrt{13}\]*\[\sqrt \frac {3}{2}\]
13.8: Работа и скалярное произведение
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 26936
- Питер Дурмашкин
- Массачусетский технологический институт через MIT OpenCourseWare88
Мы введем векторную операцию, называемую скалярным произведением или «скалярным произведением», которая берет любые два вектора и генерирует скалярную величину (число).
 Мы увидим, что физическое понятие работы может быть математически описано скалярным произведением между векторами силы и смещения.
Мы увидим, что физическое понятие работы может быть математически описано скалярным произведением между векторами силы и смещения.Скалярное произведение
Пусть \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) — два вектора. Поскольку любые два неколлинеарных вектора образуют плоскость, мы определяем угол θ как угол между векторами \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) как показано на рисунке 13.9. Обратите внимание, что θ может варьироваться от 0 до \(\pi\).
Рис. 13.9 Геометрия скалярного произведения.Скалярное произведение \(\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}\) векторов \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{ \mathbf{B}}\) определяется как произведение величины векторов \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) на косинус угол θ между двумя векторами:
\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A B \cos (\theta) \nonumber \]
где \(A=|\overrightarrow{\mathbf{ A}}| \text { и } B=\mid \overrightarrow{\mathbf{B}}\) представляют величину \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{ B}}\) соответственно.
 Скалярное произведение может быть положительным, нулевым или отрицательным, в зависимости от значения \(\cos\theta\). Скалярное произведение всегда является скалярной величиной.
Скалярное произведение может быть положительным, нулевым или отрицательным, в зависимости от значения \(\cos\theta\). Скалярное произведение всегда является скалярной величиной.Таким образом, угол, образованный двумя векторами, равен 9{1 / 2} \nonumber \]
Мы можем дать геометрическую интерпретацию скалярному произведению, записав определение как
\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}} =(A \cos (\theta)) B \nonumber \]
В этой формулировке термин Acosθ является проекцией вектора \(\overrightarrow{\mathbf{B}}\) в направлении вектора \ (\overrightarrow{\mathbf{B}}\). Эта проекция показана на рис. 13.10а. Таким образом, скалярное произведение — это произведение длины \(\overrightarrow{\mathbf{A}}\) в направлении \(\overrightarrow{\mathbf{B}}\) на длину \( \overrightarrow{\mathbf{B}}\). Обратите внимание, что мы могли бы также записать скалярное произведение как
\[\overrightarrow{\mathbf{A}} \cdot \overrightarrow{\mathbf{B}}=A(B \cos (\theta)) \nonumber \]
Теперь термин \(B \cos ( \theta)\) — это проекция вектора \(\overrightarrow{\mathbf{B}}\) в направлении вектора \(\overrightarrow{\mathbf{A}}\), как показано на рис.
Рис. 13.10 (a) и (b) Проекция векторов и скалярное произведение 13.10b. С этой точки зрения скалярное произведение есть произведение длины \(\overrightarrow{\mathbf{B}}\) в направлении \(\overrightarrow{\mathbf{A}}\) на длину из \(\overrightarrow{\mathbf{A}}\).
13.10b. С этой точки зрения скалярное произведение есть произведение длины \(\overrightarrow{\mathbf{B}}\) в направлении \(\overrightarrow{\mathbf{A}}\) на длину из \(\overrightarrow{\mathbf{A}}\).Из нашего определения скалярного произведения мы видим, что скалярное произведение двух векторов, перпендикулярных друг другу, равно нулю, поскольку угол между векторами равен \ (\pi/2\) и \(\cos (\pi/2)=0\).
Мы можем вычислить скалярное произведение двух векторов в декартовой системе координат следующим образом. Рассмотрим два вектора \(\overrightarrow{\mathbf{A}}=A_{x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{ \mathbf{k}}\) и \(\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_ {z} \шляпа{\mathbf{k}}\). Напомним, что
\[\begin{array}{l}
\hat{\mathbf{i}} \cdot \hat{\mathbf{i}}=\hat{\mathbf{j}} \cdot \hat{\mathbf {j}} = \ шляпа {\ mathbf {k}} \ cdot \ шляпа {\ mathbf {k}} = 1 \\
\ шляпа {\ mathbf {i}} \ cdot \ шляпа {\ mathbf {j}} =\шляпа{\mathbf{j}} \cdot \шляпа{\mathbf{k}}=\шляпа{\mathbf{i}} \cdot \шляпа{\mathbf{k}}=0
\end{массив} \nonumber \]Тогда скалярное произведение между \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) равно
\[\overrightarrow{\mathbf{A }} \cdot \overrightarrow{\mathbf{B}}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \nonumber \]
Производная по времени скалярного произведения двух векторов определяется выражением
\[\begin{array}{l}
\frac{d}{d t}(\overrightarrow{\mathbf{A}} \cdot \overrightarrow {\ mathbf {B}}) = \ frac {d} {d t} \ left (A_ {x} B_ {x} + A_ {y} B_ {y} + A_ {z} B_ {z} \ right) \ \
=\frac{d}{d t}\left(A_{x}\right) B_{x}+\frac{d}{d t}\left(A_{y}\right) B_{y}+\ frac{d}{d t}\left(A_{z}\right) B_{z}+A_{x} \frac{d}{d t}\left(B_{x}\right)+A_{y} \ frac{d}{d t}\left(B_{y}\right)+A_{z} \frac{d}{d t}\left(B_{z}\right) \\
=\left(\frac{ d} {d t} \ overrightarrow {\ mathbf {A}} \ right) \ cdot \ overrightarrow {\ mathbf {B}} + \ overrightarrow {\ mathbf {A}} \ cdot \ left (\ frac {d} {d t } \overrightarrow{\mathbf{B}}\right) 9{2} = \ frac {d} {d t} (\ overrightarrow {\ mathbf {A}} \ cdot \ overrightarrow {\ mathbf {A}}) = \ left (\ frac {d} {d t} \ overrightarrow {\ mathbf{A}}\right) \cdot\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{A}} \cdot\left(\frac{d}{d t} \overrightarrow{\mathbf{A} }\right)=2\left(\frac{d}{d t} \overrightarrow{\mathbf{A}}\right) \cdot \overrightarrow{\mathbf{A}} \nonumber \]Кинетическая энергия и Скалярное произведение
Для объекта, совершающего трехмерное движение, скорость объекта в декартовых компонентах определяется выражением \(\overrightarrow{\mathbf{v}}=v_{x} \hat{\mathbf{i}}+ v_ {y} \ шляпа {\ mathbf {j}} + v_ {z} \ шляпа {\ mathbf {k}} \).
 Напомним, что величина вектора определяется квадратным корнем скалярного произведения вектора на самого себя, 9{2}\right) \nonumber \]
Напомним, что величина вектора определяется квадратным корнем скалярного произведения вектора на самого себя, 9{2}\right) \nonumber \]Работа и скалярное произведение
Работа — важный физический пример математической операции скалярного произведения двух векторов. Напомним, что когда на тело действует постоянная сила и точка приложения силы смещается вдоль оси х, вклад в работу вносит только составляющая силы в этом направлении,
\[W=F_{x } \Delta x \nonumber \]
Предположим, что мы тянем тело по горизонтальной поверхности с силой \(\overrightarrow{\mathbf{F}}\). Выберите координаты так, чтобы горизонтальное направление было осью x, а сила \(\overrightarrow{\mathbf{F}}\) образовывала угол \(\beta\) с положительным направлением x. На рис. 13.11 мы показываем вектор силы \(\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{y} \hat{\mathbf{j}}\) и вектор смещения точки приложения силы \(\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}\). Обратите внимание, что \(\Delta \overrightarrow{\mathbf{x}}=\Delta x \hat{\mathbf{i}}\) является компонентом смещения и, следовательно, может быть больше, равно или меньше нуля (но показано на рисунке больше нуля для ясности).
 Скалярное произведение между вектором силы \(\overrightarrow{\mathbf{F}}\) и вектором смещения \(\Delta \overrightarrow{\mathbf{x}}\) равно
Скалярное произведение между вектором силы \(\overrightarrow{\mathbf{F}}\) и вектором смещения \(\Delta \overrightarrow{\mathbf{x}}\) равно\[\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}}=\left(F_{x} \hat{\mathbf{i}}+F_{y} \hat {\mathbf{j}}\right) \cdot(\Delta x \hat{\mathbf{i}})=F_{x} \Delta x \nonumber \]
Рисунок 13.11 Векторы силы и смещенияРабота, выполненная тогда сила равна
\[\Delta W=\overrightarrow{\mathbf{F}} \cdot \Delta \overrightarrow{\mathbf{x}} \nonumber \]
В общем случае угол \(\beta\ ) принимает значения в диапазоне \(-\pi \leq \beta \leq \pi\) (на рис. 13.11, \(0 \leq \beta \leq \pi / 2\)). Поскольку x -компонент силы равен \(F_{x}=F \cos (\beta)\), где \(F=|\overrightarrow{\mathbf{F}}|\) обозначает величину \(\ overrightarrow{\mathbf{F}}\), работа силы равна 9{\circ}\) на землю. Коэффициент кинетического трения равен \(\mu_{k}=0,2\) а) Какова работа каждой из трех сил при скольжении тела по наклонной плоскости? (b) Для каждой силы работа, совершаемая силой, положительная или отрицательная? в) Чему равна сумма работы трех сил? Это положительно или отрицательно?
Решение: (a) и (b) Выберите систему координат с началом в верхней части наклонной плоскости и положительным направлением x, указывающим вниз по наклонной плоскости, и положительным направлением y, указывающим вверх вправо, как показано на рисунке 13.
Рис. 13.12 Система координат для объекта, скользящего по наклонной плоскости Только составляющая силы тяжести вдоль положительного направления x \(F_{g x}=m g \sin \theta\) и сила трения направлены вдоль смещения и, следовательно, вносят свой вклад в работу. Нам нужно использовать второй закон Ньютона, чтобы определить величину нормальной силы. Поскольку объект вынужден двигаться в положительном направлении x, \(a_{y}=0\), второй закон Ньютона в \(\hat{\mathbf{j}}\)-направлении \(Nm g \ потому что \ тета = 0 \). Поэтому \(N=m g \cos \theta\), а величина силы трения равна \(f_{k}=\mu_{k} m g \cos \theta\). 9{\circ}\right)\right)=38,4 \mathrm{J} . 12. При скольжении тела по наклонной плоскости на него действуют три однородные силы: сила тяжести, направленная вниз и имеющая величину \(F_{g}=mg\), нормальная сила N, перпендикулярная поверхности наклонной плоскости, а сила трения, противодействующая движению и равная по величине \(f_{k}=\mu_{k} Н\). Диаграмма сил на объект показана на рисунке 13.13.
12. При скольжении тела по наклонной плоскости на него действуют три однородные силы: сила тяжести, направленная вниз и имеющая величину \(F_{g}=mg\), нормальная сила N, перпендикулярная поверхности наклонной плоскости, а сила трения, противодействующая движению и равная по величине \(f_{k}=\mu_{k} Н\). Диаграмма сил на объект показана на рисунке 13.13.


 Скалярное произведение обозначается точкой (.), а формула скалярного произведения приведена ниже:
Скалярное произведение обозначается точкой (.), а формула скалярного произведения приведена ниже: т. е. 00 < ፀ <= 900
т. е. 00 < ፀ <= 900 Здесь угол θ между векторами измеряется от первого вектора в формуле (здесь вектор X) до второго вектора (вектор Y) в формуле.
Здесь угол θ между векторами измеряется от первого вектора в формуле (здесь вектор X) до второго вектора (вектор Y) в формуле.

 Мы увидим, что физическое понятие работы может быть математически описано скалярным произведением между векторами силы и смещения.
Мы увидим, что физическое понятие работы может быть математически описано скалярным произведением между векторами силы и смещения. Скалярное произведение может быть положительным, нулевым или отрицательным, в зависимости от значения \(\cos\theta\). Скалярное произведение всегда является скалярной величиной.
Скалярное произведение может быть положительным, нулевым или отрицательным, в зависимости от значения \(\cos\theta\). Скалярное произведение всегда является скалярной величиной. 13.10b. С этой точки зрения скалярное произведение есть произведение длины \(\overrightarrow{\mathbf{B}}\) в направлении \(\overrightarrow{\mathbf{A}}\) на длину из \(\overrightarrow{\mathbf{A}}\).
13.10b. С этой точки зрения скалярное произведение есть произведение длины \(\overrightarrow{\mathbf{B}}\) в направлении \(\overrightarrow{\mathbf{A}}\) на длину из \(\overrightarrow{\mathbf{A}}\). Напомним, что величина вектора определяется квадратным корнем скалярного произведения вектора на самого себя, 9{2}\right) \nonumber \]
Напомним, что величина вектора определяется квадратным корнем скалярного произведения вектора на самого себя, 9{2}\right) \nonumber \] Скалярное произведение между вектором силы \(\overrightarrow{\mathbf{F}}\) и вектором смещения \(\Delta \overrightarrow{\mathbf{x}}\) равно
Скалярное произведение между вектором силы \(\overrightarrow{\mathbf{F}}\) и вектором смещения \(\Delta \overrightarrow{\mathbf{x}}\) равно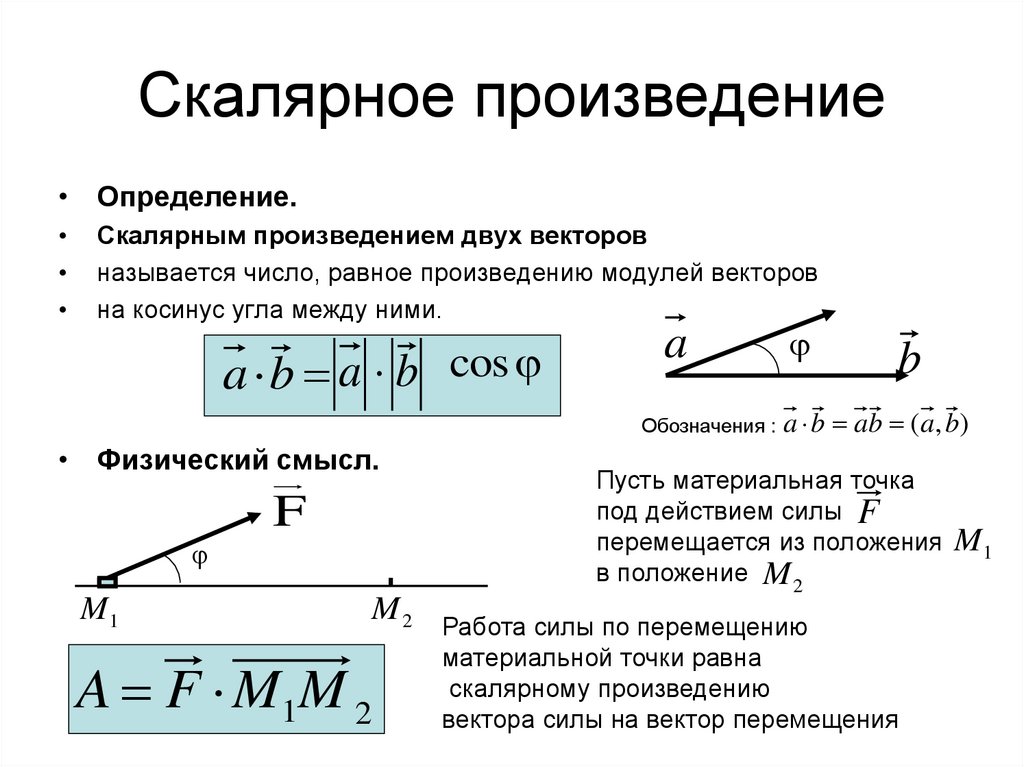 12. При скольжении тела по наклонной плоскости на него действуют три однородные силы: сила тяжести, направленная вниз и имеющая величину \(F_{g}=mg\), нормальная сила N, перпендикулярная поверхности наклонной плоскости, а сила трения, противодействующая движению и равная по величине \(f_{k}=\mu_{k} Н\). Диаграмма сил на объект показана на рисунке 13.13.
12. При скольжении тела по наклонной плоскости на него действуют три однородные силы: сила тяжести, направленная вниз и имеющая величину \(F_{g}=mg\), нормальная сила N, перпендикулярная поверхности наклонной плоскости, а сила трения, противодействующая движению и равная по величине \(f_{k}=\mu_{k} Н\). Диаграмма сил на объект показана на рисунке 13.13.