1.2 Сила, система сил, эквивалентная система сил и уравновешенная система сил
В статике рассматриваются следующие две основные задачи: 1) сложение сил и приведение системы сил, действующих на абсолютно твердое тело, к простейшему виду; 2) определение необходимых и достаточных условий равновесия действующих на абсолютно твердое тело систем сил.
Все тела в той или иной степени деформируемы. В тех случаях, когда этими деформациями можно пренебречь, тело рассматривается как абсолютно твердое, т. е. предполагается, что расстояния между любыми его точками остаются неизменными.
В статике рассматривают все тела как абсолютно твердые, но для краткости часто называют их твердыми телами или просто телами.
Если данное тело может получить любое перемещение в пространстве, то такое тело называется свободным. Примером свободного тела может служить снаряд, выпущенный из дула орудия.
Мера механического взаимодействия тел, определяющая интенсивность и направление этого взаимодействия, называется в механике
Если в результате действия одного тела на другое происходит изменение движения, в частности изменение покоя другого тела, то тогда говорят о динамическом проявлении силы. Например, в брошенном теле вследствие механического взаимодействия его с Землей происходит изменение движения, и, следовательно, мы наблюдаем динамическое проявление силы тяжести тела, с которой это тело притягивается к центру Земли.
Если же в результате действия одного тела на другое не происходит изменения движения, в частности не происходит изменения покоя другого тела (вследствие механического взаимодействия этого тела еще и с другими телами), то в этом случае говорят о
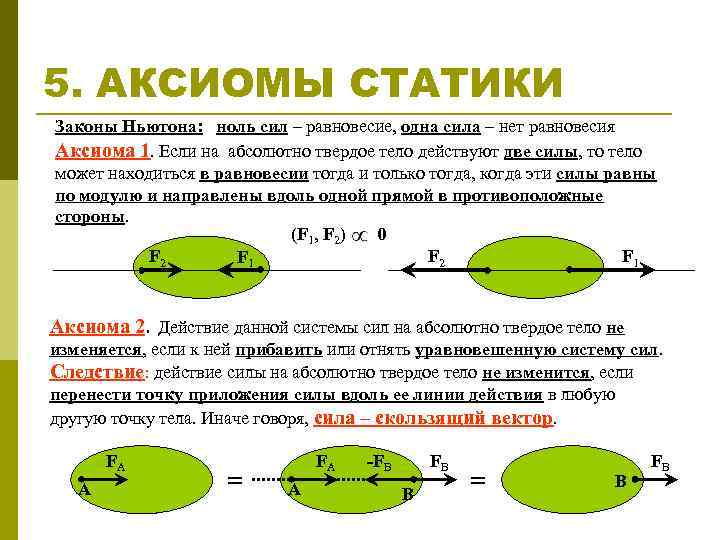
Понятие силы в механике имеет научную ценность потому, что ее можно измерять. Измерение силы в механике основано на сравнении сил. Если сравнивать динамическое или статическое проявление силы с проявлением силы, принятой за единицу измерения, то можно произвести динамическое или статическое измерение силы. При этом две сравниваемые силы считают равными, если их действия на тело в одних и тех же условиях одинаковы. За единицу силы в технической системе единиц (МКГСС) принимается сила в один килограмм (
Как известно из опыта, действие силы на тело вполне определяется численным значением (модулем), направлением и точкой приложения. Поэтому сила, действующая на тело, является величиной векторной.
Для
статического измерения сил служат
известные из курса физики приборы,
называемые динамометрами.
Главную
часть этих приборов составляет
градуированная пружина. Принцип действия
динамометра основан на том, что до
известных пределов деформация пружины
(растяжение или сжатие) пропорциональна
силе, ее вызывающей, и исчезает по
прекращении действия этой силы. При
этом о модуле силы, приложенной к пружине,
судят по величине растяжения или сжатия
пружины. Такой способ измерения модуля
силы основан, таким образом, на равновесии
между приложенной силой, модуль которой
измеряется, и силой упругости, развиваемой
пружиной динамометра. Поэтому этот
способ измерения модуля силы можно
назвать статическим. Другой, динамический,
способ измерения модуля силы будет
указан в динамике.
Кроме
модуля силы, важно еще указать направление
и точку приложения силы. Направление и
точка приложения силы зависят от
характера механического взаимодействия
тел и их взаимного положения. Например,
сила тяжести, с которой Земля действует
на тело, направлена к центру Земли и
приложена к центру тяжести тела.
Силы
давления двух прижатых друг к другу
гладких тел направлены по нормали к
поверхностям этих тел в точках их касания
и приложены в этих точках и т. д.
На практике сила давления всегда действует на некоторые поверхности, и о точке приложения силы можно говорить лишь условно, т. е. понятие точка приложения силы, в сущности, является абстракцией.
Графически сила изображается направленным прямолинейным отрезком (со стрелкой), совпадающим по направлению с направлением силы (рисунок 1). Длина этого отрезка выражает в выбранном масштабе модуль силы, направление отрезка соответствует направлению силы, его начало совпадает с точкой приложения силы. Иногда на практике бывает удобно изображать силу так, что точка ее приложения является конец вектора силы – острие стрелки. Прямая
Силу,
как и всякую векторную величину, будем
обозначать какой-нибудь буквой с чертой
над ней, например
.
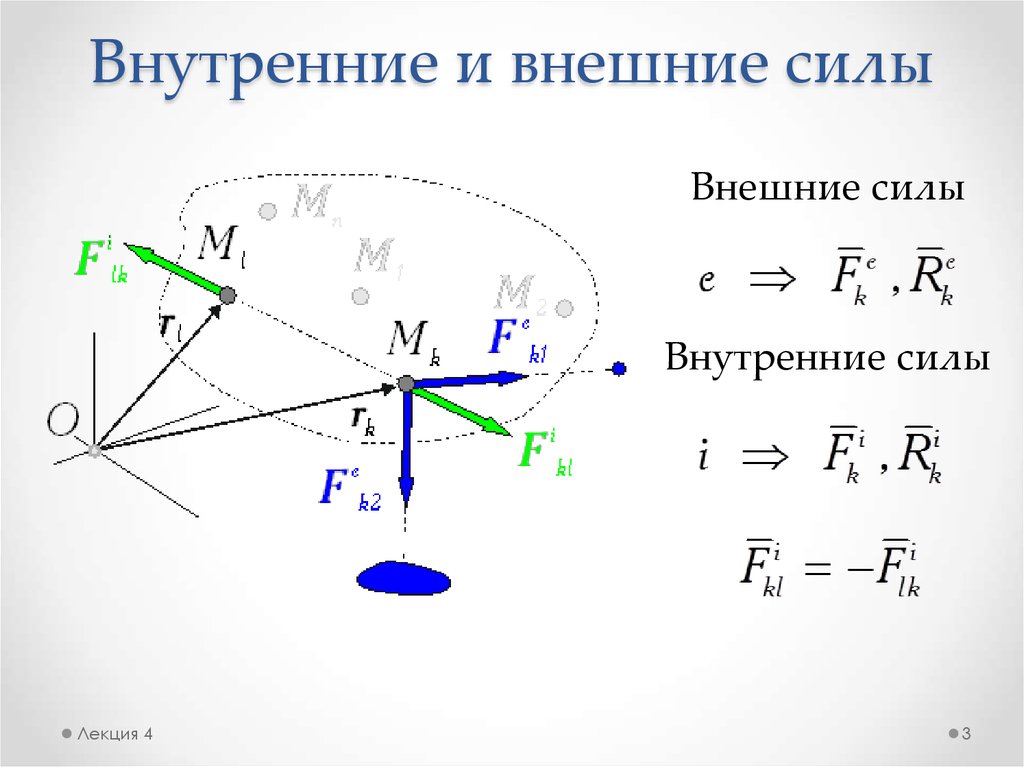Модуль
данной силы, как и всякой другой векторной
вели чины, будем обозначать той же
буквой, но без черты, например F,
или
символом.
Теперь выясним понятие системы сил, механической эквивалентности систем сил, а также понятие системы взаимно
Совокупность сил, одновременно действующих на данное тело или систему тел, называется системой сил.
Если одну систему сил, действующих на данное свободное тело, можно заменить другой системой сил, не изменяя при этом покоя или его движения, в котором находится тело, то такие две системы сил называются эквивалентными.
Если данная система сил эквивалентна одной силе, то эта сила называется равнодействующей данной системы сил, а силы, совместное действие которых может быть заменено равнодействующей, называются составляющими. Таким образом,
Нахождение равнодействующей называется сложением сил, а замену одной силы системой сил, производящей на тело то же действие, что и данная сила, называют разложением сил.
В дальнейшем мы увидим, что не всякая система сил может быть заменена одной силой, и, следовательно, не всякая система сил имеет равнодействующую.
Если под действием данной системы сил свободное тело не изменяет своего движения (выражение «тело не изменяет своего движения» надо понимать в том смысле, что это тело под действием данной системы сил движется так, как оно двигалось бы, если бы этой системы сил не было), или, в частности, продолжает оставаться в покое, то такая система сил называется
Сила,
которая, будучи присоединена к некоторой
системе сил, действующих на тело, приводит
эту систему к равновесию, называется уравновешивающей
силой данной
системы сил.
Под равновесием тела понимают состояние покоя этого тела по отношению к другим телам, играющим роль системы отсчета. Если систему отсчета, по отношению к которой изучается равновесие данного тела, можно считать неподвижной, то равновесие этого тела условно называют абсолютным, а в противном случае – относительным.
В
действительности все тела на Земле
движутся вместе с Землей вокруг ее оси,
вокруг Солнца и вместе с Солнцем в
космическом пространстве. Поэтому
абсолютного равновесия в природе нет.
Однако часто, как уже говорилось во
введении, при решении многих практических
задач движение Земли не учитывают и
считают Землю за неподвижную систему
отсчета. Вследствие этого всякое тело,
не движущееся относительно Земли,
считают находящимся в состоянии
абсолютного равновесия. В статике
изучают только абсолютное равновесие
тел.
Ясно, что уравновешенность сил, приложенных к свободному телу, является необходимым, но не достаточным условием равновесия (покоя) самого тела. В равновесии тело будет находиться лишь в том случае, если оно было в покое и до приложения к нему уравновешенных сил.
По известному из курса физики закону инерции следует, что если на тело не действуют никакие силы или если силы, действующие на него, взаимно уравновешиваются, то это тело или находится в покое, или движется по инерции.
(При
этом не следует думать, что движение
тела по инерции может быть представлено
только в виде поступательного,
прямолинейного и равномерного движения.
В динамике будет показано, что при
отсутствии сил (или при их равновесии)
тело может также находиться и в состоянии
равномерного вращения. Движение тела
по инерции в общем случае может быть
представлено в виде комбинации двух
одновременных движений: прямолинейного
равномерного движения центра тяжести
этого тела и равномерного вращения
вокруг постоянно движущейся оси,
проходящей через центр тяжести.
При
этом ось вращения может составлять
любой угол с направлением движения
центра тяжести этого тела).
Поэтому под состоянием равновесия тела можно понимать не только состояние покоя, но и движение по инерции. Однако в статике мы под состоянием равновесия материальной точки или тела будем понимать только состояние покоя.
Плоская система сходящихся сил и её равнодействующая
Системой сходящихся сил называют группу двух, трех и более сил, приложенных к телу, линии действия которых пересекаются в некоторой точке.
Пусть, к абсолютно твердому телу приложена система N сил (F1, F2, … FN), расположенных в пространстве так, что их линии действия пересекаются в одной точке О (рисунок 1).
Такую систему сил называют системой сходящихся сил. Упростим систему сходящихся сил, т.е. решим первую задачу статики.
Приведение к равнодействующей
Докажем, что данная система сил эквивалентна одной силе, т.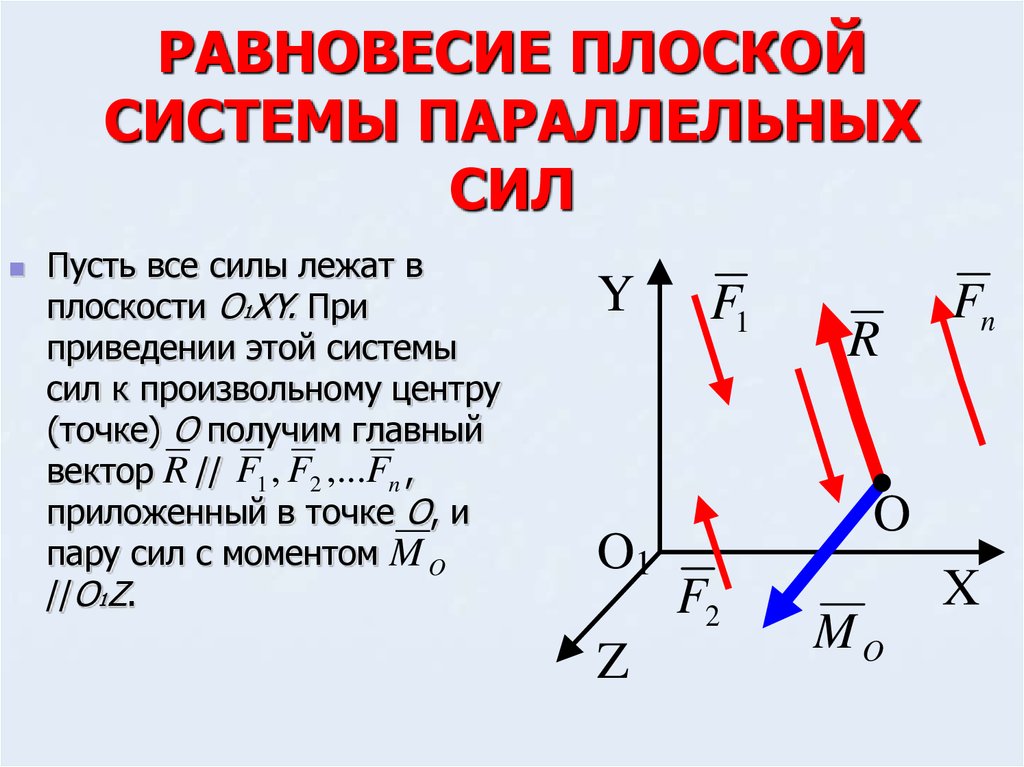
е. приводится к равнодействующей силе.
Рисунок 1
В самом деле, так как сила есть вектор скользящий, то все силы данной системы можно перенести вдоль линий их действия в точку О.
Далее, по четвертой аксиоме, силы F1 и F2 можно заменить их равнодействующей R1,2 (рисунок 1), которая определяется диагональю параллелограмма, построенного на этих силах как на сторонах, и направленной по этой диагонали, т.е.
(F1, F2) ~ R1,2,
где R1,2=F1+F2.
Далее можно записать аналогичные соотношения для полученной равнодействующей силы R*1,2 и силы F3, тогда
(R1,2 F3) ~ (F1, F2, F3) ~ R1,2,3,
где R1,2,3=F1+F2+F3 и т.д.
Для системы N сил окончательно будем иметь
(F1 F2 … FN) ~ R*,
R*= F1 + F2 + … + FN= ∑Fi .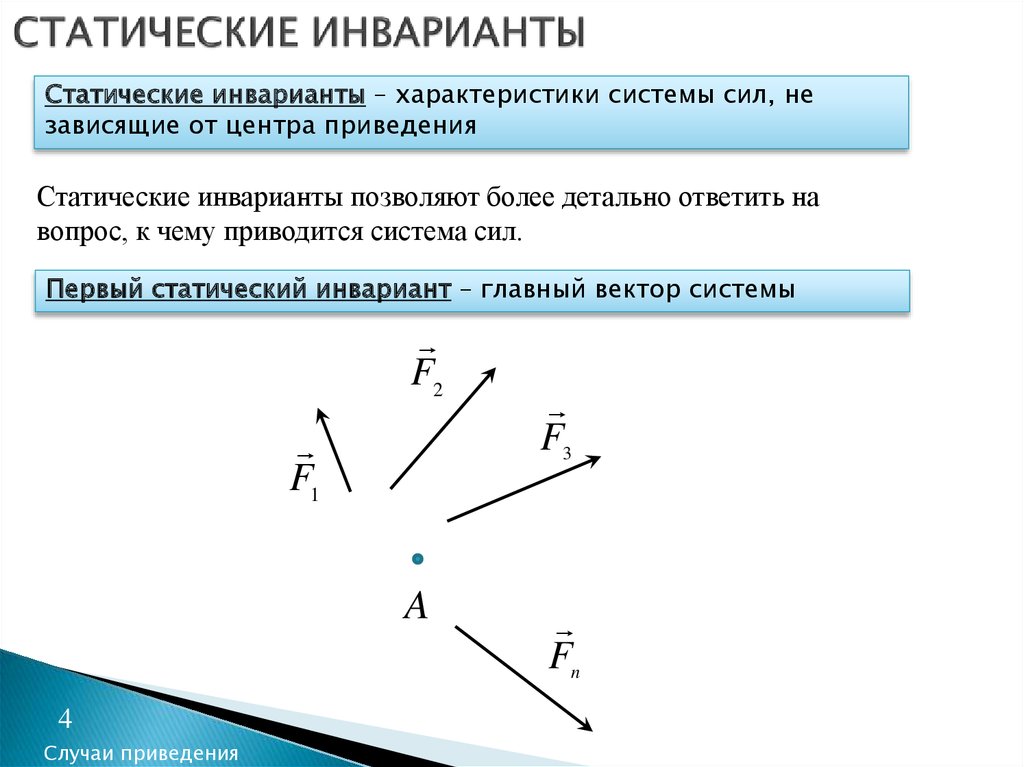
(1)
На рисунке 2, a показано построение равнодействующей указанным способом на примере системы, состоящей из четырех сил. Однако процесс определения равнодействующей удобнее вести иным путем, с помощью построения так называемого силового многоугольника.
Силовой многоугольник
Из конца вектора силы F1 (точки В) проводим вектор ВС, геометрически равный силе F2. Из конца этого вектора (точки С) проводим вектор СD равный силе F3. Из конца этого вектора (точки D) проводим вектор DE, равный силе F4.
Рисунок 2
Полученный многоугольник ABCDE называется силовым многоугольником. Процесс его построения хорошо виден на рисунке 2, б. Стороны силового многоугольника называются составляющими силами.
Вектор АЕ, соединяющий начало А первой силы с концом Е последней силы и направленный навстречу составляющим силам, называется замыкающей стороной силового многоугольника.
Следовательно, равнодействующая системы сходящихся сил изображается в выбранном масштабе замыкающей силового многоугольника, построенного на составляющих силах.
Нахождение равнодействующей системы сходящихся сил по правилу силового многоугольника называется векторным или геометрическим сложением сил.
Таким образом, мы доказали, что система сходящихся сил в общем случае эквивалентна одной силе, т.е. равнодействующей, которая приложена в точке пересечения линий действия всех сил и равна их геометрической сумме.
Вычисление равнодействующей
Для аналитического определения равнодействующей найдем ее проекции Rx, Ry, Rz на оси декартовой системы координат. Имеем
Rx = ∑ Fkx ,
Ry = ∑ Fky ,
Rz = ∑ Fkz . (2)
Тогда величина равнодействующей определится следующей формулой:
или
Для определения направления равнодействующей R* воспользуемся обычными выражениями для направляющих косинусов:
cos α = Rx/R, cos β = Ry/R, cos γ = Rz/R.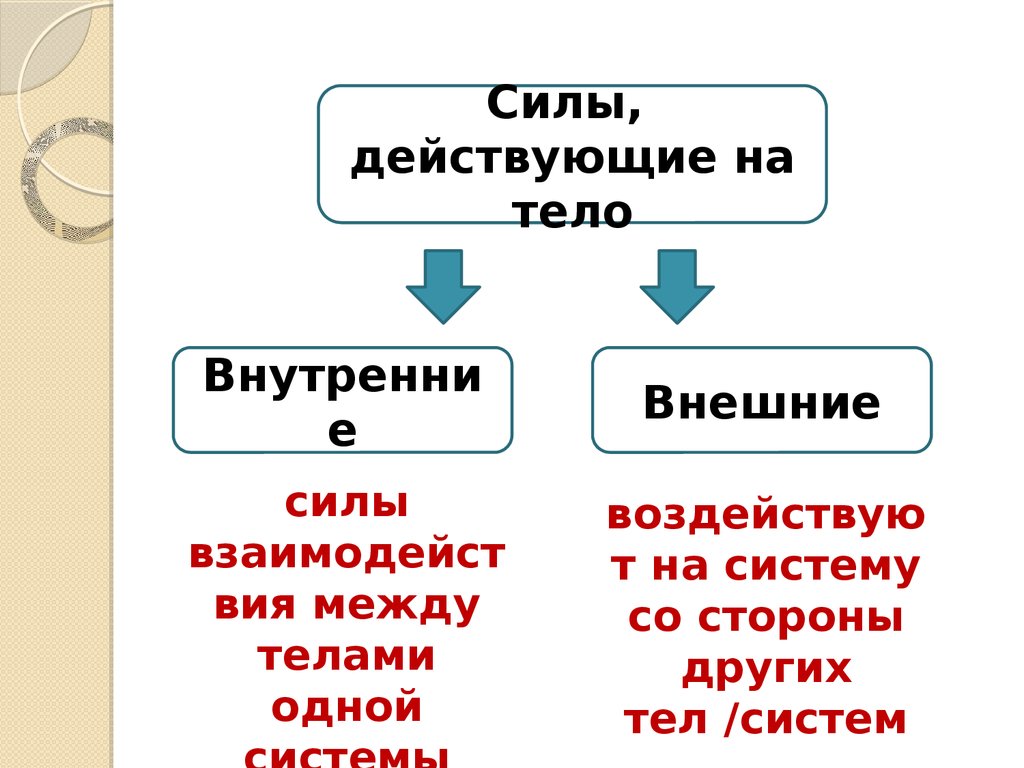
(5)
Здесь α , β , γ — углы между положительным направлением осей координат и равнодействующей.
Равенства (2)-(5) позволяют определить модуль и направление равнодействующей по заданным проекциям составляющих сил.
В случае плоской системы сходящихся сил оси координат можно взять в плоскости действия сил и тогда формулы (2)-(5) упрощаются.
Примеры решения задач >
Условия равновесия системы сходящихся сил >
Объясните систему сил в механике
Серия испытаний
Мохит Униял|Обновлено: 3 августа 2022 г. Любой внешний агент, который изменяет или пытается изменить состояние объекта, называется силой. Для представления силы требуются четыре характеристики: величина, направление, точка приложения и линия действия. Единицей силы в системе СИ является «Ньютон». В реальной жизни на многие объекты действует более чем одна сила, т. е. система сил. Анализ таких объектов несколько усложняется.
Изучение системы сил очень важно для анализа действия системы сил на объект и для расчета результатов действия системы сил.
В этой статье будут рассмотрены определение, типы и примеры системы сил.
Загрузить Формулы для машиностроения GATE – ТОМ и вибрации
Содержание
- 1. Что такое система сил?
- 2. Типы системы сил
- 3. Копланарная система сил
- 4. Некомпланарная система сил
Читать полностью
Что такое система сил?
Когда одно тело взаимодействует с другим, они действуют друг на друга с разной силой. Когда несколько сил действуют на тело одновременно, они образуют систему, известную как «система сил» или «система сил». Простыми словами, систему сил можно определить как «система сил или система сил – это группа сил, действующих на тело или ряд связанных тел». В результате этот термин используется для описания группы сил.
Силы могут действовать в одной точке или в одной плоскости. Силы могут действовать и в нескольких плоскостях трехмерного объекта. Некоторые реальные приложения для системы сил: «силы при перетягивании каната», «силы на лопастях потолочных вентиляторов», «силы на стыке фермы» и т.
д.
Скачать формулы для машиностроения GATE — Сопротивление материалов
Типы системы сил
Существуют различные системы сил, действующих на элемент. Различные типы силовых систем на одном и том же теле вызывают различное поведение. Вот почему изучение типов силовых систем очень важно. В целом силовые системы можно разделить на два типа.
- Копланарная система сил
- Некомпланарная система сил
Копланарная система сил
Термин копланарность подразумевает, что величины должны находиться в одной плоскости. Копланарная система сил – это система, в которой линии действия всех систем сил, действующих на тело, лежат в одной плоскости с телом.
Ниже приведены типы копланарной системы сил;
- Система коллинеарных копланарных сил
- Система параллельных копланарных сил
- Система параллельных копланарных сил
- Система несовпадающих копланарных сил
Загрузить формулы для машиностроения и инженерной механики GATE
Система некомпланарных сил
Термин «компланарность» означает, что величины не должны находиться в одной плоскости.
Некомпланарная система сил – это система, в которой линии действия всех систем сил, действующих на тело, не лежат в одной плоскости.
Типы некомпланарной системы сил;
- Параллельная некомпланарная система сил
- Параллельная некомпланарная система сил
- Непараллельная некомпланарная система сил
Часто задаваемые вопросы о системе сил
Что такое система сил?
Когда одно агентство действует на тело, оно называется силой. Однако, когда на тело или группу тел действуют одновременно несколько сил, система называется «системой сил » или «системой сил».
Сколько типов силовых систем существует?
В одном и том же теле разные типы силовых систем вызывают различное поведение. Основные типы систем сил:
- Копланарная система сил
- Некомпланарная система сил
Что такое копланарная система сил?
Когда на тело действует группа сил, линия действия которых лежит в одной плоскости с телом, такая группа сил называется компланарной системой сил.
Система сил в шарнирном соединении фермы является примером копланарной системы сил.Каково условие равновесия любой системы сил?
Для равновесия любой системы сил результирующая сила, действующая на тело, и результирующий момент, действующий на тело от системы сил, должны быть равны нулю. Математически условием равновесия любой системы сил является; ΣF_x =0, ΣF_y= 0 и ΣM =0
Каковы реальные примеры системы сил?
Группой войск называется система войск. Примером системы сил является любой объект, на который действуют две или более двух сил. Некоторыми реальными примерами систем сил являются силы перетягивания каната, силы на ножках стола, силы на штативе с камерой, силы на стержне, упирающемся в стену, и т. д.
Система сил в шарнирном соединении фермы является примером копланарной системы сил.ESE & GATE ME
Mechanical Engg.GATEGATE MEHPCLBARC SOESEIES MEBARC ExamISRO ExamOther Exams
Featured Articles
Follow us for latest updates
Our Apps
- BYJU’S Exam Prep: The Exam Приложение для подготовки
GradeStack Learning Pvt.
Ltd.Windsor IT Park, Tower — A, 2-й этаж,
Sector 125, Noida,
Uttar Pradesh 201303
Силовая система — Физика
силовая система – это совокупность сил , действующих в определенных местах. Различные типы силовых систем: (i) КОМПЛАНАРНЫЕ СИЛЫ: Силы, действующие только на одну плоскость, известны как компланарные силовые системы. Или мы можем сказать, что если действие сил происходит только в одной плоскости объекта, то система сил известна как копланарная сила. ii) СОВМЕСТНЫЕ СИЛЫ: Система совпадающих копланарных сил – это система двух или более сил, линии действия которых ВСЕ пересекаются в одной точке. iii) ПОДОБНЫЕ СИЛЫ параллельная копланарная система сил состоит из двух или более сил, линии действия которых параллельны друг другу. iv) РАЗЛИЧНЫЕ СИЛЫ: Если параллельные силы таковы, что их направления противоположны друг другу, то они называются «ОТЛИЧНАЯ СИЛА» . Тело находится в равновесии, если равнодействующая всех сил, действующих на него, равна нулю. Существует два основных типа статического равновесия, а именно поступательное равновесие и вращательное равновесие. Формулы σfy = 0σfy = 0 Параллельная сила Система σmo = 0 80164 9014 4 9000 2 9000 2 9000 2 9000 2 . Система ΣFy=0ΣFy=0 ΣMO=0ΣMO=0 Действие силы При изучении механики учитываются только внешние эффекты силы. Внутренние эффекты изучаются в специальных дисциплинах, например, Механика материалов (также известная как Прочность материалов 9).0227). СИЛА КАК ВЕКТОРНАЯ ВЕЛИЧИНА Сосредоточенная сила — это векторная величина. Величина силы есть величина scala r. В системе СИ он измеряется в ньютонах (Н). Сила, действующая на тело, графически изображается векторной стрелкой в точке приложения силы, где ориентация стрелки представляет направление линии действия силы, а острие стрелки представляет направление0226 смысл силы. Пусть действуют две силы, как показано на рис. Тогда результирующая сила равна F= f1+ft Подробнее о сложении векторов см. в физике и математике. https://sites.google.com/site/physicsstudywithme *На физике и математике) Добавление системы сил — |
