Резонанс напряжений
Допустим, что в цепи рис.1 действует переменная ЭДС. Она изменяется по закону:
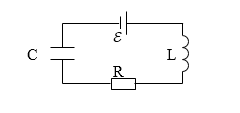
Рисунок 1.
В цепи течет ток вида:
Амплитуда силы тока${\ (I}_m)$ связана с амплитудой ${{\mathcal E}}_m$ «законом Ома» для переменного тока:
Выражение:
полное электросопротивление. Угол ($\varphi $) на который колебания тока отстают от колебаний напряжения определен выражением:
Если изменить частоту колебаний ($\omega $). Как следует из формул (3) , (5) произойдёт изменение амплитуды силы тока ($I_m$) и сдвига фаз ($\varphi $).
Если $\omega =0$, то выражение $\frac{1}{\omega C}\to \infty $. Импеданс ($Z$) становится бесконечным, следовательно, $I_m=0.$ При $\omega =0$ мы имеем дело с постоянным током, который не проходит через конденсатор. Если начать увеличивать частоту, то величина реактивного сопротивления (${\left(\omega L-\frac{1}{\omega C}\right)}^2$) сначала уменьшается, следовательно, уменьшается импеданс, увеличивается $I_m.$ Когда частота ($\omega $) становится равной резонансной частоте контура (${\omega }_0$):
полное сопротивление цепи ($Z$) становится минимальным и равным активному сопротивлению цепи ($R$). Сила тока при этом достигает максимума. При $\omega >{\omega }_0$ выражение ${\left(\omega L-\frac{1}{\omega C}\right)}^2\ne 0$ и растет при росте частоты. Импеданс вновь увеличивается, амплитуда силы тока уменьшается, приближаясь к нулю асимптотически.
Графически вышеописанный процесс изображен на рис.2.
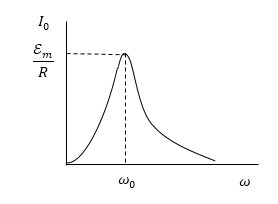
Рисунок 2.
Амплитуда силы тока при резонансной частоте ($\omega ={\omega }_0$) равна:
при этом разность фаз равна нулю ($\varphi =0$). В цепи как бы нет емкости и индуктивности. При этой частоте напряжения на емкости и индуктивности полностью взаимно компенсируются, становясь равными по модулю, так как они по фазе противоположны всегда. Такой резонанс называют резонансом напряжений. Векторная схема резонанса напряжений изображена на рис.3. При резонансе контур ведет себя как активное сопротивление.
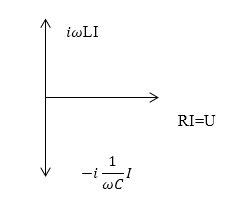
Рисунок 3.
Замечание
Итак, случай вынужденных колебаний, когда частота генератора ЭДС (или приложенного внешнего напряжения) равна резонансной частоте, представляет особый интерес. При этом амплитуда тока достигает максимума, а сдвиг фаз между током и напряжением равен нулю. Контур действует как активное сопротивление.
Применение резонанса напряжений
Явление резонанса напряжений используют в радиотехнике, если необходимо усилить колебания напряжения какой либо частоты, например в устройствах входной части радиоприемника. В этой части есть колебательный контур ($LC$). Добротность этого контура высока, напряжение с конденсатора контура подается на вход усилителя. Входные сигналы вызывают в антенне переменный ток довольно высокой частоты, который вызывает в катушке $L$ ЭДС взаимной индукции, амплитуда которой ${{\mathcal E}}_m\ \ $. Из-за резонанса на конденсаторе (значит и на входе) появляется напряжение с амплитудой ${{\mathcal E}}_mO>{{\mathcal E}}_m.$ Это усиление работает только в узком интервале частот, около резонансной частоты, что позволит выделить из большого количества сигналов разных радиостанций только колебания нужной частоты.
Пример 1
Задание: Чему равна амплитуда напряжения на конденсаторе ($U_{mC}$) при резонансе напряжений, если колебания затухают слабо? Добротность контура равна$\ O$. Внешняя ЭДС изменяется в соответствии с законом: ${\mathcal E}={{\mathcal E}}_m{sin \left(\omega t\right)\ }.$
Решение:
Амплитуда тока при резонансе достигает максимума, она равна:
\[I_{m\ }\left({\omega }_0\right)=\frac{{{\mathcal E}}_m}{R}\left(1.1\right),\]где ${\omega }_0$ — резонансная частота.
Следовательно, амплитуда напряжения на конденсаторе будет равна:
\[U_{mC}=X_CI_{m\ }\left(1.2\right),\]где емкостное сопротивление равно:
\[X_C=\frac{1}{\omega_0С}\left(1.3\right).\]Подставим в формулу (1.2) $X_C$ из (1.3) и $I_{m\ }$ из (1.1) получим амплитуду напряжения на конденсаторе при резонансе:
\[U_{mC}=\frac{{{\mathcal E}}_m}{{\omega }_0RС}(1.4).\]Учтем, что:
\[{\omega }_0=\frac{1}{\sqrt{LC}}(1.5)\]подставим выражение для резонансной частоты в формулу (1.4), получим:
где $O=\frac{1}{R}\sqrt{\frac{L}{C}}$ — добротность контура.
Ответ: $U_{mC}={{\mathcal E}}_mO.$
Пример 2
Задание: Чему равна амплитуда напряжения на индуктивности ($U_{mL}$) при резонансе напряжений, если колебания затухают слабо? Добротность контура равна$\ O$. Внешняя ЭДС изменяется в соответствии с законом: ${\mathcal E}={{\mathcal E}}_m{sin \left(\omega t\right)\ }.$
Решение:
Выражение для напряжения на индуктивности можно записать как:
\[U_{mL}=I_m{\omega }_0L\ \left(2.1\right),\]Получим:
\[U_{mL}=\frac{{{\mathcal E}}_m}{R}{\omega }_0L\ \left(2.3\right).\]Проведем замену:
\[{\omega }_0=\frac{1}{\sqrt{LC}}\left(2.4\right).\]Получим, что амплитуда напряжения на индуктивности равна:
\[U_{mL}=\frac{{{\mathcal E}}_m}{R}\frac{1}{\sqrt{LC}}L=\frac{{{\mathcal E}}_m}{R}\frac{\sqrt{L}}{\sqrt{C}}{={\mathcal E}}_mO.\]Ответ: $U_{mL}{={\mathcal E}}_mO.$
Колебания напряжения на конденсаторе и индуктивности имеют равные амплитуды, но их разность фаз равна $\pi $.
резонанс напряжений. в какой цепи и при каких условиях возникает резонанс напряжений? спасибо заранее
Резонанс напряжений может возникнуть в цепи с последовательно включенными индуктивностью и емкостью. Условие резонанса напряжений в таком контуре — равенство реактивных сопротивлений: индуктивного и емкостного.
Чем неприятен резонанс напряжений? Заранее спасибо
Резонанс напряжений — Википедия. Что такое Резонанс напряжений
Описание явления
 Резонанс напряжений основанный на трансформаторе.
Резонанс напряжений основанный на трансформаторе.Явление резонанса напряжений возникает на частоте ω0{\displaystyle \omega _{0}}, при которой индуктивное сопротивление катушки XL=ω0L{\displaystyle X_{L}=\omega _{0}L} и ёмкостное сопротивление конденсатора XC=1ω0C{\displaystyle X_{C}={\frac {1}{\omega _{0}C}}} равны между собой. При этом Электрический импеданс (полное сопротивление) цепи
- z^(jω0)=R+1jω0C+jω0L{\displaystyle {\hat {z}}(j\omega _{0})\;=R+{\frac {1}{j\omega _{0}C}}+j\omega _{0}L}
уменьшается, становится чисто активным и равным R{\displaystyle R} (сумма активного сопротивления катушки и соединительных проводов). В результате, согласно закону Ома: I=UR{\displaystyle I={\frac {U}{R}}}, ток в цепи достигает своего максимального значения.
Следовательно, напряжения как на катушке UL=IXL{\displaystyle U_{L}=IX_{L}}, так и на конденсаторе UC=IXC{\displaystyle U_{C}=IX_{C}} окажутся равными и будут максимально большой величины[1]. При малом активном сопротивлении цепи R{\displaystyle R} эти напряжения могут во много раз превысить общее напряжение U{\displaystyle U} на зажимах цепи, которое создаёт генератор. Это явление и называется в электротехнике резонансом напряжений.
Замечания
Колебательный контур, работающий в режиме резонанса напряжений, сам по себе не является усилителем мощности. Повышенные напряжения на его элементах возникают за счёт увеличения тока в цепи и следовательно потребляемой мощности от источника переменного напряжения.
Явление резонанса напряжений необходимо учитывать при разработке аппаратуры. Повышенное напряжение может повредить не рассчитанные на него элементы.
Если нужно повысить напряжение до безопасного уровня путем резонанса, то следует использовать комбинированный или параллельно-последовательный резонанс (описание в статье Резонанс токов).
Применение
При совпадении частоты генератора и собственных колебаний контура на катушке появляется напряжение, более высокое, чем на клеммах генератора. Это можно использовать для питания высокоомной нагрузки повышенным напряжением, или в полосовых фильтрах.
Если напряжение источника питания слишком маленькое, то можно его повысить если устроить последовательный резонанс на основе трансформатора. Если при этом полученное напряжение окажется больше расчетного для трансформатора, то первичная и вторичная обмотки соединяются последовательно чтобы трансформатор не вышел из строя.
См. также
Литература
- Власов В. Ф. Курс радиотехники. М.: Госэнергоиздат, 1962. С. 52.
- Изюмов Н. М., Линде Д. П. Основы радиотехники. М.: Госэнергоиздат, 1959. С. 512.
Ссылки
Примечания
- ↑ Однако, точное решение задачи о максимуме напряжения на катушке и конденсаторе с учётом величины добротности Q{\displaystyle Q}, даёт несколько другой результат. Часто́ты ωC{\displaystyle \omega _{C}} и ωL{\displaystyle \omega _{L}}, на которых напряжение на катушке и конденсаторе достигает максимума, не равны между собой, и не совпадают с частотой резонанса ω0{\displaystyle \omega _{0}}: ωC=ω02Q2−12Q2{\displaystyle \omega _{C}=\omega _{0}{\sqrt {\frac {2Q^{2}-1}{2Q^{2}}}}}
ωL=ω0{\displaystyle \omega _{L}=\omega _{0}}2Q22Q2−1{\displaystyle {\sqrt {\frac {2Q^{2}}{2Q^{2}-1}}}}
Видно, что с увеличением добротности контура, часто́ты ωC{\displaystyle \omega _{C}} и ωL{\displaystyle \omega _{L}} сближаются с резонансной частотой ω0{\displaystyle \omega _{0}}.
Источник: Бакалов В. П., Дмитриков В. Ф., Крук Б. И. Основы теории цепей: Учебник для вузов; Под ред. В.П. Бакалова. – 3-е изд., перераб. и доп. – М.: Горячая линия – Телеком, 2007. – с.: ил. (недоступная ссылка) ISBN 5-256-01472-2, с.118
Вопрос №2. Параллельное соединение приемников в однофазных цепях (10 мин.)
Расчет цепи с параллельным соединением проводников (рис. 7,а) можно осуществить различными способами: методом векторных диаграмм, методом проводимостей и методом комплексных чисел. Первый метод не позволяет с большой точностью осуществить расчеты (рис. 7, б), поэтому были введены методы комплексных чисел и метод проводимостей. Рассмотрим метод проводимостей подробнее.
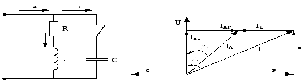
а) б)
Рис. 7. Схема разветвленной цепи и векторная диаграмма
резонанса напряжений
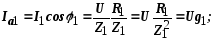
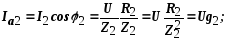
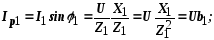
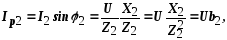
где g1, g2 – активные проводимости ветвей;
b1, b2 – реактивные проводимости ветвей.
Необходимо
отметить, что знак реактивных проводимостей
получается автоматически, т.к. 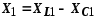 ,
,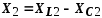 .
Т. к.XL2 и XC1 равны нулю, то b1>0, b2<0.
.
Т. к.XL2 и XC1 равны нулю, то b1>0, b2<0.
Общий ток
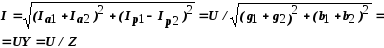 где
где 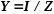 – полная проводимость цепи, См.
– полная проводимость цепи, См.
Треугольник проводимостей представлен на рис. 8.
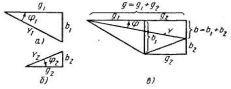
Рис. 8. Треугольники проводимостей
Функции угла φ определяют так:
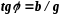 ;
; 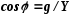
Выражения для мощностей принимают такой вид:
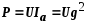 ;
; 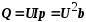
Выводы по второму вопросу: таким образом, для расчета цепей с параллельным соединением приемников используются методы векторных диаграмм, проводимостей и комплексных чисел.
Вопрос №3. Резонанс напряжений и токов (20 мин.)
Резонансным режимом работы цепи – режим, при котором ее сопротивление является чисто активным.
Различают два основных режима: резонанс напряжений и резонанс токов.
3.1. Резонанс напряжений
Резонанс напряжений – это явление в цепи с последовательным контуром, когда ток в цепи совпадает по фазе с напряжением источника.
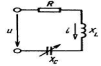
Рис. 9. Схема последовательного колебательного контура
Найдем условие резонанса напряжений. Для того чтобы ток цепи совпадал по фазе с напряжением, реактивное сопротивление должно быть равно нулю, так как tgφ=X/R.
Условие резонанса
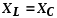
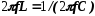
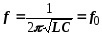
При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Выражение является формулой Томсона, определяющей зависимость собственной частоты колебаний контура от параметров L и С. Следует вспомнить, что если конденсатор контура зарядить от источника постоянного тока, а затем замкнуть его на индуктивную катушку, то в контуре возникнет переменный ток частоты f0. Вследствие потери колебания в контуре будут затухать, время затухания зависит от значения возникших потерь.
Резонансу напряжений соответствует векторная диаграмма, приведенная на рис. 10.
Признаки резонанса напряжений:
а) сопротивление цепи Z=R минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.
Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряжение на катушке и конденсаторе обусловлено накопленной в них энергией, значение которой тем больше, чем меньше потери в цепи.

Рис. 10. Векторная диаграмма и резонансная
кривая последовательного контура
Характеристики резонанса:
1)
Волновое сопротивление контура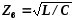
2)
Добротность контура 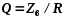
3) Резонансная кривая характеризует способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот (рис. 10, б).
4) Полное сопротивление цепи при резонансе
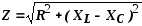
На рис. 11 показана зависимость реактивного сопротивления Х=ХL —Хс от частоты источника f. Анализ этого графика показывает, что при низких и высоких частотах реактивное сопротивление велико и ток в контуре мал. При частотах, близких к fo, реактивное сопротивление мало и ток контура велик.
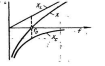
Рис. 11
Резонанс напряжений широко используется в радиотехнике и электронике для выделения сигналов заданной частоты.
Резонансные явления в электрических цепях — КиберПедия
Режим работы электрической цепи, при котором ток и напряжение на входе цепи совпадают по фазе, называют резонансом. При этом эквивалентное сопротивление всей цепи будет активным. В цепях, состоящих из резистивного, индуктивного и емкостного элементов, различают резонанс напряжений и резонанс токов.
Резонанс напряжений
Резонанс напряжений может иметь место в цепи с последовательно соединенными индуктивным и емкостным элементами. Рассмотрим схему последовательного соединения резистора, индуктивности и емкости (рис. 6.1).
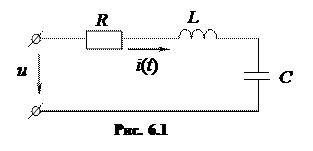 |
Второй закон Кирхгофа для данной цепи можно записать:
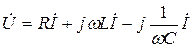 .
.
Отсюда комплексное сопротивление цепи
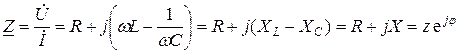 . (6.1)
. (6.1)
Построим векторную диаграмму. При этом могут иметь место три случая.
1. Пусть индуктивное сопротивление больше емкостного XL> XC , тогда и индуктивное напряжение будет больше емкостного UL> UC. Векторная диаграмма будет иметь вид (рис. 6.2).
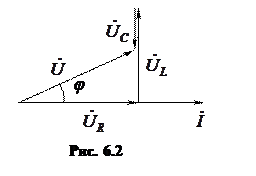 | 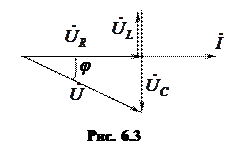 | ||
Реактивная составляющая напряжения UХ = UL – UC – положительна, и угол сдвига фаз между током и напряжением φ> 0. Такой характер цепи является активно-индуктивным.
2. Пусть индуктивное сопротивление меньше емкостного XL < XC . Тогда и индуктивное напряжение станет меньше емкостного UL< UC, так как ток через элементы протекает один и тот же, а напряжение пропорционально току и сопротивлению. Векторная диаграмма будет иметь вид (рис. 6.3).
Реактивная составляющая напряжения UХ = UL – UC – отрицательна, и угол сдвига фаз между током и напряжением φ < 0. Такой характер цепи является активно- емкостным.
3. Пусть XL = XC, в этом случае индуктивное и емкостное напряжения равны по величине UL= UC. Так как они всегда противоположны по фазе, то они полностью компенсируют друг друга, следовательно, реактивная составляющая UХ = UL – UC = 0. Общее напряжение будет активным и совпадет по фазе с током φ = 0, следовательно, в цепи имеет место резонанс напряжений. Векторная диаграмма для данного случая показана на рис. 6.4.
Из вышесказанного следует, что условием, при котором наступит резонанс напряжений, является равенство индуктивного и емкостного сопротивлений.
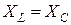 , или
, или 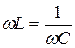 .
.
Из выражения (6.1) следует, что при резонансе полное сопротивление цепи имеет активный характер.
Резонанс напряжений можно достигнуть подбором трех параметров:
1) изменением частоты колебательного контура 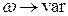 , L, C = const;
, L, C = const;
2) изменением индуктивности контура 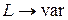 ,
, 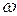 , С = const;
, С = const;
3) изменением емкости колебательного контура 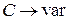 ,
, 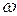 , L = const .
, L = const .
При этом все три параметра связаны между собой.
Из условия 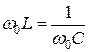 получаем:
получаем: 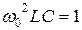 , отсюда:
, отсюда:
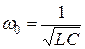 ,
, 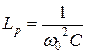 ,
, 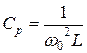 .
.
Частоту ω0, определяемую из такого условия, называют резонансной.
Если напряжение на зажимах цепи и активное сопротивление цепи R не изменяются, то ток при резонансе имеет максимальное значение
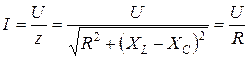 , так как
, так как 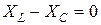 .
.
Если реактивные сопротивления 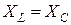 превосходят при резонансе активное сопротивление:
превосходят при резонансе активное сопротивление:
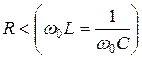 ,
, 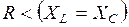 ,
,
то напряжения на зажимах катушки и конденсатора могут существенно превышать напряжение на входе цепи.
Превышение напряжения на реактивных элементах над напряжением на входе принято характеризовать величиной
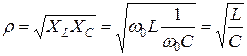 ,
,
называемой волновым или характеристическим сопротивлением цепи. Волновое сопротивление численно равно индуктивному или емкостному сопротивлению на резонансной частоте.
Кратность превышения напряжения на зажимах индуктивного и емкостного сопротивлений над входным определяют отношением напряжения на реактивном элементе к напряжению на входе цепи на резонансной частоте:
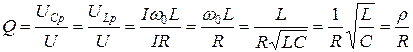 .
.
Эта величина называется добротностью контура.
Величина, обратная добротности
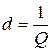 ,
,
называется затуханием контура.
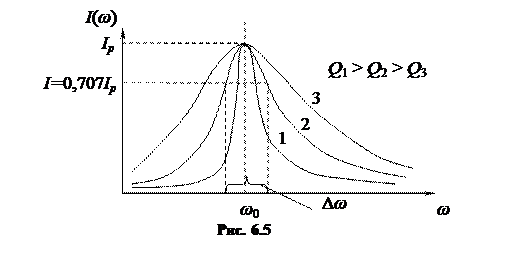 |
Избирательные свойства колебательного контура определяются его добротностью. Чем больше добротность контура, тем более узкой будет резонансная кривая (рис. 6.5).
Избирательность контура характеризуется полосой пропускания. Полоса пропускания – это диапазон частот, для которых ток ослабляется не более чем в 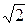 раз по отношению к максимальному значению
раз по отношению к максимальному значению
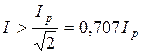 .
.
Ширину полосы пропускания можно определить по формуле
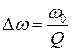 .
.
Рассмотрим резонансные кривые тока и напряжений (рис. 6.6).
При неизменных параметрах цепи и неизменном входном напряжении ток определится выражением
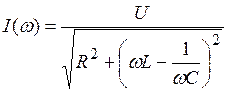 .
.
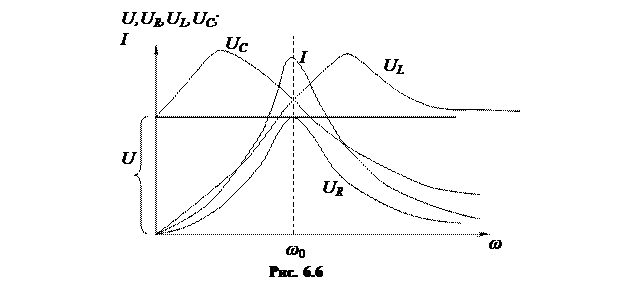 |
Рассмотрим это выражение в реперных точках:
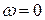 ;
; 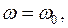
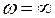 . При нулевой частоте
. При нулевой частоте 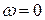 ток в цепи будет постоянным, величина тока
ток в цепи будет постоянным, величина тока 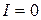 , так как конденсатор не пропускает постоянный ток, при резонансной частоте
, так как конденсатор не пропускает постоянный ток, при резонансной частоте 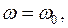 ток максимален – это признак резонанса напряжений
ток максимален – это признак резонанса напряжений 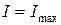 . На высоких частотах
. На высоких частотах 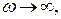 ток
ток 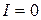 , так как сопротивление катушки становится равным
, так как сопротивление катушки становится равным 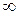 .
. Напряжение на индуктивности 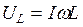 пропорционально частоте, следовательно, при нулевой частоте
пропорционально частоте, следовательно, при нулевой частоте 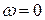 напряжение на индуктивности
напряжение на индуктивности 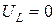 . При
. При 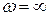 все напряжение, подаваемое от источника, приложено к индуктивности, и
все напряжение, подаваемое от источника, приложено к индуктивности, и 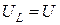 .
.
Напряжение на емкости обратно пропорционально частоте, следовательно, при 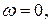 все напряжение приложено к емкости
все напряжение приложено к емкости 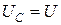 . При
. При 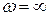
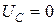 , так как равно нулю емкостное сопротивление.
, так как равно нулю емкостное сопротивление.
При резонансной частоте 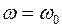 индуктивное и емкостное напряжения равны
индуктивное и емкостное напряжения равны 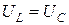 .
.
Напряжение на резистивном элементе пропорционально току и, следовательно, повторяет форму кривой тока 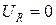 при
при 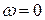 и
и 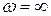 ,
, 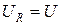 при
при 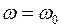 .
.
Рассмотрим энергетические соотношения при резонансе.
Мгновенные значения мощности на зажимах катушки и конденсатора определяются выражениями:
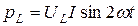 ;
;
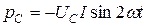 .
.
Так как при резонансе 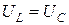 , эти мощности в любой момент времени равны и противоположны по знаку. Это значит, что происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора, но не происходит обмена между источником и реактивными элементами, так как
, эти мощности в любой момент времени равны и противоположны по знаку. Это значит, что происходит обмен энергией между магнитным полем катушки и электрическим полем конденсатора, но не происходит обмена между источником и реактивными элементами, так как
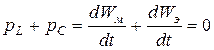 и
и 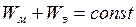 ,
,
то есть суммарная энергия электрического и магнитного полей остается постоянной. Энергия переходит из конденсатора в катушку в течение четверти периода, когда напряжение на конденсаторе убывает, а ток растет. В течение следующей четверти периода энергия переходит из катушки в конденсатор. Источник энергии питает только активное сопротивление.
Резонанс токов
Резонанс в идеальной цепи
Резонанс токов наступает при параллельном соединении индуктивности и емкости. Для обобщения анализов включим в цепь параллельно индуктивности и емкости активное сопротивление (рис. 6.7).
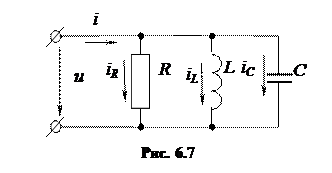 |
По первому закону Кирхгофа можно записать:
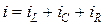 .
.
Запишем это выражение в комплексной форме:
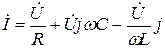 ,
,
где 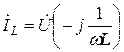 ,
, 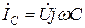 ,
, 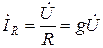 .
.
Вынесем напряжение за скобку, получим
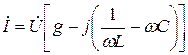 .
.
Условием резонанса токов является равенство индуктивной и емкостной проводимостей:
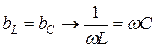 .
.
Векторная диаграмма для режима резонанса представлена на рис. 6.8. При равенстве индуктивной и емкостной проводимостей будут равны и токи 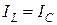 . Направленные в противофазе, эти токи компенсируют друг друга, в цепи остается только активная составляющая тока, и общий ток будет совпадать по фазе с напряжением
. Направленные в противофазе, эти токи компенсируют друг друга, в цепи остается только активная составляющая тока, и общий ток будет совпадать по фазе с напряжением 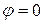 . Поэтому резонанс называют резонансом токов.
. Поэтому резонанс называют резонансом токов.
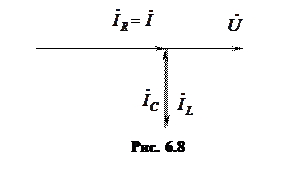 Общий ток в цепи можно представить как
Общий ток в цепи можно представить как 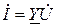 ,
,
где 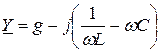 – полная комплексная проводимость, модуль которой равен
– полная комплексная проводимость, модуль которой равен
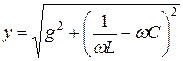 .
.
С учетом условия резонанса, получим, что 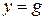 , то есть проводимость цепи минимальна, следовательно, и ток будет минимальным – это признак резонанса токов.
, то есть проводимость цепи минимальна, следовательно, и ток будет минимальным – это признак резонанса токов.
Из условия резонанса получим выражение для резонансной частоты
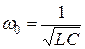 .
.
То есть, как и при резонансе напряжений, добиться резонанса токов можно, изменяя один из трех параметров ω, L, C.
Резонанс в реальной цепи
Реальная катушка и реальный конденсатор обладают не только реактивным, но и активным сопротивлением. Катушка – сопротивлением обмотки, конденсатор – сопротивлением токам утечки. В этом случае при большой добротности катушки или конденсатора активное сопротивление может оказаться функцией частоты.
Под добротностью катушки будем понимать отношение её индуктивного сопротивления к активному.
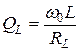 .
.
Под добротностью конденсатора – отношение его емкостного сопротивления к активному
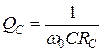 .
.
Рассмотрим цепь, содержащую реальные катушку и конденсатор, представленную на рис. 6.9.
Условием резонанса токов в такой цепи является равенство нулю реактивной проводимости 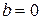 .
.
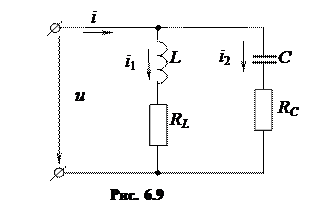 |
Комплексную проводимость цепи можно выразить через комплексные сопротивления ветвей:
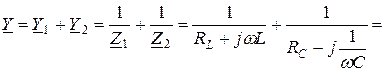
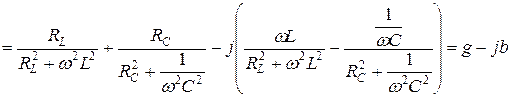 .
.
При резонансе b=0, то есть
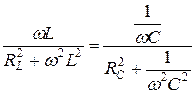 . (6.1)
. (6.1)
Из полученного выражения видно, что в отличие от идеальной цепи резонанс можно получить, регулируя не три параметра, а пять: 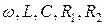 .
.
Решая уравнение (6.1) относительно частоты, получим выражение для резонансной частоты
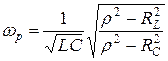 ,
,
Рассмотрим частные случаи:
1. 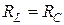 , тогда резонансная частота будет равна
, тогда резонансная частота будет равна 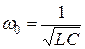 , как и в случае идеальной цепи.
, как и в случае идеальной цепи.
2. 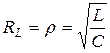 , тогда при любом значении частоты реактивная проводимость равна нулю, то есть резонанс имеет место при любой частоте.
, тогда при любом значении частоты реактивная проводимость равна нулю, то есть резонанс имеет место при любой частоте.
3. 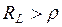 ,
, 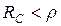 – добротность невелика, тогда выражение под корнем отрицательно. Резонансная частота мнимая, резонанс невозможен.
– добротность невелика, тогда выражение под корнем отрицательно. Резонансная частота мнимая, резонанс невозможен.
При резонансе в реальной цепи, так же, как и в идеальной, ток минимален и имеет чисто активный характер.
Векторная диаграмма для режима резонанса представлена на рис. 6.10.
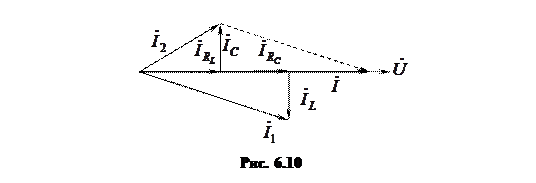 |
Из диаграммы видно, что токи в ветвях, содержащих катушку и конденсатор, различны, но равны их реактивные составляющие.
Контрольные вопросы и задания
1. Какой режим работы электрической цепи называют резонансом?
2. В каких цепях возможен резонанс напряжений?
3. Что является условием и признаком резонанса напряжений?
4. Поясните, какова природа резонанса напряжений.
5. Какой характер электрической цепи называют активно-индуктивным, активно-емкостным?
6. Как по векторной диаграмме определить характер электрической цепи?
7. Что называют волновым сопротивлением контура?
8. Что называют добротностью контура?
9. На какие свойства контура влияет добротность?
10. Что называется полосой пропускания?
11. В каких цепях возможен резонанс токов?
12. Что является условием и признаком резонанса токов?
13. Поясните природу резонанса токов.
14. Чем отличается резонанс токов в идеальной и реальной цепях?
15. Что называется добротностью катушки, конденсатора?
16. Какие частные случаи могут иметь место при резонансе в реальной электрической цепи?
17. Какие энергетические соотношения справедливы при резонансе?

