Момент силы относительно точки — презентация онлайн
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Момент силы относительно точки.
МГТУ им. Н.Э.Баумана
Алгебраическим моментом силы относительно точки называется скалярная величина, равная
произведению модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус.
Плечом h силы относительно точки O называется кратчайшее расстояние между этой точкой и линией действия силы.
B
—
+
A
( ´ ) =± h
( ´ ) =± 2∙ △
h
Алгебраический момент не зависит от переноса силы вдоль ее линии действия.

O
Векторным моментом силы относительно точки называется вектор, приложенный в этой точке, по модулю равный
произведению силы на плечо, относительно моментной точки, перпендикулярный плоскости, проходящей через моментную
точку и силу, и направленный так, что с конца этого вектора видим вращение относительно моментной точки против часовой
стрелки.
B
z
A
´
´ ( ´ )
x
´
´ (
´ )|=±2 ∙ △
|
h
O
´ ( ´ ) = ´ × ´
´ (
´ )|=± h
|
y
2. Момент силы относительно оси.
МГТУ им. Н.Э.Баумана
Моментом силы относительно оси называется алгебраический момент проекции этой силы на плоскость,
перпендикулярную оси, вычисленный относительно точки пересечения оси с этой плоскостью.
B
z
´ ) ¿ ( ´ ) =± h
(
´ ) =± 2 ∙
(
△
′
A
′
z
:
h
B
´
′
1) Сила параллельна оси;
=0
O
z
´
2) Линия действия силы пересекает
ось
=0
O
´
Таким образом, сила не создает момент относительно оси, если сила и ось
расположены в одной плоскости.

O
´
3. Момент силы относительно оси.
МГТУ им. Н.Э.Баумана
Теорема. Момент силы относительно оси равен проекции на эту ось векторного момента силы,
вычисленного относительно произвольной точки на данной оси.
´ ) =2 ∙ △
(
′
B
z
´
1
A
O1
( ´ ¿ ¿ ) ¿
´ (
´ )|=±2 ∙ △
|
| ´ ( ´ )|=± 2 ∙ △
´ 1) ¿
´ 1( ¿¿
1
′
′
B
Угол между соответствующими плоскостями есть угол
между перпендикулярами к ним.
´
O
1
;
△ = △ 1
′
1
´ ) =|
´ (
´ )| =|
´ ( ´ )| 1
(
1
Знак определяется знаком .
´
´ ´
´ ( ´ ) = ´ × ´ = =´ ( − ) + ´ ( − )+ ´ ( − )
|
′
|
Формулы для вычисления моментов относительно осей:
( ´ ) = − ; ( ´ ) = − ; ( ´ ) − .
4. Сложение параллельных сил.
´ 1 ↑↑´2
1¿
D
´ ′ 1
´ ′ 2
L
E
K
МГТУ им. Н.Э.
Баумана
;
´ ′ 2
M
;
´ 2+ ´ 2 =
´2
;
;
´ ′ 1+ ´ ′ 2= ´ ∗
( ´ ′ ¿¿1, ´ ′ 2) 0;¿
´ ´ 2) ( ¿¿1,
´ ´ 2 , ´ 1 , ´ 2)¿¿( ¿¿1,
´ ´ 2 )¿
( ¿¿1,
´∗
( ´ ′¿¿1, ´ ′ 2 , ´ ′1 , ´ ′ 2)¿( ´ ′¿¿1, ´ ′ 2)¿
´ ′ 1
Из подобия треугольников DEK, DAC и DLM, DCB:
´ 1 A
C
B
´ 2
′1 ′2 ⇒ = =
= ;
=
2 1 ∗
′ 1 ′ 2
Таким образом, две параллельные силы, направленные в
´2 ´
одну сторону, имеют равнодействующую, параллельную
2
им, по модулю равную сумме их модулей и направленную
в ту же сторону.
Верно и обратное: силу можно разложить на две параллельные силы,
направленные в ту же сторону, бесконечным числом способов.
´
´ 1 1
´∗
´ = ´ 1+
´ 2;
´ ↑↑ ´ 1 ↑ ↑ ´ 2
5. Сложение параллельных сил. Пара сил.
´ 1 ↓↑ ´ 2 ; 1 ≠ 22¿
Разложим силу на две параллельные и
´2
A
C
;
B
d
( ´ ′¿¿2, ´ 2) 0¿
∗
= 1 − 2
= =
2 1 ∗
Таким образом, две параллельные силы, направленные в
противоположные стороны и не равные по модулю, имеют
равнодействующую, параллельную им, по модулю равную
разности их модулей и направленную в сторону большей силы.
´1
3 ¿ ´ 1 ↓ ↑ ´ 2 ; 1= 2
;
∗
´
´∗
( ¿¿1,
´ 2) ( ´ 2 , ´ ′ 2 , ´ )¿
´ ′2
´∗
´1
МГТУ им. Н.Э.
Баумана
Пара сил – система двух равных по модулю параллельных сил, направленных в противоположные
стороны и не направленные вдоль одной прямой.
´2
Кратчайшее расстояние d между линиями действия сил пары называется плечом пары.

Плоскость, в которой расположены силы пары, называется плоскостью пары.
Действие пары сил на тело характеризуется моментом пары
´ 1,
´ 2 ) =± 1
(
6. Эквивалентность пар.
МГТУ им. Н.Э.Баумана
Теорема. Не изменяя действия пары сил на тело, ее можно переносить куда угодно в плоскости действия,
изменять силы и плечо, сохраняя неизменным модуль и направление момента пары сил.
´ 1,
´ 2)
(
´1
;
´ ′ 1=− ´ ′ 2 ;
´2
A
´ 2= ´ ′ 2 + ´ } rsub {2¿
´ rsub {1} =− {acute { } 2 ;
}
( }´ rsub {1} , {acute { } ¿¿2) 0¿
B
´ ′1 ,
´ ′2)
(
´ 1 ´
′1
}´ rsub {1¿ 1
( ´ 1 , ´ 2 ) =2 ∙ △
( ´ ′1 , ´ ′ 2 )=2∙ △
1
2
1
2
´ ′2
2
}´ rsub {2¿ △ 1 2= △ 1 –2 общее основание и равные высоты
( ´ 1 , ´ 2 ) = ( ´ ′ 1 , ´ ′ 2 )
Направления моментов совпадают.
7. Перенос пары в параллельную плоскость.
Теорема. Действие пары сил на тело не изменится, если эту пару перенести в параллельную плоскость.
¿¿ ¿¿
´
B 2
´ ′ 1= ´ 1 ;
´ ′ 2= ´ 2 ;
´1
A
´1
´2
B’
}´ rsub {2¿
´ ′ 1 A’
´ ′2
}´ rsub {1¿
´ 1=−
´ 2;
МГТУ им. Н.Э.
Баумана
8. Векторный момент пары сил.
МГТУ им. Н.Э.Баумана
Векторным моментом пары сил называется вектор, перпендикулярный плоскости пары, направленный в
ту сторону, откуда пара стремится повернуть тело против часовой стрелки и численно равный
произведению силы пары на ее плечо.
´ 1 =− ´ 2
´1
A
B
´
´
O
´2
Таким образом, векторный момент пары равен векторному
моменту одной из сил пары, вычисленному относительно точки
приложения второй силы.
Т.к. точка О произвольна, то можно считать векторный
момент приложенным в любой точке, т.е. векторный
момент пары сил есть свободный вектор.
Две пары сил, действующие на твердое тело, эквивалентны, если они имеют
одинаковые по модулю и направлению векторные моменты.
9.
 Сложение пар сил. Теорема. Две пары, действующие на твердое тело и лежащие в пересекающихся плоскостях, можно
Сложение пар сил. Теорема. Две пары, действующие на твердое тело и лежащие в пересекающихся плоскостях, можнозаменить одной эквивалентной парой, векторный момент которой равен сумме векторных моментов
исходных пар.
Приведем обе пары к одному плечу АВ, расположенному на
линии пересечения плоскостей.
´′
´
´ 1
A
´ ′2
B
´ ′1
´ 2
´1
´2
´ ′ 1+
´ ′ 2=
´′
;
´ (
´ ,
´ × =
´
´ × ( ´ 1+
´ 2 ) =
´ ×
´ 1 +
´ ×
´2
´ (
´ ,
´ 1 )=
´ (
´ 1,
´ ′1 ) +
´ (
´ 2,
´ ′2 )
В общем случае:
´ ∑
´
=
=1
Условия равновесия системы пар сил:
´
МГТУ им. Н.Э.
Баумана
{
=∑ =0
=1
´ ∑
´ =0 ⇒ = ∑ =0
=
=1
=1
= ∑ =0
=1
English Русский Правила
Момент силы относительно точки
В механике существует понятие о моменте силы относительно точки.
Моментом силы относительно точки называется взятое со знаком ( плюс или минус) произведение модуля силы на кратчайшее расстояние от точки до линии действия силы (рис.
М0( )= ±P h.
Точка О, относительно которой берется момент силы, называется центром момента; ОВ = h—кратчайшее расстояние от центра момента до линии действия силы — называется плечом силы относительно данной точки; знак плюс ставится в случае, если сила стремится повернуть плечо h против хода часовой стрелки, а знак минус — в противоположном направлении. Момент силы относительно точки О на рис. 12 положительный.
Из последнего равенства следует, что при
 Момент силы, как и момент пары, измеряют в ньютонометрах.
Момент силы, как и момент пары, измеряют в ньютонометрах.
Рис.12. Момент силы относительно точки O.
1.12. Уравнения равновесия плоской системы параллельных сил
Пусть к данному телу приложена система параллельных сил , , , , (рис. 13). Через произвольную точку О, взятую в плоскости действия сил, проведем ось Ох, перпендикулярную силам, и ось Оу, параллельную этим силам. Запишем для данной системы сил уравнения равновесия
Рис.13. Система параллельных сил.
Каждая сила перпендикулярна оси Ох, и ее проекция на эту ось равна нулю. Следовательно, первое уравнение обращается в тождество 0 = 0 и выполняется независимо от того, уравновешиваются силы или нет. Таким образом, для плоской системы параллельных сил остается только два уравнения равновесия, причем на ось
Система уравнений равновесия для плоской системы параллельных сил принимает вид
Уравнения равновесия для плоской системы параллельных сил можно записывать в виде
Точки А и В –произвольные точки , предпочтительно их взять на оси
Итак, для произвольной плоской системы сил мы имеем три уравнения равновесия, а для плоской системы параллельных сил только два уравнения равновесия. Соответственно при решении задач на равновесие произвольной плоской системы сил можно найти три неизвестных, а при рассмотрении равновесия плоской системы параллельных сил — не более двух.
Если количество неизвестных превышает число уравнений статики, задача становится статически неопределимой.
1.13. Типы опор балок
В машинах и сооружениях очень часто встречаются тела удлиненной формы, называемые балками.
· Подвижная шарнирная опора (рис. 14, а). Такая опора не препятствует вращению конца балки и его перемещению вдоль плоскости качения. В ней может возникать только одна реакция, которая перпендикулярна плоскости качения и проходит через центр катка.
Схематическое изображение подвижной шарнирной опоры дано на рис. 14, б.
Рис. 14. Типы опор балок.
Подвижные опоры дают возможность балке беспрепятственно изменять свою длину при изменении температуры и тем самым устраняют возможность появления температурных напряжений.
· Неподвижная шарнирная опора (рис. 14, в). Такая опора допускает вращение конца балки, но устраняет поступательное перемещение ее в любом направлении Возникающую в ней реакцию можно разложить на две составляющие — горизонтальную и вертикальную
·Жесткая заделка, или защемление (рис.
Балка с одним заделанным концом называется консольной балкойили просто консолью.
Если опорные реакции могут быть найдены из одних уравнений статики, то балки называют статически определимыми.Если же число неизвестных опорных реакций больше, чем число уравнений статики, возможных для данной задачи, то балки называют
Пример.
Определить неизвестные параметры реакций опор А и В для заданной (рис.15 ) конструкции балки, нагруженной параллельными силами и .
· Записываем уравнение равновесия балки как сумму моментов всех сил относительно опоры А.
Рис.15. Расчетная схема балки.
= RB*8 –P2*5 — P1*3 =0,
Откуда RB = = = 525Н.
· Записываем уравнение равновесия балки как сумму моментов всех сил относительно опоры В.
=-RA*8 +Р1*(8-3) +Р2*(8-5)=0,
Откуда RA = = = 475Н.
· Проверка правильности вычислений
Сумма проекций всех сил на ось Y должна равняться нулю.
= RA –Р1 –Р2 + RB=475 -400-600+525 =0
Дата добавления: 2016-10-26; просмотров: 2702; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА, ТОЧКИ И ОСИ
В дальнейшем «центром» будем называть точку в пространстве, а
«точкой» – точку на плоскости.
Момент силы относительно центра
– векторная величина, равная векторному произведению радиуса-вектора, проведен- ного из этого центра в точку приложения силы, на вектор силы:
M O (P )= r ´ P .
Рисунок 3.1
Вектор
M O (P )
(рисунок 3.1) приложен
в центре O и направлен перпендикулярно плоскости OAB , в такую сторону, чтобы, смотря ему навстречу, видеть силу
По модулю момент силы P относительно центра O будет равен:
где h – плечо, м.
M O (P )= r ´ P
= r Psin (r , P )= P r sina = P h ,
Размерность момента силы [H × м].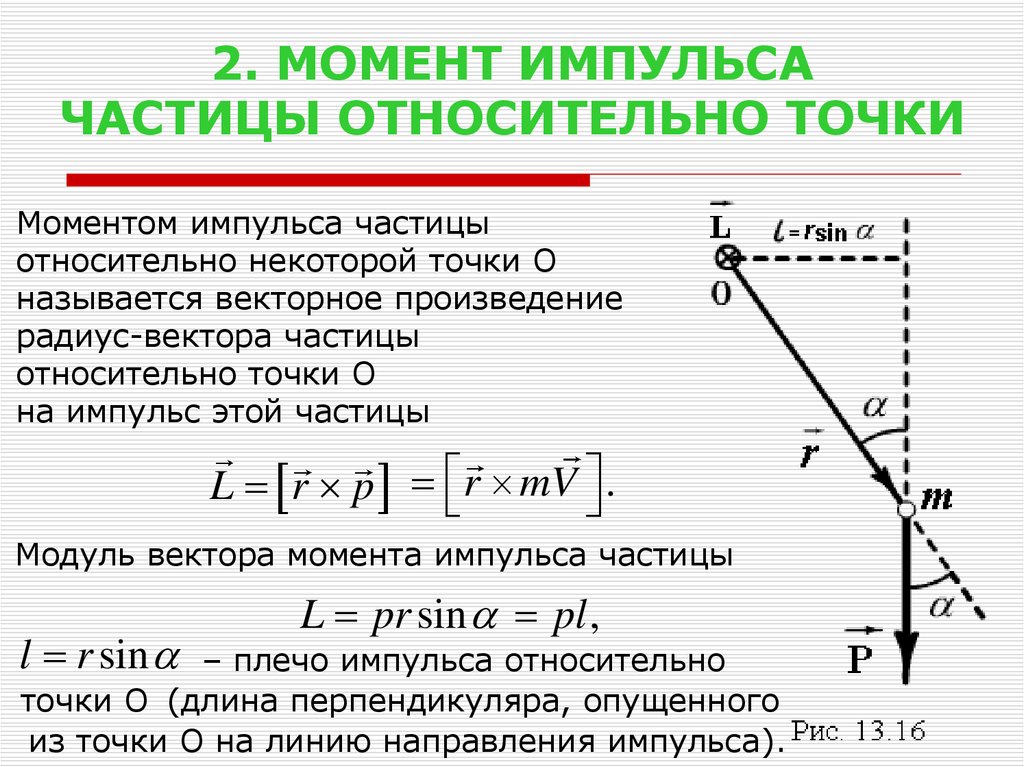
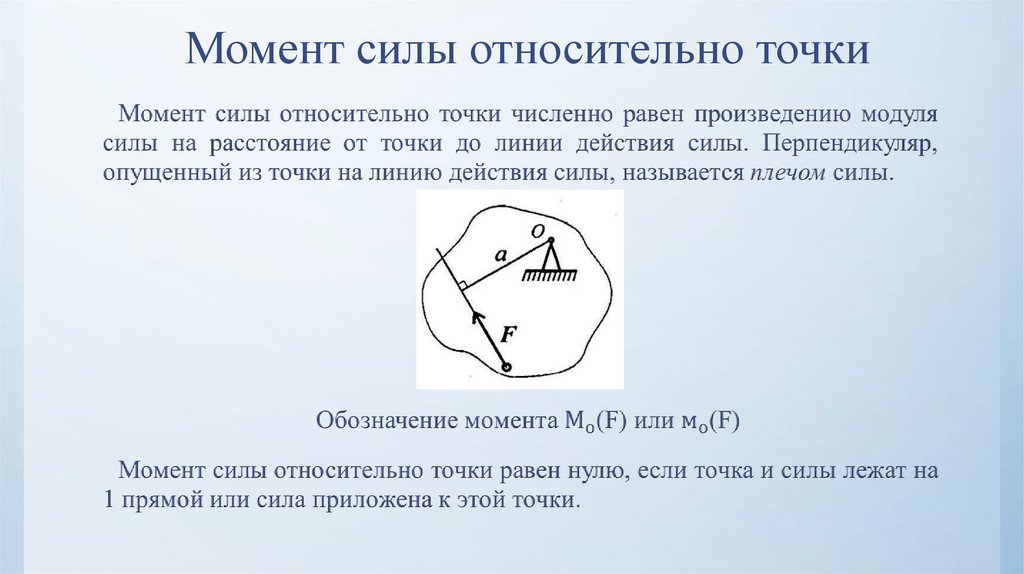
Момент силы относительно точки – произведение модуля силы на
плечо:
M A (P )= ±Ph
– момент силы P относительно точки A .
Плечом ( h ) называется кратчайшее расстояние от точки (полюса), относительно которой определяем момент, до линии действия силы.
Момент силы считается положительным « + », если мы условно видим обход заданного вектора силы P вокруг полюса (точки A ) против хода часовой стрелки, и отрицательным « » – если по ходу часовой стрелки.
| Рисунок 3.2 | Пример. Определить моменты сил P1 и P2 относи- тельно точки A (рисунок 3.2). M A (P1 )= P1h1 ; M A (P2 )= —P2h2 . |
Свойства момента силы относительно точки (центра):
1) значение момента силы не изменится, если силу переместить вдоль линии ее действия в любую точку;
2) момент силы относительно точки (центра) равен нулю, если линия действия силы проходит через полюс.
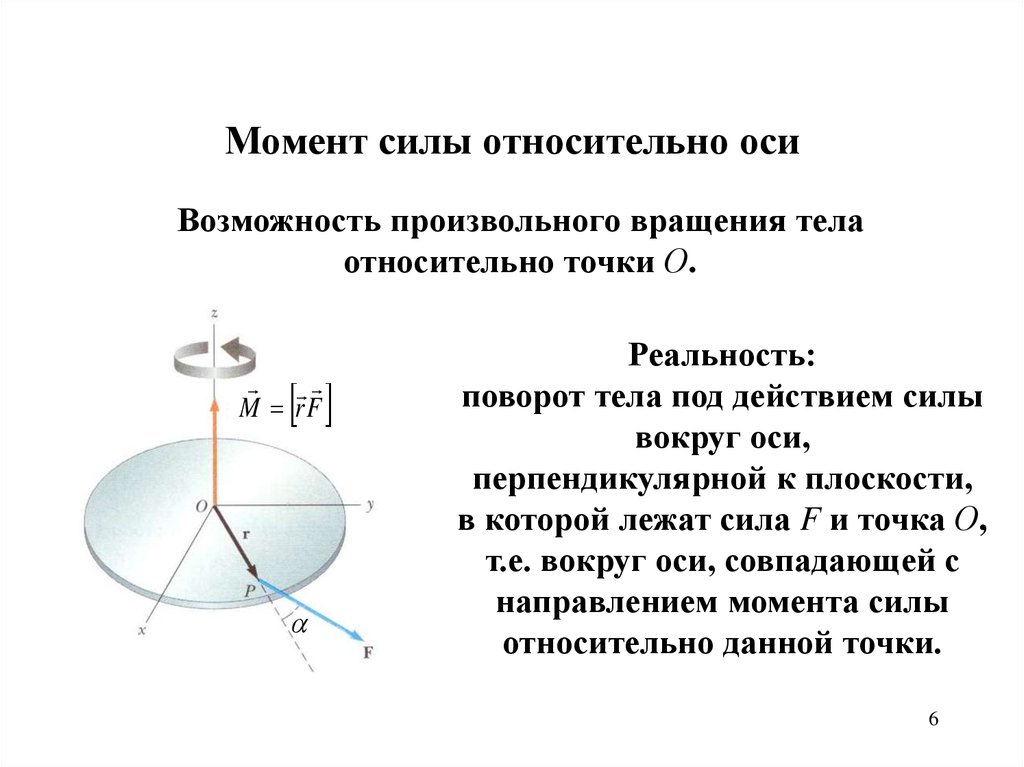
Момент силы относительно оси (рисунок 3.3). Чтобы найти момент
силы P относительно оси z , необходимо спроецировать силу на плоскость p (плоскость вращения), перпендикулярную оси вращения z , и
найти момент полученной проекции P1
Рисунок 3.3
относительно точки O пересечения оси с плоскостью.
Момент силы относительно оси – произведение модуля проекции
P1 силы P на плоскость p , перпендикулярную оси z , на ее плечо h ,
относительно точки O пересечения оси с плоскостью:
M z = P1h .
Момент силы относительно оси равен нулю, когда:
1) линия действия силы параллельна оси, относительно которой определяется момент силы;
2) линия действия силы пресекает ось, относительно которой определяется момент силы;
т. е. момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости.
е. момент силы относительно оси равен нулю, когда сила и ось лежат в одной плоскости.
Теорема Вариньона о моменте равнодействующей
Момент равнодействующей системы сил относительно какого-либо центра равняется геометрической сумме моментов сил, составляющих эту систему, относительно того же центра:
M O (R )= åM O (P i )
– относительно центра O .
Момент равнодействующей системы сил относительно точки или оси равен алгебраической сумме моментов сил, составляющих эту систему, относительно той же точки или оси:
M A (R )= åM A (P i ) – относительно точки A ;
M x (R )= åM x (P i )
– относительно оси x .
Пример (рисунок 3.4). Пусть к телу приложена сила P . Определить момент этой силы относительно точки A .
Момент силы P относительно точки A
будет равен:
Рисунок 3. 4
4
Так как
M A (P )= r ´ P .
P = P x + P y , то
M A (P)= r ´ P x + r ´ P y .
По модулю момент силы P относительно точки A будет равен:
M A (P )= —P × l .
Если силу P разложить на составляющие, то момент этой силы относительно точки A будет равен алгебраической сумме моментов этих составляющих относительно той же точки:
M A (P)= —P x × h + P y × d = —P cosa × h + Psina × d .
Уравнение линии действия равнодействующей плоской системы сил
Пусть равнодействующая R плоской системы сил приложена в точке A (рисунок 3.5). Вектор R расположен таким
образом, что его проекции
R x и R y на
Рисунок 3. 5
5
координатные оси x и y направлены в стороны положительных направлений соответствующих осей.
Согласно теореме Вариньона:
M O (R )= R y x — R x y ; (3.1)
R y x — R x y — M O (R )= 0 . (3.2) Уравнение (3.2) есть уравнение линии действия равнодействующей.
Пример. Определить уравнение линии действия равнодействующей R плоской
сходящейся системы сил (P1, P2 , P3 , P4 ),
приложенных в точке A (рисунок 3.6), если
P1 =10 Н ,
P = 8 Н ,
P3 =18 Н ,
P =14 Н ,
Рисунок 3.6
a = 3 м , b = 4 м .
Сначала определяем проекции равно- действующей на координатные оси:
R x = åP i x = P1 — P3 =10 -18 = -8 Н ;
R y = åP i y = —P2 + P4 = -8 +14 = 6 Н .
Далее определяем сумму моментов всех сил относительно произволь- ной точки, например, относительно начала координат (точки O ):
åM O (P i )= —P1b — P2a + P3b + P4a ;
åM O (P i )= -10 × 4 — 8× 3 +18× 4 +14 × 3 = 50 Н × м .
Так как
åM O (P i )= M O (R ), согласно формуле (3.1), получим:
åM O (P i )= R y x — R x y ;
50 = 6x — (-8) y ;
6x + 8y — 50 = 0 ;
3x + 4y — 25 = 0 . (3.3)
Таким образом, получили уравнение (3.3) линии действия равнодействующей R , которая находится на расстоянии d от моментной точки O :
M O (R )
d .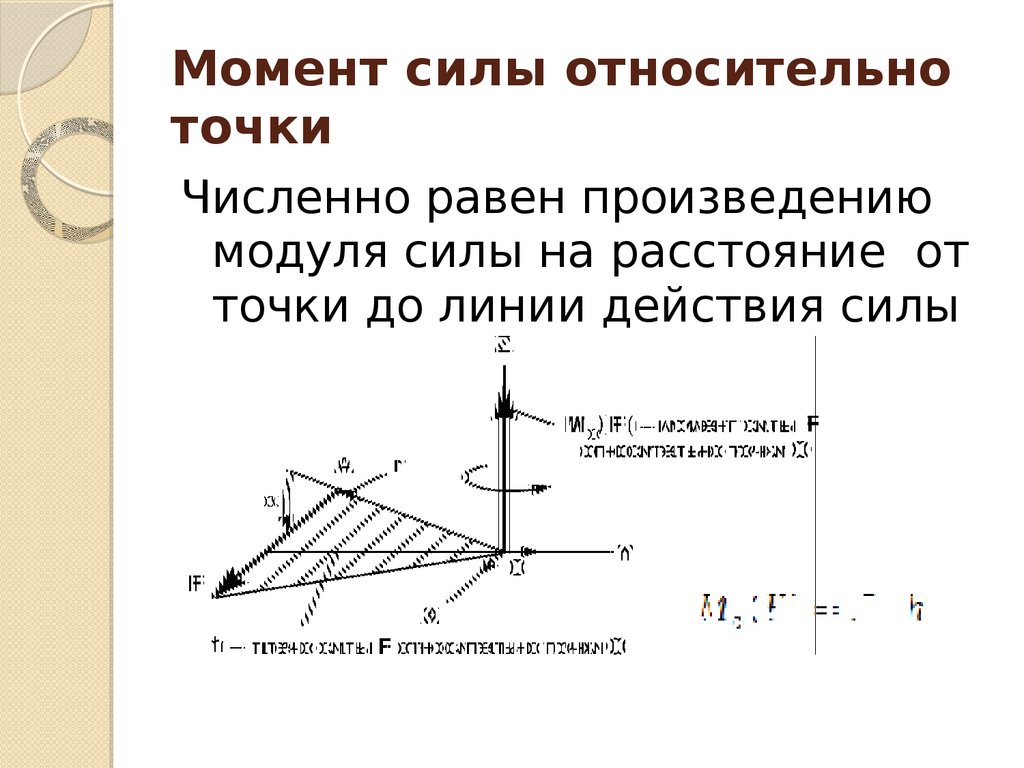
R
По величине сила R будет равна:
R = = = 10 Н .
Тогда кратчайшее расстояние d от моментной точки O до линии
действия силы R составит:
|
M O (R ) 50
d 5 м
R 10
ТЕОРИЯ ПАР СИЛ
Сложение двух параллельных сил
Равнодействующая R двух параллельных сил
P1 и
P2 одного направления (рисунок 4. 1) имеет такое же
1) имеет такое же
Рисунок 4.1
направление, а ее модуль равен алгебраической сумме модулей слагаемых сил:
R = P1 + P2 .
Точка C приложения равнодействующей делит отрезок AB на части обратно пропорциональные модулям сил:
AC = P2 .
BC P1
По свойству пропорций:
P1
= P2 =
P1 + P2
BC AC BC + AC
Откуда следует равенство:
P1 = P2
= R . (4.1)
BC AC AB
Равнодействующая R двух параллельных сил
P1 и
P2 противоположного направления (рисунок 4.2) имеет
Рисунок 4.2
направление силы, большей по модулю, и модуль, равный разности модулей этих сил:
R = P1 — P2 .
Точка C приложения равнодействующей лежит на продолжении отрезка AB за точкой приложения большей силы:
P1 = P2
= R . (4.2)
(4.2)
BC AC AB
Пара сил. Момент пары сил
Пара сил – совокупность двух равных по модулю параллельных сил, направленных в противоположные стороны (рисунок 4.3).
Пара сил – это самостоятельный, не
Рисунок 4.3
1) плоскостью действия;
2) направлением вращения;
упрощаемый элемент статики, харак- теризующийся:
3) модулем (величиной) момента пары.
P2 = —P1 ; P1 P2 .
M (P1, P2 )= A B ´ P2 = B A´ P1 ;
M (P1, P2 )= P1h = P2h ,
где h – кратчайшее расстояние между линиями действия сил, состав- ляющих пару, м.
Размерность момента пары сил [H × м].
Момент пары сил (P1, P2 )
изображают вектором M , который
перпендикулярен плоскости действия пары и направлен в ту сторону, откуда видно пару сил стремящуюся вращать плоскость ее действия против хода часовой стрелки.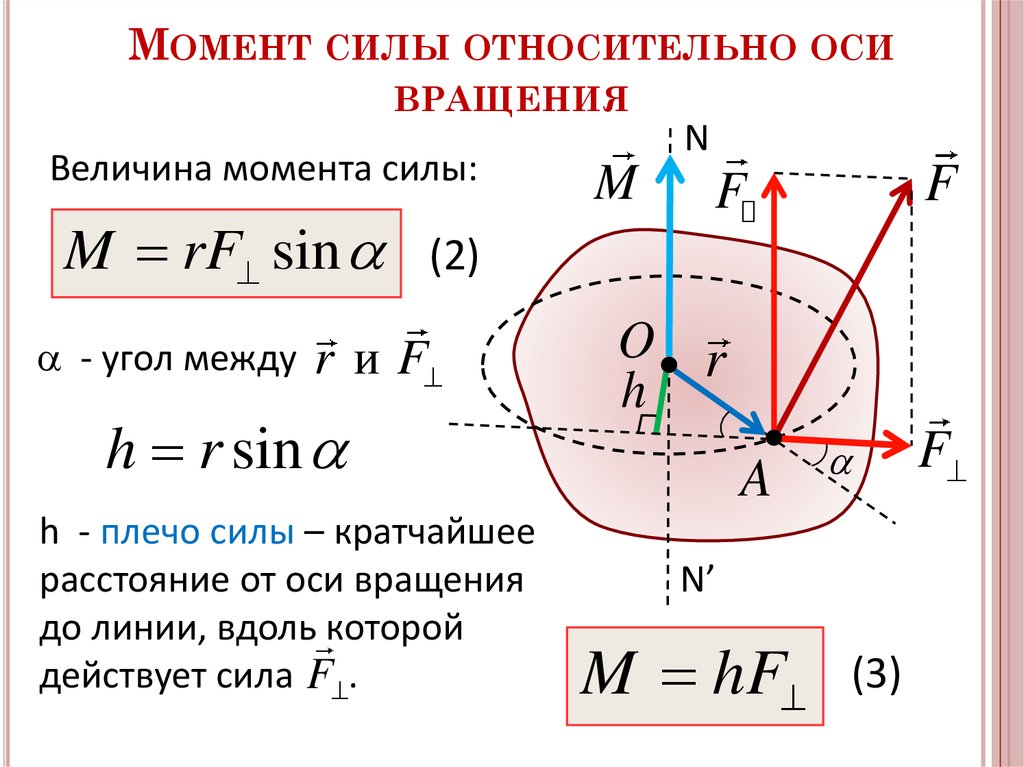
Момент пары сил считается положительным « + », если пара сил
стремится вращать плоскость в сторону противоположную ходу часовой стрелки, и отрицательным « » – если в сторону хода часовой стрелки.
| Момент положителен « + » | Момент отрицателен « – » |
Свойства пар
Проекция пары на любую ось равна нулю, что следует из определения пары сил.
Не изменяя действия пары на твердое тело, пару можно перемещать и поворачивать в плоскости ее действия, переносить в любую плоскость, параллельную плоскости действия пары, а так же изменять ее силы и плечо, сохраняя неизменным модуль и направление момента пары.
Таким образом, момент пары сил, есть вектор свободный, т.е. не имеющий определенной точки приложения.
Сложение пар, лежащих в пересекающихся плоскостях
Заменим сходящиеся силы в точках A и B их равнодействующими (рисунок 4.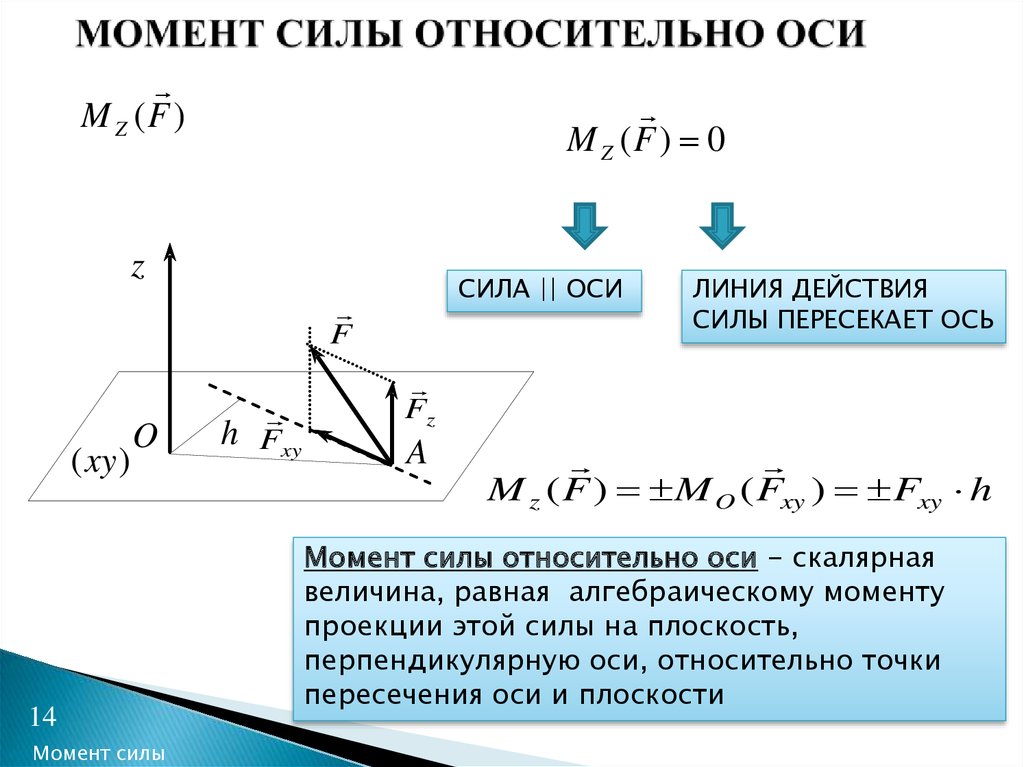 4):
4):
Так как
= и P2
P1 + P2 = R ;
P1¢+ P2¢ = R ¢.
= P2¢ , то
R = R¢ .
M1 (P1, P1¢)= A B ´ P1 ;
M2 (P2 , P2¢)= A B ´ P2 .
Две пары (P1, P1¢) и
Рисунок 4.4
При сложении нескольких пар получим:
M = åM i .
(P2 , P2¢), лежащие в пере- секающихся плоскостях,
можно заменить одной эк- вивалентной парой (R, R¢),
момент которой равен геометрической сумме мо- ментов слагаемых сил:
M = M1 + M2 ;
M = A B ´ P1 + A B ´ P2 .
Если тело под действием системы пар находится в равновесии, то момент результирующей пары равняется нулю:
M = åM i = 0 .
В проекции на оси координат получим:
ìåM i x = 0;
íåM i y = 0;
ïîåM i z = 0.
Если пары расположены в одной плоскости, векторы моментов их будут параллельны. Момент результирующей пары определится как алгебраическая сумма моментов пар:
M = åM i .
СУБХАНКАР 4 СТУДЕНТА: КОНЦЕПЦИЯ МОМЕНТА:
КОНЦЕПЦИЯ МОМЕНТА:
Момент силы (или момент) — это тенденция силы скручивать или вращать объект. Это важное, основное понятие в технике и физике. Момент математически оценивается как произведение силы и плеча момента . Плечо момента — это перпендикулярное расстояние от точки вращения до .0005 линия действия силы. Момент можно рассматривать как меру тенденции силы вызывать вращение вокруг воображаемой оси, проходящей через точку. (Примечание: в машиностроении и гражданском строительстве «момент» и «крутящий момент» имеют разные значения, тогда как в физике они являются синонимами.)
(Примечание: в машиностроении и гражданском строительстве «момент» и «крутящий момент» имеют разные значения, тогда как в физике они являются синонимами.)
Момент силы можно вычислить относительно любой точки, а не только точек, в которых линия действия силы перпендикулярно. На изображении А показаны компоненты, сила F и плечо момента x, когда они перпендикулярны друг другу. Когда сила не перпендикулярна интересующей точке, такой как точка O на изображениях B и C, величина Момента, M вектора F относительно точки O есть
- где
- — вектор из точки О в положение, где применяется величина F .
- × представляет векторное произведение векторов.
[На рисунке момент в точке O, когда компоненты перпендикулярны точке O. Изображение B и изображение C иллюстрируют компоненты момента в точке O, когда компоненты не перпендикулярны точке O . ]
]
В машиностроении (в отличие от физики) термины «крутящий момент» и «момент» не взаимозаменяемы. «Момент» — это общий термин для тенденции одной или нескольких приложенных сил вращать объект вокруг оси (концепция, которая в физике называется крутящим моментом). «Крутящий момент» является частным случаем этого: если сумма векторов приложенных сил равна нулю (т. е. их «результат» равен нулю), то силы называются «парой», а их момент называется «крутящим моментом».
Например, сила вращения на валу, например, вращающейся отвертки, образует пару, поэтому результирующий момент называется «крутящим моментом». Напротив, боковая сила, действующая на балку, создает момент (называемый изгибающим моментом), но, поскольку результирующая сила отлична от нуля, этот изгибающий момент не называется «крутящим моментом».
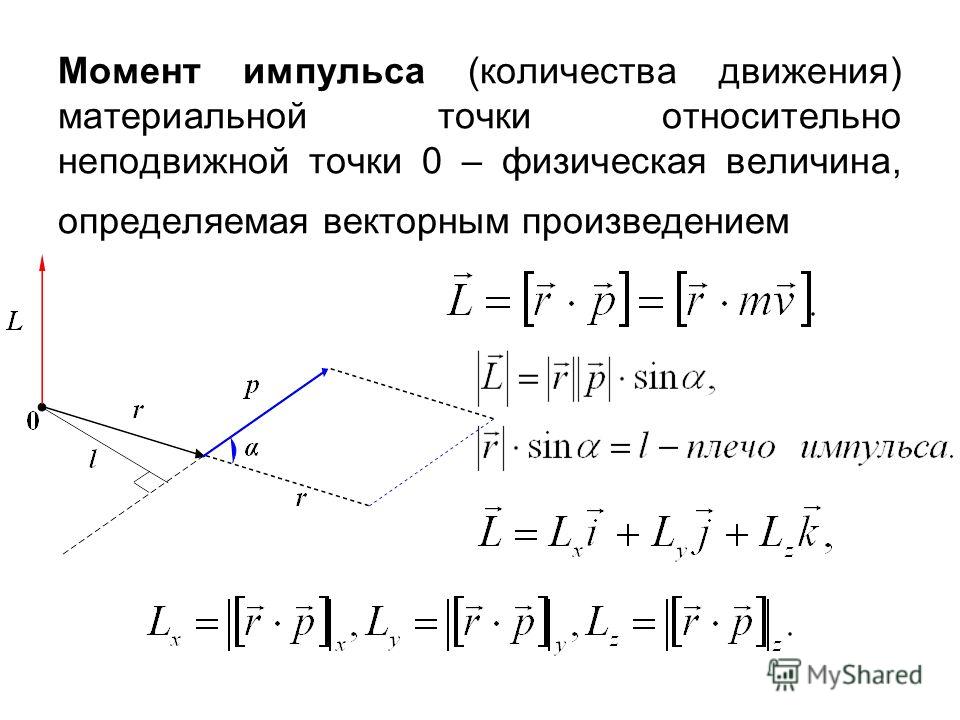
Частица находится в положении r относительно своей оси вращения. Когда к частице приложена сила F, только перпендикулярная составляющая F⊥ создает крутящий момент. Этот крутящий момент τ = r × F имеет величину τ = |r| |Ф⊥| = | г | |Ф| sinθ и направлен наружу от страницы.
Этот крутящий момент τ = r × F имеет величину τ = |r| |Ф⊥| = | г | |Ф| sinθ и направлен наружу от страницы.
A Пара — это система сил с равнодействующей (также известной как чистая или сумма) моментом, но без равнодействующей силы. Другой термин для пары чистый момент . Его эффект заключается в создании вращения без перемещения или, в более общем смысле, без какого-либо ускорения центра масс.
Результирующий момент пары называется крутящим моментом . Его не следует путать с термином крутящий момент, который используется в физике, где он является просто синонимом момента. Вместо этого крутящий момент является частным случаем момента. Крутящий момент имеет особые свойства, которых нет у момента, в частности, свойство не зависеть от точки отсчета.
Простая пара:
Простейшая пара состоит из двух равных и противоположных сил, линии действия которых не совпадают. Это называется «простая пара».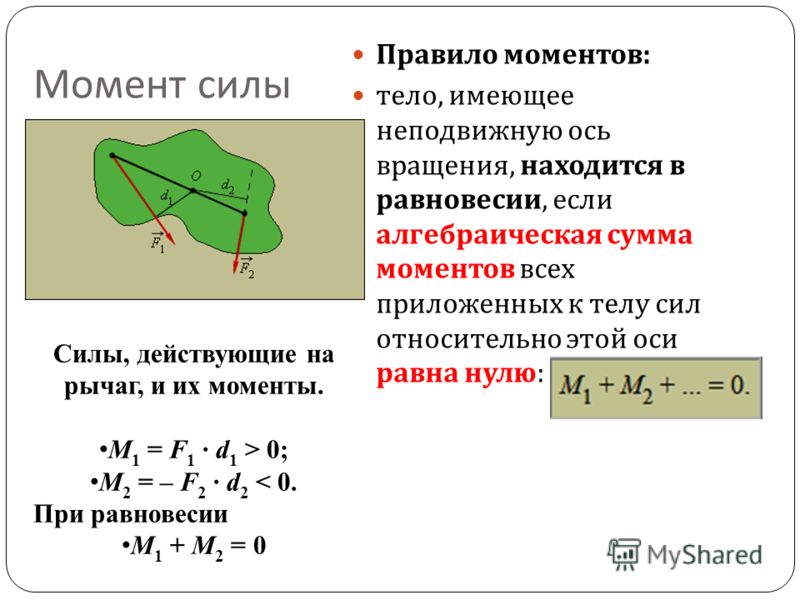 Силы имеют вращательный эффект или момент, называемый крутящим моментом, относительно оси, перпендикулярной плоскости сил. Единицей СИ для крутящего момента пары является ньютон-метр.
Силы имеют вращательный эффект или момент, называемый крутящим моментом, относительно оси, перпендикулярной плоскости сил. Единицей СИ для крутящего момента пары является ньютон-метр.
Если две силы равны F и −F , то величина крутящего момента определяется по следующей формуле:
сил
Величина крутящего момента всегда равна Fd, причем направление крутящего момента задается единичным вектором , который перпендикулярен плоскости, содержащей две силы. Когда d принять за вектор между точками действия сил, то пара представляет собой векторное произведение d и F .
Независимость от точки отсчета:
Момент силы определяется только относительно определенной точки P (говорят «момент о P «), и вообще при изменении P момент меняется. Однако момент (крутящий момент) пары независим от опорной точки P : Любая точка даст один и тот же момент. Другими словами, вектор момента, в отличие от любого другого вектора момента, является «свободным вектором». (Этот факт называется Теорема Вариньона о втором моменте .)
Однако момент (крутящий момент) пары независим от опорной точки P : Любая точка даст один и тот же момент. Другими словами, вектор момента, в отличие от любого другого вектора момента, является «свободным вектором». (Этот факт называется Теорема Вариньона о втором моменте .)
Доказательство этого утверждения следующим образом: Предположим, что существует набор силовых векторов 2 1 , F 2 1 , F 2 1 , F 9015 2 1 , F 9015 2 1 , F 9015 2 1 , F 9000 9015 2 1 , . , с векторами положения (о каком-то начале координат P ) r 1 , r 2 и т. д. соответственно. Момент около P равен
Теперь мы выбираем новую точку отсчета P’ , отличающийся от P вектором r . Новый момент —
Новый момент —
Теперь распределительное свойство перекрестного продукта подразумевает
Однако определение силы силы означает, что
Поэтому
- 9303030
,
- 930
,
- 930
,
. доказывает, что момент не зависит от точки отсчета, что является доказательством того, что пара является свободным вектором.
Подписаться на: Post Comment (Atom)
Q9 Напишите выражение для момента силы относительно заданной оси вращения…
Перейти к
- Объективные вопросы
- Вопросы с короткими/длинными ответами
- Числа
- Иметь значение
- Физические величины и измерения
- Сила и давление
- Энергия
- Световая энергия
- Теплопередача
- Звук
- Электричество
Главная > Селина Солюшнс Класс 8 Физика > Глава 3 — Сила и давление > Упражнение: Вопросы с короткими/длинными ответами > Вопрос 9
Вопрос 9 Вопросы с короткими/длинными ответами
Q9) Напишите выражение для момента силы относительно данной оси вращения.
Ответ:
Решение:
Момент силы относительно данной оси = Сила \умножить перпендикулярное расстояние силы от оси вращения.
Стенограмма видео
Привет, студенты, добро пожаловать в Лидо
Видео с вопросами и ответами от Learning
так вот у нас есть интересный вопрос
и нам нужно
понять концепцию здесь, прежде чем мы
Двигаясь вперед с
выражение, которое я написал
сразу сюда
но мы должны понять концепцию
вот так мы должны написать выражение
за
момент силы относительно заданной оси
вращения, чтобы понять, что сначала мы
должен знать
что мы понимаем под моментом силы?
правильно, момент силы равен
поворотный эффект
силы на тело
так как вы можете видеть здесь, на этой картинке
сюда
есть стержень или ось вращения
так что это ось вращения, где
это колесо вращается
правильно хорошо и
в центре есть стержень
он прикреплен
он не может двигаться в этом направлении, если мы
подать заявление
сила прямо здесь, так что это направление
движение ограничено
он может вращаться только вокруг оси
вращение или вокруг оси сейчас
этот момент силы определяется как
какую бы силу мы ни применяли
на перпендикулярном расстоянии от
вращаться
так что если вот стержень и это
перпендикулярное расстояние больше, чем
сила должна быть приложена
в этом направлении, поэтому максимальный момент
силы будет там, когда сила
прямо перпендикулярно к
расстояние от оси вращения вправо
так это момент силы предположим
мы прикладываем силу в этом направлении.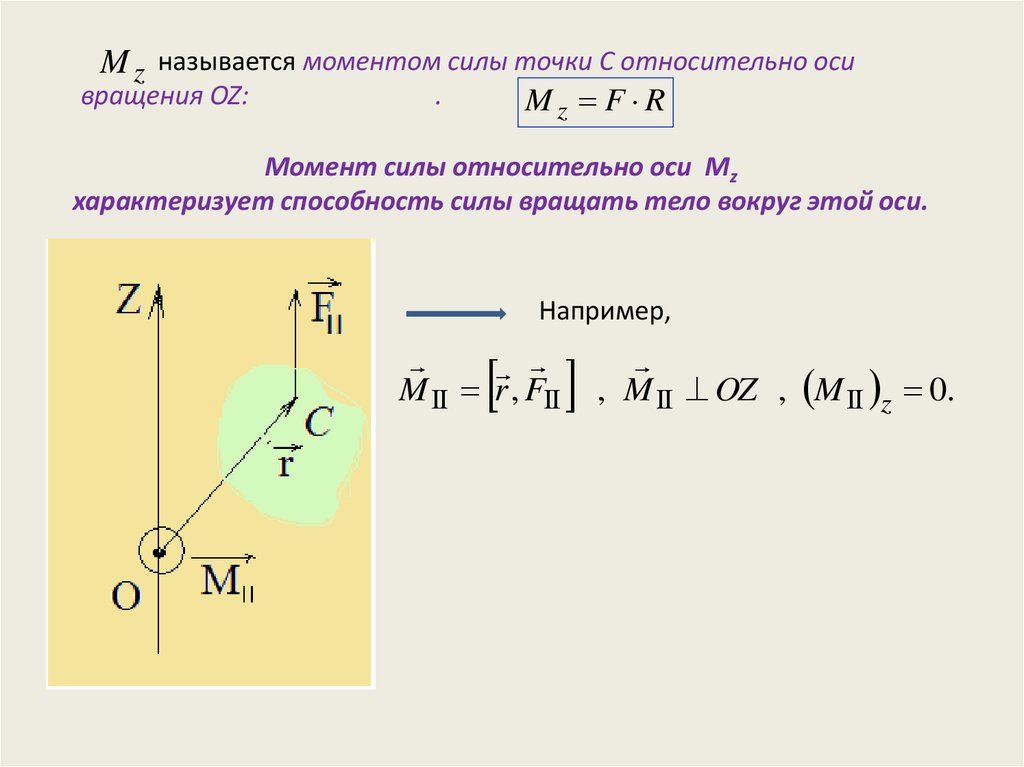 что параллельно этому, то это будет
не вращать
поэтому он должен быть перпендикулярен
направление, которое
этот момент силы также обозначается как
тау
или крутящий момент равен силе в
перпендикулярное расстояние от
точка опоры, это ваша подача
и перпендикулярное расстояние от этого
здесь, так что это будет расстояние
и сила будет в этом направлении
когда вы применяете силу, вы можете применить
сила в этом направлении
так вот как будет момент силы
рассчитывается
единица s i для момента силы равна
равно
ньютон и метр, поэтому ньютон-метр становится
единица си
почему ньютон метр потому что сила ньютон
Единицы силы — ньютон и единица
расстояния составляет метр, поэтому, когда мы объединяем
эти два у нас есть единица si на данный момент
силы
равен ньютон-метру, я надеюсь, что это
пример был простым, если у вас есть
дальнейшие вопросы
пожалуйста, оставьте свои комментарии ниже, спасибо
ты
что параллельно этому, то это будет
не вращать
поэтому он должен быть перпендикулярен
направление, которое
этот момент силы также обозначается как
тау
или крутящий момент равен силе в
перпендикулярное расстояние от
точка опоры, это ваша подача
и перпендикулярное расстояние от этого
здесь, так что это будет расстояние
и сила будет в этом направлении
когда вы применяете силу, вы можете применить
сила в этом направлении
так вот как будет момент силы
рассчитывается
единица s i для момента силы равна
равно
ньютон и метр, поэтому ньютон-метр становится
единица си
почему ньютон метр потому что сила ньютон
Единицы силы — ньютон и единица
расстояния составляет метр, поэтому, когда мы объединяем
эти два у нас есть единица si на данный момент
силы
равен ньютон-метру, я надеюсь, что это
пример был простым, если у вас есть
дальнейшие вопросы
пожалуйста, оставьте свои комментарии ниже, спасибо
ты
Связанные вопросы
Q1) Дайте определение силы. Укажите его единицу СИ.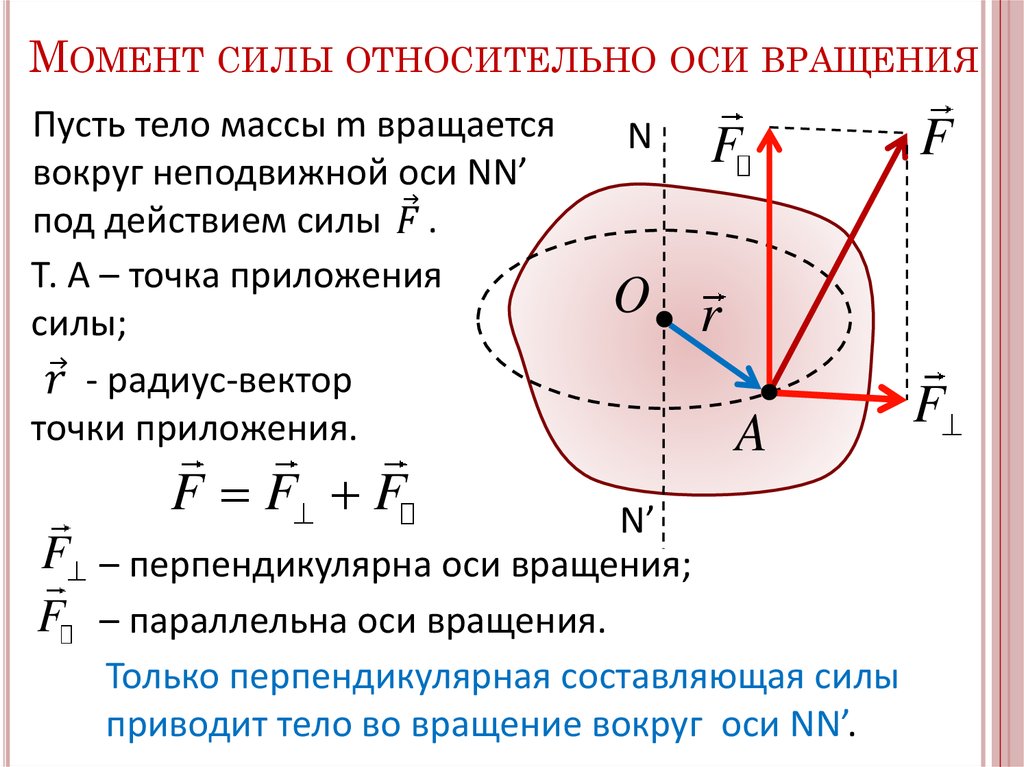
Q2) Назовите два действия силы, приложенной к телу.
В3) Чем отличается действие силы, когда она приложена к (а) твердому телу (б) нетвердому телу?
Q4) Укажите действие силы F на следующей диаграмме.
Q5) Дайте определение термину «момент силы».
Q6) Укажите единицу измерения момента силы в системе СИ.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Exercises
Objective Questions
Short/Long Answer Questions
Numericals
Chapters
Matter
Physical Quantities and Measurement
Force and Pressure
Energy
Light Energy
Heat Transfer
Sound
Электричество
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd Все права защищены
Крутящий момент | bartleby
Что такое крутящий момент?
Крутящий момент — вращательный эквивалент линейной силы в физике и механике.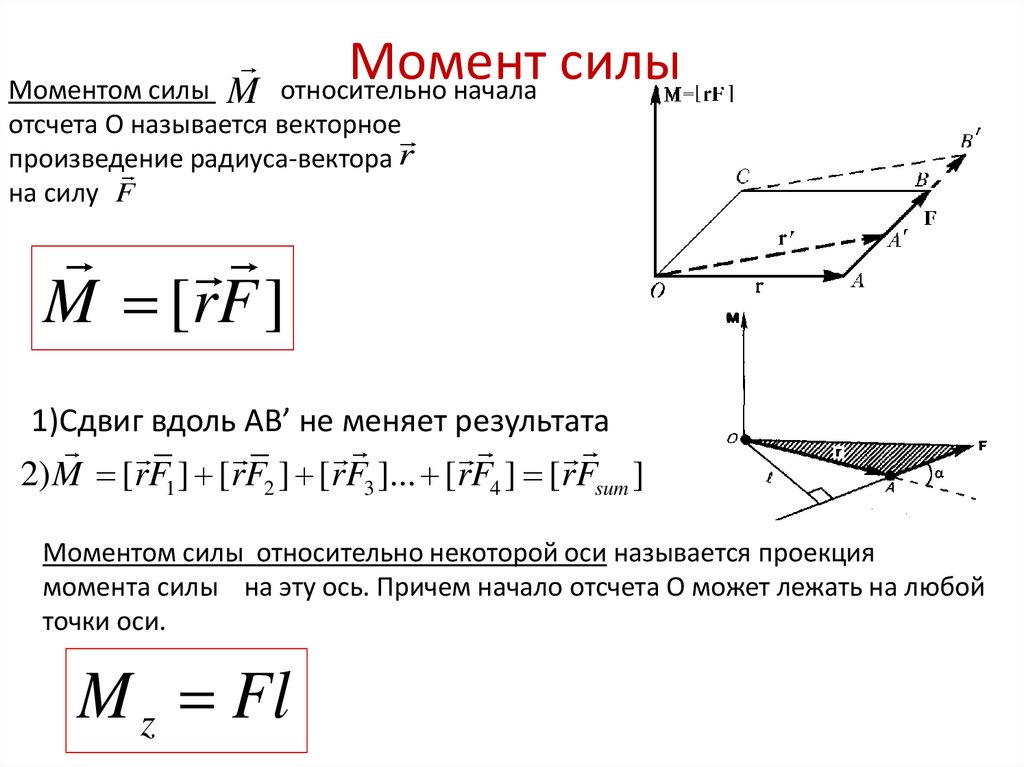 В зависимости от курса обучения он также известен как момент силы, сила вращения или эффект поворота.
В зависимости от курса обучения он также известен как момент силы, сила вращения или эффект поворота.
Крутящий момент — это векторная величина, которая используется для расчета стремления силы произвести вращательный эффект в объекте вокруг некоторой оси. Точка, в которой объект вращается, называется ось вращения . Направление вектора крутящего момента определяется направлением силы на оси.
Формула плеча момента
«Рычаг момента» показан на рисунке справа вместе с векторами r и F, упомянутыми ранее. Проблема с этим определением заключается в том, что оно не указывает направление крутящего момента, а только его величину, что затрудняет его применение в трехмерных случаях. Плечо момента равно расстоянию до центра, когда сила перпендикулярна вектору смещения r, а крутящий момент максимален для данной силы. Формула для расчета величины крутящего момента, вызванного перпендикулярной силой:
τ=(плечо момента)(сила)
Величину крутящего момента можно рассчитать, сначала определив плечо рычага, а затем умножив его на приложенную силу. Перпендикулярное расстояние между осью вращения и линией действия силы определяется как плечо рычага.
Перпендикулярное расстояние между осью вращения и линией действия силы определяется как плечо рычага.
Чтобы рассчитать величину крутящего момента, сначала вычислите плечо рычага, а затем умножьте его на приложенную силу. На основании вышеизложенного можно сделать вывод, что создаваемый крутящий момент пропорционален величине силы и перпендикулярному расстоянию между точкой, относительно которой рассчитывается крутящий момент, и точкой, в которой приложена сила. Направление крутящего момента может быть по часовой стрелке или против часовой стрелки в зависимости от направления приложенной силы. Положительный крутящий момент заставляет объект вращаться против часовой стрелки. Отрицательный крутящий момент вращает объект по часовой стрелке.
В результате крутящий момент математически представляется как:
τ = F.r. sinθ
Где r обозначает длину плеча момента, а θ обозначает угол, образованный вектором силы и плечом момента.
Единицей СИ для крутящего момента является ньютон-метр. Используя правило правой руки, мы можем определить направление вектора крутящего момента. Наш большой палец будет указывать в направлении вектора крутящего момента, если мы укажем наши пальцы в направлении r и согнем их в направлении F.
Используя правило правой руки, мы можем определить направление вектора крутящего момента. Наш большой палец будет указывать в направлении вектора крутящего момента, если мы укажем наши пальцы в направлении r и согнем их в направлении F.
В имперских единицах часто используется фут-фунт. Фунт-сила — это количество силы, с которой гравитация Земли действует на объект весом в один фунт. Величина этих единиц часто аналогична
1 Нм≃1,74 ft⋅lbs
Уравновешенные крутящие моменты
Когда крутящие моменты по обе стороны от точки опоры равны, говорят, что крутящие моменты уравновешены. Типичный пример уравновешенных крутящих моментов — двое детей на качелях. Если точка опоры качелей находится в центре, двое детей должны иметь одинаковую массу, чтобы качели были сбалансированы. Если точка опоры не находится в центре, их массы должны различаться, чтобы создавать равные крутящие моменты.
Типы крутящих моментов
Крутящий момент может быть как статическим, так и динамическим.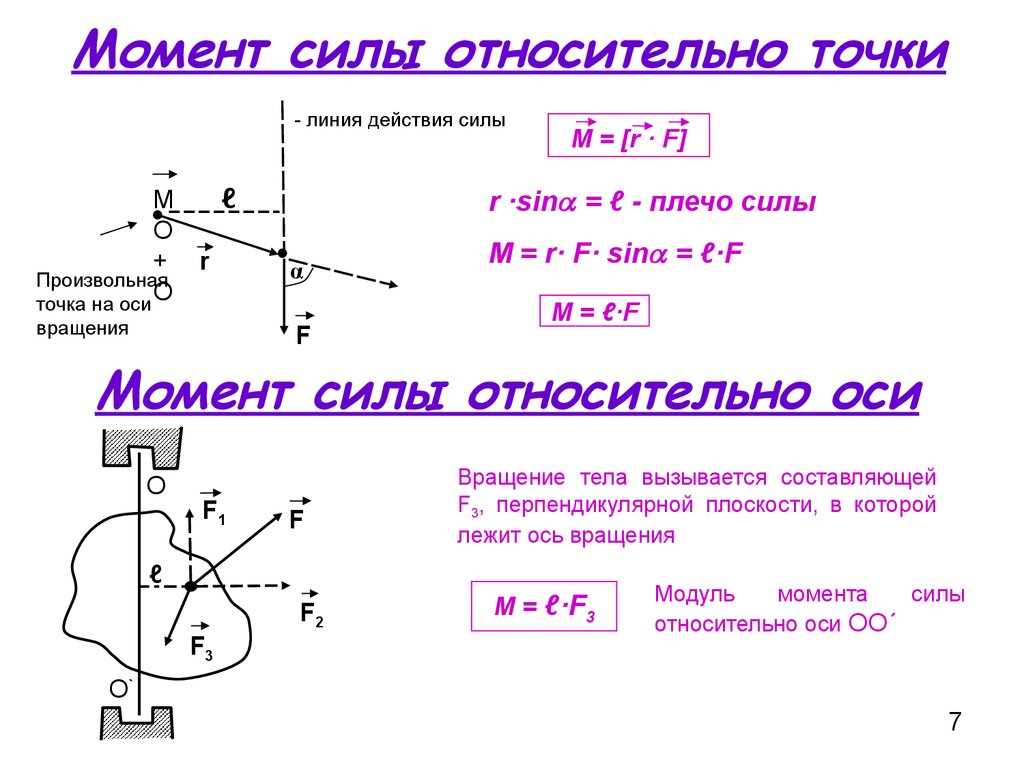 Статический крутящий момент определяется как крутящий момент, который не создает углового ускорения. Вот несколько примеров статического крутящего момента:
Статический крутящий момент определяется как крутящий момент, который не создает углового ускорения. Вот несколько примеров статического крутящего момента:
- Когда человек толкает закрытую дверь, он или она использует статическую дверь, которая не вращается, несмотря на приложенную силу. Поскольку ускорение отсутствует, вращение велосипеда с постоянной скоростью является еще одним примером статического крутящего момента.
- Приводной вал гоночного автомобиля, ускоряющегося от линии старта, создает динамический крутящий момент, поскольку он должен создавать угловое ускорение колес из-за ускорения автомобиля на трассе.
Крутящий момент в кинематике вращения
Для вращательной системы первый закон Ньютона эквивалентен понятию вращательного равновесия. Если на него не действует внешний крутящий момент, объект, который не вращается, остается таковым. Точно так же объект, вращающийся с постоянной угловой скоростью, продолжает вращаться, если на него не действует внешний крутящий момент.
Однако, если известна скорость вращения, мощность можно рассчитать по крутящему моменту. На самом деле мощность двигателя л.с. рассчитывается с использованием измеренного крутящего момента и скорости вращения. Лошадиная сила измеряет общую эффективность двигателя. Крутящий момент — это простое измерение максимальной силы крутящего момента, которую двигатель может создать при интенсивной работе.
Угловой момент
Крутящий момент и угловой момент тесно связаны. Угловой момент, обозначаемый буквой «L», является вращательным аналогом линейного количества движения «p». Это вектор. Угловой момент частицы равен
L = r × p L = rp sinθ
, где θ — угол между r и p.
Связь между угловым моментом и крутящим моментом
Теперь давайте найдем формулу или выражение.
Скорость изменения углового момента во времени = ΔL/ΔT
Сейчас,
ΔL/ΔT = Δ(I ω)/ΔT = I. Δω/ΔT ……. (1)
Здесь я буду константой для конкретного объекта.
Теперь Δω/ΔT (угловая скорость по времени) представляет собой угловое ускорение (α).
Таким образом, из уравнения 1 мы можем написать, ΔL/ΔT = I α……………………(2)
I (момент инерции) является вращательным аналогом массы (инерции). Крутящий момент (τ) относится к моменту силы. τ = r x F = r F sinθ……………. (3)
F — вектор силы, а r — вектор положения
θ — это угол между вектором силы и вектором плеча рычага. «x» определенно обозначает векторное произведение.
τ = r F sin θ = r ma sinθ = r m αr sinθ = mr 2 . αsinθ = I αsinθ = I x α ……………………… (4)
[α — угловое ускорение, I — момент инерции, x — векторное произведение.]
τ= I α( из уравнения 4)
Это означает, что создаваемый крутящий момент зависит от момента инерции и углового ускорения
Таким образом, из уравнения 2 можно получить ΔL/ΔT = τ……………………. (5)
Крутящий момент, без сомнения, скорость изменения углового момента во времени.
Кроме того, τ= I α
или, τ= I (ω 2 -ω 1 )/t [здесь α = угловое ускорение = временная скорость изменения важной угловой скорости = (ω 2 – ω 1 )/t, где ω 2 и ω 1 оказываются конечной и начальной угловыми скоростями, а t — временной интервал]
или, τ t = I (ω 2 -ω 1 ) ……………………(6)
когда τ= 0 (т. е. чистый крутящий момент равен нулю),
е. чистый крутящий момент равен нулю),
I (ω 2 -ω 1 ) = 0
т.е. факт, что угловое ускорение может быть равно нулю. Когда крутящие моменты объекта уравновешиваются, чистый крутящий момент и угловое ускорение равны нулю.
Контекст и приложения
Эта тема важна для профессиональных экзаменов как для студентов, так и для выпускников, особенно для
- 10, 11, 12 стандарт.
- Студенты инженерных специальностей
- Крутящий момент является фактором, влияющим на несколько сложных механизмов, включая электродвигатель, приводящий в действие большинство бытовых приборов. Это особенно важно для работы автомобилей, где он играет ключевую роль в двигателе и трансмиссии.
- Момент трения
- Статическое равновесие
- Псевдовектор
- Трансляционное равновесие
Мы предоставим вам пошаговые решения миллионов задач из учебников.

