Момент сил | это… Что такое Момент сил?

Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.

Момент силы приложенный к гаечному ключу

Отношение между векторами силы, момента силы и импульса во вращающейся системе

Содержание 1 Момент силы 2 Предыстория 3 Единицы 4 Специальные случаи 4.1 Формула момента рычага 4.2 Сила под углом 4.3 Статическое равновесие 4.4 Момент силы как функция от времени 5 Отношение между моментом силы и мощностью 6 Отношение между моментом силы и работой 7 Момент силы относительно точки 8 Момент силы относительно оси 9 Единицы измерения 10 Измерение момента 11 См. также

Момент силы

В физике момент силы можно понимать как «вращающая сила».

В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы!

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус вектор , а проекцию вектора силы на вектор , через угол .

В первом случае, используя теорему Пифагора, можно записать следующее равенство , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть ни что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуля вектора момента силы .

И теперь полная работа записывается очень просто или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, τ — вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

τ = МОМЕНТ РЫЧАГА * СИЛУ

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ

Сила под углом

Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.

Момент силы как функция от времени

Момент силы — производная по времени от момент импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ СИЛЫ * *

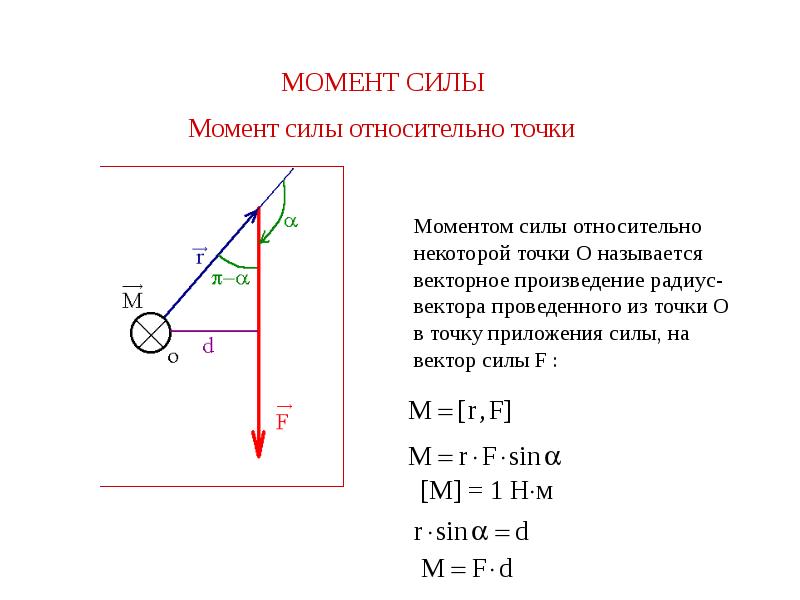
Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющий точки

O и O_F, на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

См. также

• Момент инерции
• Момент импульса
• Теорема Вариньона

Момент силы относительно точки — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1. Момент силы относительно точки.

МГТУ им. Н.Э.
Баумана
Алгебраическим моментом силы относительно точки называется скалярная величина, равная
произведению модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус.
Плечом h силы относительно точки O называется кратчайшее расстояние между этой точкой и линией действия силы.
B
—
+
A
( ´ ) =± h
( ´ ) =± 2∙ △
h
Алгебраический момент не зависит от переноса силы вдоль ее линии действия.
O
Векторным моментом силы относительно точки называется вектор, приложенный в этой точке, по модулю равный
произведению силы на плечо, относительно моментной точки, перпендикулярный плоскости, проходящей через моментную
точку и силу, и направленный так, что с конца этого вектора видим вращение относительно моментной точки против часовой
стрелки.
B
z
A
´
´ ( ´ )
x
´
´ (
´ )|=±2 ∙ △
|
h
O
´ ( ´ ) = ´ × ´
´ (
´ )|=± h
|
y

2. Момент силы относительно оси.

МГТУ им. Н.Э.
Баумана
Моментом силы относительно оси называется алгебраический момент проекции этой силы на плоскость,
перпендикулярную оси, вычисленный относительно точки пересечения оси с этой плоскостью.
B
z
´ ) ¿ ( ´ ) =± h
(
´ ) =± 2 ∙
(
△
′
A
′
z
:
h
B
´
′
1) Сила параллельна оси;
=0
O
z
´
2) Линия действия силы пересекает
ось
=0
O
´
Таким образом, сила не создает момент относительно оси, если сила и ось
расположены в одной плоскости.
O
´

3. Момент силы относительно оси.

МГТУ им. Н.Э.
Баумана
Теорема. Момент силы относительно оси равен проекции на эту ось векторного момента силы,
вычисленного относительно произвольной точки на данной оси.
´ ) =2 ∙ △
(
′
B
z
´
1
A
O1
( ´ ¿ ¿ ) ¿
´ (
´ )|=±2 ∙ △
|
| ´ ( ´ )|=± 2 ∙ △
´ 1) ¿
´ 1( ¿¿
1
′
′
B
Угол между соответствующими плоскостями есть угол
между перпендикулярами к ним.
´
O
1
;
△ = △ 1
′
1
´ ) =|
´ (
´ )| =|
´ ( ´ )| 1
(
1
Знак определяется знаком .
´
´ ´
´ ( ´ ) = ´ × ´ = =´ ( − ) + ´ ( − )+ ´ ( − )
|
′
|
Формулы для вычисления моментов относительно осей:
( ´ ) = − ; ( ´ ) = − ; ( ´ ) − .

4. Сложение параллельных сил.

´ 1 ↑↑
´2
1¿
D
´ ′ 1
´ ′ 2
L
E
K
МГТУ им. Н.Э.
Баумана
;
´ ′ 2
M
;
´ 2+ ´ 2 =
´2
;
;
´ ′ 1+ ´ ′ 2= ´ ∗
( ´ ′ ¿¿1, ´ ′ 2) 0;¿
´ ´ 2) ( ¿¿1,
´ ´ 2 , ´ 1 , ´ 2)¿¿( ¿¿1,
´ ´ 2 )¿
( ¿¿1,
´∗
( ´ ′¿¿1, ´ ′ 2 , ´ ′1 , ´ ′ 2)¿( ´ ′¿¿1, ´ ′ 2)¿
´ ′ 1
Из подобия треугольников DEK, DAC и DLM, DCB:
´ 1 A
C
B
´ 2
′1 ′2 ⇒ = =
= ;
=
2 1 ∗
′ 1 ′ 2
Таким образом, две параллельные силы, направленные в
´2 ´
одну сторону, имеют равнодействующую, параллельную
2
им, по модулю равную сумме их модулей и направленную
в ту же сторону.
Верно и обратное: силу можно разложить на две параллельные силы,
направленные в ту же сторону, бесконечным числом способов.
´
´ 1 1
´∗
´ = ´ 1+
´ 2;
´ ↑↑ ´ 1 ↑ ↑ ´ 2

5. Сложение параллельных сил. Пара сил.

´ 1 ↓↑ ´ 2 ; 1 ≠ 2
2¿
Разложим силу на две параллельные и
´2
A
C
;
B
d
( ´ ′¿¿2, ´ 2) 0¿
∗
= 1 − 2
= =
2 1 ∗
Таким образом, две параллельные силы, направленные в
противоположные стороны и не равные по модулю, имеют
равнодействующую, параллельную им, по модулю равную
разности их модулей и направленную в сторону большей силы.
´1
3 ¿ ´ 1 ↓ ↑ ´ 2 ; 1= 2
;
∗
´
´∗
( ¿¿1,
´ 2) ( ´ 2 , ´ ′ 2 , ´ )¿
´ ′2
´∗
´1
МГТУ им. Н.Э.
Баумана
Пара сил – система двух равных по модулю параллельных сил, направленных в противоположные
стороны и не направленные вдоль одной прямой.
´2
Кратчайшее расстояние d между линиями действия сил пары называется плечом пары.
Плоскость, в которой расположены силы пары, называется плоскостью пары.
Действие пары сил на тело характеризуется моментом пары
´ 1,
´ 2 ) =± 1
(

6. Эквивалентность пар.

МГТУ им. Н.Э.
Баумана
Теорема. Не изменяя действия пары сил на тело, ее можно переносить куда угодно в плоскости действия,
изменять силы и плечо, сохраняя неизменным модуль и направление момента пары сил.
´ 1,
´ 2)
(
´1
;
´ ′ 1=− ´ ′ 2 ;
´2
A
´ 2= ´ ′ 2 + ´ } rsub {2¿
´ rsub {1} =− {acute { } 2 ;
}
( }´ rsub {1} , {acute { } ¿¿2) 0¿
B
´ ′1 ,
´ ′2)
(
´ 1 ´
′1
}´ rsub {1¿ 1
( ´ 1 , ´ 2 ) =2 ∙ △
( ´ ′1 , ´ ′ 2 )=2∙ △
1
2
1
2
´ ′2
2
}´ rsub {2¿ △ 1 2= △ 1 –2 общее основание и равные высоты
( ´ 1 , ´ 2 ) = ( ´ ′ 1 , ´ ′ 2 )
Направления моментов совпадают.

7. Перенос пары в параллельную плоскость.

Теорема. Действие пары сил на тело не изменится, если эту пару перенести в параллельную плоскость.
¿¿ ¿¿
´
B 2
´ ′ 1= ´ 1 ;
´ ′ 2= ´ 2 ;
´1
A
´1
´2
B’
}´ rsub {2¿
´ ′ 1 A’
´ ′2
}´ rsub {1¿
´ 1=−
´ 2;
МГТУ им. Н.Э.
Баумана

8. Векторный момент пары сил.

МГТУ им. Н.Э.
Баумана
Векторным моментом пары сил называется вектор, перпендикулярный плоскости пары, направленный в
ту сторону, откуда пара стремится повернуть тело против часовой стрелки и численно равный
произведению силы пары на ее плечо.
´ 1 =− ´ 2
´1
A
B
´
´
O
´2
Таким образом, векторный момент пары равен векторному
моменту одной из сил пары, вычисленному относительно точки
приложения второй силы.
Т.к. точка О произвольна, то можно считать векторный
момент приложенным в любой точке, т.е. векторный
момент пары сил есть свободный вектор.
Две пары сил, действующие на твердое тело, эквивалентны, если они имеют
одинаковые по модулю и направлению векторные моменты.

9.

Сложение пар сил. Теорема. Две пары, действующие на твердое тело и лежащие в пересекающихся плоскостях, можно
заменить одной эквивалентной парой, векторный момент которой равен сумме векторных моментов
исходных пар.
Приведем обе пары к одному плечу АВ, расположенному на
линии пересечения плоскостей.
´′
´
´ 1
A
´ ′2
B
´ ′1
´ 2
´1
´2
´ ′ 1+
´ ′ 2=
´′
;
´ (
´ ,
´ 1 ) =
´ × =
´
´ × ( ´ 1+
´ 2 ) =
´ ×
´ 1 +
´ ×
´2
´ (
´ ,
´ 1 )=
´ (
´ 1,
´ ′1 ) +
´ (
´ 2,
´ ′2 )
В общем случае:
´ ∑
´
=
=1
Условия равновесия системы пар сил:
´
МГТУ им. Н.Э.
Баумана
{
=∑ =0
=1
´ ∑
´ =0 ⇒ = ∑ =0
=
=1
=1
= ∑ =0
=1

English     Русский Правила

Момент силы

Момент силы относительно точки простыми словами можно определить как меру способности тела вращаться вокруг определенной точки или оси. Это отличается от стремления тела двигаться в направлении действия силы. Момент силы развивается только тогда, когда приложенная сила не совпадает с центром тяжести тела. Это связано с тем, что сила, проходящая через центр тяжести тела, не стремится повернуть его вдоль какой-либо оси. Отсюда можно сделать вывод, что Момент обусловлен силой, не имеющей равной и противоположной силы вдоль линии ее действия.

Поскольку сила, которую мы здесь прикладываем, предназначена для вращения различных тел, мы называем ее по-другому — Крутящий момент. Крутящий момент также можно считать эквивалентным силе в линейной динамике (линейном движении).

Поскольку крутящий момент эквивалентен силе при прямолинейном движении, он также играет ту же роль, что и сила при линейном движении.

Крутящий момент можно определить как меру того, насколько сила, действующая на частицу, может заставить ее вращаться вокруг оси, называемой осью вращения.

Чем больше сила, тем больше вращательное движение объекта.

Крутящий момент является векторной величиной, что означает, что он имеет как величину, так и определенное направление. Он представлен «тау» в греческом алфавите.

Крутящий момент также можно определить как произведение силы и перпендикулярного расстояния между линией действия силы и точкой вращения.

[Крутящий момент = Сила x Перпендикулярное расстояние между осью вращения и точкой приложения силы]

[Из этой формулы мы можем понять, что крутящий момент представляет собой перекрестное произведение силы и перпендикулярного расстояния.]

Следовательно,

=rf

=rfSin

[Здесь угол между силой и перпендикулярным расстоянием]

Здесь можно развить три случая,

Случай 1: Когда θ равно 0°, крутящий момент равен ноль, так как Sin0 имеет нулевое значение.

Случай 2: Когда θ равно 180°, крутящий момент снова равен нулю, так как Sin180 имеет нулевое значение произведение F и D.

т. е. =fd

Единицей крутящего момента в системе СИ является ньютон-метр (Нм).

Используя правило правой руки, мы можем найти направление вектора крутящего момента. Если мы направим пальцы в направлении r (расстояние точки вращения и точки приложения силы) и согнем их в направлении силы, то большой палец будет указывать в направлении вектора крутящего момента.

При вращательном равновесии сумма всех крутящих моментов, действующих на тело, равна нулю, что просто означает, что на объекте нет чистого крутящего момента.

∑=0

1. Величина силы, приложенной к объекту.
2. Перпендикулярное расстояние линии действия силы от оси вращения, которая также называется плечом рычага.

Отсюда можно сделать вывод, что чем больше модуль силы и перпендикулярное расстояние между линией действия силы, тем больше будет момент силы, тем больше будет ее поворотное действие.

Можно также написать, что приложенная сила и расстояние прямо пропорциональны моменту силы.

Момент инерции:

Это физическая величина, которая выражает тенденцию тела сопротивляться угловому ускорению. Его также можно определить как сумму произведения массы частицы на квадрат расстояния между осью вращения и положением частицы.

Связь между моментом инерции и крутящим моментом.

Согласно первому закону движения Ньютона, тело остается в покое до тех пор, пока на него не действует внешняя сила.

Например, вентиляторы, стиральные машины и кондиционер работают только тогда, когда мы их включаем. Это означает, что они остаются в покое, пока мы не включим кнопку питания. Мы видим, что все вращающиеся электроприборы остаются в покое, а при подаче крутящего момента каждая частица в системе, имеющая свои вращательные массы (момент инерции), начинает вращаться вокруг своей оси вращения. Вот как мы можем понять связь между ними по первому закону движения Ньютона.

Теорема о параллельных осях:- 

Он гласит, что момент инерции твердого тела относительно своей оси равен моменту инерции относительно параллельной оси, проходящей через его центр масс, и произведению массы тела на квадрат перпендикулярного расстояния между две оси вместе

Теорема о перпендикулярной оси:- 

Она утверждает, что момент инерции плоскости относительно оси, перпендикулярной ее плоскости, равен сумме моментов инерции относительно любых двух взаимно перпендикулярных осей в ее плоскости и пересекающихся друг друга в точке, где перпендикулярная ось проходит через него.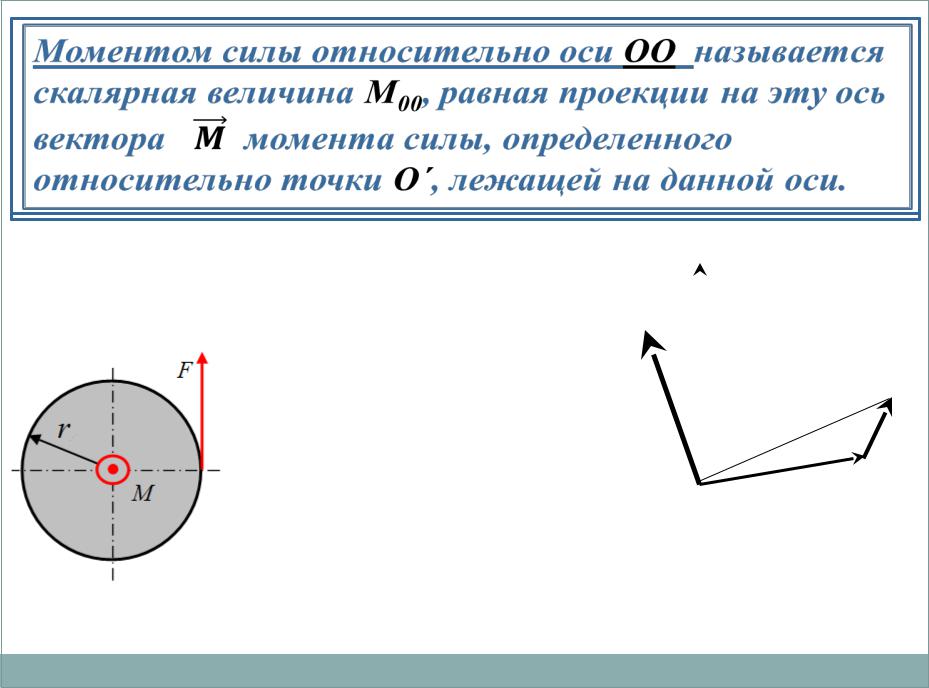

ВАЖНОЕ ЗАМЕЧАНИЕ: [Момент силы считается положительным, если сила стремится повернуть тело против часовой стрелки, и отрицательным, если она стремится повернуть объект по часовой стрелке.]

Вывод:

Момент силы Тенденция объекта совершать круговое движение вокруг фиксированной точки. Он говорит нам о силе, генерируемой для того, чтобы вызвать вращательное движение, которое называется эффектом поворота. Если объект закреплен на шарнире, и мы прикладываем силу, то это создает крутящий момент, который приводит к изменению вращательного состояния движения объекта. Мы сталкиваемся с крутящим моментом в повседневной жизни, открывая дверь, качаясь на качелях и многое другое.

НАУЧНО-ТЕХНИЧЕСКИЙ БЛОГ СУБХАНКАРА: КОНЦЕПЦИЯ МОМЕНТА:

КОНЦЕПЦИЯ МОМЕНТА:

Момент силы (или момент) — это тенденция силы скручивать или вращать объект. Это важное, основное понятие в технике и физике. Момент математически оценивается как произведение силы и плеча момента . Плечо момента представляет собой перпендикулярное расстояние от точки вращения до линия действия силы. Момент можно рассматривать как меру тенденции силы вызывать вращение вокруг воображаемой оси, проходящей через точку. (Примечание: в машиностроении и гражданском строительстве «момент» и «крутящий момент» имеют разные значения, тогда как в физике они являются синонимами.)

Момент силы можно вычислить относительно любой точки, а не только точек, в которых линия действия силы перпендикулярно. На изображении А показаны компоненты, сила F и плечо момента x, когда они перпендикулярны друг другу. Когда сила не перпендикулярна интересующей точке, такой как точка O на изображениях B и C, величина Момента, M вектора F относительно точки O есть

где

— вектор из точки О в позицию, где применяется величина F .

× представляет векторное произведение векторов.

[На рисунке момент в точке O, когда компоненты перпендикулярны точке O. Изображение B и изображение C иллюстрируют компоненты момента в точке O, когда компоненты не перпендикулярны точке O .]

В машиностроении (в отличие от физики) термины «крутящий момент» и «момент» не взаимозаменяемы. «Момент» — это общий термин для тенденции одной или нескольких приложенных сил вращать объект вокруг оси (концепция, которая в физике называется крутящим моментом). «Крутящий момент» является частным случаем этого: если сумма векторов приложенных сил равна нулю (т. е. их «результат» равен нулю), то силы называются «парой», а их момент называется «крутящим моментом».
Например, сила вращения на валу, например, вращающейся отвертки, образует пару, поэтому результирующий момент называется «крутящий момент». Напротив, боковая сила, действующая на балку, создает момент (называемый изгибающим моментом), но, поскольку результирующая сила отлична от нуля, этот изгибающий момент не называется «крутящим моментом».

Частица находится в положении r относительно своей оси вращения. Когда к частице приложена сила F, только перпендикулярная составляющая F⊥ создает крутящий момент. Этот крутящий момент τ = r × F имеет величину τ = |r| |Ф⊥| = | г | |Ф| sinθ и направлен наружу от страницы.

A Пара — это система сил с равнодействующей (также известной как чистая или сумма) моментом, но без равнодействующей силы. ^{Другой термин для пары чистый момент . Его эффект заключается в создании вращения без перемещения или, в более общем смысле, без какого-либо ускорения центра масс.}

Результирующий момент пары называется крутящим моментом . Его не следует путать с термином крутящий момент, который используется в физике, где он является просто синонимом момента. ^{Вместо этого крутящий момент является частным случаем момента. Крутящий момент имеет особые свойства, которых нет у момента, в частности, свойство не зависеть от точки отсчета.}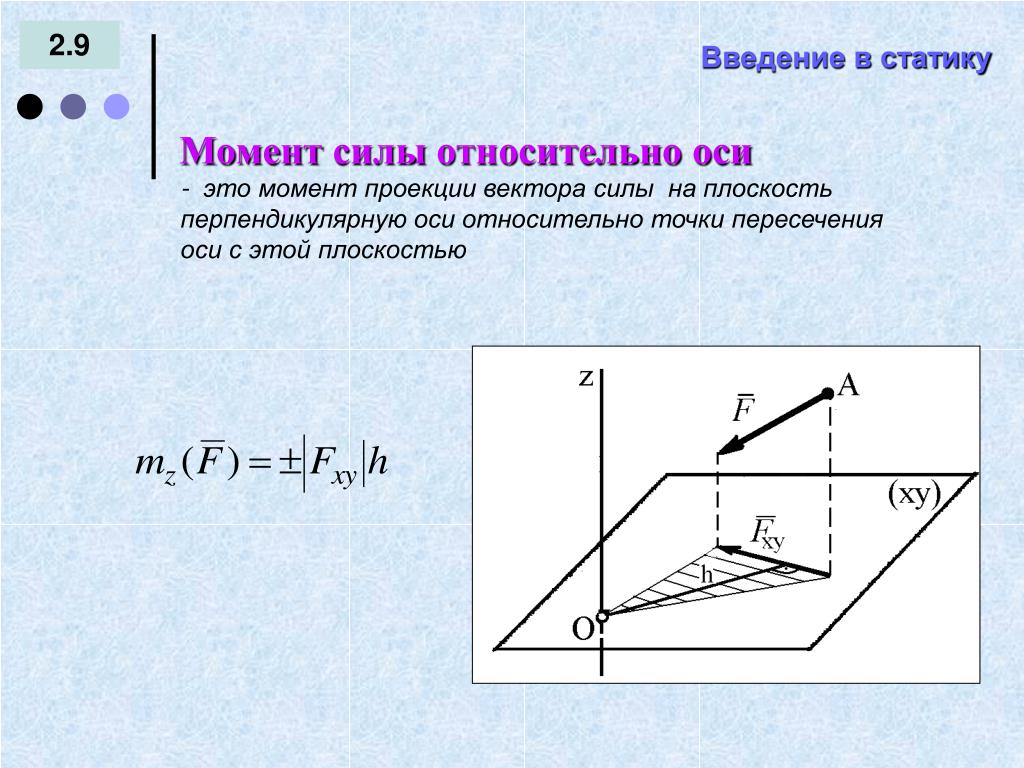

Простая пара:

Простейшая пара состоит из двух равных и противоположных сил, линии действия которых не совпадают. Это называется «простая пара». Силы имеют вращательный эффект или момент, называемый крутящим моментом, относительно оси, перпендикулярной плоскости сил. Единицей СИ для крутящего момента пары является ньютон-метр.
Если две силы равны F и −F , то величина момента определяется по следующей формуле:

0114 F — величина одного сил

d — перпендикулярное расстояние между силами, иногда называемое рычаг пары

Величина крутящего момента всегда равна Fd, причем направление крутящего момента задается единичным вектором , который перпендикулярен плоскости, содержащей две силы. Когда d принять за вектор между точками действия сил, то пара представляет собой векторное произведение d и F .

  
Независимость от точки отсчета:

Момент силы определяется только относительно определенной точки P (говорят «момент о P «), и вообще при изменении P момент меняется. Однако момент (крутящий момент) пары независим от опорной точки P : Любая точка даст один и тот же момент. <sup>Другими словами, вектор крутящего момента, в отличие от любого другого вектора момента, является «свободным вектором». (Этот факт называется Теорема Вариньона о втором моменте .)









, F ₂ и т. д., образующие пару , с векторами положения (о каком-то начале координат P ) r ₁ , r ₂ и т. д. соответственно. Момент около P равен</sup>

Теперь мы выбираем новую точку отсчета P’ , отличающийся от P вектором r . Новый момент равен

Теперь из распределительного свойства векторного произведения следует

Однако определение пары сил означает, что Следовательно,

Это доказывает, что момент не зависит от точки отсчета, что является доказательством того, что пара является свободным вектором.