Моменты инерции некоторых твердых тел — Студопедия

Тело	Положение оси вращения	Момент инерции
Полый тонкостенный цилиндр радиуса R	Ось симметрии
Сплошной цилиндр или диск радиуса R	То же
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его середину
Прямой тонкий стержень длиной l	Ось перпендикулярна стержню и проходит через его конец
Шар радиусом R	Ось проходит через центр шара

Теорема Штейнера:Момент инерции тела Jz относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния

а между осями (теорема Штейнера):

При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергияравна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:

Момент инерции –мера инертности тела при вращательном движении.

Работа вращения тела идет на увеличение его кинетической энергии и определяется выражением, где Mz – момент сил относительно оси вращения z.

.

Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:

где Lz – момент импульса твердого тела относительно оси z.
В замкнутой механической системе момент внешних сил относительно неподвижной оси M z = 0 и , откуда Lz= const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.

Вопросы для самоконтроля и повторения:

1. Что называется моментом инерции тела? Какова роль момента инерции во вращательном движении?

2. От чего зависит момент инерции тела?

3. Что называется моментом силы относительно неподвижной оси?

4.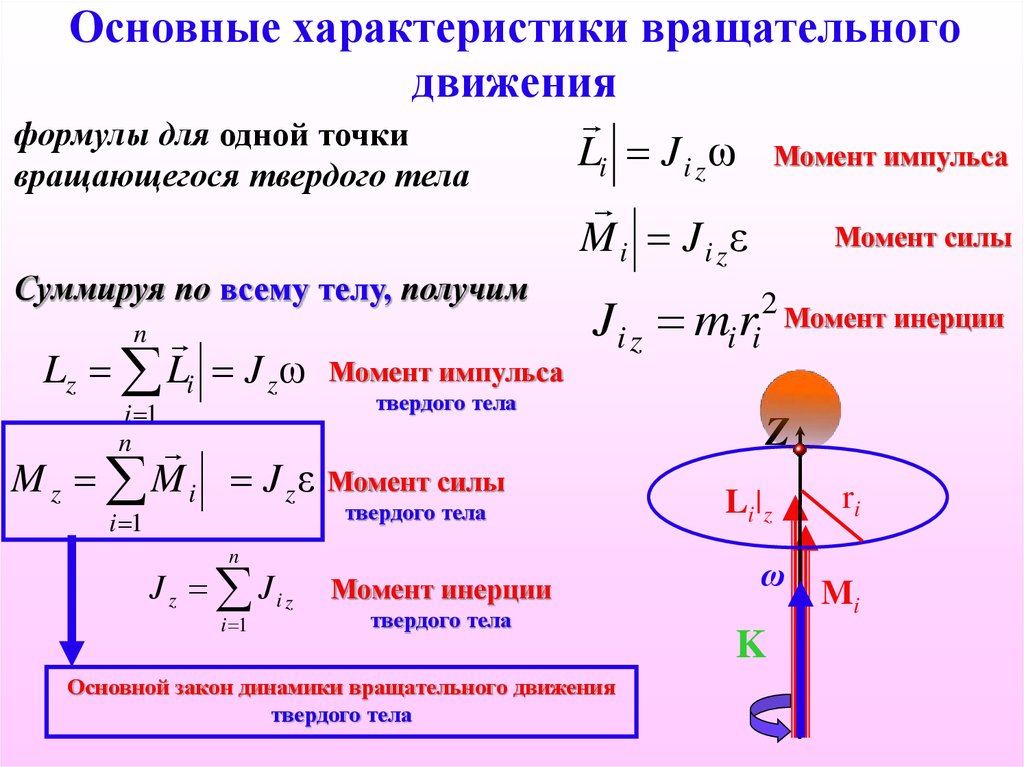 Что такое момент импульса твердого тела? Как определяется направление момента импульса?

5. Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси? Как определяется работа при вращении тела?

6. Сформулируйте уравнение динамики вращательного движения твердого тела.

7. Сформулируйте закон сохранения момента импульса. В каких системах он выполняется?

8. Сопоставьте основные величины и уравнения динамики поступательного и вращательного движений.

Заполните таблицу:

Физическая величина	Обозначение	Тип величины	Ед. измерения	Формула
1. Момент силы
2. Плечо силы				———
3. Кинетическая энергия вращающегося тела
5. Момент инерции: а) однородного цилиндра б) однородного шара
5. Момент импульса тела
6. Угловое ускорение
7. Основное уравнение вращательного движения	_______	—————	————

Решите задачи:

1. Почему, перед тем как метнуть диск, метатель совершает вместе с диском вращение?

2. Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии по закону , где

В=2 рад/с², С=-0,5 рад/с³. Определить момент сил относительно оси вращения для момента времени t = 3 c.

3. Полый тонкостенный цилиндр массой 0,3 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену 1,2 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты.

4. Сплошной однородный шар радиусом 8 см и массой 3 кг катится без скольжения с угловой скоростью 1,2 рад/с. Найдите его момент импульса L, а также полную кинетическую энергию тела.

Задания для самостоятельной работы:

1. На тело с моментом инерции J действует вращающий момент М. С каким угловым ускорением вращается тело?

Вариант

М, Н·м

L, кг·м 2

2. Фигурист за некоторое время уменьшил частоту своего вращения от ν₁ до ν₂. Его момент инерции равен J. Рассчитайте угловое ускорение ε фигуриста, тормозящий момент силы М, работу торможения А.

Вариант

н1, Гц

н2, Гц

0,5

I, кг·м 2

t, c

3. Сплошной однородный шар радиусом R и массой m катится без скольжения с угловой скоростью w. Найти его момент импульса L, а также полную кинетическую энергию тела.

Вариант

R, см

w, рад/с

m, г

Работа 21.

ИНЕРЦИАЛЬНЫЕ СВОЙСТВА ТВЁРДОГО ТЕЛА

Задание: Изучить количественные характеристики инерциальных свойств твёрдого тела с помощью тензора инерции

Рис. 1

Оборудование и принадлежности: установка для проведения измерений, весы, разновес.

ОПИСАНИЕ УСТАНОВКИ.

Внешний вид используемого в работе прибора «Крутильный маятник» представлен на рис. 1. На основании 2, оснащённом ножками с регулируемой высотой, прикреплён миллисекундомер 1. В основании закреплена колонка 3, на которой при помощи прижимных винтов закреплены кронштейны 4, 5, 6. Кронштейны 4 и 6 имеют зажимы, служащие для закрепления стальной проволоки, на которой подвешена рамка 7. На кронштейне 5 закреплена стальная плита 8, которая служит основанием фотоэлектрическому датчику 9, электромагниту 10 и угловой шкале 11. Конструкция рамки позволяет закреплять грузы 12. Фотоэлектрический датчик и электромагнит соединены с миллисекундомером.

ЭЛЕМЕНТЫ ТЕОРИИ

Рис. 2

Общие сведения. Одной из величин, характеризующих вращение твёрдого тела вокруг некоторой точки О (рис. 2) является момент импульса тела

.Чтобы определить момент импульса тела, можно мысленно разбить тело на материальные точки массами (I — номер точки), найти вектор момента импульса каждой материальной точки, который равен векторному произведению радиус-вектора точки на вектор ее импульса , тогда .

Пусть тело вращается вокруг оси, проходящей через точку О и

— его мгновенная угловая скорость. Тогда скорость i-той точки тела равна . Поэтому момент импульса тела относительно точки О равен:

(1)

Векторное равенство (1) можно записать в виде трёх проекций на оси координат:

(2)

Учитывая , что

вместо (2) имеем:

(3)

Где

(4)

И аналогично выражаются

и т. д. Из (4) видно, что и т. д. Поэтому из 9 величин . . . различны лишь 6. Величины называются осевыми моментами инерции, а — центробежными моментами инерции.

Таким образом, момент импульса тела весьма сложно зависит от распределения масс в теле и его направление не совпадает, вообще говоря, с угловой скоростью вращения тела. Совокупность величин

(5)

Называется тензором инерции тела относительно точки О. Величины

, , являются диагональными элементами тензора, а остальные — недиагональными. В данном случае величины, расположенные симметрично относительно диагонали, равны. Такой тензор называется симметричным. Если недиагональные элементы тензора равны нулю, а осевые отличны от нуля, то говорят, что оси тела, совпадающие с осями координат, являются главными осями инерции, а величины , , называют главными моментами инерции (часто их можно определить из соображений симметрии). Если главные оси проведены через центр масс, то они называются главными центральными осями. Тело, для которого , а остальные компоненты тензора равны нулю, называется шаровым волчком. При этом , т. е. направление момента импульса совпадает с направлением . Если , то тело называется симметричным волчком, а при говорят об асимметричном волчке.

Вычислим момент инерции

твёрдого тела относительно произвольной оси ОА. Свяжем с точкой О декартовую систему координат и учтем, что (рис. 3), тогда . Пусть — единичный вектор, направленный вдоль оси ОА, тогда

Рис. 3

, .

Подставляя

и в выражение для и учитывая, что , получаем:

,

Где

, , и т. д. компоненты тензора инерции.

Если оси координат являются главными центральными осями, то

. (6)

Теория метода. Колебательное движение крутильного маятника описывается уравнением, которое в проекции на ось вращения Z имеет вид:

, (7)

Где Mz — момент сил упругости относительно оси вращения, сообщающий системе угловое ускорение

, — момент инерции относительно той же оси. Для упругих деформаций (амплитуда колебаний должна быть мала) , где — проекция вектора углового перемещения маятника на ось Z (он направлен противоположно вектору момента сил упругости), — модуль кручения. Тогда:

, (8)

Или

. (9)

Уравнение (9) является уравнением гармонических колебаний переменной JZ с циклической частотой

. Следовательно .

Обозначим период колебаний рамки

, тогда

,

Где

— момент инерции рамки. Для рамки с кубиком

,

Где

— момент инерции кубика с ребром (он равен ). Если в рамке закрепить параллелепипед, то период его колебаний , где — его момент инерции относительно оси вращения. Для него получаем:

. (10)

Рис. 4

Рассчитаем момент инерции параллелепипеда относительно оси, проходящей через точки

и (см. рис. 4). Пусть , , . Тогда

. (11)

Аналогично

,

(т. к.

, , ).

С учётом (6)

. (12)

Для прямоугольного параллелепипеда

, , . (13)

Подчеркнём, что в данном случае

, , (14)

(оси координат совпадают с главными центральными осями тела). Тогда

; ; (15)

И с учётом

Для угла

и запишем

. (16)

С учётом (11) получаем

(17)

Порядок выполнения задания

1. Определение момента инерции параллелепипеда относительно оси

.

а) Измерить длину рёбер параллелепипеда и куба, определить их массу. Используя (10), определить

, , . Для этого найти периоды колебаний , , , , , измеряя время 10 колебаний и учитывая, что , где — число колебаний. По формуле (12) рассчитать ;

б) закрепив параллелепипед соответствующим образом, определить период колебаний системы и по формуле (10) рассчитать

;

в) Рассчитать

по формуле (12), используя выражения (13). Сравнить полученные результаты.

2. Определение угла между векторами

и .

а) Используя значения

, , , , измеренные при выполнении первого задания, по формуле (17) найти угол (в градусах) между и .

б) Закрепив вместо параллелепипеда кубик и выполнив соответствующие измерения

, , , убедиться в том, что вектора и совпадают по направлению.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Что представляет собой тензор инерции?

2. Какие оси называются главными центральными?

3. Рассчитайте момент инерции куба относительно оси, проходящей через центр масс перпендикулярно граням.

ЛИТЕРАТУРА

1. Кембровский Г. С. Приближённые вычисления и методы обработки результатов измерений в физике. — Минск: Изд-во «Университетское», 1990. -189 с.

2. Матвеев А. Н. Механика и теория относительности. — М.: Высшая школа, 1986. -320 с.

3. Петровский И. И. Механика. — Минск: Изд-во БГУ, 1973. -352 с.

4. Савельев И. В. Курс общей физики. — М.: Наука, 1982. Т. 1. Механика. Молекулярная физика. -432 с.

5. Сивухин Д. В. Общий курс физики. М.: Наука, 1989 Т.1. Механика. -576 с.

6. Стрелков С. П. Механика. — М.: Наука, 1975. -560 с.

7. Физический практикум. Под ред. Кембровского Г. С. — Минск: Изд-во «Университетское», 1986. -352 с.

Факторы, от которых зависит момент инерции

Момент инерции в физике есть мера объема вращательной инерции тела, т.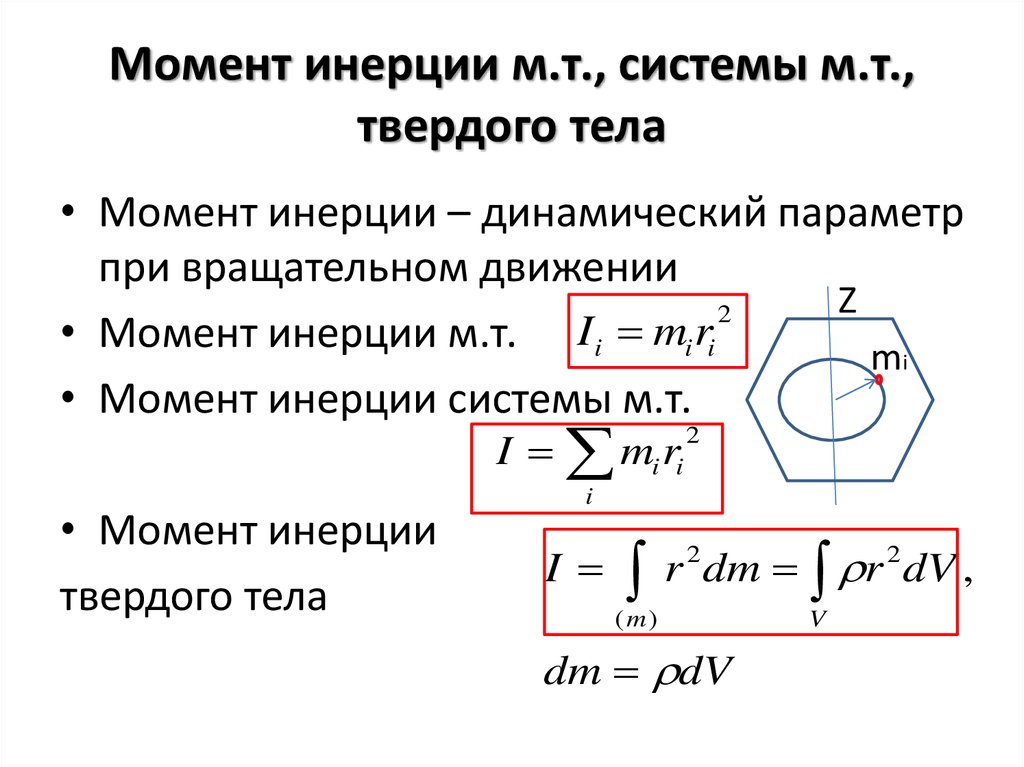 е. сопротивления тела, показывающего скорость его вращения относительно оси, изменяемой крутящим моментом.

Ось может быть внутренней или внешней, наклонной или прямой. Момент инерции (I) всегда указывается относительно этой оси. Он определяется как результат сложения всех произведений, полученных при умножении каждой частицы в теле на квадрат ее расстояния от оси.

Моментом инерции называется вращательная инерция, вращательный аналог веса прямого движения. Оно возникает из-за способности вращающегося тела сопротивляться изменению его вращательного движения. Это свойство также связано с плотностью материала, из которого состоит корпус. Для данной точки момент инерции всего в несколько раз превышает квадрат расстояния, перпендикулярного оси вращения, I = mr2.

Примеры момента инерции

Представьте, что вы сидите в движущемся автобусе. Когда через некоторое время он останавливается, ваша верхняя часть тела движется вперед, а нижняя часть тела не двигается. Это из-за инерции. Ваша нижняя часть тела подключена к шине, но верхняя часть тела не связана с шиной напрямую. Поэтому, когда автобус останавливается, ваша нижняя часть тела останавливается вместе с автобусом, но верхняя часть тела продолжает двигаться вперед. То есть сопротивляется изменениям своего положения.

Точно так же ваше тело отбрасывается назад, когда вы садитесь в движущийся поезд. Это потому, что перед посадкой в ​​поезд вы были расслаблены. Как только вы садитесь в движущийся поезд, ваша нижняя часть тела встречается с поездом, но верхняя часть тела все еще находится в состоянии покоя. Поэтому он оттесняется назад, то есть сопротивляется изменению своего положения.

Факторы, от которых зависит момент инерции

• Масса тела  

Масса оценивает количество вещества в теле. Это также сила, благодаря которой тело сопротивляется ускорению или изменению своей скорости, когда к нему прикладывается внешняя сила, действующая как инерция. Базовой единицей массы в системе СИ является килограмм (кг). Когда тело имеет большую массу, внешней силе труднее изменить состояние его движения. Точно так же, когда тело имеет большую массу или когда плотность материала, из которого сделано тело, высока, его момент инерции высок. Следовательно, для изменения вращения тела требуется более высокий крутящий момент.

Момент инерции зависит от оси вращения. Ось вращения тела зависит от размера и формы тела. По мере изменения размера и формы меняется и ось вращения тела. Это вызывает изменение момента инерции тела.

Чтобы измерить, как вес твердого вращающегося тела распределяется относительно оси вращения, мы определяем новый параметр, известный как радиус вращения. Это связано с моментом инерции и общей массой тела. Когда масса на одной стороне тяжелее, ось вращения тела ближе к ней, и момент инерции требует более высокого крутящего момента на этой стороне, чтобы изменить движение.

Это размещение тела на оси и его ориентация. Если есть изменение направления оси, направление крутящего момента также должно измениться, чтобы вызвать изменение вращения тела. Точно так же изменение точки, в которой ось вращения проходит через тело, то есть изменение его положения, изменило бы и момент инерции тела.

Формула момента инерции

Момент инерции равен I = mr2.

Где,

m = Сумма произведения массы.

r = Расстояние от оси вращения.

Промежуточная единица инерции является составной единицей измерения. В международной системе единиц (СИ) масса измеряется в килограммах, а расстояние в метрах. Следовательно, размерность момента инерции равна килограмм-метрам в квадрате.

Момент инерции любой формы тела, которую можно определить по математической формуле, обычно рассчитывается с помощью интегрального исчисления. Момент инерции диска можно измерить, разрезав его на число неподвижных колец, найдя их количество, умножив массу на их расстояния от точки отсчета и объединив эти произведения. Процесс слияния выполняется автоматически; ответ: I = (mR2) / 2, 

Вращающиеся тела можно разделить на следующие категории:

Момент инерции системы частиц

Для системы различных точечных частиц, вращающихся вокруг фиксированной оси, момент инерции может быть задан как I = ∑jmjrj2, где mj — масса каждой точечной частицы, rj — расстояние этих частиц от оси. Из-за члена r2 время инерции увеличивается, поскольку квадрат расстояния до оси вращения не изменяется. Момент инерции является вращательным аналогом веса при прямолинейном движении.

Момент инерции твердого тела

Когда мы говорим о твердом теле, мы предполагаем, что все частицы в твердом теле распределены равномерно. Если бы мы выбрали два поперечных сечения твердого тела наугад так, что оба сечения имеют одинаковую площадь, то мы имели бы одинаковое количество частиц в обоих поперечных сечениях. Будем также считать, что плотность материала тела фиксирована и не колеблется.

Таким образом, можно сказать, что момент инерции твердого тела можно описать через момент инерции системы частиц, с той лишь разницей, что формула I=∫r2dm,. То же самое верно даже для твердых тел странной формы.

Заключение

Момент инерции — это название, данное вращательной инерции, вращательный аналог веса прямого движения. Оно возникает из отношения вращения вращательного движения. Входное время должно быть указано относительно выбранной оси вращения. С точки зрения точки, момент инерции всего в несколько раз превышает квадрат перпендикулярного расстояния к оси вращения, I = mr2. Это отношение «точка-точка» становится основой всех других времен инерции, поскольку из набора точек можно построить что угодно.

Момент инерции определяется выражением I = mr2.

Промежуточная единица инерции является составной единицей измерения. В международной системе единиц (СИ) масса измеряется в килограммах, а расстояние в метрах. Следовательно, размерность момента инерции равна килограмм-метрам в квадрате.

Получите выражение момента инерции и определите его. От каких факторов зависит момент инерции? Напишите его единицу измерения и размерную формулу.

Получение изображения
Пожалуйста, подождите …

Зарегистрируйтесь сейчас для специальных предложений

+91

Дом

>

английский

>

Класс 11

>

>

>

>

4>

>44444>

>4444>

>4444>

> 444>

>

>

.