Методика определения коэффициента возвращающей силы пружины — Студопедия

Поделись с друзьями: 

Часть 1 Определение коэффициента возвращающей силы пружины.

    1. Подвесить на штатив пружину с подвеской и заметить по указателю длину ненагруженной пружины .

    2. Положить на подвеску грузик массой m =  кг и заметить по указателю длину пружины l.

    3. Добавить 2–й, 3–й, 4–й, 5–й грузики, каждый раз измерять длину  и вычислять удлинение = .

    4. Рассчитать по формуле (4.30) коэффициент возвращающей силы для пяти измерений и найти среднее значение коэффициента.

    5. Определить отклонение от среднего отдельных измерений

 Δ  = | – | и относительную погрешность δ = (Δ / )×100%. Данные опытов и расчетов занести в таблицу 4.2.

Таблица 4.2 – Результаты измерений и вычислений

№	м	m,кг	м	м	Н/м	kср,  Н/м	Δ  Н/м	Δ kср, Н/м	δ  kср, %
1	0,09	0,005	0,10
2		0,010	0,11
3		0,015	0,13
4		0,020	0,141
5		0,025	0,15

Часть 2 Определение периода колебаний нагруженной пружины

    1. Поместить на подвеску два грузика и записать массу грузиков с подвеской и указателем  (масса подвески и указателя написана на приборе).

    2. Слегка приподнять груз на пружине (на 6–8 мм), отпустить ее и, пропустив 5–6 колебаний, отсчитать по секундомеру время, за которое пружина совершит N колебаний (количество колебаний

N задает преподаватель). По формуле  определить период колебания нагруженной пружины.

    3. Опыт повторить 3 раза (число N можно взять разное), рассчитать каждый раз период и найти средний период .

    4. На подвеску добавить еще три грузика, подсчитать новую общую массу грузов и подвески  и, проделав опыт 3 раза, определить .

    5. Используя формулу (4.32), найти теоретические значения периодов нагруженной пружины, взяв за коэффициент упругости значение  из таблицы 4.2.

 = 2π      и                     (4.32)

 

    6. Приняв полученные значения и  за истинные, вычислить относительные ошибки результатов измерений по формуле:

δT

     7. Данные измерений и вычислений занести в таблицу 4.3.

Таблица 4.3 – Результаты измерений и вычислений

Масса, кг	№ опыта	N	, с	, с	, с	, с	δT, %
=0,033	1	12	11,6
	2	14	13,7
	3	16	14,9
0,048	1	12	14,2
	2	14	16,3
	3	16	18,5

8. Окончательные результаты измерений для

k записать в виде:

 

k= (  ± Δ       при   δk = …%.

Контрольные вопросы

1. Напишите уравнение гармонического колебания. Что называется гармоническим колебанием?

2. Дайте определение величин, характеризующих гармоническое колебание

(амплитуда, фаза, частота, циклическая частота, период).

3. По каким формулам определяется ускорение колеблющейся точки?

4. Какие силы вызывают гармонические колебания? Каковы их свойства?

5. Какова природа возвращающей силы в данной работе? Какая формула ее определяет?

6. Что такое коэффициент возвращающей силы? По каким формулам его определяют?   

7. Как можно рассчитать период колебаний нагруженной пружины? От чего он зависит?

Как можно практически измерить период колебаний груза на пружине?

 

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Гармонический осциллятор

30. 11.2020

Гармонический осциллятор (в классической механике) — система, которая при выведении её из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:

F = − k x {displaystyle F=-kx} ,

где k — постоянный коэффициент.

Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой.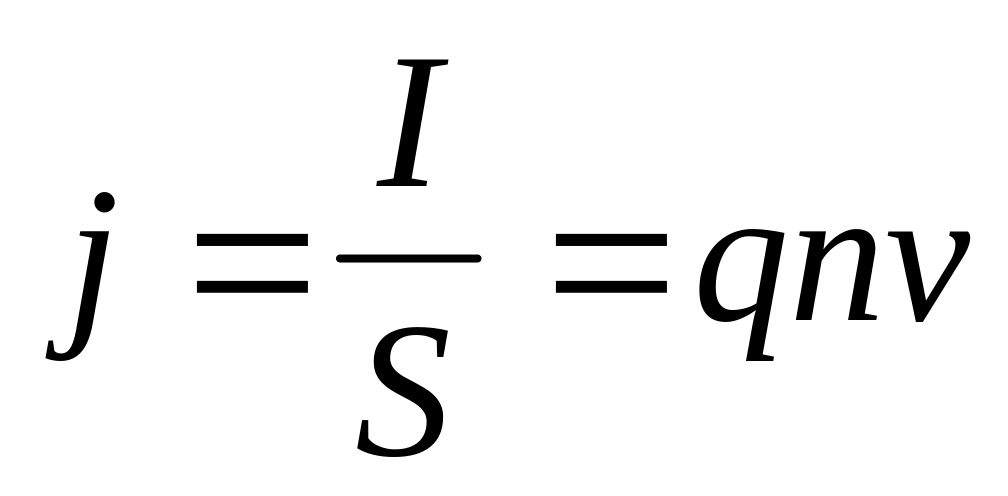 Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.

Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди немеханических аналогов гармонического осциллятора можно выделить электрический гармонический осциллятор (см. LC-цепь).

Свободные колебания консервативного гармонического осциллятора

Уравнение и его решения

Пусть x — смещение материальной точки относительно её положения равновесия, а F — действующая на точку возвращающая сила любой природы вида

F = − k x {displaystyle F=-kx} ,

где k = const. {2}x=0} .

Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Величину ω 0 {displaystyle omega _{0}} называют циклической частотой. (Имеется в виду круговая частота, измеряющаяся в радианах за секунду. Чтобы перевести её в частоту, выражающуюся в герцах, надо разделить на 2 π {displaystyle 2pi } .)

Будем искать решение этого уравнения в виде

x ( t ) = A sin ⁡ ( ω t + φ ) {displaystyle x(t)=Asin left(omega t+varphi ight)} .

Здесь A — амплитуда, ω — частота колебаний, φ — начальная фаза.

Подставляем в дифференциальное уравнение и получаем:

x ¨ ( t ) = − A ω 2 sin ⁡ ( ω t + φ ) {displaystyle {ddot {x}}(t)=-Aomega ^{2}sin(omega t+varphi )} , − A ω 2 sin ⁡ ( ω t + φ ) + ω 0 2 A sin ⁡ ( ω t + φ ) = 0 {displaystyle -Aomega ^{2}sin(omega t+varphi )+omega _{0}^{2}Asin(omega t+varphi )=0} . {2}=0,} ω = ± ω 0 . {displaystyle omega =pm omega _{0}.}

Отрицательную частоту можно отбросить, так как произвол в выборе здесь знака покрывается произволом выбора начальной фазы.

Общее решение уравнения записывается в виде:

x ( t ) = A sin ⁡ ( ω 0 t + φ ) , {displaystyle x(t)=Asin left(omega _{0}t+varphi ight),}

где A и φ — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям.

Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой.

Простое гармоническое движение

Движение, совершаемое консервативным гармоническим осциллятором, носит название простого гармонического движения. Это движение не является ни вынужденным, ни затухающим.

Оно периодическое: тело колеблется с частотой ω0 около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и предыдущее; период, частота и амплитуда колебаний остаются постоянными.

Учитывая, что ω0 = 2πf, получим

f = 1 2 π k m , {displaystyle f={frac {1}{2pi }}{sqrt {frac {k}{m}}},}

и, поскольку T = 1/f, где T — период колебаний,

T = 2 π m k . {displaystyle T=2pi {sqrt {frac {m}{k}}}.}

Эти формулы показывают, что период и частота не зависят от амплитуды и начальной фазы движения.

Частота движения определяется характерными свойствами системы (например, массой движущегося тела), в то время как амплитуда и начальная фаза определяются начальными условиями — координатой и скоростью тела в момент начала колебаний. Кинетическая и потенциальная энергии системы также зависят от этих свойств и условий.

Используя приёмы дифференциального исчисления, можно получить скорость и ускорение материальной точки как функции времени:

v ( t ) = d x d t = A ω 0 cos ⁡ ( ω 0 t + φ ) {displaystyle v(t)={frac {mathrm {d} x}{mathrm {d} t}}=Aomega _{0}cos(omega _{0}t+varphi )} , a ( t ) = d 2 x d t 2 = − A ω 0 2 sin ⁡ ( ω 0 t + φ ) {displaystyle a(t)={frac {mathrm {d} ^{2}x}{mathrm {d} t^{2}}}=-Aomega _{0}^{2}sin(omega _{0}t+varphi )} . {2}}

имеет постоянное значение. Это отражает «консервативность» осциллятора, то есть отсутствие энергетических потерь.

Простое гармоническое движение можно рассматривать как математическую модель различных видов движения, таких, например, как колебание пружины. Другими случаями, которые могут приближённо рассматриваться как простое гармоническое движение, являются движение маятника и вибрации молекул.

Простое гармоническое движение является основой некоторых способов анализа более сложных видов движения. Одним из таких способов является способ, основанный на преобразовании Фурье, суть которого сводится к разложению более сложного вида движения в ряд простых гармонических движений.

Примеры осцилляторов

Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами:

• когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие;
• возвращающая сила должна в точности или приближённо быть пропорциональна перемещению.

Ниже представлено несколько примеров.

Горизонтальная система груз—пружина

Типичным примером системы, в которой происходит простое гармоническое движение, является идеализированная система груз—пружина, в которой груз присоединён к пружине и находится на горизонтальной поверхности. Если пружина не сжата и не растянута, то на груз не действует никаких переменных сил и он находится в состоянии механического равновесия. Однако, если груз вывести из положения равновесия, пружина деформируется и с её стороны будет действовать сила, стремящаяся вернуть груз в положение равновесия. В случае системы груз—пружина такой силой является сила упругости пружины, которая подчиняется закону Гука:

F = − k x {displaystyle F=-kx} ,

где k имеет вполне конкретный смысл — это коэффициент жёсткости пружины.

Однажды смещённый груз подвергается действию возвращающей силы, ускоряющей его и стремящейся вернуть в начальную точку, то есть в положение равновесия. По мере того, как груз приближается к положению равновесия, возвращающая сила уменьшается и стремится к нулю. Однако в положении x = 0 груз обладает некоторым количеством движения (импульсом), приобретённым благодаря действию возвращающей силы. Поэтому груз проскакивает положение равновесия, начиная снова деформировать пружину (но уже в противоположном направлении). Возвращающая сила будет стремиться замедлить его, пока скорость не станет равной нулю; и сила вновь будет стремиться вернуть груз в положение равновесия.

Если нет потерь энергии, груз будет колебаться как описано выше; такое движение является периодическим.

Вертикальная система груз—пружина

В случае вертикально подвешенного на пружине груза, наряду с силой упругости, действует сила тяжести, то есть суммарно сила составит

F = − k x − m g {displaystyle F=-kx-mg} .

Если сделать замену переменной, чтобы оперировать не величиной x {displaystyle x} , а величиной X = x + m g / k {displaystyle X=x+mg/k} , то уравнение движения примет вид, идентичный случаю горизонтальной геометрии, только для переменной X {displaystyle X} .

Колебания будут происходить с той же частотой ω 0 = k / m {displaystyle omega _{0}={sqrt {k/m}}} . Однако, если в горизонтальном случае равновесию отвечало состояние недеформированной пружины, то в вертикальном варианте пружина в равновесии будет растянута. Зависимости частоты от величины ускорения свободного падения g {displaystyle g} при этом нет; g {displaystyle g} влияет лишь на сдвиг положения равновесия m g / k {displaystyle mg/k} .

Измерения частоты (или периода) колебаний груза на пружине используются в устройствах для определения массы тела — так называемых массметрах, применяемых на космических станциях, когда весы не могут функционировать из-за невесомости.

Универсальное движение по окружности Движение по кругу и гармоническое движение

Простое гармоническое движение в некоторых случаях можно рассматривать как одномерную проекцию универсального движения по окружности.

Если объект движется с постоянной угловой скоростью ω по окружности радиуса r, центром которой является начало координат плоскости x − y, то такое движение вдоль каждой из координатных осей является простым гармоническим с амплитудой r и круговой частотой ω.

Груз как простой маятник

В приближении малых углов движение простого маятника является близким к простому гармоническому. Период колебаний такого маятника, прикреплённого к стержню длиной ℓ, даётся формулой

T = 2 π ℓ g . {displaystyle T=2pi {sqrt {frac {ell }{g}}}.}

где g — ускорение свободного падения. Это показывает, что период колебаний не зависит от амплитуды и массы маятника, но зависит от g, поэтому, при той же самой длине маятника, на Луне он будет качаться медленнее, так как там слабее гравитация и меньше значение ускорения свободного падения.

Указанное приближение является корректным только при небольших углах отклонения, поскольку выражение для углового ускорения пропорционально синусу координаты:

ℓ m g sin ⁡ θ = I α , {displaystyle ell mgsin heta =Ialpha ,}

где I — момент инерции; в данном случае I = m ℓ 2. Небольшие углы реализуются в условиях, когда амплитуда колебаний значительно меньше длины стержня.

Когда угол θ мал, можно считать, что sin θ ≈ θ, и выражение принимает вид:

ℓ m g θ = I α , {displaystyle ell mg heta =Ialpha ,}

что делает угловое ускорение прямо пропорциональным углу θ, а это удовлетворяет определению простого гармонического движения.

Свободные колебания гармонического осциллятора с затуханием

Уравнение и его решения

При рассмотрении осциллятора с затуханием за основу берётся модель консервативного осциллятора, в которую добавляется сила вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и прямо пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

F = − k x − α v . {displaystyle F=-kx-alpha v.}

Используя второй закон Ньютона, получаем дифференциальное уравнение, описывающее затухающий осциллятор:

x ¨ + 2 γ x ˙ + ω 0 2 x = 0. {2}x=0.}

Здесь введены обозначения:

• 2 γ = α / m {displaystyle 2gamma =alpha /m} . Коэффициент γ {displaystyle gamma } носит название постоянной затухания. Он имеет размерность частоты.
• ω 0 = k m {displaystyle omega _{0}={sqrt {k over m}}} . Величину ω 0 {displaystyle omega _{0}} называют собственной частотой системы. Она тоже имеет размерность частоты.

Решение распадается на три случая.

• При малом трении ( γ < ω 0 {displaystyle gamma <omega _{0}} ) общее решение записывается в виде:

x ( t ) = A e − γ t s i n ( ω f t + φ ) , {displaystyle x(t)=Ae^{-gamma t}sin(omega _{f}t+varphi ),}

где ω f = ω 0 2 − γ 2 {displaystyle omega _{f}={sqrt {omega _{0}^{2}-gamma ^{2}}}} — частота свободных колебаний.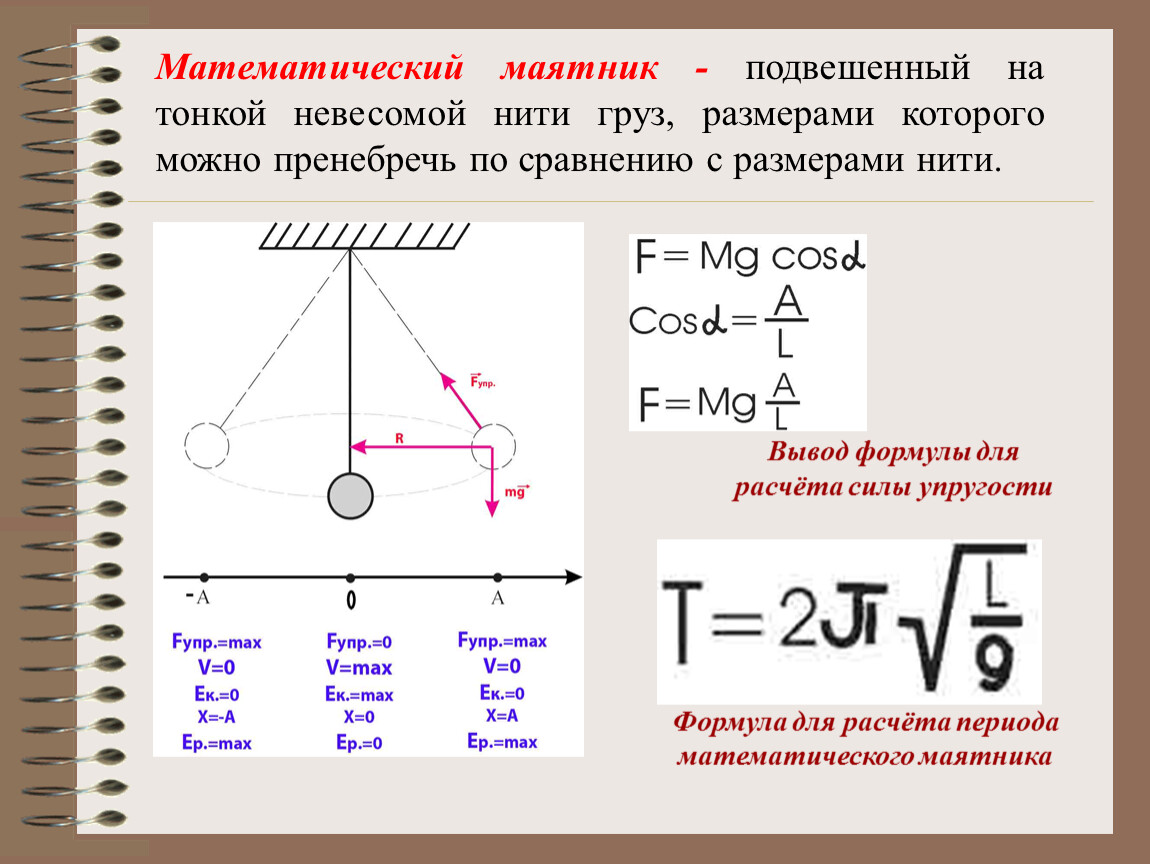 {2}}}.}

Движение при наличии затухания

Характер движения затухающего осциллятора зависит от постоянной затухания γ {displaystyle gamma } . Помимо указанной постоянной, затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой Q {displaystyle Q} . По определению, добротность равна:

Q = ω 0 2 γ . {displaystyle Q={frac {omega _{0}}{2gamma }}.}

Чем выше добротность, тем медленнее затухают колебания осциллятора.

Критическое затухание γ = ω 0 {displaystyle gamma =omega _{0}} примечательно тем, что именно при таком затухании осциллятор быстрее всего оказывается в положении равновесия. Если трение меньше критического, он дойдёт до положения равновесия быстрее, однако «проскочит» его по инерции и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.

Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы стрелка успокаивалась максимально быстро для считывания его показаний.

У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; теоретически, со временем он пересечёт положение равновесия неограниченное количество раз. Добротность, меньшая или равная 0,5, соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.

Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной частотой колебаний их амплитуда устанавливается примерно в Q {displaystyle Q} раз больше, чем при возбуждении с той же интенсивностью на низкой частоте.

Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в e {displaystyle e} раз, умноженному на π {displaystyle pi } .

В случае колебательного движения затухание ещё характеризуют такими параметрами, как:

• Время жизни колебаний (оно же время затухания, оно же время релаксации) τ — время, за которое амплитуда колебаний уменьшится в e раз.

τ = 1 / γ . {displaystyle au =1/gamma .} Это время рассматривается как время, необходимое для затухания (прекращения) колебаний (хотя, формально, свободные колебания продолжаются бесконечно долго).

• Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону: d = ln ⁡ ( x max n / x max n + 1 ) . {displaystyle d=operatorname {ln} (x_{{ ext{max}};n}/x_{{ ext{max}};n+1}).} Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.

Замечание о вынужденных колебаниях гармонического осциллятора

Колебания осциллятора называют вынужденными, когда на него производится некоторое дополнительное воздействие извне. Это воздействие может производиться различными средствами и по различным законам. Например, силовым возбуждением называется воздействие на груз силой, зависящей только от времени по определённому закону. Кинематическим возбуждением называют воздействие на осциллятор движением точки закрепления пружины по заданному закону. Возможно также воздействие трением, когда, например, среда, с которой груз испытывает трение, совершает движение по заданному закону.

---

• Сморгоньсиликатобетон
• Акиндинов, Алексей Петрович
• Флаг Арканзаса
• Блиок, Андрей Андреевич
• Dragon Age (серия игр)
• Военно-морские силы Республики Абхазия
• Кадоно, Эйко
• Гудивок, Пётр Михайлович
• Нёльтинг, Эрик
• Станнан

Физика — восстанавливающая сила и силовая постоянная

Введение

Возможно, вам знаком термин «сила». Любое притяжение, трение или отталкивание любой массы можно назвать силой. Здесь глубоко обсуждается тема восстановления силы со всеми необходимыми примерами. Возвращающая сила – это притяжение точки равновесия к удаленной от нее массе. Возвращающая сила также известна как простое гармоническое движение. Обычно это представляется как F=-kx. Роберт Гук впервые определил эту формулу. Формула содержит константу пропорциональности, известную как постоянная силы или постоянная пружины. Что касается жесткости пружины, Гук утверждает, что, когда объект гибко деформируется, смещение, соответствующее деформационной нагрузке, пропорционально.

Восстанавливающая сила 

В соответствии с этим термином восстанавливающая сила представляет собой притяжение положения равновесия к движущейся массе для восстановления размера, формы или положения. Проще говоря, возвращающая сила возвращает частицы в их равновесное состояние. Эта сила действует на частицы массы, которые удаляются от своей начальной точки. Например, когда маятник в часах выключается, он перестает двигаться и его положение возвращается в точку равновесия, т. е. в центр. Кроме того, восстанавливающая сила также называется простым гармоническим движением.

Во-первых, Простое Гармоническое Движение — это своего рода периодическое движение, при котором частица с восстанавливающей силой, пропорциональной смещению ее величины, действует в направлении положения равновесия объекта.

В простой формуле гармонического движения восстанавливающая сила может быть обозначена как F = -kx, где сила обозначена как «F», а расстояние — как «x». «К» называется константой пропорциональности. Эта константа называется константой Spring. Кроме того, в формуле стоит знак минус и возникающая возвращающая сила противодействует смещению массы и притягивает к положению равновесия.

Возвращающая сила также является одной из основных составляющих колебаний. В колебательной системе восстанавливающая сила постоянно толкает ее к положению равновесия. Когда объект стремится к равновесию, восстанавливающая сила толкает и увеличивает его скорость. Частица может наблюдать простое колебание с восстанавливающей силой, пропорциональной смещению.

Постоянная силы

Постоянная силы — это константа, которая используется при расчете восстанавливающей силы. Эта постоянная силы является константой пропорциональности и называется константой пружины. Более того, эта константа обычно обозначается «k». Эта константа была впервые представлена ​​в юриспруденции Робертом Гуком, британским физиком в 17 веке.

• Закон Гука

В двух словах закон Гука описывает, что материалы эластичны только тогда, когда сила и перемещение пропорциональны. Этот закон также известен под названием «Закон эластичности». Закон Гука гласит, что величина смещения пропорциональна силе деформации или нагрузке при сравнительно небольшой упругой деформации предмета. Изделие сохраняет свою форму и размер всякий раз, когда давление сбрасывается в этих условиях.

Он также пропорционален приложенной силе, вызывающей минимальные смещения компонентов, частиц или ионов из их стандартных положений.

Иллюстрации

Простые гармонические движения можно наблюдать в повседневной деятельности. Возьмем, к примеру, прыжки с тарзанки: эластичность шнура тарзанки заставляет прыгуна колебаться вверх и вниз, изображая простое гармоническое движение.

Точно так же гитара и другие струнные музыкальные инструменты также отражают СГМ. Всякий раз, когда струна смещается и колеблется, ее точка равновесия притягивает ее обратно, когда она возвращается в свое положение, в свое простое гармоническое движение.

Если требуется усилие в 15000 ньютонов, чтобы оттянуть пружину на 50,0 см от положения равновесия, какова постоянная силы пружины?

• Во-первых, применяя общую формулу закона Гука,

Сила = – Постоянная пружины * Расстояние

Следовательно, постоянная пружины = -ForceDistance 

= -15000 Ньютон / 0,50 м (50 см = 0,50 м)

= -30000 Ньютон на метр

Хотя, теперь мы можем скажи это сила 15000 ньютон на расстоянии 50 см от положения равновесия имеет константу пропорциональности -30000 ньютон для восстанавливающей силы.

Заключение

Мы рассмотрели все важные аспекты восстановления силы и постоянной силы и рассмотрели несколько примеров. Теперь мы можем сказать, что восстанавливающая сила — это сила, которая притягивает любую движущуюся массу к ее равновесию или исходному положению. Кроме того, формула восстанавливающей силы F = -kx имеет Константу пропорциональности (т.е. «k»), часто называемую константой пружины. Возвращающая сила также известна как простое гармоническое движение, которое является одной из основных составляющих колебаний. Мы также изучили закон Гука, формулу восстанавливающей силы и восстанавливающую силу при колебаниях.

Восстановление силы: обзор, уравнение, примеры

Вы когда-нибудь видели, как кто-то прыгает с тарзанки? Они прыгают с моста через реку, прикрепленные к пружинному шнуру, который заставляет их колебаться вверх и вниз после того, как они почти достигают поверхности реки. В этом случае сила, вызывающая колебания, представляет собой силу пружины, вызванную натяжением гибкого эластичного шнура. Когда человек начинает раскачиваться взад-вперед, действуя как маятник, сила, порождающая колебания, — гравитация. В этой статье мы обсудим восстанавливающие силы, некоторые примеры и их важность, поскольку они являются необходимым условием для простого гармонического движения.

Определение восстанавливающей силы

В физике говорят, что объект находится в равновесии, если на него не действует результирующая сила. Это может произойти, когда величина и направление сил, действующих на объект, идеально сбалансированы или просто потому, что на объект не действуют никакие силы. Не все силы пытаются вернуть объект обратно в равновесие, но силы, которые делают это, называются восстанавливающими силами .

Возвращающая сила — это сила, действующая против смещения, чтобы попытаться вернуть систему в равновесие.

Возвращающая сила — это функция, зависящая от положения объекта или системы. Этот тип силы отвечает за генерацию колебаний и необходим для того, чтобы объект двигался в простом гармоническом движении. Возвращающая сила — это то, что вызывает изменение ускорения объекта при простом гармоническом движении. Смещение от положения равновесия приводит к тому, что система запасает потенциальную энергию.

Дифференциальное уравнение второго порядка, описывающее простое гармоническое движение в одном измерении, вытекает из второго закона Ньютона, так что \(а\), ускорение объекта и восстанавливающая сила, действующая на объект, испытывающий простое гармоническое движение, будут связанные с \(\omega\), угловой частотой и \(x\) положением колеблющегося объекта как такового: 92x$$

Примеры: Пружины и маятники

Когда вы берете предмет, прикрепленный к пружине, вытягиваете его на расстояние от положения равновесия и отпускаете, восстанавливающая сила возвращает предмет обратно в равновесие. Для системы пружина-масса в горизонтальном столе единственная сила , действующая на массу в направлении смещения, представляет собой восстанавливающую силу пружины

.

Используя второй закон Ньютона, мы можем составить уравнение движения объекта. 2}.$$ 92=\frac km,$$ или явно как

$$\omega=\sqrt{\frac km}.$$

Пружина \(12\;\mathrm{cm}\) имеет жесткость пружины \ (400 \; {\ textstyle \ frac {\ mathrm N} {\ mathrm m}} \). Какая сила требуется, чтобы растянуть пружину до длины \(14\;\mathrm{см}\)?

Смещение имеет величину

$$x=14\;\mathrm{см}\;-\;12\;\mathrm{см}=2\;\mathrm{см}=0,02\;\mathrm m$$

Сила пружины имеет величину

$$F_s=kx=(400\;{\textstyle\frac{\mathrm N}{\mathrm m}})(0,02\;\mathrm m)= 8\;\mathrm N$$

Второй пример, который мы будем обсуждать, касается простого маятника. Простой маятник состоит из массы, которая качается вокруг положения равновесия, подвешенного на стержне. Возвращающая сила создается силой тяжести.

Как мы видим на изображении выше, восстанавливающая сила является составляющей силы тяжести, которая антипараллельна смещению маятника . Это уравнение получается с помощью тригонометрических соотношений и геометрии системы. 9\circ\;\mathrm{или}\;\mathrm{rad})\).

Чтобы объект считался гармоническим осциллятором, восстанавливающая сила должна быть пропорциональна смещению. В данном случае она пропорциональна силе тяжести и синусу угла смещения \(\theta\). Однако в некоторых случаях движение простого маятника считается движением простого гармонического движения.

Когда угол смещения очень мал, синус угла смещения можно аппроксимировать как сам угол, такое, что \(\sin\left(\theta\right)\приблизительно\theta\). В этом случае возвращающая сила пропорциональна смещению.

Теперь мы можем рассмотреть дифференциальное уравнение, используемое для описания движения простого маятника при малом угле смещения. Во-первых, нам нужно ввести понятие длины дуги, чтобы решить дифференциальное уравнение.

Длина дуги — это расстояние между двумя точками на кривой.

Опять же, мы начинаем подход со второго закона Ньютона, который определяется как 92=\frac gL,$$

или явно как

$$\omega=\sqrt{\frac gL}.