Определение момента инерции твердого тела методом крутильных колебаний
Лабораторная работа 7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА
МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
Цель работы: определить момента инерции твердого тела методом крутильных колебаний.
Оборудование: лабораторная установка — крутильный маятник.
1. ОБЩИЕ СВЕДЕНИЯ
Вращательным движением твердого тела называется такое движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения
В твёрдом теле все точки жестко связаны между собой и могут вращаться вокруг неподвижной оси под действием момента внешней силы. При этом вектор момента силы М и вектор углового ускорения ε всегда направлены в одну сторону и справедлив основной закон динамики вращательного движения
M = I ε
где I — момент инерции твердого тела относительно неподвижной
оси вращения, кг· м
Момент инерции I характеризует инертные свойства твердого тела при вращательном движении и зависит от распределения массы тела относительно оси вращения.
Рассмотрим твёрдое тело и выделим в нём материальную точку массой mi. Её удаление от оси вращения обозначим через ri (рис. 1). Тогда линейная скорость этой точки равна
vi = ωiri, где ωi — угловая скорость вращения, рад/с.
Момент импульса относительно оси вращения равен
Li = miViri = miriωi.
Величина равная Ii = miri2 называется
моментом инерции материальной точки.
Для твёрдого тела моменты импульсов складываются по всем материальным точкам, образующим это тело. Тогда суммарный момент импульса равен
или
L = Iω.
Здесь
и есть момент инерции твердого тела относительно оси вращения.
Суммирование производится по всем материальным точкам, входящих в твердое тело.
Практически вычисление такой суммы сводится к вычислению соответствующего интеграла, что для однородных тел симметричной формы труда не составляет, то есть
где ρ — плотность, кг/м3, V — объем, занимаемый телом, м3.
Интегрирование производится по всему объёму тела.
Для любого твёрдого тела можно указать три взаимно
перпендикулярные оси, проходящие через его центр инерции. Эти оси называются
главными осями тела. А момент инерции относительно любой оси вращения
выражается через моменты инерции тела относительно этих главных осей.
Главные оси просто определить для однородных симметричных тел (шара, куба, параллелепипеда и т.д.). Главные оси инерции таких тел всегда совпадают с осями симметрии тела.
Например, главные оси однородного прямоугольного параллелепипеда проходят через его геометрический центр перпендикулярно граням (рис. 2).
Для тел сложной формы главные оси и моменты инерции определяют экспериментально.
Если известны главные оси твердого тела, то с ними связывают прямоугольную систему координат
Возьмём произвольную ось вращения, проходящую через центр инерции, ось ОС (рис. 3).
Момент инерции тела относительно оси ОС выражается через моменты инерции главных осей, то есть
I= Ix cos2α + Iy сos2 + Iz cos2 γ (1)
где Ix, Iy, Iz

Моменты инерции Ix, Iy, Iz определяются экспериментально. Момент инерции тела относительно произвольной оси вращения находится простым суммированием по формуле (1).
Момент инерции тела зависит от выбора оси вращения. Однако это не значит, что для всякой новой оси момент инерции следует вычислять заново.
Если известен момент инерции тела относительно оси, проходящей через центр инерции, то момент инерции тела относительно любой оси, параллельной первой и смещенной на расстояние
где I0 — момент инерции относительно оси вращения, проходящей через центр инерции, кг · м3; m — масса тела, кг; d — расстояние между осями, м.
Используемый в лабораторной работе крутильный маятник позволяет определить момент инерции тел любой формы.
Такой маятник представляет собою рамку, подношенную на
тонкой упругой струне.
Mупр = —D Θ, где Θ — угол поворота рамки, рад; D — коэффициент, характеризующий момент упругих сил, Н · м.
При достаточно тонкой и длинной струне зависимость М(Θ) выполняется и для больших углов поворота, а затухания при крутильных колебаниях можно считать малыми.
Пренебрегай затуханиями, движение рамки записывают уравнением для свободных незатухающих колебаний
или
(2)
где — угловое ускорение, рад · с2, вторая производная по времени от угла попорота; ω0 — циклическая частота колебаний, рад/с. Циклическая частота колебаний выражается как
Период таких колебаний равен
(3)
Решение дифференциального уравнения (2) имеет вид
где Θ0 — угловая амплитуда колебаний, рад; α — начальная фаза
колебаний, рад.
Если известен момент инерции I, то найти период колебаний рамки не составляет труда, а следовательно, и найти постоянную
В данной лабораторной работе постоянная D не определяется. Для нахождения момента инерции рамки используется тело с известным моментом инерции. В качестве такого тела взят куб с достаточно идеальными поверхностями и гранями. Его момент инерции относительно оси, походящей через центр, вычисляется по формуле
(4)
где m — масса куба, кг, а — сторона куба, м.
Такой куб жестко закрепляется в рамке крутильного маятника. Если вывести нагруженную рамку из положения равновесия, то она будет совершать крутильные колебания, а её период колебаний равен
Страница не найдена
Поиск по сайту Авторизация
|
|
Семинары Окт 14, 2022 Семинар «Прикладная гидродинамика» Окт 14, 2022 Семинар Гемодинамика Уважаемые коллеги, Во вторник 18го октября в 14:30 НСК с докладом «Исследование механики стенок… | ||||||||||||||||
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 4 из 9Следующая ⇒ Контрольные вопросы 1. Что значит вращательное движение твердого тела? 2. Что характеризует момент инерции тела и как его вычислить? Вспомните формулы для вычисления моментов инерции стержня, диска, цилиндра, обруча, шара, сферы относительно оси вращения, проходящей через центр масс. 3. Что характеризует момент силы? Как направлен вектор момента силы и чему равен его модуль? 4. Запишите основной закон динамики вращательного движения твердого тела. 5. Что такое момент импульса? Чему равен момент импульса вращающегося тела относительно оси вращения? Как направлен вектор момента импульса? 6. Сформулируйте закон сохранения момента импульса и приведите примеры его проявления. 7. Как вычислить кинетическую энергию вращающегося тела? 8. Чему равна работа силы при вращательном движении?
Основные формулы
Момент М силы F относительно оси вращения u определяется формулой , где – радиус-вектор, проведенный от оси вращения в точку приложения силы.
Модуль , где d — плечо силы (кратчайшее расстояние между линией действия силы и осью вращения).
Момент инерции материальной точки относительно оси вращения где m – масса материальной точки и r – ее расстояние до оси вращения,
Момент инерции твердого тела относительно его оси вращения где интегрирование должно быть распространено на всю массу тела.
Момент инерции сплошного однородного цилиндра (диска) относительно оси цилиндра где – радиус цилиндра и – его масса.
Момент инерции полого цилиндра (толстого кольца) c внутренним радиусом и внешним относительно оси цилиндра для тонкостенного полого цилиндра (обруча) Момент инерции однородного шара радиусом R относительно оси, проходящей через его центр, .
Момент инерции однородного стержня относительно оси, проходящей через его середину перпендикулярно к нему, . Если для какого-либо тела известен его момент инерции Jc относительно оси, проходящей через центр масс, то момент инерции относительно любой оси, параллельной первой, может быть найден по формуле Штейнера , где m – масса тела, d – расстояние между осями.
Момент импульса материальной точки относительно оси определяется , где — импульс материальной точки.
Модуль , где Ju— момент инерции точки относительно оси u.
Аналогично и для твердого тела .
Основной закон динамики вращательного движения выражается уравнением , где М – момент внешних сил, приложенных к телу, L – момент импульса тела, J – момент инерции тела, w – его угловая скорость. Если J = const, то , где e – угловое ускорение, приобретаемое телом под действием момента сил М (второй закон Ньютона для вращательного движения).
Закон сохранения момента импульса (в замкнутой системе) . Кинетическая энергия вращающегося тела , Элементарная работа, совершаемая внешними силами за малый промежуток времени dt, при вращении тела . Полная работа при повороте на угол Dj = j 2 — j1: . При М = constA = M×Δj. Методические указания 1. После краткой записи условия задачи сделать чертеж и указать на нем все силы, действующие на тела системы, все моменты сил и все векторные кинематические характеристики движения. 2. Записать второй закон Ньютона для вращательного движения . Так как в курсе общей физики обычно рассматривается вращение твердого тела лишь вокруг неподвижной оси (или оси, перемещающейся в пространстве параллельно самой себе), то на нее и проектируют векторное уравнение. В этом случае все векторы, характеризующие вращательное движение тела: , направлены вдоль оси вращения. 3. Для тел, движущихся поступательно, записывают второй закон Ньютона в форме и проектируют его на выбранные оси координат (обычно на одну ось). 4. Используя кинематические связи между телами и соотношения между линейными и угловыми характеристиками, упрощают записанные уравнения и добиваются, чтобы их число было равно числу неизвестных. Решая их, находят искомые величины. 5. Закон сохранения механической энергии, при решении задач на вращательное движение, применяется особенно в тех случаях, когда законы вращения сложны или даже неизвестны. Следует помнить, что полная кинетическая энергия твердого тела складывается из кинетической энергии его поступательного движения со скоростью центра масс и кинетической энергии вращения вокруг оси, проходящей через центр масс. 6. Закон сохранения момента импульса при вращательном движении, как и закон сохранения импульса при поступательном движении, позволяет исключить из рассмотрения внутренние силы. Этот закон справедлив для системы, если она замкнута или результирующий момент всех внешних сил, действующих на систему, равен нулю. ЗАДАЧИ 67. К ободу однородного диска радиусом 0,2 м приложена касательная сила 98,1 H. При вращении на диск действует момент сил трения 4,9 Н×м. Найти массу диска, если известно, что диск вращается с угловым ускорением 100 рад/с2. [7,36 кг] 68. Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно к его плоскости. Зависимость угловой скорости вращения диска от времени дается уравнением w = A +Вt, где В = 8 рад/с2. Найти касательную силу F, приложенную к ободу диска. Трением пренебречь. [4,0 Н] 69. Маховик, момент инерции которого 63,6 кг×м2, вращается с угловой скоростью 31,4 рад/с. Найти момент сил торможения, под действием которого маховик останавливается через 20 с. Маховик считать однородным диском. [100 Н×м] 70. К ободу колеса, радиусом 0,5 м и массой 50 кг, приложена касательная сила 98,1 Н. [7,8 рад/с2; 80 с] 71. Маховое колесо, момент инерции которого 245 кг×м2, вращается с частотой 20 об/с. Через 1 минуту после того, как на колесо перестал действовать момент сил, оно остановилось. Найти момент сил трения и число оборотов, которое сделало колесо до полной остановки после прекращения действия сил. Колесо считать однородным диском. [513 Н×м; 600 об.] 72. Две гири с массой 2 кг и 1 кг соединены нитью, перекинутой через блок массой 1 кг. Найти ускорение, с которым движутся гири, и силы натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь. [2,8 м/с2; 14 Н; 12,6 Н] 73. Две гири с разными массами соединены нитью, перекинутой через блок, момент инерции которого 50 кг×м2 и радиус 20 см. [ 1,08 кН] 74. Блок массой 1 кг укреплен на конце стола. Гири 1 и 2 одинаковой массы по 1 кг соединены нитью, перекинутой через блок. Коэффициент трения гири 2 о стол k = 0,1. Найти ускорение, с которым движутся гири, и силы натяжения нитей. Блок считать однородным диском. Трением в блоке пренебречь. [3,53 м/с2; 6,3 Н; 4,5 Н] 75. Диск массой 2 кг катится без скольжения по горизонтальной плоскости со скоростью 4 м/с. Найти кинетическую энергию диска. [24 Дж] 76. Обруч радиуса r скатился без проскальзывания с горки высотой h. Найти скорости и ускорения точек A и B обода. (А — наивысшая точка обода, В — находится на 1/4 окружности по направлению вращения). [ ; ; ] 77. На вертикальной оси укреплена горизонтальная штанга, по которой могут свободно перемещаться два груза с массами m1 и m 2, связанные нитью длины l. Система вращается с угловой скоростью w. На каких расстояниях от оси будут находиться грузы в равновесии? Чему равны при этом сила натяжения нити и кинетическая энергия грузов? Вернутся ли грузы в положение равновесия, если их сместить из этого положения на малое расстояние? [ ; ; равновесие неустойчивое; ; ] 78. Шар диаметром 6 см и массой 0,25 кг катится без скольжения по горизонтальной плоскости с частотой вращения 4 об/с. Найти кинетическую энергию шара. [Eк= 0,1 Дж] 79. Диск диаметром 60 см и массой 1 кг вращается вокруг своей оси, проходящей через центр перпендикулярно к его плоскости, с частотой 20 об/с. Какую работу А надо совершить, чтобы остановить диск? [А = -355 Дж] 80. [L = 3,8 кг×м2/с] 81. Найти кинетическую энергию велосипедиста, едущего со скоростью 9 км/ч. Масса велосипедиста вместе с велосипедом 78 кг, причем на колеса приходится масса 3 кг. Колеса велосипеда считать обручами. [Ек = 253 Дж] 82. Мальчик катит обруч по горизонтальной дороге со скоростью 7,2 км/ч. На какое расстояние может вкатиться обруч на горку за счет его кинетической энергии? Уклон горки равен 10 м на каждые 100 м пути. [S = 4,1 м] 83. Тело массой m совершает мертвую петлю, соскальзывая с минимально необходимой для этого высоты. С какой силой тело давит на опору в точке А, радиус-вектор которой составляет угол a с вертикалью? Трением пренебречь. [ Fн = 3mg(1- cos a)] 84. [ = 7,56 м ] 85. Автомобиль массой 1000 кг движется со скоростью 36 км/ч по выпуклому мосту, имеющему радиус кривизны 50 м. С какой силой давит автомобиль на мост в середине? С какой минимальной скоростью должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост? [7,8 кН; ~ 80км/ч ] 86. Автомобиль массой 2000 кг движется со скоростью 36 км/ч по вогнутому мосту, имеющему радиус кривизны 100 м. С какой силой давит автомобиль на мост в середине? [21,6 кН] 87. Найти линейные скорости движения центров масс шара, диска и обруча, скатывающихся без скольжения с наклонной плоскости. Высота наклонной плоскости 0,5 м, начальная скорость всех тел равна нулю. [ ; v1 = 2,65 м/с; v 2 = 2,56 м/с; v 3 = 2,21 м/с; =3,13 м/с ] 88. Колесо, вращаясь равнозамедленно, уменьшило за 1 мин частоту вращения от 300 об/мин до 180 об/мин. Момент инерции колеса равен 2 кг×м2. Найти угловое ускорение колеса, момент сил торможения, работу сил торможения и число оборотов, сделанных колесом за 1 мин. [e = — 0,21 рад/с2; M = — 0,42 Н×м; A = — 630 Дж; N = 240 об.] 89. Однородный стержень длиной 85 см подвешен к горизонтальной оси, проходящей через верхний конец стержня. Какую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси? [v = 7,1 м/с ] 90. Горизонтальная платформа массой 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 10 об/мин. [n2 = 22 об/мин ] 91. Горизонтальная платформа массой 80 кг и радиусом 1 м вращается с частотой 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от 2,94 до 0,98 кг×м 2? Считать платформу однородным диском. [n2 = 21 об/мин ] 92. Человек массой 60 кг находится на неподвижной платформе массой 100 кг. С какой частотой будет вращаться платформа, если человек будет двигаться по окружности радиусом 5 м вокруг оси вращения? Скорость движения человека относительно платформы 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека — точечной массой. [n = 0,49 об/мин] ⇐ Предыдущая123456789Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
|
Последнее изменение этой страницы: 2017-01-20; просмотров: 494; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. |
Момент инерции в зависимости от массы
Введение в момент инерцииСуществует множество аналогий при сравнении линейного и вращательного движения. В основе этих сравнений лежат понятия массы с одной стороны и момента инерции с другой. Масса не только является свойством любого физического объекта, но и является мерой сопротивления объекта ускорению, когда к объекту приложена результирующая сила. Второй закон Ньютона выражает это в известном уравнении 9.0003 F = мА. По аналогии, момент инерции любого твердого объекта – это мера его сопротивления угловому ускорению относительно оси, когда к объекту прикладывается крутящий момент. Это выражается уравнением τ = Iα .
Момент инерции можно определить по уравнению0004 . Для непрерывных жестких объектов уравнение будет аналогичным, но с использованием интегралов вместо суммы. Следует отметить, что по определению момент инерции тела зависит не только от конкретной оси, вокруг которой оно вращается, но и от его формы и от того, как распределена его масса.
Следует отметить, что по определению момент инерции тела зависит не только от конкретной оси, вокруг которой оно вращается, но и от его формы и от того, как распределена его масса.
В этом уроке вы будете сравнивать моменты инерции двух объектов с одинаковыми массами . Вы начнете с использования своих навыков изготовителя, а также некоторых базовых математических навыков, включая алгебру и геометрию. Вы создадите два плоских объекта из картона. Один из объектов будет круглым диском радиуса 3,5″. Другой объект будет кольцом, внешний радиус которого также равен 3,5″, , но масса которого равна массе диска . На рис. 1 показана схема с двумя такими объектами.
Рисунок 1 – Плоский диск и плоское кольцо Вы хотите определить толщину x кольца, так что , когда два таких концентрических кольца склеены вместе , масса диска будет идентична массе пары концентрических колец. Вы вырежете диск и два кольца из трех листов картона. Вы можете предположить, что бумаги для карточек имеют одинаковую толщину с равномерным распределением массы.
Вы вырежете диск и два кольца из трех листов картона. Вы можете предположить, что бумаги для карточек имеют одинаковую толщину с равномерным распределением массы.
Хорошо, теперь применим математические и геометрические навыки, чтобы определить значение x ! Затем вырежьте плоские объекты из картона и соберите кольцо. Если вы правильно рассчитали, диск и кольцо в сборе должны быть очень близки к одной и той же массе при размещении на весах.
Задание №2. Определение периода дискового и кольцевого маятников Теперь, когда у вас есть два объекта одинаковой формы, но с разным распределением масс, вы готовы к первому шагу по определению их моментов инерции. Вы будете рассматривать каждый объект как физический маятник — любое твердое тело, которое качается в вертикальной плоскости вокруг оси, проходящей через это тело. На рис. 2 показан произвольный физический маятник и его физическая теория. Уравнение в рамке позволяет определить момент инерции I любого объекта относительно любой конкретной точки поворота на этом объекте. T, G и d поддаются измерению, а g известно.
T, G и d поддаются измерению, а g известно.
Вы будете измерять период T с помощью магнитометра PocketLab. Крошечный магнит, прикрепленный скотчем к нижней части физического маятника, будет вызывать внезапный пик магнитуды магнитного поля каждый раз, когда он проходит мимо PocketLab, пока маятник качается вперед и назад. На рис. 3 показаны изображения экспериментальной установки для двух объектов одинаковой массы. В обоих случаях были выбраны похожие опорные точки — опорные точки близко к краю объекта. Маятники качаются на металлическом стержне, который проходит через небольшие отверстия, пробитые в маятниках. Использование металлического стержня желательно и помогает снизить трение в точке поворота.
Рисунок 3. Два одинаковых маятника с одинаковой массой, но с разным распределением массы Для пояснения механизма поворота на рисунке 4 показан вид устройства под углом. Шарнир представляет собой тонкий металлический стержень, закрепленный на кольцевой стойке. Также используется деревянный стержень для дюбеля (или что-то подобное), так как винт зажима не вкручивается достаточно сильно, чтобы прижать металлический стержень к зажиму. Следует надевать защитные очки, чтобы предотвратить любую возможность попадания в глаза тонкого металлического стержня.
Также используется деревянный стержень для дюбеля (или что-то подобное), так как винт зажима не вкручивается достаточно сильно, чтобы прижать металлический стержень к зажиму. Следует надевать защитные очки, чтобы предотвратить любую возможность попадания в глаза тонкого металлического стержня.
Для успеха в этом эксперименте необходимо точное измерение периода T каждого из двух ваших маятников. PocketLab позволяет рассчитать период физического маятника гораздо точнее, чем это возможно с помощью секундомера. Использование PocketLab для этой цели исключает ошибки, связанные со временем реакции при запуске и остановке секундомера. PocketLab также должен быть настроен на максимально возможную скорость передачи данных (50 точек в секунду). Убедитесь, что вы измеряете время за несколько периодов, а затем находите среднее значение. На рис. 5 показано, как это можно сделать.
Рисунок 5 – Нахождение периода путем усреднения Теперь вы должны быть готовы к измерению периодов двух ваших физических маятников. Эти данные имеют решающее значение для успеха в этом эксперименте!
Эти данные имеют решающее значение для успеха в этом эксперименте!
Теперь, когда вы определили период для двух ваших физических маятников, вы готовы вычислить экспериментальные моменты инерции, используя уравнение в рамке в нижней части рисунка 2. . Вам нужно будет измерить массу каждого маятника. (Помните, что массы должны быть очень близки к одному и тому же значению!) Вам также необходимо измерить расстояние от точки вращения до центра масс каждого маятника. Вы можете использовать принятое значение 90,81 м/с/с для ускорения g силы тяжести. Обязательно выражайте все измерения в системе МКС (метр-килограмм-секунда). Что такое единица измерения MKS для момента инерции? (Подсказка: посмотрите на определяющее уравнение для момента инерции.)
Задача № 4 — Определение теоретических моментов инерции легко доступны в Интернете. Эти теоретические моменты инерции определяются с помощью интегрального исчисления, детали которого не важны для нашего исследования. Рисунок 6 суммирует теоретический момент уравнений инерции относительно центра масс для плоского диска и кольца. Однако наш диск и кольцо не вращались вокруг соответствующих центров масс. Они вращались вокруг оси очень близко к своим внешним краям . Помните, что момент инерции зависит не только от массы и от того, как она распределена, но и от конкретной оси, вокруг которой она вращается.
Рисунок 6 суммирует теоретический момент уравнений инерции относительно центра масс для плоского диска и кольца. Однако наш диск и кольцо не вращались вокруг соответствующих центров масс. Они вращались вокруг оси очень близко к своим внешним краям . Помните, что момент инерции зависит не только от массы и от того, как она распределена, но и от конкретной оси, вокруг которой она вращается.
Как оказалось, существует простая и чрезвычайно полезная теорема, известная как Теорема о параллельных осях 9.0009 , который выражает отношение между моментом инерции I объекта относительно любой оси и его моментом инерции относительно параллельной оси , проходящей через центр масс. Если Ic — момент инерции относительно центра масс, m — масса объекта, а w — расстояние между двумя осями, эта теорема говорит нам, что момент инерции I определяется выражением уравнение
Используйте теорему о параллельных осях вместе с некоторой алгеброй и уравнениями на рисунке 6, чтобы определить уравнения для момента инерции относительно точки вблизи края плоского диска и кольца. Если ваши оси расположены очень близко к внешнему краю диска и кольца, то можно считать, что w равно внешнему радиусу.
Если ваши оси расположены очень близко к внешнему краю диска и кольца, то можно считать, что w равно внешнему радиусу.
Наконец, вычислите теоретические значения этих моментов инерции из ваших уравнений.
Рисунок 6. Моменты инерции относительно центра масс для диска и кольца Задача № 5. Определите процентную разницу между экспериментальным и теоретическим моментами инерцииСравнение должно быть выражено как процентная разница между экспериментальным и теоретический момент инерции относительно осей вблизи краев, основанный на части теоретического момента инерции. Разница в процентах будет отрицательной, если ваш экспериментальный результат меньше теоретического, и положительной, если экспериментальный результат больше теоретического.
Задание № 6. Сравните моменты инерции диска и кольца и обсудите причины любых различий Ваш экспериментальный момент инерции кольца относительно оси его края больше, чем момент инерции диска относительно его края ось? Так и должно быть, если период для кольца был больше периода диска. Проведите обсуждение, которое интуитивно подсказывает, что момент инерции кольца должен быть больше момента инерции диска.
Проведите обсуждение, которое интуитивно подсказывает, что момент инерции кольца должен быть больше момента инерции диска.
Динамика вращения падающего измерительного стержня
PocketLab Voyager: эксперимент с маховиком
PocketLab Voyager: момент инерции и сохранение углового момента: момент инерции
Физический маятник: нахождение момента инерции
Вращение твердых тел | SpringerLink
Мгновенная мощность, передаваемая для вращения объекта вокруг фиксированной оси, находится из
$$ P=\frac{dW}{dt}=\frac{\tau _{z}d\theta}{dt}=\tau _{z}\omega _{z} $$
Табл. 7.2 приведены аналогичные уравнения для линейного движения и вращательного движения вокруг неподвижной оси
Пример 7.14
Диск радиусом \(R=0,08 \; \mathrm{m}\) и массой 5 кг вращается вокруг своей центральной оси с угловая скорость 170 об/мин. Найти: а) кинетическую энергию вращения диска; (b) Предположим, что тот же самый диск вращается с помощью двигателя, развивающего мгновенную мощность 0. \(2\mathrm {h}\mathrm {p}\), найдите в этом случае крутящий момент, приложенный к диску. 9{2}=2,5 \; \mathrm {J} $$
Найти: а) кинетическую энергию вращения диска; (b) Предположим, что тот же самый диск вращается с помощью двигателя, развивающего мгновенную мощность 0. \(2\mathrm {h}\mathrm {p}\), найдите в этом случае крутящий момент, приложенный к диску. 9{2}=2,5 \; \mathrm {J} $$
(b)
$$ P=(0,2 \; \mathrm {h}\mathrm {p}\ ) \bigg (\frac{746 \; \mathrm {W}}{ 1\mathrm{h}\mathrm{p}}\bigg)=149,2\; \mathrm {W} $$
и
$$ \tau =\frac{P}{\omega }=\frac{(149,2 \; \mathrm {W})}{(17,8 \; \mathrm {r }\mathrm {a}\mathrm {d}/\mathrm {s})}=8,4 \; \mathrm {N}\,\mathrm {m} $$
Пример 7.15
Рассмотрим легкую веревку, намотанную на однородную цилиндрическую оболочку массой 30 кг и радиусом 0,2 \(\mathrm {m}\), как на рис. 7.22. Предположим, что цилиндр может свободно вращаться вокруг своей центральной оси и что веревку тянут из состояния покоя с постоянной силой, равной 35 Н. Считая, что веревка не проскальзывает, найти: (а) крутящий момент, приложенный к цилиндру примерно его центральная ось; б) угловое ускорение цилиндра; в) ускорение точки разматывающегося каната; (d) число оборотов, совершаемых цилиндром при достижении угловой скорости 12 \(\mathrm {r}\mathrm {a}\mathrm {d}/\mathrm {s}, (\mathrm {e}) \) работа, совершаемая приложенной силой, когда веревку протягивают на расстояние \(1\mathrm {м}, (\mathrm {f})\) работа, выполняемая с использованием теоремы о работе-энергии.
Легкий канат, намотанный на однородную цилиндрическую оболочку
Изображение полного размера
Решение 7.15
(a) Поскольку линия действия как веса, так и нормальных сил проходит через центральную ось цилиндр, они не создают крутящего момента. Следовательно, полный крутящий момент, действующий на цилиндр, равен
$$ \tau =FR=(35 \; \mathrm {N})(0,2 \; \mathrm {m})=7 \; \text {Н/м} $$
(б) Момент инерции цилиндра равен
{2})}=12,4 \; \mathrm {rad} $$или
$$ \theta = (12,4 \; \mathrm {rad}) \bigg (\displaystyle \frac{1 \; \mathrm {r}\mathrm {e}\mathrm {v}}{2\pi \;\mathrm {r}\mathrm {a}\mathrm {d}}\bigg)= 2 \; \text {rev} $$
(e) Если канат переместился на расстояние lm, угловое смещение цилиндра равно
$$ \displaystyle \theta =\frac{s}{R}=\frac{ (1 \; \mathrm {m})}{(0,2 \; \mathrm {m})}=5 \; \mathrm {rad} $$
проделанная работа равна
$$ W=\int _{\theta _{0}}^{\theta}\tau d\theta =\tau (\theta -\theta _ {0})=(7 \; \mathrm {N}\,\mathrm {m})\ ((5 \; \mathrm {r}\mathrm {a}\mathrm {d})-0)=35 \ ; \mathrm {J} $$ 9{\mathrm{o}}\) к горизонтали, найти; а) начальное угловое ускорение стержня при его освобождении; б) начальное ускорение точки на конце стержня; в) по закону сохранения энергии найти угловую скорость стержня в самом нижнем положении (пренебрегая трением на оси).
Однородный стержень, свободно вращающийся на одном конце
Изображение полного размера
Решение 7.16
(a) Поскольку нормальная сила, действующая на стержень со стороны штифта, проходит через ,\), то единственная сила, вносящая вклад в крутящий момент, — это сила тяжести. Эта сила действует на центр тяжести, который находится в центре масс (см. раздел 8.4). Следовательно, чистый внешний крутящий момент равен 9{\circ}+1)}=6,64 \; \mathrm {r}\mathrm {a}\mathrm {d}/\mathrm {s}$$
Рис. 7.24Цилиндр с центральной частью может свободно вращаться вокруг своего центра. Веревки, обернутые вокруг внутренней и внешней секций, действуют с разной силой
Изображение полного размера
Рис. 7.25Блок массой м прикреплен к легкой струне, которая намотана на ободок однородного сплошного диска радиусом R и масса M
Изображение в натуральную величину
Пример 7.
 17
17Найдите чистый крутящий момент в системе, показанной на рис. 7.24, где \(r_{1}=5\) см, \(r_{2}=15\) см, \(F_{1}= 10 \; \mathrm {N}, F_{2}=20 \; \mathrm {N}\) и \(F_{3}=15 \; \mathrm {N}\). Массой и трением канатов и шкивов пренебречь.
Решение 7.17
Поскольку все силы лежат в одной плоскости, чистый крутящий момент равен
$$\begin{aligned} \tau _{\mathrm {n}\mathrm {e}\mathrm {t}}&=\ тау _ {1} + \ тау _ {2} + \ тау _ {3} = (10 \; \ mathrm {N}) (0,05 \; \ mathrm {m}) + (20 \; \ mathrm {N} )(0,05 \; \mathrm {m})\\&-(15 \; \mathrm {N})(0,15 \; \mathrm {m})=-0,75 \; \mathrm {N\, м} \end{aligned}$$
Пример 7.18
Блок массой м прикреплен к легкой струне, которая намотана на ободок однородного сплошного диска радиусом R и массой M , как показано на рис. 7.25. Считая, что струна не проскальзывает и диск вращается без трения, найти: а) ускорение бруска; (б) угловое ускорение диска, и; в) натяжение струны при выводе системы из состояния покоя.
Решение 7.18
Диаграммы свободного тела диска и блока показаны на рис. 7.25. Применение второго закона Ньютона к блоку дает
$$ T-mg=-ma $$
или
$$\begin{aligned} a=\frac{mg-T}{m} \end{align}$$
(7.13)
где положительные \(\mathrm {y}\) выбираются направленными вверх. Применение второго закона Ньютона в угловой форме к диску дает
$$ \tau =RT=I\alpha $$
или
$$ \alpha =\frac{RT}{I} $$
Поскольку ускорение блока равно (тангенциальному) ускорению точки на ободе диска, мы имеем
9{2}-0=0,6 \; \mathrm {J} $$Пример 7.20
На рис. 7.26 показана машина Этвуда с учетом массы шкива. Если систему вывести из состояния покоя (предполагая, что струна не растягивается и не проскальзывает) и трением шкива можно пренебречь, найти линейное ускорение блоков и угловое ускорение шкива.
Рис. 7.26Машина Этвуда
Изображение полного размера
Решение 7.
 {2}\), найдите угловой момент цилиндра при \(t=3\mathrm {s}(\mathrm {c})\) найти приложенный крутящий момент; (d) найти работу, проделанную после \(3\mathrm {s}.\) 9{2}/\mathrm {s} $$
{2}\), найдите угловой момент цилиндра при \(t=3\mathrm {s}(\mathrm {c})\) найти приложенный крутящий момент; (d) найти работу, проделанную после \(3\mathrm {s}.\) 9{2}/\mathrm {s} $$Пример 7.24
Однородный твердый шар радиусом 0,2 \(\mathrm {м}\) вращается вокруг своей центральной оси с угловой скоростью 5 \(\mathrm {r}\mathrm {a}\mathrm {d}/\mathrm {s}\). Если импульсная сила со средним значением 100 \(\mathrm {N}\) действует на край сферы на уровне центра в течение короткого времени 2 \(\mathrm {m}\mathrm {s}\ ):\((\mathrm{a})\) найти угловой импульс силы; б) конечная угловая скорость сферы.
{2})(\omega _{f}-(5 \; \mathrm {r}\mathrm {a}\mathrm {d}/\mathrm {s})) $$Это дает \(\omega _ {f}=5.2 \;\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}.\)
Пример 7.25
Человек стоит на платформе, которая может свободно вращаться без трения вокруг вертикальной оси, как на рис. 7.28. Если система первоначально вращается с угловой скоростью 0,3 \(\mathrm {r}\mathrm {e}\mathrm {v}/\mathrm {s}{:}\,(\mathrm {a})\) найти конечная угловая скорость системы, если груз втягивает человек; б) найти прирост кинетической энергии системы и ее источника.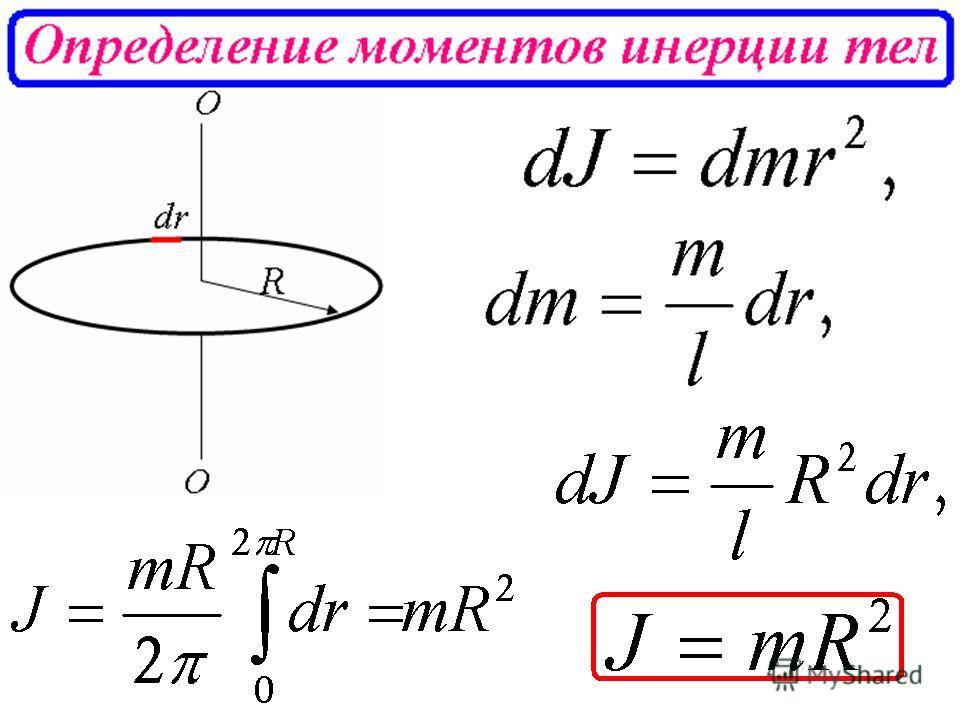 {2}/\mathrm {s})}( 0,3 \;\mathrm {r}\mathrm {e}\mathrm {v}/\mathrm {s})=1,5 \; \mathrm {r}\mathrm {e}\mathrm {v}/\mathrm {s} $$
{2}/\mathrm {s})}( 0,3 \;\mathrm {r}\mathrm {e}\mathrm {v}/\mathrm {s})=1,5 \; \mathrm {r}\mathrm {e}\mathrm {v}/\mathrm {s} $$
(b)
$$ \omega _{i}=\bigg (0,3 \; \frac{\mathrm {r}\mathrm {e}\mathrm {v}}{\mathrm {s}}\bigg ) \bigg (\frac{2\pi \; \mathrm {r}\mathrm {a}\mathrm {d}}{1 \; \mathrm {r}\mathrm {e}\mathrm {v}}\bigg )=1,9 \; \mathrm {r}\mathrm {a}\mathrm {d}/\mathrm {s} $$
$$ \omega _{f}=\bigg (1,5 \; \frac{\mathrm {r}\mathrm {e}\mathrm {v}}{\mathrm {s}}\bigg ) \bigg (\frac{2\pi \; \mathrm {r}\mathrm {a}\mathrm {d}}{1 \; \ mathrm {r} \ mathrm {e} \ mathrm {v}} \ bigg) = 9,4 \; \mathrm {r}\mathrm {a}\mathrm {d}/\mathrm {s} $$ 9{2}\), который изначально находился в покое, падает на первый, оба в конечном итоге будут вращаться с одинаковой угловой скоростью из-за трения между ними. Определить: а) конечную угловую скорость; б) изменение кинетической энергии системы.
Рис. 7.29 Однородный диск, вращающийся без трения. {2}\), найти время, необходимое колесу для изменения направления движения. 9{2}\). При \(t=2 \; \mathrm {s}\) Найдите: а) угловую скорость колеса, б) угол в радианах, на который вращается колесо, в) тангенциальное и радиальное ускорения точки в точке обод колеса.
{2}\), найти время, необходимое колесу для изменения направления движения. 9{2}\). При \(t=2 \; \mathrm {s}\) Найдите: а) угловую скорость колеса, б) угол в радианах, на который вращается колесо, в) тангенциальное и радиальное ускорения точки в точке обод колеса.
Найдите угловую скорость Земли в радианах в секунду относительно (а) ее оси, (б) солнца.
Стержень в форме \(\mathrm {L}\) вращается против часовой стрелки с угловым ускорением \(\omega \) (см. рис. 7.30). Найдите (в векторной форме) линейную скорость и ускорение точки \(\mathrm {P}\) на стержне.
Четыре массы соединены легкими жесткими стержнями, как показано на рис. 7.31. Рассчитайте момент инерции системы относительно (а) оси \(\mathrm {x}\) (б) оси \(\mathrm {y}\) (в) оси \(\mathrm {z} \)-ось.
7.31. Рассчитайте момент инерции системы относительно (а) оси \(\mathrm {x}\) (б) оси \(\mathrm {y}\) (в) оси \(\mathrm {z} \)-ось.
Найти момент инерции однородного твердого шара радиусом R и массой M относительно оси, проходящей через его центр масс.
Найдите момент инерции эллиптического квадранта относительно оси \(\mathrm{y}\) (см. рис. 7.32).
Однородный сплошной цилиндр радиусом 0,2 \(\mathrm {м}\) массой 5 кг вращается вокруг своей оси центра масс с угловой скоростью 10 об/мин. Найдите (а) его кинетическую энергию вращения, (б) его угловой момент.

Колесо массой 20 кг и радиусом 0,75 \(\mathrm {м}\) первоначально вращалось со скоростью 120 об/мин. Если его угловая скорость увеличилась до 300 об/мин за 20 \(\mathrm{s}\), найти: а) работу, совершаемую колесом, б) среднюю мощность, сообщаемую колесу.
Колесо массой 10 кг и радиусом 0,4 \(\mathrm {м}\) равномерно ускоряется из состояния покоя до угловой скорости 800 об/мин за 20 \(\mathrm {с}\). Найдите (а) крутящий момент, приложенный к колесу, (б) работу, совершаемую колесом, (в) работу, совершаемую с помощью теоремы работа-энергия.
Однородный стержень длиной L и массой M вращается в точке \(\mathrm {O}\) (см. рис. 7.33). Если снаряд массой 90 275 м 90 276, движущийся со скоростью 90 275 v 90 276, ударится о стержень и прилипнет к нему, найти момент импульса системы непосредственно перед и сразу после удара.
Диск радиусом 2,2 \(\mathrm {м}\) и массой 120 кг вращается вокруг вертикальной оси без трения, проходящей через его центр. Человек массой 65 кг медленно идет от края диска к центру. Найти угловую скорость диска, когда человек находится на расстоянии 0,7 \(\mathrm {m}\) от центра, если его угловая скорость в момент начала ходьбы человека равна 1,6 \(\mathrm {r}\mathrm {a }\mathrm{d}/\mathrm{s}.\)
. Стровая стержня с помощью L-образного стержня.
Рис. 7.33Однородный стержень длиной L и массой M вращается в точке \(\mathrm {O}\). Снаряд массой м движется со скоростью v сталкивается со стержнем и прилипает к нему
Изображение в натуральную величину
динамический — Расчет инерции многоформового твердого тела
Задавать вопрос
Спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 5 тысяч раз
9
Новинка! Сохраняйте вопросы или ответы и организуйте свой любимый контент.
Узнать больше.
Я подумал, что кто-то, возможно, задавал этот вопрос раньше, но я не смог найти ответ.
Я пишу библиотеку физики для своего игрового движка (2d, в настоящее время в actionscript3, но легко переводится на языки на основе C).
У меня проблемы с поиском хорошей формулы для расчета инерции моих игровых объектов.
Дело в том, что существует множество проверенных формул для расчета инерции вокруг центроида выпуклого многоугольника, но моя структура немного отличается: у меня есть игровые объекты со своим локальным пространством. Вы можете добавить выпуклые формы, такие как круги и выпуклые многоугольники, в это локальное пространство, чтобы сформировать сложные объекты. Сами фигуры снова имеют свое собственное локальное пространство. Итак, есть три слоя: мир, объект и пространство формы.
У меня не возникло бы проблем с расчетом инерции каждого отдельного многоугольника в форме по формулам, приведенным в статье о моментах инерции в Википедии.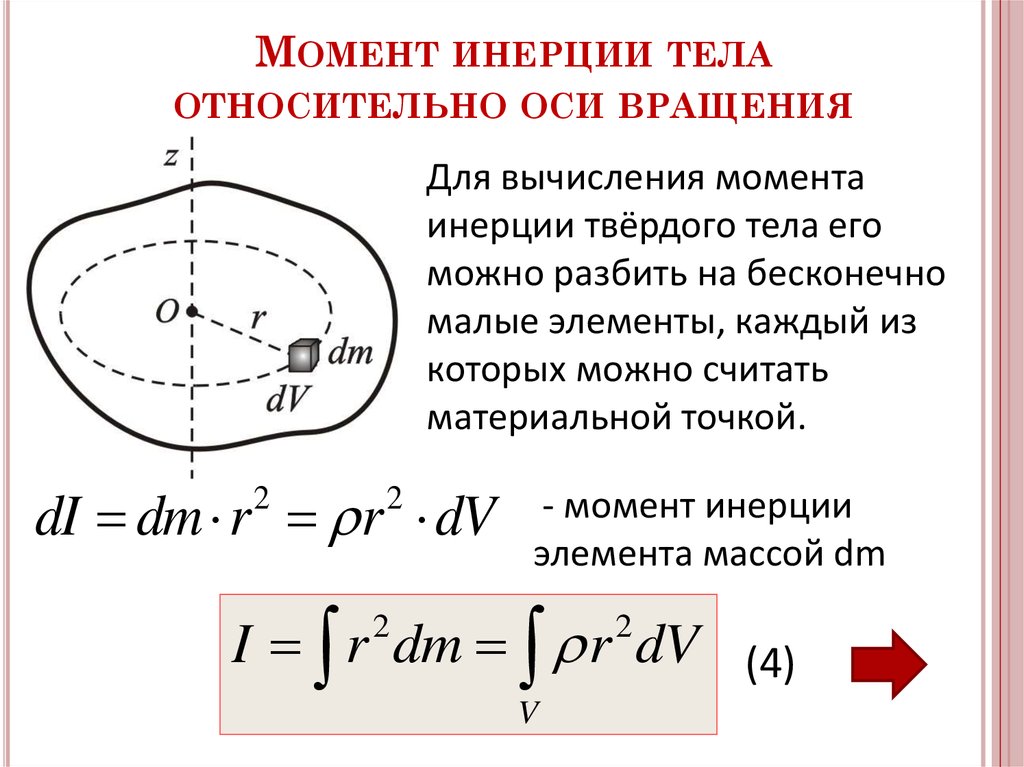
или те, которые приведены в замечательной статье об обнаружении столкновений и реагировании на них.
Но мне интересно, как связать это со структурой моего объекта, просто добавить все инерции форм объекта? Это то, что использует другой писатель для вычисления инерции треугольных многоугольников, он складывает все моменты инерции треугольников. Или есть еще что-то?
Мне сложно понять всю эту концепцию инерции, так как у меня нет сильного физического образования. Поэтому, если бы кто-нибудь мог дать мне ответ, предпочтительно с логикой инерции вокруг данного центроида, я был бы очень благодарен. Я на самом деле изучаю IT. — Разработка игр в моем университете, но, к моему большому разочарованию, ни один из преподавателей в их рядах не имеет опыта в области физики.
- динамика
- физика
2
Лоренс, физика намного проще, если вы остаетесь в двухмерном пространстве. В двумерном пространстве вращения описываются скаляром, сопротивление вращению (момент инерции) описывается скаляром, а вращения являются аддитивными и коммутативными. Вещи становятся волосатыми (намного, намного волосатее) в трехмерном пространстве.
Вещи становятся волосатыми (намного, намного волосатее) в трехмерном пространстве.
При соединении двух объектов объединенный объект имеет собственный центр масс. Чтобы рассчитать момент инерции этого комбинированного объекта, вам необходимо суммировать моменты инерции отдельных объектов, а также добавить смещение, данное теоремой Штейнера о параллельной оси для каждого отдельного объекта. Этот член смещения представляет собой массу объекта, умноженную на квадрат расстояния до составного центра масс.
Основная причина, по которой вам необходимо знать момент инерции, заключается в том, что вы можете смоделировать реакцию на крутящие моменты, действующие на ваш объект. Это довольно просто в 2D-физике. Вращательное поведение является аналогом второго закона Ньютона. Вместо F=ma вы используете T=Iα. (В трехмерном пространстве все снова намного сложнее.) Вам нужно найти внешние силы и крутящие моменты, найти линейное ускорение и ускорение вращения, а затем интегрировать численно.


 ..
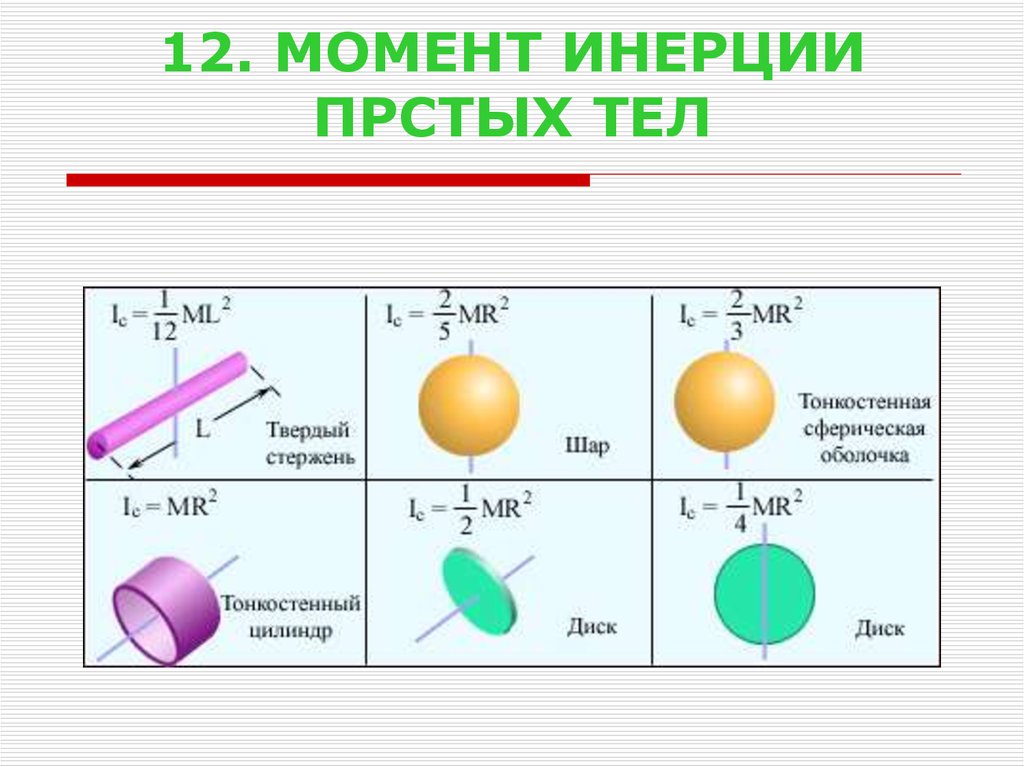
..
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления





 Найти угловое ускорение колеса. Через какое время после начала действия силы колесо будет иметь частоту вращения в 100 об/с? Колесо считать однородным диском. Трением пренебречь.
Найти угловое ускорение колеса. Через какое время после начала действия силы колесо будет иметь частоту вращения в 100 об/с? Колесо считать однородным диском. Трением пренебречь. Момент сил трения вращающегося блока 98,1 Н×м. Найти разность натяжения нити по обе стороны блока, если известно, что блок вращается с угловым ускорением 2,36 рад/с2. Блок считать однородным диском.
Момент сил трения вращающегося блока 98,1 Н×м. Найти разность натяжения нити по обе стороны блока, если известно, что блок вращается с угловым ускорением 2,36 рад/с2. Блок считать однородным диском.
 Кинетическая энергия вала, вращающегося с частотой 5 об/с, равна 60 Дж. Найти момент импульса L вала.
Кинетическая энергия вала, вращающегося с частотой 5 об/с, равна 60 Дж. Найти момент импульса L вала. С какой наименьшей высоты должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом 3 м, и не оторваться от дорожки в верхней точке петли? Масса m велосипедиста вместе с велосипедом 75 кг, причем на колеса приходится масса mo = 3 кг. Колеса велосипеда считать обручами.
С какой наименьшей высоты должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом 3 м, и не оторваться от дорожки в верхней точке петли? Масса m велосипедиста вместе с велосипедом 75 кг, причем на колеса приходится масса mo = 3 кг. Колеса велосипеда считать обручами. Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения.
Сравнить найденные скорости со скоростью тела, соскальзывающего с наклонной плоскости при отсутствии трения. Человек массой 60 кг стоит при этом на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.
Человек массой 60 кг стоит при этом на краю платформы. С какой частотой начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека — точечной массой.
 Обратная связь — 161.97.168.212 (0.014 с.)
Обратная связь — 161.97.168.212 (0.014 с.)