9. Момент инерции твердого тела
Из формулы (7.24) видно, что угловое ускорение, сообщаемое телу вращающим моментом, зависит от момента инерции тела; чем больше момент инерции, тем меньше угловое ускорение. Следовательно, момент инерции характеризует инерционные свойства тела при вращательном движении, как и масса при поступательном движении. В отличие от массы тела момент инерции зависит от радиуса окружности, описываемой точкой приложения силы, а, следовательно, от выбора оси вращения.
Из формулы следует, что единицей измерения момента инерции является кг.мІ.
Из определения момента инерции
(7.25)
видно, что момент инерции есть величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей:
(7.26)
Момент
инерции существует безотносительно к
вращению. Каждое тело независимо от
того, вращается оно или покоится, обладает
определенным моментом инерции относительно
любой оси.
Для неоднородных тел и тел неправильной формы момент инерции определяют экспериментально, а для однородных тел геометрически правильной формы – посредством интегрирования.
Как было ранее указано, в силу формулы (7.3) элементарная масса равна произведению плотности тела в данной точке на соответствующий элементарный объем: .
Следовательно, момент инерции можно представить в виде: .
Если плотность тела постоянна, её можно вынести за знак суммы задача нахождения моментов инерции сводится к интегрированию:
(7.27)
Интегралы в (7.27) берутся по всему объему тела. Величины и r в этих интегралах являются функциями точки.
В качестве примера вычислим момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис. 7.10).
Рис. 7.10.
Разобьем
диск на кольцевые слои толщиной
.
Все точки одного слоя будут находиться
на одинаковом расстоянии от оси, равном
.
Объем такого слоя равен
,
где – толщина диска. Поскольку диск однороден,
плотность его во всех точках одинакова,
(7.27) можем вынести за знак интеграла:
,
где
–
радиус диска.
Так как масса диска , то получим
Для однородных и симметричных тел обычно основной осью вращения является ось симметрии. В этом случае момент инерции, как мы видели, легко вычисляется.
Для некоторых тел правильной формы значение моментов инерции относительно осей, проходящих через центр их симметрии приведены в таблице 2.
Таблица 2
Форма тела | Расположение оси | Величина момента инерции |
Обруч | ||
Цилиндр | ||
Шар | ||
Примечание: m – масса тела, R0 – его радиус | ||
Рассмотрим
произвольное тело и две параллельные
друг другу оси, одна из которых (ось С)
проходит через центр масс тела, а другая
(ось О) отстоит от первой на расстояние а (рис.
Рис. 7.11
Момент инерции относительно оси О определяется выражением
Разобьем это выражение на три суммы:
Первая сумма представляет собой момент инерции относительно оси, проходящей через центр масс. Сумма дает массу тела . Наконец, , где – координата центра масс, которая при сделанном выборе начала координат равна нулю. Таким образом, мы приходим к соотношению:
(7.29)
Это соотношение выражает теорему Штейнера, которая гласит, что момент инерции
В
соответствии с теоремой Штейнера момент
инерции диска относительно оси ОґОґ,
отстоящей на расстоянии от
оси, проходящей через центр масс, равен
найденному нами моменту инерции (7.
28) относительно
оси, проходящей через центр диска, плюс : .
Моментом инерции системы материальных точек относительно полюса называется сумма моментов инерции всех материальных точек входящих в механическую систему
Поделись
б) Относительно оси:
Рис. 8
(35)
в) Относительно плоскости:
Рис. 9
(36)
2.3.3 Моменты инерции абсолютно твердого тела.
Для сплошных тел роль материальной точки имеет элементарный объем массы .
а) Относительно полюса:
Рис. 10
Моментом инерции твердого тела относительно полюса называется интеграл вида:
(37)
б) Относительно оси:
Рис. 11
(38)
в) Относительно плоскости:
Рис. 12
(39)
Здесь dm=ρdV, где ρ – плотность тела, V — объем тела. Моменты инерции одинаковых по форме тел, изготовленных из различных материалов, отличаются друг от друга.
2.3.4 Моменты инерции однородных тел.
Однородным называется тело, если плотность тела во всех его точках одинакова.
а) Момент инерции однородного стержня
Имеем однородный стержень длиной «l» и массой «m». Центр масс стержня точка «с».
Вычислим момент инерции стержня относительно оси СZ, проходящей через центр масс стержня и перпендикулярной к нему (рис.13)
Рис. 13
Согласно формуле (38), момент инерции тела относительно оси вычисляется по формуле: .
Если разделить стержень на отрезки длиной
(40)
тогда
(41)
Таким образом, момент инерции однородного стержня относительно центра масс вычисляется по формуле:
(42)
б) Момент инерции цилиндра, масса которого распределена по ободу (т.
е. полый цилиндр)или кольца
Имеем цилиндр, масса которого распределена по ободу, его радиус «R
Вычислим момент инерции стержня относительно оси СZ, проходящей через центр масс стержня (рис.14)
Рис. 14
(43)
в) Сплошной однородный цилиндр
Пусть радиус цилиндра равен R, его масса m, высота H. Построим цилиндрическую трубку радиуса r толщина dr (r<R)высотой H толщиной dr и длина 2 r (Рис.15). За элемент массы dm возьмем массу этой трубки. Объем равен dV=2 rHdr, а ее масса dm=ρdV=ρ2 rHdr, где ρ=m/V – плотность. Объем всего цилиндра V= R2H. Следовательно,
(44)
Рис. 15
По определению:
(45)
Получили для сплошного однородного цилиндра (диска или шкива):
(46)
2.3.5 Радиус инерции.
Характеристикой, не зависящей от массы тела, является радиус инерции. Радиус инерции измеряется в метрах и имеет простой физический смысл. Если данное тело превратить в материальную точку той же массы, то для того чтобы момент инерции оставался таким же как у исходного тела, эту точку следует поместить на расстояние от оси, равное радиусу инерции.
Зная радиус инерции тела можно определить момент инерции тела по формуле для материальной точки.
(47)
где — радиус инерции.
Пример:
Определить радиус инерции для полого цилиндра:
(48)
(49)
;
(50)
Радиус инерции используется обычно в задачах для неоднородных тел. Определяются радиусы инерции неоднородных тел экспериментальным путем.
2.3.6 Физический смысл моментов инерции.
Ввёл понятие момента инерции Гюйгенс при изучении математического маятника. Термин «момент инерции» ввел Леонард Эйлер. Физический смысл момента инерции аналогичен физическому смыслу массы, т.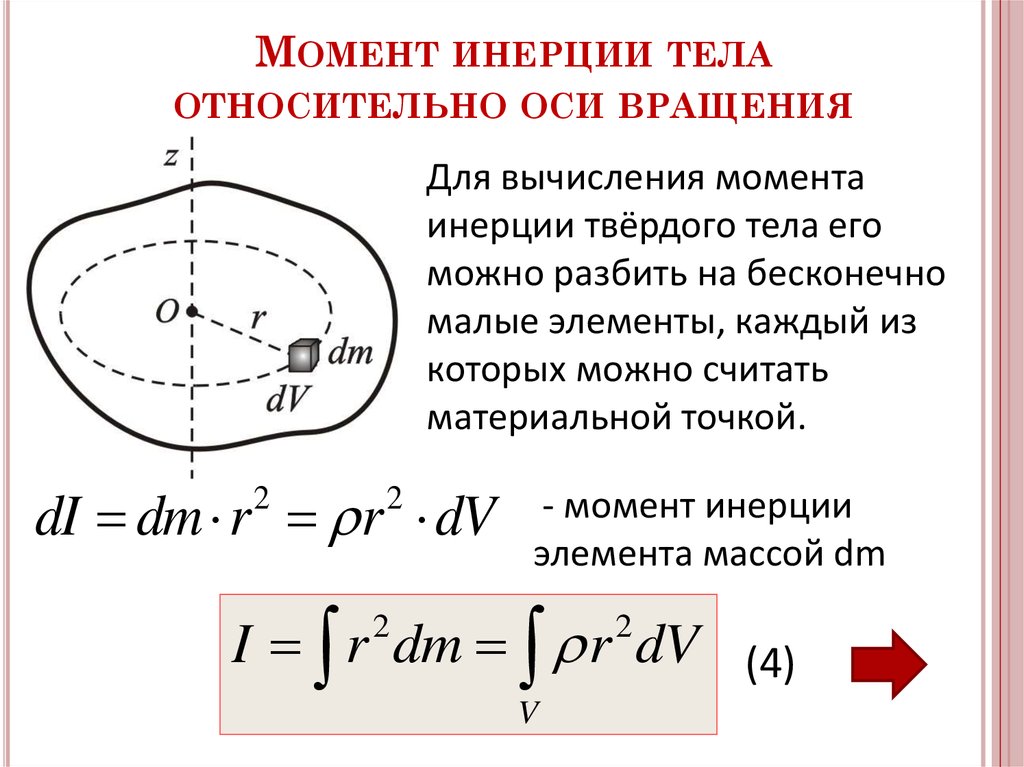
к. выражаются через массу. Масса – это мера инертности тела по отношению к поступательному движению. Масса характеризует способность тела препятствовать изменению скорости, т.е. способность тела сохранять свою скорость неизменной.
Аналогично момент инерции характеризует меру инертности тела по отношению к вращательному движению. Момент инерции характеризует способность тела сохранять угловую скорость неизменной, т.е. препятствует появлению углового ускорения тела. Таким образом, инерция вращающейся системы зависит не только от масс ее точек, но и от того, как они расположены по отношению к оси вращения.
2.3.7 Теорема Гюйгенса – Штейнера (теорема о моментах инерции относительно параллельных осей).
В справочниках приводят моменты инерции тел относительно осей координат, проходящих через центр масс. Если же ось вращения смещена из центра масс, то вопрос о величине момента инерции позволяет решить специальная теорема – теорема Гюйгенса-Штейнера или теорема о моментах инерции относительно параллельных осей.
d– перпендикулярно осям.
h– перпендикулярны осям.
Рис. 16
Формулировка: Момент инерции механической системы (тела) относительно произвольной оси равен моменту инерции этого тела относительно параллельной оси, проходящей через центр масс, и величины, равной произведению массы этой системы (тела) на квадрат расстояния (d) между осями.
Таким образом, теорема Гюйгенса – Штейнера имеет вид:
(51)
Доказательство:
По определению момента инерции:
(52)
находим по теореме косинусов:
(53)
Где «+» – для тупого угла;
«-» – для острого угла.
По определению центра масс:
(54)
Следовательно, ,
но, так как точка С это начало координат, то , а это значит, что:
(55)
Пример:
Определить момент инерции стержня относительно оси z,, проходящей через конец стержня.
Рис. 17
По теореме Гюйгенса – Штейнера:
(56)
Значит, — момент инерции стержня относительно конца.
Таким образом, момент инерции относительно оси, проходящей через конец стержня в четыре раза больше, чем момент инерции стержня относительно оси, проходящей через центр масс.
Момент инерции в любой задаче надо вычислять относительно оси вращения и, если ось вращения не проходит через центр масс надо использовать теорему Гюйгенса – Штейнера. Из всех моментов инерции механической системы относительно параллельных осей самый маленький момент инерции у системы будет относительно оси , проходящей через центр масс.
2.3.8 Осевые моменты инерции в декартовых координатах.
Рис. 18
(57)
Где — по теореме Пифагора.
Определение: осевыми моментами инерции тела в декартовых координатах называются интегралы вида:
(58)
2.3.9 Полярный момент инерции тела в декартовых координатах.
Рис. 19
Определение: полярным моментом инерции тела в декартовых координатах называется интеграл вида:
(59)
Где .
Таким образом, полярный момент инерции в декартовых координатах имеет вид:
(60)
Сложив почленно осевые моменты инерции, получим:
(61)
Учитывая, что полярный момент инерции определяется по формуле:
(62)
Получим формулу взаимосвязи между моментами инерции:
(63)
2.3.10 Центробежные моменты инерции.
Осевые моменты инерции не полностью характеризуют поведение тела при его вращении. В механике в качестве характеристик, учитывающих несимметричность в распределении масс, вводят центробежные моменты инерции.
Определение: Центробежными моментами инерции тела называются моменты инерции, вычисляемые по формулам:
(64)
Центробежные моменты инерции могут иметь не только положительные и нулевые значения, но и отрицательные. В этом их отличие от осевых моментов инерции.
2.3.11 Главные оси инерции.
Определение: Главными осями инерции называются такие оси, для которых все центробежные моменты инерции равны нулю.
Симметрия в расположении масс относительно оси (например, Х) характеризуется обращением в нуль двух центробежных моментов инерции.
Если , значит ось «Х» есть главная ось инерции.
Если , то все оси «X, Y, Z» являются главными осями инерции.
2.3.12 Главные центральные оси инерции.
Определение: Главными центральными осями инерции называются такие главные оси инерции, которые проходят через центр масс.
Если в теле есть ось симметрии, то эта ось всегда является одной из главных центральных осей инерции, так как центр масс лежит на этой оси, но не все главные оси инерции являются осями симметрии.
Если тело имеет плоскость симметрии, то любая прямая перпендикулярная этой плоскости и проходящая через центр масс является одной из главных осей симметрии для точки пересечения этой оси с плоскостью.
Через любую точку тела можно провести, по крайней мере, три взаимно перпендикулярных главных осей инерции.
Понятие о главных осях инерции играет важную роль в динамике твердого тела. Если главные оси инерции выбрать в качестве декартовых осей координат, то все центробежные моменты инерции обращаются в нули и соответствующие уравнения или формулы оказываются значительно проще, чем в других системах координат.
2.3.13 Моменты инерции относительно оси любого направления.
Рис. 20
Пусть: — направляющие косинусы оси L.
Определение: Моментом инерции тела относительно произвольной оси «L» называется момент инерции, вычисляемый по формуле:
(65)
Если оси «X, Y, Z» являются главными осями инерции, то и формула (56) будет иметь вид:
(66)
2.3.14 Тензор инерции.
Определение: Тензором инерции называется такой тензор, элементами которого являются моменты инерции (осевые и центробежные).
(67)
Это симметричный тензор, т. к. тензор называется симметричным, если он не изменяется при перестановке индексов .
Тензор называется антисимметричным, если при перестановке индексов он меняет знак .
Тензор инерции симметричный тензор, т.к. .
Тензор инерции позволяет компактно записывать моменты инерции и легко производить математические операции с ними.
2.3.15 Эллипсоид инерции.
Рис. 21
Знаем, что:
(68)
Выберем на оси «L» точку «M» такую чтобы , тогда направляющие косинусы оси «L» имеют вид:
(69)
Подставим (60) в формулу (59):
(70)
Разделив на , получим эллипсоид инерции в произвольной системе координат:
(71)
Если оси «X, Y, Z» являются главными осями инерции, то и эллипсоид имеет вид:
(72)
Канонический (простейший) вид эллипсоида инерции.
(73)
где полуоси эллипсоида инерции:
(74)
Смысл эллипсоида инерции в том, что он характеризует распределение масс в теле.
Рис. 22
3. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ И
Что такое инерция? — Определение из WhatIs.com
По
- Участник TechTarget
Инерция — это свойство материи, которое заставляет ее сопротивляться изменениям скорости (скорости и/или направления). Согласно первому закону движения Ньютона, объект с заданной скоростью сохраняет эту скорость, если на него не действует внешняя сила. Инерция — это свойство материи, которое делает этот закон верным.
Величина инерции объекта пропорциональна его массе. Однако инерция — это не то же самое, что масса или импульс (произведение скорости и массы). Массу объекта можно измерить, наблюдая степень его инерции. Это делается путем измерения величины силы, необходимой для создания определенного ускорения.
Свойство инерции полезно в навигационных системах. Массивный объект может обеспечивать постоянную точку отсчета для ускорения и, в частности, изменения направления, поскольку он имеет тенденцию поддерживать постоянную ориентацию в пространстве. Инерциальные системы наведения применяются в самолетах, космических кораблях, морских судах и ракетах.
Последнее обновление: сентябрь 2005 г.
СБОМ
Спецификация программного обеспечения (SBOM) — это перечень всех составляющих компонентов и программных зависимостей, участвующих в разработке и поставке приложения.
ПоискСеть
- беспроводная ячеистая сеть (WMN)
Беспроводная ячеистая сеть (WMN) — это ячеистая сеть, созданная путем соединения узлов беспроводной точки доступа (WAP), установленных в …
- Wi-Fi 7
Wi-Fi 7 — это ожидаемый стандарт 802.11be, разрабатываемый IEEE.
- сетевая безопасность
Сетевая безопасность включает в себя все шаги, предпринятые для защиты целостности компьютерной сети и данных в ней.
ПоискБезопасность
- Что такое модель безопасности с нулевым доверием?
Модель безопасности с нулевым доверием — это подход к кибербезопасности, который по умолчанию запрещает доступ к цифровым ресурсам предприятия и …
- RAT (троянец удаленного доступа)
RAT (троян удаленного доступа) — это вредоносное ПО, которое злоумышленник использует для получения полных административных привилегий и удаленного управления целью …
- атака на цепочку поставок
Атака на цепочку поставок — это тип кибератаки, нацеленной на организации путем сосредоточения внимания на более слабых звеньях в организации …
ПоискCIO
- пространственные вычисления
Пространственные вычисления в широком смысле характеризуют процессы и инструменты, используемые для захвата, обработки и взаимодействия с трехмерными данными.
- Пользовательский опыт
Дизайн взаимодействия с пользователем (UX) — это процесс и практика, используемые для разработки и внедрения продукта, который обеспечит позитивное и …
- соблюдение конфиденциальности
Соблюдение конфиденциальности — это соблюдение компанией установленных правил защиты личной информации, спецификаций или …
SearchHRSoftware
- Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса …
- удержание сотрудников
Удержание сотрудников — организационная цель сохранения продуктивных и талантливых работников и снижения текучести кадров за счет стимулирования …
- гибридная рабочая модель
Гибридная рабочая модель — это структура рабочей силы, включающая сотрудников, работающих удаленно, и тех, кто работает на месте, в офисе компании.
..
SearchCustomerExperience
- CRM (управление взаимоотношениями с клиентами) аналитика
Аналитика CRM (управление взаимоотношениями с клиентами) включает в себя все программные средства, которые анализируют данные о клиентах и представляют…
- разговорный маркетинг
Диалоговый маркетинг — это маркетинг, который вовлекает клиентов посредством диалога.
- цифровой маркетинг
Цифровой маркетинг — это общий термин для любых усилий компании по установлению связи с клиентами с помощью электронных технологий.
определение момента+инерции по The Free Dictionary
Момент+инерции+инерции — определение момента+инерции по The Free DictionaryМомент+инерции — определение момента+инерции по The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
