Частота колебаний — это… Что такое Частота колебаний?



Частота колебаний

        число полных колебаний (См. Колебания)в единицу времени. Для гармонических колебаний Ч. к. f = 1/T, где Т — период колебаний. Единица Ч. к. — одно колебание в секунду, или Герц. Часто пользуются величиной ω = 2πf, которая называется циклической или круговой частотой.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Частота кадров
• Частота электрического тока

Смотреть что такое «Частота колебаний» в других словарях:

• частота колебаний — число колебаний в 1 с. Обозначается f или ν. Если Т  период колебаний, то f = 1/T; измеряется в герцах (Гц). Угловая частота колебаний ω = 2πf = 2π/T рад/с. * * * ЧАСТОТА КОЛЕБАНИЙ ЧАСТОТА КОЛЕБАНИЙ, число колебаний в 1 с. Обозначается f или n.… …   Энциклопедический словарь

• частота колебаний — (f[v]) Величина, обратная периоду колебаний. [ГОСТ 7601 78] частота колебаний Число колебаний в единицу времени [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] частота колебаний частота Количество периодов… …   Справочник технического переводчика

• ЧАСТОТА КОЛЕБАНИЙ — число колебаний в 1 с. Обозначается f или ?. Если T период от колебаний, то f = 1/T; измеряется в герцах (Гц). Угловая частота колебаний ??= 2?f = 2?/T рад/с …   Большой Энциклопедический словарь

• ЧАСТОТА КОЛЕБАНИЙ — величина, обратная периоду колебаний T(f=1/Т), т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени. Обычно Ч. к. измеряется в герцах: 1 Гц соответствует одному колебанию в секунду. Часто используется также… …   Физическая энциклопедия

• Частота колебаний — 14. Частота колебаний v Средняя частота спектра лазерного излучения в пределах интервала частот линии спонтанного излучения Источник: ГОСТ 24453 80: Измерения пара …   Словарь-справочник терминов нормативно-технической документации

• частота колебаний — svyravimų dažnis statusas T sritis automatika atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d oscillation, f …   Automatikos terminų žodynas

• частота колебаний — virpesių dažnis statusas T sritis automatika atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d oscillations, f …   Automatikos terminų žodynas

• частота колебаний — svyravimų dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Svyruojamojo judesio dažnis. atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f ryšiai:… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• частота колебаний — virpesių dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Tam tikros sistemos virpėjimo dažnis. atitikmenys: angl. oscillation frequency vok. Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• частота колебаний — virpesių dažnis statusas T sritis chemija apibrėžtis Virpesių skaičius per 1 sekundę. atitikmenys: angl. oscillation frequency rus. частота колебаний …   Chemijos terminų aiškinamasis žodynas

• частота колебаний — svyravimų dažnis statusas T sritis fizika atitikmenys: angl. oscillation frequency vok. Schwingfrequenz, f; Schwingungsfrequenz, f rus. частота колебаний, f pranc. fréquence d’oscillations, f …   Fizikos terminų žodynas

Книги

• Школа музыки. 40 уроков для юных музыкантов, певцов и композиторов, Боуэн Майриг, Боуэн Рэйчел. О книгеЗамечательное продолжение одной из наших любимых книг об искусстве `Школы искусств`. Теперь пришло время обратить внимание на музыку!Мы снова стоим на пороге невероятной школы, где вас… Подробнее  Купить за 1063 грн (только Украина)
• Решение волновых задач сейсмостойкости методом граничных элементов, С.П. Гордеева. Программа вычисляет напряженно-деформированное состояние (НДС) сооружений неограниченной формы (плотины совместно с основанием, подземные сооружения, откосы каньонов) при волновом… Подробнее  Купить за 970 грн (только Украина)
• Решение волновых задач сейсмостойкости методом граничных элементов, С.П. Гордеева. Программа вычисляет напряженно-деформированное состояние (НДС) сооружений неограниченной формы (плотины совместно с основанием, подземные сооружения, откосы каньонов) при волновом… Подробнее  Купить за 863 руб

Частота в физике, теория и онлайн калькуляторы

Определение частоты

Определение

Частотой называют физическую величину, характеризующую периодический процесс.

Она равна числу повторений или реализации событий за единицу времени. Обозначают частоту $\nu ,$ могут встречаться другие варианты обозначений частоты, например $f$ или $F$.

Частота (наряду со временем) — это наиболее точно измеряемая величина.

Частота колебаний

Частота служит одним из основных параметров, характеризующих колебания.

Определение

Частота — это физическая величина обратная периоду колебаний (T). Частота — это число полных колебаний, которые совершаются за единицу времени.

\[\nu =\frac{1}{T}\left(1\right).\]

В Международной системе единиц (СИ) частота измеряется в герцах или обратных секундах:

\[\left[\nu \right]=с^{-1}=Гц.\]

Герц — единица измерения частоты периодического процесса, при которой за время в одну секунду протекает один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.

Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, о близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:

\[{\nu =\nu }_1-\ {\nu }_2\left(2\right).\]

Другой характеристикой колебаний является циклическая частота, которая равна:

\[{\omega }_0=2\pi \nu \left(3\right).\]

Циклическая частота измеряется в радианах, деленных на секунду:

\[\left[{\omega }_0\right]=\frac{рад}{с}.\]

Частота колебаний тела, массой$\ m,$ подвешенного на пружине с жесткостью $k$ равна:

\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(4\right).\]

Выражение (4) выполняется для упругих, малых колебаний. Масса пружины должна быть мала в сравнении с массой тела.

Частота колебаний математического маятника, длина нити которого $l$:

\[\nu =\frac{1}{2\pi \sqrt{{l}/{g}}}\left(5\right),\]

где $g$ — ускорение свободного падения.

Частота колебаний физического маятника:

\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(6\right),\]

где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.

Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее результаты дают эти формулы.

Частота дискретных событий, частота вращения

Определение

Частотой дискретных колебаний ($n$) — называют физическую величину, которая равна количеству действий (событий) в единицу времени.

Если время, которое занимает одно событие обозначить как $\tau $, то частота дискретных событий равна:

\[n=\frac{1}{\tau }\left(7\right).\]

Единицей измерения частоты дискретных событий является обратная секунда:

\[\left[n\right]=\frac{1}{с}.\]

Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.

Частотой вращения ($n$) — называю

Частота колебаний | Все формулы

Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени.

Разновидность частот колебаний :

Циклическая частота

Частота колебаний физического маятника

Частота пружинного маятника

Частота математического маятника

Частота электромагнитных колебаний

Частота колебаний крутильного маятника

В Формуле мы использовали :

— Частота колебаний

— Циклическая частота

— Период колебаний маятника

— Масса груза, или масса маятника

— Жесткость пружины

— Длина подвеса

— Ускорение свободного падения

— Момент инерции маятника относительно оси вращения

— Расстояние от оси вращения до центра масс

— Момент инерции тела

— Вращательный коэффициент жёсткости маятника

Частота | Virtual Laboratory Wiki

Частота́ — физическая величина, характеристика периодического процесса, равная числу полных циклов, совершённых за единицу времени. Стандартные обозначения в формулах — $ ~{\nu} $, $ ~f $ или $ ~F $. Единицей частоты в Международной системе единиц (СИ) в общем случае является герц (Гц, Hz). Величина, обратная частоте, называется периодом.

Мгновенная частота и частоты спектральных составляющих

Периодический сигнал характеризуется мгновенной частотой, являющейся скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои частоты. Свойства мгновенной частоты и частоты спектральной составляющей различны, подробнее об этом можно прочитать, например, в книге Финка.

Циклическая частота


В теории электромагнетизма, теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обозначается $ ~ {\omega} $). Циклическая частота связана с частотой колебаний соотношением $ ~\omega = 2\pi f $. В математическом смысле циклическая частота — это первая производная полной фазы колебаний по времени. Единица циклической частоты — радиан в секунду (рад/с, rad/s) .

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Частота дискретных событий

Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий секунда в минус первой степени (с⁻¹, s⁻¹), однако на практике для выражения частоты импульсов обычно используют герц.

Частота вращения

Частота вращения — физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.

Другие величины, связанные с частотой

Метрологические аспекты

Измерения

Эталоны

Литература

Ссылки

См. также

---

Эта страница использует содержимое раздела Википедии на русском языке. Оригинальная статья находится по адресу: Частота. Список первоначальных авторов статьи можно посмотреть в истории правок. Эта статья так же, как и статья, размещённая в Википедии, доступна на условиях CC-BY-SA .

---

Колебания: частота, период

Прежде, чем начинать решать “серьезные” задачи, нужно хорошо освоить терминологию, основу. Поэтому вводная статья посвящена определению периода, частоты, циклической частоты колебаний, амплитуды и общей записи закона колебаний.



Колебания

Задача 1. Грузик на пружине за с совершил колебаний. Найти период и частоту колебаний.

Период – время одного полного колебания:

   

Частота колебаний

   

Ответ: c, Гц.

Задача 2. Груз на пружине за мин совершает колебаний. Определить период колебаний и циклическую частоту.

Период – время одного полного колебания:

   

Циклическая частота (угловая частота) равна:

   

Ответ: c, рад/с.

Задача 3. За 1 с комар совершает 600 взмахов крыльями, а период колебаний крыльев шмеля 5 мс. Какое из насекомых и на сколько сделает в полете большее количество взмахов за 1 мин?

Частота колебаний крыльев комара – 600 Гц. Частота колебаний крыльев шмеля равна:

   

Следовательно, комар делает на 400 взмахов за 1 с больше, чем шмель, а за 1 минуту – на 24000 взмахов.

Ответ: комар, на 24000.

Задача 4. Крылья пчелы колеблются с частотой

Гц. Сколько взмахов крыльями сделает пчела, пока долетит до цветочного поля, расположенного на расстоянии в 500 м, если она летит со скоростью м/с?

Если скорость полета пчелы известна и известно расстояние, определим  время полета:

   

Тогда количество взмахов за это время равно:

   

Ответ: 30 000.

Задача 5. Найти амплитуду, период и частоту колебаний, если закон колебаний материальной точки имеет вид (см).

Амплитуда – первое число в законе колебаний, то есть

. Циклическая частота – множитель при , . Тогда период

   

А частота:

   

Ответ: с, Гц.

По какой формуле найти ЧАСТОТУ КОЛЕБАНИЙ???

1/T T — период колебаний

Частота равна единицу делим на период. Смотря что тебе дано в задаче

это короче герцы (hz)

частота колебаний= количество колебаний делить на время колебаний! т. е ню= эн поделить на тэ

У нас такая формула — Частота=1\период (Т)

V=N/t или 1/T (герц)

Лабораторная работа «Исследование колебаний математического маятника» (Ерюткин Е. С.)

Цель: выяснить, как зависит период и частота свободных колебаний математического маятника от его длины.

Оборудование: штатив с муфтой и лапкой, шарик с нитью, секундомер (рис. 1).



Рис. 1. Оборудование

Для выполнения работы нам потребуется таблица. Таблица будет состоять из следующих частей:

Величина/№	1	2	3	4	5
Длина (см)	5	20	45	80	125
Число колебаний	30	30	30	30	30
Время (с)
Период (с)
Частота (Гц)

Во-первых, нужно определить количество экспериментов. В данном случае их 5. По вертикали записаны те самые величины, которые мы будем измерять. В первую очередь, длина самого маятника в сантиметрах. Следующая величина – количество колебаний. Далее – полное время колебаний. Следующие две графы – это период колебаний, который измеряется в секундах, и частота в Гц. Обратите внимание, что мы заранее записали те величины, которые будем использовать. В первую очередь, это длина нитяного маятника. Начальная длина: 5 см – это очень короткий маятник. Дальше 20, 45, 80 и 125. Число колебаний мы будем использовать постоянное. Это 30 колебаний. В каждом эксперименте мы будем использовать по 30 колебаний.

Соберем экспериментальную установку. Установка состоит из шарика на нити. Нить продернута через ластик. Это сделано для того, чтобы можно было регулировать его длину. Обратите внимание, что сам ластик укреплен в лапке штатива.



Рис. 2. Грузик на нити, закрепленный в штативе

Для измерения длины будем использовать линейку и секундомер. Итак, мы отсчитали 30 колебаний, и время, которое мы зарегистрировали, оказалось равным 13,2 с (рис. 3).



Рис. 3. Первый эксперимент с длиной нити 5 см

Заносим эти данные в таблицу и можем приступать к расчетам периода и частоты колебаний. Следующий шаг: увеличиваем длину маятника до 20 см. И весь эксперимент повторяем сначала. Вновь результаты заносим в таблицу. Итак, проведя наши эксперименты, мы получили конечные результаты и занесли их в таблицу.

Период колебаний:  (с). Частота колебаний: 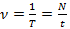 (Гц), где  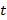– это время, а  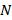– количество колебаний, совершенных за время .

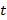Обратите внимание: когда длина маятника составляла 5 см, 30 колебаний прошли за время 13,2 с. Период колебаний составил 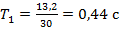, а частота .

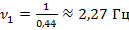Следующий результат: те же 30 колебаний, но длина маятника была уже 20 см. В этом случае увеличилось время колебаний – 26,59 с, а период колебаний составил 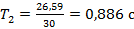. Частота уменьшилась почти в 2 раза, обратите внимание: .

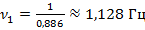Если мы посмотрим на третий результат, то увидим, что длина маятника еще больше, период стал больше, а частота уменьшилась еще на некоторое значение. Следующий, четвертый и пятый, постарайтесь посчитать сами. Обратите внимание на то, как при этом будет меняться период и частота колебаний нашего нитяного маятника.

Для 4 и 5 экспериментов посчитайте частоту и период самостоятельно.

Величина/№	1	2	3	4	5
Длина (см)	5	20	45	80	125
Число колебаний	30	30	30	30	30
Время (с)	13,2	26,59	40,32	52,81	66,21
Период (с)	0,44	0,886	1,344
Частота (Гц)	2,27	1,128	0,744

Табл. 1. Значения частоты и периода для первых трех экспериментов

Можно сделать вывод: с увеличением длины маятника увеличивается период колебаний и уменьшается частота (рис. 4). Хотелось бы, чтобы четвертый и пятый опыты вы проделали сами и убедились, что все действительно так, как мы получили в наших опытах.

Формула для вычисления периода колебания математического маятника: 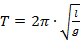, где 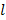 – длина маятника, а – ускорение свободного падения.

Формула для вычисления частоты колебаний: .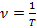



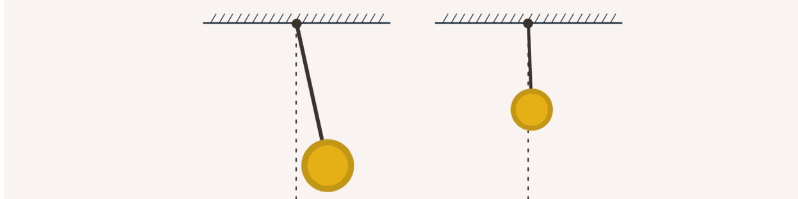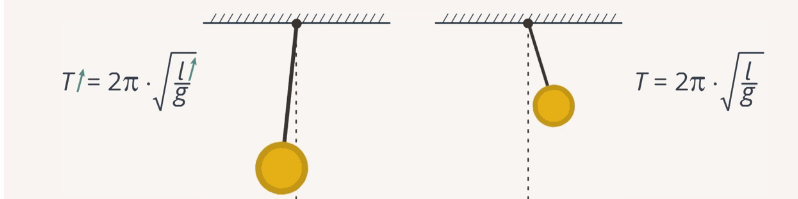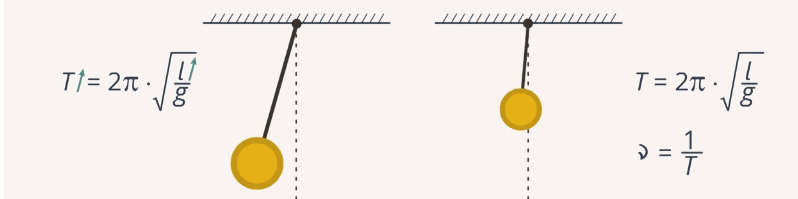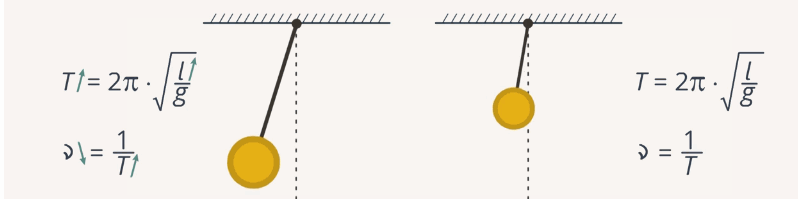
Рис. 4. Зависимость частоты и периода маятника от его длины

На этом лабораторная работа заканчивается, но есть дополнительная часть к лабораторной работе – дальнейшее исследование колебаний.

 

Ветка. Математическая зависимость между длиной маятника и периодом колебаний

Дополнительная часть лабораторной работы заключается в том, чтобы лучше определить взаимосвязь периода колебаний и длины нитяного маятника. Эта зависимость должна определяться математически. Цель дополнительного задания в том, чтобы выявить математическую зависимость между периодом и длиной маятника. Как это можно сделать? Нужно рассмотреть отношение периодов колебаний маятника и отношение длин маятника. Посмотрим на таблицу, которую используем, и обсудим те величины, которые будем туда заносить.

В первой части мы рассмотрим отношение периода из второго опыта, когда длина маятника составляла 20 см. Отношение мы будем искать к периоду, который получили, когда длина маятника составляла 5 см. Отношение самих длин мы рассмотрим в нижней строке. Итак, в верхней строке отношение периодов 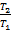, в нижней строке отношение длин маятника 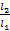. Все необходимые данные мы возьмем из предыдущей таблицы. Обратим внимание, что эти вычисления в некоторых случаях получатся приближенными, но это зависит уже от чистоты эксперимента. Если мы обратимся к первой строке, то увидим, что во всех экспериментах отношение периодов будет составлять: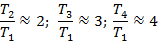


Далее рассмотрим отношение длин маятников. Обратите внимание: в первом случае это отношение равно 4, т. е. 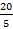. Во втором случае – 9. В третьем случае – 16. Видно сразу, как будут связаны эти величины. Посмотрите: в первом случае у нас 2 и 4. В другом случае – 3 и 9 и т. д.

Делаем вывод о том, что период будет пропорционален корню квадратному из длины маятника. Эту зависимость мы можем использовать в дальнейшем для анализа подобных колебаний: 



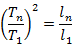
Из этого следует, что период мы можем записать как  .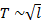

Другими словами, если мы увеличиваем длину маятника в 4 раза, то период увеличится в 2 раза. Если увеличим длину маятника в 3 раза, то увеличится период в 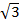 раз. И т. д. В этом и заключается результат лабораторной работы.

 

Список литературы

1. Аксенович Л.А. Физика в средней школе: Теория. Задания. Тесты: учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования/Л.А. Аксенович, Н.Н. Ракина, К.С. Фарино. Под ред. К.С. Фарино. – Минск.: Адукацыя i выхаванне, 2004.
2. Физика: механика. 10 кл.: учеб. для углубленного изучения физики/М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др. Под ред. Г.Я. Мякишева. – М.: Дрофа, 2002. – 496 с.
3. Элементарный учебник физики. П