НОУ ИНТУИТ | Лекция | Работа с числами в языке Java
Аннотация: Двоичное представление целых чисел. Позиционные и непозиционные системы счисления. Двоичное представление положительных целых чисел. Двоичное представление отрицательных целых чисел. Дополнительный код. Проблемы целочисленной машинной арифметики. Шестнадцатеричное представление целых чисел и перевод из одной системы счисления в другую. Побитовые маски и сдвиги. Двоичное представление вещественных чисел. Двоичные дроби. Мантисса и порядок числа. Стандарт IEEE 754 представления чисел в формате с плавающей точкой.
Ключевые слова: представление, система счисления, позиционная система счисления, алгоритмизация, кодирование информации, словосочетание, binary digit, архитектура компьютера, микрокоманда, порт ввода-вывода, аналого-цифровые преобразователи, двоичная система счисления, двоичное представление, дополнительный код, целочисленный тип, операции, бит, ячейка, криптография, инверсия, эквивалентность, значение, буфер, floating point, знаковый бит, мантисса, plain text, exponent, натуральный логарифмы, IEEE 754, IEC, экспонента, infinity, nan, IND, indeterminism, signaling, quiet
4.1. Двоичное представление целых чисел
Позиционные и непозиционные системы счисления
Позиционная система счисления — это такой способ записи числа, при котором вес цифры зависит от занимаемой позиции и пропорционален степени некоторого числа. Основание степени называется основанием системы счисления.
Например, число 2006 в десятичной системе счисления представляется в виде суммы тысяч, сотен, десятков и единиц:
то есть слагаемых с различными степенями числа 10. По основанию степени — числу десять — система называется десятичной. Другие позиционные системы счисления отличаются только числом в основании степени.
При написании программ чаще всего используют десятичную, шестнадцатеричную (основание шестнадцать), восьмеричную (основание восемь) и двоичную (основание два) системы. Число различных знаков — цифр, используемых для записи чисел — в каждой системе равно основанию данной системы счисления.
| 0,1 | — цифры двоичной системы |
| 0,1,2,3,4,5,6,7 | — цифры восьмеричной системы |
| 0,1,2,3,4,5,6,7,8,9 | — цифры десятичной системы |
| — цифры шестнадцатеричной системы |
intuit.ru/2010/edi»>В шестнадцатеричной системе «обычных» десятичных цифр недостаточно, и для обозначения цифр, больших девяти, используются заглавные латинские буквы A,B,C,D,E,F.В дальнейшем везде, где это необходимо, мы будем указывать основание системы счисления индексом рядом с числом: — в десятичной системе, — в шестнадцатеричной системе, — в восьмеричной системе, — в двоичной системе.
Существует множество непозиционных систем счисления, в которых числа изображаются и называются по своим правилам. Для римской системы чисел характерны сопоставление отдельного знака каждому большому числу ( V — пять, X — десять, L — пятьдесят, C — сто, M — тысяча ), повторение знака столько раз, сколько таких чисел во всем числе ( III — три, XX — двадцать), отдельные правила для предшествующих и последующих чисел (IV — четыре, VI — шесть, IX — девять). Множество непозиционных систем счисления связано с традиционными способами измерения конкретных величин — времени ( секунда, минута, час, сутки, неделя, месяц, год), длины ( дюйм, фут, ярд, миля, аршин, сажень), массы ( унция, фунт), денежных единиц.
Приведем пример самой простой из возможных систем счисления – унарную. В ней имеется всего одна цифра 1. В унарной системе счисления число 1 изображается как 1, число 2 изображается как 11, число 3 как 111, число 4 как 1111, и так далее. Первоначально вместо единицы использовались палочки (помните детский сад?), поэтому такая система счисления иногда называется палочковой. Как ни странно, она является позиционной.
Позиционные системы счисления с основанием 2 и более удобны для алгоритмизации математических операций с числами (вспомните способ сложения и умножения «столбиком»). Двоичная система является естественным способом кодирования информации в компьютере, когда сообщение представляется набором нулей («0» — нет сигнала на линии) и единиц («1» — есть сигнал на линии). Для обозначения двоичных цифр применяется термин «бит», являющийся сокращением английского словосочетания «двоичная цифра» (BInary digiT).
Машинным словом называют порцию данных, которую процессор компьютера может обработать за одну операцию (микрокоманду). Первые персональные компьютеры были 16-разрядными, т.е. работали с 16-битными (двухбайтными) словами. Поэтому операционные системы для этих компьютеров также были 16-разрядными. Например, MS DOS. Операционные системы для персональных компьютеров следующих поколений были 32-разрядны (Windows® ’95/’98/NT/ME/2000/XP, Linux, MacOS®), так как предназначались для использования с 32-разрядными процессорами.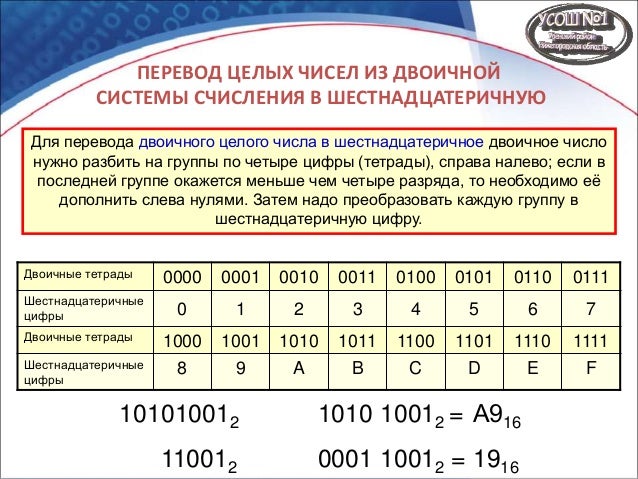
Представление чисел в двоичной и шестнадцатеричной системах счисления, а также преобразование из одной системы в другую часто необходимо при программировании аппаратуры для измерений, контроля и управления с помощью портов ввода-вывода, цифро-аналоговых и аналого-цифровых преобразователей.
Двоичное представление положительных целых чисел
Целые числа в компьютере обычно кодируются в двоичном коде, то есть в двоичной системе счисления. Например, число 5 можно представить в виде .
Показатель системы счисления принято записывать справа снизу около числа.
Аналогично, , и так далее. Все очень похоже на обозначение чисел в десятичной системе счисления:
ru/2010/edi»>. Но только в качестве основания системы счисления используется число . У чисел, записанных в десятичной системе счисления, индекс 10 обычно не пишется, но его можно писать. Так что , и так далее.В двоичной арифметике всего две цифры, 0 и 1. Двоичный код положительного целого числа – это коэффициенты разложения числа по степеням двойки.
Умножение числа на двоичное десять, то есть на , приводит к дописыванию справа нуля в двоичном представлении числа. Умножение на двоичное сто, то есть на — дописыванию двух нулей. И так далее.
Целочисленное деление на с отбрасыванием остатка производится путем отбрасывания последнего (младшего) бита, деление на — отбрасывания двух последних бит, и так далее. Обычно такие операции называют побитовыми сдвигами на n бит влево (умножение на ) или вправо (целочисленное деление на ).
intuit.ru/2010/edi»>Сложение двоичных чисел можно производить «в столбик» по полной аналогии со сложением десятичных чисел. Единственное отличие – то, что в двоичной арифметике только две цифры, 0 и 1, а не десять цифр (от 0 до 9) как в десятичной. Поэтому если в десятичной арифметике единицу более старшего разряда дает, к примеру, сложение 1 и 9, то в двоичной арифметике ее даст сложение 1 и 1. То есть(в десятичной системе это равенство выглядит как 1+1=2). Аналогично, , и так далее.
Примеры сложения «в столбик»:
Совершенно аналогично выполняется умножение:
В машинной реализации целочисленного умножения используют побитовые сдвиги влево и сложения. Поскольку эти алгоритмы очень просты, они реализуются аппаратно.
Шестнадцатеричные числа — KnowItAllNinja
До сих пор мы рассматривали две системы счисления — по основанию 2 (двоичная) и по основанию 10 (десятичная).
Другой распространенной системой счисления, используемой в информатике, является основание 16, также известное как шестнадцатеричное или сокращенно шестнадцатеричное.
Почему мы используем шестнадцатеричный код? Что ж, оно кратно 2, поэтому его относительно легко преобразовать между двоичным и шестнадцатеричным значениями, а шестнадцатеричные значения более удобочитаемы и понятны, чем более длинные двоичные значения.
Поскольку шестнадцатеричный формат хорошо подходит для представления очень больших двоичных значений, он используется во многих областях вычислений, таких как кодирование символов, адресация памяти, значения цвета RGB и адреса IPv6.
В этом уроке мы узнаем о:
- Что такое шестнадцатеричная система счисления.
- Как преобразовать числа из десятичных в шестнадцатеричные.
- Как преобразовать числа из шестнадцатеричной системы в десятичную.
- Как преобразовать числа из двоичного в шестнадцатеричный.
- Как преобразовать числа из шестнадцатеричных в двоичные.
Медиафайлы: видеопрезентация
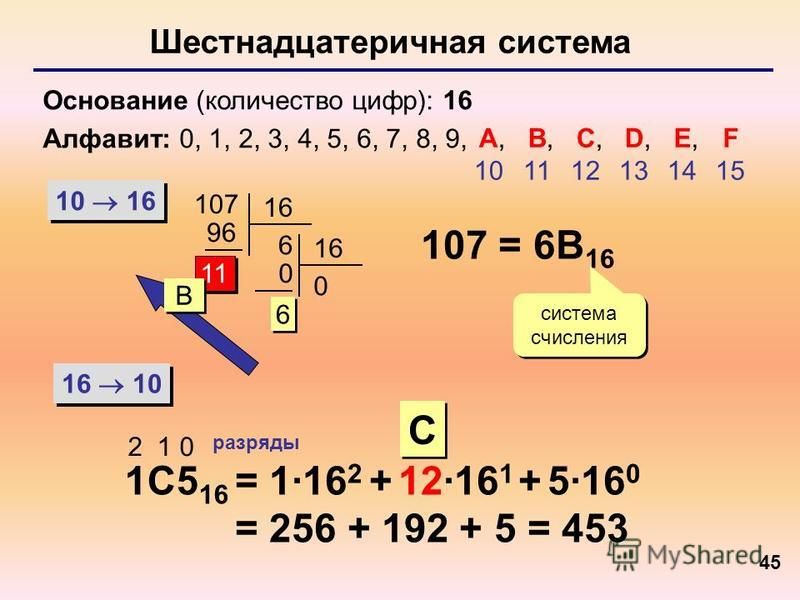
1. Что такое шестнадцатеричная система счисления?
Шестнадцатеричная система счисления — это система счисления, подобная двоичной и десятичной, но все числа кратны 16.
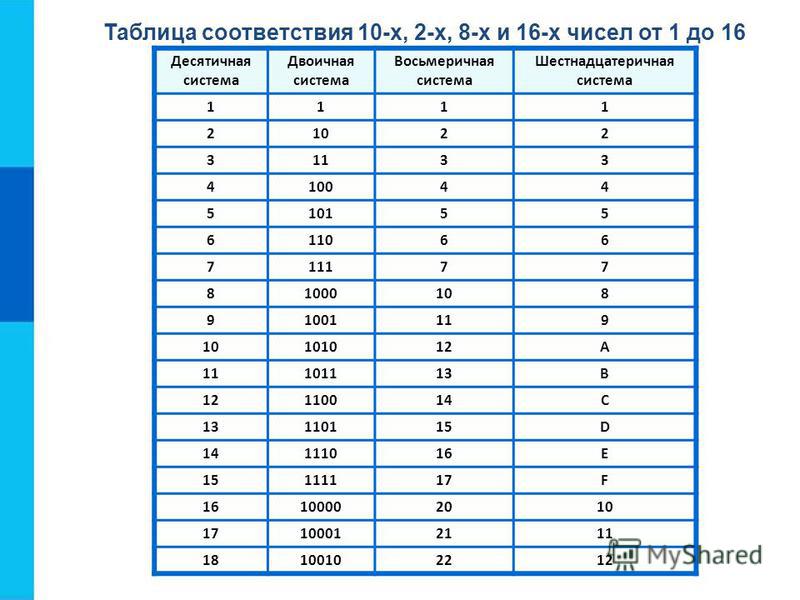
Однако, поскольку наша десятичная система счисления идет только от 0 до 9, мы используем буквы от A до F для представления остальных чисел, как показано в таблице ниже.
Как и в случае с двоичным кодом, лучший способ сделать это правильно — записать шестнадцатеричную таблицу перед началом работы.
| Decimal | Hex Value |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| Decimal | Hex Value |
|---|---|
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
So in hexadecimal, the number 6 is 6 точно так же, как десятичное число, но число 14 — это E.
Дальнейшее размышление
Во введении к уроку мы рассмотрели некоторые способы использования шестнадцатеричного числа в вычислениях. Узнайте больше об этом и о том, почему шестнадцатеричный код так важен.
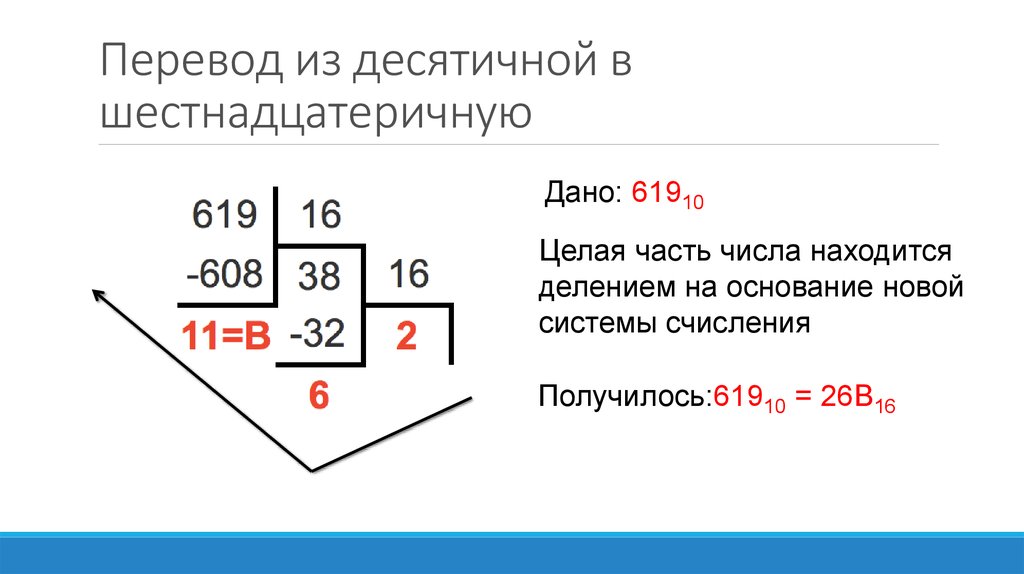
2. Как преобразовать десятичное число в шестнадцатеричное
Чтобы узнать шестнадцатеричное значение десятичного числа, мы следуем процессу, аналогичному вычислению двоичного числа.
Разница между двоичным и шестнадцатеричным преобразованием заключается в том, что теперь нам нужно вычислить, сколько РАЗ номер столбца будет вписываться в желаемое число.
Помните, что в двоичном формате каждое число слева увеличивается на кратное 2. Но в шестнадцатеричном оно увеличивается на кратное 16. Таким образом, наши столбцы выглядят следующим образом:
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
.
аналогичный процесс:Влезет ли 4096 в 20? Нет, поэтому у нас их нет, поэтому мы ставим 0 в столбце 4096.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 |
Влезет ли 256 в 20? Нет, поэтому у нас ничего из этого нет, поэтому мы ставим 0 в столбце 256.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 |
Will 16 fit into 20? Да. Сколько раз? 1 — значит ставим 1 в 16 столбце.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 1 |
Теперь у нас есть 16.
20 — 16 = 4 .
Влезет ли 1 в 4? Да. Сколько раз? 4 – значит, ставим 4 в столбец 1.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 4 |
So, the hex value for 20 is 14 (а вы говорите как ОДИН – ЧЕТЫРЕ). Не волнуйтесь, если это немного сбивает с толку — давайте попробуем другой пример с большим числом.
Рабочий пример 2
Давайте вычислим шестнадцатеричное значение десятичного числа 109.
Впишется ли 4096 в 109? Нет, поэтому у нас их нет, поэтому мы ставим 0 в столбце 4096.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0091 |
Влезет ли 256 в 109? Нет, поэтому у нас ничего из этого нет, поэтому мы ставим 0 в столбце 256.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 |
| 999999999999999999999992900 |
| . Да. Сколько раз? 6 – значит, ставим 6 в 16 столбец. |
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 6 |
6 x 16 равно 96, поэтому из 109 нужно вычесть 96.
109 – 96 = 13 .
Влезет ли 1 в 13? Да. Сколько раз? 13 конечно, но какой шестнадцатеричный код для 13? Используя таблицу в начале этого урока, мы видим, что это D.
Итак, мы поставили D в столбец 1.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | 6 | D |
Итак, шестнадцатеричное значение для 109 равно 6D .
Работал Пример 3
Давайте попробуем последнее число. На этот раз очень большой. Давайте попробуем 5078.
Влезет ли 4096 в 5078? Да. Сколько раз? 1 — поэтому мы ставим 1 в столбце 4096.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 |
Теперь нам нужно от 5078 отнять 4096.
4096 – 5078 = 982 .
Влезет ли 256 в 982? Да. Сколько раз? 3 — поэтому мы ставим 3 в столбце 256.
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 3 |
3 x 256 is 768, so we have to take 768 away from 982. 982 – 768 = 214 .
Влезет ли 16 в 214? Да. Сколько раз? 13 — но какой шестнадцатеричный код для 13? Используя таблицу в начале этого урока, мы видим, что это D.
Итак, мы поставили D в 16 столбце.
| 4096 | 256 | 16 | 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | D | 3 | D | 3 | .
214 – 208 = 6 .| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 1 | 3 | D | 6 |
Таким образом, шестнадцатеричное значение для 5078 равно 9027 9 027D6.
Дополнительные размышления
Как вы думаете, что будет после столбца 4096? Посмотрите, сможете ли вы решить это, и проверьте свой ответ в Интернете.
3. Как преобразовать шестнадцатеричное число в десятичное
Преобразование шестнадцатеричного в десятичное очень просто. Все, что нам нужно, это наша шестнадцатеричная таблица из начала этого урока.
Let’s look at the example below:
| 4096 | 256 | 16 | 1 |
|---|---|---|---|
| 0 | 0 | D | 9 |
We have nothing in the 4096 и 256 столбцов, так что мы можем оставить их в покое.
У нас есть D в 16 столбце. Мы можем видеть из нашей шестнадцатеричной таблицы, что D — это шестнадцатеричное значение для 13. Поэтому нам нужно умножить 13 x 16, что дает нам 208 .
В столбце 1 у нас есть 9, с которыми нам ничего не нужно делать.
Теперь нам просто нужно сложить эти числа. 208 + 9 = 217 .
Итак, десятичное значение для D9 равно 217 .
Дальнейшие размышления
Преобразование шестнадцатеричных чисел в десятичные несложно, но требует некоторой практики. Будет полезно, если вы выучите числа 0-F наизусть. Практикуйте это с другом.
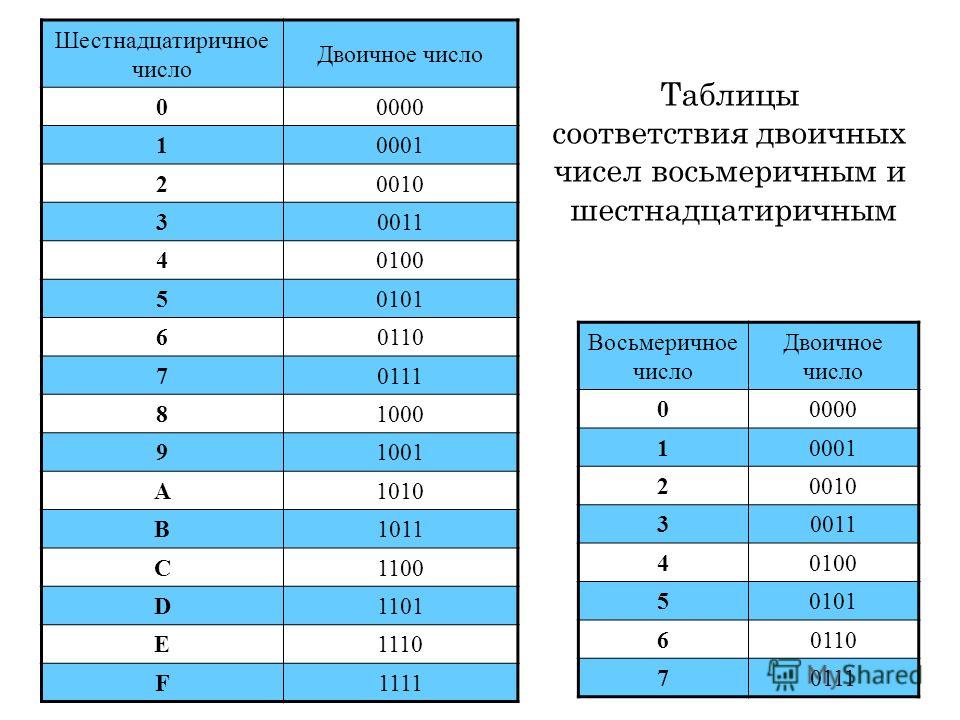
4. Как преобразовать двоичное число в шестнадцатеричное
В предыдущем уроке мы узнали, что полубайт состоит из 4 бит. Наименьшее число, которое мы можем хранить в 4 битах, равно 0,9.0003
| 8 | 4 | 2 | 1 | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | .|||||
| 8 | 4 | 2 | 1 | |||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | . представлен в виде глотка. |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 0 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 0 | 0 | 1 | 1 |
Мы можем тогда конвертировать эти два числа в Hexadecim в двоично-десятичном преобразовании.
Первое число равно 2 .
Второе число равно 3 .
Итак, двоичное число 100011 в шестнадцатеричном формате равно 23 .
Заметьте, это ДВА-ТРИ, а не двадцать три.
Рабочий пример 2
Рассмотрим число 11101010.
Это уже 8 бит, поэтому мы можем сразу разделить его на две части.
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 8 | 4 | 2 | 1 |
|---|---|---|---|
| 1 | 0 | 1 | 0 |
Теперь мы можем преобразовать эти два полубайта в их шестнадцатеричные значения.
Первое число равно 14, что в шестнадцатеричном формате равно E .
Второе число равно 10, что в шестнадцатеричном формате равно А .
Итак, двоичное число 11101010 в шестнадцатеричном формате равно EA .
Дополнительные мысли
Что бы вы сделали, если бы у вас было 9-значное двоичное число? Если вы не уверены, поищите ответ в Интернете.
5. Как преобразовать шестнадцатеричный код в двоичный
Еще раз нам нужно понять, что каждый шестнадцатеричный столбец может быть разделен на двоичный полубайт — число от 0 до 15.
Допустим, у вас есть шестнадцатеричное число, мы буду использовать 4D.
Что нам нужно сделать, так это признать, что это два отдельных кусочка, и поэтому мы обрабатываем их отдельно.
Сначала преобразуем число 4 в двоичное.
| 8 | 4 | 2 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | .
.| 8 | 4 | 2 | 1 | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 11 | 1 | 1 | 0091 |
Мы просто склеиваем их вместе.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
Дальнейшие размышления
Какое наибольшее двоичное число можно представить двумя шестнадцатеричными цифрами?
Краткое содержание урока
Подводя итог тому, что мы узнали в этом уроке:
- Шестнадцатеричная нотация включает столбцы, кратные 16.
- Шестнадцатеричная используется для облегчения чтения длинных двоичных последовательностей.
- Hex используется в IPv6 и при адресации памяти.
- Числа 10–15 представлены буквами A–F в шестнадцатеричном формате.
- Чтобы преобразовать десятичное число в шестнадцатеричное, нам нужно выяснить, сколько РАЗ номер столбца будет вписываться в желаемое число.
- Чтобы преобразовать шестнадцатеричный формат в десятичный, мы умножаем число в каждом столбце на значение столбца.
- Преобразование в двоичный файл и из него включает обработку каждого столбца как полубайта.
Продолжить…
| Двоичный: единицы и нули Компьютеры используют двоичный код. Много бинарника. Вы спросите, что такое двоичный код? Двоичный способ представления чисел и данных с использованием только двух возможных цифр: 0 и 1. 0 означает «ложь», а 1 означает «истина». Компьютеры не видят абсолютно ничего из того, что видите вы. Вы можете увидеть текст на экране. Вы можете увидеть видео или изображение. Возможно, вы играете в игру. Компьютеру все равно. Для компьютера каждый файл, который у вас есть, — это просто длинная строка двоичных цифр. Последовательность единиц и нулей, расположенных в определенном порядке. Конечно, когда эти двоичные числа обрабатываются, они (удивительно) складываются вместе, создавая нечто столь же сложное, как видео, изображение или игру, которую вы можете просматривать на своем экране. Большая проблема с двоичным кодом. У людей проблемы с чтением. Куча проблем. Я приведу вам пример. Прочтите это: 01000011011000010111011001100101001000000101001101110100011011110111001001111001Хорошо. Вы прочитали это. «Ноль, один, ноль, ноль, ноль, ноль, один, один, ноль… бла-бла-бла».  Что это значит? Вы, вероятно, понятия не имеете.Строка двоичных цифр, которую вы только что прочитали, просто создает два слова «Cave Story», как их может увидеть компьютер. Если я изменю 4-ю двоичную цифру на 1 вместо 0, теперь будет написано «Сохранить историю». Но это знает только компьютер — у вас нет простого способа перевести это. Шестнадцатеричный: Сжатый двоичный Так он и сделал. 0000 -> 0 0001 -> 1 0010 -> 2 0011 -> 3 0100 -> 4 0101 -> 5 0110 -> 6 0111 -> 7 1000 -> 8 1001 -> 9 1010 -> А 1011 -> Б 1100 -> С 1101 -> Д 1110 -> Э 1111 -> Ф( -> — это просто стрелка.) Это шестнадцатеричное число. В шестнадцатеричном формате каждая строка из 4 двоичных цифр может быть представлена как одна шестнадцатеричная цифра. В нашей обычной системе счета используются только цифры от 0 до 9. Да, в шестнадцатеричной системе, такие вещи, как A, B, C, D, E и F считаются числами, а не буквами Шестнадцатеричный: 43 61 76 65 20 53 74 6F 72 79 Текст: Cave S t o r yКак видите, шестнадцатеричный код по-прежнему не удобочитаем. Однако это намного лучше, чем двоичный код, который слишком длинный. Теперь вы должны знать, что каждый текстовый символ (по крайней мере, английский) может быть представлен двумя шестнадцатеричными цифрами. Каждая группа из двух шестнадцатеричных цифр на самом деле представляет собой число, известное как байт. Каждый символ стоит 1 байт. В ассемблере мы обычно будем использовать байты для обозначения чисел, а не текстовых символов. Кроме того, единственная причина, по которой мы это делаем, заключается в том, что OllyDbg представляет (почти) все свои числа в виде шестнадцатеричных чисел.  |
Составив воедино огромный список единиц и нулей или «истин» и «ложей», мы можем создать язык компьютеров.
Но в шестнадцатеричной системе используются цифры от 0 до F.