Системы счисления
Кодирование информации — представление информации в той или иной стандартной форме.
Например, письменность и арифметика — кодирование речи и числовой информации, музыку кодируют с помощью нот.
Чтобы использовать числа их нужно как-то записывать и называть.
Самые первые системы нумерации возникли в древнем Египте и Месопотамии — применяли иероглифы.
Системы счисления — способы кодирования числовой информации, то есть способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.
В древнем Вавилоне делили час на 60 минут, угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток.
В Риме семь чисел обозначают буквами. 1-I, 5-V, 10-X, 50- L,100-C, 500-D, 1000-M.
IV (4=5-1)
VI (6=5+1)
Значение числа определяется как сумма или разность цифр числа. Это непозиционная система счисления.
Славяне числа кодировали буквами А=1, В=2, Г=3; чтобы избежать путаницы ставился специальный знак ~ титло. Алфавитная система счисления. Славянская нумерация сохранялась до конца XVII века.
При Петре I возобладала так называемая арабская нумерация. Славянская нумерация сохранилась в богослужебных книгах.
Самой популярной системой кодирования чисел оказалась позиционная, десятичная. Используются десять цифр. Значение каждой определяется той позицией, которую цифра занимает в записи числа.
Эта система пришла из Индии, где она появилась не позднее VI века, европейцы заимствовали ее у арабов, назвав ее арабской. Из арабского языка заимствовано слово «цифра». Причина ее возникновения анатомическая — 10 пальцев. Анатомическая система счисления (существовали пятеричные, двадцатеричные системы счисления).
Например, 23 — три единицы, два десятка 32 — две единицы, три десятка 400 — 4 сотни, два 0 вклад в число не дают, нужны для того, чтобы указывать позицию 4.
В десятичной позиционной системе особую роль играет число 10 и его степени, например, 1996 — 6 единиц, 9 десятков, 9 сотен 1 тысяча или 1996=6+9*10+9*100+1*1000, т.к.1000=103, 100=102, 10=101, таким образом, 1996=1*103 + 9*102
Любое число в нулевой степени равно единице 0,10 = 1
То есть любое 4-х значное число можно записать в следующем виде:
N=a3*103+a2*102+a1*101+a0*100
a3, a2, a1, a0-десятичные цифры, от 1 до 9 или коэффициенты 3 2 1 0 — разряды, степени числа 10 со степенями называют основанием системы счисления.
Но основанием системы может быть не обязательно число 10, мы можем записать число в р-ичной системе, где основанием будут степени числа р. Любое число N в р-ичной системе мы можем представить в виде формулы:
N=an*Pn+an-1*Pn-1+.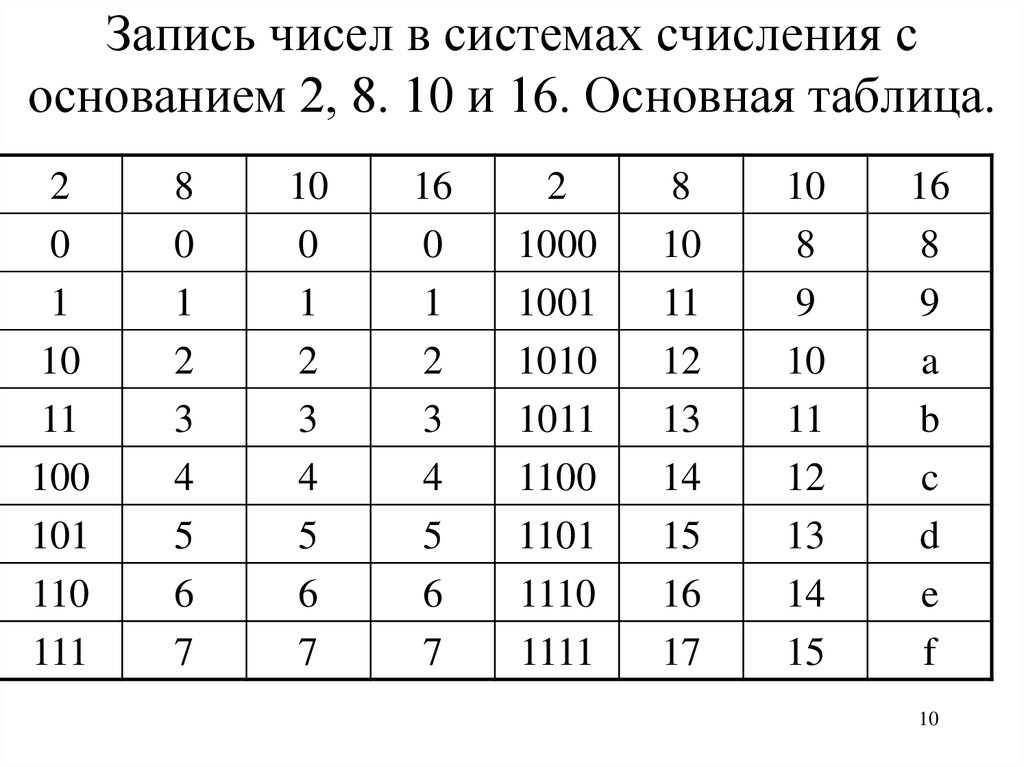 ..+a1*P1+a0*P0
..+a1*P1+a0*P0
Если взять за основание 60, то придется использовать 60 разных цифр. Такая система была в Древнем Вавилоне. Если основанием возьмем 2, получим систему всего с двумя цифрами 0 и 1. К сожалению, в этой системе даже небольшие числа записываются слишком длинно, так 1995 в двоичной системе записывается 199510=111110010112
Система счисления, где 2 является основанием системы называется двоичной системой счисления, относится к машинной системе счисления, к машинным системам счисления относятся и восьмеричная и шестнадцатеричная. Таким образом существуют следующие системы счисления: вавилонская, римская, алфавитные, анатомические, машинные.
Системы счисления делятся также на позиционные и непозиционные.
Перевод из двоичной системы счисления в десятичную.
Как узнать чему равно девятизначное двоичное число N=1111101002
Подпишем сверху каждый разряд
87654321010 — 1 разряды (степени двойки)
1111101002
В двоичной системе особую роль играет двойка и ее степени.
Таким образом:
111110100=1*28 +1*27 +1*26 +1*25 +1*24 +0*23 +1*22 +0*21 +0*20 =1*256+1*128+1*64 +1*32 +1*16 +0*8 +1*4 +0*2 +0*1=256 + 128 + 64 + 32 + 16 + 0 + 4 + 0 +0 =500
Перевод из десятичной системы счисления в двоичную.
Пусть нужно перевести в двоичную систему число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая про нулевые.
Выписав все остатки, начиная с последнего 3 в обратном порядке, получим двоичное разложение числа.
23410 = 111010102
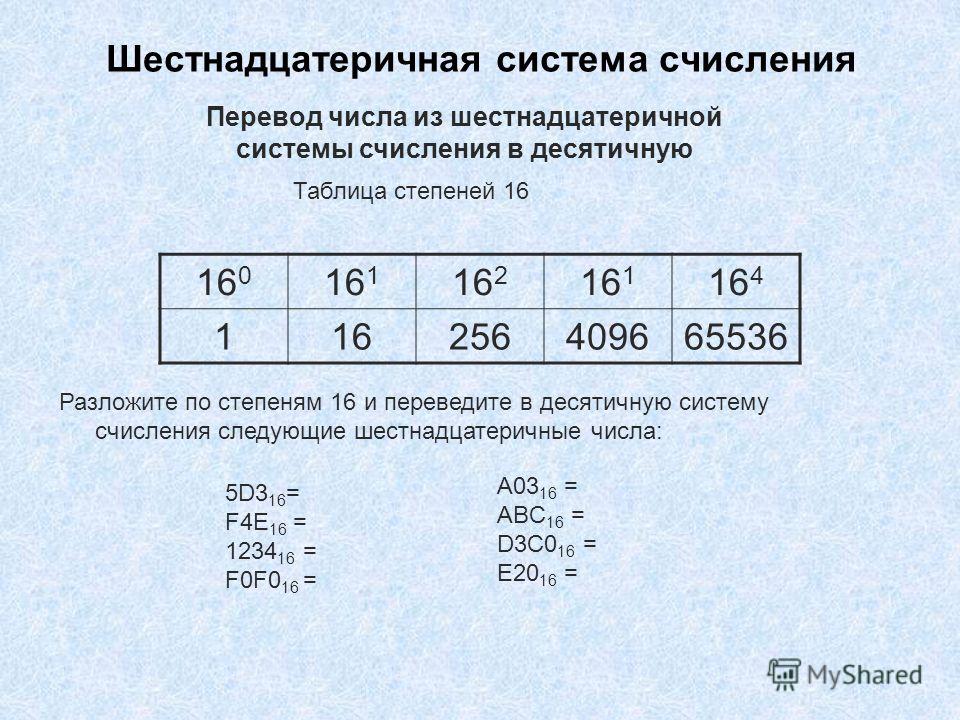
Восьмеричная и шестнадцатеричная системы счисления.
Запись числа в двоичной системе удобна для компьютера, но громоздка для человека. На помощь приходят системы, родственные двоичной восьмеричная система счисления использует 8 цифр: 0,1,2,3,4,5,6,7.
Единица, записанная в самом младшем разряде означает просто единицу (1*8 в нулевой степени), та же единица в следующем разряде обозначает 8 (1*8 в первой степени), в следующем 64 (1*8 во второй степени) и так далее.
2 1 0 1 — разряды (степени восьмерки)
1008 = 1*82 + 0*81 + 0*80
8 — это 2 в третьей степени. При переводе в восьмеричную систему двоичное число из трех цифр записывается одной цифрой.
Восьмеричная запись | Двоичное представление |
впереди стоящий 0 ничего не значит |
0 | 000 | |
1 | 001 | |
2 | 010 | |
3 | 011 | |
4 | 100 | |
5 | 101 | |
6 | 110 | |
7 | 111 |
Для перевода из двоичной в восьмеричную число, записанное в двоичной системе делим на триады справа налево
Например, 11011100011=11 011 100 011 и заменить каждую группу одной восьмеричной цифрой 2 2 4 2 и получим 22428
Для перевода числа из восьмеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную систему, представив каждую цифру в виде триады (1 в двоичной системе 1 добавляем до триады впереди 00)
6 | 1 | 1 |
110 | 001 | 001 |
Еще компактней выглядит запись двоичного числа в шестнадцатеричной системе счисления.
Для первых 10 из 16 шестнадцатеричных цифр используются привычные цифры 0 1 2 3 4 5 6 7 8 9, а для остальных используют первые буквы латинского алфавита
A-10 D-13
B-11 E-14
C-12 F-15
Цифра 1 в самом младшем разряде означает 1, в следующем разряде означает 16 (в первой степени), в следующем разряде 16*16 (162)=256, в следующем разряде 1*163 и так далее.
10016 =25610
Цифра F, записанная в самом младшем разряде означает 15 в десятичной системе, F в следующем разряде означает 15*16 в первой степени в десятичной системе и т.д.
2 1 0 — 1 разряды (степени числа 16)
Число 21016=10*162+15*161+0*160
21016=10*256+240+0*1=2560+240+0=280010
2 1 0
BAD16=11*162+1 0*161+13*1 60
16 — это 2 в четвертой степени. При переводе из двоичной системы в шестнадцатеричную число двоичное число из 4-х цифр кодируется числом из одной цифры в шестнадцатеричной системе.
При переводе из двоичной системы в шестнадцатеричную число двоичное число из 4-х цифр кодируется числом из одной цифры в шестнадцатеричной системе.
Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную, представив каждую цифру в виде сочетания четырех 1 и 0
A | O | F | AOF16 |
1010 | 0000 | 1111 |
Как осуществить перевод чисел из двоичной системы в шестнадцатеричную? Необходимо разбить число, записанное в двоичной системе на группы по 4 разряда справа налево, заменив каждую группу одной шестнадцатеричной цифрой.
1101 | 1010 | 1101 | в двоичной |
11 | 10 | 13 | в десятичной |
B | A | D | в шестнадцатеричной |
10 | 2 | 8 | 16 |
| 0 | 000 | 0 | 0 |
| 1 | 001 | 1 | 1 |
| 2 | 010 | 2 | 2 |
| 3 | 011 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
§10.
 Шестнадцатеричная система счисления | Перевод чисел
Шестнадцатеричная система счисления | Перевод чиселПланирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 8 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, базовый уровень) | §10. Шестнадцатеричная система счисления
Содержание урока
Перевод чисел
Связь с двоичной системой счисления
Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления
Алгоритм перевода двоичного числа в шестнадцатеричную систему счисления
Арифметические действия
Применение шестнадцатеричной системы
Выводы. Интеллект-карта
Вопросы и задания
Ключевые слова:
• шестнадцатеричная система • перевод чисел • связь с двоичной системой • сложение • вычитание
Шестнадцатеричная система (позиционная система с основанием 16) широко используется для записи адресов и содержимого ячеек памяти компьютера.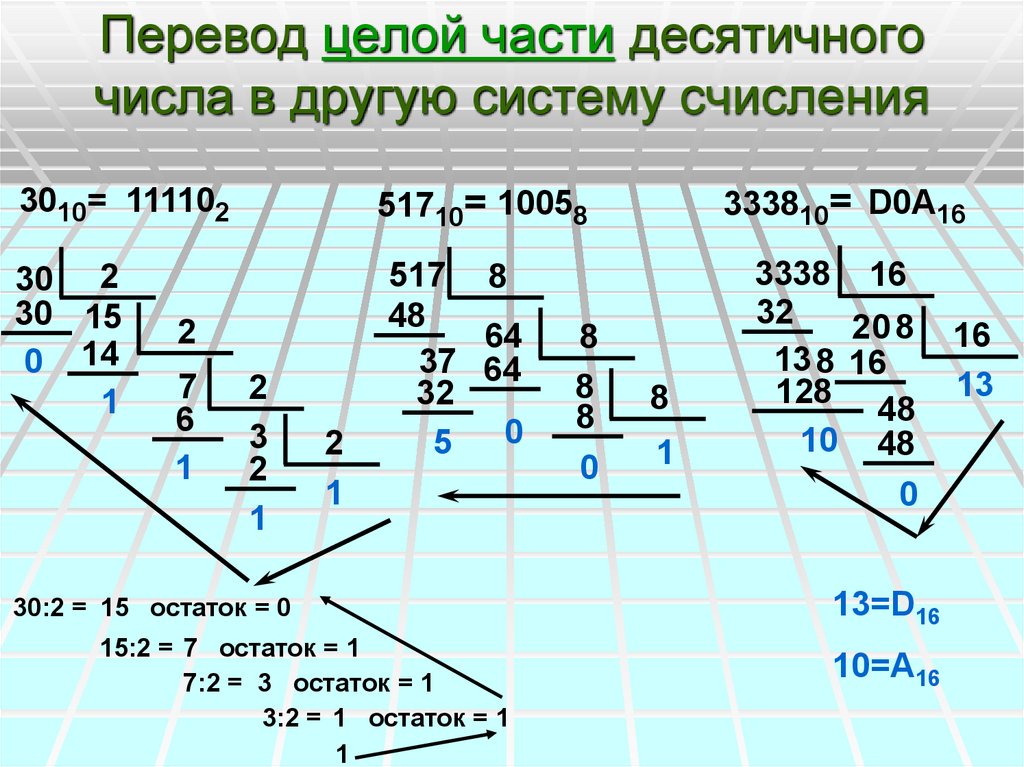 Её алфавит содержит 16 цифр. Вместе с 10 арабскими цифрами от 0 до 9 используются первые буквы латинского алфавита:
Её алфавит содержит 16 цифр. Вместе с 10 арабскими цифрами от 0 до 9 используются первые буквы латинского алфавита:
А = 10, В = 11, С = 12, D = 13, Е = 14 и F = 15.
Какие числа записаны в шестнадцатеричной системе неверно: 34AF516, 5BG616, 9FF6116, ADh3316? Как вы рассуждали?
Перевод чисел
Для перевода чисел из десятичной системы в шестнадцатеричную используют алгоритм деления на 16 и выписывания остатков. Важно не забыть, что все остатки, большие 9, заменяются на буквы:
Переведите в шестнадцатеричную систему счисления числа 31, 91, 126, 172.
Запись некоторого числа в шестнадцатеричной системе счисления заканчивается на 0. Что можно сказать о свойствах этого числа?
Запись некоторого числа в шестнадцатеричной системе счисления заканчивается на 3. Что можно сказать о свойствах этого числа?
Платон перевёл некоторое число из десятичной системы в шестнадцатеричную, полученная запись содержит 2 цифры. Какое это могло быть число (назовите наименьшее и наибольшее возможные значения)?
Какое это могло быть число (назовите наименьшее и наибольшее возможные значения)?
Для перевода числа из шестнадцатеричной системы в десятичную значение каждой цифры умножают на 16 в степени, равной её разряду, и полученные значения складывают:
Переведите числа 1216, 5716, 7916, АВ16, DD16, EF16 в десятичную систему счисления.
Не выполняя перевода чисел в другие системы счисления, выясните, может ли число 225 быть записано в шестнадцатеричной системе как 11F16. Как вы рассуждали?
Следующая страница Связь с двоичной системой счисления
Cкачать материалы урока
Эпоха 16-битной и шестнадцатеричной системы счисления
Перейти к плейлисту эпизодов
Давайте поговорим о 16-битной эпохе и новой системе нумерации. Нам нужно вычислить большие числа. Работа с двоичными и восьмеричными числами утомительна. Бам, поприветствуйте шестнадцатеричную (или шестнадцатеричную) нотацию, которую вы используете каждый день для цветовых кодов CSS.
Нам нужно вычислить большие числа. Работа с двоичными и восьмеричными числами утомительна. Бам, поприветствуйте шестнадцатеричную (или шестнадцатеричную) нотацию, которую вы используете каждый день для цветовых кодов CSS.
Основные выводы из этого эпизода:
- Шестнадцатеричное (hex) более сжатое обозначение
- Позволяет ввести до 16 цифр: 0-9 + A-F
- Одна шестнадцатеричная запись аналогична 4-битным группам в двоичном коде
- Полезно для больших чисел
- Цветовые коды используют шестнадцатеричный код
Учебные заметки
Помните : Чем больше число, тем больше мощность
Процесс преобразования двоичного числа в десятичное занимает несколько шагов. Сложнее посмотреть на образец 1 и 0 и вытащить точный десятичный эквивалент.
Преобразование больших чисел
Как упростить представление?
Новая 16-битная система счисления:
Из каких блоков состоит наша новая 16-битная система счисления? Начнем с восьмеричной.
В восьмеричном формате у нас есть семь битов, которые также являются цифрами от 0 до 7. Он использует группировку 3-битных двоичных чисел для представления цифр.
Обратите внимание, что мы использовали все образцы единиц и нулей.
16-разрядное преобразование:
Давайте рассмотрим преобразование этого двоичного числа в нашу новую 16-разрядную систему счисления. Мы группируем его по 4 битам, что означает, что для 2-байтового двоичного шаблона имеется 4 цифры. Всегда начинайте с младшего значащего бита (крайнего справа).
Обозначение этого нового числа — 0x1445, где x обозначает шестнадцатеричный или шестнадцатеричный формат. Сокращенное обозначение: 1455 16 .
Теперь сравните эту новую запись чисел с восьмеричной. Вы видите, что использование шестнадцатеричной формы лучше для больших чисел?
Хотите знать, где вы когда-нибудь будете использовать шестнадцатеричный?
Цветовые коды указаны в шестнадцатеричном формате.
Преобразуем шестнадцатеричное представление цвета «белый» в двоичный, восьмеричный и десятичный форматы.
Практическое использование Hex
- Цветовые коды
- Сообщения об ошибках
- Штрих-код
- Взаимодействие с API
Эй… эй ты… да ты!… Хорошо проводишь время? Учиться новому? Хороший!
Эпизоды
Общее время работы лаборатории: 02:59:07
- 1 Введение в лабораториюбесплатно 03:56
- 2 Электроника «включена» и «выключена» 12:11
- 3 Символ для представления свободного количества 14:26
- 4 Система счисления для Statefree 12:44
- 5 Двоичный — объединение 1 и 0 бесплатно 19:25
- 6 Улучшение бинарного представленияfree 13:45
- 7 Эпоха 16-битных и шестнадцатеричных чисел 15:15
- 8 Бинарное дополнениебесплатно 03:59
- 9 Отрицательное целочисленное представление данных — часть 1бесплатно 10:06
- 10 Отрицательное целочисленное представление данных.
 Часть 2бесплатно 18:42
Часть 2бесплатно 18:42 - 11 Представление данных в виде реальных чисел. Часть 1бесплатно 17:12
- 12 Представление данных в виде реальных чисел. Часть 2бесплатно 10:18
- 13 Представление текстовых данныхбесплатно 08:47
- 14 Представление данных цифрового изображениябесплатно 18:21
Знай код слетает на движке WP. Ознакомьтесь с решениями для управляемого хостинга от WP Engine.
WordPress® и связанные с ним товарные знаки являются зарегистрированными товарными знаками WordPress Foundation. Фреймворк Genesis и связанные с ним товарные знаки являются зарегистрированными товарными знаками StudioPress.
Этот веб-сайт не связан и не спонсируется Automattic, Inc., WordPress Foundation или WordPress® Open Source Project.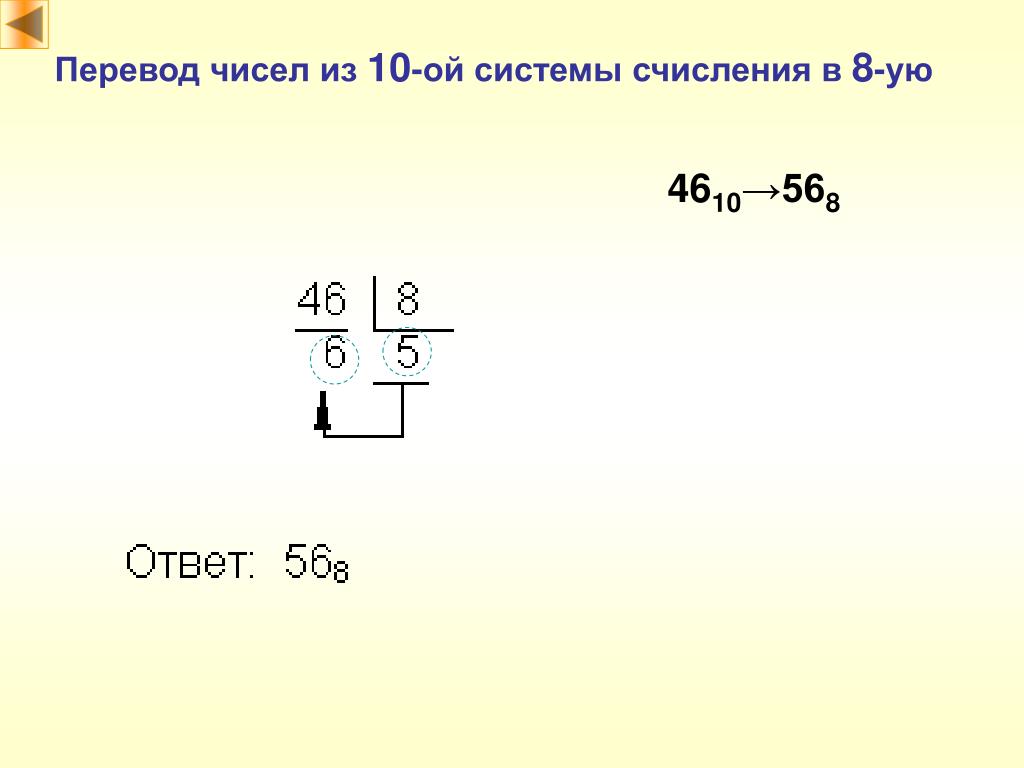
Шестнадцатеричные числа — Electronics-Lab.com
Шестнадцатеричные числа
Шестнадцатеричное число (16) представляет собой систему счисления с основанием 16 , в которой использует шестнадцать (16) чисел для представления значения своей цифры. В шестнадцатеричном числе используется группа или набор из четырех (4) двоичных цифр для формирования шестнадцатеричной цифры 9.0026 . Другими словами, шестнадцатеричная цифра эквивалентна полубайту, а из предыдущей статьи мы знаем, что полубайт — это четырехбитное двоичное число. Крайний правый полубайт образует наименее значимую шестнадцатеричную цифру, а слева от него можно добавлять полубайты для представления большего шестнадцатеричного числа.
Архитектура цифровых систем рассчитана на 8-, 16-, 32- и 64-битные и т. д. двоичные числа и представление этих чисел нулями (0) и единицами (1) становятся довольно запутанными и сложными. Чтение и запись больших двоичных чисел может привести к ошибкам, и информация действительно может стать сомнительной.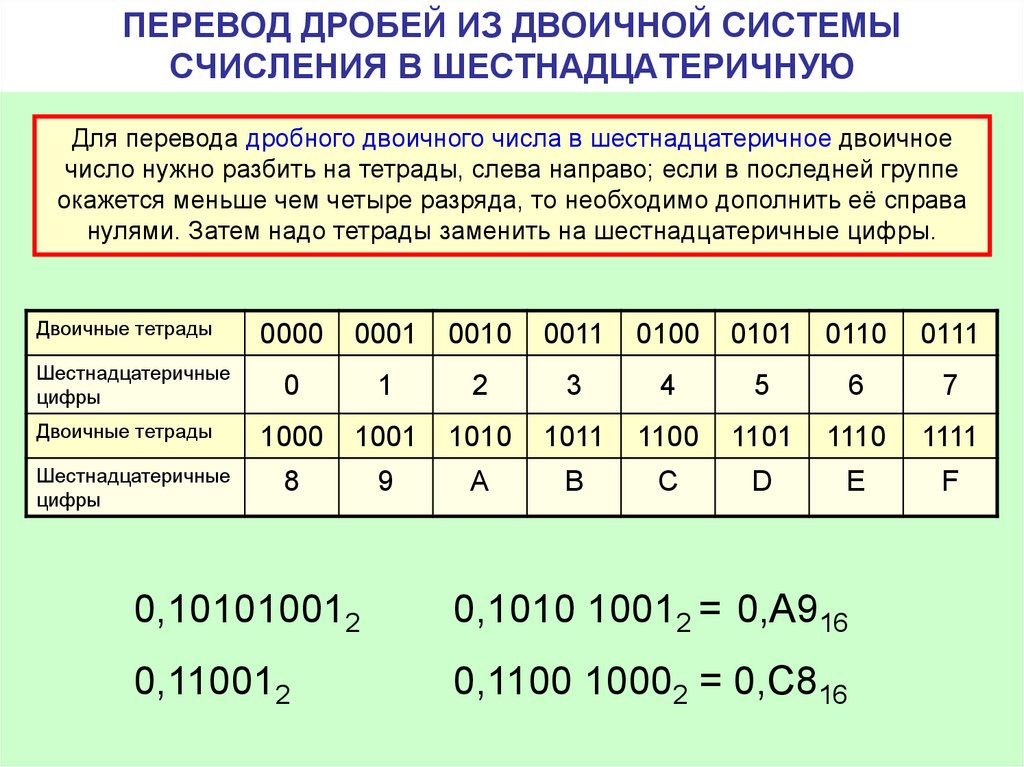 Представлением больших двоичных чисел можно управлять с помощью системы нумерации с более высоким базовым значением, которая будет вмещать больше значений в однозначных цифрах по сравнению с двоичными цифрами (битами). Восьмеричная цифра (с основанием 8) может использовать восемь (8) чисел (от 0 до 7) и может вмещать 3-битное двоичное число. 3-битное двоичное число довольно мало и не подходит для 8-, 16-, 32- и 64-битных архитектур и т. д. Точно так же десятичное число подходит для представления 3-битного двоичного числа, но тратит впустую два (8 и 9).) числовые значения. Другими словами, восьмеричная система счисления более подходит по сравнению с десятичными (десятичными) числами, когда речь идет о представлении двоичных чисел.
Представлением больших двоичных чисел можно управлять с помощью системы нумерации с более высоким базовым значением, которая будет вмещать больше значений в однозначных цифрах по сравнению с двоичными цифрами (битами). Восьмеричная цифра (с основанием 8) может использовать восемь (8) чисел (от 0 до 7) и может вмещать 3-битное двоичное число. 3-битное двоичное число довольно мало и не подходит для 8-, 16-, 32- и 64-битных архитектур и т. д. Точно так же десятичное число подходит для представления 3-битного двоичного числа, но тратит впустую два (8 и 9).) числовые значения. Другими словами, восьмеричная система счисления более подходит по сравнению с десятичными (десятичными) числами, когда речь идет о представлении двоичных чисел.
Подходящей и подходящей системой нумерации является та, которая может вмещать 4-битное двоичное число. Как мы знаем, 4-битное число может содержать шестнадцать (16) значений (два, возведенные в степень четыре). Для этого требуется система счисления, имеющая набор из шестнадцати значений, то есть от 0 до 15. Десятичная цифра имеет диапазон чисел от 0 до 9, и такие числа, как 10, 11, 12, 14 и 15, не могут быть представлены, поскольку они предполагает использование ранее использовавшихся номеров. В шестнадцатеричном формате значения выше девяти (9) представлены английскими алфавитами, такими как A, B, C и т. д. Использование этих алфавитов решает проблему повторения чисел для десяти (10) и более значений.
Десятичная цифра имеет диапазон чисел от 0 до 9, и такие числа, как 10, 11, 12, 14 и 15, не могут быть представлены, поскольку они предполагает использование ранее использовавшихся номеров. В шестнадцатеричном формате значения выше девяти (9) представлены английскими алфавитами, такими как A, B, C и т. д. Использование этих алфавитов решает проблему повторения чисел для десяти (10) и более значений.
Это означает, что A, B, C, D, E и F в шестнадцатеричном формате представляют собой десятичные числа: десять (10), одиннадцать (11), двенадцать (12), тринадцать (13), четырнадцать (14) и пятнадцать ( 15). То же самое верно для представления эквивалентных двоичных чисел «1010», «1011», «1100», «1101», «1110». и «1111» соответственно. Сложность представления большего двоичного числа можно облегчить, разбив двоичное число на группы по 4 бита. Например, рассмотрим (1101100111001010 2 ) — 16-битное двоичное число, которое можно записать как (1101 1001 1100 1010 2 ) .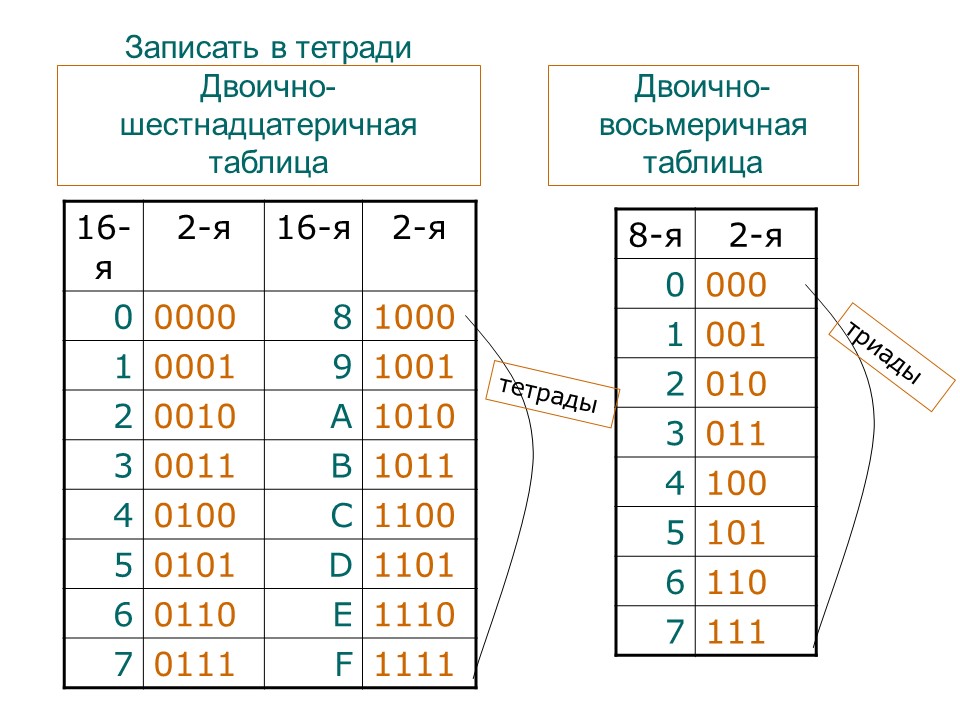 Последнее достигается путем разбиения на группу или набор из 4 битов, и полученное двоичное число намного легче читать.
Последнее достигается путем разбиения на группу или набор из 4 битов, и полученное двоичное число намного легче читать.
Длину и сложность двоичных чисел можно дополнительно уменьшить, преобразовав их в эквивалентные шестнадцатеричные числа. Однако шестнадцатеричные числа являются сложными по сравнению с десятичными числами и используются только в цифровых системах. Четырехбитные двоичные числа «0000», «0001», «0010», … и «1111» представлены одной шестнадцатеричной цифрой. Четырехбитное двоичное число называется «полубайтом», что эквивалентно шестнадцатеричной цифре. Байт состоит из 8 бит или двух полубайтов, и две шестнадцатеричные цифры представляют его эквивалент. Например, двоичное число (10100111 2 ) разделен на две половинки (1010 0111 2 ) . При этом (1010 2 ) эквивалентно (10 10 ) в десятичном виде и ( A 16 ) в шестнадцатеричном. Точно так же второй полубайт (0111 2 ) эквивалентен (7) в десятичном и шестнадцатеричном формате. Таким образом, двоичное число (10100111 2 ) эквивалентно (A7 16 ) в шестнадцатеричном формате.
Точно так же второй полубайт (0111 2 ) эквивалентен (7) в десятичном и шестнадцатеричном формате. Таким образом, двоичное число (10100111 2 ) эквивалентно (A7 16 ) в шестнадцатеричном формате.
Шестнадцатеричные числа
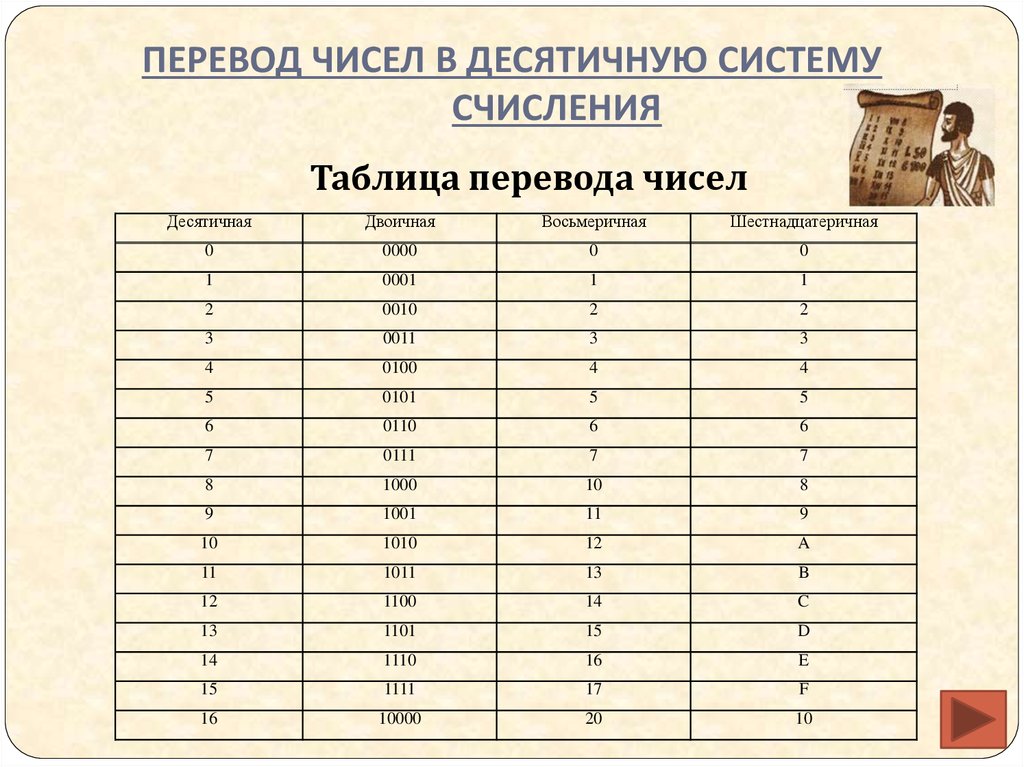
В следующей таблице перечислены десятичные числа от 0 до 15 и их эквиваленты в двоичных и шестнадцатеричных числах.
В приведенной выше таблице показаны эквивалентные десятичные числа от 0 до 15 для шестнадцатеричных цифр. Для подсчета чисел после пятнадцати (F) в шестнадцатеричном формате используется процедура, аналогичная другим системам счисления, т.е. включая значащую цифру слева. Например, число «16», преобразованное в двоичное число, равно 9.0025 (0001 0000) 2 и его шестнадцатеричный эквивалент (10 16 ). Точно так же эквивалентом 17 в шестнадцатеричном формате является (11 16 ) , и, следуя той же процедуре, шестнадцатеричное число может быть расширено до желаемого значения. Используя приведенную выше таблицу, любое двоичное число можно легко преобразовать в эквивалентное ему шестнадцатеричное число. Например, 16-битное число (1010 1100 0111 1011 2 ) , преобразованное в шестнадцатеричное, равно (AC7B 16 ) . Гораздо проще написать и запомнить это шестнадцатеричное число, чем 16-битный ряд из 0 и 1. Следовательно, рекомендуется записывать двоичные числа в шестнадцатеричной системе счисления, чтобы избежать ошибок и т. д.
Используя приведенную выше таблицу, любое двоичное число можно легко преобразовать в эквивалентное ему шестнадцатеричное число. Например, 16-битное число (1010 1100 0111 1011 2 ) , преобразованное в шестнадцатеричное, равно (AC7B 16 ) . Гораздо проще написать и запомнить это шестнадцатеричное число, чем 16-битный ряд из 0 и 1. Следовательно, рекомендуется записывать двоичные числа в шестнадцатеричной системе счисления, чтобы избежать ошибок и т. д.
В цифровых системах, особенно при написании программ, знак «#» (решётка) значащая цифра для обозначения шестнадцатеричного значения. Например, указанное выше шестнадцатеричное число (AC7B 16 ) также можно записать как 9.0025 (#AC7B) .
Счет в шестнадцатеричном формате
Как описано выше, значение шестнадцатеричного числа можно расширить, используя дополнительные значащие цифры. Одна шестнадцатеричная цифра, начинающаяся с «0», может составлять до #F (15 X 16 0 = 15 10 ) , расширенная до двух цифр, может составлять до #FF (15 X 16 1).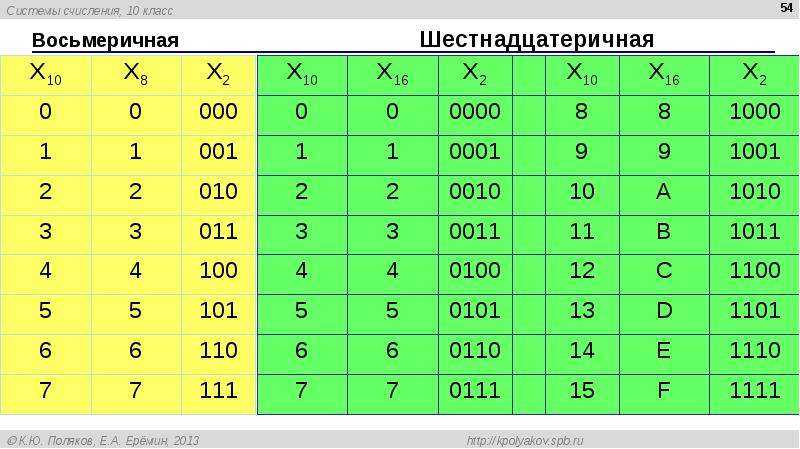 +15 х 16 0 = 255 10 ) . Точно так же #FFFF и #FFFF могут считать до 9.0025 4095 10 и 65535 10 , соответственно. В следующей таблице указан вес каждой цифры в шестнадцатеричном числе.
+15 х 16 0 = 255 10 ) . Точно так же #FFFF и #FFFF могут считать до 9.0025 4095 10 и 65535 10 , соответственно. В следующей таблице указан вес каждой цифры в шестнадцатеричном числе.
Добавление нулей к двоичному числу
Поскольку двоичное число разбивается на группы, состоящие из 4 бит, для определения его эквивалентного шестнадцатеричного числа. Для этого требуется двоичное число, состоящее из битов, кратных четырем (4), например. 4, 18, 12, 16 и 20 и т. д. Однако это может быть не так, когда речь идет о двоичных числах, а двоичные числа могут различаться по длине в битах. Решение состоит в том, чтобы начать разбивать двоичные числа на группы по 4 бита, начиная с младшего значащего бита (LSB), и, в конце концов, у нас останется менее 4 бит в конце. Ведущие нули добавляются к оставшимся битам, увеличивая их длину до 4 бит. Эта группа из 4 битов составляет старшую значащую цифру (MSD) шестнадцатеричных чисел. В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 1010 10 ) преобразуется в 16-разрядное (делящееся на 4) двоичное число путем добавления начальных нулей, а затем определяется его эквивалентное шестнадцатеричное число.
В следующей таблице нестандартное 13-битное двоичное число (1 0101 1101 1010 10 ) преобразуется в 16-разрядное (делящееся на 4) двоичное число путем добавления начальных нулей, а затем определяется его эквивалентное шестнадцатеричное число.
В приведенном выше примере 13-битное число требует добавления 3 битов с нулевыми значениями к крайней левой стороне, чтобы сделать его 16-битным двоичным числом. Точно так же 10-битное двоичное число потребует добавления шести (6) нулевых битов. Использование шестнадцатеричных чисел сокращает длину двоичных чисел в четыре (4) раза, а преобразование из двоичного в шестнадцатеричное или из шестнадцатеричного в двоичное выполняется легко и быстро.
Преобразование шестнадцатеричных чисел в десятичные
Преобразование шестнадцатеричных значений в десятичные достигается с помощью метода взвешенной суммы цифр, описанного в предыдущей статье. В следующем примере шестнадцатеричное число (#7DE5) преобразуется в десятичное число.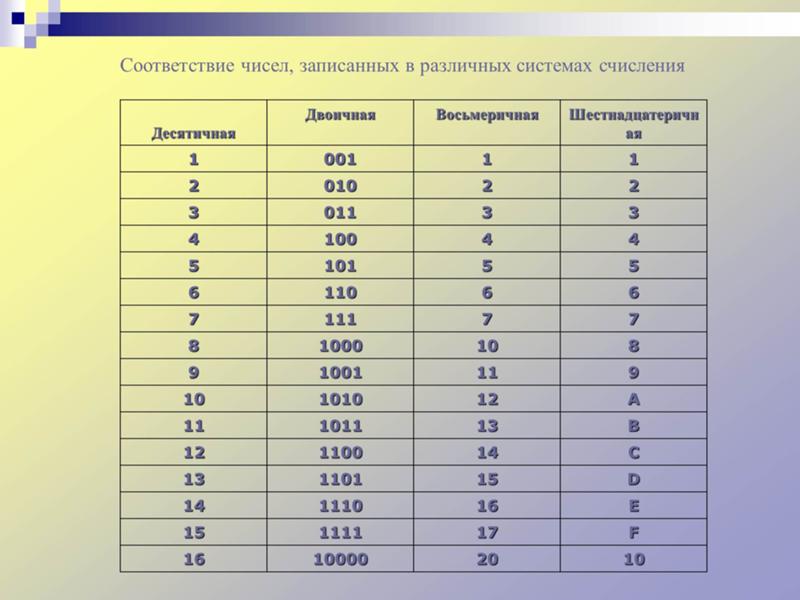
Преобразование десятичного числа в шестнадцатеричное
Преобразование десятичного числа в шестнадцатеричное требует применения метода повторного деления на 16, который использовался для преобразования десятичного числа в эквивалентное ему двоичное значение в предыдущей статье. То же десятичное число (238 10 ) используется для получения эквивалентного ему шестнадцатеричного числа в следующем примере.
Пример преобразования двоичного числа в шестнадцатеричное
Ниже показано преобразование 8-битного двоичного числа (11011001 2 ) в шестнадцатеричное число.
Шестнадцатеричный код в двоичный и десятичный Пример
Преобразование #8C4A в его эквивалентное двоичное и десятичное число показано ниже в качестве примера.
Заключение
- Шестнадцатеричный номер использует систему счисления с основанием 16, и его цифры могут состоять из шестнадцати (16) цифр от 0 до 15.
 В шестнадцатеричном коде используются заглавные буквы: A, B, C, D, E и F. эквивалентно 10, 11, 12, 13, 14 и 15 соответственно.
В шестнадцатеричном коде используются заглавные буквы: A, B, C, D, E и F. эквивалентно 10, 11, 12, 13, 14 и 15 соответственно. - В шестнадцатеричных числах каждая цифра представляет собой группу или набор из 4 битов. Эквивалент двоичного числа в шестнадцатеричном формате получается путем разбиения двоичного числа на группы по 4 бита, а затем, в зависимости от значения каждой 4-битной группы, каждой группе присваивается эквивалентное шестнадцатеричное значение от «0» до «F».
- Двоичные числа могут потребовать добавления начальных нулей в крайнюю левую (наиболее значащую) сторону для формирования 4-битных групп.
- Шестнадцатеричное число представляется с помощью «16» в качестве нижнего индекса или решетки (#) с крайней левой стороны, например. 2A7E 16 или #2A7E.
- Шестнадцатеричное число можно преобразовать в десятичное число с помощью метода взвешенной суммы цифр. Преобразование десятичного числа в шестнадцатеричное требует применения метода повторного деления на 16.



 Часть 2бесплатно 18:42
Часть 2бесплатно 18:42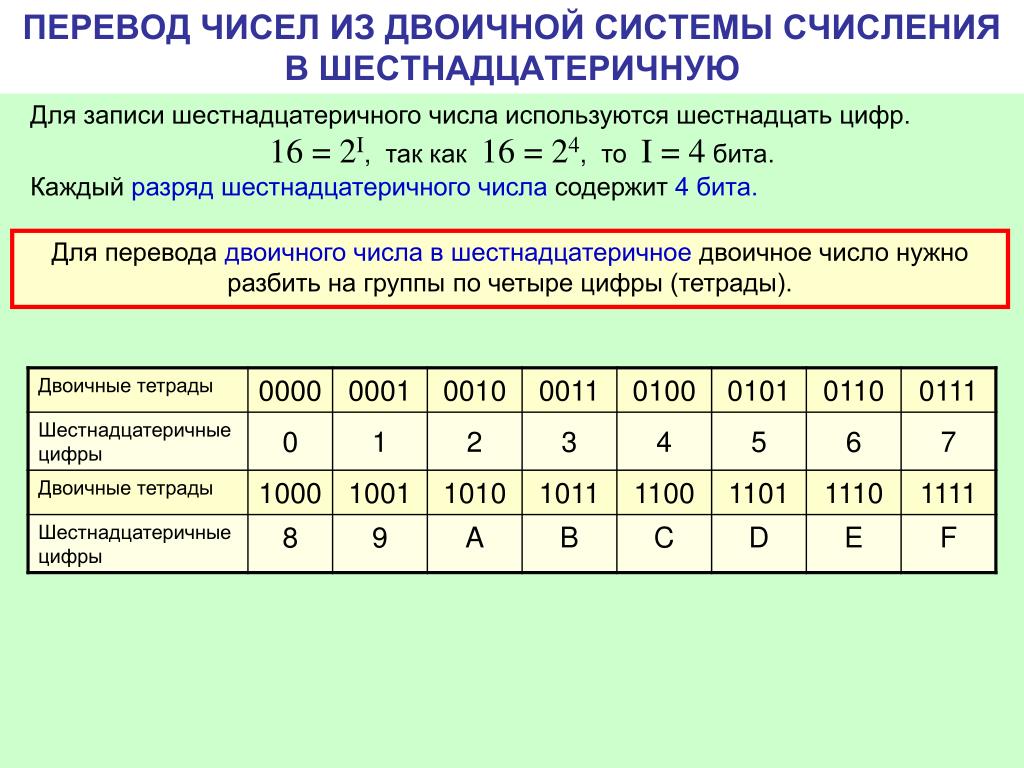 В шестнадцатеричном коде используются заглавные буквы: A, B, C, D, E и F. эквивалентно 10, 11, 12, 13, 14 и 15 соответственно.
В шестнадцатеричном коде используются заглавные буквы: A, B, C, D, E и F. эквивалентно 10, 11, 12, 13, 14 и 15 соответственно.