Чему равняется 1: Что такое дюйм? Чему равен 1 дюйм? – Фунт (единица измерения) — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Фунт (единица измерения) — Википедия

У этого термина существуют и другие значения, см. Фунт. Единицы веса по странам, табл. 1848 г.

Фунт (от лат. pondus — вес, гиря^[1]) — единица измерения массы. Исторически использовался в некоторых европейских странах, причём в эпоху феодальной раздробленности в некоторых странах (например, во Франции) его значение имел право устанавливать каждый феодал, поэтому даже в начале XVIII века в Европе было более ста разных фунтов^[2]. Наиболее распространённым сегодня является международный фунт эвердьюпойс, который юридически определён как 0,453 592 37 килограммов, и который разделён на 16 унций^[3]. Международный стандартный символ для эвердьюпойсного фунта — lb;^[4] альтернативным символом является lb_m^[5] (для большинства определений фунта), # (главным образом в США), и ℔^[6] или ″̶^[7] (специально для аптекарского фунта).

В англоязычных странах фунт (англ. pound от лат. pondus «вес»

[8] или lb сокр. от libra «весы») — одна из наиболее распространённых единиц массы и силы. При необходимости исторически традиционное смешение массы и веса разрешается через употребление для единицы силы термина «фунт-сила» (англ.)русск., сокращённо lbf.

Существовало несколько фунтов (тройский, лондонский, башенный и др.). Сейчас английский фунт соответствует:

По соглашению от 1 июля 1959 года международный фунт^[en] (символ lb) равен 0.45359237 кг^[9]. Соглашение было подписано представителями шести стран, а именно США, Великобритания, Канада, Австралия, Новая Зеландия и Южно-Африканский Союз^[10].

При использовании в качестве измерения веса в Великобритании по-прежнему использует стон (букв. «камень») весом 14 фунтов. Например, «11 камней 4 фунта» в США обозначаются «158 фунтами»

[11], или «72 килограммами» в тех местах, где пользуются метрической системой. США не приняли метрическую систему^[12], несмотря на многочисленные попытки^[en] сделать это, и фунт по-прежнему широко используется в качестве одной из основных единиц измерения в США^[en]^[13]^[14].

В настоящее время Международная организация законодательной метрологии (МОЗМ) в своих рекомендациях относит фунт к тем единицам измерения массы, «которые должны быть изъяты из обращения как можно скорее там, где они используются в настоящее время, и которые не должны вводиться, если они не используются»

[15].

В русской системе мер фунт равен 96 золотникам и с 1747 года являлся эталонным весом. В 1747 году был изготовлен «бронзовый золочёный фунт 1747 года», по которому в 1835 году был изготовлен платиновый фунт, основа мер веса в Российской империи и Советской России до декрета «О введении международной метрической системы мер и весов», подписанного В. И. Лениным в 1918 году.

В Указе от 11 октября 1835 года «О системе Российских мер и весов»^[16] говорится:

Принять за основную единицу Российского веса образцовый (фунт), сделанный комиссией согласно с выведенным результатом, что российский или английский кубический дюйм воды при температуре 13
1/₃° Реомюра в безвоздушном пространстве весит 368,361 долю, или что объём российского фунта той же воды равен 25,019 английским кубическим дюймам, что составляет совершенное равенство с известным золочёным фунтом Санкт-Петербургского монетного двора, сделанным в 1747 г. и служащим с того времени основанием Российской монетной системы.

Этот фунт называли русским фунтом торгового веса. Существовал ещё и аптекарский, или нюрнбергский фунт (единица для измерения аптекарского веса). Согласно Торговому уставу 1893 год 1 аптекарский фунт =

7/₈, или 0,875 русского фунта.

Соотношение с метрической системой^[17]:

1 г = 0,23442557 золотника;
1 г = 22,504855 долей;
1 кг = 2,441933 фунта;
1 кг = 2 фунта 42 золотника 40,855 долей;
1 квинталь (центнер) = 6 пудов 4,1933 фунта;
1 т = 61 пуд 1,933 фунта.

Миллиграммы, граммы и килограммы в аптекарском весе:

1 мг = 0,016075 грана;
1 г = 16,08 гран;
1 кг = 2 фунта 9 унций 4 драхмы;
1 аптекарский гран = 62,2088 мг;
1 драхма = 3,732527 г;
1 унция = 29,860215 г;
1 фунт аптекарский = 0,358322 кг.

В 1890-х годах Д. И. Менделеевым был изготовлен платиново-иридиевый эталон русского фунта, согласованный с весом платинового образца 1835 года. Положением о мерах и весах 1899 года новый эталон русского фунта был узаконен и выражен в метрической системе мер: 1 русский фунт = 0,40951241 кг

[18].

Русский фунт = 0,40951241 кг

Австрийский фунт равен 0,56001 кг (использовался также в Баварии)
Амстердамский фунт равен 0,4941 кг
Венецианский фунт равен 0,477 кг
Датский фунт равен 0,496 кг
Древнеримский фунт (libra) равен 0,32745 кг
Испанский фунт равен 0,451 кг
Каролингский фунт равен 0,408 кг^[19]
Португальский фунт равен 0,459 кг
Русский артиллерийский фунт равен 0,4914 кг

Французский фунт (ливр) равен 0,489505 кг
Шведский фунт равен 0,425076 кг
Ливонский/Ганзейский фунт^[20] равен 0,4847 кг (в Ливонии использовалась преобладающая на Балтике Ганзейская система мер, базировавшаяся на мерах Любека и Гамбурга)
Нюрнбергский (не аптекарский) фунт равен 0,5095 кг (как торговый распространён в средней Германии и использовался как артиллерийский в центральной Европе)
Прусский фунт равен 0,467711 кг (норма восходит к двум Кёльнским маркам и распространена во всей нижней Германии и Рейнских областях)

Во многих европейских странах, использующих метрическую систему, в обиходе используется так называемый «

метрический фунт» (нем. Pfund, фр. livre, нидерл. pond), равный ровно 0,5 кг.

↑ Pound term definition (англ.)
↑ Ирина Винокурова. Хлебная метрология // Техника — молодёжи. — 2011. — № 7 (июль). — С. 50.
↑ United States National Bureau of Standards. Notices «Refinement of values for the yard and the pound» (неопр.) (25 июня 1959). Дата обращения 12 августа 2006.
↑ IEEE Std 260.1™-2004, IEEE Standard Letter Symbols for Units of Measurement (SI Units, Customary Inch-Pound Units, and Certain Other Units)
↑ Fletcher, Leroy S. & Shoup, Terry E. (1978), Introduction to Engineering, Prentice-Hall, ISBN 978-0135018583, <https://books.google.com/books?id=tyohAQAAIAAJ> ^:257
↑ unicode chart 2100-214F (неопр.). character 2114 of the Unicode 6.0 and 5.0 standards. Unicode Consortium. Дата обращения 28 апреля 2011.
↑ The Dictionary of Medical and Surgical Knowledge (неопр.). Дата обращения 22 сентября 2016.
↑ Pound term definition (англ.) ссылка проверена 15 мая 2009.
↑ National Bureau of Standards, Appendix 8 Архивировано 18 января 2009 года.; National Physical Laboratory, P H Bigg et al. : Re-determination of the values of the imperial standard pound and of its parliamentary copies in terms of the international kilogramme during the years 1960 and 1961 ; Sizes.com: pound avoirdupois.
↑ National Institute of Standards and Technology. Research Highlights of the National Bureau of Standards (англ.). — U.S. Department of Commerce, National Bureau of Standards, 1959. — P. 13.
↑ Christine Hopkins, Ann Pope, Sandy Pepperell (2013). «Understanding Primary Mathematics». p. 195. Routledge.
↑ Appendix G – Weights and Measures // The World Factbook (неопр.). — Central Intelligence Agency, 2007.
↑ US 1988 law on metrification (неопр.). Дата обращения 21 сентября 2019.
↑ Countries not using SI (неопр.). Дата обращения 21 сентября 2019.
↑ Международный документ МОЗМ D2. Узаконенные (официально допущенные к применению) единицы измерений. Приложение В Архивная копия от 14 октября 2013 на Wayback Machine.
↑ Указ «О системе Российских мер и весов»
↑ Таблицы для перевода метрических (десятичных) мер в русские и русских — в метрические
↑ Сто лет государственной службы мер и весов в СССР. — М.: Гос. изд-во техн.-теорет. лит-ры, 1945. — С. 49.
↑ Kahnt Helmut. Karlspfund // Das große Münzlexicon von A bis Z. — 1. Auflage. — Regenstauf: Battenberg Verlag, 2005. — S. 216—217. — ISBN 3-89441-550-9.
↑ Казакова Из истории сношений Новгорода с Ганзой в XV веке (рус.) // Институт истории Академии наук СССР Исторические записки : журнал / Ответ. ред. акад. Б. Д. Греков. — [Б. м.: Издательство Академии наук СССР, 1949. — Т. 28. — С. 111—137.

Вилинов Ю. А., Шишков С. М. Рыболовные грузила или невольничья пайка? // Мелитопольский краеведческий журнал, № 7, 2016, с. 69-72.
Каменцева Е. И., Устюгов Н. В. Русская метрология. Изд. 2-е. — М.: Высшая школа, 1975. — 328 с.

Почему 0,999 равняется 1, и в чём проблема дня рождения?

Не верите, что 0,999 равняется 1? Держите доказательство без сложных вычислений и, как приятный бонус, обсуждение проблемы даты рождения и вычисление шансов выиграть спор на эту тему.

Почему 0,999… равняется 1?!

«Чуть-чуть» не считается, за исключением метания подковы, бросков ручной гранаты и… математики?

Что?! Это несерьёзно, да?

Советуем раньше времени не разочаровываться в математической точности, потому что впервые в истории близость значения на самом деле математически точна!

Сейчас вы узнаете, как с помощью базовой математики продемонстрировать друзьям то, что периодическая десятичная дробь 0,999… в действительности равняется 1.

Да, вы всё правильно поняли. Покажем, что это правда, без лишних премудростей. Никаких вычислений, никаких пределов и каких бы то ни было продвинутых концепций. Итак, начнём!

Как перевести периодические десятичные дроби в обыкновенные

Часто люди не понимают, что можно легко записать любую периодическую десятичную дробь в виде обыкновенной.

Итак, вот, что понадобится.

Если у вас одночисловое бесконечное значение, напишите повторяющуюся цифру над знаменателем 9. Таким образом, мы получим:

Если в дроби чередуются 2 числа, запишите повторяющиеся цифры в числитель над 99.

При повторении трёх чисел в значении повторяющиеся цифры записывайте над знаменателем 999.

Заметили закономерность?

С учётом N повторяющихся цифр формула обретает вид:

Демонстрация равенства 0,999… и 1

Ладно, поехали! Начните с приравнивания 0,999… эквивалентной дроби.

Конечно, 9 ÷ 9 = 1. Поэтому получаем:

Здесь, пожалуй, закончим. Коротко и ясно.

Всё ещё не убеждены?

До сих пор удивляетесь, как это может быть правдой? Понимаем, ведь это совершенно противоречит здравому смыслу и будоражит разум.

Предположим, что добавление девяток в конец числа 0,999… не только больше и больше приближает значение к 1, но и делает его равным 1.

Вот ещё один способ посмотреть на это.

1/3 равно 0,33333… и 2/3 равно 0,66666…, поэтому 1/3 + 2/3равняется0,333 +0,6666…, верно?

Суммируйте обе стороны и снова получите, что…

Любители математики, наверное, сейчас немного разочаровались, потому что это слишком легко и, как говорят в математическом мире, тривиально.

Слышу вас и тоже временами тоскую по математике. Все же задержитесь еще на немного и вы увидите, почему вышеописанная схема актуальна для бесконечных последовательностей. Вы наверняка знакомы с некоторыми замысловатыми тонкостями математики, которые мы не собирались сегодня использовать, но, кажется, придётся, ведь это будет стоить того.

Метод бесконечных последовательностей

Начнём с разложения значения 0,999… на разряды. Вспомните, как учитель в начальной школе объяснял разрядное значение числа и говорил что-то вроде:

Напишем 0,999… таким же образом, начиная примерно так:

Или в виде дроби:

Если сложим первые 5 значений, то получим 0,99999, и, продолжая представлять дробь в десятичной форме, будем делать это до бесконечности и получим точное значение 0,999…

Выписать десятичное разложение до бесконечности вручную невозможно, поэтому воспользуемся сокращением.

Сначала вынесем 9 за скобки.

Затем перепишем знаменатели в виде 10 в степени.

Теперь используем сигма-нотацию для представления бесконечной суммы.

Дополнительное примечание к сигма-нотации: если вы новичок в сигма-нотации, позвольте рассказать об этом. Греческая буква ∑ (сигма) используется в математике для обозначения многократного сложения.

Первое значение при суммировании образуется путём подстановки первого указанного значения для n, которое можно найти под символом ∑. В этом случае значение равно n = 1, поэтому получаем (1/10)¹.

Чтобы отыскать следующее значение, нужно взять следующее целое число, n = 2, для получения (1/10)². Затем подставляйте n = 3, чтобы получить (1/10)³ , и так далее. Продолжайте делать это, пока не доберётесь до значения над символом ∑. В нашем случае это бесконечность, поэтому завершения нет.

И, конечно же, все эти образованные значения складываются вместе. В нашем случае их сумма затем умножается на 9.

Думать о числах в нашей последовательности можно и по-другому: каждый последующий член получается умножением предыдущего на знаменатель прогрессии.

Это означает, что у нас есть геометрическая прогрессия, которая сходится к a/(1 - r), где a – первое значение в ряду, а r – число-множитель для получения следующего члена.

Сходимость означает, что последовательность будет всё приближаться и приближаться к конкретному значению, поскольку вы добавляете всё больше и больше членов в ряд. Последовательность становится бесконечно близкой к значению сходимости. В бесконечном масштабе сходимость превращается в равенство.

В нашем случае начинаем с 1/10 и каждый раз умножаем на 1/10, так что a и r = 1/10.

Завершим арифметические операции с правой стороны.

Теперь мы доказали, что 0,999… сходится к или равняется 1.

Заключительные мысли

Если это кажется нелепым, то всё в порядке! Вы знаете, что два разных числа должны на самом деле быть разными числами. Противоречащий здравому смыслу характер этой проблемы присущ странности, которая сопровождает работу с бесконечностью.

Даже в такой простой проблеме, как эта, вы выходите за границы осязаемого для человеческого сознания в масштаб за пределами нашего понимания. Как конечные существа, мы хватаемся за понимание концепции бесконечности или вечности, но никогда не сможем по-настоящему испытать её. Это означает, что часто вещи, правдивые для нашего конечного мира, ведут себя по-другому на бесконечном уровне.

Принятие перехода от легкодоступной и воспроизводимой математики к тому, что можно проверить и представить только в наших умах, – часть красоты и чуда науки.

Так что не принимайте сегодняшний урок близко к сердцу.

Пусть некий слой тумана останется между вами и полным пониманием. Пусть мозг взрывается от факта, что бесконечность ведёт себя странно. И пусть это вызывает страстную жажду исследования и, прежде всего, более углубленного изучения математики.

Проблема дня рождения в реальной жизни

Впервые я услышала эту задачу на курсе математической статистики 300-го уровня в небольшом университете на Тихоокеанском северо-западе. В классе было 30 студентов, и профессор поспорил, что как минимум у двоих один и тот же день рождения.

Затем он попросил всех назвать свой день рождения. Когда подошла моя очередь, я объявила дату рождения как «два в кубе, три в кубе», что заставило класс рассмеяться, поскольку наш высокоинтеллектуальный профессор завис на некоторое время, прежде чем расшифровать дату.

В любом случае, как он и предсказывал, ещё не добрались до последнего студента, а пара совпадающих дней рождения нашлась.

Так как же ему повезло найти соответствующую пару?

Разминка

Ограничение: ради простоты будем игнорировать возможность рождения 29 февраля.

Начнём с простого примера, чтобы размять наш мозг:

Какова вероятность того,что у двух человек одинаковый день рождения?

Человек А родился в любой день года, так как он первый, кого спрашиваем. Вероятность рождения в любой день года составляет 1 или 365/365.

Поскольку человек B должен родиться в тот же день, что и человек A, его вероятность составляет 1/365.

Мы хотим, чтобы оба события произошли, поэтому перемножаем вероятности:

Вероятность того, что у любых случайно выбранных двух человек одинаковая дата рождения.

Таким образом, с вероятностью 0,27% вы подойдёте к незнакомцу и обнаружите, что его день рождения совпадает с вашим. Негусто.

Но что насчёт большей группы?

Какова вероятность, что по крайней мере у 2 из 4 человек одинаковый день рождения?

Чтобы решить эту проблему, придётся вычислить все следующие вероятности:

у А и В одинаковый день рождения;
у А и С совпадает день рождения;
у D и A одинаковый день рождения;
у B и C одинаковый день рождения;
у B и D один и тот же день рождения;
у C и D одинаковый день рождения;
у A, B и C одинаковый день рождения;
у B, C и D одинаковый день рождения;
у C, A и D одинаковый день рождения;
у A, B и D одинаковый день рождения;
у A, B, C и D одинаковый день рождения.

Фу, как много расчётов! Представьте себе, сколько вероятностей пришлось бы рассчитать на класс из 30 студентов!

Должен быть способ получше…

Лучший способ – хитрость с дополнением

Самый простой способ вычислить что-то среди гигантиллиона вероятностей – посмотреть на проблему под другим углом.

Какова вероятность того, что никто не разделяет один и тот же день рождения?

Это альтернативное упражнение полезно, потому что представляет собой противоположность нашей первоначальной проблеме (то есть дополнение). Исходя из теории вероятности, мы знаем, что сумма всех возможных результатов – то есть выборочное пространство – всегда равна 1 или 100% вероятности.

Поскольку вероятность того, что по крайней мере у 2 человек одинаковый день рождения и вероятность отсутствия одинакового дня рождения, покрывают все возможные сценарии, сумма их вероятностей равна 1.

Или эквивалентно:

Использование дополнения для решения нашей проблемы

Ура! Это будет намного легче рассчитать.

Расчёт

Потрясающе! Мы наконец-то готовы выяснить, насколько безопасную ставку сделал профессор.

Определим вероятность того, что ни у кого из 30 человек день рождения не повторяется.

Разбиваем расчёт на последовательные операции:

Первый студент может родиться в любой день, поэтому назначаем ему вероятность 365/365.
Следующий студент теперь ограничен 364 возможными днями, поэтому вероятность второго студента составляет 364/365.
Третий студент может родиться в любой из оставшихся 363 дней, то есть 363/365.

Этот шаблон продолжается, и у нашего последнего студента вероятность составляет 336/365 (365 – 29 дней, так как ученики до него израсходовали 29 потенциальных дней).

Снова перемножьте все 30 вероятностей между собой:

Вероятности с 361/365 по 338/365 не показаны

Держитесь! Вышло чуточку грязно. Дальше подправим.

Поскольку знаменатель – помноженное само на себя тридцать раз число 365, перепишем его следующим образом:

Используем факториалы (символически: !) для дальнейшей очистки этого расчёта.

С использованием факториала 365! будет равно произведению всех убывающих целых чисел с 365 до 1. Нам нужно произведение целых чисел только с 365 до 336, поэтому убираем посторонние числа делением 365! на 335!.

Примечание: если это приводит вас в замешательство, попробуйте меньшее значение, например, 5!/3! = 5 • 4 • 3 • 2 • 1/3 • 2 • 1. Обратите внимание на 3 • 2 • 1 в числителе и знаменателе. Они «сокращаются» и превращают 5!/3! = 5 • 4.

Собрав всё это вместе, получим выражение, которое можно легко ввести в инженерный калькулятор:

Упрощённая форма произведения 30 вероятностей выше

Результат составляет 0,294 или 29,4% вероятности того, что ни у кого в классе нет одинакового дня рождения. Конечно, нам нужно дополнение, поэтому вычтем значение из 1, чтобы определить вероятность того, что во всяком случае у 2 студентов в группе из 30 человек дни рождения совпали.

Получается, наш профессор сделал довольно безопасную ставку! У него был почти 71% вероятности того, что двое или более из нас родились в один день.

Шанс пятьдесят на пятьдесят

Знаете, чему многие удивляются? Если вы повторите этот расчёт с группой из 23 человек, то обнаружите 50% шанса, что во всяком случае двое человек родились в один и тот же день.

Это относительно маленькая группа людей с учётом 365 возможных дней рождения! И это означает, что в любом коллективе, где больше 23 человек, скорее всего, хотя бы 2 человека родились в один день.

Какой безумный маленький факториал!

Что вас удивило больше: равенство 0,999 и 1 или проблема дня рождения?

1 (число) — Википедия

Материал из Википедии — свободной энциклопедии

Символ со сходным начертанием: ᛐ

1 (оди́н, един, едини́ца, раз) — число, мысленное представление отдельного абстрактного объекта. Наименьшее натуральное число, целое число между 0 и 2.

Ряд знаменитых учёных Древней Греции рассматривали каждое из натуральных чисел как собрание единиц; сама же единица числом не считалась^[1]. Платон рассматривал единицу не как начало числового ряда, а как нечто неделимое (какой-нибудь непрерывный процесс, геометрическая фигура, мысли о чём-либо)^[2].

Это единственное положительное число, которое равно своему обратному. Поэтому привело к одному из основных понятий в теории групп — единице.

Для любого числа x:

x·1 = 1·x = x (см.: умножение). Как результат, 1 является автоморфным числом в любой позиционной системе счисления. Так же, в связи с этим свойством, число 1 называется мультипликативной единицей, и является нейтральным элементом.

x/1 = x (см.: деление)

x¹ = x, 1^x = 1, и для ненулевого числа x, x⁰ = 1 (см.: возведение в степень)

x↑↑1 = x и 1↑↑x = 1 (см.: суперстепень).

Число 1 не может быть использовано как основа позиционной системы счисления, но существует унарная система счисления, являющаяся суммарной. Поскольку квадрат, куб и любая другая степень числа 1 равняется единице, невозможно брать логарифмы от числа, не равного 1, по основанию 1.

В настоящее время в математике принято не относить единицу ни к простым, ни к составным числам, так как это нарушает важную для теории чисел единственность разложения на простые множители. Последним из профессиональных математиков, кто рассматривал 1 как простое число, был Анри Лебег в 1899 году.

Число 1 — наименьшее натуральное число, большее нуля (является ли нуль натуральным числом — зависит от принятых соглашений). Иногда за определение 1 принимают утверждение «при умножении единицы на любое другое число в результате получается это же число», а натуральные числа определяют, исходя из определений единицы и операции сложения.

Единица также используется в тождестве Эйлера — математическом соотношении пяти констант математики — собственно единицы, нуля, e, π и i:

e(πi)+1=0{\displaystyle e^{(\pi i)}+1=0}

В представлении фон Неймана для натуральных чисел, 1 определяется как множество {0}. Это множество имеет кардинальность 1 и наследственный ранг 1. Такие множества с единственным элементом называются синглетонами.

Единица обозначается арабской цифрой «1»^[3].

В математике инков единица обозначалось в кипу в виде одного узла на свисающей нити. В кириллице числовое значение буквы а (азъ).

Единица // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 113-114. — 352 с.
Ламберто Гарсия дель Сид. Первые натуральные числа и их значение → 1 // Замечательные числа. Ноль, 666 и другие бестии. — DeAgostini, 2014. — Т. 21. — С. 15-16. — 159 с. — (Мир математики). — ISBN 978-5-9774-0716-8.
David Wells. 1 // The Penguin Dictionary of Curious and Interesting Numbers. — Penguin Books, 1986. — С. 30-32. — 229 с. — ISBN 0-14-008029-5.

Мнимая единица — Википедия

Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляться также в обобщённом смысле не только для комплексных чисел^[⇨].

В математике, физике мнимая единица обозначается как латинская i{\displaystyle i} или j{\displaystyle j}. Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.

Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x)=0{\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x2+1=0{\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».

Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.

Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «−i» и «−i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i{\displaystyle i} через радикал (как −1{\displaystyle {\sqrt {-1}}}).

Мнимая единица — это число, квадрат которого равен −1. Т.е. i{\displaystyle i} — это одно из решений уравнения

x2+1=0,{\displaystyle x^{2}+1=0,} или x2=−1.{\displaystyle x^{2}=-1.}

И тогда его вторым решением будет −i{\displaystyle -i}, что проверяется подстановкой.

Степени i{\displaystyle i} повторяются в цикле:

…{\displaystyle \ldots }

i−3=i{\displaystyle i^{-3}=i}

i−2=−1{\displaystyle i^{-2}=-1}

i−1=−i{\displaystyle i^{-1}=-i}

i0=1{\displaystyle i^{0}=1}

i1=i{\displaystyle i^{1}=i}

i2=−1{\displaystyle i^{2}=-1}

i3=−i{\displaystyle i^{3}=-i}

i4=1{\displaystyle i^{4}=1}

…{\displaystyle \ldots }

Что может быть записано для любой степени в виде:

i4n=1{\displaystyle i^{4n}=1}

i4n+1=i{\displaystyle i^{4n+1}=i}

i4n+2=−1{\displaystyle i^{4n+2}=-1}

i4n+3=−i.{\displaystyle i^{4n+3}=-i.}

где n — любое целое число.

Отсюда: in=inmod4{\displaystyle i^{n}=i^{n{\bmod {4}}}} где mod 4 — это остаток от деления на 4.

Из тождества Эйлера следует, что число ii{\displaystyle i^{i}} является вещественным:

ii=e(iπ/2)i=ei2π/2=e−π/2=0,20787957635…{\displaystyle i^{i}={e^{(i\pi /2)i}}=e^{i^{2}\pi /2}=e^{-\pi /2}=0{,}20787957635\ldots }.

Точнее, в комплексном анализе возведение в степень: xy=exp⁡(y⋅Ln⁡x){\displaystyle x^{y}=\exp(y\cdot \operatorname {Ln} x)} является многозначной функцией, поэтому

ii=e−π(1+4n)2{\displaystyle i^{i}=e^{-{\frac {\pi (1+4n)}{2}}}}, где n∈Z{\displaystyle n\in \mathbb {Z} }.

Также верно, что (−i)(−i)=ii{\displaystyle (-i)^{(-i)}=i^{i}}.

Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:

i!=Γ(1+i)≈0.4980−0.1549i.{\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}

Также

|i!|=πsinh⁡(π)≈0.521564….{\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….}^[1]

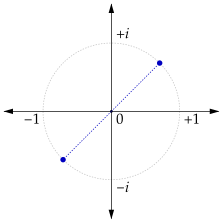$i!=\Gamma (1+i)\approx 0.4980-0.1549i.$ Корни квадратные из мнимой единицы Корни кубические из мнимой единицы (вершины треугольника)

В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.

uk=cos⁡π2+2πkn+i sin⁡π2+2πkn,k=0,1,…,n−1{\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}

В частности, i={1+i2; −1−i2}{\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i3={−i; i+32; i−32}{\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}

Также корни из мнимой единицы могут быть представлены в показательном виде:

uk=e(π2+2πk)in,k=0,1,…,n−1{\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}

В конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду «мнимых единиц расширения» может быть несколько. Но в этом случае могут возникать делители нуля и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения x2=−1{\displaystyle x^{2}=-1}.

К вопросу об интерпретации и названии[править | править код]

Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в.

Обычное обозначение i{\displaystyle i}, но в электро- и радиотехнике мнимую единицу принято обозначать j{\displaystyle j}, чтобы не путать с обозначением мгновенной силы тока: i=i(t){\displaystyle i=i(t)}.

В языке программирования Python мнимая единица записывается как 1j.

В языке программирования Wolfram Language мнимая единица записывается как I.

Ответы@Mail.Ru: чему равняется 1 миля?

Ми́ля (от лат. milia passuum — тысяча двойных римских шагов) — путевая мера для измерения расстояния. Миля применялась в ряде стран в древности, а также во многих современных странах до введения метрической системы мер. В странах с неметрической системой мер миля применяется до настоящего времени. Величина мили различна в различных странах и колеблется от 0,58 км (Египет) до 11,2 км (старочешская миля) . * Древнеримская (миллиатрий) : 1 миля = 1598 м (по другим данным 1480 м) * Старорусская: 1 миля = 7 вёрст = 7467,6 м * Британская и американская: 1 миля = 8 фурлонгов = 1609,344 м (обычно, говоря просто «миля» , имеют в виду её) * Морская: 1 миля = 1852 м * Географическая (немецкая) : 1 миля = 1/15° экватора = 7420 м * Французская: 1 миля =1/25° экватора = 4,17 русских вёрст= 4448 м. Морска́я ми́ля — единица измерения расстояния, применяемая в мореплавании и авиации. Первоначально морская миля определялась как длина дуги большого круга на поверхности земного шара размером в одну угловую минуту. Таким образом, перемещение на одну морскую милю вдоль меридиана примерно соответствует изменению географических координат на одну минуту широты. По современному определению, международная морская миля равна 1852 метрам (точно) . Морская миля не является единицей СИ, однако, по решению Генеральной конференции по мерам и весам, её использование допускается, хотя и не рекомендуется. Общепринятого обозначения не существует; иногда используются сокращения «NM», «nm» или «nmi» (от англ. nautical mile). Следует отметить, что сокращение «nm» совпадает с официально принятым обозначением нанометра. Международная морская миля = 10 кабельтовых = 1/3 морской лиги Морская миля Великобритании = 1853,184 метрам (до 1970 г.).

морская или сухопутная?

морская 1852метра

А их много.. . Самая «распространенная» — английская морская, по-моему, 1670 метров. 1/10 называется кабельтов… Моряки ими расстояние меряют

Число Авогадро — Википедия

Число́ Авога́дро, конста́нта Авогадро, постоянная Авогадро — физическая величина, численно равная количеству специфицированных структурных единиц (атомов, молекул^[1], ионов, электронов или любых других частиц) в 1 моле вещества^[2]. Ранее определялось как количество атомов в 12 граммах (точно) чистого изотопа углерода-12. Обозначается обычно как N_A^[3], а иногда и L^[4].

Значение числа Авогадро в Международной системе единиц СИ согласно изменениям определений основных единиц СИ точно равно

N_A = 6,022 140 76⋅10²³ моль⁻¹.

Иногда в литературе проводят различие между постоянной Авогадро N_A, имеющей размерность моль⁻¹, и численно равным ей безразмерным числом Авогадро А^[5]^{[K 1]}.

Моль — количество вещества, которое содержит N_A структурных элементов (то есть столько же, сколько атомов содержится в 12 г ¹²С, согласно старому определению), причём структурными элементами обычно являются атомы, молекулы, ионы и др. Масса 1 моля вещества (молярная масса), выраженная в граммах, численно равна его молекулярной массе, выраженной в атомных единицах массы. Например:

1 моль натрия имеет массу 22,9898 г и содержит примерно 6,02⋅10²³ атомов;
1 моль фторида кальция CaF₂ имеет массу (40,08 + 2 · 18,998) = 78,076 г и содержит 6,02⋅10²³ ионов кальция и 12,04⋅10²³ ионов фтора;
1 моль тетрахлорида углерода CCl₄ имеет массу (12,011 + 4 · 35,453) = 153,823 г и содержит 6,02⋅10²³ молекул тетрахлорида углерода;
и т. п.

В конце 2011 года на XXIV Генеральной конференции по мерам и весам единогласно принято предложение^[7] определить моль в будущей версии Международной системы единиц (СИ) таким образом, чтобы избежать его привязки к определению килограмма. Предполагалось, что моль в 2018 году будет определён на основе числа Авогадро, которому будет приписано точное значение без погрешности, базирующееся на результатах измерений, рекомендованных CODATA. До 20 мая 2019 года число Авогадро являлось измеряемой величиной, не принимаемой по определению. В 2015 году из наиболее прецизионных измерений получено рекомендованное значение числа Авогадро N_A = 6,022 140 82(11)⋅10²³ моль⁻¹, полученное в результате усреднения результатов различных измерений^[8]^[9]^[10].

На заре развития атомной теории (1811) А. Авогадро выдвинул гипотезу, согласно которой при одинаковых температуре и давлении в равных объёмах идеальных газов содержится одинаковое количество молекул. Позже было показано, что эта гипотеза есть необходимое следствие кинетической теории, и сейчас она известна как закон Авогадро. Его можно сформулировать так: один моль любого газа при одинаковых температуре и давлении занимает один и тот же объём, при нормальных условиях равный 22,41383 литра. Эта величина известна как молярный объём газа.

Сам Авогадро не делал оценок числа молекул в заданном объёме, но понимал, что это очень большая величина. Первую попытку найти число молекул, занимающих данный объём, предпринял в 1865 году Йозеф Лошмидт. Из вычислений Лошмидта следовало, что для воздуха количество молекул на единицу объёма составляет 1,81⋅10¹⁸ см⁻³, что примерно в 15 раз меньше истинного значения. Через 8 лет Максвелл привёл гораздо более близкую к истине оценку «около 19 миллионов миллионов миллионов» молекул на кубический сантиметр, или 1,9⋅10¹⁹ см⁻³. По его оценке число Авогадро было приблизительно 1022{\displaystyle 10^{22}}.

В действительности в 1 см³ идеального газа при нормальных условиях содержится 2,68675⋅10¹⁹ молекул. Эта величина была названа числом (или постоянной) Лошмидта. С тех пор было разработано большое число независимых методов определения числа Авогадро. Превосходное совпадение полученных значений является убедительным свидетельством реального количества молекул.

В 1908 г. Перрен даёт приемлемую оценку 6,8⋅1023{\displaystyle 6,8\cdot 10^{23}} вычисленной из параметров Броуновского движения.

$6,8\cdot 10^{23}$

Один из оптиков австралийского ACPO держит однокилограммовый монокристаллический шар из кремния для проекта International Avogadro Coordination.

Данные в этой статье приведены по состоянию на декабрь 2011 года.

Вы можете помочь, обновив информацию в статье.

Официально принятое в 2010 году значение числа Авогадро было измерено при использовании двух сфер, изготовленных из кремния-28. Сферы были получены в Институте кристаллографии имени Лейбница и отполированы в австралийском Центре высокоточной оптики настолько гладко, что высоты выступов на их поверхности не превышали 98 нм. Для их производства был использован высокочистый кремний-28, выделенный в нижегородском Институте химии высокочистых веществ РАН из высокообогащённого по кремнию-28 тетрафторида кремния, полученного в Центральном конструкторском бюро машиностроения в Санкт-Петербурге.

Располагая такими практически идеальными объектами, можно с высокой точностью подсчитать число атомов кремния в шаре и тем самым определить число Авогадро. Согласно полученным результатам, оно равно 6,02214084(18)·10²³ моль⁻¹^[11].

Однако в январе 2011 года были опубликованы результаты новых измерений, считающиеся более точными^[12]: N_A = 6,02214078(18)⋅10²³ моль⁻¹.

На 24-й Генеральной конференции по мерам и весам 17—21 октября 2011 года была единогласно принята резолюция^[7], в которой, в частности, предложено в будущей ревизии СИ переопределить моль таким образом, чтобы число Авогадро было равным точно 6,02214X⋅10²³ моль⁻¹, где Х заменяет одну или более значащих цифр, которые будут определены в окончательном релизе на основании наиболее точных рекомендаций CODATA^[13]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Планка, элементарный заряд, постоянную Больцмана и максимальную световую эффективность монохроматического излучения для дневного зрения.

Значение числа Авогадро, рекомендованное CODATA в 2010 году, составляло:

N_A = 6,022 141 29(27)⋅10²³ моль⁻¹.

Значение числа Авогадро, рекомендованное CODATA в 2014 году, составляло^[14]:

N_A = 6,022 140 857(74)⋅10²³ моль⁻¹

↑ Число Авогадро A есть кратная единица измерения очень больших безразмерных величин, численно равная постоянной Авогадро, то есть A в N_A раз больше исходной величины — 1-й штуки. Число Авогадро используют для количественного описания систем, содержащих настолько большое число любых объектов (обычно частиц и групп частиц вещества), что указывать количество этих объектов в штуках становится малоудобно и малонаглядно. Например, 1 А теннисных мячей покроют поверхность планеты Земля слоем толщиной 100 км; 1 А долларовых банкнот закроют все материки Земли плотным двухкилометровым слоем; в пустыне Сахара содержится немногим менее 3 А песчинок^[6].

↑ Ранее выводилось как количество молекул в грамм-молекуле или атомов в грамм-атоме.
↑ Авогадро постоянная // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1. — С. 11. — 704 с. — 100 000 экз.
↑ в отличие от N, обозначающее количество частиц (англ. Particle number)
↑ http://www.iupac.org/publications/books/gbook/green_book_2ed.pdf
↑ Пресс И. А., Основы общей химии для самостоятельного изучения, 2012, с. 22—23.
↑ Пресс И. А., Основы общей химии для самостоятельного изучения, 2012, с. 23.
↑ ¹ ² On the possible future revision of the International System of Units, the SI. Resolution 1 of the 24th meeting of the CGPM (2011).
↑ Точная оценка числа Авогадро поможет дать новое определение килограмма : Наука: Наука и техника: Lenta.ru
↑ The Correlation of the NA Measurements by Counting 28Si Atoms
↑ More Precise Estimate of Avogadro’s Number to Help Redefine Kilogram | American Institute of Physics (неопр.) (недоступная ссылка). Дата обращения 15 июля 2015. Архивировано 16 июля 2015 года.
↑ Физики уточнили число Авогадро для будущего эталона килограмма (рус.) (недоступная ссылка). РИА Новости (20 октября 2010). Дата обращения 20 октября 2010. Архивировано 23 октября 2010 года.
↑ B. Andreas et al., Determination of the Avogadro Constant by Counting the Atoms in a ²⁸Si Crystal, Phys. Rev. Lett. 106, 2011, 030801
↑ Agreement to tie kilogram and friends to fundamentals — physics-math — 25 October 2011 — New Scientist
↑ CODATA Value: Avogadro constant
↑ Больцмана постоянная, 1988.
↑ Фарадея постоянная, 1998.

Щас читаю Властелина Колец и там расстояния измеряются в «лигах». (30 лиг, 24 лиги и тд)….

Лига – одна из самых старых единиц измерения, а сейчас используется в США, Британии и Латинской Америке. Под лигой понимается расстояние, которое может пройти человек (или проехать всадник) за 1 час. Оттого в разных странах она разная. Где-то считают скорость пешехода, где-то скорость всадника, где-то дороги ровные и за час можно проехать больше, чем в горах. Подобные единицы измерения очень практичны для путешественников того времени (в отличие от километров и миль) , поскольку позволяют определить не расстояние, а время в пути и рассчитать припасы. Впервые лига встречается в Древнем Риме. Она принята раной 1,5 римских мили или 3000 шагов. По нашему счету это примерно 2220 метров. Во Франции лига (читается лье, помните, у Жюля Верна) и равнялась от 3 до 5 км в зависимости от местности В Латинской Америке, где ездят на лошадях, лига равняется от 5 км в Аргентине до 6 в Бразилии. Ну а в США и Британии равняется ок. 4,8 км. (см. ответ выше) Так что для Толкиена лигу следует понимать по своему исходному значению – один час пути Благодарю за интересный вопрос

Лига — британская и американская единица измерения расстояния.<br><br>1 лига = 3 милям = 24 фурлонгам = 4828,032 метрам.<br>