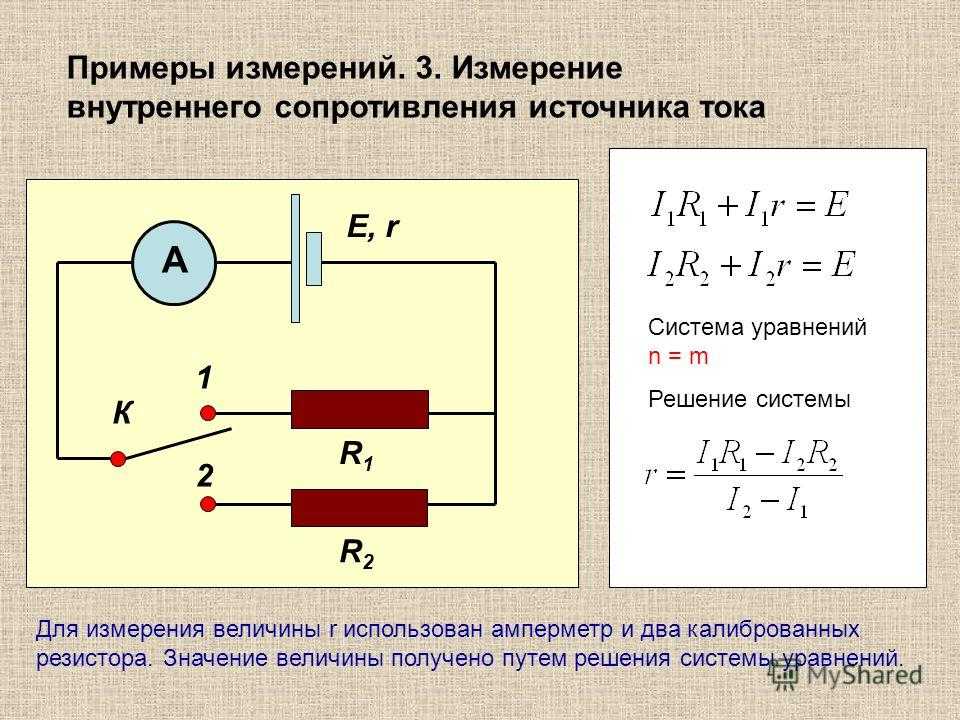
Идеальный источник ЭДС — Студопедия

Идеальный источник ЭДС имеет неизменные ЭДС и напряжение на зажимах при всех токах нагрузки. У реального источника ЭДС и напряжение на зажимах изменяются при изменении нагрузки, например вследствие падения напряжения в обмотках генератора постоянного тока. Поэтому реальные источники ЭДС изображается с помощью двух последовательно включенных элементов – идеального источника ЭДС и сопротивления, которое учитывает внутреннее сопротивление реального источника (рисунок 2.3 а). Свойства реального источника ЭДС отражает вольт-амперная характеристика (ВАХ) или внешняя характеристика – зависимость напряжения между его выводами от тока источника (рисунок 2.3 б). Уравнение внешней характеристики реального источника ЭДС:

.

Рисунок 2.3. Схема замещения (а) и внешняя характеристика(б) реального источника ЭДС

Уменьшение напряжения источника электрической энергии при увеличении тока объясняется увеличением падения напряжения на его внутреннем сопротивлении. В большинстве случаев внутреннее сопротивление источника ЭДС относительно мало и напряжение на его зажимах мало изменяется с нагрузкой.

Идеальный источник токаобеспечивает протекание неизменного тока в приемниках при изменении их сопротивления. У реального источника ток во внешней цепи изменяется при изменении сопротивления. Поэтому реальный источник тока изображается на схемах как идеальный источник тока с параллельно включенным сопротивлением, величина которого определяется из характеристики элемента (рисунок 2.4 а). Внешняя характеристика источника тока приведена на рисунке 2.4 б.

Рисунок 2.4 Схема замещения (а) и внешняя характеристика (б) реального источника тока

Различают несколько режимов работы источников энергии. В режиме холостого хода приемники электрической энергии отключены и ток источника равен нулю. Напряжение на зажимах источника равно его ЭДС, так как отсутствует падение напряжения на внутреннем сопротивлении. Короткое замыкание является аварийным режимом, когда зажимы источника энергии замкнуты накоротко. При этом ток в цепи определяется только внутренним сопротивлением источника, которое обычно достаточно мало, поэтому токи короткого замыкания достигают недопустимо больших значений. В номинальном режиме источник энергии может работать неопределенно длительное время без перегрева или других недопустимых последствий. Согласованный режим работы осуществляется, когда источник отдает в нагрузку максимальную мощность. Условие передачи максимальной мощности может быть получено из уравнения внешней характеристики источника:

,

если выразить из этого уравнения ток нагрузки:

,

получим закон Ома для замкнутой цепи с последовательной схемой замещения источника. Мощность, отдаваемая источником ЭДС (с последовательной схемой замещения) в нагрузку:

.

Для источника тока (с параллельной схемой замещения) мощность, отдаваемая в нагрузку:

.

Мощность, отдаваемая источником в нагрузку будет максимальна, при максимальном значении соотношения . Максимум этого соотношения можно определить, взяв первую производную дроби по и приравняв ее к нулю. Максимум будет при . Следовательно, мощность, отдаваемая источником во внешнюю цепь будет максимальна, когда сопротивление внешней цепи равно внутреннему сопротивлению источника .

Лабораторная работа. Исследование источников постоянного напряжения и тока

 Лабораторная работа №1

 

Исследование источников

постоянного напряжения и тока

 

Цель работы:

Изучить внешние характеристики независимых и зависимых (управляемых) источников постоянного напряжения и тока на ПК с помощью программы  Electronics Workbench

 

1. 1 .Теоретические сведения

 

Элементы электрических цепей (ЭЦ) можно разделить на активные и пассивные. К активным элементам относятся элементы генерирующими электрическую энергию. В ТЭЦ используют идеализированные независимые и зависимые (управляемые) источники напряжения и тока.

Независимыми источниками напряжения (рис.1.1) называют такие источники электрической энергии, напряжение на зажимах которых не зависит от тока, протекающего через них. Внутреннее сопротивление таких источников равно нулю.

 

 

 

а)                                   б)                                             в)

 

 

Рис. 1.1.Обозначение независимых источников напряжения.

Стандарт: а) Россия; б) США; в) Германия

 

          Независимыми источниками тока (рис.1.2), называют такие источники электрической энергии, ток которых не зависит от напряжения на его зажимах.

Внутреннее сопротивление таких источника равно бесконечности.

 

 

 

 

 

Рис. 1.2. Обозначение независимых источников тока.

Стандарт: а) Россия; б) США; в) Германия

 

Основной характеристикой источника напряжения и тока является его внешняя характеристика, представляющая зависимость напряжения на его зажимах от протекающего через него тока U(I). Внешние характеристики идеализированных источников напряжения и тока приведены на рис. 1.3.

 

         

 

 

 

 

Рис. 1.3. Внешние характеристики источника постоянного:

а — напряжения; б – тока.

 

В отличие от независимых идеализированные зависимые источники энергии имеют не одну пару зажимов, а две: входную управляющую и выходную, т.е. зависимые источники являются четырёхполюстниками. Различают зависимые источники напряжения и зависимые источники тока (табл. 1.1).

 Таблица 1.1

 

n	Наименование	Обозначение	Ki
1	Источник напряжения управляемый напряжением (ИНУН)	U1                                             U2=K1U1	U2/U1
2	Источник напряжения управляемый током (ИНУТ)	I 1                              U2=K2I1	U2/I1
3	Источник тока управляемый напряжением (ИТУН)	U1                                              i 2=K3U1	I2/U1
4	Источник тока, управляемый током	I1                                      I 2=K4I1	I2/I1

 

Коэффициент пропорциональности К_i называется коэффициентом управления, которым в зависимости от типа источника может иметь размерность сопротивления (ИНУТ), проводимости (ИТУН) или быть безразмерной величиной. Если управляющее воздействие такого источника равно нулю, то на выходе такого источника будет равно нулю напряжение или ток. Каждый активный элемент (подобно пассивному) характеризуется только одним параметром – напряжением или током на его выходных зажимах.

С помощью идеализированных активных и пассивных элементов, можно промоделировать любой реальный элемент электрической цепи – представить его в виде схемы замещения, которая с достаточной для данного элемента точностью отражает процессы, происходящие в таком элементе.

Реальный источник электрической энергии можно представить двумя схемами замещения: последовательной (рис.1.4, а) и параллельной (рис.1.4, б)

 

 

 

 

 

 

Рис.1.4.  Схемы замещения реальных источников

 

Последовательная схема замещения реального источника (Рис.1.4,а) содержит последовательные соединения источника ЭДС (e,E) и внутреннего сопротивления R

вн. Параллельная схема замещения реального источника (Рис. 1.4,б) содержит параллельное соединение источника тока (i,J) и внутренней проводимости G_вн=1/ R_вн. Обе схемы эквиваленты и в конкретных случаях пользуются той схемой замещения реального источника электрической энергии, которая позволяет проще и быстрее решить поставленную задачу.

Внешняя характеристика реального источника

U(I)=E-R_внI= J/G_вн-I/G_вн=( J-I)/G_вн.

 апроксимируется прямой линией (рис.1.5)

 

 

 

 

 

 

Рис.1.5. Внешняя характеристика реального источника

 

В простейшем случае к реальному источнику подключается сопротивление нагрузки R_н (рис.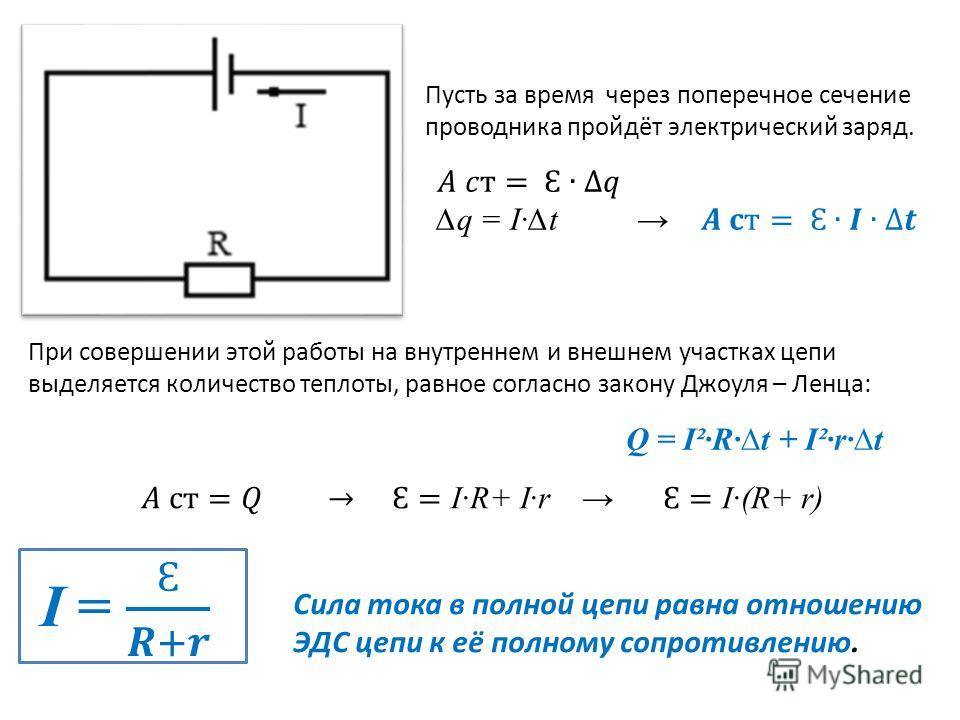 1.6, а).

 

 

 

 

 

 

 

 

 

 

             Рис.1.6. Схема нагуженного реального источника (а) и

                                его нагрузочные характеристики (б)

 

В сопротивлении нагрузки R_н ток I, напряжение U_н, мощность P_н и к.п.д. источника h определяются по формулам:

      ;  ;             (1.1)

 

  ; .                               (1.2)

 

В режиме холостого хода (ХХ) источника R_н=∞ и в режиме короткого замыкания (К3) R_н=0 мощность в нагрузке не выделяется (P_н=0). Максимальная мощность в сопротивлении нагрузки выделяется при согласованном режиме работы, когда сопротивление нагрузки равно внутреннему сопротивлению источника  (R

н=R_вн).

                                                    (1.3)

При этом к. п.д. источника будет равен h=0,5=50%. В связи с таким низким к.п.д. согласованный режим широко применяется в проводной электросвязи, где используются малые мощности (до 10 Вт). В электротехнических установках большой мощности применяется режим работы, при котором R_н>>R_вн, при этом достигается высокий коэффициент полезного действия системы передачи.

 

2. Предварительный расчёт

 

         Для  исследуемой цепи (рис.1.6,а) в соответствии с номером варианта задания (см. табл.1.2) рассчитать зависимости I(R_н), U_н(R_н), P_н(R_н), h(R_н) по формулам (1.1), (1.2).

 

Таблица 1.2

Исходные данные для предварительного расчёта.

 

Вар. №	1	2	3	4	5	6	7	8	9	10	11	12
Е, В	5	10	15	20	25	30	35	40	45	50	55	60
Rвн, Ом	5	10	15	20	25	30	35	40	45	50	55	60

 

   

    Расчёты выполнить при R_н равном:  0,1R_вн; 0,5R_вн; R_вн; 1,5R_вн;

2R_вн; 4R_вн; 10R_вн. Результаты предварительного расчёта свести в табл.1.3.

 

 

 

 

 

 

 

Таблица 1.3.

Результаты предварительного расчёта и эксперимента.

 

Задано			Е = ….В;   Rвн= ….Ом.
№	Rн	Rн,Ом	Предварительный расчёт				Результаты измерений
			I,А	Uн,В	Рн,Вт	h	I,A	Uн,В	Рн,Вт	h
1	0,1RВН
2	0,5Rвн
3	Rвн
4	1,5Rвн
5	2 Rвн
6	4 Rвн
7	10Rвн

 

По результатам предварительного расчёта (см. табл.1.3) построить графики зависимостей  I(R_н), U_н(R_н), P_н(R_н), h(R_н).

 

3.Порядок выполнения работы

 

3.1. Исследование идеального источника

постоянного напряжения

 

Производится загрузка программы EWB; раскрывается, каталог файлов папки Lab_TEC, загружается файл Lab1_1, при этом на дисплее монитора появляется схема, приведённая на рис.1.7.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рис. 1.7.   Исследование идеального источника постоянного напряжения

 

Устанавливается величина ЭДС. идеального источника напряжения согласно номера варианта (см. табл.1.1).

Изменяя сопротивление резистора R через 20% путём изменения положения движка этого резистора, записать показания амперметра М₁ и вольтметра М₂. Результат измерений занести в таблицу 1.3.

 

 

Таблица 1.3

Исследование идеального источника напряжения.

n	R,Ом	U,В	I,мА
1	200
2	400
3	600
4	800
5	1000

По результатам измерений построить внешнюю характеристику идеального источника напряжения U(I).

 

3.2. Исследование идеального источника постоянного тока

 

Загрузить файл Lb1_2, при этом на дисплее монитора появится схема, приведённая на рис.1.8.

Рис. 1.8. Исследование идеального источника постоянного тока

 

  Установить величину тока источника тока I, равную 100 мА. Изменяя сопротивление резистора R через 20% путём изменения положения движка этого резистора, записать показания вольтметра М₁ и амперметра М₂ в табл. 1.4.

 

Таблица 1.4.

 

n	R,Ом	U,В	I,А
1	0
2	200
3	400
4	600
5	800
6	1000

 

По результатам измерений (см. табл.1.4) построить внешнюю характеристику идеального источника тока U(I).

 

3.3. Исследование ИНУТ

Загрузить файл Lb1_3, при этом на дисплее монитора появится схема, приведённая на рис.1.9.

Рис. 1.9. Исследование ИНУТ

         

       Изменяя сопротивление резистора R путём изменения положения движка этого резистора, записать показания амперметра М₁ и вольтметра М₂ в табл.1.5.

Таблица 1.5

Исследование ИНУТ

n	R,Ом	U,В	I,mA	Rупр,Ом
1	200
2	400
3	600
4	800
5	1000

 

По результатам измерений (см. табл.1.5) построить внешнюю характеристику ИНУТ    U(I).

Определить управляющее сопротивление      R_упр=U₂/I₁.

 

3.4. Исследование реального независимого источника

Загрузить файл Lb1_4, при этом на дисплее монитора появится схема, приведённая на рис.1.10.

 

 

 

 

 

 

 

Рис. 1.10. Исследование реального источника

 

          Установить значения сопротивлений резисторов R_вн согласно номера варианта (см. табл.1.1). Изменяя значения  R_н, используемые в предварительном расчёте (см. табл. 1.2), записать показания амперметра М₁ и вольтметра М₂ в таблицу 1.2. По результатам измерений I и U_н рассчитать значения

                                            и                                 (1. 4)

 

и занести их в таблицу 1.2, а по ним построить графики I(R_н), U_н(R_н), P_н(R_н),  h(R_н) вместе c графиками этих функций, полученных в результате предварительного расчета.

3.5. Дополнительное задание

 

        Исследовать неразветвлённую цепь постоянного тока при согласном (рис.1.11,а) и встречном (рис.1.11,б) включении источников E₁, E₂ .

Рис.1.11. Исследование неразветвленной ЛЭЦ  постоянного тока с двумя источниками  напряжения  E1  и E2

 

     Для получения схемы рис.1.11,а загружается файл Lb1_5 и измеряются ток

амперметром М₁ и напряжение вольтметром М₂. Для получения схемы рис.1.11,б загружается файл Lb1_6 и измеряется ток амперметром М₁ и напряжение вольтметром М₂.

          Ток в первой и второй схемах рассчитываются соответственно по формулам:

 

                                      ;         U_R3=I_R3.

 

          Знак «плюс» для первой схемы (рис.1.10,а), знак «минус» для второй схемы R2 (рис.1.10,б).

 

 

 

4. Содержание отчёта

 

          В отчёте по лабораторной работе должны  быть приведены:

4.1. Название и цель работы.

4.2. Электрические схемы исследуемых цепей.

4.3. Расчётные формулы.

4.4 . Результаты предварительного расчёта и эксперимента.

4.5 .Графики нагрузочных характеристик I(R_н),U_н(R_н),Pн(R_н),h(R_н) и внешняя характеристика реального источника U(I_н).

4.6 . Выводы по результатам исследований.

 

5. Контрольные вопросы

 

5.1 . Перечислите все типы источников напряжения (ЭДС), имеющиеся в программе Electronics Workbench. Каковы их свойства и условные обозначения?

5.2 . Перечислите все типы источников тока, имеющихся в программе   Electronics Workbench. Каковы их свойства и условные обозначения?

5.3 . Чему равно внутреннее сопротивление источника напряжения и источника тока?

5.4. Чем отличается неидеальные источники электрической энергии от     идеальных?

5.5 . Как осуществить эквивалентное преобразование неидеального источника напряжения в неидеальный источник тока и обратное преобразование?

5.6 .  Какие режимы работы неидеального источника Вы знаете?

5.7 . Что такое режим холостого хода и короткого замыкания реального источника?

5.8 . Что такое согласованный режим реального источника?

5.9 . При каком сопротивлении нагрузки в ней выделяется максимальная мощность?

5.10        Какие типы зависимых источников Вам известны?

5.11. Для чего применяются зависимые источники?

5.12.  Как выполняется изменение параметров резисторов в программе EWB?

5. 13. Как выполняется изменение сопротивление потенциометра в программе EWB?

5.14        Как осуществляется запуск схемы на расчёт (моделирование) в программе EWB?

5.15        Каким образом можно приостановить и остановить процесс моделирования в программе EWB?

5.16. Как выполняется регулировка параметров независимых источников электрической энергии в программе EWB?

5.17. Как выполняется изменение параметров зависимых источников электрической энергии?

Полное руководство по формуле внутреннего сопротивления, электродвижущей силе и т. д.

Согласно теореме Тевенина полезная разность потенциалов между клеммами в линейной электрической цепи может быть описана как идеальный источник напряжения, последовательно соединенный с импедансом. Этот импеданс известен как внутреннее сопротивление источника.

Когда источник питания подает ток, измеренное выходное напряжение ниже напряжения холостого хода; разница в падении напряжения (произведение тока и сопротивления). Внутреннее сопротивление — это понятие, которое применимо ко всем видам электрических источников и полезно для изучения множества различных типов электрических цепей. Ячейки, ЭДС и внутреннее сопротивление взаимосвязаны друг с другом.

Формула внутреннего сопротивления

Внутреннее сопротивление — это сопротивление внутри батареи или любого другого источника напряжения, которое вызывает падение напряжения источника при наличии тока. Это барьер для прохождения тока, обеспечиваемый элементами и батареями, что приводит к выделению тепла. Внутреннее сопротивление выражается в единицах Ом. Во-первых, дано соотношение между внутренним сопротивлением (r) и ЭДС ячейки (e) .

е = I (r + R)

Здесь e — электродвижущая сила (выраженная в вольтах) , R — сопротивление нагрузки, I — ток, а r — внутреннее сопротивление элемента, измеренное в омах.

Преобразование предыдущего уравнения дает:

e = IR + Ir

Согласно закону Ома, V=IR.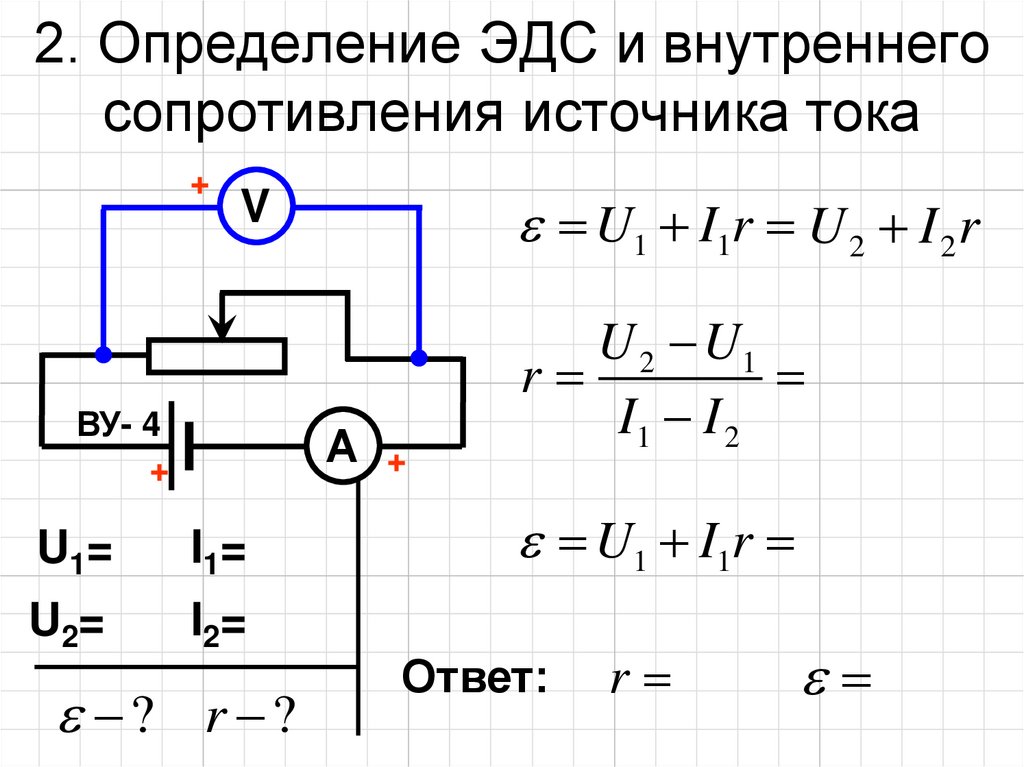 Заменив IR, мы получим

e = V + Ir

Когда ток (I) протекает по цепи, V представляет собой разность потенциалов между клеммами на ячейке в предыдущем уравнении.

ЭДС (e) ячейки всегда больше, чем разность потенциалов между клеммой по ячейке.

Пример: Когда ток не протекает через цепь, разность потенциалов на ячейке составляет 3 В. Разность потенциалов на клеммах уменьшается до 2,8 В, в то время как протекает ток I = 0,37 Ампер. Чему равно внутреннее сопротивление элемента (r)?

Решение:

e = V + Ir

Или, e – V = Ir

Или, (e – V)/I = r

Следовательно, r = (3,0 – 2,8)/0,37 = 0,54 Ом.

Электроны, протекающие через элемент, преобразуют часть электрической энергии в тепловую за счет внутреннего сопротивления элемента. В результате разность потенциалов, доступная для остальной части схемы, выглядит следующим образом.

В = E (ЭДС ячейки) – Ir (полная доля полного сопротивления внутреннего резистора).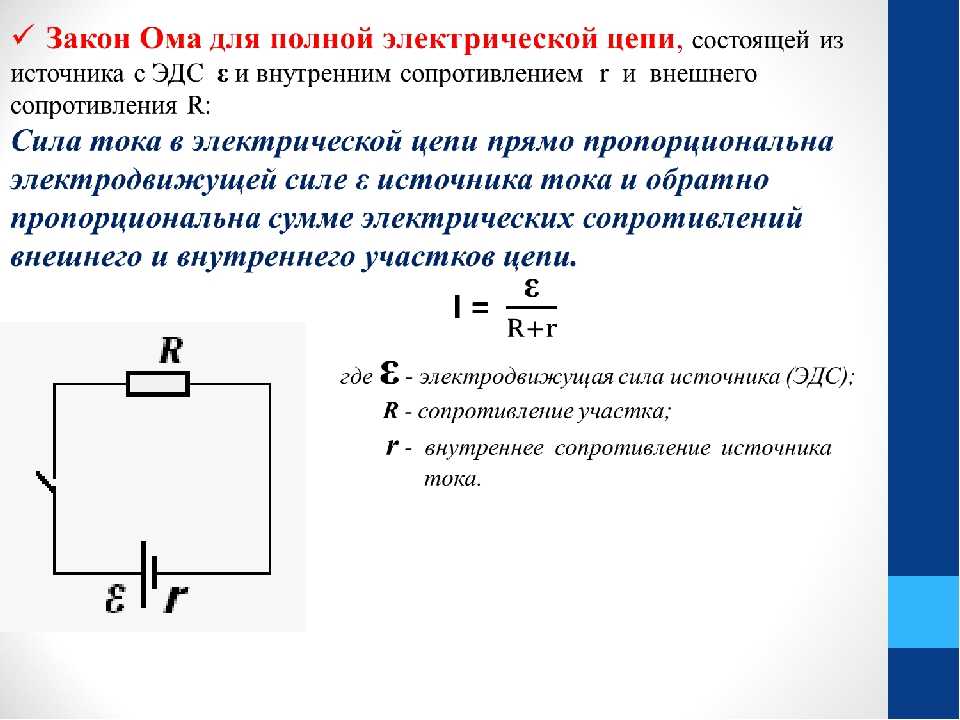

Внутреннее сопротивление обеспечивается электродами и электролитом, препятствующими прохождению тока внутри элемента.

Теорема Тевенина

Теорема Тевенина, первоначально сформулированная в терминах только резистивных цепей постоянного тока, утверждает, что «любая линейная электрическая сеть, содержащая только источники напряжения, источники тока и сопротивления, может быть заменена на клеммах A и B комбинацией эквивалентного источника напряжения Vth при последовательном соединении с сопротивлением Rth». С точки зрения внутрисхемной теории, это позволяет свести любую однопортовую сеть к одному источнику напряжения и импедансу.

Применение внутреннего сопротивления:

Внутреннее сопротивление важно исследовать следующими способами:

Его можно применять для повышения эффективности электродвигателя или любого другого электрического оборудования, необходимо сначала понять, насколько Внутреннее сопротивление у него есть и как его можно снизить.

При изучении внутреннего сопротивления аккумуляторов используется термин «внутреннее сопротивление». Внутреннее сопротивление — фундаментальное понятие в электротехнике, которое можно использовать в самых разных проектах и ​​экспериментах с использованием электричества.

Внутреннее сопротивление особенно важно при конструировании двигателей для автомобилей, грузовиков и других крупных транспортных средств. Внутреннее сопротивление (IR) может использоваться в двигателях внутреннего сгорания (ICE) для повышения производительности двигателя и топливной экономичности.

Заключение

Формула внутреннего сопротивления — это понятие, которое может быть применено к широкому спектру двигателей и электрического оборудования. Формулы внутреннего сопротивления рассматриваются в их самой базовой форме, прежде чем перейти к более сложным приложениям. Формула внутреннего сопротивления используется по-разному, но очень важно понимать, где и как следует использовать внутреннее сопротивление. Внутреннее сопротивление чаще всего используется в электродвигателях и электрическом оборудовании, но может использоваться для исследования внутреннего сопротивления аккумуляторов. Эта статья поможет вам получить отличное представление о концепции внутреннего сопротивления и зависимость между внутренним сопротивлением (r) и ЭДС (e) ячеек.

Видео с вопросами: определение взаимосвязи между напряжением на клеммах, внутренним сопротивлением, электродвижущей силой и током в батарее

Стенограмма видео

Какое из следующих утверждений правильно связывает электродвижущую силу ε батареи с током 𝐼 через батарею , напряжение на клеммах 𝑉 батареи и внутреннее сопротивление 𝑟 батареи? (A) ε равно 𝑉 минус 𝐼𝑟, (B) ε равно 𝑉𝑟 плюс 𝐼, (C) ε равно 𝑉 плюс 𝐼𝑟, (D) 𝑉 равно ε𝐼𝑟, или (E) 𝑉 равно ε𝑟 плюс 𝐼.

Итак, в этом вопросе нам дали кучу разных переменных, относящихся к батарее. Это электродвижущая сила, обозначенная символом ε, ток, обозначенный символом 𝐼, напряжение на клеммах, обозначенное символом 𝑉, и внутреннее сопротивление, обозначенное строчной буквой 𝑟. Нам нужно решить, какое из этих выражений дает правильную связь между этими четырьмя переменными. Итак, для начала давайте вспомним, как ведут себя аккумуляторы.

Батарея — это устройство, которое преобразует химическую энергию в электрическую, и мы можем использовать батарею для создания разности потенциалов в цепи. В этом смысле батарея очень похожа на идеальную ячейку, которую мы часто используем в принципиальных схемах. Однако между ними есть некоторые важные различия. Итак, ячейка или идеальная ячейка — это своего рода теоретическая составляющая. Он обеспечивает разность потенциалов, и мы предполагаем, что он не имеет никакого сопротивления. Батарея, с другой стороны, является реальным устройством. Он обеспечивает разность потенциалов. Тем не менее, он имеет некоторое сопротивление. Это означает, что когда мы имеем дело с батареей, мы не можем точно описать ее поведение, рассматривая ее как элемент.

На самом деле, поскольку у батареи есть некоторое сопротивление, она фактически ведет себя как идеальная ячейка, последовательно соединенная с постоянным резистором.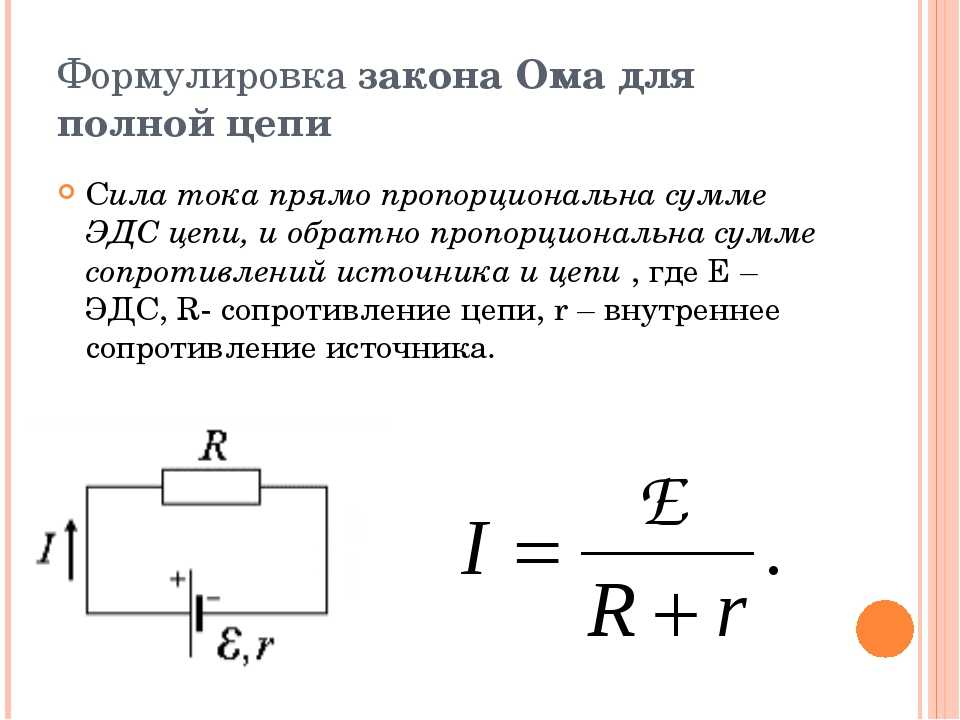 Когда мы представляем батарею таким образом, этот резистор представляет собой внутреннее сопротивление батареи, которое мы можем обозначить строчной буквой 𝑟. Эта идеальная ячейка представляет собой источник электродвижущей силы батареи, которую мы обозначаем через ε. Теперь, наряду с электродвижущей силой и внутренним сопротивлением батареи, этот вопрос требует от нас учитывать ток через батарею. А для того, чтобы был ток, аккумулятор должен быть подключен к цепи.

Итак, давайте представим, что наша батарея просто соединена в простую последовательную цепь с резистором. С аккумулятором, подключенным таким образом, мы обнаружим, что заряд начинает течь. Другими словами, в цепи будет ток. Обозначим этот ток 𝐼, отметив, что здесь мы показываем ток, идущий в направлении обычного тока, то есть от положительного к отрицательному полюсу батареи.

Теперь, поскольку мы показали, что батарея фактически аналогична идеальной ячейке и резистору, соединенным последовательно, мы можем нарисовать эти компоненты внутри нашей батареи, чтобы показать, как она работает. На данный момент мы пометили три из заданных величин на нашей диаграмме. Это ε, электродвижущая сила батареи; строчная 𝑟, внутреннее сопротивление батареи; и 𝐼, ток через батарею. Оставшаяся величина, упомянутая в вопросе, — это напряжение на клеммах 𝑉. На этом этапе нам нужно помнить, что напряжение на клеммах — это напряжение или разность потенциалов между положительной и отрицательной клеммами батареи, когда она подключена к цепи и идет заряд. Таким образом, мы можем обозначить это количество на нашей диаграмме следующим образом.

Итак, теперь у нас есть эти величины, представленные и обозначенные на принципиальной схеме, нам нужно выяснить взаимосвязь между всеми четырьмя из них. И мы можем сделать это, подумав о влиянии внутреннего сопротивления батареи. Теперь мы знаем, что подключение батареи к цепи, подобной этой, вызывает протекание заряда. Другими словами, он создает ток. Важно отметить, что этот ток присутствует не только в самой цепи; он также присутствует внутри батареи. Теперь мы показали, что батарея ведет себя так же, как ячейка и резистор, соединенные последовательно, а это означает, что ток 𝐼 эффективно проходит через резистор. Всякий раз, когда через резистор проходит ток, мы видим, что на этом резисторе есть разность потенциалов.

Мы можем думать, что резисторы потребляют часть разности потенциалов, подаваемой в цепь. Итак, в случае батареи мы можем думать об электродвижущей силе, которую мы представляем с помощью этой ячейки, как о максимальной разности потенциалов, которую мы когда-либо могли измерить на батарее. Однако, как только мы подключаем батарею к цепи и начинает течь заряд, внутреннее сопротивление батареи эффективно использует часть разности потенциалов и уменьшает величину разности потенциалов, подаваемой на остальную часть цепи.

Теперь мы можем рассчитать точную величину этого уменьшения разности потенциалов, вызванного внутренним сопротивлением батареи, используя закон Ома, который представлен уравнением 𝑉 равно 𝐼 умноженному на 𝑅. Закон Ома говорит нам, что разность потенциалов 𝑉 на компоненте равна току 𝐼 в этом компоненте, умноженному на сопротивление 𝑅 этого компонента. Давайте применим закон Ома к резистору, который мы используем для представления внутреннего сопротивления батареи. Итак, в этом случае 𝑉 будет разностью потенциалов на этом резисторе. Поскольку это фактически величина разности потенциалов, которая теряется из-за внутреннего сопротивления батареи, ее часто называют потерянными вольтами батареи, что мы можем представить с помощью символа 𝑉 sub L.

Далее, ток 𝐼 в этом случае будет током в этом резисторе, который совпадает с током в остальной части этой цепи, и мы просто называем это 𝐼. И 𝑅 в этом случае будет сопротивлением этого резистора, которое мы обозначаем строчной буквой 𝑟. Итак, мы использовали закон Ома, чтобы показать, что потерянные вольты в батарее равны току, умноженному на внутреннее сопротивление. Но как это поможет нам найти взаимосвязь между четырьмя переменными, указанными в вопросе?

Что ж, если учесть тот факт, что батарея ведет себя точно так же, как идеальная ячейка, подключенная к резистору, то мы знаем, что разность потенциалов по всей батарее равна разности потенциалов, обеспечиваемой этой ячейкой, за вычетом величины разности потенциалов.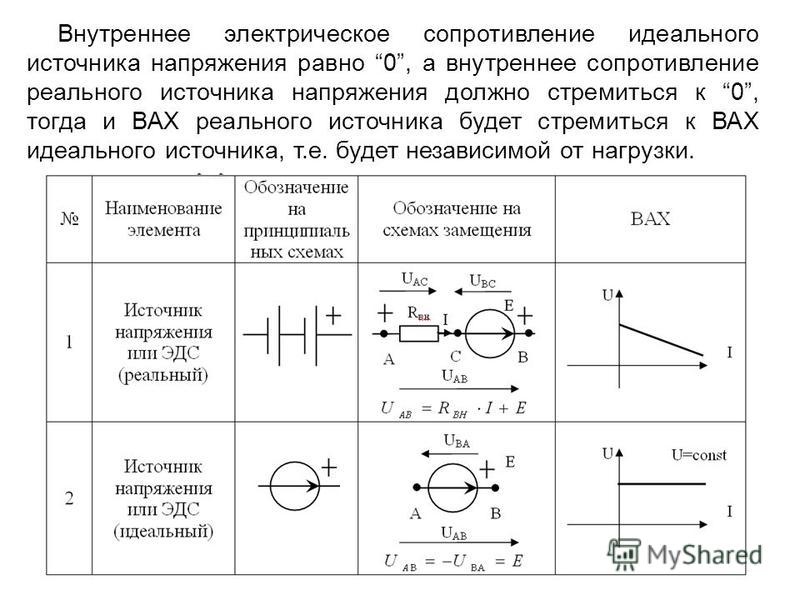 это потеряно или израсходовано этим резистором. Другими словами, напряжение на клеммах 𝑉 равно электродвижущей силе ε за вычетом потерянных вольт 𝑉 sub L. А поскольку мы показали, что потерянные вольты равны 𝐼 умноженному на строчные буквы 𝑟, мы можем заменить 𝐼 умноженное на строчные буквы 𝑟 на место из 𝑉 sub L в этом выражении. Это дает нам 𝑉 равно ε минус 𝐼 умноженное на строчные буквы 𝑟. Напряжение на клеммах батареи равно электродвижущей силе этой батареи минус ток через батарею, умноженный на ее внутреннее сопротивление.

В нынешнем виде это выражение не соответствует в точности ни одному из предложенных нам вариантов ответа, но мы можем исправить это, переставив его. Если мы добавим 𝐼𝑟 к обеим частям этого выражения, мы получим 𝑉 плюс 𝐼𝑟 равно ε. А затем, поменяв местами левую и правую части этого уравнения, мы получим ε равно 𝑉 плюс 𝐼𝑟, что, как мы видим, соответствует варианту (C). Итак, это наш окончательный ответ. Если у нас есть батарея с электродвижущей силой ε, напряжением на клеммах 𝑉 и внутренним сопротивлением 𝑟, через которую проходит ток 𝐼, то эти четыре величины связаны уравнением ε равно 𝑉 плюс 𝐼𝑟.