Методическая разработка по информатике и икт по теме: Системы счисления

Вариант 2

1.        Система счисления — это:

A)        представление чисел в экспоненциальной форме;

Б) представление чисел с постоянным положением запятой;

B) способ представления чисел с помощью символов, имеющих определенное количественное значение.

2.        Пятеричная система счисления имеет основание:
          А) 5;        Б) 3;                В) 4

3.        Для представления чисел в восьмеричной системе счисления используются цифры:

            А) 1-8;              Б) 0 — 9;                В) 0-7.

4.        В какой системе счисления может быть записано число 750?

А) в восьмеричной;   Б) в семеричной;        В) в шестеричной.

5.        Чему равно число CDXIV в десятичной системе счисления?

                А) 616;        Б) 614;        В) 414.

6.        Преимуществом позиционной системы счисления является:

A)        сложно выполнять арифметические операции;

Б) ограниченное число символов, необходимых для записи числа;

B)        различное написание цифр у разных народов.

7.        Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 692:

1. отсутствует в десятичной системе счисления;

Б) отсутствует в восьмеричной;

2. существует во всех названных системах счисления.

8.        Какие цифры используются в семеричной системе счисления?  
А) 0,1,6;        Б) 0,8,9;        В) 1,6,7.

9.        Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 432, 768, 568, 243?

                А) 10;        Б) 8;        В) 9.

10.        Когда 2 · 3 =11?

1. в пятеричной системе счисления;

Б) в троичной системе счисления;

2. в четверичной системе счисления.

11.        Как записывается максимальное 3-разрядное положительное число в четверичной системе счисления?

                А) 333;        Б) 222;        В) 3333.

12.        Число — это:

A)        ряд символов;

Б) обозначение некоторой величины;

B)        набор знаков.

Вариант 1

1.        В зависимости от способа изображения чисел системы счисления делятся на:

A)        арабские и римские;

Б) позиционные и непозиционные;

B)        представление в виде ряда и в виде разрядной сетки.

2.        Двоичная система счисления имеет основание:

                  А) 10;        Б) 8;        В) 2.

3.        Для представления чисел в шестнадцатеричной системе счисления используются:

А) цифры 0 — 9 и буквы A-F;          Б) буквы А — Q;                В) числа 0-15.

4.        В какой системе счисления может быть записано число 402?

        А) в двоичной;        Б) в троичной;   В) в пятеричной.

5.        Чему равно число DXXVII в десятичной системе счисления?

        А) 527;        Б) 499;        В) 474.

6.        Недостатком непозиционной системы счисления является:

A) сложно выполнять арифметические операции;

Б) ограниченное число символов, необходимых для записи числа;

B) различное написание цифр у разных народов.

7.        Даны системы счисления: 2-ая, 8-ая, 10-ая и 16-ая. Запись вида 352:

1. отсутствует в двоичной системе счисления;

Б) отсутствует в восьмеричной;

2. существует во всех названных системах счисления.

8.        Какие цифры используются в шестеричной системе счисления?

                А) 0,6,5,2;        Б) 8,6,1,0;        В) 0,3,2,1.

9.        Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 341, 123, 222,111.

                А)3;        Б) 4;        В) 5.

10.        Когда 2 · 2 = 11?

1. в двоичной системе счисления;
2. Б) в троичной системе счисления;
3. в четверичной системе счисления.

11.Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?

                А) 2222;            Б) 1111;        В) 3333.

12.        Цифры — это:

A)        символы, участвующие в записи числа;

Б) буквы, участвующие в записи числа;        

B)        пиктограммы, участвующие в записи числа.

Перевод чисел из любой системы счисления в десятичную – УчМет

Тема урока: «Перевод чисел из любой системы счисления в десятичную».
Предмет: Информатика
Класс: 9
Учебник: Н.В.Макарова. Информатика. Учебник для 7-9 класса
Тип урока: урок изучения нового материала.

Этапы урока:  

• Организационный. 

• Повторение теоретического материала. 

• Сообщение темы и цели урока. 

• Изучение нового материала 

• Закрепление изученного материала.   

• Задание на дом. 

• Подведение итогов.

Оборудование: 

Цели урока:
1. Развитие знаний, умений и навыков по теме.

2. Формирование у учащихся навыков и умений переводить числа из любой системы счисления в десятичную.
3. Повышение интереса к изучаемой теме и предмету.
4. Развитие логического мышления.

5. Воспитание аккуратности, настойчивости и целеустремлённости в достижении поставленной цели.

Ход урока

1) Организационная часть.
Приветствие учащихся и контроль посещаемости.

2) Повторение теоретического материала.

Выполнение теста:
Тест по теме «Системы счисления»

1 вариант

1. В зависимости от способа изображения чисел системы счисления делятся на:

А) арабские и римские;

Б) позиционные и непозиционные;

В) представление в виде ряда и в виде разрядной сетки.

2. Двоичная система счисления имеет основание:

А) 10; Б) 8; В) 2.

3. Для представления чисел в шестнадцатеричной системе счисления используются:

А) цифры от 0 до 9 и буквы латинского алфавита от A до F;

Б) буквы латинского алфавита от A до Q;

В) числа от 0 до 16.

4. В какой системе счисления может быть записано число 402:

А) двоичной; Б) троичной;

В) пятеричной; Г) восьмеричной.

5. Чему равно число DXXVII в десятичной системе счисления:

А) 527; Б) 499; В)474.

6. Недостатком непозиционной системы счисления является:

А) сложно выполнять арифметические действия;

Б)ограниченное число символов, необходимых для записи числа;

В) различное написание цифр у разных народов.

7. Даны системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Запись вида 352:

А) отсутствует в двоичной системе счисления;

Б) отсутствует в восьмеричной системе счисления;

В) существует во всех названных системах счисления.

8. Какие цифры используются в семеричной системе счисления:

А) 0, 1, 6; Б) 0, 8, 9; В) 0, 6, 7.

9. Какое минимальное основание должна иметь система счисления, если в ней можно записать числа 341, 123, 222, 111:

А) 3; Б) 4; В) 5.

10. Когда 2 • 2 = 11?

А) в двоичной системе счисления;

Б) в троичной системе счисления;

В) в четвертичной системе счисления.

11. Как записывается максимальное 4-разрядное положительное число в троичной системе счисления?

А) 2222; Б) 1111; В) 3333

12. Цифры – это:

А) символы, участвующие в записи числа;

Б) буквы, участвующие в записи числа;

В) пиктограммы, участвующие в записи числа.

2 вариант

1. Система счисления – это:

А) представление числа в экспотенциальной форме;

Б) представление чисел с постоянным положением запятой;

В) способ представления чисел с помощью символов, имеющих определенное количественное значение;

2. Пятеричная система счисления имеет основание:

А) 5; Б) 3; В) 4.

3. Для представления числа в восьмеричной системе счисления используются цифры:

А) от 1 до 8; Б) от 0 до 9; В) от 0 до 7.

4. В какой системе счисления может быть записано число 750?

А) в восьмеричной; Б) в семеричной;

В) в шестнадцатеричной.

5. Чему равно число CDXIV в десятичной системе счисления?

А) 616; Б) 614; В) 414.

6. Преимуществом позиционной системы счисления является:

А) сложно выполнять арифметические действия;

Б)ограниченное число символов, необходимых для записи числа;

В) различное написание цифр у разных народов.

7. Даны системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Запись вида 692:

А) отсутствует в десятичной системе счисления;

Б) отсутствует в восьмеричной системе счисления;

В) существует во всех называемых системах счисления

8. Какие цифры используются в семеричной системе счисления?

А) 0, 1, 6; Б) 0, 8, 9; В) 1, 6, 7

9. Какое минимальное основание должна иметь система счисления, если в ней можно записать числа: 432, 768, 568, 243?

А) 10; Б) 8; В) 9.

10. Когда 2 • 2 = 11?

А) в пятеричной системе счисления;

Б) в троичной системе счисления;

В) в четвертичной системе счисления.

11. Как записывается максимальное 3-разрядное положительное число в четверичной системе счисления:

А) 333; Б) 222; в) 3333.

12. Число – это:

А) ряд символов;

Б) обозначение некоторой величины;

В) набор знаков.

Ключ ответов

вариант

1

2

3

4

5

6

7

8

9

10

11

12

1

б

в

а

в

а

а

а

а

в

в

а

а

2

в

а

в

а

в

б

б

а

а

а

в

б

3) Сообщение темы и цели урока.
Сегодня мы познакомимся с правилами перевода чисел из любой системы счисления в десятичную и выполним задания по переводу чисел из любой системы счисления в десятичную.

4) Изучение нового материала (презентация)

Слайд №2

Алгоритм перевода чисел из любой системы счисления в десятичную

1. Представьте число в развернутой форме. При этом основание системы счисления должно быть представлено в десятичной системе счисления

2. Найдите сумму ряда. Полученное число является значением числа десятичной системы счисления.

Слайд №3

Перевод чисел из любой системы счисления в десятичную

Например, переведем число 1011₂ в десятичную систему счисления. Для этого представим это число в виде степеней двойки и произведем вычисления в десятичной системе счисления.

1011₂ = 1*2³ + 0*2² + 1*2¹ + 1*2⁰ = 1*8 + 0*4 + 1*2 + 1*1 = 8 + 0 + 2 + 1 = 11₁₀

Рассмотрим еще один пример. Переведем число 52,74₈ в десятичную систему счисления.

52,74₈ = 5*8¹ + 2*8⁰ + 3*8^-1 + 4*8^-2 = 5*8 + 2*1 + 7*1/8 +4*1/64 = 40 + 2 + 0,875 + 0,0625 = 42,9375₁₀

Слайд №4

Перевод чисел из 8-ой системы счисления в 10-ую

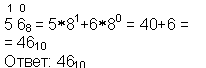
Перевод чисел из 16-ой системы счисления в 10-ую

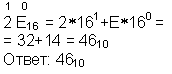
Слайд №5

Алгоритм перевода целых двоичных чисел в систему счисления с основанием q = 2ⁿ.

1. Двоичное число разбить справа налево на группы по n в каждой.

2. Если в левой последней группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.

3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q = 2ⁿ

Слайд №6

Пример

Перевести число 1100101001101010111₂ в восьмеричную систему счисления.

Разбиваем число на группы по три цифры – триады (т.к. Q =8, 8=2ⁿ, n =3) слева на право и, пользуясь таблицей, записываем соответствующее восьмеричное число

001	100	101	001	101	010	111
1	4	5	1	5	2	7

Дополняем.

Получаем: 145127₈

Слайд №7

Пример

Перевести число 1100101001101010111₂ в шестнадцатеричную систему счисления.

Разбиваем число на группы по три цифры – триады (т.к. q =16, 16=2n, n =4) слева направо и, пользуясь таблицей, записываем соответствующее шестнадцатеричное число

0110	0101	0011	0101	0111
6	5	3	5	7

Дополняем.

Получаем: 65357₁₆

III.Закрепление

1. Переведите число 1101₂ в десятичную систему счисления.

2. Переведите число 0,123₅ в десятичную систему счисления.

3. Переведите число 16,4₈ в десятичную систему счисления.

IV.Домашнее задание Н.В.Макарова Информатика. Учебник тема 23.2стр 306, учебник-конспект (Составитель Сумцова О.В.) стр. 81, 82

ПР Перевод чисел из одной системы счисления в другую

Инфоурок › Информатика ›Другие методич. материалы›ПР Перевод чисел из одной системы счисления в другую

Курс профессиональной переподготовки

Учитель информатики

Курс профессиональной переподготовки

Учитель математики и информатики

Курс повышения квалификации

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-459944

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Перевод чисел из одной системы счисления в другую

Цели урока:

• повторить изученный материал по теме система счисления ;
• научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот;
• освоить принципы перевода чисел из одной системы в другую;
• развивать логическое мышление.

Ход урока

Вначале урока краткое повторение и проверка домашнего задания..

Вопросы:

— В каком виде представлена числовая информация в памяти компьютера?

— Для чего используются системы счисления?

— Какие виды систем счисления вы знаете? Привести свои примеры.

— Чем отличаются позиционные системы от непозиционных?.

Цель нашего урока научится переводить число из десятичной системы в любую другую позиционную систему счисления и наоборот. Но в начале мы рассмотрим, как можно

представить любое целое неотрицательное чисело:

В позиционных системах значение записи целого числа определяется по следующему правилу: пусть a _na _n-1a _n-2…a ₁a ₀ — запись числа A, а _i – цифры, тогда

A = a n·pn+a n-1·pn-1 +a n-2·pn-2+…+a 1·p1+ a0·p0        (1),

где p — целое число большее 1, которое называется основанием системы счисления

 Для того, чтобы при заданном p любое неотрицательное целое число можно было бы   записать по формуле (1) и притом единственным образом, числовые значения различных цифр должны быть различными целыми числами, принадлежащими отрезку от 0 до p-1.

Пример:

1) Десятичная система

p = 10

цифры: 0,1,2,3,4,5,6,7,8,9

число 5735 = 5·10³+7·10²+3·10¹+8·10⁰

2) Троичная система

p = 3

цифры: 0,1,2

число 201₃ = 2·3²+0·3¹+1·3⁰

Замечание: нижним индексом в записи числа обозначается основание системы счисления, в которой записано число. Для десятичной системы счисления индекс можно не писать.

Представление отрицательных и дробных чисел:

Во всех позиционных системах для записи отрицательных чисел так же как и в десятичной системе используется знак ‘–‘.  Для отделения целой части числа от дробной используется запятая. Значение записи a _na _n-1a _n-2…a ₁a ₀, a _-1 a _-2…a _m-2 a _m-1a _m числа A определяется по формуле, являющейся обобщением формулы (1):

A = an·pn+a n-1·p n-1+a n-2·p n-2+…+a1·p1+a0·p0+a-1·p-1+a -2·p-2+…+am-2·p–(m–2)+am–1·p–(m–1)+amp–m     (2),

Пример:

75,6 = 7·10¹+5·10⁰+6·10^–1

 –2,314₅ = –(2·5⁰+3·5^–1+1·5^–2+4·5^–3)

Перевод чисел из произвольной системы счисления в десятичную:

Следует понимать, что при переводе числа из одной системы счисления в другую количественное значение числа не изменяется, а меняется только форма записи числа, так же как при переводе названия числа, например, с русского языка на английский.

Перевод чисел из произвольной системы счисления в десятичную выполняется непосредственным вычислением по формуле (1) для целых и формуле (2) для дробных чисел.

Перевод чисел из десятичной системы счисления в произвольную.

Перевести число из десятичной системы в систему с основанием p – значит найти коэффициенты в формуле (2). Иногда это легко сделать простым подбором. Например, пусть нужно перевести число 23,5 в восьмеричную систему. Нетрудно заметить, что 23,5 = 16+7+0,5 = 2·8+7+4/8 = 2·8¹+7·8⁰+4·8^–1 =27,48. Понятно, что не всегда ответ столь очевиден. В общем случае применяется способ перевода отдельно  целой и дробной частей числа.  

Для перевода целых чисел применяется следующий алгоритм (полученный на основании формулы (1)):

1. Найдем частное и остаток от деления числа на p. Остаток  будет очередной цифрой ai (j=0,1,2 …) записи числа в новой системе счисления.

2. Если частное равно нулю, то перевод числа закончен, иначе применяем к частному пункт 1.

Замечание 1. Цифры ai в записи числа нумеруются справа налево.

Замечание 2. Если p>10, то необходимо ввести обозначения для цифр с числовыми значениями, большими или равными 10.

Пример:

Перевести число 165 в семеричную систему счисления.

165:7 = 23 (остаток 4) => a₀ = 4

23:7 = 3 (остаток 2) => a₁ = 2

3:7 = 0 (остаток 3) => a₂ = 3

Выпишем результат: a₂a₁a₀, т.е. 3247.

Выполнив проверку по формуле (1), убедимся в правильности перевода:

3247=3·7²+2·7¹+4·7⁰=3·49+2·7+4 = 147+14+4 = 165.

Для перевода дробных частей чисел применяется алгоритм, полученный на основании формулы (2):

1. Умножим дробную часть числа на p.

2. Целая часть результата будет очередной цифрой am (m = –1,–2, –3 …) записи  числа в новой системе счисления. Если дробная часть результата равна нулю, то перевод числа закончен, иначе применяем к ней пункт 1.

Замечание 1.  Цифры a_m в записи числа располагаются слева направо в порядке возрастания абсолютного значения m.

Замечание 2.  Обычно количество дробных разрядов в новой записи числа ограничивается заранее. Это позволяет выполнить приближенный перевод с заданной точностью. В случае бесконечных дробей такое ограничение обеспечивает конечность алгоритма.

Пример 1:

Перевести число 0,625 в двоичную систему счисления.

 0,625·2 = 1,25 (целая часть 1) => a_-1 =1

0,25·2  = 0,5 (целая часть 0) => a-₂ = 0

0,5·2 = 1,00 (целая часть 1) => a-₃ = 1

Итак, 0,62510 = 0,1012

Выполнив проверку по формуле (2), убедимся в правильности перевода:

0,1012=1·2^-1+0·2-²+1·2^-3=1/2+1/8 = 0,5+0,125 = 0,625.

 Пример 2:

Перевести число 0,165 в четверичную систему счисления, ограничившись четырьмя четверичными разрядами.

0,165·4 = 0,66 (целая часть 0) => a_-1=0

0,66·4  = 2,64 (целая часть 2) => a_-2= 2

0,64·4 = 2,56 (целая часть 2) => a_-3= 2

0,56·4 = 2,24 (целая часть 2) => a_-4= 2

Итак, 0,16510 ” 0,02224

Выполним обратный перевод, чтобы убедиться, что абсолютная погрешность не превышает 4–4:

0,02224 = 0·4^-1+2·4^-2+2·4^-3+2·4^-4= 2/16+2/64+2/256 = 1/8+1/32+1/128 = 21/128 = 0,1640625

|0,1640625–0,165| = 0,00094 < 4–4 = 0,00390625

Перевод чисел из одной произвольной системы в другую

В этом случае сначала следует выполнить перевод числа в десятичную систему, а затем из десятичной в требуемую.

Особым способом выполняется перевод чисел для систем с кратными основаниями.

Пусть p и q – основания двух систем счисления. Будем называть эти системы системами счисления с кратными основаниями, если p = qn или q = pn, где n – натуральное число. Так, например, системы счисления с основаниями 2 и 8 являются системами счисления с кратными основаниями.

Пусть p = qn и требуется перевести число из системы счисления с основанием q в систему счисления с основанием p.  Разобьем целую и дробную части записи числа на группы по n последовательно записанных цифр влево и вправо от запятой. Если количество цифр в записи целой части  числа не кратно n, то надо дописать слева соответствующее количество нулей. Если количество цифр в записи дробной части  числа не кратно n, то нули дописываются справа. Каждая такая группа цифр числа в старой системе счисления будет соответствовать одной цифре числа в новой системе счисления.

Пример:

Переведем 1100001,111₂  в четверичную систему счисления.

Дописав нули и выделив пары цифр, получим 01100001,11102.

Теперь выполним перевод отдельно каждой пары цифр, пользуясь пунктом Перевод чисел из одной   произвольной системы в другую.

01₂=1₁₀=1₄

10₂=2₁₀=2₄

00₂=0₁₀=0₄

01₂=1₁₀=1₄

11₂=3₁₀=3₄

10₂=2₁₀=2₄

Итак,  1100001,1112 = 01100001,11102 = 1201,324.

Пусть теперь требуется выполнить перевод из системы с большим основанием q, в систему с меньшим основанием p, т.е. q = p_n. В этом случае одной цифре числа в старой системе счисления соответствует n цифр числа в новой системе счисления.

Пример: Выполним проверку предыдущего перевода числа.

1201,324 = 1100001,11102=1100001,1112

В шестнадцатеричной системе есть цифры с числовыми значениями 10,11,12, 13,14,15. Для их обозначения используют первые шесть  букв латинского алфавита A, B, C, D, E, F.

Приведем таблицу чисел от 0 до 16, записанных в системах счисления с основаниями 10, 2, 8 и 16.

Число в десятичной системе счисления	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
В восьмеричной	0	1	2	3	4	5	6	7	10	11	12	13	14	15	16	17	20
В двоичной	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111	10000
В шестнадцатеричной	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10

 Для записи шестнадцатеричных цифр можно использовать также строчные латинские буквы a-f.

Пример: Переведем число 110101001010101010100,11₂ в шестнадцатеричную систему счисления.

Воспользуемся кратностью оснований систем счисления (16=2⁴). Сгруппируем цифры по четыре, дописав, слева и справа  нужное количество нулей

000110101001010101010100,1100₂

и, сверяясь с  таблицей, получим: 1A9554,C₁₆

Вывод:

В какой системе счисления лучше записывать числа – это вопрос удобства и традиций. С технической точки зрения, в ЭВМ удобно использовать двоичную систему, так как в ней для записи числа используются только  две цифры 0 и 1, которые можно представить двумя легко различимыми состояниями “нет сигнала ” и “есть сигнал”.

А человеку, напротив, неудобно иметь дело с двоичными записями чисел из-за того, что они более длинные, чем десятичные и в них много повторяющихся цифр. Поэтому, при необходимости работать с машинными представлениями чисел используют восьмеричную или шестнадцатеричную системы счисления. Основания этих систем – целые степени двойки, и поэтому числа легко переводятся из этих систем в двоичную и обратно.

Записываем задание на дом:

а) Запишите дату рождения всех членов вашей семьи в различных системах счисления.

б) Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:

а) 1001111110111,011₂ ;

б) 1110101011,1011101₂