Энергетические процессы в резистивном, индуктивном и емкостном элементах

 

Энергетические процессы в электрических цепях синусоидального тока достаточно сложные, так как физические процессы в различных элементах неодинаковы.

Чтобы яснее представить энергетические процессы в цепях синусоидального тока, рассмотрим графики мгновенных значений мощности, напряжения и тока отдельно для резистивного, индуктивного и емкостного элементов, подключенных к источнику электрической энергии.

В резистивном элементе с сопротивлением r при напряжении

ток в этом элементе

,

то есть совпадает по фазе с напряжением. В любой момент времени мощность резистивного элемента

.

Мгновенная мощность в резистивном элементе в любой момент времени положительна, то есть в течение любого интервала времени в резистивный элемент поступает энергия и происходит необратимое преобразование электрической энергии в другие ее виды.

Средняя за период мощность, то есть активная мощность, резистивного элемента равна:

,

где , – действующие значения напряжения и тока.

 

 

Для индуктивного элемента L напряжение равно:

.

Напряжение опережает по фазе ток

.

Мгновенная мощность индуктивного элемента

.

Мгновенная мощность изменяется по синусоидальному закону с частотой, в 2 раза большей частоты тока. Мгновенная мощность положительна при нарастании по абсолютному значению тока в индуктивном элементе; в это время энергия накапливается в магнитном поле индуктивного элемента.

Определим энергию, поступающую в индуктивный элемент за четверть периода, в течение которого ток и мгновенная мощность положительны:

.

После подстановки мгновенного значения напряжения на индуктивном элементе и соответствующей замены переменных получим:

.

В течение следующей четверти периода мгновенная мощность p_L отрицательна, то есть индуктивный элемент не получает энергию от источника e, а наоборот, источник получает энергию от индуктивного элемента.

Среднее значение мощности за период

.

Синусоидальный ток в индуктивном элементе не совершает работы. Поэтому в отличие от резистивного элемента энергетический режим индуктивного элемента принято определять не активной, а реактивной индуктивной мощностью, равной максимальной мгновенной мощности:

.

Хотя размерности активной и реактивной мощностей совпадают, для измерения реактивной индуктивной мощности выбрана своя единица: вар.

 

В емкостном элементе С напряжение

отстает по фазе от тока на угол . Мгновенная мощность в емкостном элементе равна:

.

В емкостном элементе, так же как и в индуктивном, мгновенная мощность – синусоидальная величина, частота которой вдвое больше частоты тока.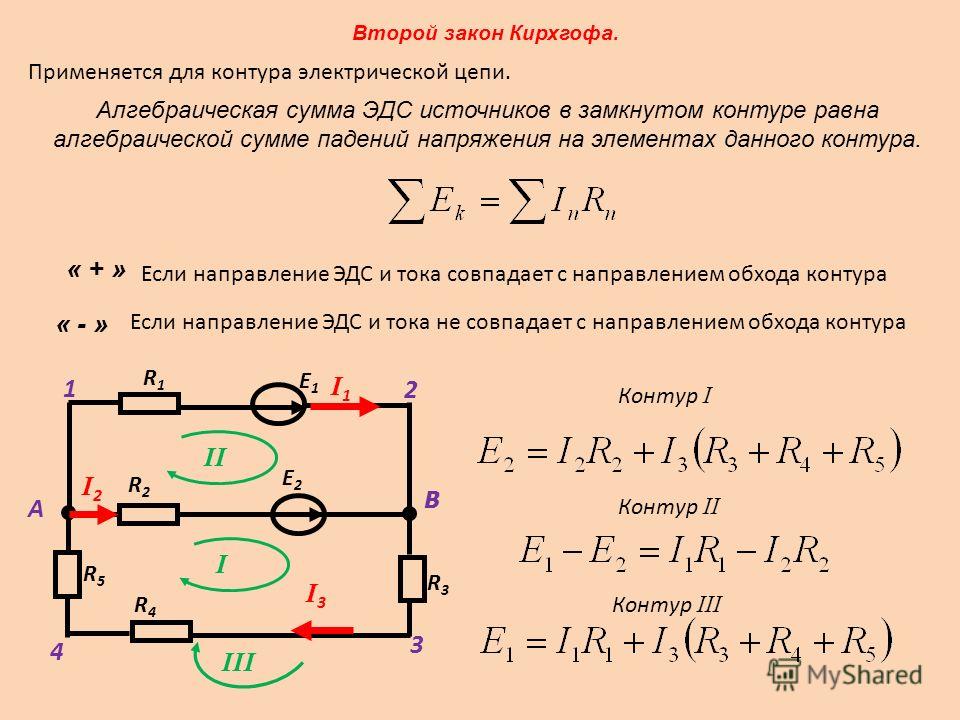

Но в емкостном элементе мгновенная мощность положительна в те интервалы времени, в течение которых напряжение возрастает по абсолютному значению. В течение этих интервалов времени происходит зарядка емкостного элемента и в его электрическом поле накапливается энергия. При уменьшении по абсолютному значению напряжения на емкостном элементе мгновенная мощность отрицательна, то есть этот элемент разряжается и энергия, запасенная в его электрическом поле, возвращается источнику.

К концу первой четверти периода энергия электрического поля достигает максимального значения:

.

После подстановки мгновенного значения тока в емкостном элементе и соответствующей замены переменных получим:

.

В емкостном элементе, так же как и в индуктивном, синусоидальный ток не совершает работы.

Энергетический режим емкостного элемента принято определять реактивной емкостной мощностью, равной максимальной мгновенной мощности:

.

Если индуктивный и емкостной элементы соединены последовательно, то в моменты времени, когда энергия магнитного поля индуктивного элемента увеличивается, энергия электрического поля емкостного элемента уменьшается и наоборот. Следовательно, эти элементы могут обмениваться энергией не только с источниками, но и друг с другом.

 

---

Дата добавления: 2018-05-10; просмотров: 1354; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

---

Сообщество Экспонента

• вопрос
• 31.05.2023

Цифровая обработка сигналов, Математика и статистика, Системы управления, Другое

Добрый день, нужна помощь в работе с таблицей. У меня есть определенный коэф. Kg=2.53, в таблице идет столбец значений Kg, как осуществить поиск и выбор нужного значения, между теми, что идут в таблиц…

Добрый день, нужна помощь в работе с таблицей. У меня есть определенный коэф. Kg=2.53, в таблице идет столбец значений Kg, как осуществить поиск и выбор нужного значения, между теми, что идут в таблиц. ..

• вопрос
• 28.05.2023

Другое, Математика и статистика

Здравствуйте, помогите пожалуйста разобраться с преобразованием Фурье. Желательно с объяснением решения (см. вложенный скрин). Заранее всем спасибо!

Здравствуйте, помогите пожалуйста разобраться с преобразованием Фурье. Желательно с объяснением решения (см. вложенный скрин). Заранее всем спасибо!

1 Ответ

• фурье

28.05.2023

• вопрос
• 26.05.2023

Другое

Возможны ли облачные вычисления в среде MatLab, без установки приложения на собственный компьютер? Если » да», то как это сделать?

Возможны ли облачные вычисления в среде MatLab, без установки приложения на собственный компьютер? Если » да», то как это сделать?

1 Ответ

• вопрос
• 20.05.2023

Электропривод и силовая электроника, Другое

Нужно смоделировать устройство (Блок схемы уже есть) которые изготавливают упругие элементы из проволоки для амортизаторов бортовой радиоэлектронной аппаратуры.

Там есть обратная связь ( в виде датчик…

Нужно смоделировать устройство (Блок схемы уже есть) которые изготавливают упругие элементы из проволоки для амортизаторов бортовой радиоэлектронной аппаратуры. Там есть обратная связь ( в виде датчик…

6 Ответов

• Simulink
• Моделирование систем
• математическое моделирование

20.05.2023

• вопрос
• 20.05.2023

Электропривод и силовая электроника

Добрый день! Мне нужна структурная схема (и может быть ее описание) блока Synchronous Machine Round Rotor. Помогите пожалуйста найти источник информации.

Добрый день! Мне нужна структурная схема (и может быть ее описание) блока Synchronous Machine Round Rotor. Помогите пожалуйста найти источник информации.

• вопрос
• 15.05.2023

Электропривод и силовая электроника

Здравствуйте! Мог бы кто помочь построить схему в Симулинке?

Здравствуйте! Мог бы кто помочь построить схему в Симулинке?

10 Ответов

• вопрос
• 14. 05.2023

Изображения и видео

Необходимо было моделировать возможные искажения изображения, проблемы возникли в моделировании процесса преломления света при прохождении через сферическую поверхность, полученное изображение было в…

Необходимо было моделировать возможные искажения изображения, проблемы возникли в моделировании процесса преломления света при прохождении через сферическую поверхность, полученное изображение было в…

3 Ответа

• моделирование

14.05.2023

• вопрос
• 11.05.2023

Системы управления, Робототехника и беспилотники, Автоматизация испытаний, Глубокое и машинное обучение(ИИ), Цифровая обработка сигналов, Другое

У кого нибудь есть модель электропривода механизма подъема экскаватора и оптимизации контуров? Спасибо за ранее

У кого нибудь есть модель электропривода механизма подъема экскаватора и оптимизации контуров? Спасибо за ранее

6 Ответов

• вопрос
• 02. 05.2023

Другое

Мне нужно сделать интегральную частотно-импульсную систему автоматического управления теплопотреблением помещения. Я никак не могу разобраться как сделать регулятор ичим

Мне нужно сделать интегральную частотно-импульсную систему автоматического управления теплопотреблением помещения. Я никак не могу разобраться как сделать регулятор ичим

1 Ответ

• MATLAB

02.05.2023

• вопрос
• 02.05.2023

ПЛИС и СнК, Системы связи, Цифровая обработка сигналов, Другое, Встраиваемые системы

Задача — LDPC декодер внутри FPGA.  Первый пришедший в голову вариант — декодер из MATLAB с последующей генерацией HDL. Источник : https://www.mathworks.com/help/wireless-hdl/ref/dvbs2ldpcde…

Задача — LDPC декодер внутри FPGA.  Первый пришедший в голову вариант — декодер из MATLAB с последующей генерацией HDL. Источник : https://www.mathworks.com/help/wireless-hdl/ref/dvbs2ldpcde. ..

1 Ответ

• Simulink
• ПЛИС и СнК
• Системы связи

02.05.2023

Реальная, реактивная и полная мощность

За кулисами происходит сложный процесс при включении любого электрического устройства. Электричество должно подаваться в сеть и, в конечном счете, на компонент. В процесс вносят вклад различные типы мощности, которые мы более подробно объясним в этой статье, включая активную мощность, реактивную мощность, комплексную мощность и полную мощность.

Реальная мощность находится в цепи переменного тока (AC) и измеряется в ваттах. Он выполняет фактическую работу в цепи, обеспечивая электричеством каждый элемент, находящийся под напряжением. Он также известен как «активная мощность», потому что это тип, который направляется через сеть, прежде чем подавать питание на предметы, начиная от вашего телефона и заканчивая лампочками.

Реактивная мощность отличается от реальной мощности. Он не электрифицирует предметы напрямую, но все же играет роль в энергосистеме, обеспечивая равномерное движение электричества между генераторами и конденсаторами (область хранения электроэнергии). Он подается в систему по мере необходимости, чтобы обеспечить баланс между высокими и низкими напряжениями. Рассмотрим идеальную цепь переменного тока, состоящую из источника и обобщенной нагрузки, где ток и напряжение синусоидальны. Если нагрузка чисто резистивная, две величины одновременно меняют свою полярность, направление потока энергии не меняется на обратное — и течет только реальная мощность. Если нагрузка чисто реактивная, то напряжение и ток равны 90 градусов не совпадают по фазе, и поток чистой мощности отсутствует. Эта энергия, текущая назад и вперед, известна как реактивная мощность. Если конденсатор и катушка индуктивности соединены параллельно, то токи, протекающие через катушку индуктивности и конденсатор, противодействуют друг другу и имеют тенденцию компенсировать, а не добавлять. Обычно считается, что конденсаторы генерируют реактивную мощность, а катушки индуктивности — потребляют ее. Это основной механизм управления коэффициентом мощности при передаче электроэнергии; конденсаторы (или катушки индуктивности) вставляются в цепь, чтобы частично компенсировать реактивную мощность нагрузки. Практическая нагрузка будет иметь резистивную, индуктивную и емкостную части, поэтому в нагрузку будет поступать как активная, так и реактивная мощность.

Комплексная мощность представляет собой сумму реальной мощности и реактивной мощности. Полная мощность представляет собой векторную сумму активной и реактивной мощности. Он представляет собой два типа мощности — реальный тип, который был отправлен для включения элементов, и реактивный, который остается в цепи переменного тока. Полная мощность представляет собой среднеквадратичное значение (RMS или rms) напряжения и тока. Полная мощность удобна для определения размеров оборудования или проводки. Однако суммирование кажущейся мощности для двух нагрузок не даст точного значения полной кажущейся мощности, если они не имеют одинакового смещения между током и напряжением.

Инженеры используют следующие термины для описания потока энергии в системе (и назначают каждому из них разные единицы):

• • Активная мощность (P) [Единица измерения: Вт]
• • Реактивная мощность (Q) [единица измерения: вар]
• • Комплексная мощность (S): Комплексное значение S называется комплексной мощностью.
• • Полная мощность (|S|) [единица измерения: ВА]: абсолютное значение комплексной мощности S.

На схеме P – активная мощность, Q – реактивная мощность (в данном случае отрицательная), S – комплексная мощность; а длина S — кажущаяся мощность.

---

Единицей измерения всех форм мощности является ватт (обозначение: Вт). Однако эта единица обычно зарезервирована для активной составляющей мощности. Полная мощность обычно выражается в вольт-амперах (ВА), поскольку она представляет собой простое произведение среднеквадратичного значения напряжения и среднеквадратичного значения тока. Единице реактивной мощности присваивается специальное сокращение «ВАР», что означает реактивный вольт-ампер (поскольку поток реактивной мощности не передает полезной энергии в нагрузку, ее иногда называют «безваттной» мощностью).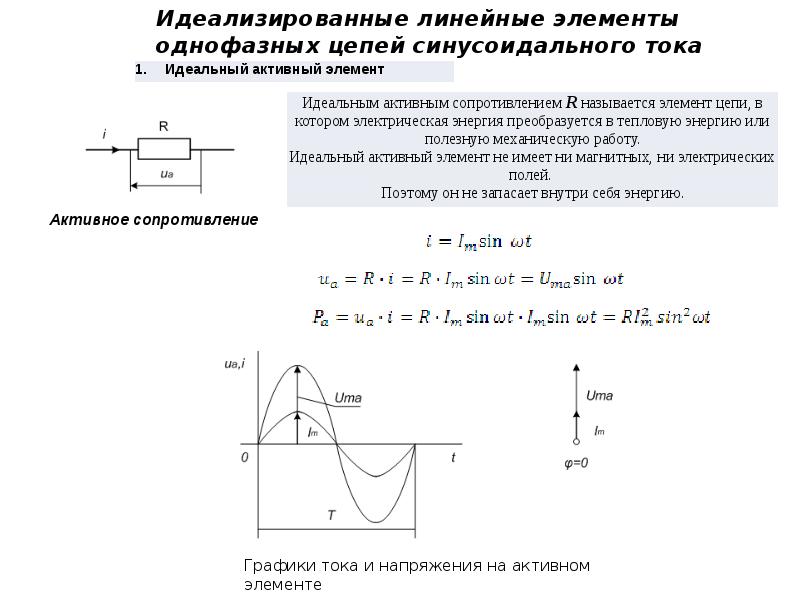 Обратите внимание, что не имеет смысла присваивать комплексной мощности одну единицу, потому что это комплексное число; поэтому он определяется как пара из двух единиц: W и VAR.

Понимание соотношения между этими тремя величинами лежит в основе понимания энергетики. Математическая связь между ними может быть представлена ​​векторами или выражена комплексными числами (где j — мнимая единица).

---

КОЭФФИЦИЕНТ МОЩНОСТИ:

Коэффициент мощности измеряет эффективность системы электропитания переменного тока. Коэффициент мощности – это реальная мощность на единицу полной мощности. (pf = Вт·ч/ВА·ч) Коэффициент мощности, равный единице, идеален, а 99% это хорошо. Там, где сигналы чисто синусоидальные, коэффициент мощности равен косинусу фазового угла (f) между синусоидальными сигналами тока и напряжения. По этой причине в технических паспортах оборудования и на паспортных табличках коэффициент мощности часто указывается как «cosf». Коэффициент мощности равен 1, когда напряжение и ток совпадают по фазе; и равен нулю, когда ток опережает или отстает от напряжения на 90 градусов. Коэффициенты мощности обычно обозначаются как «опережающие» или «отстающие», чтобы показать знак фазового угла, где опережение указывает на отрицательный знак. Для двух систем, передающих одинаковое количество активной мощности, система с более низким коэффициентом мощности будет иметь более высокие циркулирующие токи. Это происходит из-за энергии, которая возвращается к источнику из запасов энергии в нагрузке. Эти более высокие токи в практической системе приведут к более высоким потерям и снизят общую эффективность передачи. Цепь с более низким коэффициентом мощности будет иметь более высокую полную мощность и потери при том же самом количестве передаваемой мощности. Чисто емкостные цепи вызывают реактивную мощность, при этом форма волны тока опережает волну напряжения на 90 градусов, в то время как чисто индуктивные цепи вызывают реактивную мощность, при этом форма волны тока отстает от формы волны напряжения на 90 градусов. Результатом этого является то, что емкостные и индуктивные элементы схемы имеют тенденцию компенсировать друг друга.

---

ПОТОК РЕАКТИВНОЙ МОЩНОСТИ:

При передаче и распределении электроэнергии значительные усилия прилагаются для контроля потока реактивной мощности. Обычно это делается автоматически путем включения и выключения катушек индуктивности или конденсаторных батарей, регулировки возбуждения генератора и другими способами. Розничные торговцы электроэнергией могут использовать счетчики электроэнергии, которые измеряют реактивную мощность, чтобы финансово наказать клиентов с низким коэффициентом мощности. Это особенно актуально для заказчиков, эксплуатирующих высокоиндуктивные нагрузки, такие как двигатели на водяных насосных станциях.

---

ИНТЕЛЛЕКТУАЛЬНАЯ БАТАРЕЯ:

Выходной ток зависит от состояния батареи. Интеллектуальное зарядное устройство может контролировать напряжение, температуру и/или время зарядки аккумулятора, чтобы определить оптимальный зарядный ток в данный момент. Зарядка прекращается, когда сочетание напряжения, температуры и/или времени указывает на то, что батарея полностью заряжена.

Для Ni-Cd и NiMH аккумуляторов напряжение на аккумуляторе медленно увеличивается в процессе зарядки, пока аккумулятор не будет полностью заряжен. После этого напряжение снижается, что указывает интеллектуальному зарядному устройству на то, что аккумулятор полностью заряжен. Такие зарядные устройства часто маркируются буквой «V» или «дельта-V», что указывает на то, что они контролируют изменение напряжения.
Типичное интеллектуальное зарядное устройство быстро заряжает аккумулятор примерно до 85% от его максимальной емкости менее чем за час, а затем переключается на подзарядку, которая занимает несколько часов, чтобы полностью зарядить аккумулятор.

---

ВОЛЬТ-АМПЕР:

Вольт-ампер в электрическом выражении означает количество полной мощности в цепи переменного тока, равное току в один ампер при ЭДС в один вольт. Это эквивалентно ваттам для нереактивных цепей следующим образом:

• • 10 кВ·А = мощность 10 000 Вт (где префикс k равен килограмму)
• • 10 МВ·А = мощность 10 000 000 Вт (где M равно мега)

Несмотря на то, что вольт-ампер и ватт эквивалентны по размеру, можно найти продукты, рассчитанные как в ВА, так и в ваттах с разными номерами. Это обычная практика в системах ИБП (источник бесперебойного питания). Номинальная мощность в ВА — это полная мощность, которую может производить ИБП, а номинальная мощность в ваттах — это реальная мощность (или реальная мощность), которую он генерирует, в отличие от реактивной мощности. Реактивная мощность возникает из-за емкости и индуктивности компонентов нагрузки, которая питается от цепи переменного тока. При чисто резистивной нагрузке (например, лампы накаливания) кажущаяся мощность равна реальной мощности, а количество используемых ВА и ватт будет эквивалентным. Однако в более сложных нагрузках, таких как компьютеры (для питания которых предназначены ИБП), потребляемая кажущаяся мощность (ВА) будет больше фактической используемой мощности (ватты). Отношение этих двух величин называется коэффициентом мощности.

---

Покупайте в CableOrganizer® электрические блоки, зарядные устройства, настольные розетки, системы бесперебойного питания (ИБП) и многое другое.

Похожие материалы

Портативные устройства PowerVer от Tripp Lite

Устройство защиты от перенапряжения на розетке Grouper™ 6

Настольная втулка Nightcap

Что подразумевается под коэффициентом мощности?

Низкий коэффициент мощности снижает пропускную способность электрической системы за счет увеличения протекающего тока. Поэтому иметь низкий коэффициент мощности неэффективно и дорого. Но что такое коэффициент мощности и что на него влияет?

Типичная распределительная система ограничена по величине тока, которую она может нести; коэффициент мощности, выраженный в процентах, является показателем величины полного тока, который может быть использован для создания работы (активной мощности). Чем ближе коэффициент мощности к 1,00 (100%), тем меньше ток, необходимый для выполнения указанной работы.

Например, нагрузка с коэффициентом мощности 0,80 означает, что только 80% мощности эффективно используется для выполнения работы. В идеальном мире вся мощность, получаемая из энергосистемы, должна быть преобразована в полезную работу, но в реальном мире это не так. Для полного описания коэффициента мощности необходимы сложные уравнения. Однако для более простого понимания Министерство энергетики США использует простую аналогию с мощностью, необходимой лошади, чтобы тянуть тележку по рельсам.

В идеале лошадь должна быть размещена перед вагоном, чтобы обеспечить наиболее эффективное тяговое усилие; однако это не всегда возможно. Угол буксировки отражает изменение коэффициента мощности: чем меньше угол, тем лучше коэффициент мощности, чем больше угол, тем ниже коэффициент мощности (рис. 1).

1. Углы влияют на полезную работу. Показанная здесь аналогия обеспечивает визуализацию, помогающую понять коэффициент мощности. Коэффициент мощности определяется как отношение реальной (рабочей) мощности к полной (полной) мощности. Если лошадь вести ближе к центру следа, угол бокового увода уменьшается, и реальная мощность приближается к значению кажущейся мощности. Источник: Министерство энергетики США

Полная энергия, необходимая для тяги вагона, равна полной мощности. Фактическая энергия, движущая вагон, является реальной силой. Энергия, не используемая из-за угла тяги лошади, является реактивной мощностью. Другими словами, реальная мощность, также называемая рабочей мощностью (кВт), выполняет фактическую работу движения, тепла и света. Реактивная мощность или нерабочая мощность (кВар) поддерживает магнитное поле реактивной нагрузки (обычно индуктивной). Ток, используемый для создания реактивной мощности, не используется для создания работы; однако этот ток ложится бременем на систему распределения, поставщика электроэнергии и счета за электроэнергию объекта.

Векторная сумма рабочей мощности и нерабочей мощности равна общей мощности (полная мощность):

Полная мощность = √ (активная мощность ² + реактивная мощность ² )

, которая используется для расчета коэффициента мощности:

9000 2 Коэффициент мощности = Активная мощность / Полная мощность = косинус угла (ϕ)

Основы напряжения и тока

Чтобы понять коэффициент мощности, мы должны сначала понять некоторые основы теории переменного тока (AC) и связанные с ней формы сигналов. Напряжение в системе переменного тока чередуется между положительным и отрицательным (в синусоидальной форме) и заставляет ток вести себя аналогичным образом. Это происходит 60 раз в секунду (в системе с частотой 60 Гц) в диапазоне от 0 до 360 градусов. В отличие от систем переменного тока, напряжение в системе постоянного постоянного тока (DC) не изменяется.

Поскольку мгновенное значение напряжения переменного тока постоянно изменяется, наука определила другую меру для величин переменного тока, а именно среднеквадратичное значение. Среднеквадратичное значение сигнала переменного тока дает тот же эффект нагрева, что и сигнал постоянного тока того же значения.

Среднеквадратичное значение представляет собой квадратный корень из среднего арифметического квадратов набора мгновенных значений за период (цикл). Когда напряжение и ток являются чисто синусоидальными, среднеквадратичное значение напряжения и тока можно найти по пиковому (pk) напряжению и току:

В _СКЗ = В _шт. / √2

119,5 В _СКЗ = 169 В _шт.

I _RMS = I _шт. / √2

75 A _RMS = 106 A _pk / 1,414

Вы можете спросить себя, какое отношение это имеет к коэффициенту мощности? Для расчета мощности переменного тока требуется знание среднеквадратичного значения напряжения, среднеквадратичного значения тока и синусоидального фазового соотношения. Итак, резюмируя, среднеквадратичное значение — это мера нагревательного эффекта, рассчитанная по форме волны, которая позволяет сравнивать переменный ток с постоянным. Любой фазовый сдвиг от чистой синусоидальной формы сигнала указывает на коэффициент мощности.

Ниже приведено сравнение того, как коэффициент мощности влияет на выходную мощность кВА при двух разных однофазных нагрузках.

Для электрического обогревателя мощностью 9 кВт (120 В переменного тока, 75 А) с входным коэффициентом мощности (PF) 1,0:

P = √1ϕ x 120 В переменного тока x 75 A x 1,0 PF = 9 кВт

кВА = √1ϕ x 120 В переменного тока x 75 A = 9 кВА

Для зарядного устройства мощностью 9 кВт (120 В переменного тока, 75 A) с входным коэффициентом мощности 0,866:

P = √1ϕ x 120 В переменного тока x 86,6 A x 0,866 PF = 9 кВт

кВА = √1ϕ x 120 В переменного тока x 86,6 A = 10,392 кВА

Хотя каждая нагрузка потребляет 9 кВт мощности, входной коэффициент мощности зарядного устройства составляет 0,866. Более низкий коэффициент мощности требует для работы дополнительных 11,6 А, которые в конечном итоге предоставляются энергетической компанией. Необходимо не только приобрести дополнительный реактивный ток, но и увеличить размер распределительной системы, чтобы справиться с дополнительным током.

Что влияет на коэффициент мощности?

Коэффициент мощности относится к соотношению между активной (полезной мощностью) и полной (полной) мощностью. Это отношение является мерой того, насколько эффективно используется электроэнергия.

Линейные резистивные нагрузки. В системе переменного тока нагрузки классифицируются по способу потребления тока. Линейная резистивная нагрузка — это чисто резистивная нагрузка, не содержащая ни индуктивных, ни емкостных компонентов, таких как электрические обогреватели и лампы накаливания. Кривые напряжения и тока пересекают нулевую координату в одной и той же точке.

Кривая мощности (P) на рис. 2 рассчитана по напряжению (V) и току (I), показанным в положительной области графика. В этом примере напряжение и ток составляют 120 ВСКЗ и 75 АСКЗ соответственно. Произведение двух равно 9кВА или 9 кВт. Напряжение и ток находятся «в фазе», и 100% мощности (рабочей мощности) эффективно используются для выполнения полезной работы. Коэффициент мощности для этого типа нагрузки равен 1,0.

2. Линейные активные нагрузки. Напряжение и ток совпадают по фазе с коэффициентом мощности, равным 1,0 для чисто резистивных нагрузок. Предоставлено Ametek Solidstate Controls

Линейные нерезистивные/реактивные нагрузки. Необычно найти чисто активные нагрузки; большинство нагрузок имеют дополнительную реактивную составляющую. Эти нерезистивные/реактивные нагрузки составляют большой процент всех нагрузок. Форма волны тока смещена от формы волны напряжения так, что она находится «в противофазе». Если нагрузка индуктивная, ток отстает от напряжения; если нагрузка емкостная, ток опережает.

Промышленные объекты, как правило, имеют отстающие нагрузки коэффициента мощности (индуктивные нагрузки). Этими типами нагрузок могут быть асинхронные двигатели, дроссели и трансформаторы. Нагрузки с опережающим коэффициентом мощности (емкостные нагрузки) менее распространены и обычно представляют собой подземные кабели или некоторые импульсные источники питания.

На рис. 3 та же нагрузка, что и на рис. 2, теперь имеет кривые напряжения и тока, сдвинутые по фазе на 30 градусов. Поскольку это индуктивная форма волны, ток теперь отстает.

3. Индуктивные нагрузки. Напряжение и ток не совпадают по фазе для линейных нерезистивных/реактивных нагрузок. В этом примере с индуктивной нагрузкой ток отстает от напряжения на 30 градусов при коэффициенте мощности 0,866. Предоставлено Ametek Solidstate Controls

Нелинейные нагрузки — гармоники. Сегодняшние промышленные установки имеют не только резистивные, индуктивные и емкостные нагрузки, но многие из них также включают полупроводниковое оборудование, такое как импульсные источники питания, приводы постоянного тока, частотно-регулируемые приводы (VFD), электронные балласты, дуговые сварочные аппараты и датчики температуры. -управляемые печи. Это все нелинейные нагрузки или нагрузки, для которых ток несинусоидален, даже когда напряжение синусоидально. Несинусоидальный характер этих сигналов выражается с помощью гармоник.

Гармоники — это сигналы различной амплитуды на частотах, кратных основной частоте напряжения (50 Гц или 60 Гц). Они накладываются на синусоидальную форму волны тока для создания общей формы волны тока. Рисунок 4 является примером такой формы волны тока.

4. Нелинейные нагрузки. На этом графике показаны формы сигналов напряжения и тока нелинейного источника питания с гармониками. Для наглядности он показан без 30-градусного фазового сдвига тока. Предоставлено Ametek Solidstate Controls

Среднеквадратичное значение всего тока находится путем суммирования среднеквадратичного значения каждой гармоники тока. При частоте сигнала 60 Гц это означает, что частота 2-й гармоники будет равна 120 Гц (60 Гц x 2 = 120 Гц), а частоты 3-й, 4-й и 5-й гармоник будут равны 180 Гц, 240 Гц и 300 Гц соответственно. Гармоники, кратные основной частоте, могут быть выражены как 2f, 3f, 4f и т. д.

Текущее полное гармоническое искажение (THD) представляет собой сумму всех гармонических составляющих формы волны тока по сравнению с основной составляющей волны тока. . Как показано ниже, это отношение среднеквадратичного значения гармоник тока к среднеквадратичному значению основного тока.

I _THD = СКЗ гармоник тока / СКЗ основного тока = √(I ₂ ² + I ₃ ² + I ₄ ² + …) / I ₁ x 100%

Для чисто синусоидальных сигналов фазовый сдвиг между напряжением и током достаточен для количественного определения коэффициента мощности (PF). Для сигналов, которые не являются синусоидальными, термин «коэффициент мощности смещения» (DpPF) используется для количественной оценки фазового сдвига между основными частотами двух сигналов (составляющими 50 Гц или 60 Гц). Для тех же несинусоидальных сигналов определен термин для количественной оценки влияния гармоник на коэффициент мощности. Этот термин называется коэффициентом мощности искажения (DF).

DF = 1 / √(1 + THD ² )

Чтобы найти общий коэффициент мощности (PF _T ), используется следующее уравнение:

PF _T = DF x D _p ПФ

Корреляция коэффициента мощности

Для линейных нагрузок треугольник мощности представляет собой прямоугольный треугольник, показывающий взаимосвязь между рабочей, реактивной и полной мощностью. Соотношение между рабочей и полной мощностью – это PF. Значение может варьироваться от 0,0 до 1,0.

Рабочая мощность, также называемая истинной мощностью, реальной мощностью или активной мощностью, выполняет фактическую работу движения/нагрева/освещения и т. д. и измеряется в ваттах (Вт). Реактивная мощность поддерживает магнитное или электрическое поле в устройствах, таких как соленоидные катушки, обмотки двигателей, обмотки трансформаторов, конденсаторы и балласты, не выполняя реальной работы. Эта дополнительная энергия измеряется в реактивных вольт-амперах (ВАР) и иногда называется «безваттной» мощностью.