Исследование зависимости мощности и КПД источника тока от внешней нагрузки

ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИ:

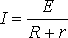, (1)

I- сила тока в цепи; Е- электродвижущая сила источника тока, включённого в цепь; R- сопротивление внешней цепи; r- внутреннее сопротивление источника тока.

МОЩНОСТЬ, ВЫДЕЛЯЕМАЯ ВО ВНЕШНЕЙ ЦЕПИ

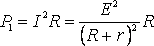. (2)

Из формулы (2) видно, что при коротком замыкании цепи (R®0) и при R®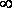эта мощность равна нулю. При всех других конечных значениях R мощность Р₁> 0. Следовательно, функция Р₁ имеет максимум. Значение R₀, соответствующее максимальной мощности, можно получить, дифференцируя Р

1 по R и приравнивая первую производную к нулю:

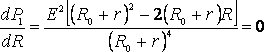. (3)

Из формулы (3), с учётом того, что R и r всегда положительны, а Е ? 0, после несложных алгебраических преобразований получим:

R₀ = r. (4)

Следовательно, мощность, выделяемая во внешней цепи, достигает наибольшего значения при сопротивлении внешней цепи равном внутреннему сопротивлению источника тока.

При этом сила тока в цепи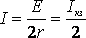

(5)

равна половине тока короткого замыкания. При этом мощность, выделяемая во внешней цепи, достигает своего максимального значения, равного

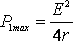. (6)

Когда источник замкнут на внешнее сопротивление, то ток протекает и внутри источника и при этом на внутреннем сопротивлении источника выделяется некоторое количество тепла. Мощность, затрачиваемая на выделение этого тепла равна

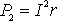
. (7)

Следовательно, полная мощность, выделяемая во всей цепи , определится формулой

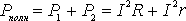= I²(R+r) = IE (8)

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ

КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ источника тока равен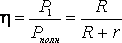

. (9)

Из формулы (8) следует, что

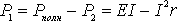, (10)

т.е. Р₁ изменяется с изменением силы тока в цепи по параболическому закону и принимает нулевые значения при I = 0 и при 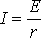. Первое значение соответствует разомкнутой цепи ( R>> r ), второе – короткому замыканию ( R<< r). Зависимость к.п.д. от силы тока в цепи с учётом формул (8), (9), (10) примет вид

(11)

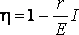
Таким образом, к.п.д. достигает наибольшего значения h =1 в случае разомкнутой цепи ( I = 0), а затем уменьшается по линейному закону, обращаясь в нуль при коротком замыкании.

Зависимость мощностей Р₁, Р_полн = EI и к.п.д. источника тока от силы тока в цепи показаны на рис.1.

Рис.1. I

₀ E/r

Из графиков видно, что получить одновременно полезную мощность и к.п.д. невозможно. Когда мощность, выделяемая на внешнем участке цепи Р₁, достигает наибольшего значения, к.п.д. в этот момент равен 50%.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ

Рис. 2.

Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.

Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку в нижней части экрана) и амперметр (кнопка там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр

, измеряющий напряжение на нагрузке.

Подключите соединительные провода. Для этого нажмите кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.

4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой

. Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашего варианта.

Таблица 1. Исходные параметры электрической цепи

Номер варианта	1	2	3	4	5	6	7	8
Е, В	10,0	9,5	9,0	8,5	8,0	8,5	9,0	9,5
r, Ом	4,8	5,7	6,6	7,5	6,4	7,3	8,2	9,1

5. Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.

6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.

7. Вычислите по формулам (2), (7), (8), (9) Р₁, Р₂, Р_полн и h для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.

8. Постройте на одном листе миллиметровой бумаге графики зависимости P₁ = f(R), P₂ = f(R), P_полн=f(R), h = f (R) и U = f(R).

9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.

Таблица 2. Результаты измерений и расчётов

R, Ом	2,0	2,5	3,0	…			20
U, В
I, А
P1, Вт
P2, ВТ
Pполн, ВТ
h

Вопросы и задания для самоконтроля

1. Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.
2. Что такое ток короткого замыкания?
3. Что такое полная мощность?
4. Как вычисляется к.п.д. источника тока?
5. Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.
6. Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?
7. К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.
8. Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.
9. Объясните явление.
10. При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.

Закон Ома для участка цепи. Где мне найти в инете такой? Бесплатно

Я вот радиоэлектронщик, но кроме формулы напряжение равно силе тока, умноженному на сопротивление ничего не «конспективится».

Закон Ома Три основные электрические величины — ток, сопротивление и напряжение — связаны между собой зависимостью, выражен¬ной законом Ома, который формулируется следующим образом: сила тока в замкнутой цепи прямо пропорциональна электродви¬жущей силе источника и обратно пропорциональна сопротивлению всей цепи. Ток в цепи возникает под действием ЭДС; чем больше ЭДС источника энергии, тем больше и сила тока в замкнутой цепи. Сопротивление цепи препятствует прохождению тока, следовательно, чем больше сопротивление цепи, тем меньше сила тока. Закон Ома может быть выражен так: I = E/R+ Ro, где R — сопротивление внешней части цепи. Ом; Ro — сопротивление внутренней части цепи, Ом; I — сила тока, А, Е — ЭДС, В. Закон Ома для участка цепи. Если участок цепи не содержит источника энергии, то положительные заряды на этом участке перемещаются из точки более высокого потенциала к точкам более низкого потенциала. Источник энергии затрачивает определенную энергию, поддерживая разность по-тенциалов между началом и концом этого участка. Эта разность потенциалов называется напряжением между началом и концом рассматриваемого участка. Ток на участке электрической цепи равен напряжению на зажимах этого участка, деленному на его сопротивление: I= U/R. где U — напряжение, В; I — сила тока, A; R — сопротивление, Ом. Сила тока в цепи измеряется амперметром (миллиамперметром) , а напряжение — вольтметром (милливольтметром) . Для включения амперметра цепь тока разрывается, и в месте разрыва концы проводов присоединяются к зажимам амперметра (рис. 2). В этом случае через амперметр проходит весь измеряе¬мый ток. Вольтметр показывает падение напряжения на данном участке. Если воль¬тметр подключить к началу внешней це¬пи — положительному полюсу источника энергии, то он покажет падение напряже¬ния во всей внешней цепи, которое будет в то же время напряжением на зажимах источников энергии. Напряжение на зажимах источника энергии равно разности между ЭДС и паде¬нием напряжения на внутреннем сопротив-лении этого источника, т. е. U == Е — IRo. Если уменьшить сопротивление внешней цепи R, то сопротивле-ние всей цепи R + Ro также уменьшится, а ток в цепи увеличит-ся. Рис. 2. Схема включе¬ния амперметра и воль¬тметра С увеличением тока падение напряжения внутри источника энергии (IRo) возрастает, так как внутреннее сопротивление Ro источника остается неизменным. Следовательно, с уменьшением сопротивления внешней цепи напряжение на зажимах источника энергии также уменьшается. При соединении зажимов источника энергии с проводником, сопротивление которого практически рав¬но нулю, ток в цепи I == E/Ro. Это выражение определяет наибольший ток, который может быть получен в цепи данного источника. Режим, при котором сопротивление внешней цепи практически равно нулю, называется коротким замыканием. Короткое замыка¬ние может возникнуть, например, из-за нарушения изоляции проводов, соединяющих приемник с источником энергии. Лишен¬ные изолирующего слоя металлические провода при взаимном соприкосновении образуют весьма малое сопротивление, которое по сравнению с сопротивлением приемника равно нулю. Для защиты электротехнической аппаратуры от токов коротко¬го замыкания применяют различные предохранительные устройст¬ва.

Чем определяется сила тока короткого замыкания батарейки?

как всегда-внутренним сопротивлением.

Ее внутренним сопротивлением…

Внутренним сопротивлением.

В основном внутренним сопротивлением.

1.При режиме холостого хода источника внешний участок электрической цепи отключён. Какое внешнее сопротивление цепи в этом случае со стороны выводов источника.

Внешняя цепь разомкнута и тока в цепи нет, вследствие чего напряжение на зажимах источника равно его ЭДС U=Е, I=0, Рист=0, Rнагр=∞

Так как нагрузка отключается от источника питания и ток в нагрузке становится равным нулю, то внешнее сопротивление равно 0.

2. Зависит ли напряжение на выводах источника электрической энергии от электрического сопротивления внешнего участка цепи.

Да, зависит. Согласно закону Ома для полной цепи, сила тока в полной цепи равна электродвижущей силе источника e, деленной на сумму внутреннего сопротивления источника r и сопротивления внешнего участка цепи R: I = e / (R + r).

Следовательно, сила тока в цепи ЗАВИСИТ от сопротивления внешнего участка цепи. Далее, согласно закону Ома для участка цепи, напряжение на зажимах источника (оно же — напряжение на концах внешнего участка) равно произведению силы тока на сопротивление внешнего участка. Таким образом, напряжение на зажимах источника зависит от электрического сопротивления внешнего участка:

U = I * R = e * R / (R + r).

3.При режиме короткого замыкания источника, напряжение на его зажимах равно нулю. Почему ток короткого замыкания достигает больших величин?

Коротким замыканием (к.з.) называют такой режим работы источника, когда его зажимы замкнуты проводником, сопротивление которого можно считать равным нулю. Практически к. з. возникает при соединении друг с другом проводов, связывающих источник с приемником, так как эти провода имеют обычно незначительное сопротивление и его можно принять равным нулю.

К. з. может происходить в результате неправильных действий персонала, обслуживающего электротехнические установки или при повреждении изоляции проводов.

При коротком замыкании ток равен:

Iк.з = E / R

Ввиду того что внутреннее сопротивление источника R обычно очень мало, проходящий через него ток возрастает до весьма больших значений (ток идет по пути наименьшего сопротивления). Напряжение же в месте к. з. становится равным нулю, т. е. электрическая энергия на участок электрической цепи, расположенный за местом к. з., поступать не будет.

Короткое замыкание является аварийным режимом, так как возникающий при этом большой ток может привести в негодность как сам источник, так и включенные в цепь приборы, аппараты и провода. Лишь для некоторых специальных генераторов, например, сварочных, короткое замыкание не представляет опасности и является рабочим режимом.

4. При анализе сложной цепи c помощью закона Кирхгофа следует ли принимать одинаковое направление обхода для всех контуров?

Правила Кирхгофа (Зако́ны Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.

а) первый закон Кирхгофа (применяется для узлов электрической цепи)

Алгебраическая сумма токов в узле электрической цепи равна нулю, или сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от узла электрической цепи.

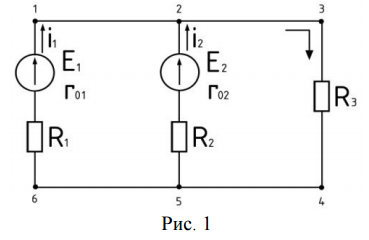
Пример: для узла 2 (Рис. 1).

I1 + I2 — I3=0

Токи, направленные к узлу имеют знак «+»; направленные от узлf имеют знак «–».

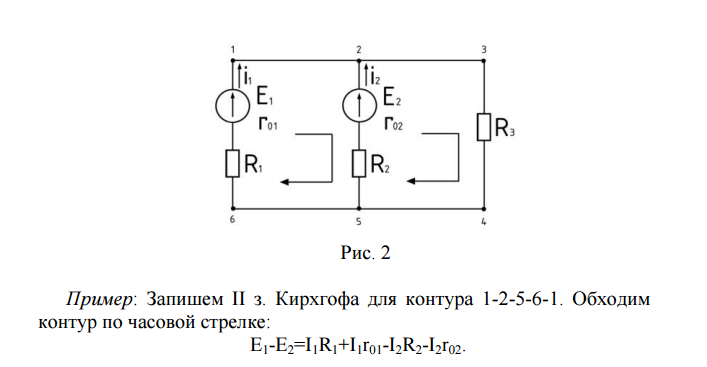
б) второй закон Кирхгофа

Алгебраическая сумма всех действующих ЭДС в любом контуре электрической цепи равна алгебраической сумме всех падений напряжения на сопротивлениях, входящих в данный контур.

Раскрытие алгебраических сумм ЭДС и падения напряжения следует производить в соответствии с правилом знаков:

1. Если направление ЭДС совпадает с условно выбранным направлением обхода по контуру, то ЭДС берут со знаком «+», если направление ЭДС не совпадает с выбранным направление обхода, то со знаком «–».

2. Если направление тока на участке цепи совпадает с выбранным направлением обхода контура, то падение напряжения на этом участке будет со знаком «+», если направление тока не совпадает с направлением обхода контура, то со знаком «–».

5. Можно ли индуктивную катушку, предназначенную для работы в цепи переменного тока, включить в цепь постоянного тока, сохранив при этом значение подведенного к ней напряжения равным номинальному?

Нельзя. Из-за влияния X_L ток катушки в цепи переменного тока меньше, чем в цепи постоянного тока. Поэтому катушки, рассчитанные на включение в цепь переменного тока, нельзя включать в цепь постоянного тока на то же напряжение(они сгорят).

Определить ток короткого замыкания источника тока, если при внешнем сопротивлении

Условие задачи:

Определить ток короткого замыкания источника тока, если при внешнем сопротивлении 50 Ом ток в цепи 0,2 А, а при сопротивлении 110 Ом ток — 0,1 А.

Задача №7.2.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(R_1=50\) Ом, \(I_1=0,2\) А, \(R_2=110\) Ом, \(I_2=0,1\) А, \(I_{кз}-?\)

Решение задачи:

Запишем три раза закон Ома для полной цепи — для случая, когда внешнее сопротивление цепи равно \(R_1\), когда внешнее сопротивление цепи равно \(R_2\), и когда в цепи течет ток короткого замыкания (то есть когда внешнее сопротивление цепи равно нулю).

\[\left\{ \begin{gathered}
{I_1} = \frac{{\rm E}}{{{R_1} + r}} \;\;\;\;(1)\hfill \\
{I_2} = \frac{{\rm E}}{{{R_2} + r}} \;\;\;\;(2)\hfill \\
{I_{кз}} = \frac{{\rm E}}{r} \hfill \;\;\;\;(3)\\
\end{gathered} \right.\]

Поделим уравнение (1) на уравнение (2), тогда получим:

\[\frac{{{I_1}}}{{{I_2}}} = \frac{{{R_2} + r}}{{{R_1} + r}}\]

Перемножим «крест-накрест»:

\[{I_1}\left( {{R_1} + r} \right) = {I_2}\left( {{R_2} + r} \right)\]

Раскроем скобки:

\[{I_1}{R_1} + {I_1}r = {I_2}{R_2} + {I_2}r\]

Все члены с \(r\) перенесем в левую сторону, остальные — в правую:

\[{I_1}r — {I_2}r = {I_2}{R_2} — {I_1}{R_1}\]

Вынесем в левой части внутреннее сопротивление \(r\) за скобки, чтобы в дальнейшем выразить его:

\[r\left( {{I_1} — {I_2}} \right) = {I_2}{R_2} — {I_1}{R_1}\]

\[r = \frac{{{I_2}{R_2} — {I_1}{R_1}}}{{{I_1} — {I_2}}}\;\;\;\;(4)\]

Из формулы (3) видно, что для расчета тока короткого замыкания нам нужно еще знать ЭДС источника \(\rm E\). Его можно выразить из формул (1) или (2):

\[{\rm E} = {I_1}\left( {{R_1} + r} \right)\;\;\;\;(5)\]

В итоге, сначала по формуле (4) произведем расчет внутреннего сопротивления, далее по формуле (5) найдем значение ЭДС, а потом уже по формуле (3) найдем искомый ток короткого замыкания.

\[r = \frac{{0,1 \cdot 110 — 0,2 \cdot 50}}{{0,2 — 0,1}} = 10\;Ом\]

\[{\rm E} = 0,2 \cdot \left( {50 + 10} \right) = 12\;В\]

\[{I_{кз}} = \frac{{12}}{{10}} = 1,2\;А = 1200\;мА\]

Ответ: 1200 мА.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.