Чему равен момент пары сил: Пара сил, момент пары сил в технической механике с примерами — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Пара сил с примерами решения и образцами выполнения

Содержание:

Теория пар сил
Силы, направленные в одну сторону
Силы направлены в противоположные стороны и различные по модулю
Пара сил и ее момент
Эквивалентность пары сил
Добавление пар сил
Условия равновесия пар сил
Момент силы относительно точки на оси. Момент пары сил
Момент силы относительно точки
Теорема о моменте равнодействующей системы сходящихся сил
Момент сил относительно оси
Момент пары сил и его свойства

Парой сил называется система двух равных по модулю, противоположных по направлению параллельных сил.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Теория пар сил

Пару сил в механике рассматривают как одно из основных понятий наряду с понятием силы.

Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны. Пара сил не составляет системы сил, эквивалентной нулю. Пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.

Пара сил, действующая на твердое тело, характеризуется, прежде всего, плоскостью действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.

Силы, направленные в одну сторону

Пусть в абсолютно твердого тела в точках А и В приложены две параллельные силы и направленные в одну сторону (рис. 4.1). Найдем их равнодействующую. Для этого в точках

А и В к телу приложим две равные по величине и противоположные по направлению силы и, действующих по прямой АВ.

Поскольку , то согласно первой аксиомой статики , а согласно второй аксиомой .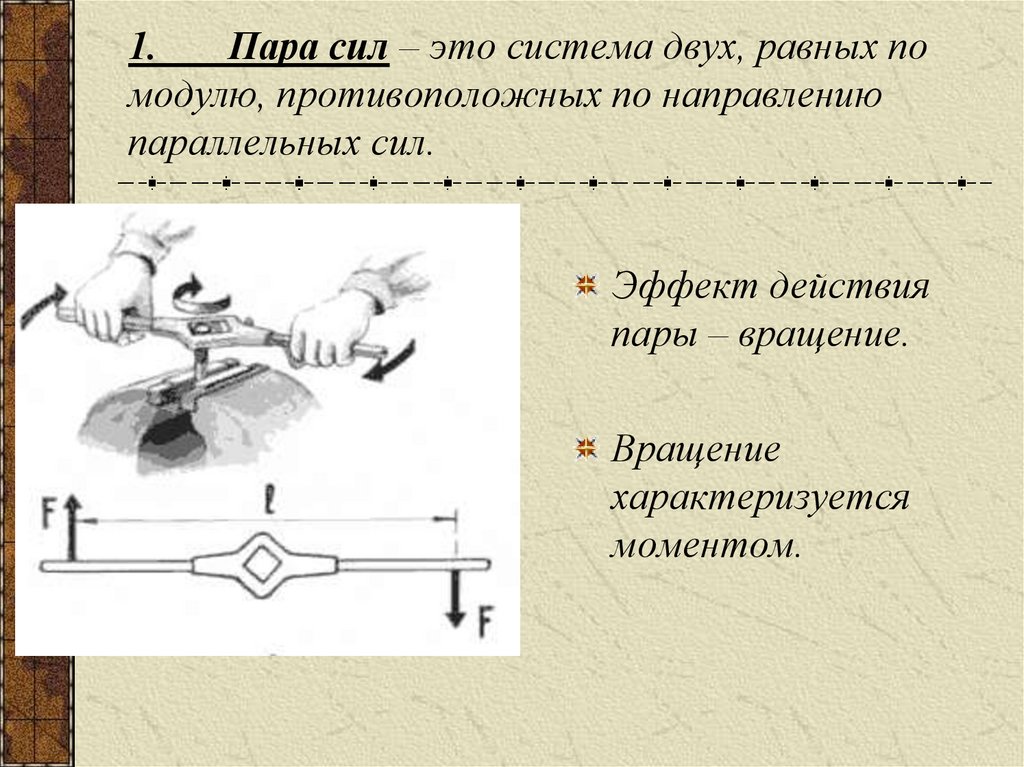 Добавляя попарно силы и , и , используя аксиому параллелограмма сил, получим:

то есть

Итак,

Силы и не является параллельными лежат в одной плоскости, поэтому их линии
действия имеют точку пересечения А. Перенесем силы и вдоль их линий действия в эту точку. Получим силы

Сила — скользящий вектор, поэтому Разложим теперь силу на составляющие , а силу — на составляющие так, чтобы:

Получим:

Поскольку силы и направлены по одной прямой в одну сторону, то их равнодействующая cпрямована по той же прямой в том же направлении и ее величина равна сумме этих сил, то есть Учитывая (4.1), запишем Перенесем силу вдоль линии ее действия в точку С отрезка АВ. Получим силу Это означает, что сила — равнодействующая сил

Найдем точку приложения равнодействующей сил и . С сходства одинаково заштрихованных треугольников запишем:

Поскольку, то, откуда, учитывая свойство пропорции, имеем

Итак, равнодействующая двух параллельных сил, направленных в одну сторону, параллельна этих сил, направленная в ту же сторону, что и составляющие силы; модуль
равнодействующей равна сумме модулей составляющих сил, а линия ее действия разделяет расстояние между точками приложения этих сил внутри на части, обратно
пропорциональны величинам этих сил.

Из изложенного следует, что произвольную силу можно разложить на две параллельные силы. Если то

Силы направлены в противоположные стороны и различные по модулю

Пусть параллельные силы и направлены в разные стороны и (рис. 4.2).

Найдем равнодействующую сил и Для этого разложим силу на две параллельные силы: , прилагаемую в точке В, принимая и , прилагаемую в точке С. Сила является равнодействующей сил и поэтому

Согласно (4.3), откуда

Поскольку Но поэтому Следовательно, сила — равнодействующая сил Из формулы (4.4) получим

Равнодействующая двух параллельных, разных по модулю, противоположно направленных сил параллельная им и направлена в сторону большей силы; модуль равнодействующей равна разности модулей составляющих сил. Линия действия равнодействующей проходит через точку, лежащую вне отрезка АВ со стороны большей силы и разделяет расстояние между точками приложения сил внешне на отрезки, обратно пропорциональны величинам этих сил.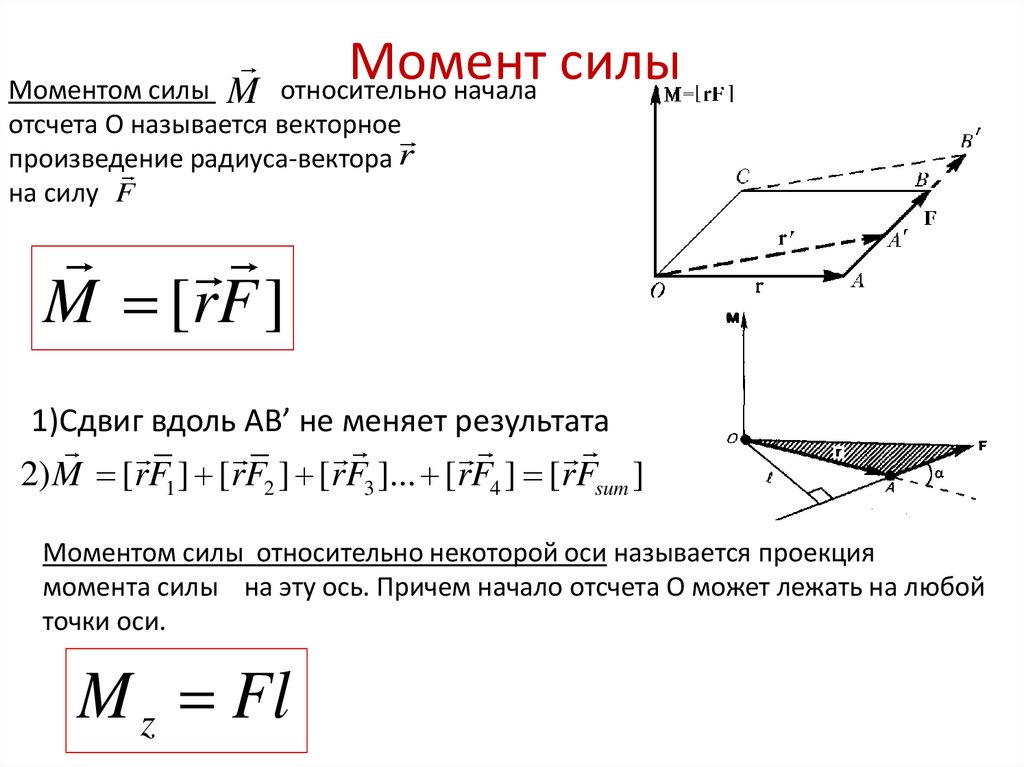

Пара сил и ее момент

Система двух равных по модулю, параллельных, противоположно направленных сил, линии действия которых не совпадают, называется парой сил.

Пусть к некоторому абсолютно твердого тела приложена пара сил (Рис. 4.3, а).
Согласно определению пары сил:

Элементами пары есть силы, составляющие пару, плечо пары, плоскость действия пары.

Плечо пары — это кратчайшее расстояние между линиями действия сил пары, то есть длина перпендикуляра h, опущенного из любой точки линии действия одной из сил пары на линию действия второй силы (рис. 4.3, а). Поскольку сила -скользящий вектор, то силы в паре всегда можно разместить так, чтобы расстояние АВ между точками их приложения было плечом пары (Рис. 4.3, б).

Плоскость действия пары — это плоскость, в которой размещены силы пара. Она единственная, поскольку через две параллельные линии можно провести только одну
плоскость.

Как будет показано в § 5.3, пара сил не имеет равнодействующей.

Пара сил не является системой уравновешенных сил, ибо в первой аксиомой статики две равные по модулю и противоположны по направлению силы будут уравновешенной системой сил только тогда, когда имеют общую линию действия. Силы, составляющих пару, не имеют общей линии действия.

Пара сил, действующая на тело, пытается вращать его. По мере вращательного действия силы в статике, как известно, является момент. Следовательно, и действие пары сил на тело должна характеризоваться моментом. Докажем это с помощью следующей теоремы.

Теорема 4.1. Векторная сумма моментов сил пары относительно произвольного центра
(Точки) в пространстве является величиной постоянной для данной пары.

Доказательство. Пусть задано пару сил плечо которой h (рис. 4.4). Поскольку
действие пары на тело характеризуется вращательным эффектом, найдем сумму моментов сил пары относительно центра О, произвольно расположенного в пространстве.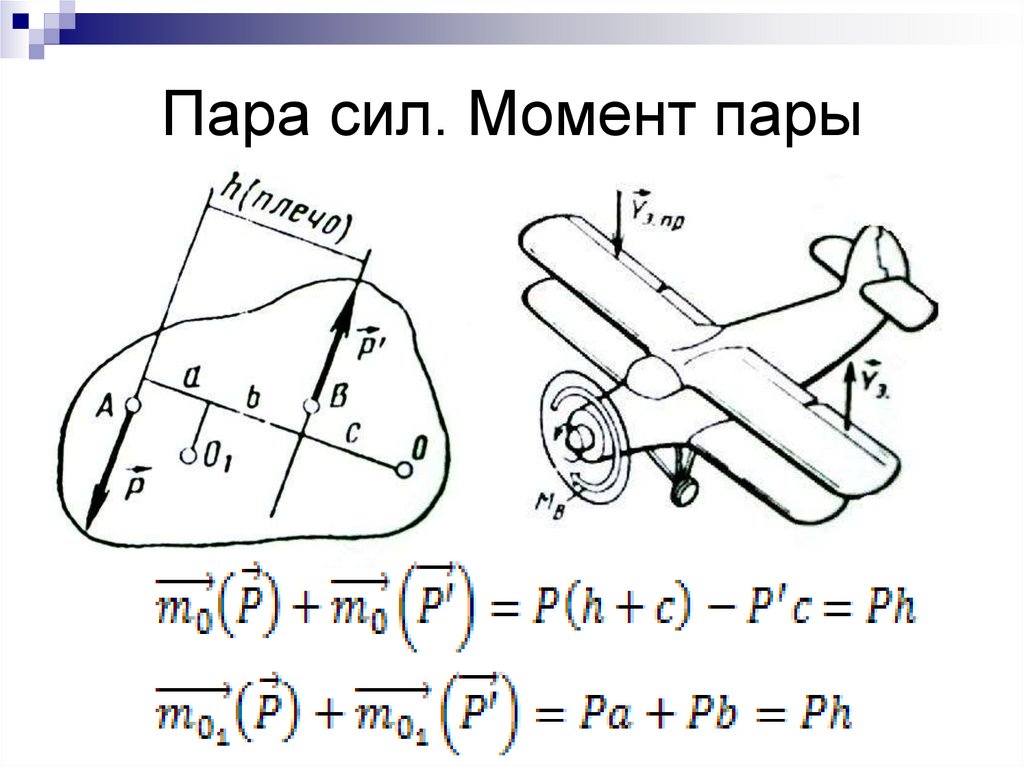

Получим:

где — радиусы-векторы точек приложения сил и относительно центра О. С учетом формул (4.7) равенство (4.8) запишется так:

Здесь — радиус-вектор точки А, в которой приложено силу пары, относительно центра В, а потому Итак,

Известно, что вектор перпендикулярен плоскости векторов и , а его модуль

Аналогично, учитывая, что , получим

где вектор перпендикулярен плоскости векторов и , а модуль этого вектора

Следовательно, сумма моментов сил пары относительно произвольного центра в пространстве не зависит от выбора этого центра и равен моменту одной из сил пары относительно точки приложения другой силы. Теорема доказана.

Эта сумма моментов характеризует вращательное действие пары сил на тело. Назовем ее вектор-моментом пары сил. Обозначим вектор-момент пары сил или просто. Итак, вектор-момент пары сил равен векторному моменту одной силы пары относительно точки приложения другой силы данной пары, то есть

С доказательства теоремы следует, что момент пары сил является вектором. Определим его величину и направление.

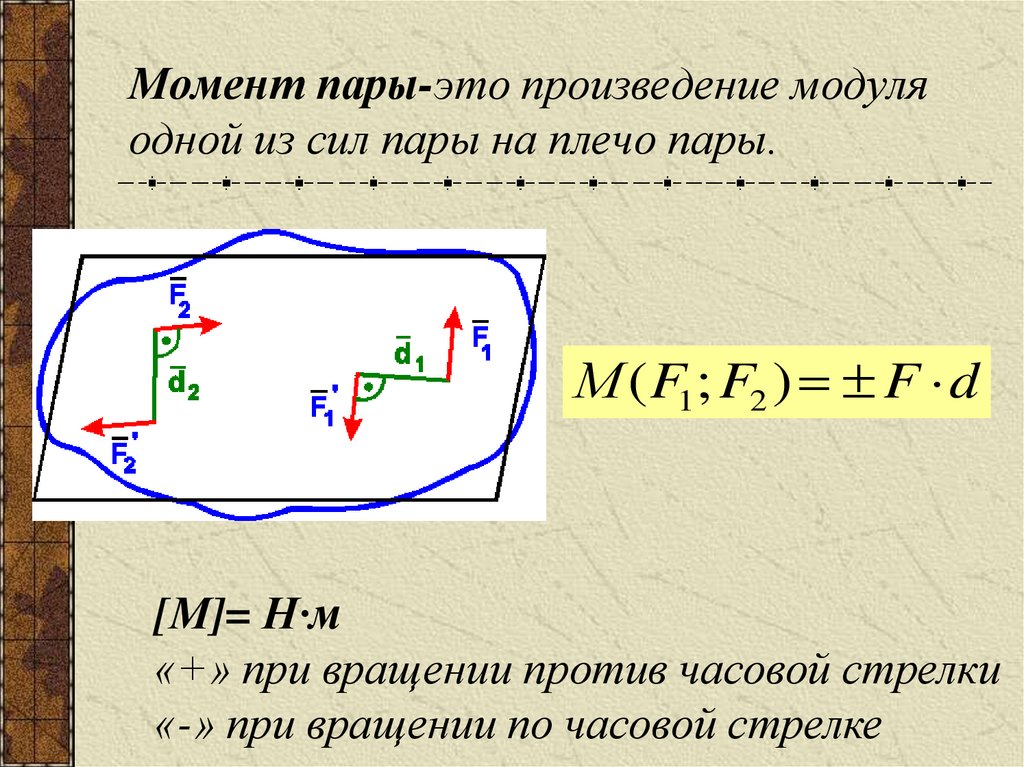
Величина момента пары по формулам (4.10) — (4.14) равна произведения величины одной из сил пары на плечо пары:

Вектор-момент пары сил направляется перпендикулярно к плоскости действия пары так, чтобы с его конца было видно попытки пары сил вращать тело против часовой стрелки (рис. 4.4).

Если на тело действует система пары сил, расположенных в одной плоскости, то вектор-моменты всех пар сил системы перпендикулярны этой плоскости. Итак, вектор-моменты такой системы пар является системой параллельных векторов, для составления которых достаточно знать их величины и знаки. Поэтому целесообразно ввести понятие алгебраического момента пары сил.

Алгебраическим моментом пары сил называется взятый со знаком «+» или «-» произведение одной из сил пары на плечо пары:

Алгебраический момент пары сил считаем положительным, если пара сил пытается вращать тело против часовой стрелки (рис. 4.5, а) и отрицательным, если пара сил пытается вращать тело по часовой стрелке (рис. 4.5, б). Алгебраические моменты пар сил на рисунках показывают дуговыми стрелками.

Эквивалентность пары сил

Рассмотрим теоремы, из которых вытекают основные свойства пары сил, которые предоставят нам возможность выполнять определенные действия над ними.

Теорема 4.2. Действие пары сил на тело не изменится при произвольном переносе этой пары в плоскости ее действия.

Доказательство. Пусть к некоторому телу приложена пара сил плечо которой АВ = h и расположенной в плоскости П (рис. 4.6). Возьмем произвольную точку С в плоскости П и отложим от нее под произвольным углом отрезок СD = h (рис. 4.7). В точках С и D приложим к телу две системы уравновешенных сили размещенных в плоскости П, линии действия которых параллельны.

Силы выбираем так, чтобы

Согласно второй аксиомой статики

Перенесем силы и силы вдоль линий их действия в точки пересечения (рис.

4.7). Пользуясь аксиомой параллелограмма сил, заменим системы сил и из них равнодействующимии

Учитывая формулы (4.7) и (4.17), получим

Поскольку фигура является ромбом, то — биссектриса углов
и Согласно с равенством (4.19) параллелограммы, построенные на силах и — также ромбы. Поэтому их диагонали и является биссектрисами указанных углов, потому что две стороны каждого из этих ромбов совпадают со сторонами ромба Отсюда следует, что силы и имеют одну линию действия, которая совпадает с диагональю Учитывая формулу (4.20) и первую аксиому статики, делаем вывод, что силы и уравновешиваются. Итак, система сил и ее можно отбросить, то есть

Это означает согласно формуле (4.18), заданной паре сил эквивалентна паре сил .

Покажем, что величина и направление векторов-моментов пар сил и совпадают. Действительно, величина момента заданной пары сил а знак (как видно из рис. 4.6) — положительный. Величина момента эквивалентной пары с учетом равенств (4. 17).

Из рис. 4.8 видно, что знак момента также положительный, то естьСледовательно, можно считать, что полученная пара сил не что иное, как пара сил которая перенесена из исходного положения ее плеча АВ в положение плеча СD, и этот перенос не изменил кинематического состояния тела. Теорема доказана.

Теорема 4.3. Действие пары сил на твердое тело не изменится, если перенести эту пару в плоскость, параллельную плоскости ее действия.

Доказательство. Пусть на некоторое твердое тело действует пара сил с плечом АВ = h, которая размещена в плоскости (рис. 4.9, а).

Выберем в теле плоскость параллельную плоскости . В плоскости возьмем точки С и D так, чтобы и

Приложим к телу в точках С и D две системы уравновешенных сил линии действия которых параллельны. Эти силы размещены в плоскости и удовлетворяют условию (4. 17), а следовательно,

Проведем отрезки АС и ВD, точкой пересечения которых есть точка А.

Поскольку и то ABCD — параллелограмм с диагоналями АС и BD, а потому

Добавим попарно силы и , и Они параллельны и равны по модулю, поэтому их равнодействующая и будут приложены в точке О пересечения диагоналей параллелограмма АВСD (рис. 4.9, б).

Равнодействующая силы и равны по модулю и направлены в противоположные
стороны. Итак, система сил уравновешена, то есть

и можно записать

Сравнивая соотношения (4.21) и (4.22), получим Это означает, что воздействие на тело пар сил и одинакова. Легко показать, что вектор-моменты этих пар сил равны. Действительно, учитывая формулу (4.17), имеем:

Вектор-моменты и направлены перпендикулярно плоскостям и в одно и ту же сторону. Таким образом,, а следовательно, .
Теорема доказана.

Теорема 4. 4. Действие пары на тело не изменится, если изменить силы и плечо пары, оставляя неизменным ее вектор-момент.

Доказательство. Пусть к телу приложена пара сил с плечом АВ = h, размещена в плоскости П (рис. 4.10).

Приложим к телу в точках А и В две силы , действующих по прямой АВ. Это означает, что , а

За аксиомой параллелограмма сил найдем равнодействующие систем сил и

Учитывая, что и получим

Итак, . Это означает, что линии действия сил и параллельные, то есть
силы , образуют пару сил, которая лежит в плоскости П. Итак, учитывая формулу (4.23), получим

Плечо новой пары Величина момента заданной пары сил, а полученной пары Из рис. 4.10
видно, что поскольку находим , а с получаем Тогда или Очевидно, что знаки моментов и также совпадают. Итак, изменив силу и плечо заданной пары сил, оставив неизменным ее вектор-момент, получили эквивалентную пару сил.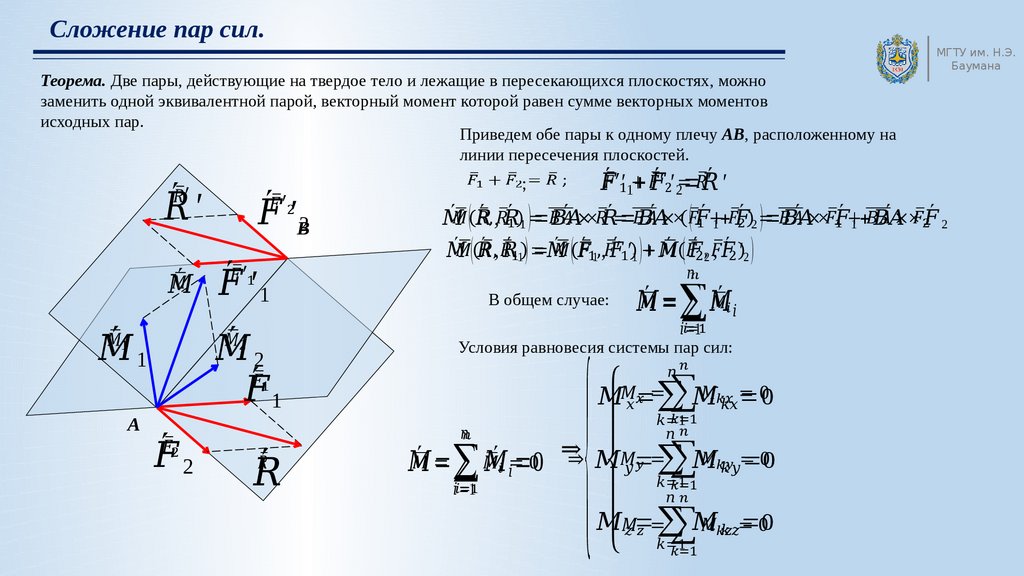 Теорема доказана.

Из доказанных теорем следует:
1) пары эквивалентны, если равны их векторы-моменты;
2) вектор-момент пары сил является вектором свободным. Это означает, что его можно приложить в произвольной точке твердого тела.
Сформулированы три теоремы можно объединить в одну теорему: пары сил являются эквивалентными, если равны их векторы-моменты.
Из всего сказанного можно сделать вывод, что вектор-момент пары сил является полной характеристикой статическому воздействию пары на твердое тело. Поэтому действия над парами сил можно заменить эквивалентными операциями над их векторами-моментами.

Добавление пар сил

1. Геометрическое определение момента результирующей пары сил
Установим правило сложения пар сил, лежащих в плоскостях, которые пересекаются. Это правило вытекает из следующей теоремы.

Теорема 4.5. Две пары сил, которые лежат в плоскостях, пересекающихся эквивалентны одной паре, вектор-момент которой равен геометрической сумме векторов-моментов данных пар.

Доказательство. Пусть пары сил и размещены соответственно в плоскостях П1 и П2, пересекающихся (рис. 4.11).

Пользуясь теоремой 4.4, приведем обе пары к плечу АВ, размещенного на линии пересечения плоскостей П1 и П2 , то есть

При этом должны выполняться равенства

Добавим согласно аксиоме параллелограмма силы, приложенные в точках А и В. Получим и . Принимая во внимание, что и будем иметь . Итак, система пари эквивалентна одной паре Найдем вектор — момент этой пары:

Теорема доказана.

Аналогично можно добавить n пар сил в пространстве. В результате получим одну пару сил, вектор-момент которой равен векторной сумме векторивмоментив составляющих пар сил, а именно:

2. Аналитическое определение момента результирующей пары сил
Спроектируем равенство (4.25) на оси прямоугольной декартовой системы координат и используем теорему о проекции суммарного вектора на ось.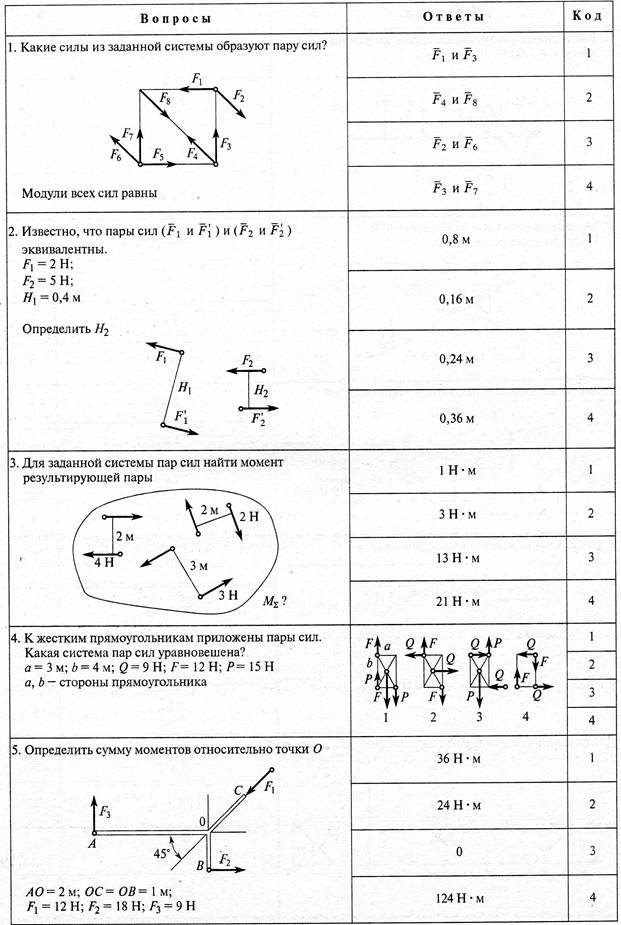 Получим проекции момента результирующей пары сил на оси координат:

где , — проекции вектора момента результирующей пары на соответствующие оси координат; , — проекции вектора момента
и-й пары на оси выбранной системы координат.

Тогда величина вектора момента пары

а направление его найдем по формулам:

Известно (§ 4.2), что вектор-моменты пар, размещенных в одной плоскости, есть коллинеарными и поэтому добавляются алгебраически. Итак, момент результирующей
пары плоской системы пар равна сумме алгебраических моментов составляющих пар

Условия равновесия пар сил

1. Геометрическое условие равновесия пространственной системы пар сил

Пусть на тело действует n пар сил, произвольно расположенных в пространстве, вектори-моменты которых равны

В § 4.4 было доказано, что такая система пар сил эквивалентна одной паре сил, вектор-момент которой определяется формулой (4. 25). очевидно, что тело под действием системы пар сил остается в равновесии, если вектор-момент результирующей пары будет равняться нулю

Это условие равновесия, учитывая формулу (4.25), запишем в виде

Формула (4.29) является геометрической условием равновесия пространственной системы пар, которую можно сформулировать так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда вектор-момент результирующей пары или геометрическая сумма векторов-моментов составляющих пар будет равняться нулю.

2. Аналитические условия равновесия пространственной системы пар сил

Из условия (4.29), учитывая формулу (4.26), получаем, что в случае равновесия пространственной системы пар сил то есть

Формулы (4.30) являются аналитическими условиями равновесия пространственной системы пар сил, которые формулируются так: пространственная система пар сил будет
находиться в равновесии тогда и только тогда, когда алгебраические суммы проекций
векторов-моментов составляющих пар на три взаимно перпендикулярные оси координат будут равны нулю.

3. Условие равновесия плоской системы пар сил

Условие равновесия плоской системы пар сил получаем из равенства (4.28).
Плоская система пар сил будет находиться в равновесии тогда и только тогда, когда сумма алгебраических моментов составляющих пар сил будет равняться нулю:

Условие равновесия плоской системы пар можно получить также из условий равновесия (4.30).

Действительно, пусть система пар сил размещена в координатной плоскости . Тогда вектор-моменты всех пар сил данной системы перпендикулярны плоскости , то есть или . Отсюда получим такое условие равновесия

Поскольку , то условия равновесия (4.32) и (4.31) эквивалентны для системы пар сил, расположенных в плоскости .

Момент силы относительно точки на оси. Момент пары сил

Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны, приложенных к телу в двух разных точках.

Момент силы относительно точки

Моментом силы относительно точки (Центра) (рис. 2.1) называется вектор, который равен векторному произведению радиуса- вектора , проведенного из центра в точку приложения силы, на вектор

(2.1)

Модуль этого векторного произведения:

(2.2)

Опустим перпендикуляр из точки на линию действия силы . Длину этого перпендикуляра назовем плечом силы относительно точки . Тогда (2.2) запишем в виде:

(2.3)

Итак, момент силы относительно центра численно равен произведению модуля силы на
плечо, и направленный перпендикулярно к плоскости, проходящей через точку и линию действия силы, в ту сторону, откуда «вращение» тела под действием силы вокруг точки (или самый короткий поворот вектора направлению вектора ) видит наблюдатель, находящийся на конце вектора-момента, таким, что происходит против часовой стрелки (рис 2. 2).

Очевидно, момент силы относительно точки имеет все свойства векторного произведения. Из формулы (2.1) можно найти проекции вектора на координатные оси. Как известно из векторной алгебры,
(2.4)

Раскрывая этот определитель по элементам первой строки и раскладывая вектор на составляющие на осях координат, получим

(2.5)

Сравнивая левую и правую части равенства (2.5), имеем

(2.6)

Модуль, и направление момента силы относительно точки можно определить еще и так:

Заметим, что формулы (2.6) легко получить, пользуясь правилом циклической
перестановки индексов.
По определению момента силы относительно точки имеем:
1) если переместить силу вдоль линии ее действия, то момент силы относительно точки не изменится;
2) момент силы относительно точки всегда равен нулю, когда линия действия силы проходит через эту точку (в этом случае плече равно нулю),
3) момент силы относительно точки численно равен удвоенной площади треугольника (Рис. 2.3), построенного на силе и центре момента (О).

Теорема о моменте равнодействующей системы сходящихся сил

Теорема Вариньона. Момент равнодействующей сходящейся системы сил относительно произвольного центра равен векторной (геометрической) сумме моментов составляющих сил относительно того самого центра:

(2.8)

Доказательство. Пусть в точке А пересекаются линии действия системы сходящихся сил
(рис. 2.4, а). Обозначим через радиус-вектор, проведенный из точки О в точку А. Равнодействующую заданной системы найдем, построив многоугольник сил
(рис. 2.4, б). Тогда по определению момента силы относительно точки О
получим:
(2. 9)

что и требовалось доказать.

Если силы и точка О размещены в одной плоскости, то их моменты перпендикулярны этой плоскости и лежат на одной прямой. Поэтому момент равнодействующей такой системы сил равен алгебраической сумме моментов составляющих сил относительно этой
точки.

Момент сил относительно оси

Моментом силы относительно оси называется проекция на эту ось момента силы относительно любой точки, лежащей на этой оси (рис. 2.5).
Из этого определения следует, что моменты сил относительно координатных осей вычисляются по формулам (2.6). Эти формулы, в частности, показывают, что момент силы
относительно оси не зависит от выбора точки на оси.

При решении конкретных задач моменты сил относительно осей удобно вычислять более наглядным способом (рис. 2.6) по следующему правилу.
1. Проводим произвольную плоскость перпендикулярную оси и находим точку
пересечения этой плоскости с осью.
2. Проектируем силу на указанную плоскость.
3. Вычисляем момент проекции , силы на эту плоскость относительно точки О:

При этом момент силы относительно оси считается положительным, если наблюдатель видит со стороны положительного направления оси , что сила пытается повернуть тело вокруг оси против часовой стрелки.
Как видно из рис. 2.6, численное значение момента силы относительно оси можно выразить удвоенной площадью треугольника который лежит в плоскости

Из определения момента силы относительно оси следует, что он равен нулю, если линия действия силы и ось лежат в одной плоскости.
Пример 1. Сила приложена в точке А с координатами (2; 3,4) и составляет
с осью угол , с осью — угол , а с осью — угол . При этом
Вычислить момент этой силы относительно оси
Решение.

По формулам (2.6), есть

для определения предварительно нужно найти
Известно, что откуда

или

Если то Тогда,

Момент пары сил и его свойства

Парой сил называется система двух равных по величине сил . параллельных между собой, что направлены в противоположные стороны вдоль несовпадающих линий действия и приложенные к одному телу (рис. 2.7, а). Плоскость называется плоскостью действия пары сил, или плоскостью пары. Плечом пары называется самое короткое расстояние между линиями действия сил пары.

Определим, чему равна сумма моментов сил, составляющих пар относительно произвольной точки.

Пусть О — произвольная точка пространства (Рис. 2.7, б), a — силы, составляющие пару и приложенные соответственно в точках А и В. Пусть Из определения момента силы относительно точки имеем:

(2.10)

Полученная векторная сумма не зависит от положение точки , в отношении которой вычисляются моменты, а определяется лишь точками приложения сил, составляющих пару.
Векторное произведение называется моментом пары сил и обозначается
Модуль момента пары сил равен произведению модуля одной из сил пары на
плечо пары.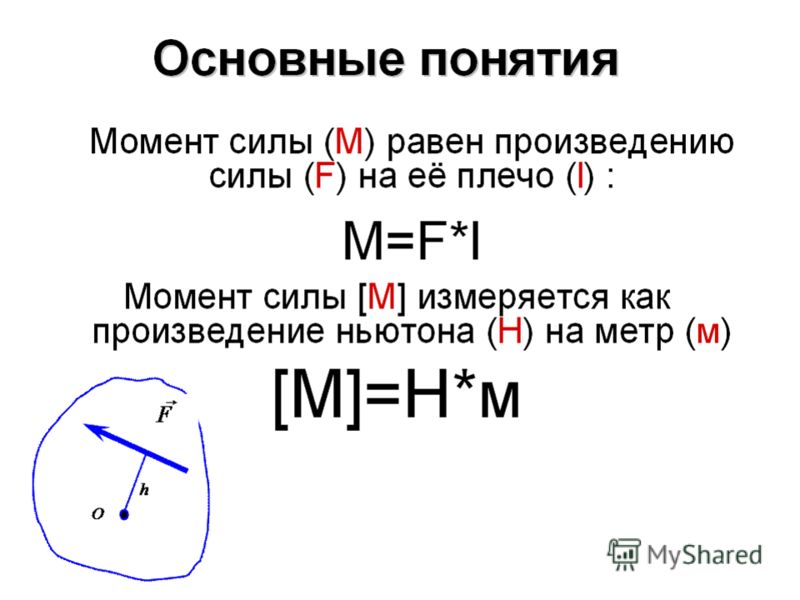
Как видим, момент пары направленный перпендикулярно к плоскости действия пары в ту
сторону, откуда «вращение» пары происходит против часовой стрелки.

Итак, момент пары сил — вектор свободный и математически определен в виде

(2.11)

Ниже показано, что момент пары полностью определяет статическое действие пары сил на твердое тело, то есть полной характеристикой механического воздействия пары сил на это тело. Из определения момента пары сил и аксиомы I о двух силах следует, что пара сил является уравновешенной системой (система сил, эквивалентная нулю) тогда и только тогда, когда момент пары равна нулю. Другие свойства пары сил определяются следующими теоремами.

Теорема 1. Не меняя действия пары сил на твердое тело, его можно переносить и произвольно вращать в плоскости действия, изменяя величину силы, входящей в нее, и длину плеча так, чтобы момент пары оставался неизменным.

Доказательство. Пусть задано пару сил и с плечом . В плоскости действия этой пары выберем произвольный отрезок (рис. 2.8, а). В точках с и d этого отрезка
на линиях, перпендикулярные к нему, приложим соответственно две системы сил
и каждая из которых эквивалентна нулю. Причем Продолжим линии действия сил и к пересечению их с линиями действия и сил Полученные точки пересечения обозначим через
Перенесем теперь силы и а также силы и как скользящие векторы в точки и Пусть — равнодействующая сходящихся сил и , приложенных в точке, а равнодействующая сходящихся сил и приложенных в точке Понятно, что система сил эквивалентна нулю, поскольку по построению силы и равны по величине, направлены в противоположные стороны и приложенные к концам диагонали параллелограмма Итак, систему можно отбросить, не нарушая состояния тела. Таким образом, пару сил которая осталась, эквивалентна заданной паре сил

Покажем, что при указанном перемещении пары сил можно изменять величину
силы, входящей в нее, и длину плеча, о чем говорится в теореме. Для этого рассмотрим исходную пару сил (рис. 2.8, б).
Приложим к точкам а и b систему сил эквивалентную нулю. Пусть и
равнодействующие сходящихся систему сил и , приложенных соответственно в точках а и Ь. Тогда система сил эквивалентна системе сил а следовательно, паре сил Момент пары сил , равен а момент пары сил равна . Легко убедиться, что алгебраические значения этих моментов одинаковы. Кроме того, из рис. 2.8, а видно, что направления вращений, создаваемых парами, совпадают. Итак, моменты пар сил и равны между собой. Теорема доказана.

Теорема 2. Две пары сил, которые лежат в одной или параллельных плоскостях и имеют одинаковые по величине, но противоположные по направлению моменты, составляют систему пар сил, эквивалентную нулю.

Доказательство. Пусть в плоскости заданы две пары сил и , в которых одинаковые алгебраические значения моментов, но противоположные направления вращений, создаваемых этими парами. По теореме 1, преобразуем пару сил так, чтобы эти пары имели общие точки приложения сил, которые составляют пары (рис. 2.9). Из рисунка и условия видим, что мы получили систему сил эквивалентную нулю. Итак, система с двух пар и эквивалентна нулю. Моменты этих пар соответственно равны:

(2.12)

С другой стороны, сумма моментов всех сил, которые составляют эти пары, определяется выражением:

(2.13)

которое является суммой моментов составляющих пар, равных нулю. Следовательно, эта система двух пар сил эквивалентна нулю.

Поскольку момент пары сил — вектор свободный, то доказанные теоремы справедливы также для случая пар сил, лежащих в параллельных плоскостях.
Из доказанных теорем следует вывод об эквивалентности двух пар сил, имеющих геометрически одинаковые моменты.
Кроме того, эти теоремы позволяют установить правило составления пар сил, которые лежат не только в параллельных плоскостях, но и в тех, которые пересекаются.
Так, если задан систему n пар то она может быть заменена одной, эквивалентной заданной системе пар — результирующей парой. Причем момент результирующей пары равен векторной (геометрической) сумме моментов составляющих пар:

(2.14)

Отметим, что пару сил нельзя заменить одной силой, которая была бы эквивалентна по действию на твердое тело двум равным по величиной, параллельным и противоположно направленным силам. Действительно, если предположить, что пара сил эквивалентна некоторой силе , то через их эквивалентность момент пары сил и момент силы относительно произвольной точки, должны быть одинаковыми. Выбрав эту точку на линии действия силы , мы приходим к противоречию, поскольку момент пары сил остается без изменений, он не зависит от выбора центра, а момент силы равен нулю. Этим доказывается приведенное утверждение.

Итак, пара сил, действующих на твердое тело, образует новый самостоятельный элемент статики, который вместе с силой составляет важное понятия механики. Основные свойства этого элемента и основные преобразования, которым он подлежит, вполне устанавливаются доказанными теоремами о парах.
Эти свойства и превращения будут выглядеть так:

1) пару сил можно переносить в плоскости ее действия, в том числе и вращать на любой угол;
2) пару сил можно переносить в любую плоскость, параллельную плоскости действия этой пары;
3) можно изменять силы, образующие пару и плечо, не меняя момента пары;
4) несколько пар сил, произвольно расположенных в пространстве, можно заменить одной парой, момент которой равен геометрической сумме моментов составляющих пар.
Из изложенного в главах 1 и 2 приходим к такому важному выводу: механическое влияние в статике характеризуется тремя типами векторов: силой — скользящим вектором, моментом силы относительно точки — приложенным вектором и парой сил — свободным вектором.

Услуги по теоретической механике:

Заказать теоретическую механику
Помощь по теоретической механике
Заказать контрольную работу по теоретической механике

Учебные лекции:

Статика
Система сходящихся сил
Момент силы
Произвольная система сил
Плоская произвольная система сил
Трение
Расчет ферм
Расчет усилий в стержнях фермы
Пространственная система сил
Произвольная пространственная система сил
Плоская система сходящихся сил
Пространственная система сходящихся сил
Равновесие тела под действием пространственной системы сил
Естественный способ задания движения точки
Центр параллельных сил
Параллельные силы
Система произвольно расположенных сил
Сосредоточенные силы и распределенные нагрузки
Кинематика
Кинематика твердого тела
Движения твердого тела
Динамика материальной точки
Динамика механической системы
Динамика плоского движения твердого тела
Динамика относительного движения материальной точки
Динамика твердого тела
Кинематика простейших движений твердого тела
Общее уравнение динамики
Работа и мощность силы
Обратная задача динамики
Поступательное и вращательное движение твердого тела
Плоскопараллельное (плоское) движение твёрдого тела
Сферическое движение твёрдого тела
Движение свободного твердого тела
Сложное движение твердого тела
Сложное движение точки
Плоское движение тела
Статика твердого тела
Равновесие составной конструкции
Равновесие с учетом сил трения
Центр масс
Колебания материальной точки
Относительное движение материальной точки
Статические инварианты
Дифференциальные уравнения движения точки под действием центральной силы и их анализ
Динамика системы материальных точек
Общие теоремы динамики
Теорема об изменении кинетической энергии
Теорема о конечном перемещении плоской фигуры
Потенциальное силовое поле
Метод кинетостатики
Вращения твердого тела вокруг неподвижной точки

Техническая механика — Тема1.

3. Пара сил и момент силы

§1. Момент силы относительно центра (или точки)

Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее моментом.

Рассмотрим силу , приложенную в точке А твердого тела (рис. 1). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы

, называется плечом силы относительно центра О. Так как точку приложения силы можно произвольно перемещать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть:

1) от модуля силы F и длины плеча h;

2) от положения плоскости поворота ОАВ, проходящей через центр О и силу F;

3) от направления поворота к этой плоскости.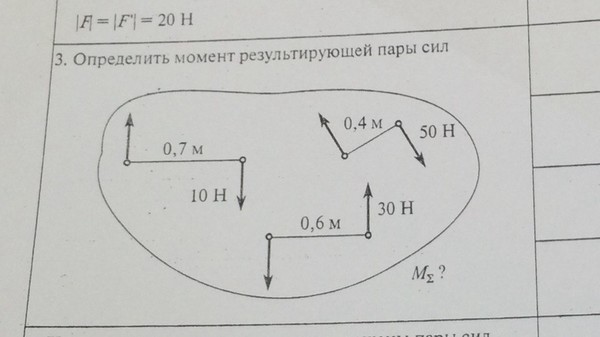

Рис.1. Сила, приложенная к телу

Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.

Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Момент силы относительно центра О будем обозначать M.

Следовательно, М= ±Fh. Единицы измерения в системе СИ : Н·м,

Правило знаков для момента силы: момент пары сил будем считать положительным, если пара стремиться повернуть тело по направлению хода часовой стрелки, и отрицательным, если пара сил стремится вращать тело против хода часовой стрелки.

Отметим следующие свойства момента силы:

1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.

2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).

3) Момент силы численно выражается удвоенной площадью треугольника ОАВ (рис. 1)

M= ± 2пл.ΔOAB

§2.Теорема Вариньона о моменте равнодействующей

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.

Рис.2. Сходящаяся система сил

Рассмотрим систему сил , сходящихся в точке А (рис. 2). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие выражения моментов М(), М(), … .

По формуле М() = +2пл.ΔОАВ_1. Но, как видно из рисунка, где F_1x — проекция силы на ось Ох; следовательно М() = ОА · F_1x

Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил , через , где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

или .

§3. Пара сил. Момент пары

Парой сил (или просто парой) называются две силы, равные по величине, параллельные и направленные в противоположные стороны (рис. 3). Очевидно, и

Рис. 3. Пара сил

Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:

Расстояние a между линиями действия сил называется плечом пары.

Если пара вращает тело против часовой стрелки, момент её считается отрицательным (как на рис. 3), если по часовой стрелке – положительным.

Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.

Вектор момента пары направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть оттуда, увидим вращение тела против часовой стрелки (рис. 4).

Нетрудно доказать, что вектор момента пары – есть вектор этого векторного произведения (рис. 4). И заметим, что он равен вектору момента силы относительно точки А, точки приложения второй силы:

Рис.4. Вектор момента пары сил

Видео-урок «Пара сил и ее свойства»

§4. Свойства пар сил

1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.

2) Найдём сумму моментов сил оставляющих пару, относительно какой-либо точки О (рис.5).

Рис.5. Пара сил

Покажем радиусы-векторы точек А₁ и А₂ и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О

Но

. Поэтому .

Но .

Значит .

Момент пары сил относительно любой точки равен моменту этой пары.

Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, равный моменту этой пары

3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.

4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F₁=F₂=5 H и плече а = 4 см момент пары m = 20 H∙см. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Н∙см и действие пары на тело не изменится.

Все эти свойства можно объединить и, как следствие, сделать вывод, что пары с одинаковым вектором момента и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны.

Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m (рис. 6). Или, если это пространственная конструкция, показывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары

– свободный вектор. Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.

Рис.6. Эквивалентные пары сил

И ещё одно дополнительное замечание. Так как момент пары равен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары

на эту ось: , где – угол между вектором и осью z.

Видео-уроки «Эквивалентность пар»

§5. Сложение пар

Пусть даны две пары с моментами m₁ и m₂, расположенные в пересекающихся плоскостях (рис. 7).

Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а образующих вторую пару:

Эти пары показаны на рис. 7, где . И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересечения плоскостей.

Рис.7. Пары сил с моментами m₁ и m₂

Сложив силы, приложенные к точкам А и В, построением параллелограммов, получим их равнодействующие . Так как , то эти силы и будут образовывать пару, момент которой

, где – радиус-вектор точки В, совпадающий с АВ.

Так как

, то момент полученной пары .

Следовательно, в результате сложения пар, расположенных в пересекающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоскостях, получим пару с моментом .

Конечно, эта результирующая пара будет располагаться в плоскости перпендикулярной вектору .

Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие равновесия пар =0.

Это является необходимым и достаточным условием равновесия систем пар.

Если пары расположены в одной плоскости, векторы моментов их будут параллельны.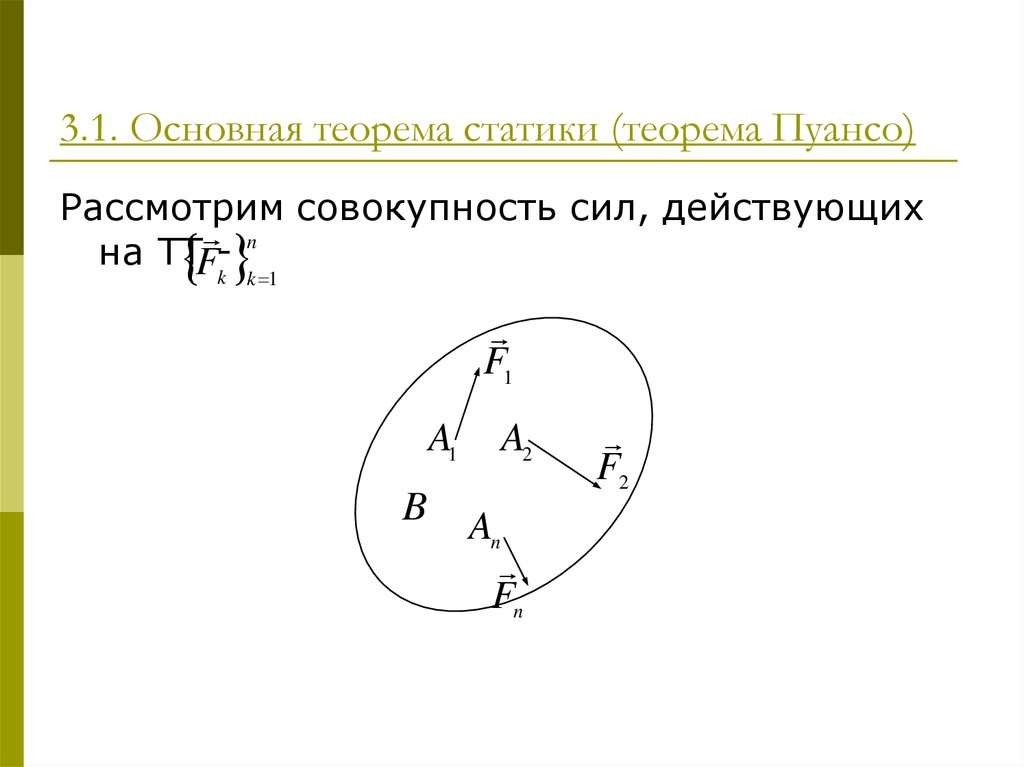 И момент результирующей пары можно определить как алгебраическую сумму моментов пар.

Рис.8. Моменты пар сил, расположенные в одной плоскости

Например, пары, показанные на рис.8, расположены в одной плоскости и моменты их:

m₁=2 Hсм , m₂=5 Hсм, m₃=3 Hсм. Пары уравновешиваются, потому что алгебраическая сумма их моментов равна нулю:

Вопросы для самопроверки:

— Что называется моментом силы относительно центра на плоскости?

— Какая система сил называется парой?

— Можно ли заменить действие пары сил на тело одной силой?

— Что такое момент пары?

— Какая плоскость называется плоскостью действия пары?

— Какие пары называются эквивалентными?

— Что называется плечом пары?

— Запишите векторную и скалярную зависимости между элементами пары.

— Почему пара сил не имеет равнодействующей?

— Имеет ли пара сил равнодействующую?

— Каким образом можно уравновесить действие на тело пары сил?

— Что такое момент пары сил?

— Изменятся ли моменты пар сил, если положения сил, показанные на рис. а, изменить на положения, показанные на рис. б?

— Какие пары называются эквивалентными?

— Эквивалентны ли пары сил, изображенные на рисунке?

— Каким образом производится сложение пар сил?

— Сформулируйте условие равновесия пар сил.

— Чем характеризуется действие пары сил на твердое тело?

— Как направлен вектор момента пары сил?

— Как определяются моменты пар сил, лежащих в одной плоскости?

— Какие преобразования пары сил не изменяют ее действия на твердое тело?

— Сформулируйте теоремы об эквивалентности пар.

— Что называется результирующей парой?

— Запишите формулу для определения результирующей системы пар.

— Назовите условия равновесия плоской системы пар.

— Приведите векторную запись условия равновесия произвольной системы пар.

— Будет ли изменяться момент силы относительно точки, если, не меняя направления, переносить силу вдоль линии ее действия?

— На тело действуют две силы F₁ = 40 Н и F₂ = 50 Н, как показано на рисунке (а = 0,5 м, b = 0,8 м, ). Какая из сил создает больший момент относительно точки О?

— Что такое главный вектор и главный момент плоской системы сил?

— Как аналитически найти главный вектор и главный момент данной плоской системы сил?

— В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?

— Сформулируйте теорему Вариньона.

— Приведите векторную запись теоремы Вариньона.

— Чему равен главный вектор системы сил?

— Чему равен главный момент системы сил при приведении ее к точке?

— Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?

Теория пар сил в теоретической механике

Содержание:

Теория пар:

Пару сил в механике рассматривают как одно из основных понятий наряду, с понятием силы.

Парой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (рис. 24).

Пара сил не составляет системы сил, эквивалентной нулю.

Рис. 24

Рис. 25

Известно, что под действием пары сил свободное твердое тело выходит из равновесия. Обычно пару сил прилагают к телу, которое должно вращаться, например к маховику вентиля при его закрывании и открывании (рис. 25). Поэтому пару сил нельзя заменить одной силой и, следовательно, она не имеет равнодействующей, а является такой системой сил, упростить которую нельзя. Каждая из сил, входящих в состав пары сил, имеет свойства обычных сил.

Рис. 26

Пара сил, действующая на твердое тело, характеризуется прежде всего плоскостью действия, аналогично тому, как сила характеризуется линией действия. Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.

Для количественной характеристики действия пары сил на твердое тело и указания направления, в котором пара сил стремится вращать тело в плоскости действия, введем понятие алгебраического момента пары сил.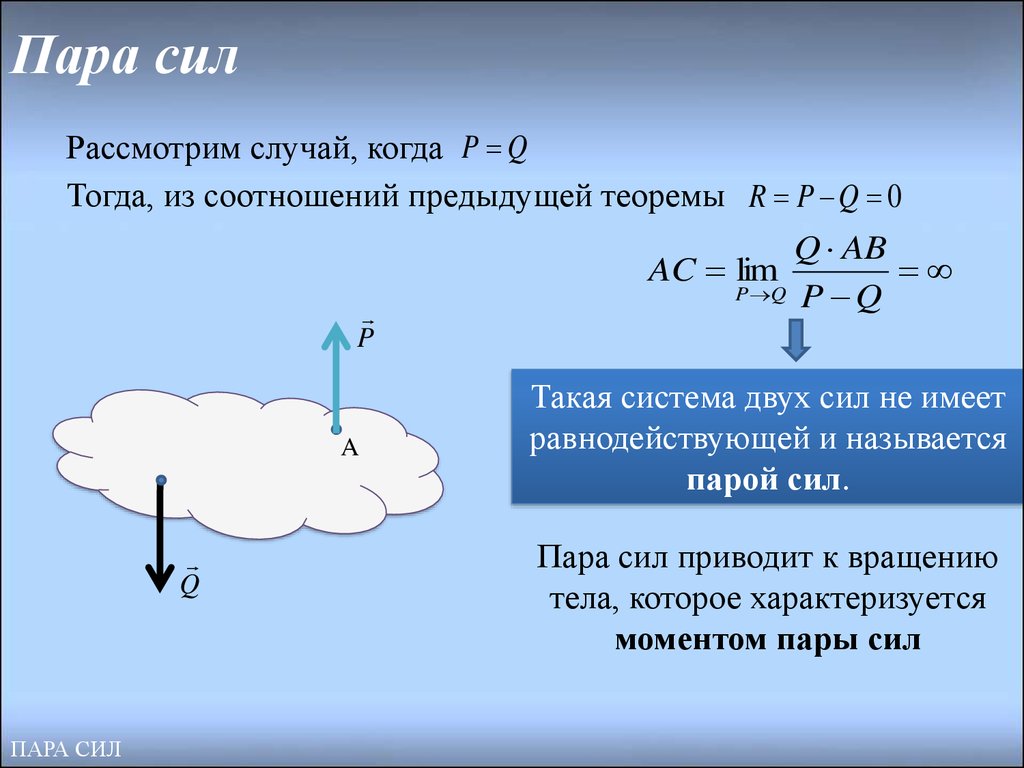

Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил.

Плечом пары сил называют кратчайшее расстояние между линиями действия сил пары (рис. 26).

Алгебраический момент пары обозначим или . Согласно определению,

Алгебраический момент пары сил выражается в тех же единицах, что и алгебраический момент силы относительно точки.

Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрелке.

Алгебраический момент пары сил не зависит от переноса сил пары вдоль своих линий действия и может быть равен нулю, если линии действия сил пары совпадают, т. е. в случае двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой. Такая система двух сил, как известно, эквивалентна нулю. Алгебраический момент пары сил численно равен площади параллелограмма, построенной на силах пары:

Теорема об эквивалентности двух пар сил, расположенных в одной плоскости

Докажем, что пары сил, расположенные в одной плоскости, по своему действию на тело отличаются одна от другой только алгебраическими моментами.

Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Докажем теперь следующую теорему об эквивалентности двух пар сил: пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент. Иначе: две пары сил, расположенные в одной плоскости, эквивалентны, если они имеют одинаковые алгебраические моменты.

Пусть на твердое тело действует пара сил с алгебраическим моментом (рис. 27). Перенесем силу в точку , а силу — в точку , проведем через точки и две любые параллельные прямые, пересекающие линии действия сил пары и лежащие, следовательно, в плоскости действия заданной пары сил. Соединив прямой точки и , разложим силы в точке и в точке по правилу параллелограмма, как указано на рис. 27. Тогда

Так как силы и образуют пару сил, то

и, следовательно,

Итак,

так как

следовательно, эту систему двух сил можно отбросить.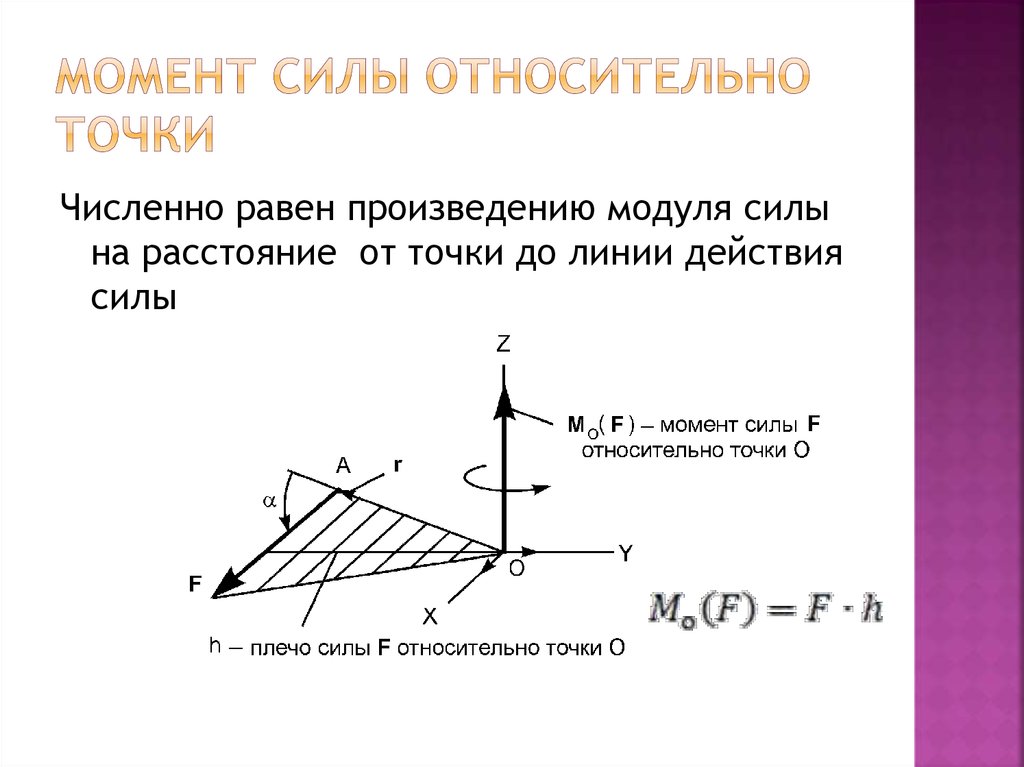

Рис. 27

Таким образом, заданную пару сил заменим другой парой сил . Докажем, что алгебраические моменты у этих пар сил одинаковы. Направление вращения у них одно и то же. Имеем

Но так как эти треугольники имеют общее основание и равные высоты (их вершины расположены на общей прямой, параллельной основанию).

Таким образом, теорема доказана и можно сделать следующие выводы:

а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;
б) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Эти операции над парами сил не изменяют их действия на твердое тело.

Теорема о переносе пары сил в параллельную плоскость

Действие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость (рис. 28).

Для доказательства этой теоремы к паре сил в точках и , где перпендикуляры, опущенные из точек и плоскости , пересекаются параллельной ей плоскостью , приложим две системы сил и , каждая из которых эквивалентна нулю, т. е.

Выберем силы и так, чтобы они удовлетворяли условиям

Рис. 28

Сложим две равные и параллельные силы и . Их равнодействующая параллельна этим силам, равна их сумме и приложена посередине отрезка в точке , так как складываются равные параллельные силы. Равнодействующая двух равных параллельных сил и тоже равна их сумме, параллельна им и приложена на середине отрезка , т. е. в точке , где пересекаются диагонали прямоугольника . Так как , то система сил эквивалентна нулю и ее можно отбросить.

Таким образом, пара сил эквивалентна такой же паре сил , но лежащей в другой, параллельной плоскости. Пару сил, не изменяя ее действия на твердое тело, можно перенести из одной плоскости в другую, параллельную ей.

Векторный момент пары сил

Пару сил, приложенную к твердому телу, можно охарактеризовать плоскостью действия, моментом пары сил и направлением вращения пары. Все эти элементы пары сил в пространстве можно выразить одной величиной — векторным моментом пары сил.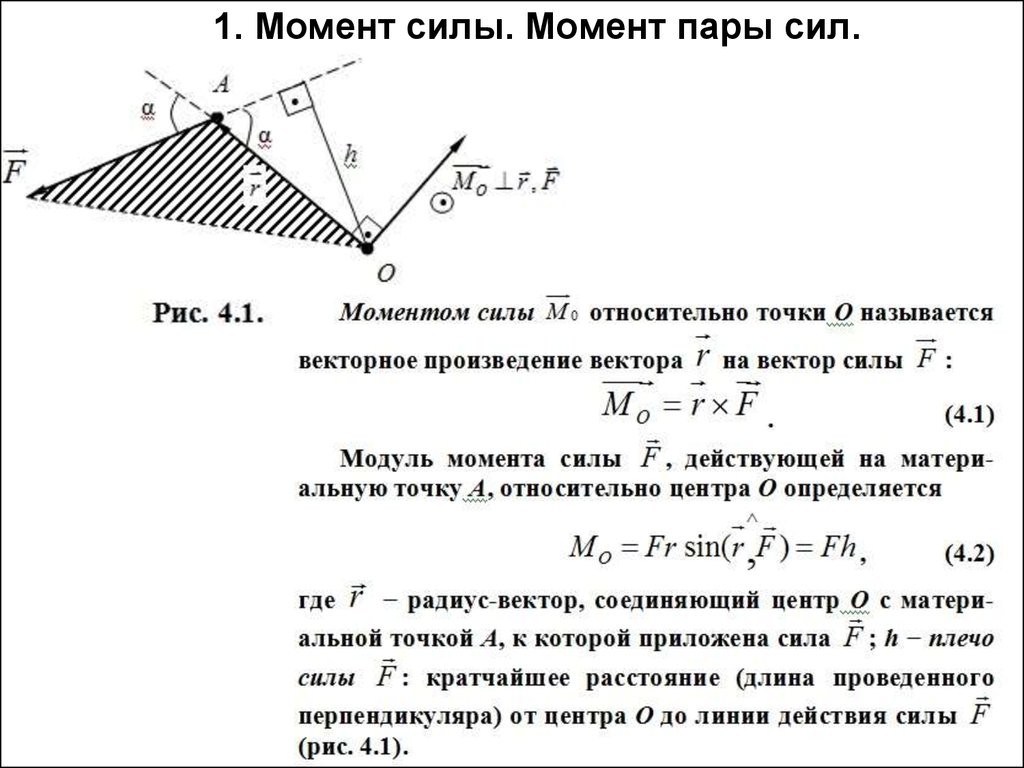

Векторным моментом пары сил назовем вектор, числовое значение которого равно произведению силы пары на ее плечо. Векторный момент пары сил направлен перпендикулярно плоскости действия пары сил так, чтобы с его направления можно было видеть стремление пары сил вращать тело против часовой стрелки. Векторный момент пары сил условимся временно прикладывать посередине отрезка, соединяющего точки приложения сил пары (рис. 29). Его можно прикладывать также, как будет доказано ниже, в любой точке тела, _на которое действует пара сил. Векторный момент пары сил обозначим или .

Согласно определению, числовое значение векторного момента пары сил совпадает с модулем алгебраического момента пары сил и, следовательно,

где — плечо пары сил.

Векторный момент пары сил численно выражается площадью параллелограмма, построенного на силах пары:

Отметим простейшие свойства векторного момента пары сил: его числовое значение не зависит от переноса сил пары вдоль своих линий действия, и он может быть равен нулю, если одна из сторон параллелограмма превратится в точку, т. е. плечо пары или сила пары становится равной нулю.

Векторный момент пары сил можно выразить в виде векторного произведения двух векторов:

Действительно,

но

и, следовательно,

что совпадает с модулем векторного момента пары сил.

Направления векторных произведений и перпендикулярны плоскости, где лежат сомножители векторных произведений, а следовательно, и плоскости действия пары сил. Они совпадают с направлением векторного момента пары сил .

Рис. 29

Эквивалентность пар сил

Сформулируем условия эквивалентности двух пар сил, используя наиболее общую характеристику пары сил — ее векторный момент.

Известно, что пару сил можно как угодно поворачивать и переносить в плоскости ее действия; действие пары сил на твердое тело не изменяется, если алгебраический момент пары сил остается таким же. Следовательно, векторный момент пары сил можно переносить параллельно самому себе в любую точку твердого тела, лежащую в плоскости действия пары сил. Так как к тому же пару сил можно переносить в параллельную плоскость, то векторный момент пары сил можно переносить параллельно самому себе в любую точку тела, не изменяя действия пары сил на твердое тело. Поэтому векторный момент пары сил, действующей на твердое тело, есть свободный вектор, т. е. он характеризуется только модулем и направлением, а точкой приложения у него может быть любая точка тела; следовательно, векторный момент пары сил не обязательно прикладывать посередине отрезка, соединяющего точки приложения сил пары.

Итак, две пары сил, действующие на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению векторные моменты.

Теорема о сумме моментов сил пары

Сумма векторных моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора точки и равна векторному моменту этой пары сил, т. е. для пары сил

где — любая точка (рис. 30).

Эту теорему докажем, вычисляя левую часть равенства (3):

так как для пары сил

Но

и не зависит от выбора точки ; следовательно,

что на основании формулы (2) совпадает с векторным моментом пары сил . Таким образом,

Взяв за точку последовательно точки и , по формуле (3) имеем

т. е. векторный момент пары сил равен векторному моменту одной из сил пары относительно точки приложения другой силы пары.

Эта теорема имеет важное значение при решении задач, когда надо вычислять сумму моментов сил пары относительно какой-либо точки. Для этого достаточно взять момент пары сил, что справедливо для любой точки.

Если моментная точка выбирается в плоскости действия сил пары как частный случай, справедлива теорема о сумме алгебраических моментов сил пары: сумма алгебраических моментов сил, входящих в состав пары сил, относительно точки, лежащей в плоскости действия пары сил, равна алгебраическому моменту пары сил и, следовательно, не зависит от выбора моментной точки, т. е.

Выбирая и за моментные точки, лежащие на линиях действия сил пары, получаем

т. е. алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки, лежащей на линии действия другой силы этой пары.

Рис. 30

Сложение пар сил

Рассмотрим случай, когда пары сил не лежат в одной или параллельных плоскостях, а расположены в пересекающихся плоскостях. Докажем, что две пары сил, действующие на одно и то же тело и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, векторный Момент которой равен сумме векторных моментов заданных пар сил.

Рис. 31

Пусть имеются две пары сил и (рис.31), лежащие в пересекающихся плоскостях. Эти пары сил можно получить из пар сил, как угодно расположенных в пересекающихся плоскостях, путем параллельного переноса, поворота в плоскости действия и одновременного изменения плеч и сил пар. Сложим силы в точках и по правилу параллелограмма. После сложения получим две силы и :

R = Fi F2′> R’ = F\+F’2.

Силы и составляют пару сил, так как они приложены в разных точках и как равнодействующие равных, но противоположных сил, образующих пары сил.

Итак, при сложении двух пар сил, лежащих в пересекающихся плоскостях, получается эквивалентная пара сил. Обозначим векторный момент пары сил . Тогда на основании формул (4) и (7)

Учитывая, что

где и — векторные моменты заданных пар сил и , имеем

т. е. векторный момент эквивалентной пары сил равен сумме векторных моментов заданных пар.

Заказать решение задач по теоретической механике

Таким образом, чтобы сложить две пары сил, лежащие в пересекающихся плоскостях, надо сложить их векторные моменты по правилу параллелограмма в какой-либо точке тела, например в точке (рис. 31). Сложение пар сил, лежащих в одной плоскости или параллельных плоскостях, есть частный случай сложения пар сил в пересекающихся плоскостях, так как в этом случае их векторные моменты параллельны и, следовательно, векторное сложение перейдет в алгебраическое.

Последовательно применяя правило параллелограмма ко всем векторным моментам пар сил, можно любое количество пар сил в общем случае заменить одной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил:

Если это сложение выполнять графически, особенно когда векторные моменты пар сил находятся в одной плоскости, то векторный момент эквивалентной пары сил изобразится замыкающей векторного многоугольника, построенного из векторных моментов заданных пар сил.

Для пар сил, расположенных в одной плоскости, теорема об их сложении формулируется так: пары сил, действующие на твердое тело и расположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил, т. е.

Так же складываются пары сил, расположенные в параллельных плоскостях, так как их предварительно можно перенести в одну плоскость.

Рис. 32

Пример 1.

Определить векторный момент пары сил, которая получается при сложении двух пар сил с моментами и , действующих на одно и то же твердое тело. Пары сил расположены в пересекающихся плоскостях, двугранный угол между которыми равен .

Решение. Складываем по правилу параллелограмма векторные моменты заданных пар сил. Для модуля векторного момента эквивалентной пары сил имеем

так как угол между и равен двугранному углу между плоскостями действия пар сил.

Пример 2.

Пары сил с моментами и противоположного направления вращения находятся в параллельных плоскостях. Пара, имеющая момент , расположена в перпендикулярной плоскости (рис. 32). Определить момент эквивалентной пары сил.

Решение. Сложим сначала алгебраически моменты пар сил, расположенных в параллельных плоскостях. Получим пару сил с моментом , так как моменты пар сил имеют противоположные знаки. Пару сил с моментом сложим с парой сил, имеющей момент . Так как угол между и прямой, то момент эквивалентной пары

Условия равновесия пар сил

Если на твердое тело действуют пары сил, как угодно расположенные в пространстве, то эти пары сил можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил, т. е.

Векторный момент геометрически изображается замыкающей векторного многоугольника, построенного на векторных моментах заданных пар сил.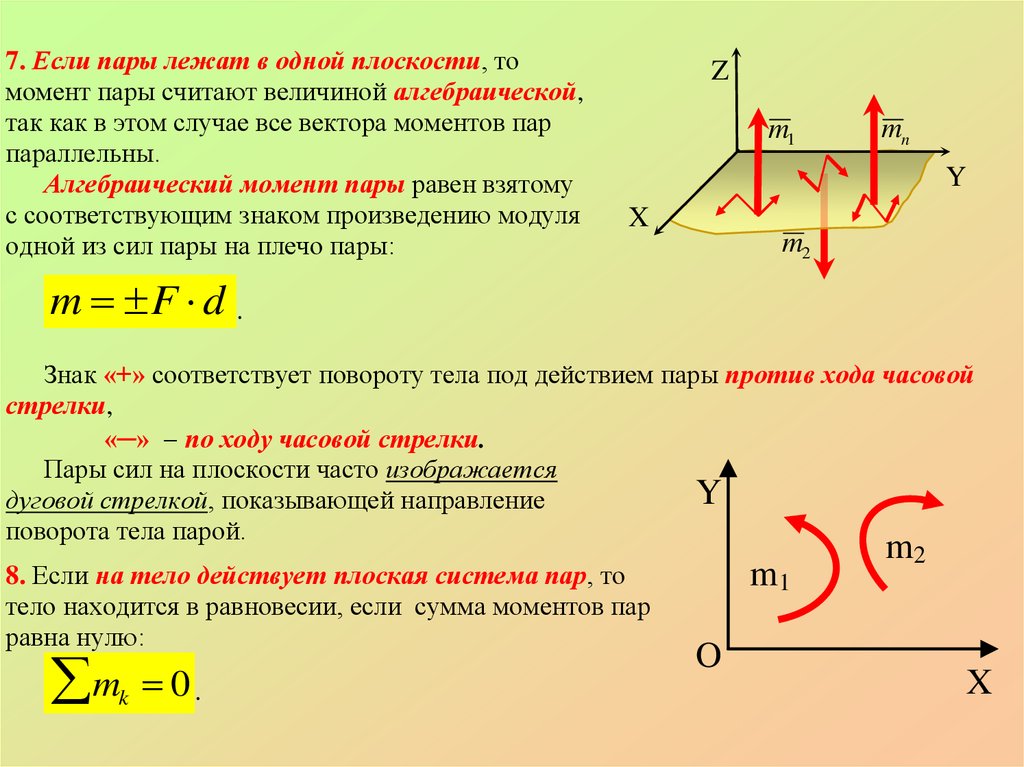

Для равновесия пар сил, действующих на твердое тело, необходимо и достаточно, чтобы модуль векторного момента эквивалентной пары сил был равен нулю или чтобы векторный многоугольник, построенный на векторных моментах заданных пар сил, был замкнут.

Итак, . Отсюда

Таким образом, для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторных моментов пар сил на каждую из трех координатных осей была равна нулю.

В общем случае пары сил можно уравновесить только парой сил и нельзя уравновесить одной силой или какой-либо другой системой сил, отличной от пары сил.

В том случае, когда пары сил действуют на твердое тело, находясь в одной плоскости, их можно заменить одной эквивалентной парой сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил:

Для равновесия таких пар сил необходимо и достаточно, чтобы алгебраический момент эквивалентной им пары сил был равен нулю, т. е. для равновесия пар сил, действующих на твердое тело в одной плоскости, необходимо и достаточно, чтобы сумма алгебраических моментов этих пар сил была равна нулю.

Если на твердое тело действуют только пары сил, лежащие в одной плоскости, то реакции опор, уравновешивающие заданные пары сил, составляют пару сил. Например, если одной из двух опор тела в его точке является катковая опора (рис. 33), а другой — неподвижный шарнир в точке , то направление реакции в шарнире противоположно направлению реакции в точке , так как эти реакции составляют пару сил. Реакция катковой опоры перпендикулярна плоскости опоры катков и направлена вверх; следовательно, направлена параллельно вниз.

Величины этих реакций равны. Их можно найти приравняв момент пары сил опорных реакций сумме алгебраических моментов пар сил, действующих на тело. Таким образом,

Рис. 33

Теория пар, расположенных в одной плоскости

При сложении двух параллельных сил и , направленных в разные стороны (рис.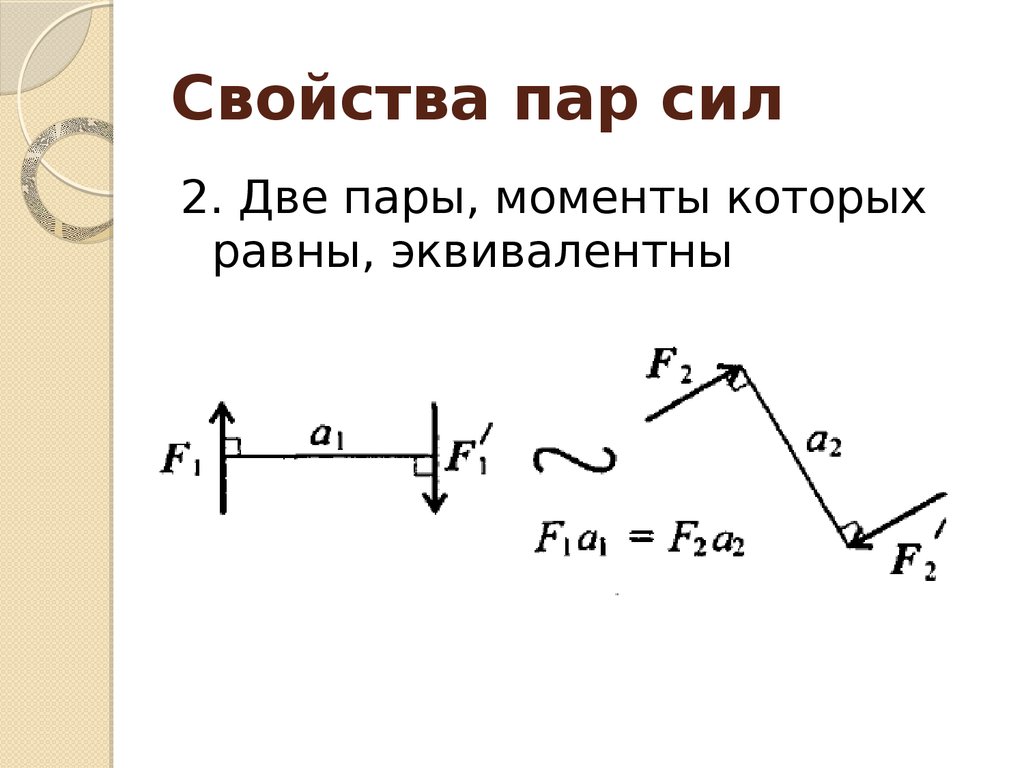 35), может оказаться, что ; в этом случае равнодействующая таких сил а ее точка приложения С, определяемая одним из равенств:

находится в бесконечности.

Поэтому силы и не могут быть заменены одной равнодействующей силой. Такая система двух равных параллельных сил Р и —Р, направленных в противоположные стороны, называется парой сил (рис. 37). Расстояние р между линиями действия сил Р и —Р называется плечом пары, а произведение одной из сил пары на плечо — моментом пары, который равен:

где знак плюс берется, если пара поворачивает плоскость чертежа по направлению против часовой стрелки, а знак минус — по часовой стрелке. Будем изображать пару так, чтобы начало каждой из сил совпадало с концами плеча пары (рис. 38).

Рис. 37. Рис. 38.

Пары сил имеют следующие свойства:

Пару сил нельзя заменить равнодействующей силой, а следовательно, и уравновесить силой; действие пары определяется ее моментом.
Равновесие тела не нарушается при переносе пары в любое положение в ее плоскости.

Дана пара с плечом АВ (рис. 39). Пусть повернуто плечо пары АС. Прикладывая к точкам А и С четыре равные и взаимно уравновешивающиеся силы , перпендикулярные к АС, находим равнодействующие и сил и , а также и .

Рис. 39.

Равнодействующие Р и Р’ равны между собой и направлены по одной прямой, так как делят пополам углы соответствующих ромбов. На основании изложенного заключаем, что силы и , а также и попарно уравновешиваются. Удаляя их, поручаем пару с плечом АС, эквивалентную заданной паре. Этим мы доказали, что пару можно повернуть на любой угол. Отсюда делаем вывод, что пару можно также перенести в ее плоскости в любое положение, так как перенос пары можно осуществить рядом ее поворотов.

3. При изменении величин сил и длин плеч двух пар эти пары остаются статически эквивалентными, если их момент при этом сохраняет свою величину и знак.

Пусть дана пара с плечом АВ (рис. 40). Разлагаем силу на две силы и из которых приложена к точке А, a — к неизвестной пока точке С на прямой АВ. Так как и , то силы и , приложенные в точке A, заменяем силой . Отсюда следует, что пару мы заменили парой , эквивалентной данной, так как из равенств и заключаем, что моменты указанных пар равны между собой. Следовательно, две пары, лежащие в одной плоскости, эквивалентны, если они имеют равные моменты и одинаковое направление вращения.

Рис. 40.

4. Для пар, расположенных в равнодействующей пары равен алгебраической сумме моментов пар составляющих.

Рис. 41.

Если имеются, например, три пары (рис. 41) с неодинаковыми плечами, то, задавшись плечом р, одинаковым для всех пар, получаем силы пар, получаем силы пар равными .

Совместив затем плечи всех пар, получаем одну пару с силами . Момент этой пары равен:

Вообще, если имеется пар, то можем написать:

где —момент равнодействующей пары;

— моменты составляющих пар.

5. Пары, взаимно уравновешиваются, если алгебраическая сумма моментов их равна нулю.

Это следует из того, что при сложении сил в точках А и В (рис. 41) сумма их может оказаться равной нулю, а потому и момент равнодействующей пары также будет равен нулю.

Полагая в уравнении (32) , получим условие равновесия пар на плоскости:

Задача с решением

На свободную жесткую систему ABCD (рис.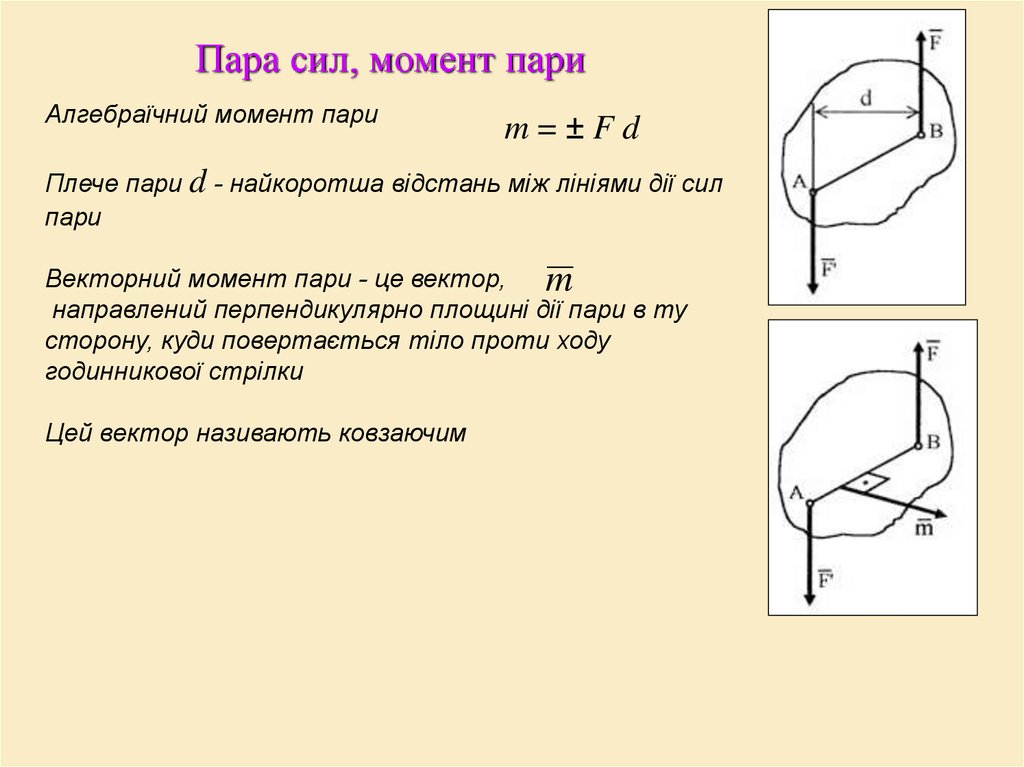 42) действуют четыре
силы и плечи которых соответственна равны:

Определить величину и направление сил и четвертой пары так, чтобы система находилась в равновесии.

Рис. 42.

Решение. Применим уравнение (33) равновесия пар:

Выражая моменты пар через произведения сил и плеч, имеем:

или

откуда т. е. искомая пара будет стремиться повернуть систему по направлению часовой стрелки, а каждая из неизвестных сил пары

Теория пар сил — презентация онлайн

Новосибирский Государственный Архитектурно-Строительный
Университет (Сибстрин)
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.
СТАТИКА
ЛЕКЦИЯ 5.
ТЕОРИЯ ПАР СИЛ
Кафедра теоретической механики

2. План лекции

Введение
Сложение параллельных сил, направленных
в разные стороны
Пара сил. Момент пары сил
Теорема об эквивалентности пар сил
Теорема о сложении пар сил
Условие равновесия тела под действием
системы пар сил
Заключение

3.

На предыдущей лекцииСложение параллельных сил направленных в одну сторону
B
C
A
Q
P
R
ВВЕДЕНИЕ
P || Q
R P Q
P
Q
R
CB AC AB

4. Цель лекции

Научиться работать с
парами сил.
ВВЕДЕНИЕ

5. Актуальность. Практические примеры

…что тело под действием одной силы F (~системе сходящихся сил)
Движется прямолинейно и
равноускоренно.
… что тело под действием системы параллельных сил
Движется прямолинейно и
равноускоренно.
ВВЕДЕНИЕ

6. Актуальность. Практические примеры

В этой лекции вы узнаете…
Какую систему сил необходимо приложить, чтобы заставить
тело вращаться
ВВЕДЕНИЕ

7. Теорема о сложении двух сил, направленных в разные стороны, но линии действия которых параллельны

Система двух не равных по модулю сил, линии
действия которых параллельны, но силы
направлены противоположно, имеет
равнодействующую, которая равна по модулю
разности модулей этих сил, им параллельна и
направлена в сторону большей силы.

Линия
действия равнодействующей проходит через
точку, которая лежит на продолжении отрезка АВ
и делит этот отрезок внешним образом на части,
обратно пропорциональные силам.
Сложение параллельных сил, направленных в разные стороны
Доказательство
(Q, P), Q || P, P Q
Представим силу
P ~ (Q , R )
причем Q Q
Тогда R P Q
P
R
Q
C
A
B
Q
а точка ее приложения
Q AB
AC
P Q
(Q, P) ~ (Q, Q , R)
Заметим, что (Q , Q) ~ 0
(Q, P ) ~ R
Сложение параллельных сил, направленных в разные стороны

9. Пара сил

Рассмотрим случай, когда P Q
Тогда, из соотношений предыдущей теоремы R P Q 0
P
A
Q
ПАРА СИЛ
Q AB
AC lim
P Q P Q
Такая система двух сил не имеет
равнодействующей и называется
парой сил.
Пара сил приводит к вращению
тела, которое характеризуется
моментом пары сил

10. Пара сил. Момент пары сил

Плоскость, проходящая через линии
действия сил, называется
F
плоскостью действия пары.

А
B
Расстояние между линиями действия
F1
сил называется
плечом пары.
Моментом пары сил называется вектор M , модуль которого равен
произведению модуля одной из сил пары на плечо пары: M=Fd.
Направлен этот вектор перпендикулярно плоскости действия
пары в сторону, откуда вращение пары видно происходящим
против часовой стрелки.
M
Для пар сил, расположенных в одной плоскости, как и для
обычных сил, часто используют понятие алгебраического
момента пары: M=±Fd. Знак «плюс» берется, если пара стремится
повернуть тело против хода часовой стрелки, «минус» – по ходу.
ПАРА СИЛ

11. Пара сил. Вращательный эффект пары

Вращательный эффект пары
F1
z
A
rA
F2
B
rB
O
y
x
складывается из вращательных
эффектов составляющих ее сил
M AB F2 (OB OA) F2
OB F2 OA F2 OB F2 OA F1
M O ( F1 ) M O ( F2 )
M M O ( F1 ) M O ( F2 )
Сумма моментов сил пары относительно любой точки О равна
моменту пары этих сил.

Поскольку момент пары сил
перпендикулярен плоскости
пары, а его модуль равен
M AB F1 sin( AB, F1 ) , то момент пары не зависит от точек
приложения сил пары. Он определяется лишь плечом пары.
ПАРА СИЛ
Пара сил. Пример
Пример пар сил вызывающих одинаковое вращательное
воздействие на тело (равные моменты)
Выбор отвертки
10мм
ПАРА СИЛ
F=10кН
20мм
F=5кН
Теорема об эквивалентности пар сил
Все пары сил, имеющие один и тот
же момент, эквивалентны.
Доказательство проведем в два этапа:
1. Для случая когда плоскости действия пар совпадают.
2. Когда плоскости действия пар параллельны.
Так как вектор момента пары направлен перпендикулярно
плоскости действия пары, то равенство моментов
подразумевает, что плоскости действия пар либо совпадают
либо параллельны.
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ

14. Доказательство

плоскости действия пар совпадают
Пара сил ( F , F ) с моментом m Fh
( F , F ) ~ ( f , Q, f , Q )
Q F
A
h
F
Q
( f , Q, f , Q ) ~ (Q, Q )
C
d
f
Так как ( f , f ) ~ 0 то
B
f
Момент пары (Q, Q ) равен m Qd
Так как ABC ~ FQf то d hF Q
F
m Qd Qh Fh m
Q
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ

15.

Доказательствоплоскости
действия пар параллельны
F2
B
R
F2
F1
A
D
F1
F1
R
C
( F1 , F2 )
Добавим уравновешенную
систему сил
( F1 , F2 ) ~ ( F1 , F2 , F1 , F2 , F1 , F )
F2
Заметим, что
( F2 , F1 ) ~ R, ( F1 , F2 ) ~ R
Тогда
( F1 , F2 , F1 , F2 , F1 , F2 ) ~
~ ( R1 , R2 , F1 , F2 ) ~ ( F1 , F2 )
По построению M ( F1 , F2 ) M ( F1 , F2 )
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ
Теорема об эквивалентности пар сил
Применение теоремы об эквивалентности пар сил
Если нет крестовой отвертки, а есть только плоская с узким
шлицем. Воспользуемся теоремой и перенесем усилие…
ТЕОРЕМА ОБ ЭКВИВАЛЕНТНОСТИ ПАР СИЛ
Теорема о сложении пар сил
Действие на тело системы пар с
моментами
M1 , M 2 ,…, M N
эквивалентно действию одной
пары с моментом
N
M Mk
k 1
ТЕОРЕМА О СЛОЖЕНИИ ПАР СИЛ

18. Доказательство

Докажем сначала теорему для двух пар сил
( F1 , F1 ) и (Q1 , Q1 )
Q1
R1
A
F1
B
R1
Q1
Из теоремы об эквивалентности пар
следует, что для доказательства достаточно
рассмотреть две пары, точки приложения
F1 сил которых A и B совпадают.

Действие рассматриваемых двух пар
эквивалентно действию одной пары ( R1 , R1 )
момент которой равен
M AB R1 AB ( F1 Q1 ) AB F1 AB Q1 M1 M 2
Доказательство для общего случая N пар теперь
можно просто получить по индукции.
ТЕОРЕМА О СЛОЖЕНИИ ПАР СИЛ

19. Условия равновесия тела под действием системы пар сил

Для того чтобы тело под действием системы пар
M1 , M 2 ,…, M N находилось в равновесии, необходимо и
достаточно, чтобы результирующая пара была эквивалентна
нулю:
N
M Mk 0
k 1
Для проекций на оси координат получаем
три скалярных уравнения:
N
M x M kx 0
k 1
N
M y M ky 0
k 1
Условия равновесия тела под действием системы пар сил
N
M z M kz 0
k 1

20. Условия равновесия тела под действием системы пар сил

Пример решения задачи
Задача. В плоскости Оxy расположены три пары сил.
Определить момент пары m3, при котором эта система пар
находится в равновесии, если m1 = 510 Н·м, m2 = 120 Н·м
y
m1
m2
m3
Решение.

Моменты пар m1, m2
положительны. Следовательно, уравнение
равновесия пар имеет вид:
510 120 m3 0
O
x
m3 670 Н м
Условия равновесия тела под действием системы пар сил

21. Вопросы для самоконтроля

1. В каком случае можно найти равнодействующую двух
сил, направленных в противоположные стороны, линии
действия которых параллельны?
2. Чему равна эта равнодействующая?
3. Можно ли силу разложить на две ей параллельные, но
направленные противоположно?
4. Что такое пара сил?
5. Как найти плечо пары?
6. Чему равен момент пары?
7. Какие пары являются эквивалентными?
ЗАКЛЮЧЕНИЕ

22. Вопросы для самоконтроля

8. Почему момент пары сил называют свободным вектором?
9. Как сложить пары?
10. Могут ли две эквивалентные пары иметь разные плечи?
11. Можно ли пару сил уравновесить одной силой?
12. Сформулируйте условия равновесия тела под действием
системы пар. Запишите уравнения равновесия тела под
действием системы пар.

1.7. Тождественное преобразование систем сил

Преобразование может быть выполнено графическим или аналитическим способом.

1.7.1. Преобразование сходящейся системы сил Равнодействующая R двух сходящихся сил находится на основании аксиомы о параллелограмме сил. (рис.1.9). Геометрическая сумма любого числа сходящихся сил может быть определена путем последовательного сложения двух сил (рис.1.19) – способ векторного многоугольника.

Вывод: система сходящихся сил (n) приводится к одной равнодействующей силе .

Рис.1.19 Рис.1.20. Рис.1.21.

Аналитически равнодействующая сила может быть определена через ее проекции на оси координат

, (1.5 )

Согласно теореме: проекция равнодействующей на ось равна сумме проекций слагаемых сил на эту ось (рис.1.20). Rx = F1 x + F2 x + F3 x , или в общем виде

Rx = å Fkx (1.6)

С учетом (1.6) равнодействующая определяется выражением

, (1.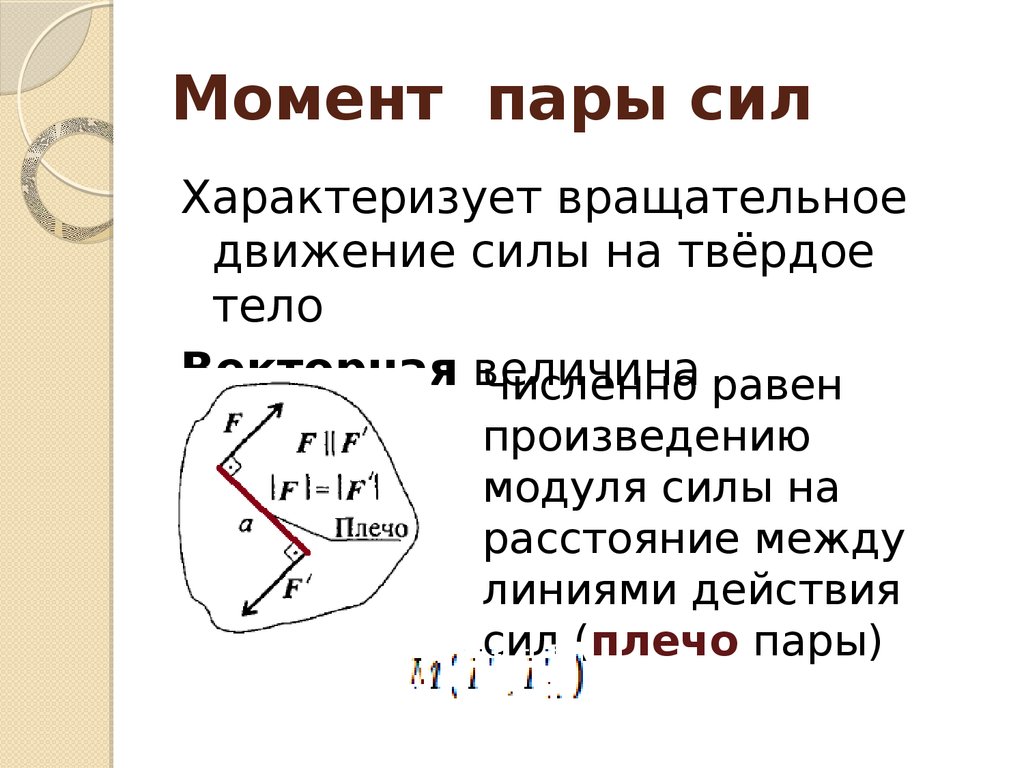 7)

Направление вектора равнодействующей определяется косинусами углов между вектором и осями x, y, z (рис.1.20)

где

1.7.2. Преобразование произвольной системы сил.

Применить правило параллелограмма сил непосредственно к произвольной системе сил нельзя, так как линии действия сил не пересекаются в одной точке. Предварительно систему сил приводят к одному центру на основании теоремы о параллельном переносе силы.

Теорема: силу, приложенную к твердому телу, можно, не изменяя оказываемого ею действия, перенести параллельно в другую точку тела, прибавляя при этом пару сил с моментом, равным моменту переносимой силы относительно точки, в которую она переносится (рис.1.22).

В результате указанного преобразования получается сходящаяся система сил и сумма моментов пар сил. Действие сходящейся системы сил заменяют действием суммарной силы, действие моментов — суммарным моментом. Суммарный вектор * называют главным вектором системы сил, суммарный момент * — главным моментом системы сил. 1.8 Условия равновесия систем сил

1.8.1. Равновесие системы сходящихся сил

По определению (см.п.1.1) действие системы сходящихся сил эквивалентно действию одной равнодействующей силы . Для равновесия тела крайне важно и достаточно, чтобы равнодействующая равнялась нулю = 0.

Из формулы (1.7) следует, что для равновесия пространственной системы сходящихся сил крайне важно и достаточно, чтобы сумма проекций всех сил на оси X,Y,Z равнялась нулю

å Fkx = 0

å Fky = 0 ( 1.10) åFkz = 0

Для равновесия плоской сходящейся системы сил крайне важно и достаточно, чтобы сумма проекций всех сил на оси X,Y равнялась нулю

å Fkx = 0

å Fky = 0 ( 1.11 )

1.8.2. Равновесие произвольной системы сил.

Действие произвольной системы сил эквивалентно действию главного вектора и главного момента. Для равновесия крайне важно и достаточно выполнения условия

* = 0 (1. 1.9. Вопросы для самоконтроля по разделу

1. Дайте определение абсолютно твердого тела, материальной точки, силы, линии действия силы, системы сил (плоской, пространственной, сходящейся) произвольной систем сил.

2. Что принято называть проекцией силы на ось, на плоскость?

3. Что принято называть моментом силы, как определяется момент силы относительно точки?

4. Изменяется ли момент силы относительно данной точки при переносе силы вдоль линии ее действия?

5. В каком случае момент силы относительно данной точки равен нулю?

6. Какая система сил принято называть парой сил, чему равен момент пары сил?

7. Что называют связью? В чем заключается принцип освобождения от связей? Перечислите основные типы связей, покажите их реакции.

8. Каковы условия и уравнения равновесия системы сходящихся и произвольной систем сил, расположенных в пространстве и в плоскости?

9. Сформулируйте порядок решения задач статики.

— Момент пары сил.

Парой сил приложенных к твердому телу, называется система двух равных по величине, параллельных между собой сил , направлены в противоположный стороны по несовпадающим линиям действия. (рис.4.3.) Плоскость , cсодержащая параллельные силы и и , называют плосколстью действия… [читать подробенее]

— Пара сил, момент пары сил

Тема 1.3. Пара сил и момент силы относительно точки ЛЕКЦИЯ 4 Темы 1.1, 1.2. Статика. Плоская сходящаяся система сил Задание для самостоятельной работы 1. Определить величину и направление реакций связей по данным одного из… [читать подробенее]

— Момент пары сил как вектор.

Действие пары сил на тело характеризуется: 1) величиной модуля момента пары, 2) плоскостью действия, 3) направлением поворота в этой плоскости. При рассмотрении пар, не лежащих в одной плоскости, для характеристики каждой из пар необходимо будет задать все эти три. .. [читать подробенее]

— Момент пары сил

Пара сил оказывает на тело вращающее действие. Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (рис.1.18) , (1.4) где: -силы, составляющие пару; h — плечо пары Рис.1.18. … [читать подробенее]

— Момент пары сил

— Момент силы. Момент пары сил

При вращательном движении все точки твердого тела движутся по окружностям, центры которых лежат на оси вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения, угловую скорость и угловое ускорение в каждый момент времени. При… [читать подробенее]

Плоская система пар сил.

Пара сил и момент пары

В предыдущей статье мы рассматривали сложение пары антипараллельных сил, не равных по модулю и пришли к выводу, что равнодействующая таких сил существует и ее величина равна алгебраической сумме сил; точка приложения равнодействующей пары антипараллельных сил находится в пропорциональной зависимости от соотношения между модулями сил пары.

Если пара антипараллельных сил состоит из одинаковых по модулю сил, то такая система сил называется парой сил или просто парой.
Понятие пары сил введено в механику в начале XIX века французским ученым Л. Пуансо (1777-1859), который разработал теорию пар.

Плоскость, в которой расположена пара, называется плоскостью действия пары. Расстояние между линиями действия сил, составляющих пару, называется плечом пары.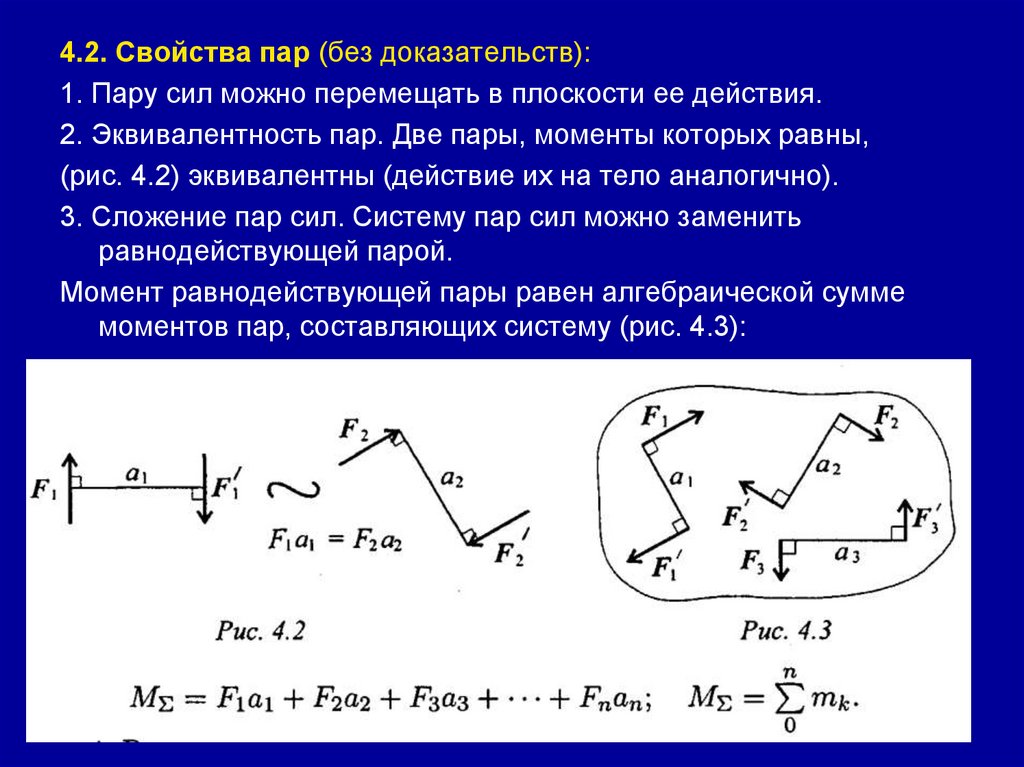
Эффект действия пары состоит в том, что она стремится вращать тело, к которому приложена. Ее вращающее действие определяется моментом пары.

Моментом пары называется произведение модуля одной из сил, составляющих пару, на плечо:

M(F₁, F₂) = F₁h =F₂h = m .

Момент пары и момент силы имеют одинаковую размерность — ньютон×метр (Нм).

Правило знаков для моментов пары.

Условимся считать момент пары положительным, если она стремится вращать свое плечо против часовой стрелки, и наоборот.

Если сделать геометрические построения (см. рисунок 1), то можно сделать вывод, что момент пары численно равен удвоенной площади треугольника, у которого основанием является вектор одной из сил пары, а высотой – плечо пары (как известно, площадь треугольника равна половине произведения основания на высоту).
Очевидно, что перенос любой из сил пары вдоль линии ее действия не влияет на вращающее действие всей пары, т. е. не изменяет момент пары, поскольку и основание треугольника (модуль силы) и его высота (плечо пары) в этом случае не меняются (перенос сил, составляющих пару вдоль линий их действия приводит к образованию равновеликих треугольников).

***

Основные свойства пары сил

Основные свойства пары сил характеризуются следующими тремя теоремами.

Теорема I. Пара сил не имеет равнодействующей.

Дана пара сил (F₁, F₂) с плечом h. (см. рисунок 2а).
Ранее мы доказали, что равнодействующая пары антипараллельных сил может быть определена, как алгебраическая сумма сил, составляющих такую пару, т. е., с учетом направленности векторов сил в разные стороны: F_Σ = |F₁| — |F₂|.
Применим это утверждение к случаю, когда силы равны между собой по модулю, и получим, что равнодействующая будет равна нулю: F₁ – F₂ = 0.
Из этого следует, что пара силы не имеет равнодействующей (или равнодействующая пары равна нулю).

Теорема II. Алгебраическая сума моментов сил, составляющих пару, относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары.

Дана пара сил (F₁, F₂) с плечом h. (см. рисунок 2b).
Момент пары: m = F₁h = F₂h.

Выберем в плоскости действия пары произвольную точку А и примем ее за центр моментов:

M_A(F₁) = -F₁a; M_A(F₂) = F₂(a+h).

Сложим правые и левые части этих равенств (не забываем, что |F₁| = |F₂|):

M_A(F₁) + M_A(F₂) = -F₁а + F₂(a+h) = -F₁а + F₂а + F₂h = F₂h = m .

Теорема доказана.

Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.

***

Теорема III. Алгебраическая сумма проекций сил пары на любую ось всегда равна нулю.

Дана пара сил (F₁, F₂) и ось z, лежащая в плоскости действия пары (см. рисунок 3). Из равенства заштрихованных треугольников видно, что F_1z = F_2z, при этом проекция одной из сил положительная, проекция другой силы – отрицательная, следовательно, сумма этих проекций равна нулю.
Теорема доказана.

Из теорем I и III следует, что пара сил не может входить ни в уравнение сил, ни в уравнение проекций сил, поскольку ее нельзя заменить ни равнодействующей, ни проекцией силы.

***

Эквивалентные пары

Две пары называют эквивалентными, если одну из них можно заменить другой, не нарушая механического состояния свободного твердого тела.

Теорема об эквивалентных парах формулируется так: если моменты двух пар алгебраически равны, то эти пары эквивалентны.

Пусть даны две пары (F₁, F₂) и (Q₁, Q₂), моменты которых алгебраически равны (см. рисунок 4), т. е.:

M(F₁, F₂) = M(Q₁, Q₂), или Fa = Qh.

Продолжим линии действия сил пары до их взаимного пересечения в точках А и В. На основании следствия из III и IV аксиом статики перенесем силы F и F₁ вдоль линий их действия в точки А и В.
Соединим эти точки прямой линией и разложим силы F и F₁ по направлению АВ и вдоль линий действия сил Q и Q₁.
Из равенства треугольников Akd и Bmn вытекет, что T = T₁ и S = S₁.

Силы T и Т₁ представляют собой уравновешенную систему, так как они равны по модулю и действуют по одной прямой в противоположные стороны. На основании аксиомы IV такую систему можно отбросить.

Силы S и S₁ представляют собой пару сил с плечом b.
Таким образом, пара (F₁, F₂) ≡ паре (S₁, S₂).

Рассмотрим треугольники AmB и AnB.
Они имеют общее основание АВ, и высоты их равны, следовательно площади тоже будут равны.
Поскольку площадь треугольника AnB равна половине момента пары (F₁, F₂), а площадь треугольника AmB равна половине момента пары (S₁, S₂), то можно записать:

М(F, F₁) = М(S, S₁) или Fa = Sb.

По условиям теоремы Fa = Qb, следовательно Sb = Qb, отсюда S = Q, S₁ = Q₁.

Силы S и Q равны по модулю, действуют вдоль одной прямой в одном направлении, следовательно они эквивалентны друг другу; на этом же основании можно сделать вывод об эквивалентности сил S₁ и Q₁. Очевидно, что тогда пара (Q,O₁) ≡ паре (S,S₁).

Так как две пары порознь эквивалентны одной и той же третьей паре, то эти пары тоже будут эквивалентны между собой:

М(F, F₁) = М(Q, Q₁), что и требовалось доказать.

Из доказательства теоремы об эквивалентных парах вытекает четыре следствия:

не изменяя механического состояния тела, пару можно переносить как угодно в плоскости ее действия;
не изменяя механического состояния тела, можно менять силы и плечо пары, но так, чтобы ее момент оставался неизменным;
чтобы задать пару, достаточно задать ее момент, поэтому иногда слово «пара» заменяют словом «момент»;
условия равновесия плоской системы параллельных сил будут справедливы, если вместе с такой системой действуют и пары сил, так как их можно повернуть в плоскости действия и поставить силы пары параллельно другим силам системы.

***

Теорема о сложении пар

Теорема: Всякая плоская система пар эквивалентна одной результирующей паре, момент которой равен алгебраической сумме моментов данных пар.

Пусть даны три пары с моментами m₁, m₂ и m₃, действующие в одной плоскости (рис. 1а).
На основании следствия из теоремы об эквивалентных парах преобразуем эти пары так, чтобы их плечи стали равными d, и перенесем к произвольно взятому на плоскости отрезку АВ длиной d.

Тогда вместо заданной системы пар получим новую систему, эквивалентную данной, причем моменты данных и новых пар будут равны, т. е.

m₁ = -P₁d ; m₂ = F₁d ; m₃ = -Qd .

Сложив три силы в точке А, получим равнодействующую R₁, модуль которой R₁ = P₁ + Q₁ – F₁.

Сложив три силы в точке В (рис. 4b) , получим равнодействующую R₂, модуль которой R₂ = P₂ + Q₂ – F₂, причем очевидно, что силы R₁ и R₂ равны по модулю, параллельны и противоположно направлены.
Значит, система (R₁, R₂) представляет собой пару с плечом d, эквивалентную данной системе пар.

Момент этой результирующей пары:

m = -R₁d = -( P₁ + Q₁ – F₁)d = -P₁d – Q₁d + F₁d, или

m = m₁ +m₂ + m₃.

Аналогичное доказательство можно привести для любой плоской системы пар, т. е. в общем виде можно записать:

m = Σm_i, что и требовалось доказать.

***

Условие равновесия плоской системы пар

Применяя доказанную ранее теорему о сложении пар к плоской системе пар, находящихся в равновесии, запишем:

m = Σm_i = 0.

Следовательно, условие равновесия плоской системы пар в общем виде будет выглядеть так:

Σm_i = 0,

а формулируется следующим образом: для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов данных пар равнялась нулю.

***

Опоры и опорные реакции балок

Опоры балок по их устройству могут быть разделены на три основных типа (см. рисунок 6): шарнирно-подвижная (опора А), шарнирно-неподвижная (опора В) и жесткая заделка (опора С). На приведенном рисунке показаны два способа условного изображения шарнирно-неподвижной опоры (опора А).

Применим правило для определения направления реакций связей и определим, какое направление могут иметь реакции представленных опор в зависимости от ограничений, накладываемых на балку.

Шарнирно-подвижная опора допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Если пренебречь трением на опоре и в шарнире, то реакция такой связи будет направлена перпендикулярно опорной плоскости, и неизвестна только по модулю (одно неизвестное).

Шарнирно-неподвижная опора допускает только поворот вокруг оси шарнира, и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира; модуль и направление ее заранее не известны (два неизвестных).

Жесткая заделка (защемление) не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Жесткую заделку заменяют реактивной силой, неизвестной по модулю и направлению, и реактивным моментом (три неизвестных).
Реактивную силу, неизвестную по направлению, раскладывают на две взаимно-перпендикулярные составляющие. Если при решении задачи реактивная сила или реактивный момент получаются отрицательными, то их действительное направление противоположно принятому.

Кроме перечисленных выше трех основных типов опор балок в конструкциях нередко балка свободно опирается на плоскость (поверхность) или ребро призмы (угол). В этих случаях направление реакций определяют, как для аналогичных типов связей, рассмотренных здесь.

***

Пример решения задачи по определению реакций опор балки

Пусть горизонтальная балка длиной l = 4 м закреплена на опорах, как показано на рисунке 7, и нагружена парой сил с моментом m = 420 Нм.
Не учитывая силу тяжести балки, определим реакции R опор А и В.

Решение.

Отбросим опоры, заменив их реакциями, и рассмотрим равновесие балки.
Так как пару сил можно уравновесить только парой, то реакции R опор А и В должны образовывать пару сил, причем реакция шарнирно подвижной опоры В перпендикулярна опорной плоскости.

Применим условие равновесия плоской системы пар и составим уравнение равновесия:

Σm_i = 0; -m + Rh = 0, где h = lcos30˚ .

Подставив известные значения, получим: R = m/h = m/(l cos30˚) = 420/(4×0,866) ≈ 120 Н.

Задача решена.

***

Пример решения задачи по определению реакции в жесткой заделке

Пусть консольная балка длиной l = 2 м нагружена на свободном конце силой F = 3000 Н (рис. 8).
Не учитывая силу тяжести балки, определим реакцию заделки.

Решение.

Отбросим заделку, заменив ее реакциями, и рассмотрим равновесие балки.
Реакция заделки представляет собой реактивную силу R и реактивный момент m.
Так как реактивный момент m может быть уравновешен только парой сил, то нагрузка F и реакция R должны образовывать пару, следовательно:

R = F = 3000 Н .

Далее применим условие равновесия плоской системы пар и составим уравнение равновесия:
Σm_i = 0; m – F₁ – 0, откуда получим:

m = Fl = 3000×2 = 6000 Нм.

Задача решена.

***

Плоская система произвольно расположенных сил

Главная страница

Страничка абитуриента

Дистанционное образование

Группа ТО-81
Группа М-81
Группа ТО-71

Специальности

Ветеринария
Механизация сельского хозяйства
Коммерция
Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

Инженерная графика
МДК. 01.01. «Устройство автомобилей»
Карта раздела
Общее устройство автомобиля
Автомобильный двигатель
Трансмиссия автомобиля
Рулевое управление
Тормозная система
Подвеска
Колеса
Кузов
Электрооборудование автомобиля
Основы теории автомобиля
Основы технической диагностики
Основы гидравлики и теплотехники
Метрология и стандартизация
Сельскохозяйственные машины
Основы агрономии
Перевозка опасных грузов
Материаловедение
Менеджмент
Техническая механика
Советы дипломнику

Олимпиады и тесты

«Инженерная графика»
«Техническая механика»
«Двигатель и его системы»
«Шасси автомобиля»
«Электрооборудование автомобиля»

3-й закон Ньютона

Рассмотрим следующие ситуации:

Вы с другом сидите на стульях с роликами. У вас обоих есть оторвите ноги от земли и своими ногами упираетесь в ноги своего друга стул. Ваш друг начинает отдаляться от вас, и вы начинаете двигаться подальше от своего друга. Вы оба ускоряетесь. Направление вашего ускорения противоположно направлению ускорения вашего друга ускорение.
Вы оба протягиваете руки, хватаете своего друга и тянете его к вам. Он ускоряется к вам, и вы ускоряетесь к его. Вы снова ускоряетесь.

Происходящее является следствием третьего закона Ньютона .

Для каждой силы, объект действует на другой объект, существует сила, равная по величине, но противоположное по направлению воздействие второго объекта на первый объект. Силы являются результатом взаимодействий.

Ты тянешь меня, я тяну тебя. Если других сил нет, я устремлюсь к вам. У меня ускорение величина силы, деленная на моей массы. Вы ускорите ко мне. Ваше ускорение имеет величину силы, деленную на вашей массы.

Вопрос:

Ты давишь на стол, стол давит на тебя. Ты ускориться от стола. Почему стол не ускоряется от вас?

Если стол на роликах, он будет ускоряться от вас. Если таблица очень массивен, величина его ускорения будет намного меньше, чем величина вашего ускорения. Если не на роликах, то усилие на него также действует трение покоя, и векторная сумма двух силы равны нулю.

Стоя на очень скользкой поверхности или на скейтборде, вы бросаете тяжелый объект от вас в северном направлении. Для этого нужно приложить воздействие на объект в северном направлении. Объект действует с силой на вы, который имеет равную величину, но указывает на юг. Вы ускоряетесь на юг.

Третий закон Ньютона также называют законом Ньютона. действие и противодействие . Для каждой силы действия существует сила противодействия, равная по модулю и противоположные по направлению. Объекты взаимодействуют.

Сила действия и противодействия всегда действуют на разные объекты.
Две силы, действующие на один и тот же объект, даже если они имеют одинаковую величина и точка в противоположном направлении никогда не образуют пару действие-противодействие.

Проблема:

Яблоко массой 0,2 кг лежит на столе в равновесии.
а) Какие силы действуют на него? Укажите их величину и направление.
б) Какова сила реакции на каждую из сил, действующих на яблоко?
(c) Что такое пары действие-реакция?

Решение:

Обоснование:
(a) Силы, действующие на яблоко, равны его весу W = mg = 1,96 Н, направленному вниз и нормальное усилие, указанное в таблице F _Н = 1,96 Н указывая вверх. Суммарная сила, действующая на яблоко, равна нулю.
(b) Сила реакции на W представляет собой силу F _WR = 1,96 Н, направленную вверх и действующую в центре Земли. (Земля тянет яблоко и яблоко тянет землю.)
Реакция на F _N есть сила F _NR = 1,96 Н направленная вниз действует на стол. (Стол давит на яблоко, яблоко давит на стол.)
(c) Пары действие-противодействие: W − F _WR и N − F _NR.

Пары действие-противодействие представляют собой силы равной величины и противоположного направления которые действуют на разных объектов . Они никогда не действуют на один и тот же объект.

Третий закон Ньютона говорит нам, что силы — это взаимодействия. Объект не может воздействовать на другой объект, не чувствуя самой силы реакции. Сила реакции имеет ту же величину и направлена в противоположном направлении. как сила, с которой объект действует на другой объект. Что и объект делает в результате действия силы реакции зависит не только от силы реакции, а на результирующую силу, действующую на объект. Чистая сила сумма силы реакции и всех других сил, действующих на объект.

Примеры пар действие-противодействие:

Ружье давит на пулю — пуля давит на ружье (отдача)
Игрок бросает мяч вперед, прилагая усилие рукой к мячу — мяч отталкивается от руки
Ученик тянет за стол — стол тянет за ученика (вот как вы может «тянуть» себя вперед. )
Земля притягивает человека (гравитация) — человек притягивает Землю

Примеры сил, имеющих одинаковую величину и противоположное направление, но НЕ пары действие-противодействие.

Земля притягивает объект к полу — нормальная сила толкает человека вверх и предотвращает падение человека на пол (обе силы действуют на тот же объект.)
Человек 1 толкает объект влево — человек 2 толкает объект в вправо, но объект остается в покое (обе силы действуют на один и тот же объект.)
Автомобиль движется с постоянной скоростью. Мотор тянет машину вперед — точки трения в обратном направлении (обе силы действуют на одну и ту же объект.)

Ссылка: Физика Футбол — Третий закон движения Ньютона — YouTube

Модуль 2: Вопрос 2

Устройство, используемое с 1940-х годов для измерения толчка или отдачи тела из-за к ударам сердца – «баллистокардиограф». Какой принцип(ы) физики участвуют здесь для измерения силы сердечного сокращения? Как может мы конструируем такое устройство?

Обсудите это со своими однокурсниками на дискуссионном форуме!

Модуль 2: Вопрос 3

Предположим, вы держите в руке чашку кофе. Определить все силы, действующие на чашку, и реакция на каждую силу.

Обсудите это со своими однокурсниками на дискуссионном форуме!

Растяжение и сжатие

Предположим, что две противоборствующие команды и противоборствующая команда тянут веревку в противоположные направления. Есть ли результирующая сила на веревке?

Если веревка ускоряется в сторону одной из команд, то нет есть ненулевая результирующая сила. F = m a . Чистая сила представляет собой векторную сумму силы тяжести и сил приложили обе команды.
Противоборствующая команда, так как веревка начинает ускоряться в их направление.

Если веревка не ускоряется, даже при этом каждая команда тянет изо всех сил может тогда нет чистой силы, действующей на веревку. Однако есть напряжение в веревка. Натяжение возникает из-за того, что на разные части тела действуют разные силы. тело. Напряжение может сломать вещи. Чистая сила, т. е. та же самая сила действуя на все части тела, не может сломать вещи.
Если вместо потянув за веревку, две команды толкают тяжелый камень, но камень не двигаться, то снова результирующая сила, действующая на камень, равна нулю. Однако теперь порода находится под сжатием .

Натяжение T является скаляром. Он определяется как величина сила, с которой натянутая веревка тянет все, к чему она прикреплена. Эту силу часто обозначают цифрой 9.0019 Т . Направление Т зависит от того, какой конец веревки рассматривается.

Суммарная сила, действующая на объект, всегда является векторной суммой всех сил. воздействуя на объект. Ускорение тела направлено в сторону эта чистая сила и имеет величину a = (чистая сила / масса объекта).

Проблема:

Блок весом 15 фунтов лежит на полу. (Примечание: фунт – это единица силы, вес блока 15 фунтов)
(а) Что сила, с которой пол действует на блок?
(b) Если веревка привязана к блок и проходят вертикально над шкивом, а другой конец прикреплен к свободно висящий груз массой 10 фунтов, какова сила, с которой пол действует на 15-фунтовый блок?
(c) Если мы заменим 10-фунтовый груз в части (b) 20-фунтовый вес, какова сила, с которой пол действует на 15-фунтовый блок?

Решение:

Обоснование:
(а) Блок находится в состоянии покоя, результирующая сила равна нулю. Вес блок находится на 15 фунтов вниз. Таким образом, пол должен оказывать усилие 15 фунтов. вверх.
(б) Блок по-прежнему находится в состоянии покоя. Вес 15 фунтов вниз, веревка тянет 10 фунтов вверх. из-за натяжения троса. Поэтому пол должен приложить силу 5 фунтов вверх.
(c) Вес на 15 фунтов направлен вниз, веревка тянет вверх с силой 20 фунтов из-за натяжения веревки. Блок будет ускоряться вверх, так как результирующая сила направлена вверх. Блок не давит на землю, и земля не отталкивание назад. Земля не оказывает на блок нулевой силы.

Проблема:

Два блоки, один из которых стоит на столе, а другой, более тяжелый, свисает с его края, соединены легкой нитью, как показано на рисунке. Какая сила заставляет блок на столе ускоряться, натяжение струны или вес подвесной блок? Запишите выражение для ускорения а.

Решение:

15.1 Виды сил | Силы

Обзор главы

2 недели

В этой главе учащиеся знакомятся с концепцией силы. В предыдущих классах учащиеся познакомились с некоторыми концепциями сил, например:

Учащиеся обнаружат, что существуют две основные категории сил, а именно контактные и бесконтактные силы. Они познакомятся с концепцией силовых полей. В этой главе есть много возможностей для того, чтобы учащиеся физически познакомились с понятиями. Предложите учащимся тянуть и толкать предметы и перемещать друг друга по классу или за пределами школьной территории. Пусть они надавят на здания, чтобы испытать сопротивление поверхностей. Позвольте им пройтись по разным поверхностям и почувствовать эффект трения.

В эту главу включено множество задач. Возможно, у вас не будет времени охватить их все. Некоторые из них являются дополнительными задачами, а некоторые задачи являются пересмотром Gr. 7 и 8. Вам нужно будет оценить требования и возможности вашего класса, чтобы решить, какие задания выполнять. В этой главе содержится большой объем информации, и многие концепции составляют основу того, что учащиеся будут изучать в разделе «Физические науки в Гр. 10-12. Возможно, вам придется потратить больше, чем выделенные 2 недели времени, указанные в CAPS. Некоторые другие главы этого семестра могут потребовать меньше времени.

Знаете ли вы, что эти рабочие тетради были созданы в Сиявула при участии многих участников и волонтеров? Просто повернитесь вперед, чтобы увидеть длинный список! Узнайте больше о Siyavula на нашем сайте:[ссылка]www.siyavula.com. Вы также можете зарегистрироваться на странице нашего сообщества, если хотите оставаться на связи и участвовать в наших проектах.

Siyavula также создал серию учебников для других классов и предметов, и мы собираемся выпускать больше. Этих учебников и рабочих тетрадей с открытой лицензией и в свободном доступе для использования, загрузки, копирования, переработки и распространения. Учебники Siyavula, которые в настоящее время доступны:

Гр. 4-6 Естественные науки и технологии: [ссылка] www.thunderboltkids.co.za
Физические науки Гр. 10-12:[ссылка]www.everythingscience.co.za
Математика гр. 10-12, Математическая грамотность гр. 10: [ссылка] www.everythingmaths.co.za

1.1 Виды войск (1,5 часа)

Задачи	Навыки	Рекомендация
Упражнение: Что могут силы?	Групповая работа, выполнение инструкций, выполнение и наблюдение	CAPS рекомендуется
Упражнение: Это толчок или притяжение?	Доступ и вызов, идентификация, сортировка и классификация, описание, объяснение	Рекомендовано
Деятельность: Пары сил	Групповая работа, интерпретация (сценариев и образов) описание, объяснение	CAPS рекомендуется
Упражнение: Могут ли силы действовать на расстоянии?	Демонстрация, наблюдение, описание, объяснение	Дополнительно

Дополнительное/альтернативное задание:

Упражнение: Перетягивание каната — Дополнительное расширение с использованием моделирования PhET.

1.2 Контактные усилия (1 час)

Задачи	Навыки	Рекомендация
Исследование: Какова связь между нормальной силой и трением?	Проведение расследования, наблюдение, запись, анализ, интерпретация, составление заключения	Предлагаемое (расширение)

Дополнительная/альтернативная задача:

Упражнение: Трение — Дополнительное расширение, использующее моделирование PhET.

1.3 Полевые силы (3,5 часа)

Задачи	Навыки	Рекомендация
Расследование: падение объектов	Групповая работа, прогнозирование, выдвижение гипотез, проведение исследования, наблюдение, запись, сравнение, интерпретация, подведение итогов	CAPS рекомендуется
Исследование: Какова связь между массой объекта и его весом?	Выдвижение гипотез, измерение, запись, построение графика, интерпретация, расчет, вывод	Рекомендовано
Деятельность: Расчет веса и массы	Расчет	CAPS рекомендуется
Задание: Сколько бы вы весили на других планетах?	Измерение, расчет, интерпретация информации в таблице	Опционально/дополнительно
Исследование: магнитные или немагнитные материалы	Выдвижение гипотез, наблюдение, запись, заключение	CAPS рекомендуется
Деятельность: Может ли магнитная сила действовать через вещества?	Осуществление деятельности, наблюдение, запись, описание, объяснение	CAPS рекомендуется
Упражнение: Визуализация магнитных полей	Осуществление деятельности, наблюдение, запись, рисование изображений, сообщение (графическое), описание, объяснение	CAPS рекомендуется
Деятельность: Зарядка объектов	Групповая работа, выполнение инструкций, наблюдение, описание, объяснение,	CAPS рекомендуется
Упражнение: Вращение колеса	Наблюдение, описание	CAPS рекомендуется
Деятельность: Генератор Ван де Граафа	Наблюдение, описание	Дополнительное расширение

Что такое сила?
Какое воздействие может оказать сила на объект?
Должны ли силы быть между соприкасающимися объектами?

Виды сил

сила
чистая сила
контактное усилие
бесконтактная сила
ньютон
деформация
скорость
скорость
ускорение

Что такое сила?

Подумайте о следующей ситуации: вы все помогаете своей учительнице переставить классную комнату, и она просит вас передвинуть ее парту с одного конца классной комнаты на другой. Как бы Вы это сделали? Парта слишком тяжелая для вас, чтобы ее поднять, так как же вы перетащите ее через класс?

Верно, вы будете либо толкать его, либо тянуть через всю комнату. При этом вы приложили силу к столу, чтобы заставить его двигаться.

Ньютон определяется как сила, необходимая для ускорения 1 килограмма массы на 1 метр в секунду в квадрате (м/с ² ).

Сила — это толчок или притяжение объекта. Единицей, в которой мы измеряем силу, является ньютонов (Н) . Он назван в честь сэра Исаака Ньютона, английского физика и математика. Сэр Исаак Ньютон признан одним из самых влиятельных ученых всех времен. Единица силы названа в его честь в знак признания его работ в области механики и его трех законов движения.

Сэр Исаак Ньютон (25 декабря 1642 — 20 марта 1727).

Вы заметили, что в одном из полей Знаете ли вы, что полей в этих рабочих тетрадях есть рисунок Ньютона?

В 1687 году Ньютон опубликовал Philosophæ Naturalis Principia Mathematica , которую часто считают одной из самых важных книг в истории науки. В нем он описывает вселенское тяготение и три закона движения.

Мы используем силы каждый день нашей жизни. Наши собственные тела полагаются на силы. Наши мышцы тянут наши кости, чтобы мы могли двигаться. Наши ноги отталкиваются от земли, когда мы ходим. Открывать двери, забирать еду — все, что мы делаем, требует какой-то силы.

Что могут силы? Давайте поэкспериментируем с силами и посмотрим, что мы можем сделать.

Это задание посвящено экспериментам с различными объектами и изучению того, что происходит с ними, когда мы их толкаем и тянем. Учащиеся должны видеть, что нажатие на твердые предметы ускоряет их. Когда вы толкаете или тянете губки, воздушные шары и тесто для лепки, их форма искажается, и мяч можно заставить двигаться. Каждой группе потребуются материалы, перечисленные ниже.

МАТЕРИАЛЫ:

блоки (деревянные или металлические)
губка или кусок пенопласта
шар
надутый воздушный шар
замазка или тесто для лепки

ИНСТРУКЦИИ:

Работайте в группах по 2 или 3 человека, следуя инструкциям и описывая воздействие сил, которые вы применяете.

Начните с мяча и положите его на землю. Подтолкните его к партнеру. Что вы смогли заставить сделать мяч, толкнув его?

Учащиеся могут заставить мяч двигаться.

Когда один из вас подталкивает мяч к другому, третий человек должен еще раз подтолкнуть мяч под углом к направлению, в котором он уже движется. Что вы смогли сделать с направлением, в котором двигался мяч?

Толкание мяча меняет его направление по мере движения.

Приложите силу в направлении, противоположном его движению, пока он уже движется. Что вы можете заставить мяч сделать?

Учащиеся могут замедлить или остановить мяч.

Приложите силу в том же направлении к его движению, когда оно уже движется. Что вы можете заставить мяч сделать?

Учащиеся могут заставить мяч двигаться быстрее.

Возьмите кусок пластилина или пластилина. Приложите к нему тянущее или толкающее усилие. Попробуйте сделать это и с надутым воздушным шаром. Что вы делаете с формой пластилина или пластилина и надутым шариком?

При воздействии сил на пластилин или пластилин изменяет свою форму и остается деформированным. Воздействие силы на воздушный шар также меняет его форму, но он снова восстанавливает свою форму, как только вы перестаете воздействовать на него силой.

Толкайте и тяните деревянные блоки. Способны ли вы изменить их движение? Умеете ли вы менять их форму?

Да, вы можете изменить их движение, заставив их двигаться. Нет, вы не можете изменить форму.

Возьмите кусок губки и скрутите его. Это также тип силы, которая изменяет форму губки.

Сожмите губку обеими руками. Это называется сжатием.

Эффекты сил

Из последнего занятия вы должны были видеть, что силы могут иметь следующие эффекты:

Силы могут изменить форму объекта. Это называется деформацией.
Силы могут изменить движение объекта. Если объект неподвижен, сила может заставить объект начать движение. Или, если объект уже движется, сила может заставить объект ускориться или замедлиться.
Силы могут изменить направление , в котором движется объект.

Как описать движение объекта? Когда объект движется, мы говорим, что он имеет скорость . Скорость – это скорость изменения положения объекта. Скорость – это скорость объекта и направление, в котором он движется. Скорость описывает только то, насколько быстро движется объект, тогда как скорость показывает, как быстро и в каком направлении движется объект.

Объект может двигаться с постоянной скоростью. Это означает, что он движется с той же скоростью в том же направлении. Например, автомобиль, движущийся по шоссе со скоростью 100 км/ч по прямой, имеет постоянную скорость. Однако что происходит, когда автомобиль движется быстрее или замедляется?

В последнем упражнении мы увидели, что можем изменить движение объекта, применив силу, которая заставит его ускориться или замедлиться. Скорость тела меняется со временем из-за действующей на него силы. это называется ускорение . Ускорение – это скорость изменения скорости тела во времени. Другими словами, это мера того, как скорость объекта меняется каждую секунду.

ИНСТРУКЦИИ:

Посмотрите на картинки в таблице.
Опишите действие на каждом изображении.
Решите, является ли приложенная сила толчком или тягой.
Опишите действие силы.

Действие	Толкать или тянуть?	Эффект
Удар по мячу.
Формовочная глина.
Игра с игрушечной тележкой.
Ракета взлетает в космос.
Упражнения на турнике.

Действие	Толкать или тянуть?	Эффект
Удар по мячу.	Нажмите	Удар по мячу меняет направление и скорость мяча.
Формовочная глина.	Нажмите	Толчок, оказываемый на глину, изменяет форму глины.
Игра с игрушечной тележкой.	Тянуть	Тяга изменяет движение повозки.
Ракета взлетает в космос.	Нажмите	Толкающая сила изменяет движение ракеты (т.е. ускоряет ее)
Упражнения на турнике.	Тянуть	Подтягивание вверх изменяет движение тела мальчика.

ВОПРОСЫ:

Эти вопросы об идентификации объекта, на который действует сила, и агента, вызывающего силу, концептуально важны при применении законов Ньютона в более поздних классах.

В примере с девочкой, пинающей мяч, что является объектом, на который действует сила, и что является агентом силы (т. е. телом, прилагающим силу)?

Футбольный мяч подвергается воздействию силы, а ступня девушки является агентом, применяющим силу.

При лепке глины какой объект испытывает силу, а какой объект является агентом?

Глина испытывает силу, а руки — агент.

Пары сил

Теперь мы собираемся выполнить еще одно практическое задание, чтобы исследовать другое понятие о силах.

ИНСТРУКЦИИ:

Для этого задания работайте в группах по три человека.

Сначала подойдите к стене класса и нажмите на нее. Опишите, что вы чувствуете ниже.

Ответ зависит от учащегося. Учащиеся могут заметить, что они чувствуют, как стена давит на их руки.

Когда вы нажимаете на стену, вы думаете, что стена отталкивает ваши руки? Как эта сила соотносится с силой, действующей на стену?

Да, отталкивает.

Сила, испытываемая учащимися, равна по величине и противоположна по направлению, что будет обсуждаться позже.

Встаньте треугольником с двумя партнерами и возьмитесь за руки. Потяните друг друга за руки. Вы чувствуете, как руки ваших партнеров оттягиваются назад, когда вы тянете?

Все еще стоя в треугольнике, положите ладони друг на друга и нажмите на руки друг друга. Чувствуете ли вы, как руки ваших партнеров отталкиваются назад, когда вы толкаете?

Затем встаньте плечом к плечу с двумя партнерами. Два ученика снаружи должны упираться в плечи ученика в середине.

Что происходит, когда вы оба толкаете с одинаковой силой?

Учащийся в середине остается неподвижным.

Что происходит, когда один из вас толкает сильнее, чем другой?

Средний ученик будет двигаться в направлении большей силы.

Затем ученик в середине должен вытянуть руки. Учащиеся снаружи должны тянуть за руки среднего ученика в противоположных направлениях.

Что происходит, когда вы оба тянете с одинаковой силой?

Средний ученик остается неподвижным.

Это важно на потом. Важно определить силы, действующие на конкретный объект.

Что происходит, когда один из вас тянет с большей силой, чем другой?

Средний ученик будет двигаться в направлении большей силы.

Что происходит, когда один из вас тянет, а другой толкает?

Обе эти силы действуют в одном направлении, поэтому учащийся движется в направлении толкания и притяжения.

В последнем упражнении мы видели, что всякий раз, когда один объект воздействует на другой объект, второй объект оказывает обратное воздействие на первый объект. Вы видели это, когда толкались о стену. Мы говорим, что силы действуют парами. Ньютон назвал единую силу девятой.0011 действие , а другое вызывает реакцию , как показано на следующей диаграмме.

Мы также видели, что когда вы прикладывали силу к стене, вы чувствовали, что стена оказывает обратное воздействие на вас. Силы действуют попарно на разные объекты. Сила, приложенная вторым объектом, равна по силе и противоположна по направлению первой силе.

То, что мы здесь описали, на самом деле является третьим законом движения Ньютона. Закон гласит, что когда одно тело действует на другое тело с силой, второе тело одновременно действует с силой, равной по силе и противоположной по направлению силе первого тела.

Если вы изучаете физические науки в гр. 10-12, вы более подробно изучите законы Ньютона в Гр. 11. Вы увидите, как эти три закона легли в основу классической механики, одного из старейших и крупнейших предметов в науке, технике и технике.

В последнем упражнении мы также увидели, что на объект одновременно могут воздействовать несколько сил. Например, когда двое из вас толкали или тянули своего друга посередине. Эффект различных сил, действующих вместе, зависит от того, насколько велика каждая сила и в каком направлении действует каждая сила.0011 чистая (общая) сила.

Что произошло, когда вы оба толкнули или потянули с одинаковой силой?

Ничего не произошло, так как учащийся оставался неподвижным.

Когда силы равны друг другу и противоположны по направлению, они уравновешивают друг друга, и мы говорим, что результирующая сила равна 0 Н.

Что произошло, когда один из вас толкнул или потянул сильнее, чем другой?

Ученик в середине двигался в направлении большей силы.

Когда силы действуют в противоположных направлениях, но не равны, мы говорим, что результирующая сила больше 0 Н. Существует равнодействующая сила . Если силы равны и действуют в одном направлении, то также будет равнодействующая сила.

Представьте себе перетягивание каната. Люди с обеих сторон тянут веревку. Если они прикладывают силы равной величины, то веревка остается неподвижной. Если одна группа способна приложить большую силу, чем другая группа, то веревка будет двигаться в направлении большей силы. Это потому, что силы неуравновешены и есть чистая (результирующая) сила, действующая в направлении большей силы.

Игра в перетягивание каната

Если у вас есть веревка, вы можете устроить учащимся перетягивание каната на школьном поле. Вы можете попросить детей с одной стороны тянуть, а другая сторона будет бездействовать. Затем потяните обе стороны одновременно. Это был бы хороший способ дать учащимся почувствовать воздействие сил на их собственные тела.

Вы также видели, что один из вас может тянуть, а другой толкать в одном направлении. В этом случае результирующая сила была намного больше, так как обе силы действовали в одном направлении и, таким образом, они складываются вместе, создавая большую результирующую силу.

Мы можем рассчитать результирующие силы, действующие на тело. Для этого нам сначала нужно поговорить о том, как мы представляем силы, действующие на тело.

Представление сил

Как изобразить силу? Когда мы хотим нарисовать диаграмму, чтобы показать, какие силы действуют, мы используем стрелки для представления сил. Мы всегда показываем силы, действующие из центра объекта, на который они действуют. Если бы мы изобразили силу, действующую на мяч, когда его толкают, это могло бы выглядеть так:

Направление стрелки показывает направление, в котором действует сила, а длина стрелки указывает на размер силы. Небольшая сила будет показана короткой стрелкой. Большая сила будет показана длинной стрелкой.

На объект одновременно могут действовать несколько сил. Эффект различных сил, действующих вместе, зависит от того, насколько велика каждая сила и в каком направлении действует каждая сила.

Давайте посмотрим, как мы можем представить следующую ситуацию: Джабу тянет руку Рода с силой 10 Н, а Вианта тянет другую руку Рода с силой 6 Н.

Мы можем изобразить силы, действующие на Рода, следующим образом: мы используем круг для обозначения Рода и стрелки разной длины для обозначения сил, действующих на него. Это называется диаграммой свободного тела.

Какая результирующая сила действует на Род? Мы можем рассчитать это следующим образом:

чистая сила = 10 Н + (- 6 Н) = 4 Н влево.

Силе, действующей Вианте, присваивается отрицательное значение, поскольку она направлена в противоположную сторону от силы, действующей Джабу.

Если все силы действуют в одном направлении, то результирующая сила представляет собой сумму различных сил.

Представьте, что вы толкаете кого-то в тележке, и ваш друг приходит помочь вам толкать сильнее. Теперь на человека в тележке действуют две силы. Эти силы действуют в одном и том же направлении, поэтому они складываются вместе, чтобы создать результирующую силу, которая является суммой двух меньших сил.

Как мы увидим позже, на эту систему действуют и другие силы, такие как трение и вес.

Узнайте больше в Интернете, взаимодействуя с этой симуляцией сил и движения. http://phet.colorado.edu/en/simulation/forces-and-motion-basics

Это дополнительное задание, которое вы можете выполнять с учащимися, если у вас есть доступ в Интернет для запуска симуляций PhET.

Упражнение: Перетягивание каната

МАТЕРИАЛЫ:

Было бы неплохо ознакомиться с симуляцией, прежде чем разрешить учащимся ее использовать. Это гарантирует, что вы сможете помочь им, если у них возникнут проблемы с симуляцией. При использовании программы важно, чтобы учащиеся каждый раз останавливали симуляцию, прежде чем добавлять другую силу. Эта ссылка представляет собой загрузку в формате pdf с полезными советами по использованию моделирования: http://phet.colorado.edu/files/teachers-guide/forces-and-motion-basics-guide.pdf

ИНСТРУКЦИИ:

Откройте веб-страницу. Нажмите на кнопку с надписью «Выполнить».
Отметьте все поля в правом верхнем углу.
Разместите синюю и красную команды таким образом, чтобы силы были уравновешены.
Нарисуйте диаграмму свободного тела, чтобы показать силы, действующие на тележку. Показать результирующую силу (сумма сил)

Примечание: Диаграмма будет зависеть от учащегося. Они выберут определенную комбинацию синих и красных членов команды, чтобы добиться сбалансированного набора сил. Предложите им поиграть с симуляцией, а не просто выбирать первый найденный ответ. Покажите им, что есть много правильных комбинаций. На диаграмме, которую они рисуют, должны быть две стрелки одинаковой длины, направленные в противоположные стороны, а результирующая сила должна быть равна нулю. Помните, что никогда нельзя рисовать чистую силу. Симуляция покажет им правильный ответ.

Сброс моделирования.
Разместите синих и красных членов команды таким образом, чтобы создать неуравновешенную силу.
Нарисуйте диаграмму свободного тела, чтобы показать силы, действующие на тележку.

Примечание: Векторная диаграмма будет зависеть от учащегося. Они выберут определенную комбинацию синих и красных членов команды, чтобы добиться несбалансированного набора сил. Предложите им поиграть с симуляцией, а не просто выбирать первый найденный ответ. Покажите им, что есть много правильных комбинаций. На диаграмме, которую они рисуют, должны быть две стрелки разной длины, направленные в противоположные стороны. Моделирование покажет им правильный ответ.

Обратите внимание учащихся на то, что неуравновешенные силы приводят к изменению движения (ускорения) тела. В случае тележки неуравновешенные силы действуют в противоположных направлениях и объединяются путем вычитания. Но неуравновешенные силы также могут действовать в одном и том же направлении, например, если два человека толкают тележку с разными силами, заставляя ее ускоряться вперед, неуравновешенные силы объединяются путем сложения, а не вычитания.

Как измерить силу? Мы используем такой инструмент, как весенние весы. Пружинные весы представляют собой простое устройство, состоящее из пружины, которая при растяжении дает показания силы, используемой для растяжения пружины.

Пружинные весы.

Работа пружинных весов зависит от закона Гука, который гласит, что когда сила растягивает или сжимает пружину, расстояние, на которое пружина перемещается из положения покоя, прямо пропорционально величине силы.

Узнайте больше о законе Гука и о том, как пружины растягиваются в зависимости от массы, с помощью этой симуляции. http://phet.colorado.edu/en/simulation/mass-spring-lab

Типы сил

До сих пор мы рассматривали силы, действующие на объект, когда объект, создающий силу, находится в контакте с объектом, испытывающим сила. Всегда ли мы должны быть в контакте с объектом, чтобы применить силу?

Это короткое дополнительное задание для ознакомления с идеей различных типов сил. Это можно сделать в виде краткой демонстрации перед классом, чтобы сэкономить время.

МАТЕРИАЛЫ:

стержневые магниты
металлические скрепки

ИНСТРУКЦИИ:

Поместите один из стержневых магнитов на стол.

Приблизьте северный конец другого стержневого магнита к южному концу первого стержневого магнита. Что случается?

Стержневые магниты движутся навстречу друг другу

Приблизьте северный конец одного стержневого магнита к северному концу другого стержневого магнита. Что случается?

Магниты пытаются оттолкнуть друг друга.

Положите скрепки на стол.

Поднесите стержневой магнит к скрепкам. Что вы наблюдаете?

Скрепки притягиваются к стержню магнита.

ВОПРОСЫ:

Приходилось ли вам соприкасаться стержневыми магнитами, чтобы они притянулись друг к другу?

Скрепки двигались к магниту?

Что вызвало движения?

Магнит приложил силу к другому магниту или скрепкам.

Магниты прикладывали силы, но они не должны были касаться друг друга. Это означает, что вам не нужно находиться в контакте с чем-то, чтобы воздействовать на это силой.

Есть два типа сил:

Теперь мы рассмотрим эти две широкие группы сил более подробно.

Контактные силы

Трение
нормальное усилие
напряжение
сжатие

Контактные силы – это силы между объектами, которые соприкасаются друг с другом. Большинство сил, которые мы рассмотрели в предыдущем разделе, были контактными силами, например, когда вы толкаете стол или тянете тележку. Вы касаетесь объекта.

Трение

Что происходит, когда вы пинаете мяч по траве? Мяч сначала движется быстро, но затем снова замедляется. Что-то заставило мяч замедлиться и перестать двигаться. Если движение мяча изменилось, то на него должна была действовать сила. Сила, противодействующая движению, называется 9.0011 трение . Силы трения всегда действуют в направлении, противоположном движению тела. Трение сопротивляется движению, когда объект и поверхность соприкасаются. Что это значит? Это означает, что если мяч движется вперед, то трение действует на мяч назад.

На следующем рисунке показан мяч, по которому только что ударили ногой. Нарисуйте стрелку, чтобы показать, в каком направлении будет действовать трение.

Учащиеся должны нарисовать стрелку в направлении, противоположном красной стрелке.

Какие факторы влияют на величину силы, необходимой для перемещения объектов? Нам нужно посмотреть на все силы, действующие на объект. Помните следующую диаграмму из начала главы?

Мы показали только силы двух учеников, толкающих тележку. Какие еще силы действуют на тележку при ее движении?

Трение действует на тележку в направлении, противоположном движению тележки. Тележка также имеет вес. Как мы узнали в Гр. 8 Планета Земля и не только, объект на Земле имеет вес из-за гравитационной силы притяжения Земли к объекту. Это сила, действующая на объект.

Мы узнаем больше о весе и силе гравитации в следующем разделе.

Теперь мы можем изобразить трение и вес на диаграмме свободного тела сил, действующих на тележку, следующим образом.

На тележку действует другая сила. Подумайте о том, когда вы стоите на земле: вы чувствуете землю под ногами. Эта контактная сила мешает вам проникнуть в землю. Это называется нормальной силой . Нормальная сила всегда действует перпендикулярно поверхности, на которой находится объект.

В простых ситуациях, например, когда вы стоите на земле или тележка движется по ровной поверхности, нормальная сила равна весу объекта, но в противоположном направлении. Вспомните, что мы узнали о силах, действующих парами. На плоской горизонтальной поверхности нормальная сила является силой реакции на вес объекта. Это показано на диаграмме для коробки, покоящейся на полу.

Теперь мы можем завершить диаграмму свободных тел сил, действующих на тележку, следующим образом:

Как вы думаете, существует ли связь между трением тела и нормальной силой? Давайте исследовать.

Узнайте, какие силы действуют, когда вы пытаетесь толкнуть картотечный шкаф в этой симуляции. http://phet.colorado.edu/en/simulation/forces-and-motion

Это исследование покажет учащимся, что сила трения связана с нормальной силой . Нормальная сила – это реакция поверхности на вес объекта.

Пока у вас есть весы, вы можете использовать любые предметы в качестве масс. Учащиеся должны будут использовать пружинные весы для измерения сил, которые они воздействуют на блоки. Важно, чтобы они измеряли силу, когда блок начинает двигаться, потому что показание упадет, когда блок начнет двигаться, поскольку кинетическое трение меньше статического трения.

Учащиеся уже познакомились с весом в предыдущих классах и расскажут об этом более подробно в следующем разделе, где они фактически вычислят гравитационное ускорение для себя. Пока просто используйте значение g = 9,8 м/с ², а затем вы можете вернуться к этому исследованию, когда учащиеся позже решат для себя гравитационное ускорение.

ИССЛЕДОВАТЕЛЬСКИЙ ВОПРОС: Какая связь между нормальной силой и трением?

ЦЕЛЬ: Определить зависимость между нормальной силой и величиной силы трения.

В ситуациях, которые мы собираемся исследовать, объект будет тянуться по плоской ровной поверхности. Увеличим его массу и измерим результирующую силу трения. Но как это связано с нормальной силой?

Если объект находится на плоской ровной поверхности, нормальная сила равна весу. Как вы узнали из гр. 8 Планета Земля и за ее пределами, и в следующем разделе мы увидим, что мы можем рассчитать вес объекта. Таким образом, мы можем вычислить нормальную силу, действующую на объект.

Для этого исследования рассчитайте вес по формуле W = m × g, где m — масса объекта в кг, а g — 9,8 м/с ² . Мы узнаем больше об этом в следующем разделе.

МАТЕРИАЛЫ И ОБОРУДОВАНИЕ:

деревянные бруски различной массы или куски массы
деревянный брусок с крюком
пружинный баланс
трехбалочные весы или электронные весы

Для этого исследования подойдет любой прибор для измерения массы.

МЕТОД:

Измерьте массу деревянного бруска с помощью крюка на трехбалочных весах. Запишите массу в таблицу. Рассчитайте и запишите нормальную силу.
Положите деревянный брусок с крюком на стол. Прикрепите пружинный баланс к крючку. Сделайте небольшую отметку на столе, с которой нужно начать тянуть блок.
Потяните в сторону, пока блок не начнет двигаться.
Запишите показания усилия в таблице ниже. Повторите это три раза для деревянного блока.
Поместите кусок массы поверх деревянного бруска. Запишите общую массу. Рассчитайте и запишите нормальную силу. Потяните его в сторону, пока он не начнет двигаться. Запишите силу. Повторите это три раза. В каждом случае запускайте блок из одного и того же положения и осторожно тяните.
Повторите эксперимент для больших масс и заполните таблицу.

Мы измеряем статическое трение , то есть трение между двумя НЕ движущимися объектами. Мы измеряем его как минимальную силу, необходимую для начала движения блока.

РЕЗУЛЬТАТЫ:

Полученные результаты будут зависеть от массы используемых блоков и поверхности, на которой проводится исследование. Важно, чтобы учащиеся видели, что по мере увеличения массы увеличивается нормальная сила, а также увеличивается показание на пружинных балансах, измеренное, когда блок начинает двигаться.

Таблица для записи усилия, необходимого для преодоления силы трения и перемещения блока.

Масса (кг)	Нормальная сила (Н)	Показание 1 (N)	Показание 2 (N)	Показание 3 (N)	Среднее (N)

Мы берем три показания, а затем вычисляем среднее значение. Это повышает достоверность результатов.

Постройте график зависимости средней силы, приложенной к блоку в состоянии покоя, от нормальной силы блока.

Сила, приложенная к точке начала движения бруска, равна силе трения, действующей на брусок.

Какая зависимая переменная?

Величина силы трения.

Какая независимая переменная?

Нормальная сила от массы блоков.

АНАЛИЗ:

Нарисуйте помеченную диаграмму свободного тела всех сил, действующих на блок, когда он собирается начать движение.

Пример диаграммы свободного тела. Вес и нормальная сила должны иметь стрелки одинакового размера. Тяговая сила должна быть равна силе трения, поскольку на диаграмме этот объект изображен в тот момент, когда он вот-вот начнет двигаться.

Почему груз на бруске меняется, когда целью исследования является выяснить, как нормальная сила влияет на силу трения?

Объект находится на плоской поверхности, поэтому нормальная сила равна весу. Увеличение массы увеличивает вес как W = m × g, поэтому нормальная сила увеличивается.

Почему для каждой настройки берутся три показания и вычисляется среднее значение?

Повторение эксперимента повышает достоверность результатов.

Какова форма вашего графика?

Форма должна представлять собой прямую линию, проходящую через начало координат. Фактическая форма будет зависеть от точности результатов учащихся и построения графика. Важно только, чтобы график показывал возрастающую тенденцию, чтобы можно было установить связь между нормальной силой и трением.

Что форма графика говорит нам о связи между нормальной силой блока и силой трения?

Форма говорит нам о том, что по мере увеличения нормальной силы` увеличивается и величина силы трения.

Как вы думаете, что произойдет, если положить кубик не на гладкий стол, а на шероховатую или гораздо более гладкую поверхность? Повлияет ли это на результаты?

Да, это повлияет на результат, так как сила трения между разными типами поверхностей различна, например, между гладкими и шероховатыми поверхностями.

ВЫВОД:

Напишите заключение по данному расследованию.

Сила трения увеличивается по мере увеличения нормальной силы объекта.

Повторите исследование и снимите показания пружинных весов, пока блок движется. Как соотносятся показания стационарного блока и подвижного блока? Есть ли разница?

Когда блок движется с постоянной скоростью, трение уменьшается по сравнению с трением, которое необходимо преодолеть, чтобы заставить блок двигаться.

Статическое трение — это максимальное значение трения в тот момент, когда блок начинает двигаться. Затем, когда блок движется с постоянной скоростью, трение уменьшается и называется трением подвижного состава. В первой части исследования мы измеряли только среднее статическое трение с разными массами. Это расширение покажет учащимся, что как только объект начинает двигаться, трение уменьшается.

Упражнение: Трение

МАТЕРИАЛЫ:

Примечание: Было бы неплохо, если бы вы ознакомились с симуляцией, прежде чем разрешить учащимся ее использовать. Это гарантирует, что вы сможете помочь им, если у них возникнут проблемы с симуляцией. Эта ссылка представляет собой загрузку в формате pdf с полезными советами по использованию моделирования: http://phet.colorado.edu/files/teachers-guide/forces-and-motion-basics-guide.pdf

ИНСТРУКЦИИ:

Откройте веб-страницу. Нажмите на кнопку с надписью «Выполнить».
Выберите вкладку «Трение».
Отметьте все поля в правом верхнем углу.
Выберите один из ящиков в поле выбора и перетащите его рядом с человеком.
Приложите усилие к ящику. Медленно увеличивайте усилие, пока ящик не начнет двигаться.

ВОПРОСЫ:

Прежде чем объект начнет двигаться, что вы заметите в величине силы трения по сравнению с величиной приложенной силы? Они сбалансированы или не сбалансированы?

Силы неуравновешены. Сила трения больше приложенной силы.

После того, как объект начнет двигаться, что вы заметите в величине силы трения по сравнению с величиной приложенной силы? Они сбалансированы или не сбалансированы?

Силы неуравновешены. Приложенная сила больше силы трения.

Что вы узнали о том, как заставить объект двигаться?

Чтобы объект двигался, необходима неуравновешенная сила. Приложенная сила должна быть больше силы трения.

Сила трения зависит от типа поверхности, по которой движется объект, и нормальной силы. Чтобы заставить объект двигаться, необходимо приложить силу, превышающую силу трения, чтобы преодолеть трение между объектом и поверхностью.

Теперь мы можем снова рассмотреть пример толкания друга в тележке. Между тележкой и землей возникает трение. Трение действует в направлении, противоположном силам, толкающим тележку вперед. Следовательно, если есть две силы 7 Н и 10 Н, толкающие тележку вперед, и трение равно 5 Н, мы можем изобразить только эти силы следующим образом:

Какова результирующая сила, действующая на тележку?

12 N вправо.

Трение между двумя поверхностями также вызывает нагрев объектов. Попробуйте это, энергично потирая руки друг о друга, а затем ощупайте ладони.

Трение выгодно по ряду причин. Например, трение между нашими ногами и землей позволяет нам двигаться вперед и предотвращает скольжение. Трение также участвует в предотвращении заноса автомобилей, поскольку шины испытывают трение между протектором и проезжей частью.

Узнайте больше о том, как трение вызывает нагрев и плавление материала. Потрите два предмета друг о друга, и они нагреются. Когда достигается температура плавления, частицы вырываются на свободу по мере того, как материал тает. http://phet.colorado.edu/en/simulation/friction

Растяжение и сжатие

Чтобы представить эти силы, предлагается принести в класс различные объекты для экспериментов. Идеальным объектом является кусок пенопласта, так как вы можете показать растяжение и сжатие, потянув и толкнув его соответственно, а также согнув его.

Существуют и другие силы, которые являются контактными силами. Посмотрите на следующий рисунок мальчика, который тянет за веревку блок.

Человек тянет веревку, которая тянет блок. Человек не касается блока напрямую. Человек тянет веревку, а блок тянет веревку в противоположном направлении. Это вызывает натяжение сила, существующая в веревке. Веревка натянута, поэтому в веревке есть натяжение. Напряжение – это контактная сила. Натяжение веревки тянет блок по полу.

Другим примером контактной силы является сжатие . Сила сжатия — это сила, которая деформирует или сдавливает объект. Давайте подумаем о некоторых примерах.

Раздайте классу тесто для лепки и попросите их сформировать шарики, которые они затем могут сжимать в руках, как показано на рисунке ниже.

Если вы возьмете шарик теста и раздавите его пальцами, вы приложите к тесту силу сжатия. Тесто меняет форму. Он деформируется. Другой пример — раздавить теннисный мяч или банку из-под прохладительного напитка между ладонями.

Измельчение теста. Прессование теннисного мяча.

На следующей диаграмме показана разница между растяжением и сжатием.

Силы натяжения — это две силы, действующие на один объект в противоположных направлениях (в направлении друг от друга) для растяжения объекта. Силы сжатия — это две силы, действующие на один объект в противоположных направлениях (навстречу друг другу), сжимающие или деформирующие объект.

Есть много других примеров сил сжатия в повседневной жизни. Мост испытывает как сжатие, так и растяжение из-за веса автомобилей и других транспортных средств, которые проезжают по нему, как показано на следующей диаграмме.

Мы рассмотрели контактные силы, которые включают трение, нормальные силы, сжатие и растяжение. Теперь мы рассмотрим силы, действующие между несоприкасающимися телами.

Полевые (бесконтактные) силы

сила тяжести
магнитная сила
электростатическая сила
полевых войск
аттракцион
отталкивание

Поле — это область в пространстве, где на объект (с определенными свойствами) действует сила. Полевые силы являются бесконтактными силами. Бесконтактные силы – это силы, действующие на расстоянии. Они не должны соприкасаться. Наиболее распространенные примеры полей:

гравитационное поле
магнитное поле
электрическое поле

Когда мы обсуждали контактные силы, мы говорили о толчках и притяжениях. Однако с полевыми силами лучше говорить о отталкивании и притяжении .

Силы гравитации

Вы когда-нибудь задумывались, почему предметы падают вниз, а не вверх?

Вы можете продемонстрировать гравитационный эффект, сбрасывая предметы разной массы с одинаковой высоты. Используйте теннисный мяч и скрученный лист бумаги (чтобы они были примерно одинакового размера и формы). Бросьте их с одной высоты и посмотрите, заметят ли ученики разницу в том, как они падают. Спросите учащихся, почему, по их мнению, предметы упали. Что-то давит на них? Или тянуть их вниз? Попросите их обсудить свои идеи друг с другом.

Модели, представленные в этой главе, очень полезны, если у вас есть доступ в Интернет. В противном случае поощряйте учащихся взаимодействовать с ними в свободное время дома или по мобильному телефону.

Мы уже сталкивались с гравитацией на планете Земля и за ее пределами в предыдущих классах.

Сила, которая заставляет предметы падать на Землю и не дает нам упасть с планеты, называется гравитационной силой . Силы гравитации существуют между любыми двумя объектами с массой, и они являются силами притяжения (тяги).

Ньютон разработал свой Закон всемирного тяготения, описывающий силу притяжения между телами с массой в 1687 году. Работа Ньютона по описанию теории гравитации могла быть вдохновлена наблюдением за падением яблока с дерева.

Строго говоря, говоря о «гравитации», мы имеем в виду именно гравитационную силу притяжения, возникающую между Землей (или другим небесным телом, например планетой) и другими объектами, в отличие от гравитационной силы вообще, которая действует между любые два объекта с массой. Например, мы бы назвали гравитационную силу, притягивающую объекты к Луне, гравитационной силой Луны.

Что такое гравитация?

Сила гравитации — это сила, которая притягивает объекты с массой друг к другу. Любой объект с массой оказывает гравитационное воздействие на любой другой объект с массой . Земля притягивает вас, парты в вашем классе и стулья в вашем классе, удерживая вас на поверхности и не давая улететь в космос.

Гравитация — это сила, поэтому она измеряется в ньютонах.

Сила притяжения Земли притягивает все к центру Земли, поэтому, когда вы роняете предмет, например книгу или яблоко, он падает на землю. Однако знаете ли вы, что вы, ваш стол, ваш стул, падающее яблоко и книга оказывают одинаковое, но противоположное притяжение на Землю? Как вы думаете, почему эти силы на Земле не вызывают заметного движения Земли?

Земля имеет гораздо большую массу, чем человек или стол, и поэтому она ускоряется гораздо меньше, хотя сила, действующая на Землю со стороны стола, равна силе, действующей на стол со стороны Земля (только в противоположных направлениях). Вот почему Земля не движется заметно.

Стрелки показывают направление гравитационного поля Земли. Все стрелки указывают на центр Земли, потому что гравитационная сила всегда притягивает.

Взаимодействуйте с этой симуляцией, чтобы увидеть взаимосвязь между гравитацией, массами объектов и расстоянием между ними. http://phet.colorado.edu/en/simulation/gravity-force-lab http://phet.colorado.edu/sims/html/gravity-force-lab/latest/gravity-force-lab_en.html

Моделирование PhET в боксе для посещений можно использовать для очень простой демонстрации того, как гравитационная сила между двумя объектами увеличивается с массой и уменьшается с увеличением расстояния между объектами. Вы можете отключить значения и использовать положение фигурок, дергающих за веревки, чтобы качественно продемонстрировать отношения.

Земля притягивает нас, потому что у нее такая большая масса, и поэтому мы все время притягиваемся вниз к центру Земли.

Эти армейские парашютисты только что выпрыгнули из задней части самолета и упали на Землю из-за гравитации.

Чем больше масса объектов, тем больше сила между ними. Это означает, что два небольших объекта будут иметь очень слабое гравитационное притяжение, поэтому оно не оказывает заметного эффекта. Однако более крупные объекты, такие как Луна и Земля, обладают гораздо большей гравитационной силой.

Переместите Солнце, Землю, Луну и космическую станцию, чтобы увидеть, как это повлияет на их гравитационные силы и орбитальные траектории. http://phet.colorado.edu/en/simulation/gravity-and-orbits

Как мы знаем из «Планеты Земля и за ее пределами», все планеты в нашей Солнечной системе удерживаются на орбитах вокруг Солнца силой гравитационного притяжения. между Солнцем и планетами.

Планеты движутся вокруг Солнца в нашей Солнечной системе. Существует гравитационная сила притяжения между Солнцем и планетами, а также между планетами и их лунами.

Создайте свою собственную солнечную систему с помощью этой симуляции и поэкспериментируйте с массами и орбитами. http://phet.colorado. edu/en/simulation/my-solar-system

Вторым фактором, влияющим на гравитационную силу притяжения между объектами, является расстояние между ними. Чем дальше объекты друг от друга, тем меньше гравитационная сила.

Между нами и Солнцем существует гравитационная сила притяжения, но мы этого не замечаем, так как находимся так далеко друг от друга и очень малы.

Все компоненты нашей Вселенной удерживаются вместе гравитационной силой. Подводя итог, мы можем сказать:

Чем больше масса объектов, тем сильнее гравитационная сила притяжения между ними.
Чем ближе объектов друг к другу, тем сильнее гравитационная сила между ними.

Заметка о падающих предметах

Полезный способ продемонстрировать гравитацию Земли — посмотреть на падающие предметы. Ниже приведено дополнительное дополнительное задание, в котором учащиеся бросают различные предметы. Вы можете проголосовать в классе, чтобы узнать, думают ли учащиеся, что яблоко или пакетик сахара упадут на землю первыми. (Ответ: они упадут на землю одновременно, если сопротивление воздуха незначительно.) Очень вероятно, что у учащихся сложится предубеждение, что более тяжелые предметы падают быстрее. В данный момент не важно, чтобы ответы учащихся были правильными, и не пытайтесь подвести их к правильному ответу. Они, надеюсь, откроют это для себя в следующем эксперименте.

В этом исследовании учащиеся должны работать в парах. Сначала они одновременно роняют целое яблоко и половинку яблока с одинаковой высоты. Затем они будут экспериментировать с мячами разной массы (но одинакового размера) и мячами одинаковой массы (но разного объема). Очень сложно ронять предметы в одно и то же время так, чтобы они упали на пол одновременно, поэтому позвольте учащимся повторить эксперимент несколько раз, пока они не будут уверены, что роняют предметы одновременно. Если им трудно увидеть, какой предмет падает на землю первым, предложите учащимся прислушаться к тому количеству звуков, которые они слышат — один или два — при ударе предметов. Учащимся, возможно, придется повторить это исследование много раз, поскольку оно, скорее всего, противоречит их предубеждениям. Совет по безопасности: лучше заранее разрезать яблоки пополам.

Когда учащиеся закончат свой эксперимент, вы можете продемонстрировать эффект сопротивления воздуха, бросив молоток и перо. Предложите учащимся проголосовать за то, что произойдет, если вы бросите молоток и перо. Будьте готовы объяснить учащимся, что сопротивление воздуха замедляет падение пера и что, если бы не было сопротивления воздуха, оба пера падали бы с одинаковой скоростью и одновременно ударялись об пол.

ИССЛЕДОВАТЕЛЬСКИЙ ВОПРОС: Падают ли разные предметы с одинаковой скоростью?

ГИПОТЕЗА:

Как вы думаете, что произойдет?

Ответ зависит от учащегося.

МАТЕРИАЛЫ И ОБОРУДОВАНИЕ:

молоток
перо
два мяча одинаковой массы, разного объема (один комплект на пару)
два мяча одинакового объема, разной массы (один комплект на пару)

Видео перьев и монет, падающих в вакууме

МЕТОД:

Работайте в парах, по очереди будьте тем, кто роняет предмет (экспериментатор), и тем, кто наблюдает за падением предметов (наблюдателем).
Заполните столбец «прогноз» в таблице ниже.
Экспериментатор: встаньте на стул или стол и возьмите два шара одинаковой массы, один в одну руку, а другой в другую.
Экспериментатор: поднимите два мяча на одной высоте перед собой и бросьте их в одно и то же время.
Наблюдатель: обратите внимание на то, что происходит, в частности, что приземлится первым.
Поменяйтесь местами и повторите эксперимент, используя два шара одинакового объема, но разной массы.
Теперь ваш учитель продемонстрирует вам и бросит молоток и перо. Перед тем, как учитель бросит молоток и перо, запишите в колонку прогнозов падение молотка и пера.
Запишите, что произошло с молотком и пером, и ответьте на приведенные ниже вопросы.

РЕЗУЛЬТАТЫ И НАБЛЮДЕНИЯ:

Что вы оставили постоянным в этом эксперименте?

Высота, с которой падают предметы.

Что вы изменили в этом эксперименте?

Тип сбрасываемых объектов, в частности масса и объем объектов.

В приведенной ниже таблице запишите, что, по вашему мнению, произойдет в столбце «прогноз», прежде чем проводить эксперимент. Как вы думаете, что произойдет, если вы бросите каждую пару предметов с одной и той же высоты в одно и то же время? Как вы думаете, что приземлится первым?

Объекты	Прогноз	Наблюдение
Мячи: одинаковой массы, разного объема
Мячи: разная масса, одинаковый объем
Молоток и перо

ОЦЕНКА:

Насколько надежным был ваш эксперимент? Как бы вы могли улучшить свой метод?

Ответ зависит от учащегося. Примеры ответов могут включать: Трудно бросать предметы одновременно. Лучше сбрасывать предметы с большей высоты. На результаты могло повлиять сопротивление воздуха, и было бы лучше сбрасывать предметы в вакууме.

ВЫВОДЫ:

Напишите заключение по данному исследованию.

Учащиеся должны были обнаружить, что половина яблока и целое яблоко упали на пол одновременно. Они также должны были обнаружить, что шары одинаковой массы падают на пол в одно и то же время, а также шары одного объема падают на пол в одно и то же время. Из этого они должны сделать вывод, что все падающие предметы падают с одинаковой скоростью, независимо от их формы или размера, если сопротивлением воздуха можно пренебречь. (Дополнительно: они ускоряет с той же скоростью). В случае падения молотка и пера учащиеся должны были обнаружить, что молоток приземлился первым. Это происходит из-за эффекта сопротивления воздуха, замедляющего падение пера.

Заблуждения о падающих предметах (видео) youtube.com/embed/_mCC-68LyZM»/>

ВОПРОСЫ:

Что приземлилось первым, яблоко или половинка яблока?

Они оба должны были приземлиться в одно и то же (или почти в одно и то же) время.

Считая шары одинаковой массы, какой из них приземлился первым, больший или меньший?

Они оба должны были приземлиться одновременно.

Учитывая шары одинакового объема, какой из них приземлился первым, более тяжелый или более легкий?

Они оба должны были приземлиться одновременно.

Как вы думаете, почему два упавших мяча всегда приземлялись одновременно?

В идеальной ситуации все объекты, сброшенные с одной высоты, приземлятся одновременно. Это связано с тем, что гравитационная сила Земли заставляет каждый объект ускоряться на одну и ту же величину каждую секунду, независимо от того, насколько он тяжелый или каков его объем.

Примечание для опытных учителей:

Согласно универсальному закону гравитации, сила земного притяжения притягивает объект с силой, пропорциональной массе объекта и массе Земли. Во всех случаях масса Земли одинакова, поэтому любые различия в силе гравитации на объекты на Земле зависят только от разницы в массе сбрасываемых объектов.

Согласно второму закону Ньютона результирующая сила, действующая на объект F, определяется как F=ma, где m — масса объекта, а a — ускорение, создаваемое результирующей силой F.

Как вы думаете, почему молот приземлился раньше пера?

В реальной ситуации воздух вокруг нас влияет на то, как предметы падают. Когда объект движется по воздуху, он испытывает сопротивление воздуха. Перо намного легче молотка, поэтому влияние сопротивления воздуха на перо гораздо больше. Суммарная сила, действующая вниз на падающий объект, представляет собой силу гравитации за вычетом силы сопротивления воздуха. Поскольку перо намного легче молотка, результирующая сила, действующая на него, будет меньше, поэтому оно будет испытывать меньшее ускорение по направлению к земле и падать медленнее.

Примечание для опытных преподавателей:

Сопротивление воздуха — это сила сопротивления, действующая для замедления объекта. Величина силы зависит от квадрата скорости падающего объекта, площади поверхности падающего объекта и плотности жидкости, в которую он падает (в данном случае воздуха). Очень легкие объекты замедляются за счет сопротивления воздуха, например, перья или тонкие листы бумаги. Это потому, что их гравитационная сила очень мала по сравнению с сопротивлением воздуха. Очень большие объекты также замедляются из-за сопротивления воздуха. Это объясняет, почему парашют замедляет ваше падение. Перед раскрытием парашюта сопротивление воздуха невелико. После раскрытия широкий парашют испытывает большее сопротивление воздуха, которое затем замедляет вас.

Очень важно, чтобы учащиеся понимали разницу между массой и весом. В науке вес — это сила, но учащиеся привыкли использовать слово «вес» при описании своей массы. Вес – это сила, с которой объект сталкивается под действием силы тяжести. На Земле все объекты притягиваются вниз к центру Земли, и наш вес указывает на величину этого притяжения. Вес будет варьироваться в зависимости от нашего положения в пространстве, но наша масса должна оставаться постоянной независимо от нашего положения.

Вы, вероятно, уже много раз слышали термин «вес» на уроках естественных наук или в разговорах с другими людьми. Многие люди неправильно используют термин «вес» в повседневном языке. Например, родственник может сказать вам: «Мой вес увеличился на 2 кг за праздники, так как я съел слишком много еды». Что не так с этим утверждением? Обсудите это со своим классом и учителем.

Это утверждение неверно, так как родственница приравнивает свой вес к килограммам. Килограммы — это мера массы, а не веса. Ее масса могла увеличиться на 2 килограмма.

вес
масса
свободное падение
гравитационное ускорение

Слово «масса» происходит от греческого слова maza , что означает кусок теста или пирог.

Масса объекта – это количество вещества в объекте. Он говорит вам, сколько частиц у вас есть. Вы помните, что узнали об атомах в «Материи и материалах»? Так, например, масса деревянного бруска говорит нам, сколько в нем атомов. Масса измеряется в килограммах (кг) и не зависит от того, где вы ее измеряете. Деревянный брусок массой 10 кг на Земле также имеет массу 10 кг на Луне.

Однако вес объекта может меняться, так как он зависит от массы объекта, а также от силы гравитационной силы, действующей на него. Вес измеряется в ньютонах (Н), так как это гравитационная сила притяжения, действующая на объект со стороны Земли (или Луны, или любой другой планеты). Следовательно, вес объекта будет меняться при взвешивании в разных местах. Вес 10-килограммового блока на Земле будет отличаться от веса на Луне. Как вы думаете, почему это так? Будет ли вес больше или меньше, чем на Луне?

Земля намного больше Луны, поэтому сила притяжения между Землей и блоком будет больше, чем сила между Луной и блоком.

Масса, вес и гравитация (видео).

СЛЕДИТЕЛЬНЫЙ ВОПРОС: Какая связь между массой предмета и его весом?

ГИПОТЕЗА: Напишите гипотезу для этого исследования.

Ответ зависит от учащегося.

МАТЕРИАЛЫ И ОБОРУДОВАНИЕ

четыре куска массы с шагом 500 г (один по 500 г, один по 1 кг, один по 1,5 кг и один по 2 кг)
пружинный баланс
Трехбалочные весы

Для измерения массы объектов можно использовать любой измеритель массы. Также можно использовать кухонные весы или электронные весы.

МЕТОД:

Измерьте массу штук на трехбалочных весах.
Измерьте вес каждой части груза с помощью пружинных весов.
Запишите массу и соответствующую массу в таблицу результатов.
Нарисуйте график своих результатов.
Рассчитать градиент графика.

РЕЗУЛЬТАТЫ:

Запишите свои результаты в следующую таблицу.

Масса (кг)	Вес (Н)

Пример результатов при использовании предложенных массовых штук:

Масса (кг)	Вес (Н)
0,5	4,8
1	9,8
1,5	14,7
2	19,6

Что такое зависимая переменная?

Вес

Что такое независимая переменная?

Масса

Таким образом, вес отложен по оси Y в зависимости от массы по оси X

Начертите график в отведенном ниже месте.

Ваш график должен быть прямой линией. Используйте пространство ниже, чтобы вычислить градиент вашего графика.

Градиент должен быть 9,8.

Возможно, вам придется напомнить учащимся о вычислении уклона прямой линии. Они должны были рассмотреть эту тему в математике, но было бы полезно напомнить им. Им нужно выбрать две координаты на своей прямой. Они могут выбрать любые две координаты, которые следует обозначить как (x1; y1) и (x2; y2). Формула градиента прямой линии: градиент = подъем/разгон = (y2 — y1)/(x2 — x1)

Пример расчета: градиент = (9,8 — 4,8)/(1 — 0,5) = 9,8

Учащиеся могут не получить правильный ответ для градиента, если они неправильно построили график или если пружинные балансы не откалиброван должным образом. Они могут получить ответ ближе к 10. Градиент графика дает гравитационное ускорение на Земле. Это будет объяснено в тексте после расследования.

ЗАКЛЮЧЕНИЕ:

Напишите заключение по этому исследованию.

Вес объекта прямо пропорционален его массе.

Вес — это сила тяжести, притягивающая вас к центру Земли. Измеряется в ньютонах. На Земле гравитационная сила заставляет нас всех ускоряться по направлению к центру Земли. Ускорение называется гравитационным ускорением . На Земле это 9,8 м/с ² . Градиент, который мы рассчитали в последнем исследовании, должен был дать вам число, близкое к 9,8 м/с ² — гравитационное ускорение.

Объекты находятся в состоянии свободного падения , когда на них действует только сила тяжести.

Вес (W) рассчитывается путем умножения массы объекта (m) на ускорение свободного падения (g):

W = m × g

Мы использовали эту формулу в последнем разделе о трении для расчета веса и, следовательно, нормальная сила, действующая на объект.

А что, если бы вы отправились на Луну?

Луна в 6 раз меньше Земли.

Масса Земли 5,972 × 10 ²⁴ кг.

Луна тоже имеет собственную гравитацию. Сила гравитации на поверхности Луны составляет одну шестую силы тяжести на поверхности Земли, поэтому вы будете весить одну шестую того, что вы делаете на Земле на Луне. На Юпитере вы будете весить в 2,5 раза больше, чем на Земле, поскольку гравитация Юпитера в 2,5 раза больше земной. Несмотря на то, что вы будете весить по-разному (и чувствовать себя легче на Луне и тяжелее на Юпитере), ваша фактическая масса останется неизменной в обоих случаях.

Масса космонавта остается неизменной, где бы ее ни измеряли. Однако вес астронавта зависит от того, где вы его измеряете, так как вы можете видеть, что астронавт весит 1200 Н на Земле и только 200 Н на Луне.

Так сколько бы ты весил на Луне? Представьте, что у вас есть масса 60 кг. Ваш вес на Земле будет 60 х 9,8 = 588 Н. Гравитационное ускорение на Луне 1,6 м/с ² , поэтому ваш вес на Луне будет 60 х 1,6 = 96 Н.

Весы измеряют вес и преобразуют его в массу.

Расчет веса и массы

Это короткое упражнение для тренировки некоторых расчетов. Учащиеся могут выполнить это задание в качестве домашнего задания.

ВОПРОСЫ:

Феррари имеет массу 1485 кг. Каков его вес на Земле?

Феррари.

вес = 1485 х 9,8 = 14553Н

Линдиве имеет массу 50 кг на Земле. Какова ее масса на Луне?

50 кг, так как масса объекта не зависит от положения.

Ян имеет массу 78 кг. Его друг Сэм говорит, что на Луне он будет весить 24 Н. Сэм прав? Объясните с помощью расчета.

вес на Луне = 78 X 1,6 = 124,8 N

Сэм неверен.

У вас есть яблоко массой 220 г, каков его вес на Земле и на Луне?

масса = 220 г = 0,22 кг.

вес на Земле = 0,22 х 9,8 = 2,156 Н

вес на Луне = 0,22 х 1,6 = 0,352 Н

Если корова весила 1340 Н на Луне, какова ее масса?

Трикотажная корова.

масса = 1340 / 1,6 = 837,5 кг

Узнайте больше онлайн, взаимодействуя с этой симуляцией, используя детали и пружины различной массы. Перевозите лабораторию на разные планеты. http://phet.colorado.edu/en/simulation/mass-spring-lab

Моделирование PhET, указанное в ссылке для посещения, можно использовать, чтобы легко показать, как изменяется вес объектов. Эту симуляцию можно использовать на многих различных уровнях, в зависимости от сложности концепций, которые вы хотите проиллюстрировать. Ссылка на pdf-файл с советами по обучению от команды PhET доступна здесь: http://phet.colorado.edu/files/teachers-guide/mass-spring-lab-guide.pdf

Вы когда-нибудь задумывались, на что это будет похоже? ходить по другим планетам? Узнайте, сколько бы вы весили на других планетах, в следующем упражнении.

Это необязательное действие . В этом упражнении учащиеся рассчитывают свой вес на семи других планетах нашей Солнечной системы. Хотя их масса останется прежней, они будут «чувствовать» себя легче или тяжелее из-за различий в силе гравитационного поля на поверхностях других планет. Следует подчеркнуть, что их масса всегда остается неизменной, а меняется только их вес. Если у вас нет доступа к весам, вы можете либо попросить учащихся оценить свою массу, либо предоставить им примерный номер.

МАТЕРИАЛЫ:

весы
калькулятор

ИНСТРУКЦИИ:

Измерьте свою массу в килограммах. Запишите значение в таблицу ниже.

Используйте значения ускорения свободного падения на разных планетах, чтобы вычислить, сколько вы будете весить на этой планете.

Планета	Ваша масса (кг)	Значение g (м/с ² )	Ваш вес (Н)
Земля		9,8
Меркурий		3,6
Венера		8,8
Марс		3,8
Юпитер		26
Сатурн		11,2
Уран		10,5
Нептун		13,3

Пример ответов для ученика весом 50 кг

Планета	Ваша масса (кг)	Значение g (м/с 2 )	Ваш вес (Н)
Земля	50	9,8	490
Меркурий	50	3,6	180
Венера	50	8,8	440
Марс	50	3,8	190
Юпитер	50	26	1300
Сатурн	50	11,2	560
Уран	50	10,5	525
Нептун	50	13,3	665

ВОПРОСЫ:

На каких планетах вы бы чувствовали себя тяжелее, чем на Земле?

Вам будет тяжелее на Юпитере и Нептуне.

На каких планетах вы бы чувствовали себя легче, чем на Земле?

Вам будет легче на Меркурии, Венере, Марсе, Сатурне и Уране.

Вес человека – это сила гравитационного притяжения к Земле, которую испытывает человек. Кто-то в свободном падении чувствует себя невесомым, но не потерял в весе. Они все еще испытывают гравитационное притяжение Земли.

Единственная причина, по которой астронавты плавают, заключается в том, что они находятся в свободном падении, и их движущийся космический корабль также находится в свободном падении вместе с ними, падая с той же скоростью. Следовательно, астронавты кажутся парящими по сравнению с космическим кораблем, потому что оба они падают с одинаковой скоростью.

Космонавты испытывают невесомость.

Наблюдайте за сверхзвуковым свободным падением Феликса Баумгартнера обратно на Землю. Он испытал свободное падение или невесомость.

Замечание о невесомости

Термин «невесомость» вызывает много путаницы у учащихся. Смешение фактического веса человека с его ощущением веса является источником многих заблуждений. Невесомость относится только к чьему-то ощущению своего веса или его отсутствия. Невесомость — это чувство, которое испытывает человек, когда никакие внешние объекты не соприкасаются с человеком, оказывающим на них давление или притяжение (мы называем эти контактные силы, потому что они возникают из-за того, что предметы соприкасаются или соприкасаются друг с другом).

Вес человека – это сила гравитационного притяжения к Земле, которую испытывает человек. Кто-то в свободном падении чувствует себя невесомым, но не потерял своего веса. Они все еще испытывают гравитационное притяжение Земли.

Учащиеся также часто не понимают, почему астронавты на орбите Земли парят в своих космических кораблях. Одно распространенное заблуждение состоит в том, что в космосе нет гравитации, поэтому астронавты могут летать. На самом деле, на низкой околоземной орбите гравитация Земли составляет около 90% своей силы на поверхности Земли. Единственная причина, по которой астронавты плавают, заключается в том, что они находятся в свободном падении, и их космический корабль также находится в свободном падении вместе с ними, падая с той же скоростью. Следовательно, астронавты кажутся парящими по сравнению с космическим кораблем, потому что оба они падают с одинаковой скоростью. Другим примером является то, что орбитальные космические корабли по существу находятся в свободном падении, поскольку «ничто» не замедляет их движение к центру Земли, но из-за их орбитальной скорости они никогда не приближаются к Земле.

Прекрасная ссылка на видео человека, переживающего свободное падение, указана в поле «Посетить».

Магнитные силы

магнит
магнитный материал

Некоторые материалы имеют сильные магнитные поля вокруг себя. Их называют магнитами. Все магниты имеют два полюса, северный и южный.

Пример стержневого магнита с северным и южным полюсами.

Другие материалы сильно притягиваются к магнитам. Эти материалы называются магнитными. Магниты воздействуют на другие магниты и магнитные материалы. Какие материалы являются магнитными? Давайте исследовать.

ИССЛЕДОВАТЕЛЬСКИЙ ВОПРОС: Какие материалы являются магнитными, а какие нет?

ГИПОТЕЗА:

Напишите гипотезу для этого исследования.

Ответ зависит от учащегося. Есть много различных возможных гипотез для этого исследования. Примером может быть: Только некоторые материалы являются магнитными.

МАТЕРИАЛЫ И ОБОРУДОВАНИЕ:

стержневые магниты
бумага
дерево
пластик
железо
алюминий
сталь

МЕТОД:

Держите различные предметы рядом с стержневым магнитом (не касаясь), чтобы увидеть, притягиваются ли они к магниту.
Заполните таблицу, указав, притягиваются ли предметы к магниту.

Учащиеся должны заметить, что неметаллы не притягиваются к магнитам и что медь, даже если это металл, не притягивается.

Как уничтожить магнит.

РЕЗУЛЬТАТЫ:

Заполните следующую таблицу.

Материал	Магнитный (ДА/НЕТ)
бумага
дерево
пластик
железо
алюминий
сталь
медь

Материал	Магнитный (ДА/НЕТ)
Бумага	НЕТ
дерево	НЕТ
пластик	НЕТ
железо	ДА
алюминий	НЕТ
сталь	ДА
медь	НЕТ

ЗАКЛЮЧЕНИЕ:

Какой вывод вы можете сделать из ваших результатов?

Не все материалы являются магнитными. Лишь некоторые металлы обладают магнитными свойствами, например железо.

Не все металлы притягиваются к магнитам. Те, которые притягиваются к магнитам, известны как магнитные материалы . Магнитных материалов очень мало. Это железо, никель и кобальт. Сплавы, в состав которых входят любые магнитные материалы, также могут притягиваться к магнитам. Сталь — это сплав, содержащий железо, поэтому сталь может притягиваться к магниту.

Сплав представляет собой смесь металлов.

Итак, теперь мы знаем, что магнитные силы могут действовать на расстоянии, но могут ли они действовать, если что-то мешает? Давай выясним.

Магнитные силы являются бесконтактными силами и могут действовать на расстоянии. Однако обычные магниты не имеют очень сильных магнитных полей. Чем дальше объект от магнита, тем слабее сила, которую он испытывает. Магнит должен действовать через большинство веществ. Если объект, помещенный между магнитом и металлом, слишком толстый, то металл может быть слишком далеко от магнита, чтобы испытывать достаточно сильную силу. Таким образом, это отсутствие притяжения связано с силой магнитного поля, а не с «блокирующей» способностью материала. В этом исследовании вы можете исследовать это, используя тонкий кусок дерева и толстый кусок дерева. Магнитное поле может действовать через тонкую древесину, что означает, что древесина не является «блокатором» магнитной силы. Таким образом, если толстая древесина препятствует притяжению скрепок, видно, что имеет значение расстояние между скрепками и магнитом, а не материал (дерево).

МАТЕРИАЛЫ:

стержневые магниты
бумага
тонкий кусок дерева
толстый кусок дерева
фольга
скрепки

ИНСТРУКЦИИ:

Держите два северных полюса близко друг к другу. Что ты заметил?

Два полюса отталкиваются друг от друга. Есть «толкающая» сила.

Держите два южных полюса близко друг к другу. Что ты заметил?

Два полюса отталкиваются друг от друга. Есть «толкающая» сила.

Держите северный полюс и южный полюс близко друг к другу. Что ты заметил?

Два полюса притягиваются друг к другу. Между полюсами действует сила притяжения.

Положите скрепки на стол.

Попробуйте подобрать скрепки магнитом, но поместите один из других материалов между магнитом и скрепками. Скрепки все еще притягиваются к магниту?

Магнит должен проходить сквозь любые материалы, если они достаточно тонкие. Именно расстояние между магнитом и скрепками будет влиять на притяжение. Таким образом, тонкий кусок дерева не должен препятствовать притяжению, но более толстая древесина будет удерживать скрепки достаточно далеко от магнита, чтобы сделать притяжение слишком слабым, чтобы поднять скрепки.

Попробуйте разные материалы между магнитом и скрепкой.

ВОПРОСОВ:

Имелись ли материалы, препятствовавшие захвату скрепок магнитом?

Единственным материалом, который мог помешать магниту захватить скрепки, является толстый кусок дерева.

Что эта деятельность говорит нам о природе магнитной силы?

Действует на расстоянии. Он сильнее всего ближе к магниту и слабее по мере удаления от магнита.

В последнем упражнении мы видели, что одноименные полюса отталкиваются, а противоположные полюса притягиваются. Мы также видели, что магнитная сила действует на расстоянии. Магниту не нужно касаться чего-либо, чтобы воздействовать на него силой. Таким образом, магнитная сила является бесконтактной или полевой силой.

Что такое силовое поле? Можем ли мы это увидеть? Давайте исследуем, возможно ли увидеть магнитное поле.

Что такое магнитное поле?

Железные опилки выравниваются с магнитным полем. Объясните учащимся, что железные опилки показывают поле в двух измерениях, но на самом деле поле окружает магнит в трех измерениях.

МАТЕРИАЛЫ:

железные опилки
два стержневых магнита
бумага

ИНСТРУКЦИИ:

Положите стержневой магнит на стол.
Положите бумагу на магнит.
Встряхните железные опилки на бумагу.
Пальцем медленно протолкните опилки вокруг магнита.
Запишите образец и нарисуйте его ниже.

Здесь показан рисунок вокруг стержневого магнита.

Снимите бумагу с магнита.
Поместите второй магнит рядом с первым так, чтобы разные полюса были обращены друг к другу.
Верните бумагу на магниты.
Переместите железные опилки вокруг двух магнитов, особенно между магнитами.
Нарисуйте узор в поле ниже.

Схема притяжения двух противоположных полюсов.

Снимите бумагу с магнита.
Переместите второй магнит так, чтобы его полюса были обращены друг к другу.
Верните бумагу на магниты.
Переместите железные опилки вокруг двух магнитов, особенно между магнитами.
Нарисуйте узор в поле ниже.

Узор между двумя одинаковыми полюсами отталкивания.

Как мы видели, можно визуализировать магнитное силовое поле вокруг магнита. Мы знаем из нашей предыдущей деятельности, что магнитная сила действует на расстоянии. Поле — это пространство вокруг магнита, в котором он может притягивать или отталкивать другой магнит.

В последнем упражнении железные опилки показали двухмерное изображение поля, но на самом деле поле окружает магнит в трех измерениях.

Магнитное поле вокруг подковообразного магнита.

Как нарисовать силовое поле? Образец, который вы видели с помощью ваших магнитов, может быть представлен силовыми линиями . Линии поля используются, чтобы показать то, что мы на самом деле не можем видеть. Чем ближе сближены силовые линии, тем сильнее описываемое поле. Чем больше линий поля нарисовано, тем сильнее поле. Силовые линии идут от северного полюса к южному полюсу. На следующей диаграмме показаны линии поля вокруг стержневого магнита.

На следующих рисунках показаны силовые линии между стержневыми магнитами, которые притягивают и отталкивают.

Противоположные полюса притягиваются.

Как полюса отталкиваются.

Поле сильнее всего рядом с магнитом и ослабевает по мере удаления от магнита.

Знаете ли вы, что Земля похожа на стержневой магнит с северным и южным полюсами? Земля имеет магнитное поле. Вы можете представить себе магнитное поле Земли так, как будто через ядро проходит стержневой магнит, южный полюс которого находится под северным полюсом Земли. Никто не знает наверняка, но теория состоит в том, что сверхгорячее жидкое железо в ядре Земли движется вращательно, и эти вращательные силы приводят к слабым магнитным силам вокруг оси вращения Земли.

Земля имеет магнитное поле, как будто через ядро проходит большой стержневой магнит, южный полюс которого находится под северным магнитным полюсом Земли.

Магнитное поле Земли. http://science.howstuffworks.com/environmental/29143-100-greatest-discoveries-earths- Magnetic-field-video.htm

Где находится настоящий Северный полюс.

Вот почему мы можем использовать компас, чтобы определить направление. У компаса есть стрелка с небольшим магнитом. Стрелка указывает на магнитный север, потому что маленький магнит притягивается к противоположному магнитному полю и может использоваться для определения направления.

Компас со стрелкой, указывающей на север.

Южное сияние также называют Aurora Australis, а северное сияние называют Aurora Borealis.

Вы когда-нибудь слышали о южном или северном сиянии? Вы знаете, как происходит это явление?

Южное сияние, вид с Международной космической станции.

Заряженные частицы покидают поверхность Солнца и движутся наружу во всех направлениях. Когда заряженные частицы достигают Земли, некоторые из них захватываются магнитным полем Земли в областях в космосе вокруг земной атмосферы, называемых поясами. Иногда заряженные частицы покидают пояса и движутся по спирали вдоль силовых линий магнитного поля к магнитным полюсам, где они входят в атмосферу Земли. Затем они взаимодействуют с частицами атмосферного газа, вызывая красивые световые шоу.

Что вызывает северное сияние?

Некоторые жидкости также могут намагничиваться в присутствии сильного магнитного поля. Их называют феррожидкостями.

Пример феррожидкости, жидкости, которая может намагничиваться в магнитном поле.

Магнитная жидкость (видео).

Электростатические силы

Помните ли вы, что изучали статическое электричество в Гр. 8? Давайте быстро повторим некоторые из уже известных нам понятий.

Несмотря на то, что эти эксперименты проводились в Гр. 8, важно, чтобы учащиеся выполняли их снова в качестве деятельности. Это поможет им понять, как работают электроскоп и генераторы Ван де Граафа.

Вы также можете выполнять это упражнение, используя пластиковую расческу, а не воздушные шарики. В противном случае вы можете использовать кусочки бумаги вместо волос ученика, так как не все волосы будут вести себя следующим образом.

МАТЕРИАЛЫ:

воздушные шары (или пластиковая расческа)
стеклянная палочка
кусок трикотажа (шерсть)
Пруток из ПВХ
пластиковая линейка
маленькие кусочки бумаги
водопроводный кран

ИНСТРУКЦИИ:

Работайте в парах.

Надуйте воздушный шар и завяжите его, чтобы воздух не выходил.

Держите шарик на небольшом расстоянии от волос. Что ты заметил?

Ничего не происходит.

Потрите волосы шариком.

Теперь держите шарик на небольшом расстоянии от волос. Что ты видишь?

Волосы должны «подняться» и прилипнуть к шарику.

Затем держите стеклянную палочку над маленькими кусочками бумаги. Что ты заметил?

Ничего не происходит.

Натрите стеклянную палочку трикотажем.

Держите стеклянную палочку над кусочками бумаги. Что ты заметил?

Кусочки бумаги прилипают к стеклянной палочке.

Снова протрите стеклянную палочку трикотажем.

Откройте кран, чтобы потекла тонкая струйка воды.

Поднесите стеклянную палочку к струе воды. Что ты заметил?

Струя воды наклоняется к стеклянной палочке.

ВОПРОСЫ:

Что вы сделали, чтобы ваши волосы прилипали к шарику?

Энергично потер баллоном.

Что будет, если потереть стеклянную палочку о трикотаж?

Электроны переносятся со стеклянного стержня на трикотаж за счет трения. Стеклянная палочка становится положительно заряженной, а вата – отрицательно.

Почему стеклянная палочка притянула струю воды?

Вода имеет положительные и отрицательные заряды. Отрицательные заряды притягивались к положительно заряженному стержню.

Давайте рассмотрим пример расчесывания волос подробнее, чтобы понять, что происходит. Вы провели пластиковой расческой по поверхности волос. Когда две поверхности трутся друг о друга, между ними возникает трение . Трение между двумя поверхностями может вызвать перенос электронов с одной поверхности на другую.

Чтобы понять, как могут переноситься электроны, нам нужно вспомнить, что мы узнали о структуре атома.

Где расположены электроны в атоме?

Электроны расположены в пространстве вокруг ядра.

Какой заряд имеет протон?

Положительный заряд.

Каков тип заряда электрона?

Отрицательный заряд.

Каков заряд нейтрона?

Нейтроны не заряжены. Они нейтральны.

Атом удерживается вместе благодаря электростатическому притяжению между положительно заряженным ядром и отрицательно заряженными электронами. Внутри атома электроны, находящиеся ближе всего к ядру, удерживаются сильнее всего, в то время как те, что находятся дальше, испытывают более слабое притяжение.

Обычно атомы содержат одинаковое количество протонов и электронов. Это означает, что атомы обычно нейтральны , потому что они имеют одинаковое количество положительных и отрицательных зарядов, поэтому заряды уравновешивают друг друга. Все объекты состоят из атомов, и поскольку атомы обычно нейтральны, объекты также обычно нейтральны.

Однако, когда мы трёмся друг о друга двумя поверхностями, например, когда вы расчёсываете волосы или трёте о волосы воздушный шар, трение может привести к переносу электронов с одного объекта на другой. Помните, что протоны зафиксированы в ядре и поэтому не могут перемещаться между атомами. Между атомами могут передаваться только электроны. Некоторые объекты отдают электроны легче, чем другие объекты. Посмотрите на следующую диаграмму, которая объясняет, как это происходит.

Какой объект на диаграмме отдал часть своих электронов?

Волосы.

У этого объекта теперь больше положительных или больше отрицательных зарядов?

Имеет больше положительных зарядов.

Какой объект на диаграмме получил электроны?

Гребень.

У этого объекта теперь больше положительных или больше отрицательных зарядов?

Имеет больше отрицательных зарядов.

Когда в объекте больше электронов, чем протонов, мы говорим, что объект отрицательно заряжен .

Когда в объекте меньше электронов, чем протонов, мы говорим, что объект положительно заряжен .

Помните, что движутся только внешние электроны, а не протоны, находящиеся в ядре атома.

Взгляните на следующие схемы, иллюстрирующие это.

Моделирование трения между ковром и ногой Джона Траволты. http://phet.colorado.edu/en/simulation/travoltage

Теперь мы понимаем перенос электронов, происходящий в результате трения между объектами. Но как это привело к тому, что ваши волосы встали дыбом, когда вы поднесли заряженный шарик к волосам в последнем упражнении? Давайте посмотрим, что происходит, когда противоположно заряженные объекты сближаются.

Это забавная демонстрация того, как одноименные заряды отталкиваются, а разноименные притягиваются. Если у вас достаточно материалов, позвольте учащимся попробовать это сделать самостоятельно. Если у вас недостаточно материалов, сделайте это в качестве демонстрации, но дайте учащимся возможность немного поиграть.

Сначала потренируйтесь в этом упражнении несколько раз, чтобы убедиться, что метод у вас правильный. Помните, что очень легко случайно заземлить стержни, поэтому работайте с осторожностью. Лучше всего это будет работать в сухой день. Это будет зависеть от района, в котором вы живете.

На семинаре по мозговому штурму с учителями-добровольцами и учеными в начале 2013 года мы сняли быструю демонстрацию этой задачи, когда группа ее обсуждала. Вы можете просмотреть этот короткий клип здесь: bit.ly/1fFbbbJ

МАТЕРИАЛЫ:

2 изогнутых стекла для часов
2 стержня из плексигласа
ткань: шерсть или нейлон
пластиковый стержень
маленьких кусочков рваной бумаги

ИНСТРУКЦИИ:

Положите на стол вверх дном часовое стекло.
Установите второе часовое стекло вертикально на первое часовое стекло.
Энергично потрите тканью один из стержней из плексигласа.
Сбалансируйте плексигласовый стержень на верхней части часового стекла.
Энергично протрите второй стержень из плексигласа той же тканью.
Поднесите второй стержень из плексигласа к стороне первого заряженного стержня из плексигласа. Что, по вашему мнению, происходит?

Второй стержень из плексигласа должен отталкивать первый, поскольку у них одинаковые заряды, поэтому учащиеся должны видеть, как второй стержень «толкает» первый по кругу.

Возможно, вам придется снова потереть первый плексигласовый стержень между попытками, так как заряд рассеивается.

Повторите упражнение, но вместо второго плексигласового стержня используйте пластиковый стержень. Что, по вашему мнению, происходит?

Теперь стержни имеют противоположные заряды, поэтому второй стержень должен «тянуть» другой стержень по кругу.

Далее поднесите палочку, которую вы натерли, ближе к маленьким кусочкам рваной бумаги на столе. Что вы наблюдаете?

Учащиеся должны уметь поднимать листы бумаги заряженным стержнем.

ВОПРОСЫ:

Что произошло, когда вы поднесли второй стержень из плексигласа близко к первому стержню из плексигласа?

Когда стержни одинаковые (т.е. оба плексигласовые), то первый стержень должен отойти от второго и верхнее часовое стекло будет вращаться по кругу.

Что произошло, когда вы поднесли пластиковый стержень к первому плексигласовому стержню?

При использовании двух разных материалов первый стержень должен двигаться к пластиковому стержню, а часовое стекло поворачивается по кругу к пластиковому стержню.

Что произошло, когда вы поднесли пластиковый стержень близко к кусочкам бумаги?

Кусочки бумаги притянулись к стержню.

Когда мы натирали стержни из плексигласа тканью, электроны переносились с плексигласа на ткань. Какой заряд теперь имеют стержни из плексигласа?

Положительный заряд.

Оба плексигласовых стержня теперь имеют одинаковый заряд . Вы замечали, что объекты с одинаковым зарядом стремятся оттолкнуть друг друга? Мы говорим, что они отталкивают друг друга. Это электростатическая сила отталкивания.

Когда мы натирали пластиковый стержень тканью, электроны переносились с ткани на пластиковый стержень. Какой заряд теперь имеет пластиковый стержень?

Отрицательный заряд.

Стержень из плексигласа и пластиковый стержень теперь имеют противоположных зарядов. Вы замечали, что объекты с разным зарядом притягиваются друг к другу? Мы говорим, что они притягивают друг друга. Это электростатическая сила притяжения.

Как и в случае с гравитационной и магнитной силой, расстояние между заряженными объектами влияет на силу электростатической силы. Чем ближе заряженные объекты, тем сильнее сила. Чем больше заряжены объекты, тем сильнее электростатическая сила между ними.

Узнайте больше онлайн с симуляцией натирания воздушных шаров и джерси. http://phet.colorado.edu/en/simulation/balloons

Теперь мы рассмотрели фундаментальное поведение зарядов. Подводя итог, мы можем сказать:

Если два отрицательно заряженных объекта приблизить друг к другу, то они будут отталкиваться друг от друга.
Если сблизить два положительно заряженных объекта, они будут отталкиваться друг от друга.
Если положительно заряженный объект приблизить к отрицательно заряженному объекту, они будут притягиваться друг к другу.

Помните, одинаковых зарядов отталкиваются и противоположных зарядов притягиваются.

Противоположности притягиваются и как бы отталкиваются (видео)

Вы когда-нибудь задумывались, откуда берется молния? Продемонстрируем электростатическую искру.

Это необязательное действие , расширение . Генератор Ван де Граафа можно использовать для самых разных развлечений. Вы можете использовать его для объяснения различных концепций статического электричества. Есть несколько веб-сайтов с идеями и предложениями для забавных мероприятий и видео демонстраций, например, этот: http://www.nationalstemcentre.org.uk/elibrary/resource/2088/van-de-graaff-generator

[ссылка]

Цель этого упражнения — показать, как образуются искры, чтобы вы могли объяснить, как работает молния. Если у вас нет генератора Ван-де-Граафа, используйте видеоклип (например, этот, представленный в поле для посещений) из Интернета.

Большие искры, маленькие искры.

МАТЕРИАЛЫ:

Генератор Ван де Граафа

ИНСТРУКЦИИ

Включите генератор.

Поднесите небольшой металлический шар к генератору. Что ты видишь?

Учащиеся должны увидеть искру между генератором и шаром.

Генератор Ван де Граафа.

Вы видели искры? Генератор Ван де Граафа можно использовать для демонстрации эффектов электростатического заряда. Большой металлический купол наверху заряжается положительно при включении генератора. Когда купол заряжен, его можно разрядить, поднеся к куполу другую изолированную металлическую сферу. Электроны прыгнут на купол из металлической сферы и вызовут искру.

Фундаментальная идея использования трения в машине для создания заряда восходит к 17 веку, но генератор был изобретен Робертом Ван де Граафом только в 1929 году в Принстонском университете.

Какое отношение эта маленькая искра имеет к мощному удару молнии?

Молния — это огромный электростатический разряд.

Как выжить при ударе молнии.

Во время грозы облака заряжаются. Трение между облаками и влага в облаках заставляют облака заряжаться. Нижняя часть облаков (ближайшая к земле) становится отрицательно заряженной, а верхняя часть облака становится положительно заряженной. Когда накопление заряда становится слишком большим, электроны перемещаются из нижней части облака на землю, где они «заземляются». Передача энергии массивна и приводит к чрезвычайно яркому свету, теплу и звуку. Вспышка молнии — это массивный разряд между заряженными областями внутри облаков или между облаками и Землей. Удар грома, который мы слышим, — это движение воздуха в результате движения электронов.

Молния чрезвычайно опасна. Если электроны движутся через человека по пути к земле, то большое количество энергии наносит значительный ущерб. Такой человек может получить серьезную травму, вплоть до смерти.

Южная Африка имеет один из самых высоких показателей ударов молнии в мире.

Какие меры предосторожности следует принимать во время грозы? Молния может ударить далеко от дождевой тени грозы. Это означает, что даже если буря кажется далекой, все равно лучше принять меры предосторожности. Самое безопасное место во время грозы – это помещение. Держитесь подальше от окон и металлических предметов. Если вы не можете попасть внутрь, не стойте рядом с высокими объектами или металлическими предметами, потому что, если ударит молния, она обычно поразит самый высокий объект в этом районе. Если вы едете в машине во время грозы, оставайтесь в машине, пока не утихнет гроза.

Резюме

Сила определяется как толчок или притяжение объекта.
Силы измеряются в ньютонах (Н).
Сила может изменить форму, направление и движение объекта.
Силы действуют парами. Сила, действующая на объект, называется действием, а сила, которую объект оказывает обратно в противоположном направлении и равная по величине, называется реакцией.
На объект может действовать более одной силы. Чистая или равнодействующая сила представляет собой сумму всех сил, действующих на объект.
Силы, действующие на тело, могут быть представлены в виде диаграммы свободного тела, где стрелки указывают направление и величину различных сил.
Есть две основные группы войск; контактные и бесконтактные (полевые) силы.
Контактные силы действуют, когда объекты соприкасаются (соприкасаются) друг с другом. Трение, растяжение и сжатие являются примерами контактных сил.
Трение – это сила, противодействующая движению двух поверхностей, когда они трутся друг о друга.
Силы сжатия — это две силы, действующие на один объект, движущиеся в противоположных направлениях (навстречу друг другу) для сжатия или деформации объекта.
Силы натяжения — это две силы, действующие на один объект, движущиеся в противоположных направлениях (в направлении друг от друга) для растяжения объекта.
Неконтактные силы могут действовать на расстоянии, и объекты не обязательно должны соприкасаться друг с другом. Типичными примерами полевых сил являются магнитные, электростатические и гравитационные силы.
Неконтактные силы известны как силы поля. Поле — это область в пространстве, в которой на определенный объект с определенными свойствами будет действовать сила.
Гравитационная сила — это сила притяжения между двумя телами из-за их массы. Гравитационная сила увеличивается с массой и уменьшается с расстоянием между телами.
Вес тела — это гравитационная сила, действующая на объект со стороны Земли (или Луны, или другой планеты). Вес будет варьироваться в зависимости от того, где он измеряется.
Масса объекта является мерой того, сколько материи он содержит. Масса остается постоянной независимо от того, где она определяется.
Вес рассчитывается как W = m × g, где g — ускорение свободного падения. На Земле g = 9,8 м/с ² .
Магнит — это материал, вокруг которого существует сильное магнитное поле.
Магнитные силы притяжения существуют между магнитом и магнитным веществом, таким как железо, сталь, кобальт и никель.
Магнит имеет два полюса, северный и южный. Противоположные полюса притягиваются друг к другу, а одноименные полюса отталкиваются.
Вокруг Земли есть магнитное поле. Мы можем использовать компас, чтобы определить направление, поскольку стрелка — это магнит, указывающий на магнитный север.
Когда определенные материалы трутся друг о друга, трение между ними заставляет электроны перемещаться из одного материала в другой. Затем объекты приобретают электростатический заряд из-за потери или приобретения электронов.
Заряд – фундаментальное свойство материи. Электроны несут отрицательные заряды, а протоны несут положительные заряды.
Объект, получивший электроны, будет заряжен отрицательно. Объект, потерявший электроны, будет заряжен положительно.
Существует электростатическая сила притяжения между объектами с противоположными зарядами и отталкивания между объектами с одинаковыми зарядами.
Грозовые облака могут заряжаться, когда частицы воды и воздуха трутся друг о друга. Удар молнии возникает, когда между грозовыми тучами и землей возникает огромный разряд.
Молния опасна, и во время грозы следует соблюдать меры предосторожности.

Концептуальная карта

Заполните концептуальную карту, чтобы обобщить то, что вы узнали о силах в этой главе. Вы также можете использовать пространство вокруг концептуальных карт, чтобы добавить к ним свои собственные примечания, которые помогут составить более полное резюме. Это поможет вам подготовиться к экзаменам, когда вам нужно будет повторить все за год.

Версия для учителя

Дайте по одному термину для каждого из следующих описаний. [5 баллов]

Воздействие, которое может деформировать гибкий объект или изменить движение объекта с массой.
Область в космосе, где на объект с определенными свойствами будет действовать сила.
Когда единственной силой, действующей на объект, является сила тяжести.
Два противоположных конца магнита.
Фундаментальное свойство материи, которое бывает двух типов и передается протонами и электронами.

Сила.
Поле.
Свободное падение
поляка.
Зарядка.

На каждый из следующих вопросов даны четыре возможных ответа. Есть только один правильный ответ. Напишите букву в строке под каждым вопросом. [6 x 2 = 12 баллов]

Какое из следующих утверждений НЕВЕРНО?
A. Для того, чтобы неподвижный объект начал движение, на этот объект должна действовать результирующая сила.
B. Контактные силы наиболее сильны, когда объекты, на которые действует сила, соприкасаются.
C. Силы поля действуют на расстоянии, но они также могут действовать, когда объекты соприкасаются.
D. Силы всегда действуют парами равной силы, но эти пары действуют на разные объекты.
Что из нижеперечисленного НЕ является полевыми силами?
А. Гравитационная сила
Б. Сила трения
С. Электростатическая сила
Д. Магнитная сила
Правильная единица измерения гравитационной силы:
.
А. Ньютон
Б. килограмм
C. ньютон на килограмм
D. килограмм на ньютон
Какое из следующих веществ является магнитным?
А. алюминий
Б. медь
С. кобальт
Д. олово
Электростатическая сила между двумя заряженными объектами равна F. Расстояние между ними увеличивается. Как изменится электростатическая сила?
А. Увеличивает
Б. Уменьшается
C. Остается прежним
D. Недостаточно информации.
Масса космонавта на Земле 80 кг. Какой ОДИН из следующих утверждений о массе и весе астронавта на Луне верен?
A. Масса будет такой же, как и вес.
B. Масса будет меньше и вес тоже будет меньше.
C. Масса будет такой же, а вес будет меньше.
D. Масса будет меньше, а вес останется прежним.

Определите, какое из следующих утверждений верно или неверно. Если они ложны, перепишите их, чтобы сделать их истинными. [5 х 2 = 10 баллов]

Сила не может заставить двигаться неподвижный объект.
Сила может заставить движущийся объект изменить направление.
Сила может изменить форму объекта.
Сила натяжения замедляет или останавливает объект из-за трения поверхностей друг о друга.
Молния — это приложение магнитной силы.

Ложь. Сила может заставить неподвижный объект двигаться.
Правда
Правда
Ложь. Сила трения замедляет или останавливает объект из-за трения поверхностей друг о друга
Ложь. Молния — это приложение электростатической силы.

Взгляните на следующие изображения.

Какая ситуация показывает толчок, а какая ситуация показывает вытягивание? [1 балл]
Мальчик тянет стол с силой 70 Н. Сила трения равна 20 Н. Нарисуйте диаграмму свободного тела в пространстве ниже, чтобы показать эти силы, действующие на стол. [4 балла]
Какая сила действует на стол? [1 балл]

Изображение слева показывает толчок, а справа — вытягивание.
1 балл дается за рисование точки для стола.
1 балл присваивается за правильное использование значений.
2 балла присваиваются правильному направлению стрелок и длине стрелок, чтобы показать разницу в величине сил.
50 Н вправо.

На блок действует сила 50 Н и 80 Н. Рассчитайте чистую силу, действующую на брусок, если:

силы действуют в одном направлении [1 балл]
силы действуют в противоположных направлениях [1 балл]

110 Н
30 Н

Запишите три различных воздействия силы на объект. [3 балла]

изменение движения (быстрее или медленнее)
изменение направления
изменение формы

Что иллюстрирует следующая диаграмма? Поясните свой ответ. [4 балла]

На изображении A показан объект в состоянии покоя, а на изображениях B и C показан объект с приложенными к нему различными силами. На изображении B показаны силы сжатия, применяемые для сжатия объекта. На изображении C показаны силы натяжения, применяемые для растяжения объекта.

Сведите в таблицу разницу между массой и весом, используя определения массы и веса и сравнив единицы, в которых они измеряются. [5 баллов]

Таблица, показывающая разницу между массой и весом.

	Масса	Вес
Определение	Масса определяется количеством материи, из которой состоит объект, и остается постоянной независимо от того, где ее измеряют.	Вес объекта определяется гравитационной силой, действующей на него со стороны Земли или другого крупного объекта, такого как Луна или другая планета. Вес меняется в зависимости от того, где он определяется и силы гравитационной силы.
Единицы	килограмма (кг)	ньютона (Н)

Запишите формулу, связывающую вес предмета с его массой. Объясните, что обозначает каждый символ. [4 балла]

W = m × g, где W — вес объекта в Н, m — масса объекта в кг и g — ускорение свободного падения в м/с ² .

Какие ДВА фактора влияют на гравитационную силу между двумя объектами? Объясните отношения. [2 балла]

Расстояние между предметами, чем они ближе, тем сильнее сила, и масса предметов, так как чем больше масса, тем сильнее сила.

Астронавт проводит эксперимент по определению взаимосвязи между массой и весом на разных планетах. Он берет весы и отправляется на космическом корабле и измеряет собственный вес на разных планетах Солнечной системы. В следующей таблице показаны его результаты.

Планета	Вес (Н)
Меркурий	287
Венера	710
Земля	?
Марс	302
Юпитер	2076
Сатурн	886
Уран	854
Нептун	1126

Рассчитайте вес космонавта на Земле, если его масса 80 кг. [3 балла]
Постройте соответствующий график веса астронавта на разных планетах Солнечной системы. Вашему графику потребуется подходящий заголовок и метки для осей. [8 баллов]
На какой планете у Кевина самый маленький вес? Что это говорит вам о размере этой планеты по отношению к другим планетам? [2 балла]

Учащиеся должны указать формулу, затем заменить ее значениями и дать ответ с единицами измерения.
Вт = м × г
= 80 х 9,8
= 784 Н
Учащиеся должны нарисовать гистограмму с промежутками между столбцами [2 балла], указать заголовок [1 балл], метку по оси X [1 балл], метку по оси Y с единицами измерения [1 балл], соответствующий вертикальный масштаб [1 балл], точность прорисовки [2 балла].
Его вес самый маленький на Меркурии, так как Меркурий — самая маленькая планета по массе.

Нарисуйте схему магнитного поля вокруг стержневого магнита. [3 балла]

Вы проводите в классе эксперимент по исследованию стержневых магнитов. Вы кладете два магнита рядом друг с другом на стол, кладете лист бумаги на магниты и посыпаете бумагу железными опилками. Затем вы переворачиваете один магнит и делаете это снова. Вы видите следующие закономерности. Что показывает нам каждая фотография (A и B)? [2 балла]

Фото A. Фото B.

Фото A показывает магнитное поле между двумя противоположными полюсами, которые притягиваются друг к другу. На фото B показано магнитное поле между двумя одинаковыми полюсами (северным и северным или южным и южным), которые отталкивают друг друга.

Заполните таблицу, определив общую стоимость каждого объекта. Покажите свои расчеты. Укажите, является ли объект положительно заряженным, отрицательно заряженным или нейтральным и почему. [9 баллов]

Объект	Общий заряд	Почему он положительный, отрицательный или нейтральный?

По 3 балла за каждый из объектов, 1 балл присуждается за расчет и 2 балла за объяснение.

Объект	Общий заряд	Почему он положительный, отрицательный или нейтральный?
	Заряд = 4 + (-4) = 0	Он нейтрален, так как имеет одинаковое количество положительных и отрицательных зарядов.
	Заряд = 3 + (-6) = -3	Он заряжен отрицательно, так как отрицательных зарядов на 3 больше, чем положительных.
	Заряд = 7 + (-3) = 4	Он заряжен положительно, так как положительных зарядов на 4 больше, чем отрицательных.

Воздушный шар трется о футболку, и он получает отрицательный заряд.

Объясните, откуда взялся этот отрицательный заряд. В своем ответе укажите как протоны, так и электроны. [3 балла]
Назовите тип силы, которую будут испытывать баллон и майка ВО ВРЕМЯ трения. [1 балл]
Назовите тип силы, которую будут испытывать баллон и майка ПОСЛЕ трения. [1 балл]
Будет ли сила, упомянутая в (c), притягательной или отталкивающей? [1 балл]

Электроны переносятся с майки на воздушный шар. Протоны не переносятся. Электроны заряжены отрицательно, поэтому воздушный шар приобретает отрицательный заряд.
Трение.
Электростатическая сила.
Привлекательный.

Как вы думаете, к чему прикасаются эти две девушки слева на фото? Объясните свой ответ и что с ними происходит. [3 балла]

Что происходит на этом фото?

Девушки касаются полого купола генератора Ван де Граафа. Купол заряжен положительно, поэтому электроны переходят от их тел к куполу, чтобы разрядить его. Это приводит к тому, что их тела и волосы становятся положительно заряженными. Пряди их волос теперь отталкиваются друг от друга, поскольку все они положительны (как отталкиваются заряды), и они поднимаются вверх.

Напишите короткий абзац, чтобы объяснить, как формируется молния. [4 балла]

Трение между частицами воды и воздуха в облаках вызывает накопление отрицательного заряда. Когда в облаках имеется большой избыточный заряд, избыточный заряд перемещается по воздуху на землю и разряжается. Этот разряд образует яркую искру, поскольку энергия, выделяемая движущимися зарядами, имеет форму тепла, света и звука. Это молния.

Что не так со следующей сценой? Поясните свой ответ. [2 балла]

Учащиеся играют на улице во время грозы, что опасно. Кроме того, они находятся под деревом, что еще более опасно, так как молния бьет в высокие объекты, например деревья, и поэтому они рискуют получить удар током.

Итого [94 балла]

Третий закон Ньютона — AP Physics 1

Все AP Physics 1 Ресурсы

7 Диагностические тесты 170 практических тестов Вопрос дня Карточки Учитесь по концепции

← Предыдущая 1 2 Следующая →

AP Physics 1 Справка » Ньютоновская механика » Силы » Основы силы и законы Ньютона » Третий закон Ньютона

Кошка массой 5 кг прыгает на обеденный стол массой 30 кг. Какова средняя сила, с которой стол действует на кошку, когда кошка ходит по столу?

Возможные ответы:

Правильный ответ:

Объяснение:

Этот вопрос проверяет ваше понимание третьего закона Ньютона (равные и противоположные силы). Силы между кошкой и столом зависят исключительно от массы кошки; следовательно, масса стола не имеет значения.

Сила, которую кошка прикладывает к столу, это просто ее вес. Согласно третьему закону Ньютона, стол действует на кошку с такой же силой. Сила на кошку со стола:

Сообщить об ошибке

Блок массой 15 кг и блок массой 10 кг висят на противоположных сторонах шкива (см. рисунок). Предполагая, что шкив не имеет трения и не имеет массы, определите ускорение блоков после того, как они выйдут из состояния покоя.

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку два блока соединены веревкой шкива, они будут иметь одинаковое ускорение, и мы можем рассматривать их как единую систему. Начните с рисования диаграммы свободного тела, включая все силы, действующие на каждый объект. Кроме того, выберите направление, которое будет считаться положительным (+), и отрицательное (-).

На каждый блок действуют две силы: вес и напряжение. Вес каждого блока можно найти по уравнению:

Следовательно, вес блока массой 10 кг равен 100 Н, а вес блока массой 15 кг равен 150 Н.

Согласно третьему закону Ньютона, для каждая сила есть равная и противодействующая сила. Две силы натяжения в данном случае представляют собой пару действие/противодействие; они равны по величине, но противоположны по направлению.

Теперь, используя второй закон Ньютона:

Поскольку мы рассматриваем систему как единое целое или как будто она движется как единый объект, мы суммируем все силы, действующие на каждый объект.

Все силы, направленные в положительном (+) направлении, как показано на приведенной выше диаграмме свободного тела, также будут положительными, если их ввести в уравнение. Все силы, направленные в отрицательном (-) направлении, также будут отрицательными в уравнении.

Что мы должны использовать вместо «» в уравнении? Поскольку мы рассматриваем всю систему как единый объект, мы должны сложить все массы вместе. Другими словами, 10 кг плюс 15 кг, что составляет общую массу 25 кг.

Теперь обратите внимание, что две силы натяжения будут уравновешены, поскольку они представляют собой пары действие/противодействие и, таким образом, равны, но противоположны по знаку. Итак, найдем ускорение:

Сообщить об ошибке

Дэйв катается на скейтборде и отталкивается от земли ногой. Это заставляет его ускоряться со скоростью . Дейв весит 589 Н. Насколько сильным был его толчок от земли?

Возможные ответы:

Правильный ответ:

Объяснение:

Дэйв весит 589 Н. Это означает, что его масса равна

. Он ускоряется с , что означает, что его толкнула сила

. Согласно третьему закону движения Ньютона, Дейв также должен был оттолкнуться от земли. с силой 240 ньютонов.

Сообщить об ошибке

Мужчина стреляет из винтовки, и сила выстрела вызывает отдачу. Величина силы, действующей на винтовку, __________ величины силы, действующей на пулю, и величина ускорения винтовки, __________ ускорения пули.

Возможные ответы:

равно . . . равно

больше . . . меньше

равно . . . меньше

меньше . . . больше

меньше . . . меньше

Правильный ответ:

равно . . . меньше

Пояснение:

В соответствии с третьим законом Ньютона, который гласит, что каждая сила имеет равную и противоположную реакцию, сила, действующая на винтовку, равна силе, действующей на пулю. Однако винтовка имеет большую массу, поэтому величина ее ускорения меньше, чем у пули.

Сообщить об ошибке

Две машины, одна массой 500 кг и одна массой 250 кг, столкнулись лоб в лоб. Автомобиль с большей массой испытывает (n) __________ силу и (n) __________ ускорение по сравнению с меньшим автомобилем.

Возможные ответы:

больше . . . больше

больше . . . меньше

равно . . . меньше

равно . . . больше

Правильный ответ:

равно . . . меньше

Пояснение:

В соответствии с третьим законом Ньютауна на машины действует одинаковая сила. Поскольку больший автомобиль испытывает ту же силу и имеет большую массу, по первому закону Ньютона он будет иметь меньшее ускорение.

Сообщить об ошибке

Книга прикладывает силу 2 Н вниз к стулу, который прикладывает силу 5 Н вниз к полу, на котором стоит. С какой силой пол давит на стул вверх?

Возможные ответы:

Правильный ответ:

Пояснение:

По третьему закону Ньютона для каждой реакции существует равная и противоположная реакция. Пол должен воздействовать на кресло с силой 7 Н, чтобы система оставалась в состоянии покоя. Если бы он прилагал меньше усилий, то стул с ускорением врезался бы в пол. Эта сила, действующая на поверхность, перпендикулярную ей, называется нормальной силой.

Сообщить об ошибке

Футболист, чувствуя агрессию, придирается к ребенку, намного меньшему, чем он сам. Футболист утверждает: «Все мои часы в тренажерном зале доказывают, что я могу ударить вас сильнее, чем вы меня!» Меньший и более сдержанный джентльмен отвечает: «Да, конечно, можешь. Я намного слабее тебя». Предполагая, что под «ударом» они подразумевают «приложить силу», правы ли эти двое, думая, что футболист может ударить сильнее? Почему?

Возможные ответы:

Нет, первый закон Ньютона гласит, что сила, с которой два объекта действуют друг на друга, всегда ОДИНАКОВА по величине и противоположна по направлению.

Да, второй закон Ньютона гласит, что школьные хулиганы, играющие в футбол, всегда бьют сильнее.

Да, второй закон Ньютона гласит, что футболист заставит меньшего джентльмена разогнаться в большей степени. Поэтому он проявляет большую силу.

Нет, третий закон Ньютона гласит, что силы, действующие на два объекта друг на друга, всегда ОДИНАКОВЫ по величине и противоположны по направлению.

Правильный ответ:

Пояснение:

Относительная масса двух взаимодействующих объектов не влияет на величину силы, с которой эти два объекта действуют друг на друга. Третий закон Ньютона гласит, что силы должны быть равны по величине. Если вы пытаетесь примириться с тем, что футболист не может «бить сильнее», чем тот, кто не поднимает тяжести, ответ заключается во втором законе Ньютона.

Футболист весит больше и поэтому испытывает небольшое ускорение. Меньший джентльмен испытывает большое ускорение из-за своей относительно небольшой массы. Это большое ускорение — это то, что мы видим, когда видим, как крупный футболист ударил кого-то поменьше. Футболист почти не меняет своего движения, а человек поменьше будет лететь назад.

Сообщить об ошибке

Опишите явление, когда ремень безопасности удерживает человека на сиденье во время автомобильной аварии. Другими словами, почему человек не покидал своего места?

Возможные ответы:

Первый закон Ньютона

Закон о напряжении

Второй закон Ньютона

Все законы описывают, почему это лицо не было вырвано с их места

Третий закон Ньютона

Правильный ответ:

Третий закон Ньютона

Объяснение:

Хотя в случае автомобильной аварии действуют все три закона, только один конкретно отвечает за удержание человека на сиденье. Непосредственно перед столкновением пассажир двигался с той же скоростью, что и автомобиль. Когда автомобиль сталкивается с другим автомобилем и замедляется, тело человека продолжает двигаться вперед. Это первый закон Ньютона, или закон инерции. Но именно третий закон Ньютона удерживает человека от выброса со своего места. Сила движения тела человека вперед соответствовала силе ремня безопасности. На каждое действие есть равное и противоположное противодействие. Если бы ремень безопасности не мог «сопоставить» силу тела человека, движущегося вперед против него, он бы порвался, и человек продолжил бы движение вперед.

Сообщить об ошибке

Локомотив толкает поезд с постоянной скоростью . Как зависит сила, с которой локомотив действует на поезд, от силы поезда, действующей на локомотив?

Возможные ответы:

Они одинаковы по величине и противоположны по направлению

Ни один из них

Они противоположны по направлению и имеют разные величины

Они одинаковы по величине и направлению в том же направлении и имеют одинаковую величину

Правильный ответ:

Они одинаковы по величине и противоположны по направлению

Пояснение:

Это третий закон Ньютона. Каждое действие имеет равное противодействие. Причина, по которой поезд вообще может двигаться, связана с силой, которую локомотив прикладывает к рельсам, что позволяет ему ускорять вагоны.

Сообщить об ошибке

Два объекта прикладывают силы друг к другу. Сила, действующая на один из блоков как функция времени в направлении x, равна , где и являются константами. Какова зависимость силы от времени в направлении x на другом блоке? Предположим, что нет других сил, кроме сил, действующих на объекты друг на друга.

Возможные ответы:

Правильный ответ:

Пояснение:

По третьему закону Ньютона каждое действие имеет равную и противоположную реакцию. Таким образом, сила действует на другой блок с равной и противоположной силой. Математически это просто означает отрицание силы.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все ресурсы AP Physics 1

7 диагностических тестов 170 практических тестов Вопрос дня Карточки Изучайте понятия

Силы и законы движения Ньютона

Определение и интерпретация нормальной силы

Во многих ситуациях объект находится в контакте с поверхностью, например со столешницей. Из-за контакта на объект действует сила. В настоящем разделе обсуждается только одна составляющая этой силы, составляющая, действующая перпендикулярно поверхности. В следующем разделе обсуждается компонент, который действует параллельно поверхности. Перпендикулярная составляющая называется нормальной силой.

Определение нормальной силы

Нормальная сила — это одна составляющая силы, с которой поверхность действует на объект, с которым она соприкасается, а именно та составляющая, которая перпендикулярна поверхности.

На рис. 4.13 показан блок, лежащий на горизонтальном столе, и указаны две силы, действующие на блок: вес и нормальная сила. Чтобы понять, как неодушевленный предмет, такой как столешница, может оказывать нормальную силу, подумайте о том, что происходит, когда вы сидите на матрасе. Под вашим весом пружины матраса сжимаются. В результате сжатые пружины оказывают на вас направленное вверх усилие (нормальное усилие). Точно так же вес блока заставляет невидимые «атомные пружины» на поверхности стола сжиматься, создавая нормальную силу на блоке.

Рис.
На блок действуют две силы: его вес и нормальная сила, действующая на поверхность стола.

Третий закон Ньютона играет важную роль в связи с нормальной силой. Например, на рис. 4.13 блок воздействует на стол, нажимая на него. В соответствии с третьим законом стол оказывает на брусок противоположно направленную силу равной величины. Эта сила реакции является нормальной силой. Величина нормальной силы показывает, насколько сильно два объекта прижимаются друг к другу.

Если объект покоится на горизонтальной поверхности и нет вертикально действующих сил, кроме веса объекта и нормальной силы, то величины этих двух сил равны; то есть, . Это ситуация на рис. 4.13. Вес должен быть уравновешен нормальной силой, чтобы объект оставался неподвижным на столе. Если бы величины этих сил не были равны, на брусок действовала бы результирующая сила, и брусок ускорялся бы вверх или вниз в соответствии со вторым законом Ньютона.

Если другие силы в дополнение к и действуют в вертикальном направлении, величины нормальной силы и веса больше не равны. Например, на рис. 4.14а ящик весом 15 Н прижимают к столу. Толкающая сила имеет величину 11 Н. Таким образом, общая направленная вниз сила, действующая на ящик, равна 26 Н, и она должна быть уравновешена направленной вверх нормальной силой, если ящик должен оставаться в покое. В этом случае нормальная сила равна 26 Н, что значительно больше веса ящика.


(a) Нормальная сила больше веса ящика, потому что ящик давит вниз с силой 11 Н. (b) Нормальная сила меньше веса, потому что веревка создает направленную вверх силу 11 Н, которая частично поддерживает коробку.

Рисунок 4.14b иллюстрирует другую ситуацию. Здесь коробку тянет вверх веревка, которая прикладывает силу 11 Н. Суммарная сила, действующая на коробку из-за ее веса и веревки, составляет всего 4 Н, направленную вниз. Чтобы уравновесить эту силу, нормальная сила должна быть всего 4 Н. Нетрудно представить, что произойдет, если усилие, прикладываемое веревкой, увеличить до 15 Н, что точно равно весу ящика. В этом случае нормальная сила стала бы равной нулю. На самом деле стол можно было убрать, так как блок целиком держался на веревке. Ситуации на рис. 4.14 согласуются с идеей о том, что величина нормальной силы показывает, насколько сильно два объекта давят друг на друга. Ясно, что коробка и стол сильнее прижимаются друг к другу в части а рисунка, чем в части б.

Подобно ящику и столу на рис. 4.14, различные части человеческого тела прижимаются друг к другу и прикладывают нормальные силы. Пример 8 иллюстрирует замечательную способность человеческого скелета выдерживать широкий диапазон нормальных сил.

Пример

Физика человеческого скелета

Во время циркового эквилибристики женщина выполняет стойку на голове над головой стоящего артиста, как показано на рис. 4.15а. Женщина весит 490 Н, а голова и шея стоящего исполнителя весят 50 Н. В первую очередь именно седьмой шейный позвонок в позвоночнике поддерживает весь вес над плечами. Какова нормальная сила, с которой этот позвонок действует на шею и голову стоящего исполнителя (а) до акта и (б) во время акта?

Рисунок 4.15

(а) Молодая женщина удерживает равновесие во время выступления китайской акробатической группы Сычуани. Диаграмма свободного тела показана для тела стоящего исполнителя над плечами (б) перед актом и (в) во время акта. Для удобства масштабы, используемые для векторов в частях b и c, различны. (a. Supri/Reuters/Landov LLC)

Рассуждение

Для начала нарисуем диаграмму свободного тела для шеи и головы стоящего исполнителя. Перед актом действуют только две силы: вес головы и шеи стоящего исполнителя и нормальная сила. Во время акта присутствует дополнительная сила за счет веса женщины. В обоих случаях восходящие и нисходящие силы должны уравновешиваться, чтобы голова и шея оставались в покое. Это условие равновесия приведет нас к значениям нормальной силы.

Решение


(а)	На рис. 4.15b показана диаграмма свободного тела головы и шеи стоящего исполнителя перед актом. Единственными действующими силами являются нормальная сила и вес 50 Н. Эти две силы должны уравновешиваться, чтобы голова и шея стоящего исполнителя оставались в покое. Таким образом, седьмой шейный позвонок оказывает нормальную силу.
(б)	На рис. 4.15c показана диаграмма свободного тела, применяемая во время акта. Теперь общая направленная вниз сила, действующая на голову и шею стоящего исполнителя, равна , которая должна быть уравновешена направленной вверх нормальной силой, так что .

Таким образом, нормальная сила не обязательно имеет ту же величину, что и вес объекта. Значение нормальной силы зависит от того, какие другие силы присутствуют. Это также зависит от того, ускоряются ли соприкасающиеся объекты. В одной ситуации, связанной с ускорением объектов, величина нормальной силы может рассматриваться как своего рода «кажущийся вес», как мы сейчас увидим.

Кажущийся вес

Обычно вес объекта можно определить с помощью весов. Однако, несмотря на то, что весы работают правильно, бывают ситуации, когда они не дают правильного веса. В таких ситуациях показания весов дают только «кажущийся» вес, а не гравитационную силу или «истинный» вес. Кажущийся вес — это сила, с которой объект действует на весы, с которыми он соприкасается.

Чтобы увидеть расхождения, которые могут возникнуть между истинным весом и кажущимся весом, рассмотрите весы в лифте на рис. 4.16. Причины расхождений будут объяснены в ближайшее время. На весы встает человек, чей истинный вес равен 700 Н. Если лифт находится в состоянии покоя или движется с постоянной скоростью (либо вверх, либо вниз), весы регистрируют истинный вес, как показано на рис. 4.16а.

Рисунок 4.16

(a) Когда лифт не ускоряется, весы регистрируют истинный вес человека. (b) Когда лифт ускоряется вверх, кажущийся вес (1000 Н) превышает истинный вес. (c) Когда лифт ускоряется вниз, кажущийся вес (400 Н) меньше истинного веса. (d) Кажущийся вес равен нулю, если лифт падает свободно, т. е. если он падает с ускорением свободного падения.

Если лифт ускоряется, кажущийся вес и истинный вес не равны. Когда лифт поднимается с ускорением, кажущийся вес больше истинного, как показано на рис. 4.16b. И наоборот, если лифт движется вниз с ускорением, как в части с, кажущийся вес меньше истинного веса. На самом деле, если лифт падает свободно, так что его ускорение равно ускорению свободного падения, кажущийся вес становится равным нулю, как показывает часть d. В такой ситуации, когда кажущийся вес равен нулю, человек считается «невесомым». Таким образом, кажущийся вес не равен истинному весу, если весы и человек на них движутся с ускорением.

Расхождения между истинным весом и кажущимся весом можно понять с помощью второго закона Ньютона. На рис. 4.17 показана диаграмма свободного тела человека в лифте. На него действуют две силы: истинный вес и нормальная сила, действующая на платформу весов. Применение второго закона Ньютона в вертикальном направлении дает

где а — ускорение лифта и человека. В этом результате символ g обозначает величину ускорения свободного падения и никогда не может быть отрицательной величиной. Однако ускорение a может быть как положительным, так и отрицательным, в зависимости от того, ускоряется ли лифт вверх или вниз. Решение для нормальной силы показывает, что

(4.6)

В уравнении 4. 6 это величина нормальной силы, действующей на человека со стороны весов. Но в соответствии с третьим законом Ньютона, это также величина силы, направленной вниз, которую человек оказывает на весы, а именно кажущийся вес.


Схема свободного тела, показывающая силы, действующие на человека, едущего в лифте на рис. 4.16. — истинный вес, нормальная сила, действующая на человека со стороны платформы весов.

Уравнение 4.6 содержит все функции, показанные на рис. 4.16. Если лифт не ускоряется, а кажущийся вес равен истинному весу. Если лифт поднимается с ускорением, a положительно, и уравнение показывает, что кажущийся вес больше истинного веса. Если лифт движется вниз с ускорением, a отрицательно и кажущийся вес меньше истинного веса. Если лифт падает свободно, и кажущийся вес равен нулю. Кажущийся вес равен нулю, потому что, когда и человек, и весы свободно падают, они не могут столкнуться друг с другом. В этом тексте, когда указан вес, предполагается, что он является истинным весом, если не указано иное.

Проверьте, понимаете ли вы

11.	Стопка книг весом 165 Н помещена на весы в лифте. На шкале указано 165 Н. Только по этой информации можете ли вы сказать, движется ли лифт с постоянной скоростью вверх, движется с постоянной скоростью вниз или находится в состоянии покоя? Ответ:

12.

Чемодан весом 10 кг помещается на весы в лифте. В каком направлении ускоряется лифт, когда шкала показывает 75 Н и когда она показывает 120 Н?

Вниз при значении 75 Н и вверх при значении 120 Н
Вверх при 75 Н и вниз при 120 Н
Вниз в обоих случаях
Наверх в обоих случаях

Ответ:

а.	Вниз при значении 75 Н и вверх при значении 120 Н

13.

Вы стоите на весах в лифте, который движется вверх с постоянной скоростью. Весы показывают 600 Н. В следующей таблице показаны пять вариантов того, что показывают весы, когда лифт замедляется, когда он останавливается, когда он останавливается и когда он набирает скорость на обратном пути вниз. Какой из пяти вариантов правильно описывает показания весов? Обратите внимание, что символ означает «меньше чем» и означает «больше чем».

Опция	Лифт замедляется, когда останавливается	Лифт остановлен	Лифт набирает скорость на обратном пути вниз
(а)	600 Н	600 Н	600 Н
(б)	600 Н	600 Н	600 Н
(в)	600 Н	600 Н	600 Н
(г)	600 Н	600 Н	600 Н
(д)	600 Н	600 Н	600 Н

Ответ:

Сила, энергия и моменты: определение, формула, примеры

Проще говоря, сила — это не что иное, как толчок или притяжение. С научной точки зрения, сила — это движение, производимое объектом в результате его взаимодействия с другим объектом или полем, таким как электрическое или гравитационное поле.

Рис. 1. Сила может быть толчком или притяжением объекта

Конечно, сила используется не только для того, чтобы толкать или тянуть объекты. Фактически мы можем выполнять три типа функций с помощью силы.

Изменение формы объекта: если, например, вы сгибаете, растягиваете или сжимаете объект, вы изменяете его форму.
Изменение скорости объекта: если во время езды на велосипеде вы увеличиваете педаль или кто-то толкает вас сзади, скорость велосипеда увеличивается. Таким образом, приложение большей силы заставляет велосипед ускоряться.
Изменение направления движения объекта: в крикетном матче, когда игрок с битой ударяет по мячу, сила, прилагаемая битой, вызывает изменение направления мяча. Здесь сила используется для изменения направления уже движущегося объекта.

Что такое энергия?

Энергия — это способность совершать работу, а работа равна силе, приложенной для перемещения объекта на определенное расстояние в направлении, определяемом этой силой. Таким образом, энергия — это то, сколько работы совершается этой силой над объектом. Уникальность энергии в том, что ее можно трансформировать.

Сохранение энергии

Сохранение энергии утверждает, что энергия передается только из одного состояния в другое, так что полная энергия замкнутой системы сохраняется.

Например, когда объект падает, его потенциальная энергия преобразуется в кинетическую энергию, но общая сумма обеих энергий (механическая энергия системы) одинакова в каждый момент падения.

Рис. 2 — Преобразование кинетической энергии в потенциальную в случае американских горок

Что такое момент?

Эффект поворота или сила, создаваемая вокруг оси, называется моментом силы или крутящим моментом. Примерами шарниров являются петли открывающейся двери или гайка, поворачиваемая гаечным ключом. Ослабление затянутой гайки и открывание двери на неподвижной петле требуют некоторого момента.

Рис. 3. Сила на расстоянии от неподвижной оси создает момент

Хотя это вращательное движение вокруг неподвижной оси, существуют и другие типы вращательных эффектов.

Какие бывают виды моментов силы?

Помимо аспекта вращения, нам также необходимо отметить направление, в котором движется объект. Например, в случае аналоговых часов все их стрелки вращаются в одном направлении вокруг неподвижной оси, расположенной в их центре. Направление, в данном случае, по часовой стрелке.

Момент по часовой стрелке

Когда момент или эффект вращения силы вокруг точки вызывает движение по часовой стрелке, этот момент направлен по часовой стрелке. В расчетах мы принимаем момент по часовой стрелке как отрицательный.

Момент против часовой стрелки

Точно так же, когда момент или вращательный эффект силы вокруг точки вызывает движение против часовой стрелки, этот момент является против часовой стрелки. В расчетах мы принимаем момент против часовой стрелки как положительный.

Рис. 4 – По часовой стрелке и против часовой стрелки

Как рассчитать момент силы?

Вращающее действие силы, также известное как крутящий момент, можно рассчитать по формуле:

T = крутящий момент.
r = расстояние от приложенной силы.
F = приложенная сила.
𝜭 = Угол между F и плечом рычага.

Рис. 5 – Моменты, приложенные к перпендикулярному уровню (F1) и моменту, действующему под углом (F2)

На этой диаграмме действуют две силы: F1 и F2. Если мы хотим найти момент силы F1 вокруг точки вращения 2 (куда действует сила F2), его можно вычислить, умножив F1 на расстояние от точки 1 до точки 2:

Однако, чтобы вычислить момент силы F2 вокруг точки вращения 1 (где действует сила F1), нам придется немного импровизировать. Взгляните на рисунок 6 ниже.

Рис. 6 – Разрешение вектора F2 для расчета момента силы F2

F2 не перпендикулярен стержню. Поэтому нам нужно найти составляющую силы F2, которая перпендикулярна линии действия этой силы.

В этом случае формула принимает вид F2sin𝜭 (где 𝜭 — угол между F2 и горизонталью). Итак, формула для расчета крутящего момента вокруг силы F2:

Принцип момента

Принцип момента гласит, что когда тело балансирует вокруг точки вращения, сумма момента по часовой стрелке равна сумме момента против часовой стрелки. Мы говорим, что объект находится в равновесии и не будет двигаться, пока не изменится одна из сил или не изменится расстояние от центра вращения любой из сил. См. иллюстрацию ниже:

Рис. 7 – Примеры равновесия

Рассчитайте расстояние от точки опоры силы 250 Н, которое необходимо приложить, чтобы качели уравновесились, если сила на другом конце качелей составляет 750 Н с на расстоянии 2,4 м от оси.

Сумма моментов по часовой стрелке = сумма моментов против часовой стрелки.

Следовательно, расстояние силы 250 Н должно быть 7,2 м от оси вращения, чтобы качели были сбалансированы.

Что такое пара?

В физике момент пары – это две равные параллельные силы, находящиеся в противоположных направлениях друг от друга и на одинаковом расстоянии от точки вращения, действующие на объект и производящие эффект вращения. Примером может быть водитель, поворачивающий руль своей машины обеими руками.

Отличительной особенностью пары является то, что, несмотря на эффект вращения, результирующая сила в сумме равна нулю. Следовательно, нет поступательного, а есть только вращательное движение.

Рис. 8. Пара образуется, если две равные силы действуют в противоположных направлениях на одинаковом расстоянии от точки вращения

Чтобы вычислить момент пары, нам нужно умножить любую из сил на расстояние их. В случае нашего примера выше вычисление:

Какова единица момента силы?

Поскольку единицей силы является ньютон, а единицей расстояния — метр, единицей момента становится ньютон на метр (Нм). Таким образом, крутящий момент является векторной величиной, поскольку он имеет величину и направление.

Момент силы 10 Н относительно точки равен 3 Нм. Вычислите расстояние между точками опоры и линией действия силы.

Force Energy — основные выводы

Сила — это толчок или притяжение объекта.
Сила может изменить форму объекта вместе с его скоростью и направлением, в котором он движется.
Сохранение энергии означает, что энергия передается только из одного состояния в другое, так что сохраняется полная энергия замкнутой системы.
Эффект поворота или сила, создаваемая вокруг оси вращения, представляет собой момент силы или крутящего момента.
Момент может быть направлен по часовой стрелке или против часовой стрелки.
Принцип момента гласит, что когда тело балансирует вокруг точки вращения, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки.
Момент пары – это две равные параллельные силы, находящиеся в противоположных направлениях друг от друга и на одинаковом расстоянии от точки вращения, действующие на предмет и производящие эффект поворота.

Момент Руки, векторы силы и анализ приседаний — PT Direct

Понимание этих важных биомеханических терминов позволит вам понять, почему одни вариации приседаний более или менее эффективны, чем другие, и почему некоторые вариации просто опасны!

Что такое рычаги момента и как они воздействуют на суставы?

Плечо момента — это просто длина между осью сустава и линией силы, действующей на этот сустав.

У каждого сустава, задействованного в упражнении, есть плечо момента. Чем длиннее плечо момента, тем большая нагрузка будет приложена к оси сустава за счет рычага. В качестве примера подумайте о попытке разъединить гайку и болт. Если вы не можете сделать это вручную из-за малого плеча момента, вы используете полумесяц (как показано на рисунке), который дает вам гораздо большее плечо момента и позволяет меньшему усилию (приложенному вами) привести к гораздо большему крутящему моменту (вращательному). сила), приложенная к гайке. Это потому, что крутящий момент на оси:

Сила x Момент руки = Крутящий момент

В следующих примерах упражнений вы увидите момент руки, который воздействует на тазобедренные и коленные суставы с некоторыми распространенными вариациями приседаний. Понимание этих моментных рычагов позволит вам определить, какие варианты безопасны или опасны, и какие мышцы работают больше/меньше всего при каждом варианте. Результаты могут вас удивить, поэтому читайте дальше…

Что такое векторы силы и как они применяются в упражнениях?

Вектор силы — это направление силы. На странице, посвященной основам механики движения, мы говорили о силовой линии гравитации. Когда мы поднимаем объект, действует множество векторов силы. У нас есть гравитация, сила трения об объект, силы реакции земли, мышечные силы (генерируемые на линии, существующей между началом и местом прикрепления мышцы), силы импульса и так далее.

Результатом движения является сумма всех векторов и их соответствующих сил.

Чтобы представить это в контексте упражнений, если бы я собирался ударить боксерский мешок, в игру вступили бы следующие силы и векторы

Силы реакции опоры, которые я генерировал бы ногами, чтобы начать удар
Внутренние силы каждой задействованной мышцы стопы, ног, туловища и руки
Импульс моей руки
Сумка инерционная

Главное, что нужно сделать при анализе любого упражнения, — это определить основные силы, то, как тело может управлять ими и как тело будет стабилизировать суставы, участвующие в движении. Как только вы это сделаете, вы будете знать:

Какие мышцы будут работать во время движения
Является ли поза, связанная с движением, практичной и той, которую вы хотели бы поощрять
Какие мышцы будут работать стабилизаторами
Когда техника упражнения пойдет не так, если человек технически потерпит неудачу в этом упражнении

В качестве примера можно рассмотреть приседание, первоначально с приседанием на спине:

1. В этом приседании вы можете увидеть момент, когда руки обхватывают бедро и колено – они измеряются от оси сустава до линии сила. В этом положении штанги рука вокруг бедра немного длиннее руки вокруг колена. Это означает, что разгибатели бедра (ягодичные мышцы) будут выполнять немного больше работы, чем разгибатели колена (квадрицепсы) с точки зрения силы, которую им необходимо создать для преодоления нагрузки.

2. Осанка здесь хорошая, ее следует поощрять

3. Стабилизаторы туловища, коленей и бедер будут работать значительно, особенно при увеличении нагрузки.

4. Этот присед, скорее всего, будет потерян из корпуса, в результате чего поясничный отдел позвоночника скруглится, а штанга упадет вперед, что означает «грудь вверх», «животик втянут», «толкай бедра и вверх». поможет. Как и во всех приседаниях, выравнивание коленей, если оно нарушено, может вызвать встречное вращение в поясничном отделе, поэтому также важно следить за положением коленей, когда ваши клиенты утомляются.

Теперь давайте сравним присед на спине с приседом на груди:

1. В этом приседе вы можете увидеть момент, когда руки слегка изменились. Теперь они примерно равны, что означает, что нагрузки вокруг бедра и колена будут одинаковыми. Это означает, что разгибатели бедра и разгибатели колена должны будут генерировать одинаковое количество силы на протяжении всего движения.

2. Эта поза тоже хороша, и ее следует поощрять.

3. Стабилизаторы плеча, туловища, бедра и колена будут значительно задействованы, как и в приседаниях со спиной.

4. Этот присед также будет потерян из корпуса или плечевого пояса из-за расположения грифа, поэтому помогут сигналы «локти вверх», «грудь наружу» и «живот напряжен». Как и во всех приседаниях, выравнивание коленей, если оно нарушено, может привести к обратному вращению в поясничном отделе, поэтому также важно следить за положением колена во время усталости.

Теперь давайте рассмотрим некоторые варианты приседаний, заявив, что приседания со штангой на спине:

1. В этом приседе вы можете видеть, что моментная рука вокруг бедра как минимум в два раза длиннее моментной руки вокруг колена. Это низкое положение грифа чаще всего используют пауэрлифтеры, так как оно задействует разгибатели бедра гораздо больше, чем разгибатели колена, а разгибатели бедра способны создавать большее усилие, чем разгибатели колена, и воздействовать на сустав с лучшей артикуляцией (глубокий мяч). и впадина против колена, который является неглубоким суставом). Поскольку разгибатели бедра способны производить большее усилие, чем разгибатели колена, этот вариант приседаний позволяет поднимать более тяжелые грузы.

2. Поза не будет поощряться, за исключением случаев, когда это необходимо для участия в соревнованиях (например, в пауэрлифтинге или других видах спорта, где это положение требуется при нагрузке), так как огромные нагрузки возлагаются на поясничный отдел позвоночника, а также на бедра, и эти области должны постепенно кондиционироваться, чтобы противостоять этим силам. Это «продвинутая» поза лифтеров.

3. Стабилизаторы бедра и туловища будут существенно изменены в этом варианте.

4. Этот присед будет потерян из кора, что приведет к округлению поясницы, поэтому вам помогут команды «напрячь живот», «подъехать вверх и вперед», «голова неподвижна». Как и во всех приседаниях, колени должны быть выровнены.

Наконец, чтобы немного лучше понять векторы силы, давайте взглянем на присед в машине Смита со слегка разведенными ногами, а затем на присед со швейцарским мячом, которые обычно рекомендуются в фитнес-клубах.

1. Здесь можно увидеть момент, когда рука вокруг колен значительно длиннее руки вокруг бедра. Это со временем будет способствовать укреплению квадрицепсов и лишь незначительному развитию ягодичных мышц. К сожалению, это научит человека приседать с бедрами, а не использовать ягодичные мышцы в обычном режиме. В конечном итоге это приведет к смещению модели движения и со временем может привести к травме колена или проблемам с поясницей. Вы также можете видеть, что линия силы проходит по пяткам, а не по середине стопы. Это не естественная позиция.

2. Хотя торс здесь в хорошей осанке, в булавах обычно видна плоская спина. Поскольку ягодичные мышцы не очень активны, ядро не всегда активно. Кроме того, гриф мешает человеку двигаться вперед, так как он может держаться за него, поэтому нет необходимости в том, чтобы разгибатели туловища были активны. Эту позу и ее механику не следует поощрять.

3. Будет использоваться очень мало стабилизаторов, поскольку в упражнении устранено большинство требований к естественной сагиттальной плоскости из-за фиксированного грифа и практически все требования к передней и поперечной плоскостям.

4. Если человек потерпит неудачу в этом упражнении, он будет в районе поясницы для устойчивости. Наиболее вероятной неудачей будет очень плохое положение позвоночника, так как вы можете продолжать подниматься дольше до мышечной усталости, когда вам не нужно стабилизировать свое положение.

Интересно, что когда мы спрашиваем, почему это приседание предписано, нам часто говорят, что оно помогает кому-то нарастить приседания со свободным весом, потому что они еще не могут приседать, или чтобы укрепить ягодичные мышцы и научить их движению. Ничто из этого не кажется разумным, когда вы понимаете биомеханику. Лучший способ помочь клиентам перейти к приседаниям со свободным весом — это обучение приседаниям с собственным весом с диапазоном движений, который подходит каждому отдельному клиенту.

Последняя точка. Когда вы делаете это приседание, чем дальше вы расставляете ноги, тем больше активизируются разгибатели колена (квадрицепсы) и тем меньше разгибатели бедра (ягодичные мышцы). Когда это происходит, вектор силы, вызывающий сдвиг колена, развивается и увеличивается, так что при использовании в течение долгого времени коленный сустав почти гарантированно травмируется. Вы увидите это более ярко в приседаниях со швейцарским мячом.

1. Силовая линия, проходящая через центр масс, отмечена синим цветом. Основание опоры находится далеко от линии силы, а центр масс будет располагаться вокруг самой верхней части бедер. Моментная рука колена выделена зеленым цветом — в основном это упражнение задействует все квадрицепсы и очень мало ягодичных мышц (если они есть), учитывая, что у них практически нет моментной руки, с которой они могли бы действовать.

2. Желтая линия представляет собой вектор силы четырехглавой мышцы – мы знаем, что мышца укорачивается от начала до места прикрепления. Из-за моментного плеча четырехглавой мышцы и из-за того, что человек должен постоянно отталкиваться назад, чтобы удержать мяч на стене, в коленном суставе действует постоянная сила сдвига. Чтобы справиться с работой четырехглавой мышцы, внутренняя часть колена будет постоянно подвергаться нагрузке (внутренняя часть включает в себя крестообразные связки, латеральные и коллатеральные связки, а также подколенные сухожилия). Туловище бездействует, так как опирается на мяч (во всяком случае, только мышцы, выпрямляющие позвоночник, могут быть активны, чтобы удерживать туловище на мяче), а ягодичные мышцы бездействуют, поскольку они не могут участвовать в упражнении. Никакие знания, полученные мозгом в ходе этого упражнения, бесполезны и небезопасны в долгосрочной перспективе. Так что это не та поза, которую мы когда-либо поощряли бы.

3. Хотя на мяче требуется меньшая устойчивость в поперечной и фронтальной плоскостях, чем в приседаниях со свободным положением. Стабильность в сагиттальной плоскости создается за счет трения с мячом.

4. Неудача в этом упражнении, скорее всего, связана с мышцами и в районе колена или бедра. В колене может быть значительный дискомфорт, заставляющий клиента остановиться.

Пара сил с примерами решения и образцами выполнения

Техническая механика — Тема1.

Теория пар сил в теоретической механике

Теория пар сил — презентация онлайн

2. План лекции

3.

4. Цель лекции

5. Актуальность. Практические примеры

6. Актуальность. Практические примеры

7. Теорема о сложении двух сил, направленных в разные стороны, но линии действия которых параллельны

9. Пара сил

10. Пара сил. Момент пары сил

11. Пара сил. Вращательный эффект пары

14. Доказательство

15.

18. Доказательство

19. Условия равновесия тела под действием системы пар сил

20. Условия равновесия тела под действием системы пар сил

21. Вопросы для самоконтроля

22. Вопросы для самоконтроля

Плоская система пар сил.

Пара сил и момент пары

Основные свойства пары сил

Эквивалентные пары

Теорема о сложении пар

Условие равновесия плоской системы пар

Опоры и опорные реакции балок

Пример решения задачи по определению реакций опор балки

Пример решения задачи по определению реакции в жесткой заделке

Главная страница

Дистанционное образование

Специальности

Учебные дисциплины

Олимпиады и тесты

3-й закон Ньютона

Вопрос:

Проблема:

Примеры пар действие-противодействие:

Примеры сил, имеющих одинаковую величину и противоположное направление, но НЕ пары действие-противодействие.

Модуль 2: Вопрос 2

Модуль 2: Вопрос 3

Растяжение и сжатие

Проблема:

Проблема:

15.1 Виды сил | Силы

Виды сил

Что такое сила?

Эффекты сил

Пары сил

Представление сил

Типы сил

Контактные силы

Трение

Растяжение и сжатие

Полевые (бесконтактные) силы

Силы гравитации

Магнитные силы

Электростатические силы

Резюме

Третий закон Ньютона — AP Physics 1

Все AP Physics 1 Ресурсы

Все ресурсы AP Physics 1

Силы и законы движения Ньютона

Сила, энергия и моменты: определение, формула, примеры

Что такое энергия?

Сохранение энергии

Что такое момент?

Какие бывают виды моментов силы?

Момент по часовой стрелке

Момент против часовой стрелки

Как рассчитать момент силы?

Принцип момента

Что такое пара?

Какова единица момента силы?

Force Energy — основные выводы

Момент Руки, векторы силы и анализ приседаний — PT Direct

Что такое рычаги момента и как они воздействуют на суставы?

Что такое векторы силы и как они применяются в упражнениях?

alexxlab

Добавить комментарий Отменить ответ