Краткий курс теоретической механики

Краткий курс теоретической механики

Тарг С. М. Краткий курс теоретической механики: Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с. В книге изложены основы механики материальной точки, системы материальных точек и твердого тела в объеме, соответствующем программам технических вузов. Приведено много примеров и задач, решения которых сопровождаются соответствующими методическими указаниями. В 10-м издании (9-е — 1974 г.) значительно изменены и более компактно изложены вопросы статики; в разделе «Динамика» дополнительно рассмотрены приложения общих теорем к изучению движения жидкости, малые колебания системы и некоторые другие вопросы. Для студентов очных и заочных технических вузов. Оглавление ПРЕДИСЛОВИЕ К ДЕСЯТОМУ ИЗДАНИЮ ВВЕДЕНИЕ Раздел первый. СТАТИКА ТВЕРДОГО ТЕЛА § 1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО; СИЛА. ЗАДАЧИ СТАТИКИ § 2. ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ § 3. СВЯЗИ И ИХ РЕАКЦИИ Глава II. СЛОЖЕНИЕ СИЛ. СИСТЕМА СХОДЯЩИХСЯ СИЛ § 4. ГЕОМЕТРИЧЕСКИЙ СПОСОБ СЛОЖЕНИЯ СИЛ. РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩИХСЯ СИЛ; РАЗЛОЖЕНИЕ СИЛ § 5. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ И СЛОЖЕНИЯ СИЛ § 6. РАВНОВЕСИЕ СИСТЕМЫ СХОДЯЩИХСЯ СИЛ § 7. РЕШЕНИЕ ЗАДАЧ СТАТИКИ Глава III. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА. ПАРА СИЛ § 8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ЦЕНТРА (ИЛИ ТОЧКИ) § 9. ПАРА СИЛ. МОМЕНТ ПАРЫ § 10. ТЕОРЕМЫ ОБ ЭКВИВАЛЕНТНОСТИ И О СЛОЖЕНИИ ПАР Глава IV. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ЦЕНТРУ. УСЛОВИЯ РАВНОВЕСИЯ § 11. ТЕОРЕМА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ § 12. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ДАННОМУ ЦЕНТРУ § 13. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ. ТЕОРЕМА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ Глава V. ПЛОСКАЯ СИСТЕМА СИЛ § 14. АЛГЕБРАИЧЕСКИЕ МОМЕНТЫ СИЛЫ И ПАРЫ § 15. ПРИВЕДЕНИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 16. РАВНОВЕСИЕ ПЛОСКОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ § 17. РЕШЕНИЕ ЗАДАЧ § 19. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ ТЕЛ (КОНСТРУКЦИИ) § 20. ОПРЕДЕЛЕНИЕ ВНУТРЕННИХ УСИЛИЙ § 21. РАСПРЕДЕЛЕННЫЕ СИЛЫ § 22. РАСЧЕТ ПЛОСКИХ ФЕРМ Глава VI. ТРЕНИЕ § 23. ЗАКОНЫ ТРЕНИЯ СКОЛЬЖЕНИЯ § 24. РЕАКЦИИ ШЕРОХОВАТЫХ СВЯЗЕЙ. УГОЛ ТРЕНИЯ § 25. РАВНОВЕСИЕ ПРИ НАЛИЧИИ ТРЕНИЯ § 26. ТРЕНИЕ НИТИ О ЦИЛИНДРИЧЕСКУЮ ПОВЕРХНОСТЬ § 27. ТРЕНИЕ КАЧЕНИЯ Глава VII. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ § 28. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ. ВЫЧИСЛЕНИЕ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА СИСТЕМЫ СИЛ § 29. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ПРОСТЕЙШЕМУ ВИДУ § 30. РАВНОВЕСИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. СЛУЧАЙ ПАРАЛЛЕЛЬНЫХ СИЛ Глава VIII. ЦЕНТР ТЯЖЕСТИ § 31. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ § 32. СИЛОВОЕ ПОЛЕ. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА § 33. КООРДИНАТЫ ЦЕНТРОВ ТЯЖЕСТИ ОДНОРОДНЫХ ТЕЛ § 34. СПОСОБЫ ОПРЕДЕЛЕНИЯ КООРДИНАТ ЦЕНТРОВ ТЯЖЕСТИ ТЕЛ § 35. ЦЕНТРЫ ТЯЖЕСТИ НЕКОТОРЫХ ОДНОРОДНЫХ ТЕЛ Раздел второй. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА § 36. ВВЕДЕНИЕ В КИНЕМАТИКУ § 37. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ § 38. ВЕКТОР СКОРОСТИ ТОЧКИ § 39. ВЕКТОР УСКОРЕНИЯ ТОЧКИ § 40. ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ ПРИ КООРДИНАТНОМ СПОСОБЕ ЗАДАНИЯ ДВИЖЕНИЯ § 41. РЕШЕНИЕ ЗАДАЧ КИНЕМАТИКИ ТОЧКИ § 42. ОСИ ЕСТЕСТВЕННОГО ТРЕХГРАННИКА. ЧИСЛОВОЕ ЗНАЧЕНИЕ СКОРОСТИ § 43. КАСАТЕЛЬНОЕ и НОРМАЛЬНОЕ УСКОРЕНИЯ ТОЧКИ § 44. НЕКОТОРЫЕ ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ТОЧКИ § 45. ГРАФИКИ ДВИЖЕНИЯ, СКОРОСТИ И УСКОРЕНИЯ ТОЧКИ § 46. РЕШЕНИЕ ЗАДАЧ § 47. СКОРОСТЬ И УСКОРЕНИЕ ТОЧКИ В ПОЛЯРНЫХ КООРДИНАТАХ Глава X. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 48. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ § 49. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ ОСИ, УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ § 50. 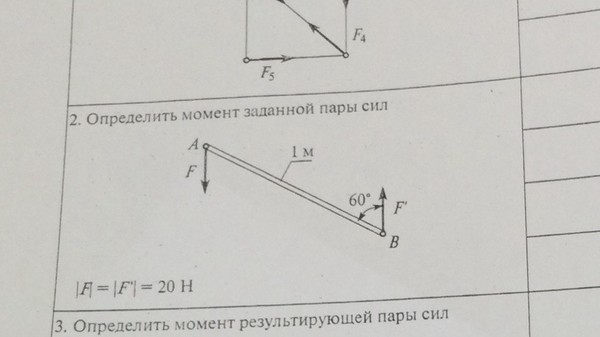РАВНОМЕРНОЕ И РАВНОПЕРЕМЕННОЕ ВРАЩЕНИЯ § 51. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛА Глава XI. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 52. УРАВНЕНИЯ ПЛОСКОПАРАЛЛЕЛЬНОГО ДВИЖЕНИЯ (ДВИЖЕНИЯ ПЛОСКОЙ ФИГУРЫ). РАЗЛОЖЕНИЕ ДВИЖЕНИЯ НА ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ § 53. ОПРЕДЕЛЕНИЕ ТРАЕКТОРИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 54. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 55. ТЕОРЕМА О ПРОЕКЦИЯХ СКОРОСТЕЙ ДВУХ ТОЧЕК ТЕЛА § 56. ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ С ПОМОЩЬЮ МГНОВЕННОГО ЦЕНТРА СКОРОСТЕЙ. ПОНЯТИЕ О ЦЕНТРОИДАХ § 57. РЕШЕНИЕ ЗАДАЧ § 58. ОПРЕДЕЛЕНИЕ УСКОРЕНИЙ ТОЧЕК ПЛОСКОЙ ФИГУРЫ § 59. МГНОВЕННЫЙ ЦЕНТР УСКОРЕНИЙ ГЛАВА XII. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 60. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ § 61. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА § 62. СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ТЕЛА § 63. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XIII. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ § 64. ОТНОСИТЕЛЬНОЕ, ПЕРЕНОСНОЕ И АБСОЛЮТНОЕ ДВИЖЕНИЯ § 65. ТЕОРЕМА О СЛОЖЕНИИ СКОРОСТЕЙ § 66. ТЕОРЕМА О СЛОЖЕНИИ УСКОРЕНИЙ (ТЕОРЕМА КОРИОЛИСА) § 67. РЕШЕНИЕ ЗАДАЧ Глава XIV. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 68. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНЫХ ДВИЖЕНИЙ § 69. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ДВУХ ПАРАЛЛЕЛЬНЫХ ОСЕЙ § 70. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ § 71. СЛОЖЕНИЕ ВРАЩЕНИЙ ВОКРУГ ПЕРЕСЕКАЮЩИХСЯ ОСЕЙ § 72. СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ. ВИНТОВОЕ ДВИЖЕНИЕ Раздел третий. ДИНАМИКА ТОЧКИ Глава XV. ВВЕДЕНИЕ В ДИНАМИКУ. ЗАКОНЫ ДИНАМИКИ § 74. ЗАКОНЫ ДИНАМИКИ. ЗАДАЧИ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ § 75. СИСТЕМЫ ЕДИНИЦ § 76. ОСНОВНЫЕ ВИДЫ СИЛ Глава XVI. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ, РЕШЕНИЕ ЗАДАЧ ДИНАМИКИ ТОЧКИ § 77. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ § 78. РЕШЕНИЕ ПЕРВОЙ ЗАДАЧИ ДИНАМИКИ (ОПРЕДЕЛЕНИЕ СИЛ ПО ЗАДАННОМУ ДВИЖЕНИЮ) § 79. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ § 80. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ § 81. ПАДЕНИЕ ТЕЛА В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ (В ВОЗДУХЕ) § 82. РЕШЕНИЕ ОСНОВНОЙ ЗАДАЧИ ДИНАМИКИ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ ТОЧКИ Глава XVII. ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ § 83. КОЛИЧЕСТВО ДВИЖЕНИЯ ТОЧКИ. ИМПУЛЬС СИЛЫ § 84. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ § 85. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ ТОЧКИ (ТЕОРЕМА МОМЕНТОВ) § 86. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ. ЗАКОН ПЛОЩАДЕЙ § 87. РАБОТА СИЛЫ. МОЩНОСТЬ § 88. ПРИМЕРЫ ВЫЧИСЛЕНИЯ РАБОТЫ § 89. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ТОЧКИ Глава XVIII. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЯ ТОЧКИ § 90. НЕСВОБОДНОЕ ДВИЖЕНИЕ ТОЧКИ § 91. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 92. ВЛИЯНИЕ ВРАЩЕНИЯ ЗЕМЛИ НА РАВНОВЕСИЕ И ДВИЖЕНИЕ ТЕЛ § 93. ОТКЛОНЕНИЕ ПАДАЮЩЕЙ ТОЧКИ ОТ ВЕРТИКАЛИ ВСЛЕДСТВИЕ ВРАЩЕНИЯ ЗЕМЛИ Глава XIX. ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ ТОЧКИ § 94. СВОБОДНЫЕ КОЛЕБАНИЯ БЕЗ УЧЕТА СИЛ СОПРОТИВЛЕНИЯ § 95. СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ (ЗАТУХАЮЩИЕ КОЛЕБАНИЯ) § 96. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. РЕЗОНАНС Глава XX. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ЗЕМНОГО ТЯГОТЕНИЯ § 97. ДВИЖЕНИЕ БРОШЕННОГО ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ § 98. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ЭЛЛИПТИЧЕСКИЕ ТРАЕКТОРИИ § 99. ПОНЯТИЕ О НЕВЕСОМОСТИ. МЕСТНЫЕ СИСТЕМЫ ОТСЧЕТА Раздел четвертый. ДИНАМИКА СИСТЕМЫ И ТВЕРДОГО ТЕЛА § 100. МЕХАНИЧЕСКАЯ СИСТЕМА. СИЛЫ ВНЕШНИЕ И ВНУТРЕННИЕ § 101. МАССА СИСТЕМЫ. ЦЕНТР МАСС § 102. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ОСИ. РАДИУС ИНЕРЦИИ § 103. МОМЕНТЫ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ. ТЕОРЕМА ГЮЙГЕНСА § 104. ЦЕНТРОБЕЖНЫЕ МОМЕНТЫ ИНЕРЦИИ. ПОНЯТИЯ О ГЛАВНЫХ ОСЯХ ИНЕРЦИИ ТЕЛА § 105. МОМЕНТ ИНЕРЦИИ ТЕЛА ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ Глава XXII. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС СИСТЕМЫ § 106. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ § 107. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС § 108. ЗАКОН СОХРАНЕНИЯ ДВИЖЕНИЯ ЦЕНТРА МАСС § 109. РЕШЕНИЕ ЗАДАЧ Глава XXIII. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ СИСТЕМЫ § 110. КОЛИЧЕСТВО ДВИЖЕНИЯ СИСТЕМЫ § 111. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ § 112. ЗАКОН СОХРАНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ § 113. ПРИЛОЖЕНИЕ ТЕОРЕМЫ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 114. ТЕЛО ПЕРЕМЕННОЙ МАССЫ. ДВИЖЕНИЕ РАКЕТЫ Глава XXIV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 115. ГЛАВНЫЙ МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ § 116. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ СИСТЕМЫ (ТЕОРЕМА МОМЕНТОВ) § 117. ЗАКОН СОХРАНЕНИЯ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ § 118. РЕШЕНИЕ ЗАДАЧ § 119. ПРИЛОЖЕНИЕ ТЕОРЕМЫ МОМЕНТОВ К ДВИЖЕНИЮ ЖИДКОСТИ (ГАЗА) § 120. УСЛОВИЯ РАВНОВЕСИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ Глава XXV. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 121. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ § 122. НЕКОТОРЫЕ СЛУЧАИ ВЫЧИСЛЕНИЯ РАБОТЫ § 123. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ СИСТЕМЫ § 124. РЕШЕНИЕ ЗАДАЧ § 125. СМЕШАННЫЕ ЗАДАЧИ § 126. ПОТЕНЦИАЛЬНОЕ СИЛОВОЕ ПОЛЕ И СИЛОВАЯ ФУНКЦИЯ § 127. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ Глава XXVI. ПРИЛОЖЕНИЕ ОБЩИХ ТЕОРЕМ К ДИНАМИКЕ ТВЕРДОГО ТЕЛА § 128. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 129. ФИЗИЧЕСКИЙ МАЯТНИК. ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ § 130. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 131. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ГИРОСКОПА § 132. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ И ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА Глава XXVII. ПРИНЦИП ДАЛАМБЕРА § 133. ПРИНЦИП ДАЛАМБЕРА ДЛЯ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 134. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ИНЕРЦИИ § 135. РЕШЕНИЕ ЗАДАЧ § 136. ДИНАМИЧЕСКИЕ РЕАКЦИИ, ДЕЙСТВУЮЩИЕ НА ОСЬ ВРАЩАЮЩЕГОСЯ ТЕЛА. УРАВНОВЕШИВАНИЕ ВРАЩАЮЩИХСЯ ТЕЛ Глава XXVIII. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ И ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ § 137. КЛАССИФИКАЦИЯ СВЯЗЕЙ § 138. ВОЗМОЖНЫЕ ПЕРЕМЕЩЕНИЯ СИСТЕМЫ. ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ § 139. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ § 140. РЕШЕНИЕ ЗАДАЧ § 141. ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ Глава XXIX. УСЛОВИЯ РАВНОВЕСИЯ И УРАВНЕНИЯ ДВИЖЕНИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 142. ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СКОРОСТИ § 143. ОБОБЩЕННЫЕ СИЛЫ § 144. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ В ОБОБЩЕННЫХ КООРДИНАТАХ § 145. УРАВНЕНИЯ ЛАГРАНЖА § 146. РЕШЕНИЕ ЗАДАЧ Глава XXX. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ ОКОЛО ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ § 147. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ § 148. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 149. МАЛЫЕ ЗАТУХАЮЩИЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ § 150. МАЛЫЕ СВОБОДНЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ Глава XXXI. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ УДАРА § 151. ОСНОВНОЕ УРАВНЕНИЕ ТЕОРИИ УДАРА § 152. ОБЩИЕ ТЕОРЕМЫ ТЕОРИИ УДАРА § 153. КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ ПРИ УДАРЕ § 154. УДАР ТЕЛА О НЕПОДВИЖНУЮ ПРЕГРАДУ § 155. ПРЯМОЙ ЦЕНТРАЛЬНЫЙ УДАР ДВУХ ТЕЛ (УДАР ШАРОВ) § 156. ПОТЕРЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПРИ НЕУПРУГОМ УДАРЕ ДВУХ ТЕЛ. ТЕОРЕМА КАРНО § 157. УДАР ПО ВРАЩАЮЩЕМУСЯ ТЕЛУ. ЦЕНТР УДАРА

Техническая механика — Тема1.3. Пара сил и момент силы

§1. Момент силы относительно центра (или точки)

Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее момен­том.

Рассмотрим силу , приложенную в точке А твердого тела (рис. 1). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы

, на­зывается плечом силы от­носительно центра О. Так как точку приложения силы можно произвольно переме­щать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть:

1) от модуля силы F и длины плеча h;

2) от поло­жения плоскости поворота ОАВ, проходящей через центр О и силу F;

3) от направления поворота к этой плоскости.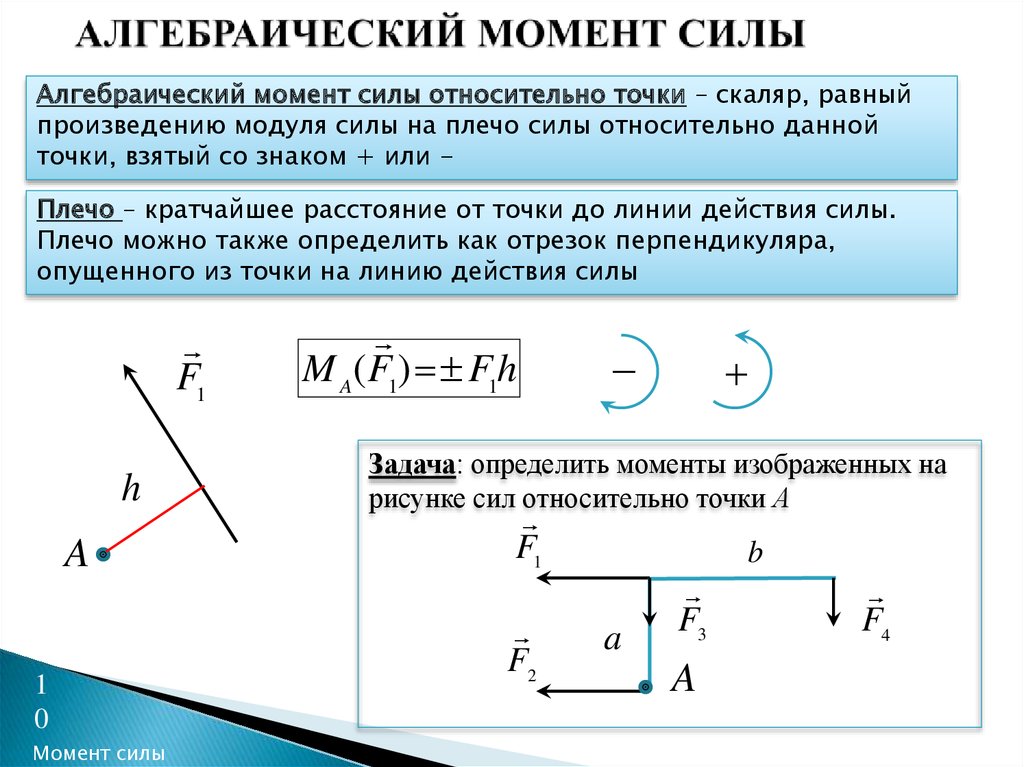

Рис.1. Сила, приложенная к телу

Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае плоскость поворота для всех сил является общей и в дополнительном задании не нуждается.

Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Момент силы относительно центра О будем обозначать M.

Следовательно, М= ±Fh. Единицы измерения в системе СИ : Н·м,

Правило знаков для момента силы: момент пары сил будем считать положительным, если пара стремиться повернуть тело по направлению хода часовой стрелки, и отрицательным, если пара сил стремится вращать тело против хода часовой стрелки.

Отметим следующие свойства момента силы:

1) Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия.

2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).

3) Момент силы численно выражается удвоенной площадью тре­угольника ОАВ (рис. 1)

M= ± 2пл.ΔOAB

§2.Теорема Вариньона о моменте равнодействующей

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил от­носительно любого центра равен алгеб­раической сумме моментов слагаемых сил относительно того же центра.

Рис.2. Сходящаяся система сил

Рассмотрим систему сил , сходящихся в точке А (рис. 2). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Для доказательства теоремы найдем соответствующие выражения моментов М(), М(), … .

По формуле М() = +2пл.ΔОАВ_1. Но, как видно из рисунка, где F_1x — проекция силы на ось Ох; сле­довательно М() = ОА · F_1x

Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил , через , где . Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

или .

§3. Пара сил. Момент пары

Парой сил (или просто парой) называются две силы, равные по ве­личине, параллельные и направленные в противоположные стороны (рис. 3). Очевидно, и

Рис. 3. Пара сил

Несмотря на то, что сумма сил равна нулю, эти силы не уравновешиваются. Под действием этих сил, пары сил, тело начнёт вращаться. И вращательный эффект будет определяться моментом пары:

.

Расстояние a между линиями действия сил называется плечом пары.

Если пара вращает тело против часовой стрелки, момент её считается отрицательным (как на рис. 3), если по часовой стрелке – положительным.

Для того, чтобы момент пары указывал и плоскость, в которой происходит вращение, его представляют вектором.

Вектор момента пары направляется перпендикулярно плоскости, в которой расположена пара, в такую сторону, что если посмотреть от­туда, увидим вращение тела против часовой стрелки (рис. 4).

Нетрудно доказать, что вектор мо­мента пары – есть вектор этого векторного произведения (рис. 4). И за­метим, что он равен вектору момента силы относительно точки А, точки приложения второй силы:

.

Рис.4. Вектор момента пары сил

Видео-урок «Пара сил и ее свойства»

§4. Свойства пар сил

1) Проекция пары на любую ось равна нулю. Это следует из определения пары сил.

2) Найдём сумму моментов сил оставляющих пару, относительно какой-либо точки О (рис.5).

Рис.5. Пара сил

Покажем радиусы-векторы точек А₁ и А₂ и вектор , соединяющий эти точки. Тогда момент пары сил относительно точки О

.

Но

. Поэтому .

Но .

Значит .

Момент пары сил относительно любой точки равен моменту этой пары.

Отсюда следует, что, во-первых, где бы не находилась точка О и, во-вторых, где бы не располагалась эта пара в теле и как бы она не была повёрнута в своей плоскости, действие её на тело будет одинаково. Так как момент сил, составляющих пару, в этих случаях один и тот же, рав­ный моменту этой пары

.

3) Пару можно перемещать в пределах тела по плоскости действия и переносить в любую другую параллельную плоскость.

4) Так как действие на тело сил, составляющих пару, определяется лишь её моментом, произведением одной из сил на плечо, то у пары можно изменять силы и плечо, но так, чтобы момент пары остался прежним. Например, при силах F₁=F₂=5 H и плече а = 4 см момент пары m = 20 H∙см. Можно силы сделать равными 2 Н, а плечо а = 10 см. При этом момент останется прежним 20 Н∙см и действие пары на тело не из­менится.

Все эти свойства можно объединить и, как следствие, сделать вы­вод, что пары с одинаковым вектором момента и неважно где расположенные на теле, оказывают на него равное действие. То есть такие пары эквивалентны.

Исходя из этого, на расчётных схемах пару изображают в виде дуги со стрелкой, указывающей направление вращения, и рядом пишут величину момента m (рис.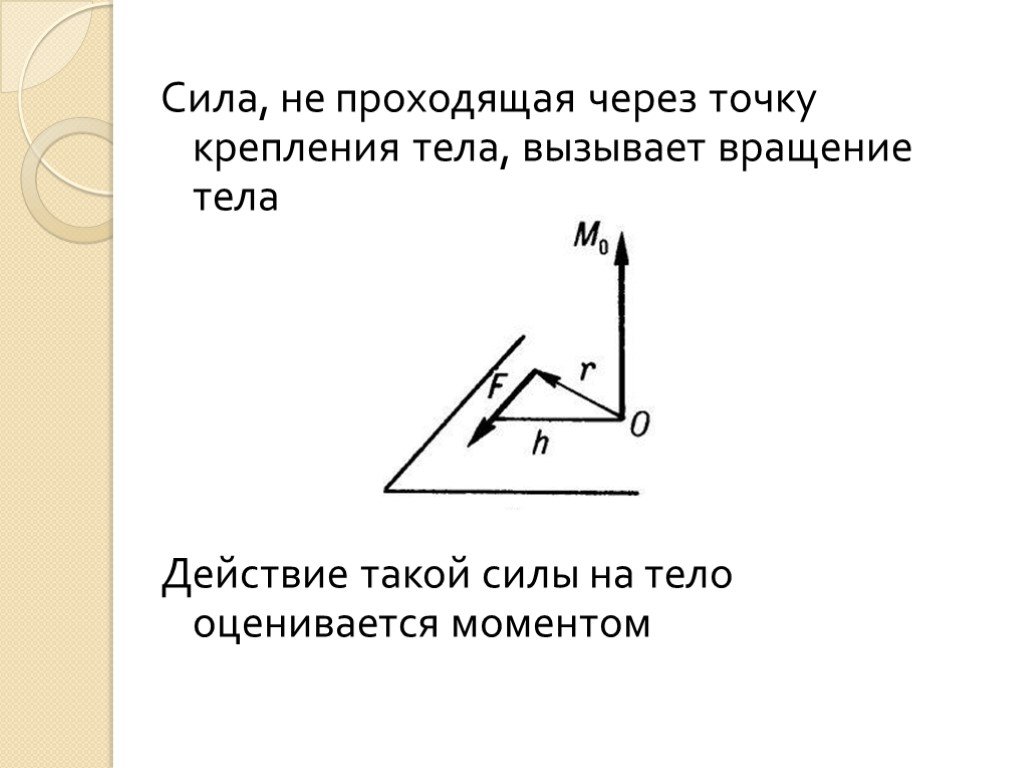 6). Или, если это пространственная конструкция, по­казывают только вектор момента этой пары. И вектор момента пары можно прикладывать к любой точке тела. Значит вектор момента пары

– свободный вектор. Такое упрощенное изображение оправдано тем, что пара сил характеризуется моментом, а не ее положением в плоскости. Но если необходимо определять не внешние силы, а внутренние в разных сечениях элемента, как это делается в сопротивлении материалов, то важен знак и место приложения пары сил.

Рис.6. Эквивалентные пары сил

И ещё одно дополнительное замечание. Так как момент пары ра­вен вектору момента одной из сил её относительно точки приложения второй силы, то момент пары сил относительно какой-либо оси z – есть проекция вектора момента пары

на эту ось: , где – угол между вектором и осью z.

Видео-уроки «Эквивалентность пар»

§5. Сложение пар

Пусть даны две пары с моментами m₁ и m₂, расположенные в пере­секающихся плоскостях (рис. 7).

Сделаем у пар плечи одинаковыми, равными а = АВ. Тогда модули сил, образующих первую пару, должны быть равны: , а об­разующих вторую пару:

.

Эти пары показаны на рис. 7, где . И расположены они в своих плоскостях так, что плечи пар совпадают с прямой АВ на линии пересе­чения плоскостей.

Рис.7. Пары сил с моментами m₁ и m₂

Сложив силы, приложенные к точкам А и В, построением паралле­лограммов, получим их равнодействующие . Так как , то эти силы и будут образовывать пару, мо­мент которой

, где – радиус-вектор точки В, совпадающий с АВ.

Так как

, то момент полученной пары .

Следовательно, в результате сложения пар, расположенных в пере­секающихся плоскостях, получится пара сил. Момент её будет равен векторной сумме моментов слагаемых пар.

При сложении нескольких пар, действующих в произвольных плоско­стях, получим пару с моментом .

Конечно, эта результирующая пара будет располагаться в плоско­сти перпендикулярной вектору .

Равенство нулю результирующей пары будет означать, что пары, действующие на тело, уравновешиваются. Следовательно, условие рав­новесия пар =0.

Это является необходимым и достаточным условием равновесия систем пар.

Если пары расположены в одной плоско­сти, векторы моментов их будут параллельны. И момент результирующей пары можно опре­делить как алгебраическую сумму моментов пар.

Рис.8. Моменты пар сил, расположенные в одной плоскости

Например, пары, показанные на рис.8, расположены в одной плоскости и моменты их:

m₁=2 Hсм , m₂=5 Hсм, m₃=3 Hсм. Пары урав­нове­шива­ются, потому что алгебраиче­ская сумма их моментов равна нулю:

Вопросы для самопроверки:

— Что называется моментом силы относительно центра на плоскости?

— Какая система сил называется парой?

— Можно ли заменить действие пары сил на тело одной силой?

— Что такое момент пары?

— Какая плоскость называется плоскостью действия пары?

— Какие пары называются эквивалентными?

— Что называется плечом пары?

— Запишите векторную и скалярную зависимости между элементами пары.

— Почему пара сил не имеет равнодействующей?

— Имеет ли пара сил равнодействующую?

— Каким образом можно уравновесить действие на тело пары сил?

— Что такое момент пары сил?

— Изменятся ли моменты пар сил, если положения сил, показанные на рис.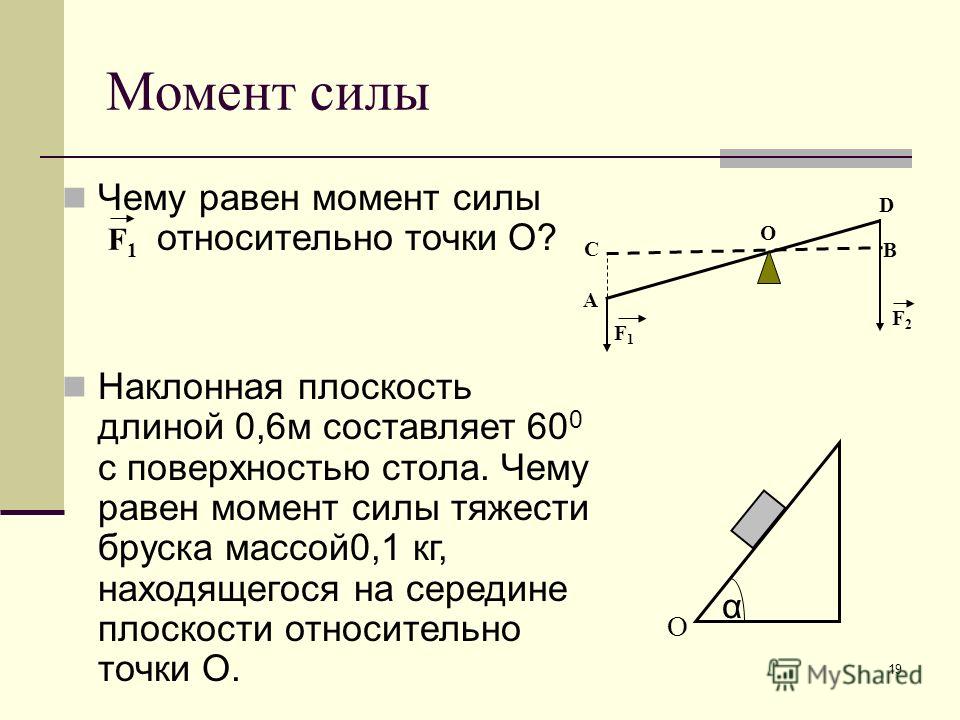 а, изменить на положения, показанные на рис. б?

— Какие пары называются эквивалентными?

— Эквивалентны ли пары сил, изображенные на рисунке?

— Каким образом производится сложение пар сил?

— Сформулируйте условие равновесия пар сил.

— Чем характеризуется действие пары сил на твердое тело?

— Как направлен вектор момента пары сил?

— Как определяются моменты пар сил, лежащих в одной плоскости?

— Какие преобразования пары сил не изменяют ее действия на твердое тело?

— Сформулируйте теоремы об эквивалентности пар.

— Что называется результирующей парой?

— Запишите формулу для определения результирующей системы пар.

— Назовите условия равновесия плоской системы пар.

— Приведите векторную запись условия равновесия произвольной системы пар.

— Будет ли изменяться момент силы относительно точки, если, не меняя направления, переносить силу вдоль линии ее действия?

— На тело действуют две силы F₁ = 40 Н и F₂ = 50 Н, как показано на рисунке (а = 0,5 м, b = 0,8 м, ). Какая из сил создает больший момент относительно точки О?

— Что такое главный вектор и главный момент плоской системы сил?

— Как аналитически найти главный вектор и главный момент данной плоской системы сил?

— В чем сходство и в чем различие между главным вектором плоской системы сил и ее равнодействующей?

— Сформулируйте теорему Вариньона.

— Приведите векторную запись теоремы Вариньона.

— Чему равен главный вектор системы сил?

— Чему равен главный момент системы сил при приведении ее к точке?

— Тело движется равномерно и прямолинейно (равновесие). Чему равны главный вектор и главный момент системы?

Момент силы — Mini Physics

28 января 2020 г. 27 декабря 2011 г. от Mini Physics

Показать/скрыть подтемы (Силы и вращательное действие сил | Уровень O) Показать/скрыть подтемы (Силы и динамика | Уровень A)

Момент силы или крутящий момент, r определяется как эффект поворота силы вокруг оси вращения и является произведением силы (F) и перпендикулярного расстояния (d) от линии действия силы до оси вращения.

• Единицей момента силы в системе СИ является ньютон-метр (Нм). Это векторная величина.
• Его направление задается правилом правой руки, перпендикулярным плоскости действия силы, и точкой вращения, параллельной оси вращения.

$$r = F \times d$$

,где
r – момент силы/крутящего момента
F – сила
d – расстояние по перпендикуляру от линии действия силы до оси вращения

Пара

Пара – это пара сил, равных по величине, но противоположных по направлению, линии движения которых не совпадают.

• Будет продолжать вращаться, так как есть результирующий момент
• Поскольку силы равны и противоположны, результирующая сила равна нулю и поэтому нет линейного ускорения
• $r = F \times d$

Крутящий момент (момент пара) есть произведение одной из сил и перпендикулярного расстояния между их линиями действия сил.

• Может снимать момент с любой точки

---

Вопросы для самопроверки

Рассмотрим рисунок выше.

Учитывая, что вес кота 150 Н, а расстояние от кота до оси вращения равно 30 см, вычислить момент силы относительно оси вращения. Показать/скрыть ответ

$$\begin{aligned} r &= F \times d \\ &= 150 \times 0.30 \\ &= 45 \text{ Нм} \end{aligned}$$

---

Почему крышку контейнера легче открыть ложкой, чем монетой?

Показать/скрыть ответ

Ложка длиннее монеты. Если вы используете их, чтобы открыть крышку контейнера путем поворота, перпендикулярное расстояние (d) будет больше для ложки, чем для монеты.

Предположим, что для открытия крышки требуется момент силы $x \text{ Нм}$, и что $d_{\text{ложка}} = 2 d_{\text{монета}}$.

Найдите силу, необходимую для открытия крышки, если мы используем ложку :

$$\begin{aligned} r &= F \times d \\ x &= F_{\text{ложка}} \times d_{\text{ложка}} \\ F_{\text{ложка}} &= \frac{x}{d_{\text{ложка}}} \end{aligned}$$

Найти силу, необходимую для откройте крышку, если мы используем монету :

$$\begin{aligned} r &= F \times d \\ x &= F_{\text{coin}} \times d_{\text{coin}} \\ F_{\text{coin}} &= \frac{x}{d_{\text{coin}}} \end{align}$$

Поскольку $d_{\text{ложка}} = 2 d_{\text{монета}}$,

$$\begin{align} F_{\text{coin}} &= \frac{x}{\ frac{d_{\text{spoon}}}{2}} \\ &= 2 \frac{x}{d_{\text{spoon}}} \\ &= 2 F_{\text{spoon}} \end {align}$$

Из приведенных выше расчетов ($F_{\text{coin}} = 2 F_{\text{ложка}}$) вам потребуется в два раза больше силы, чтобы открыть крышку контейнера, если вы использовать монету.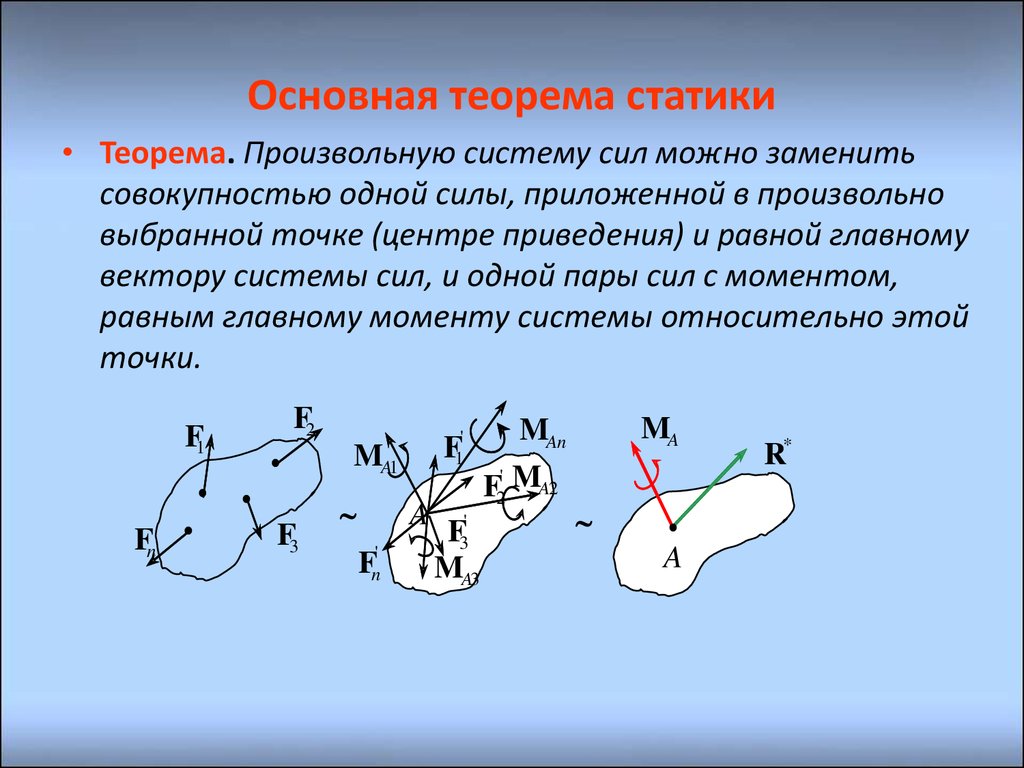

Назад к Силам и динамике (Уровень A)

Вернуться к списку тем A Level

Вернуться к Силам и вращению Действие сил (Уровень O)

Назад к списку тем уровня O

Делиться значит заботиться:

Симметрия сил – Колледж физики

Глава 4 Динамика: сила и законы движения Ньютона

Резюме

• Поймите третий закон движения Ньютона.
• Примените третий закон Ньютона для определения систем и решения задач движения.

В мюзикле «Человек из Ламанчи » есть отрывок, относящийся к третьему закону движения Ньютона. Санчо, описывая ссору своей жены с Дон Кихотом, говорит: «Конечно, я ударил ее в ответ, ваша светлость, но она намного сильнее меня, и вы знаете, что они говорят: «камень попадет в кувшин или кувшин». попадет в камень, кувшину будет плохо». Именно это и происходит всякий раз, когда одно тело действует с силой на другое — на первое тоже действует сила (равная по величине и противоположная по направлению). Многочисленные распространенные случаи, такие как ушиб пальца ноги или бросание мяча, подтверждают это. Точно сказано в Третий закон движения Ньютона .

ТРЕТИЙ ЗАКОН НЬЮТОНА

Всякий раз, когда одно тело воздействует на другое тело, на первое тело действует сила, равная по величине и противоположная по направлению силе, которую оно оказывает.

Этот закон представляет определенную симметрию в природе : Силы всегда действуют парами, и одно тело не может воздействовать силой на другое, не испытывая на себе силы. Иногда мы в общих чертах называем этот закон «действие-противодействие», где прилагаемая сила является действием, а сила, воспринимаемая как следствие, является противодействием. Третий закон Ньютона имеет практическое применение при анализе происхождения сил и понимании того, какие силы являются внешними по отношению к системе.

Мы легко можем увидеть третий закон Ньютона в действии, взглянув на то, как люди передвигаются.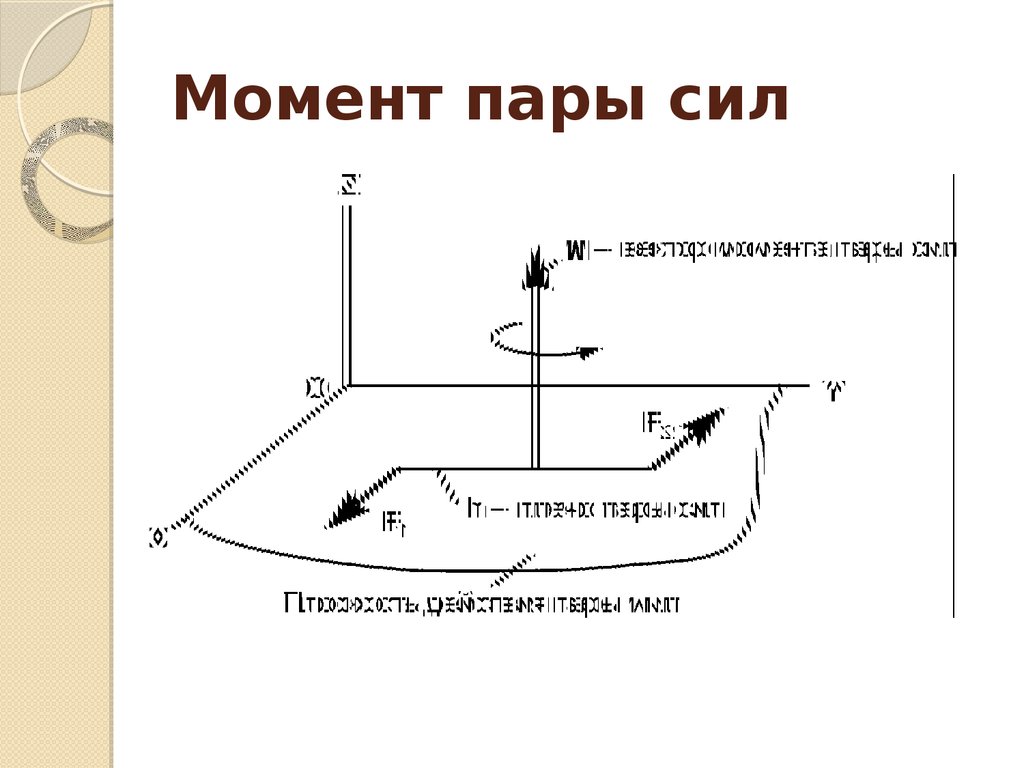 Рассмотрим пловца, отталкивающегося от края бассейна, как показано на рис. 1. Он отталкивается ногами от стенки бассейна и ускоряется в направлении , противоположном направлению своего толчка. Стена воздействовала на пловца равной и противоположной силой. Вы можете подумать, что две равные и противоположные силы нейтрализуют друг друга, но это не так, потому что они действуют на разные системы9.0112 . В этом случае есть две системы, которые мы могли бы исследовать: пловец или стена. Если мы выберем пловца в качестве интересующей системы, как на рисунке, то [латекс]\textbf{F}_{\text{стена на ногах}}[/латекс] будет внешней силой, воздействующей на эту систему и воздействующей на ее движение. Пловец движется в направлении [латекс]\textbf{F}_{\text{стена на ногах}}.[/latex] Напротив, сила [латекс]\textbf{F}_{\text{ноги на ногах стена}}[/латекс] действует на стену, а не на нашу интересующую систему. Таким образом, [латекс]\textbf{F}_{\text{ноги на стене}}[/латекс] не влияет напрямую на движение системы и не отменяет [латекс]\textbf{F}_{\text{стену на ногах}}. [/latex] Обратите внимание, что пловец отталкивается в направлении, противоположном тому, в котором он хочет двигаться. Таким образом, реакция на ее толчок идет в желаемом направлении.

Рисунок 1. Когда пловец прикладывает силу F _{фута к стене} к стене, он ускоряется в направлении, противоположном направлению его толчка. Это означает, что чистая внешняя сила, действующая на нее, направлена ​​в направлении, противоположном F _{футам на стене} . Это противодействие возникает потому, что в соответствии с третьим законом движения Ньютона стена оказывает на нее силу F _{стена на ногах} , равную по величине, но в направлении, противоположном тому, которое она прикладывает к ней. Линия вокруг пловца указывает интересующую систему. Обратите внимание, что F _{ноги на стене} не действует на эту систему (плавателя) и, таким образом, не отменяет F _{стена на ногах} . Таким образом, на диаграмме свободного тела показаны только F _{стена на ногах} , w , гравитационная сила, и BF , выталкивающая сила воды, поддерживающая вес пловца. Вертикальные силы w и BF компенсируются, так как нет вертикального движения.

Легко найти и другие примеры третьего закона Ньютона. Когда профессор шагает перед доской, она оказывает давление на пол назад. Пол оказывает на профессора реактивную силу, которая заставляет ее двигаться вперед с ускорением. Точно так же автомобиль ускоряется, потому что земля давит на ведущие колеса вперед в ответ на то, что ведущие колеса толкают землю назад. Вы можете увидеть следы отталкивания колес назад, когда шины пробуксовывают на гравийной дороге и отбрасывают камни назад. В другом примере ракеты движутся вперед, выбрасывая газ назад с большой скоростью. Это означает, что ракета оказывает большую обратную силу на газ в камере сгорания ракеты, и поэтому газ оказывает большую реактивную силу на ракету вперед. Эта сила реакции называется тяга . Это распространенное заблуждение, что ракеты движутся сами по себе, отталкиваясь от земли или воздуха позади себя. На самом деле они лучше работают в вакууме, где они легче удаляют выхлопные газы. Точно так же вертолеты создают подъемную силу, толкая воздух вниз, тем самым испытывая восходящую силу реакции. Птицы и самолеты также летают, воздействуя на воздух в направлении, противоположном тому, в котором они нуждаются. Например, крылья птицы толкают воздух вниз и назад, чтобы подняться и двигаться вперед. Осьминог передвигается в воде, выбрасывая воду через воронку из своего тела, подобно водному мотоциклу. В ситуации, похожей на ситуацию с Санчо, профессиональные бойцы в клетке испытывают силы реакции при ударе, иногда ломая себе руку, ударяя по корпусу соперника.

Пример 1. Приступая к работе: выбор правильной системы

Профессор физики толкает тележку с демонстрационным оборудованием в лекционный зал, как показано на рис. 2. Ее масса составляет 65,0 кг, масса тележки — 12,0 кг, масса оборудования составляет 7,0 кг. Вычислите ускорение, возникающее, когда профессор прикладывает к полу обратную силу 150 Н. Все силы, противодействующие движению, такие как трение о колеса тележки и сопротивление воздуха, составляют в сумме 24,0 Н.

Рис. 2. Профессор толкает тележку с демонстрационным оборудованием. Длины стрелок пропорциональны величинам сил (кроме f , так как он слишком мал для масштабирования). В каждом примере задаются разные вопросы; таким образом, система интересов должна быть определена по-разному для каждого. Система 1 подходит для примера 2, так как требует ускорения всей группы объектов. Только F _пол и f являются внешними силами, действующими на Систему 1 вдоль линии движения. Все остальные силы либо отменяют, либо воздействуют на внешний мир. Система 2 выбрана для этого примера так, что F _prof будет внешней силой и войдет во второй закон Ньютона. Обратите внимание, что диаграммы свободного тела, которые позволяют нам применить второй закон Ньютона, зависят от выбранной системы.

Стратегия

Поскольку они ускоряются как единое целое, мы определяем систему как профессора, тележку и оборудование. Это система 1 на рис. 2. Профессор толкает назад с силой [латекс]\textbf{F}_{\text{фут}}[/латекс] в 150 Н. Согласно третьему закону Ньютона, пол действует вперед сила реакции [латекс]\textbf{F}_{\text{пол}}[/латекс] равна 150 Н в Системе 1. Поскольку все движения горизонтальны, мы можем предположить, что результирующая сила в вертикальном направлении отсутствует. Таким образом, задача является одномерной в горизонтальном направлении. Как уже отмечалось, [latex]\textbf{f}[/latex] препятствует движению и, таким образом, находится в направлении, противоположном [latex]\textbf{F}_{\text{floor}}.[/latex] Обратите внимание, что мы не включайте силы [latex]\textbf{F}_{\text{prof}}[/latex] или [latex]\textbf{F}_{\text{cart}}[/latex], поскольку они являются внутренними силы, и мы не включаем [латекс]\textbf{F}_{\text{фут}}[/латекс], потому что он действует на пол, а не на систему. На Систему 1 не действуют другие значительные силы. Если из всей этой информации можно найти результирующую внешнюю силу, мы можем использовать второй закон Ньютона, чтобы найти требуемое ускорение. См. диаграмму свободного тела на рисунке.

Решение

Второй закон Ньютона определяется как

[латекс] {а\:=}[/латекс] [латекс]{\ гидроразрыва {F _ {\ текст {сеть}}} {м}.} [ /latex]

Суммарная внешняя сила, действующая на Систему 1, выводится из рисунка 2 и приведенного выше обсуждения и составляет

[latex]{\textbf{F}_{\text{net}}=\textbf{F}_{ \text{floor}}-\textbf{f}=150\text{ N}-24.0\text{ N}=126\text{ N}.}[/latex]

Масса Системы 1 равна

[ латекс]{м=(65,0 + 12,0 + 7,0)\текст{кг} = 84\текст{кг}.}[/латекс] 92} \end{array}[/latex]

Обсуждение

Никакие силы между компонентами Системы 1, например, между руками профессора и тележкой, не вносят вклад в результирующую внешнюю силу, поскольку они являются внутренними для Системы.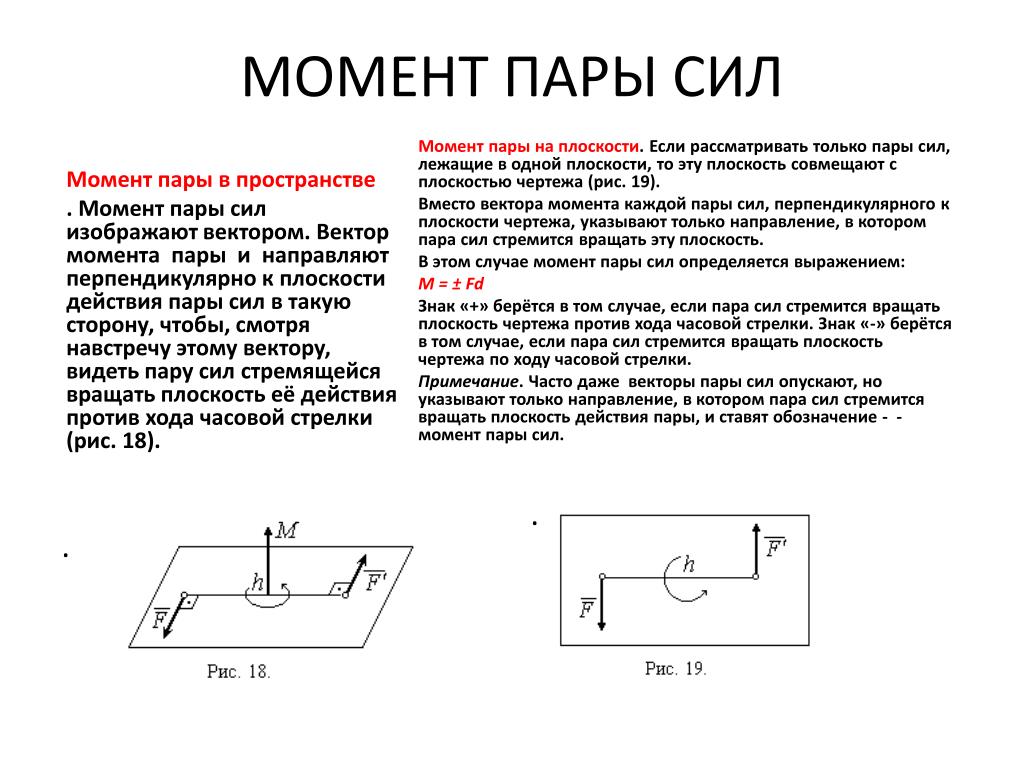 1. Другой способ взглянуть на это — отметить, что силы между компонентами системы сокращаются, потому что они равны по величине и противоположны по направлению. Например, сила, приложенная профессором к тележке, приводит к тому, что на нее действует равная и противоположная сила. В этом случае обе силы действуют на одну и ту же систему и, следовательно, сокращаются. При этом внутренние силы (между компонентами системы) сокращаются. Выбор Системы 1 имел решающее значение для решения этой проблемы.

Пример 2. Сила тележки — выбор новой системы

Рассчитайте силу, с которой профессор воздействует на тележку на рис. 2, используя при необходимости данные из предыдущего примера.

Стратегия

Если теперь мы определим интересующую нас систему как тележку плюс оборудование (система 2 на рис. 2), то чистая внешняя сила, действующая на систему 2, будет равна силе, которую профессор оказывает на тележку за вычетом трения. Сила, которую она оказывает на тележку, [latex]\textbf{F}_{\text{prof}},[/latex] является внешней силой, действующей на Систему 2. [latex]\textbf{F}_{\text {prof}}[/latex] был внутренним по отношению к Системе 1, но является внешним по отношению к Системе 2 и входит во второй закон Ньютона для Системы 2.

Решение

Второй закон Ньютона можно использовать для нахождения [латекс]\textbf{F}_{\text{проф}}.[/латекс] Начиная с

[латекс]{а\:=}[ /latex] [latex]{\frac{F_{\text{net}}}{m}}[/latex]

и отметив, что величина суммарной внешней силы на Систему 2 равна

[latex]{F_ {\text{net}}=F_{\text{prof}}-f,}[/latex]

находим для [latex]{F_{\text{prof}}},[/latex] искомое количество :

[латекс] {F_{\text{prof}}=F_{\text{net}}+f.}[/latex] 92)=29\text{ N}.}[/latex]

Теперь мы можем найти искомую силу:

[latex]{F_{\text{prof}}=F_{\text{net}}+f ,}[/латекс]

[латекс]{F_{\текст{проф}}=29\текст{N}+24,0\текст{N}=53\текст{N}.}[/латекс]

Обсуждение

Интересно, что эта сила значительно меньше силы в 150 Н, которую профессор приложил назад к полу.