Контрольная работа по физике Магнетизм 11 класс
Контрольная работа по физике Магнетизм 11 класс с ответами. Контрольная работа включает 4 варианта, в каждом варианте по 7 заданий.
1 вариант
1. Длина активной части проводника 15 см. Угол между направлением тока и индукцией магнитного поля равен 90°. С какой силой магнитное поле с индукцией 40 мТл действует на проводник, если сила тока в нем 12 А?
2. На протон, движущийся со скоростью 107 м/с в однородном магнитном поле перпендикулярно линиям индукции, действует сила 0,32 · 10-12 Н. Какова индукция магнитного поля?
3. Определите индуктивность катушки, которую при силе тока 8,6 А пронизывает магнитный поток 0,12 Вб.
4. Электрон движется по окружности радиусом 4 мм перпендикулярно к линиям индукции однородного магнитного поля. Скорость электрона равна 3,5 · 106 м/с. Рассчитайте индукцию магнитного поля.
5. Плоская прямоугольная катушка из 200 витков со сторонами 10 см и 5 см находится в однородном магнитном поле с индукцией 0,05 Тл. Какой максимальный вращающий момент может действовать на катушку в этом поле, если сила тока в ней 2 А?
6. В вертикальном однородном магнитном поле на двух тонких нитях подвешен горизонтально проводник длиной 20 см и массой 20,4 г. Индукция магнитного поля равна 0,5 Т л. На какой угол от вертикали отклонятся нити, если сила тока в проводнике равна 2 А?
7. Два протона движутся в однородном магнитном поле в плоскости, перпендикулярной линиям индукции магнитного поля, по окружностям, имеющим радиусы, равные соответственно 1 см и 2 см. Определите отношение кинетических энергий протонов.
2 вариант
1. Определите силу тока, проходящего по прямолинейному проводнику, перпендикулярному однородному магнитному полю, если на активную часть проводника длиной 40 см действует сила в 20 Н при магнитной индукции 10 Тл.
2. Электрон со скоростью 5 · 107 м/с влетает в однородное магнитное поле под углом 30° к линиям индукции. Индукция магнитного поля равна 0,8 Тл. Найдите силу, действующую на электрон.
3. В катушке с индуктивностью 0,6 Гн сила тока 20 А. Какова энергия магнитного поля катушки?
4. Электрон влетел в однородное магнитное поле с индукцией 2 · 10-3 Тл перпендикулярно линиям индукции со скоростью 3,6 · 106 м/с и продолжает свое движение по круговой орбите радиусом 1 см. Определите отношение заряда электрона к его массе.
5.
6. Проводящий стержень лежит на горизонтальной поверхности перпендикулярно однородному горизонтальному магнитному полю с индукцией 0,2 Т л. Какую силу в горизонтальном направлении нужно приложить перпендикулярно проводнику для его равномерного поступательного движения? Сила тока в проводнике равна 10 А, масса проводника равна 100 г, его длина 25 см, коэффициент трения равен 0,1.
Какую силу в горизонтальном направлении нужно приложить перпендикулярно проводнику для его равномерного поступательного движения? Сила тока в проводнике равна 10 А, масса проводника равна 100 г, его длина 25 см, коэффициент трения равен 0,1.
7. В однородное магнитное поле с индукцией 10 мТл перпендикулярно линиям индукции влетает электрон с кинетической энергией 30 кэВ. Каков радиус кривизны траектории движения электрона в поле?
3 вариант
1. Под каким углом расположен прямолинейный проводник к линиям индукции магнитного поля с индукцией 15 Тл, если на каждые 10 см длины проводника действует сила в 3 Н, когда сила тока в проводнике 4 А?
2. В однородное магнитное поле с индукцией 8,5 · 10-3 Тл влетает электрон со скоростью 4,6 · 106 м/с, направленной перпендикулярно линиям индукции. Рассчитайте силу, действующую на электрон в магнитном поле.
3. Магнитный поток, пронизывающий виток катушки, равен 0,015 Вб. Сила тока в катушке 5 А. Сколько витков содержит катушка, если ее индуктивность 60 мГн?
Сила тока в катушке 5 А. Сколько витков содержит катушка, если ее индуктивность 60 мГн?
4. Чему равен максимальный вращающий момент сил, действующих на прямоугольную обмотку электродвигателя, содержащую 100 витков провода, размером 4 х 6 см, по которой проходит ток 10 А, в магнитном поле с индукцией 1,2 Тл?
5. Ядро атома гелия, имеющее массу 6,7 · 10-27 кг и заряд 3,2 · 10-19 Кл, влетает в однородное магнитное поле с индукцией 10-2 Тл и начинает двигаться по окружности радиусом 1 м. Рассчитайте скорость этой частицы.
6. Пылинка с зарядом 10 мкКл и массой 1 мг влетает в однородное магнитное поле с индукцией 1 Тл и движется по окружности. Сколько оборотов сделает пылинка за 3,14 с?
7. Прямолинейный проводник массой 3 кг, сила тока в котором 5 А, поднимается вертикально вверх с ускорением 5 м/с2 в однородном магнитном поле с индукцией 3 Тл перпендикулярно линиям индукции.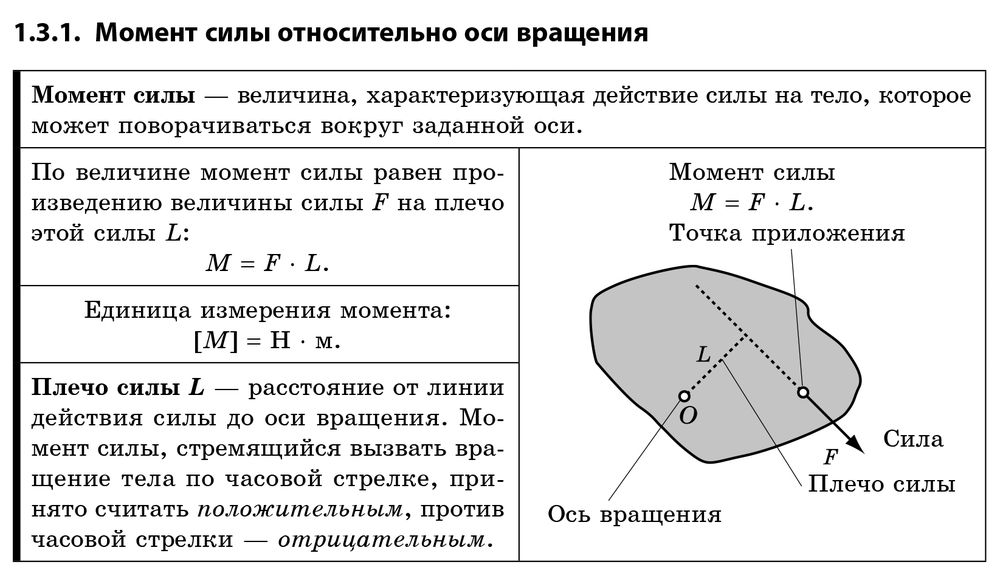 Определите длину проводника.
Определите длину проводника.
4 вариант
1. Определите длину активной части прямолинейного проводника, помещенного в однородное магнитное поле с индукцией 400 Т л, если на него действует сила 100 Н. Проводник расположен под углом 30° к линиям индукции магнитного поля, сила тока в проводнике 2 А.
2. С какой скоростью влетел электрон в однородное магнитное поле, индукция которого равна 10 Тл, перпендикулярно линиям индукции, если на него действует поле с силой 8 · 10
3. Магнитное поле катушки с индуктивностью 95 мГн обладает энергией 0,19 Дж. Чему равна сила тока в катушке?
4. Сила тока в горизонтально расположенном проводнике длиной 20 см и массой 4 г равна 10 А. Найдите индукцию магнитного поля, в которое нужно поместить проводник, чтобы сила тяжести уравновесилась силой Ампера.
5. Протон влетает в однородное магнитное поле, индукция которого равна 3,4 · 10-2 Тл, перпендикулярно линиям индукции со скоростью 3,5 · 105 м/с.
6. Два электрона движутся по окружностям в однородном магнитном поле в плоскости, перпендикулярной линиям индукции поля. Найдите отношение периодов обращения электронов, если кинетическая энергия первого электрона в 4 раза больше кинетической энергии второго.
7. На двух нитях висит горизонтально расположенный стержень длиной 2 ми массой 0,5 кг. Стержень находится в однородном магнитном поле, индукция которого 0,5 Тл и направлена вниз. Какой ток нужно пропустить по стержню, чтобы нити отклонились от вертикали на 45°?
Ответы на контрольную работа по физике Магнетизм 11 класс
1 вариант
1. 7,2 · 10-2 Н
2. 0,2 Тл
3. 14 мГн
4. 5 · 10-3 Тл
5. 0,1 Н·м
6. 45°
7. 1 : 4
2 вариант
1. 5 А
2. 3 · 10-12 Н
3 · 10-12 Н
3. 120 Дж
4. ≈ 1,8 · 1011 Кл/кг
5. 2,7 А
6. 0,148 Н или 0,048 Н в зависимости от направлений силы тока и магнитной индукции
7. 5,8 см
3 вариант
1. 30 °
2. 6,3 · 10-15 Н
3. 20
4. 2,88 Н · м
6. 5
7. 3 м
4 вариант
1. 0,25 м
2. 5 · 107 м/с
3. 2 А
4. 20 мТл
5. 10 см
6. 1 : 1
7. 5 А
PDF-версия
Контрольная работа Магнетизм 11 класс
(97 Кб, pdf)
Сборник задач абитуриенту. МАГНЕТИЗМ. Работа магнитного поля. Момент сил. Тема 22-3
Опубликовано ср, 07/24/2019 — 10:01 пользователем fizportal.ru
МАГНЕТИЗМ. Работа магнитного поля. Момент сил. Тема 22-3
22.20. Проводник длиной l = 30 см с током силой I = 20 A расположен под углом $\alpha$ = 30° к однородному магнитному полю с индукцией B = 0,4 Тл.
22.21. Прямоугольный контур площадью 150 см2 с током силой 4 A, на который действует только однородное магнитное поле с индукцией 0,1 Тл, занял положение устойчивого равновесия. Какую после этого надо совершить работу (в мДж), чтобы медленно повернуть его на 90° вокруг оси, проходящей через середины противоположных сторон?
Ответ22.22. Определите работу (в мДж), совершаемую силой Ампера при перемещении проводника длиной 0,2 м с током силой 5 A в однородном магнитном поле на расстояние 0,5 м. Проводник расположен перпендикулярно линиям поля и движется в направлении силы Ампера. Индукция магнитного поля 0,1 Тл.
22.23. Прямоугольный контур площадью 150 см2 с током силой 3 A, на который действует только однородное магнитное поле с индукцией 0,1 Тл, занял положение устойчивого равновесия. Какую после этого надо совершить работу (в мДж), чтобы медленно повернуть его на 180° вокруг оси, проходящей через середины противоположных сторон?
Ответ22. 24. С какой силой взаимодействуют два параллельных провода с токами силой 300 A, если длина проводов 50 м и каждый из них создает в месте расположения другого провода магнитное поле с индукцией 1,2 мТл?
24. С какой силой взаимодействуют два параллельных провода с токами силой 300 A, если длина проводов 50 м и каждый из них создает в месте расположения другого провода магнитное поле с индукцией 1,2 мТл?
22.25. Максимальный момент сил, действующих на прямоугольную рамку с током силой 50 A в однородном магнитном поле, равен 1 Н·м. Какова индукция поля, если ширина рамки 0,1 м, а длина 0,2 м?
Ответ22.26. Определите индукцию магнитного поля, если максимальный момент сил, действующих на рамку площадью 1 см2, равен 5 × 10−2 Н·м при силе тока 1 A. Рамка состоит из 100 витков провода.
Ответ22.27. Определить индукцию магнитного поля, если максимальный вращающийся момент сил, действующий на рамку площадью 1 см
Tags:
Абитуриенту
магнетизм
момент силы
работа МП
9 класс. fizportal.ru | ||
Домашняя работа 10 класс. 3 Электростатика. Напряженность электрического поля fizportal.ru | ||
Домашняя работа 11 класс. 5 Элементы волновой оптики. Дифракция света 2 fizportal.ru | ||
9 класс. Тема 2. ДИНАМИКА. Прямолинейное движение тел — 1 fizportal.ru | ||
9 класс. Тема 4. ДИНАМИКА. Наклонная плоскость -1 fizportal.ru | ||
Домашняя работа 8 класс. Повторение. ДУ №43 Электрическое поле fizportal.ru | ||
Домашняя работа 8 класс. Повторение. ДУ №44 Электрический ток. Источники тока fizportal.ru | ||
9 класс. Тема 1. ДИНАМИКА. Второй закон Ньютона fizportal.ru | ||
Домашняя работа 11 класс. 1 Геометрическая оптика. Прямолинейное распространение света fizportal. | ||
Домашняя работа 11 класс. 3 Элементы волновой оптики. Интерференция света 2 fizportal.ru |
Объяснение урока: Крутящий момент на прямоугольной проволочной петле с током в магнитном поле
В этом объяснении мы узнаем, как рассчитать крутящий момент на прямоугольная петля из проволоки в однородном магнитном поле.
Начнем с рассмотрения прямоугольной проволочной петли в горизонтальной плоскости, с текущим 𝐼 через него. Магнитное поле с напряженностью 𝐵 также существует. в горизонтальной плоскости. На следующей схеме показана эта петля провода.
Рассмотрим прямоугольную петлю более подробно. Следующая диаграмма показывает каждую сторону петли, обозначенную цифрами.
Как мы видим, прямоугольная петля состоит из двух отрезков провода, обеспечивающего ток
от середины основания прямоугольника. Зазор между этими двумя частями
провода 𝑑, что очень мало:
𝑑≈0.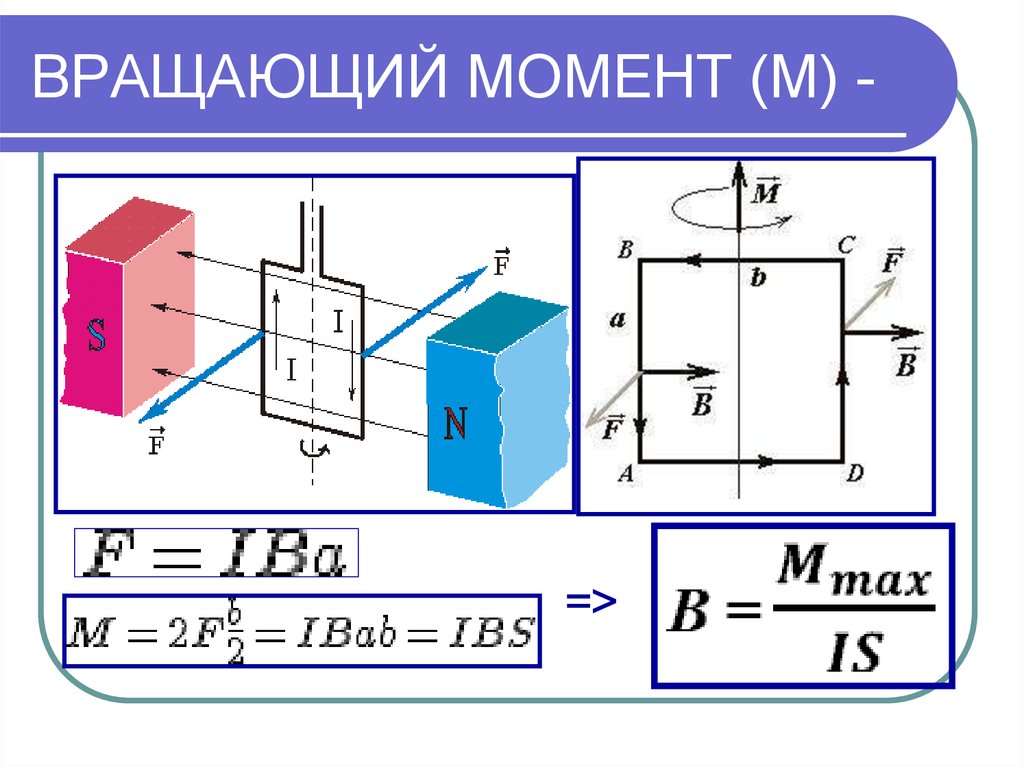
Будем также говорить, что длина двух отрезков провода, подающих ток маленький. Это означает, что нам нужно рассматривать только прямоугольное сечение (от 2 до 5) проволоки.
Напомним, что сила 𝐹 на проводе длиной 𝑙, по которому течет ток 𝐼, перпендикулярно магнитному полю 𝐵, равно 𝐹=𝐵𝐼𝑙.
Если мы посмотрим на каждый отрезок провода, то увидим, что там только сила действующие на сечения 3 и 5. Приняв вертикально вверх положительное, сила, действующая на каждую из них, равна 𝐹=−𝐵𝐼𝑑,𝐹=𝐵𝐼𝑑.
Итак, на два отрезка проволоки действуют силы равной величины, но в противоположных направлениях. Направление силы можно найти с помощью Правило левой руки Флеминга.
Правило левой руки Флеминга — это соглашение, используемое для нахождения направления
сила, действующая на провод со стороны магнитного поля, в котором находится провод
и направление тока по проводу. На следующей диаграмме показано
Правило левой руки Флеминга и оси, сделанные из магнитного поля,
силы и тока.
В правиле левой руки Флеминга большой палец указывает в направлении силы, указательный палец указывает в направлении магнитного поля, а средний палец указывает направление тока в проводе.
Мы можем использовать правило левой руки Флеминга, чтобы найти направление действующей силы на участках 3 и 5 петли проволоки. Следующая диаграмма иллюстрирует это.
Как видим, сила, действующая на участок 3 провода, направлена вниз, и сила, действующая на участок 5 провода, направлена вверх. Следующая диаграмма показаны силы, действующие на прямоугольную проволочную петлю; 𝐹 действует вниз, и 𝐹 действует вверх.
Теперь рассмотрим ось, проходящую через центр прямоугольника, представленную пунктирной линией на следующей диаграмме.
Крутящий момент вокруг этой оси можно рассчитать, умножив каждую силу на перпендикулярное расстояние к оси: 𝜏=𝐹−𝑑2+𝐹𝑑2.
Подставляя в выражения 𝐹 и
𝐹, получаем
𝜏=−𝐵𝐼𝑑−𝑑2+𝐵𝐼𝑑𝑑2𝜏=𝐵𝐼𝑑𝑑.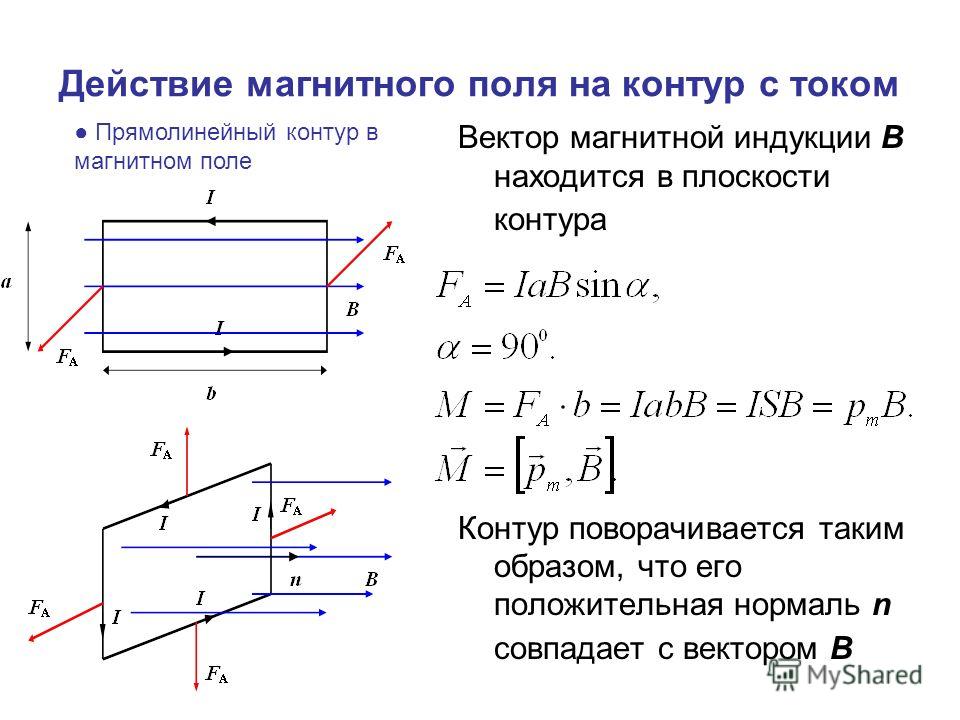
Можно видеть, что это содержит 𝑑, умноженное на прямоугольника, 𝐴. Таким образом, крутящий момент можно записать как 𝜏=𝐵𝐼𝐴.
Мы также можем рассчитать магнитный дипольный момент проволочной петли. магнитный дипольный момент определяется как крутящий момент на проводе, деленный на напряженность магнитного поля: 𝑚=𝜏𝐵.
Определение: Магнитный дипольный момент
Магнитный дипольный момент проволочной петли, по которой течет ток в магнитном поле. поле определяется как крутящий момент, действующий на петлю провода, деленный на магнитное напряженность поля: 𝑚=𝜏𝐵.
Для прямоугольного провода мы можем заменить выражение для крутящего момента, которое мы рассчитано ранее: 𝑚=𝐵𝐼𝐴𝐵𝑚=𝐼𝐴.
Теперь мы рассмотрим примерный вопрос расчета крутящего момента и магнитный дипольный момент прямоугольного провода.
Пример 1. Расчет крутящего момента и магнитного дипольного момента Прямоугольная петля из провода с током в магнитном поле
На схеме показана прямоугольная петля из провода с током между
полюса магнита. Стороны петли, параллельные линии 𝑑, равны
параллельно магнитному
поле, а стороны петли параллельны линии 𝑑
перпендикулярны к
магнитное поле. Ток в петле равен
350 мА,
а напряженность магнитного поля равна
0,12 т. Длина
𝑑=0,025м и
длина 𝑑=0,015м.
Стороны петли, параллельные линии 𝑑, равны
параллельно магнитному
поле, а стороны петли параллельны линии 𝑑
перпендикулярны к
магнитное поле. Ток в петле равен
350 мА,
а напряженность магнитного поля равна
0,12 т. Длина
𝑑=0,025м и
длина 𝑑=0,015м.
- Найти крутящий момент, действующий на петлю, с точностью до микроньютон-метр.
- Найти магнитный дипольный момент петли с точностью до микроньютон-метр на тесла.
Ответ
Часть 1
Крутящий момент, действующий на проволочную петлю, 𝜏, можно найти с помощью формула 𝜏=𝐵𝐼𝐴, где 𝐵 — напряженность магнитного поля, 𝐼 — ток в петле провода, а 𝐴 — площадь петля из проволоки.
Сначала мы переведем ток в проводе в единицы СИ ампер: 𝐼=350𝐼=0,35 мАА
Петля провода прямоугольная, поэтому площадь петли просто
𝐴=𝑑𝑑,
где 𝑑=0,025м и
𝑑=0,015м, как указано
в вопросе. Это дает площадь
𝐴=3,75×10,м
Это дает площадь
𝐴=3,75×10,м
Подставляя значения 𝐼 и 𝐴 в уравнение для крутящего момента вместе с напряженностью магнитного поля 𝐵=0,12T, дает 𝜏=0,12×0,35×3,75×10𝜏=1,575×10⋅.TAmNm
В микроньютон-метрах это равно 𝜏=15,75⋅.мкНм
К ближайшему микроньютон-метр, крутящий момент, действующий на проволочную петлю, равен 16 мкН⋅м.
Часть 2
Магнитный дипольный момент 𝑚 проволочной петли, по которой течет ток в магнитном поле равен крутящему моменту, действующему на петлю провода, 𝜏, деленная на напряженность магнитного поля, 𝐵: 𝑚=𝜏𝐵.
Подставляя ранее рассчитанное значение 𝜏=1,575×10⋅Нм и заданное значение 𝐵=0,12T дает 𝑚=1,575×10⋅0,12𝑚=1,313×10⋅/.NmTNmT
В микроньютон-метрах на тесла это 𝑚=131,3⋅/.мкНмТл
Магнитный дипольный момент петли с точностью до
микроньютон-метр на тесла равен
131 мкН⋅м/Тл.
Теперь рассмотрим, что произойдет, если будет несколько петель или поворотов, из прямоугольной проволоки. На следующей диаграмме показана та же прямоугольная петля, что и раньше, за исключением того, что теперь на проводе много витков.
Каждый кусок проволоки создает одинаковую силу. Если есть 𝑁 провода, момент на оси равен 𝜏=𝐵𝐼𝐴𝑁.
Теперь мы рассмотрим пример вопроса, где прямоугольная петля провод имеет несколько витков.
Пример 2. Расчет крутящего момента, действующего на прямоугольную проволочную петлю с несколькими витками, по которым течет ток в магнитном поле
На схеме показана прямоугольная проводящая катушка с 3 витками, находящаяся в магнитном поле. В катушке протекает ток 8,5 А. Стороны петли параллельны линии
𝑑 параллельны магнитному полю, а стороны петли
параллельные линии 𝑑 перпендикулярны магнитному полю. Длина
𝑑=0,035м и длина 𝑑=0,025м.
крутящий момент на петле 15 мН⋅м.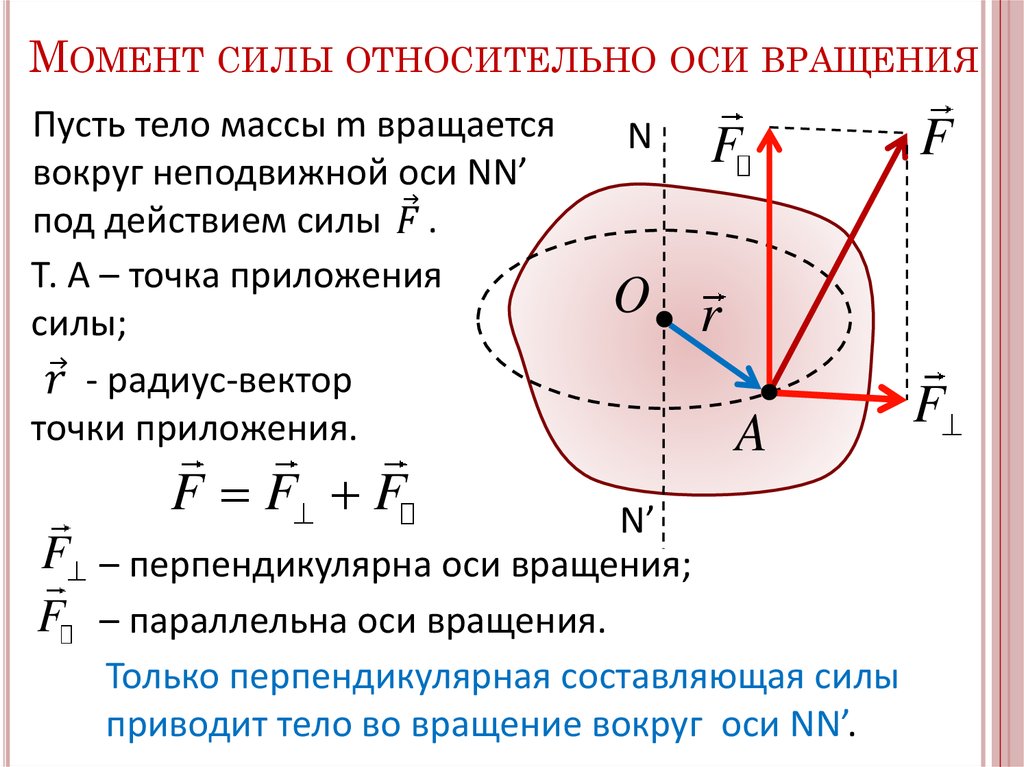 Найдите величину магнитного поля с точностью до
миллитесла.
Найдите величину магнитного поля с точностью до
миллитесла.
Ответ
Формула для расчета крутящего момента на прямоугольной проволочной петле с несколько витков, по которым течет ток в магнитном поле, 𝜏=𝐵𝐼𝐴𝑁.
Мы можем изменить это уравнение для напряженности магнитного поля, 𝐵: 𝐵=𝜏𝐼𝐴𝑁.
Во-первых, площадь прямоугольной петли провода, 𝐴, можно рассчитать, умножив 𝑑 и 𝑑: 𝐴=𝑑×𝑑𝐴=0,035×0,025𝐴=0,000875,ммм
Крутящий момент на петле можно преобразовать в единицы СИ ньютон-метры: 𝜏=15⋅=0,015⋅.мНмНм
Эти значения можно подставить в уравнение для магнитного поля прочности, наряду с заданными значениями 𝐼=8,5А и 𝑁=3: 𝐵=0,015⋅8,5×0,000875×3𝐵=0,672.NmAmT
С точностью до миллитесла это 𝐵=672.mT
Теперь давайте рассмотрим, что происходит, когда проволочная петля вращается вокруг
ось. Мы будем измерять угол 𝜃 от направления, перпендикулярного
петля провода (направление нормали к прямоугольнику) к магнитному
поле.
Силы, действующие на провод, теперь немного изменились.
Силы, действующие на секции 3 и 5, по-прежнему имеют одинаковую величину и остаются вертикальными. Однако участки 2 и 4 теперь не параллельны магнитное поле. Это означает, что будет действовать некоторая сила, перпендикулярная направление магнитного поля и направление тока в этих провода.
Это означает, что сила на этих участках проволоки направлена вдоль оси вращение в противоположных направлениях, поэтому нет крутящего момента вокруг оси от эти силы.
Мы можем обозначить эти силы на схеме провода, как показано.
Крутящий момент на тросе можно рассчитать, умножив каждую силу на ее перпендикулярное расстояние к оси. Для проволоки, повернутой на угол 𝜃, перпендикулярное расстояние, 𝑥, от сечения 3 до ось 𝑥=−𝑑2𝜃.sin
Аналогично, для перпендикулярного расстояния 𝑥 от сечения 5 до оси: 𝑥=𝑑2𝜃.sin
Мы можем использовать эти значения для расчета крутящего момента на оси:
𝜏=𝐹𝑥+𝐹𝑥.
Подставляя выражения для 𝑥 и 𝑥, это равно 𝜏=𝐹𝑑2𝜃+𝐹−𝑑2𝜃.sinsin
Подставляя в известные выражения 𝐹=−𝐵𝐼𝑑 и 𝐹=𝐵𝐼𝑑, это равно 𝜏=−𝐵𝐼𝑑−𝑑2𝜃−𝐵𝐼𝑑𝑑2𝜃𝜏=𝐵𝐼𝑑𝑑𝜃.sinsinsin
Опять же, в терминах площади этого прямоугольника можно выразить 𝐴: 𝜏=𝐵𝐼𝐴𝜃.sin
При 𝑁 витках провода момент равен 𝜏=𝐵𝐼𝐴𝑁𝜃.sin
Определение: Крутящий момент на прямоугольной проволочной петле с током в магнитном поле
Крутящий момент, 𝜏, на прямоугольной проволочной петле площадью 𝐴 и количество петель 𝑁, изн. ток 𝐼 в магнитном поле напряженностью 𝐵, под углом 𝜃 от перпендикуляра к магнитному полю является 𝜏=𝐵𝐼𝐴𝑁𝜃.sin
Теперь мы рассмотрим пример вопроса, где прямоугольная петля провод расположен под углом к магнитному полю.
Пример 3. Расчет крутящего момента, действующего на прямоугольную проволочную петлю Перенос тока в магнитном поле под углом
На схеме показана прямоугольная петля токоведущей
провод между полюсами магнита.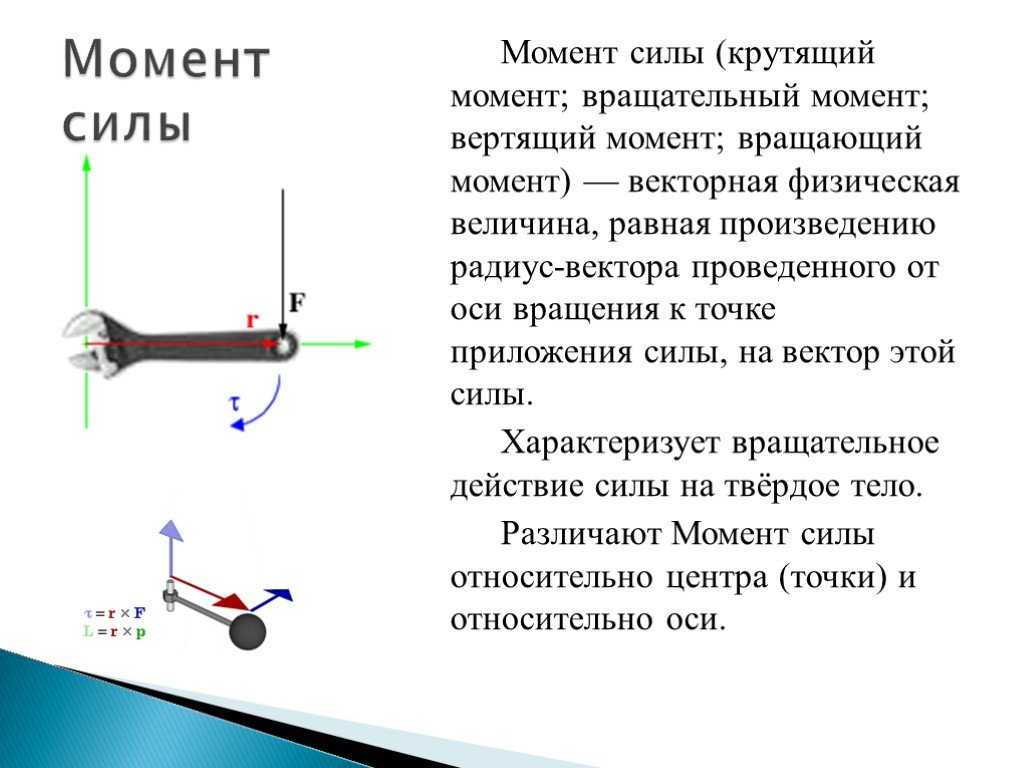 Секции петли
аб и постоянный ток
перпендикулярны магнитному полю. Диагональные линии
до н.э. и
объявление выровнено под углом
𝜃=33∘ от
направление магнитного поля. Ток в петле равен
1,75 А, а
напряженность магнитного поля
0,15 т. Длина
асм=0,065
и длина abm=0,045. Найдите момент, действующий на петлю, с точностью до
микроньютон-метр.
Секции петли
аб и постоянный ток
перпендикулярны магнитному полю. Диагональные линии
до н.э. и
объявление выровнено под углом
𝜃=33∘ от
направление магнитного поля. Ток в петле равен
1,75 А, а
напряженность магнитного поля
0,15 т. Длина
асм=0,065
и длина abm=0,045. Найдите момент, действующий на петлю, с точностью до
микроньютон-метр.
Ответ
В этом вопросе нам нужно рассчитать крутящий момент, действующий на прямоугольную петлю. провода, по которому течет ток в магнитном поле под углом.
Во-первых, мы можем вычислить площадь 𝐴 прямоугольника с помощью умножив длины двух сторон, ab и переменный ток: 𝐴=×𝐴=0,045×0,065𝐴=0,0029.abacmmm
Далее мы можем вычислить угол 𝜙, который является нормалью прямоугольника
делает с магнитным полем. Угол, указанный в вопросе,
𝜃, это угол, который прямоугольник образует с магнитным полем.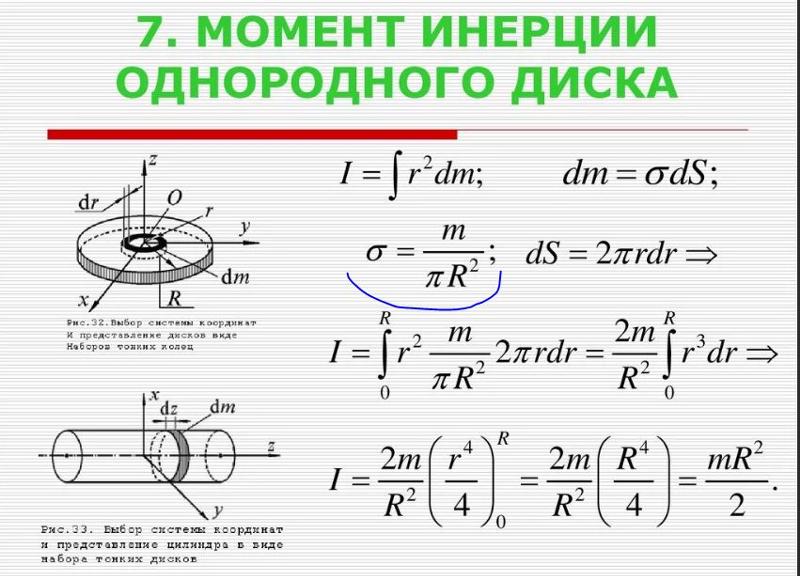 поле, так
𝜙=90−𝜃𝜙=90−33𝜙=57.∘
поле, так
𝜙=90−𝜃𝜙=90−33𝜙=57.∘
Крутящий момент на проволочной петле можно рассчитать по формуле 𝜏=𝐵𝐼𝐴𝜙, грех где 𝐵=0,15T и 𝐼=1,75 А, как указано в вопрос.
Итак, 𝜏=0,15×1,75×0,0029×57𝜏=0,000644⋅.TAmsinNm
В микроньютон-метрах это 𝜏=644⋅.мкНм
Теперь мы рассмотрим вопрос о том, как угол петли проволоки влияет на крутящий момент, действующий на петлю.
Пример 4: Влияние угла на крутящий момент, действующий на прямоугольную петлю провода с током в магнитном поле
На схеме показана прямоугольная петля токоведущей провод между полюсами магнита. Сначала более длинные стороны петли параллельны магнитному полю, а более короткие стороны петли изначально перпендикулярно магнитному полю. Затем петля поворачивается на 90∘, так что все его стороны перпендикулярны магнитному полю. Какая из строк на график правильно представляет изменение крутящего момента, действующего на петлю, как угол, который его самые длинные стороны составляют с направлением магнитного поля, варьируется от 0∘ до 90∘?
- Синий
- Зеленый
- Красный
- Оранжевый
- Ни одна из этих линий
Ответ
меняется угол петли.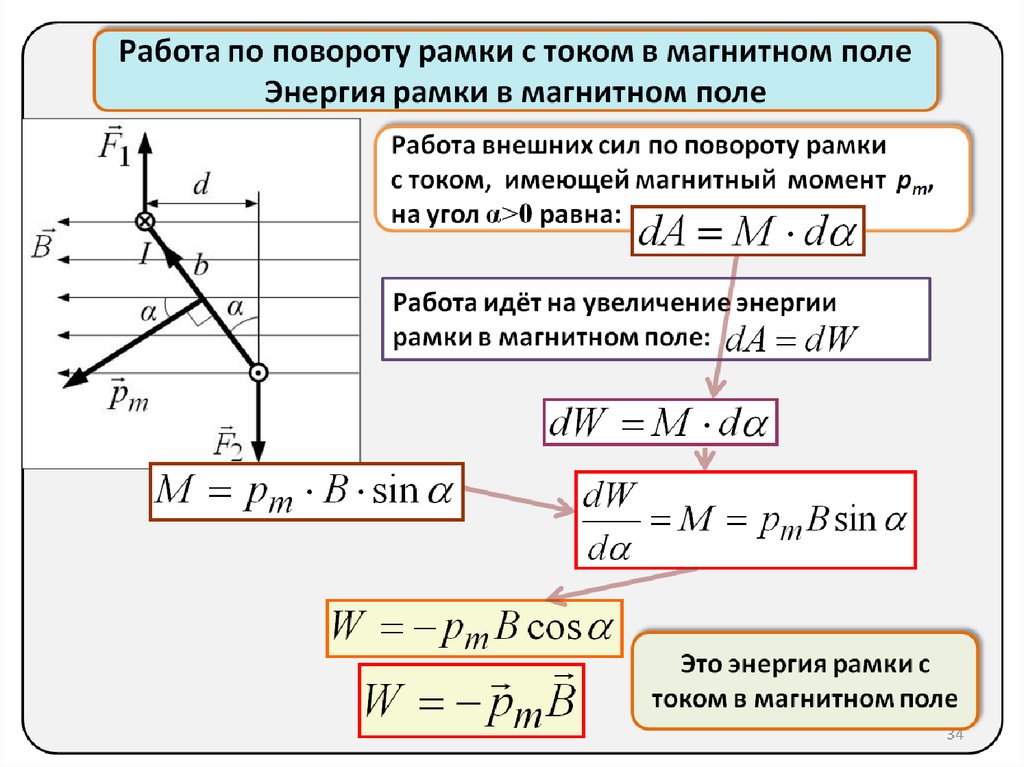
Напомним, что крутящий момент 𝜏 на прямоугольной петле провод, по которому течет ток в магнитном поле, равен 𝜏=𝐵𝐼𝐴𝜙, грех где 𝐵 — напряженность магнитного поля, 𝐼 — ток, который течет по проводу, 𝐴 — площадь прямоугольная петля, а 𝜙 — угол, нормаль к прямоугольник составляет с магнитным полем.
Однако в этом вопросе угол измеряется от сторон прямоугольник к магнитному полю. Этот угол записывается как 𝜃: 𝜙=90−𝜃.
Итак, уравнение для крутящего момента можно записать в виде 𝜏=𝐵𝐼𝐴(90−𝜃).sin
Учитывая, что sincos(90−𝜃)=𝜃, это можно записать как 𝜏=𝐵𝐼𝐴𝜃.cos
Итак, когда 𝜃=0, момент будет максимальным, а когда 𝜃=90∘, крутящий момент будет равен нулю. Линия на графике, соответствующая этому Красная линия.
Ответ — вариант C, «Красный».
Наконец, мы рассмотрим пример вопроса, объединяющий все мы узнали.
Пример 5.
 Расчет крутящего момента, действующего на прямоугольную проволочную петлю
Перенос тока в магнитном поле от момента магнитного диполя
Расчет крутящего момента, действующего на прямоугольную проволочную петлю
Перенос тока в магнитном поле от момента магнитного диполяНа схеме показана прямоугольная петля из провода с током между полюсами магнита. который создает поле с величиной 250 мТ. Сначала более длинные стороны петли параллельно магнитному полю, а более короткие стороны петли изначально перпендикулярны к магнитному полю. Петля имеет магнитный дипольный момент 500 мкН⋅м/т. Затем петля вращается внешним крутящим моментом через 90∘ так, что все его стороны перпендикулярны магнитное поле.
- На сколько изменится крутящий момент на петле из-за ее вращения? Ответ на ближайший микроньютон-метр.
- По мере увеличения угла поворота контура до значений, превышающих
90∘, но меньше
чем 180∘,
как направление приложенного крутящего момента на петле по сравнению с
направление магнитного момента, действующего на него?
- Направление крутящего момента на петле противоположно
к направлению магнитного момента на петле.

- Направление крутящего момента на петле одинаковое как направление магнитного момента на петле.
- Направление крутящего момента на петле противоположно
к направлению магнитного момента на петле.
Ответ
Часть 1
В этой части вопроса нам нужно рассчитать крутящий момент на петле провод до и после вращение на 90∘.
Напомним, что крутящий момент 𝜏, действующий на проволочную петлю равно 𝜏=𝐵𝐼𝐴𝑁𝜃, грех где напряженность магнитного поля 𝐵=250 мТл, 𝐼 ток, который течет по проводу, 𝐴 — площадь прямоугольная петля провода, 𝑁 — количество витков проволоки, а 𝜃 — угол нормали к петле делает с магнитным полем.
Перед вращением нормаль петли проволоки перпендикулярна магнитное поле, поэтому 𝜃=90∘. После петля повернулась на 90∘, нормаль петли провода будет параллельна магнитному полю, поэтому крутящий момент в этой точке равен нулю.
Таким образом, изменение крутящего момента из-за вращения точно равно крутящему моменту
перед вращением.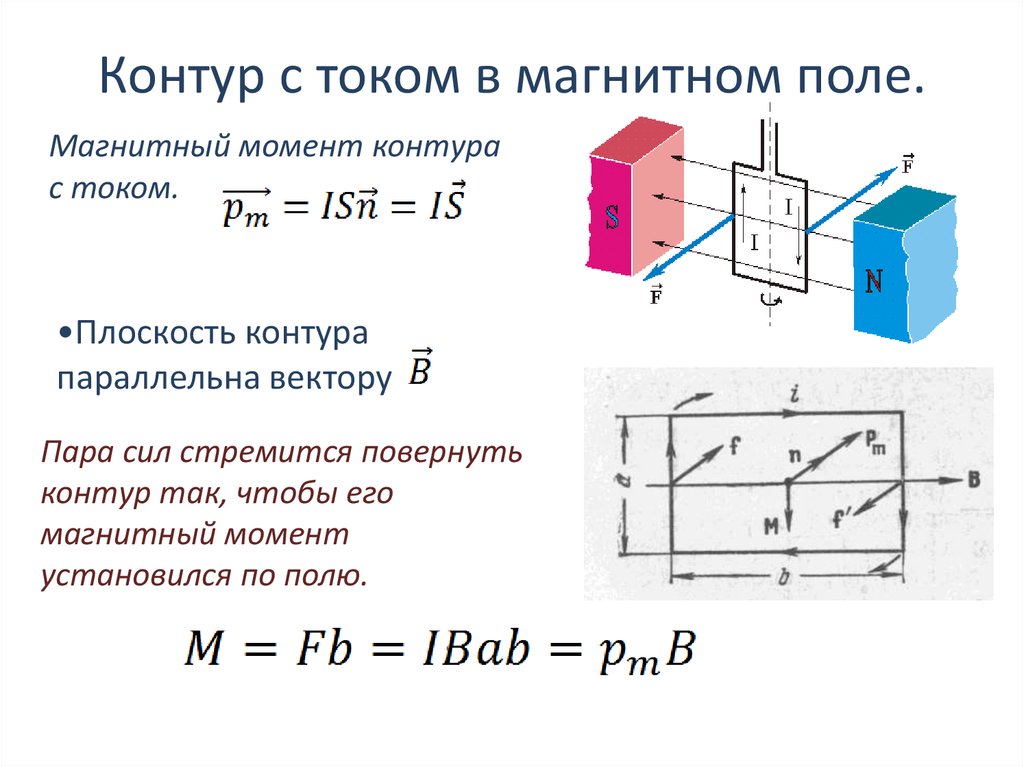
В этом случае нам дан магнитный дипольный момент петли перед вращение и напряженность магнитного поля. Напомним, что магнитный дипольный момент, 𝑚, связан с крутящим моментом на проволочной петле, 𝜏, и напряженность магнитного поля, 𝐵, следующим уравнением: 𝑚=𝜏𝐵.
Мы можем изменить это для крутящего момента на проволочной петле: 𝜏=𝑚𝐵.
Нам даны значения 𝑚=500⋅/мкНмТл и 𝐵=250мТл. Преобразовав их в единицы СИ, мы получим 𝑚=500⋅/𝑚=0,0005⋅/,𝐵=250𝐵=0,25.μNmTNmTmTT
Теперь мы можем рассчитать крутящий момент на проволочной петле: 𝜏=𝑚𝐵𝜏=0,0005⋅/×0,25𝜏=0,000125⋅.NmTTNm
В микроньютон-метрах это 𝜏=125⋅.мкНм
Часть 2
В этой части вопроса нам предлагается рассмотреть, что происходит с крутящим моментом действует на проволочную петлю, когда она вращается больше, чем 90∘ от его начальный угол.
Мы можем нарисовать схему этой конфигурации.
Как видно, есть сила, действующая вниз на правую часть петля, и есть сила, действующая вверх на левую часть петли.
Это означает, что магнитный момент будет действовать по часовой стрелке на петля, когда петля была повернута между 90∘ и 180∘.
Крутящий момент, приложенный к петле, чтобы повернуть ее из 9от 0∘ до 180∘ тоже по часовой стрелке.
Это означает, что направление крутящего момента, приложенного к петле, совпадает с направлением магнитного момента на петле. Ответ вариант B.
Мы можем обобщить то, что мы узнали из этого объяснения, следующим образом. ключевые моменты.
Ключевые моменты
- Магнитный дипольный момент 𝑚 проволочной петли, несущей
ток в магнитном поле равен крутящему моменту, действующему на петлю провода,
𝜏, деленная на напряженность магнитного поля, в котором находится провод,
𝐵:
𝑚=𝜏𝐵.

- Крутящий момент, 𝜏, действующий на прямоугольную проволочную петлю с площадью 𝐴, несущей ток, 𝐼, в магнитное поле величиной 𝐵, когда петля провода параллельно магнитному полю, равно 𝜏=𝐵𝐼𝐴.
- Когда прямоугольная петля состоит из 𝑁 витков проволоки, крутящий момент, действующий на петлю, равен 𝜏=𝐵𝐼𝐴𝑁.
- Если нормаль к прямоугольному контуру находится под углом 𝜃 к магнитному полю момент, действующий на петлю, равен равно 𝜏=𝐵𝐼𝐴𝑁𝜃.sin
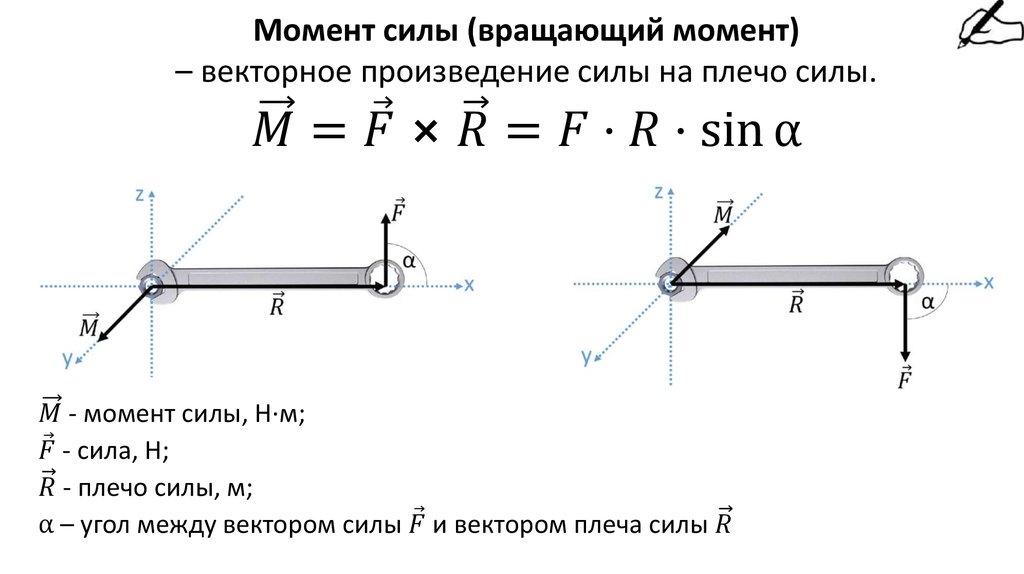
Крутящий момент в прямоугольной токовой петле
Крутящий момент — это сила, которая может заставить объект вращаться вокруг оси. Сила — это то, что заставляет объект ускоряться в линейной кинематике. Угловое ускорение также вызвано крутящим моментом. В результате крутящий момент можно определить как вращательный эквивалент линейной силы. Точка, в которой вращается элемент, называется осью вращения. В физике крутящий момент — это тенденция силы поворачиваться или скручиваться. Крутящий момент может быть выражен различными способами, включая момент и момент силы. В этом посте мы рассмотрим, как рассчитать крутящий момент на прямоугольной проволочной петле с током в однородном магнитном поле.
В физике крутящий момент — это тенденция силы поворачиваться или скручиваться. Крутящий момент может быть выражен различными способами, включая момент и момент силы. В этом посте мы рассмотрим, как рассчитать крутящий момент на прямоугольной проволочной петле с током в однородном магнитном поле.
Крутящий момент на прямоугольной токовой петле
Рассмотрим прямоугольную петлю, по которой течет ток величиной I. При помещении в магнитное поле эта петля испытывает крутящий момент, но не результирующую силу, подобно тому, как электрический диполь испытывает в однородном электрическое поле. Рассмотрим случай, когда прямоугольная петля находится в той же плоскости, что и магнитное поле B. На плечи петли, параллельные магнитам, не действует сила поля, но на плечи, перпендикулярные магнитам, действует сила, равная F 1 .
F 1 = IbB
Эта сила направлена в сторону плоскости. Точно так же мы можем записать формулу для силы F 2 , приложенной к плечу CD.
F 2 = IbB = F 1
Крутящий момент петли определяется выражением, а чистая сила петли равна нулю.
τ = F 1 (а/2) + F 2 (а/2)
= IbB(a/2) + IbB(a/2)
= I(ab)B
τ = IAB
Площадь прямоугольника равна ab. Петля вращается против часовой стрелки из-за крутящего момента.
Рассмотрим ситуацию, когда плоскость петли не параллельна магнитному полю. Пусть — угол, создаваемый полем, и пусть — нормаль катушки задается θ. Силы, действующие на плечи ВС и DA, всегда будут равны по величине и всегда будут действовать в противоположных направлениях, как видно. Результаты действия этих сил компенсируются, потому что они равно противоположны и коллинеарны во всех точках, что приводит к нулевой силе или крутящему моменту. Силы на плечах АВ и CD определяются по F 1 и F 2 . Эти силы схожи по размеру и направлению и могут быть созданы:
F 1 = F 2 = IbB
Поскольку эти силы не коллинеарны, пара на катушке вызывает крутящий момент.
Величину крутящего момента можно вычислить, используя
τ = F 1 (a/2) sin θ + F 2 (a/2) sin θ
= I(ab)B sin θ
τ = IAB sin θ
Объяснение крутящего момента в токовой петле
Когда вы оказываете давление на объект, он перемещается или оказывает определенное усилие. Например, откручивание крышки от бутылки, снятие крышки с упаковки, открывание дверной ручки, завязывание шнурка и так далее. Это вращательное движение, представляющее собой вращательное движение с некоторым движением. Если концепция крутящего момента не уяснена, движения не будет. Крутящий момент — это фраза, которая относится к вращательному движению, которое есть у всех предметов и без которого мы не смогли бы работать должным образом.
Формула для крутящего момента: τ = F × r, поскольку крутящий момент равен крутящей силе, которая стремится вызвать движение или вращение. Эта формула используется, когда сила (f) приложена к элементу в зависимости от расстояния (r) между центром вращения и местом приложения силы.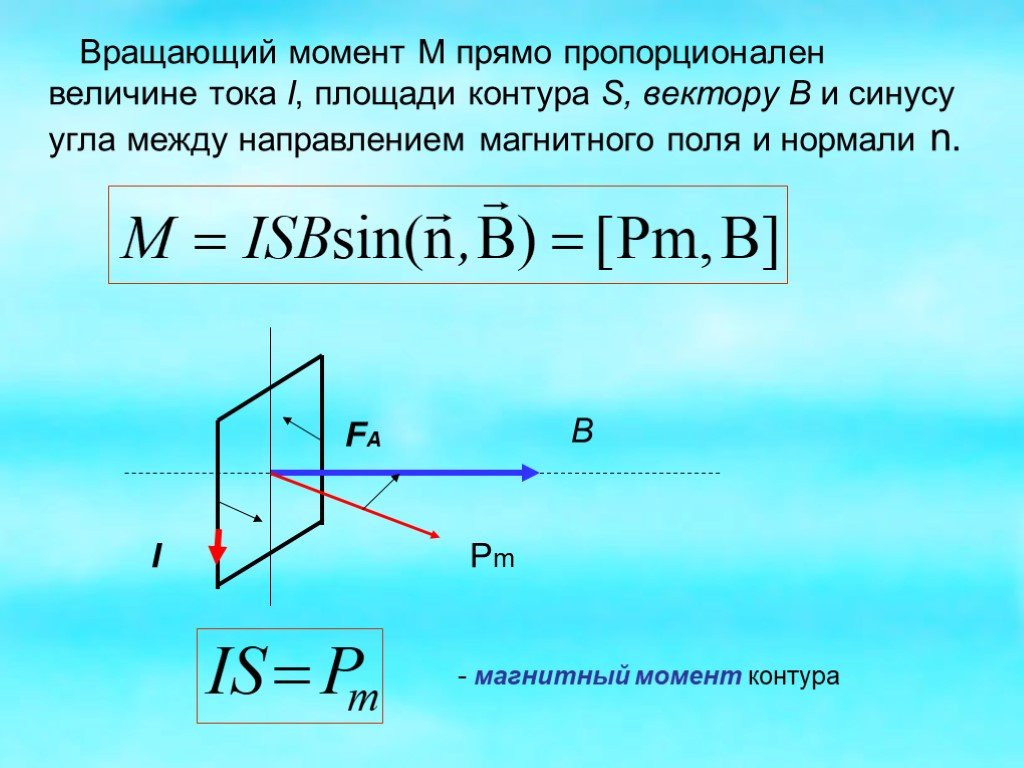 Чтобы определить направление крутящего момента, учащиеся должны согнуть пальцы правой руки в направлении тока, а их большой палец должен быть оттопырен и указывать на вектор площади в соответствии с правилом правой руки.
Чтобы определить направление крутящего момента, учащиеся должны согнуть пальцы правой руки в направлении тока, а их большой палец должен быть оттопырен и указывать на вектор площади в соответствии с правилом правой руки.
Момент на прямоугольной токовой петле Уравнение в векторной форме
Рассмотрим прямоугольную катушку PQRS, подвешенную в индукционном поле B с однородным магнитным полем. Пусть PQ = RS = l и QR = SP = b — две переменные. Пусть I представляет собой ток, протекающий через катушку в направлении PQRS, и пусть θ будет углом, образованным плоскостью катушки с направлением магнитного поля. Силы будут действовать на четыре рукава Катушки.
Вектор сил F 1 и вектор F 3 , действующие на стороны PQ и RS, равны и противоположны, но их пути действия различны согласно правилу левой руки Флеминга; таким образом, результирующая сила вектора F 1 и вектора F 3 равна нулю, но они образуют пару, известную как отклоняющая пара .
Расстояние по перпендикуляру между вектором F 1 и вектором F 3 равно bsinθ, когда нормальная плоскость петли образует угол с направлением магнитного поля B.
Так как, Крутящий момент, τ = IAB sinθ
Таким образом, когда контур содержит N витков, тогда
τ = NI ABsinθ
В векторной форме направление крутящего момента перпендикулярно
2 90 направление площади петли, а также направление магнитного поля, т. е. вдоль
Вывод
Катушка вращается вокруг своей оси за счет этого момента. Его значение меняется в зависимости от угла, образованного плоскостью катушки, и направления магнитного поля.
- Если электрический диполь находится в электрическом поле, то крутящий момент становится равным , где P — электрический дипольный момент, а E — электрическое поле.
- Если Магнитный диполь находится в магнитном поле, то крутящий момент становится равным, , где M – это Магнитный дипольный момент, а B – Магнитное поле.

Особые случаи
Случай 1: Если катушка параллельна направлению магнитного поля B,
Тогда θ = 0 o и cos θ = 9.0003
τ = niba cos θ
= niba cos 0
= NIBA
∴ τ = NIBA (максимум)
Случай 2: если катушка является перпендикулярной с магнитным полем B,
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
. , θ = 90 o и cos θ = 0.
τ = niba cos θ
= NIBA COS 90
= NIBA (0)
∴ τ = 0 (минимум)
.
Задача 1. Каков максимальный крутящий момент, который может создать ручка шириной 40 см, если ее отпустить силой 2 Н на ее краю?
Solution:
Given that: F = 2 N,
d = 40 cm = 0.
40 m
τ = F × d
= 20 × 0.40
= 8 N-m
Задача 2: Крутящий момент величиной 4,5 × 10 -2 Дж испытывает короткий стержневой магнит с осью в положении 30 o и однородным внешним магнитным полем 0,25 Тл. Насколько велик магнитный момент магнита?
Решение:
Учитывая, что:
τ = 4,5 × 10 -2 J,
θ = 30 O ,
B = 0,25 T
Мы имеем
τ = MB SIN θ
9000 4. -2 = M × 0,25 sin 30 o∴ M = 0,36 Дж/Тл
30 o угол. Крутящий момент в 4 Нм испытывается им. Диполь имеет заряд 2 см на нем.
Решение:
Учитывая, что:
E = 2 × 10 5 N/C,
τ = 4 нм,
L = 2 см = 0,02 M
Мы τ = pE sin θ
4 = p × 2 × 10 5 × sin θ
p = 4 × 10-5 См
q = p/l
q = (4 × 10
-5 90) /0,02
q = 2 мКл
Задача 4: В однородном магнитном поле напряженностью 0,8 Вебера/м 2 , прямоугольная катушка длиной 0,56 м и шириной 0,2 м с 40 витками провода подвешена вертикально. По катушке протекает ток силой 6 А. Крутящий момент, необходимый для удержания катушки в устойчивом равновесии, будет, если плоскость катушки наклонена под углом 90 o к направлению поля.
По катушке протекает ток силой 6 А. Крутящий момент, необходимый для удержания катушки в устойчивом равновесии, будет, если плоскость катушки наклонена под углом 90 o к направлению поля.
Решение:
M = Niπr2
= 40 × 6 × 0,56 × 0,2
= 26,88
B = 0,8 T
Мы имеем,
τ = MB θ
.0003
= 26,88 × 0,8 sin 90 o
= 21,504 Н·м
производится дверью.
Solution:
Given that:
F = 2 N,
d = 80 cm = 0.80 m
τ = F × d
= 20 × 0.80
= 16 Nm
Задача 6. Короткий стержневой магнит с осью 90 o и однородное внешнее магнитное поле напряженностью 0,27 Тл испытывает момент величиной 2,51 × 10 2 Дж. Чему равен магнитный момент магнита?
Решение:
Указано, что:
τ = 2,51 × 10 2 J,
θ = 90 O ,
B = 0,277 T W We Ha Ha HA HA HA HA HA HA HAS ,
B = 0,27 sin θ
2,51 × 10 2 = M × 0,27 sin 90 o
M = 929 Дж/Тл
Задача 7: Получить выражение для крутящего момента прямоугольной формы с током в однородном магнитном поле B.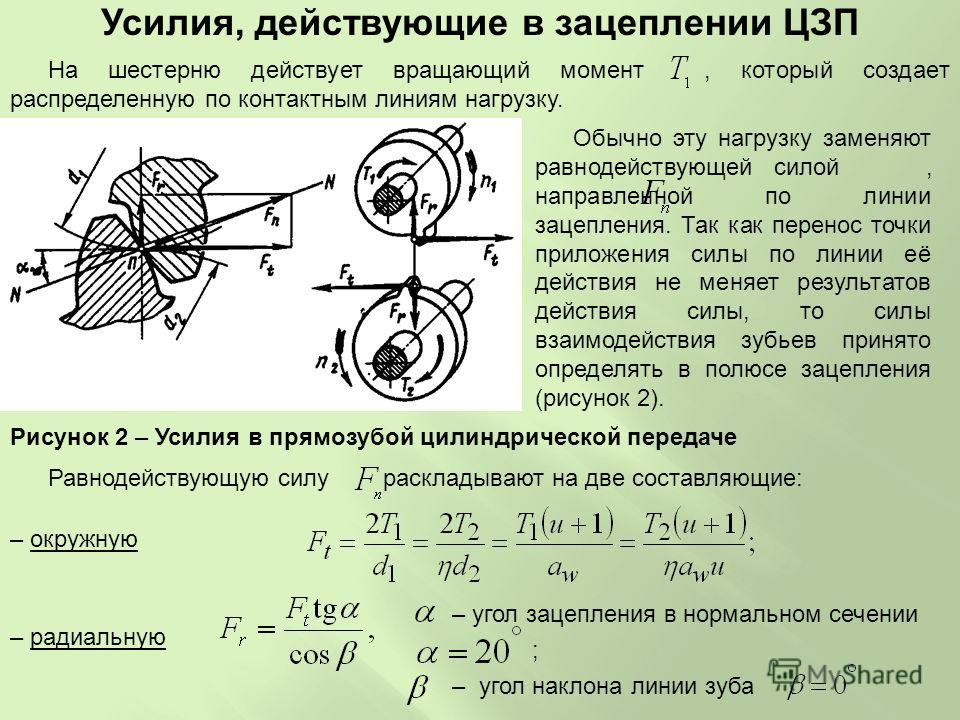 Укажите, в какую сторону закручивается петля.
Укажите, в какую сторону закручивается петля.
Решение:
Рассмотрим прямоугольную катушку PQRS, подвешенную в индукционном поле B с однородным магнитным полем. Пусть PQ = RS = l и QR = SP = b — две переменные. Пусть I представляет собой ток, протекающий через катушку в направлении PQRS, и пусть θ будет углом, образованным плоскостью катушки с направлением магнитного поля. Силы будут действовать на четыре рукава Катушки.
Вектор сил F 1 и вектор F 3 , действующие на стороны PQ и RS, равны и противоположны, но их пути действия различны, согласно правилу левой руки Флеминга; таким образом, результирующая сила вектора F 1 и вектора F 3 равна нулю, но они образуют пару, известную как отклоняющая пара . Расстояние по перпендикуляру между вектором F 1 и вектором F 3 равно bsinθ , когда нормальная плоскость петли образует угол с направлением магнитного поля B.


 Тема 8. ДИНАМИКА. Прямолинейное движение системы тел — 1
Тема 8. ДИНАМИКА. Прямолинейное движение системы тел — 1

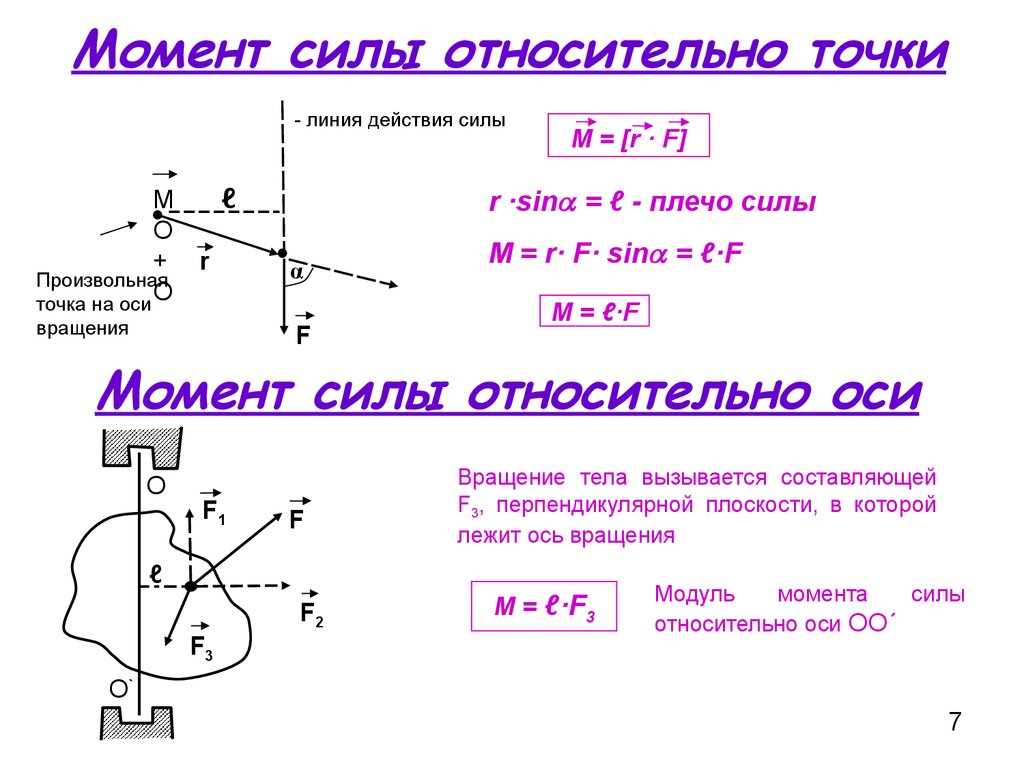
 Величину крутящего момента можно вычислить, используя
Величину крутящего момента можно вычислить, используя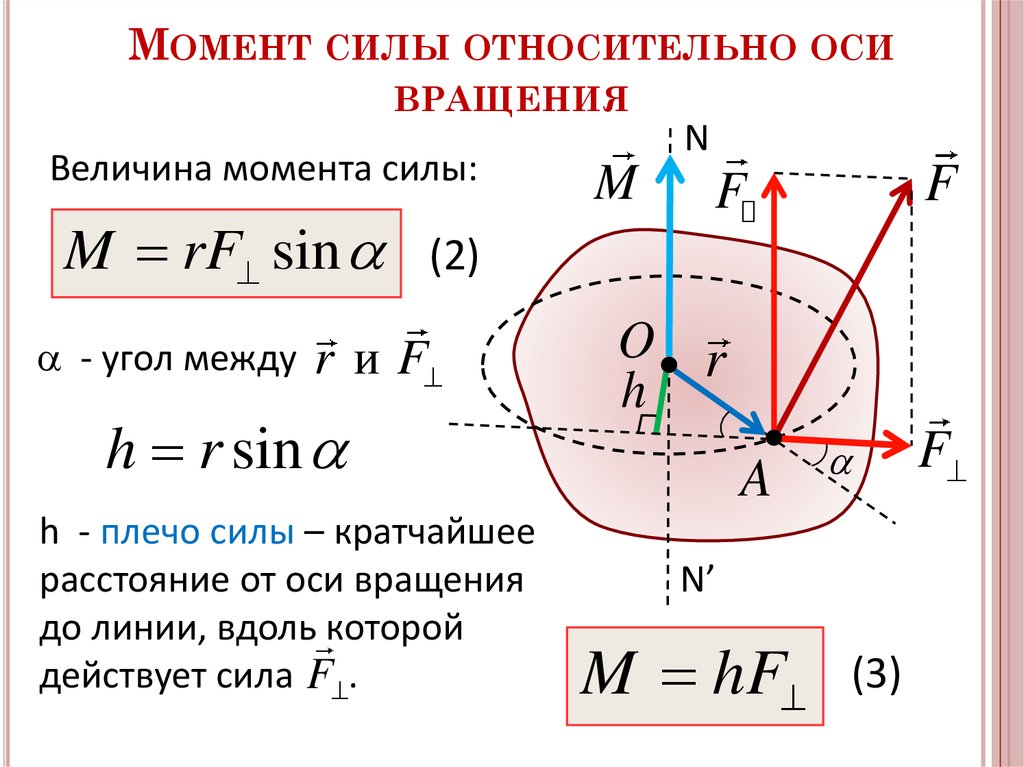 Расстояние по перпендикуляру между вектором F 1 и вектором F 3 равно bsinθ, когда нормальная плоскость петли образует угол с направлением магнитного поля B.
Расстояние по перпендикуляру между вектором F 1 и вектором F 3 равно bsinθ, когда нормальная плоскость петли образует угол с направлением магнитного поля B.
 40 m
40 m 