Закон Кулона 10 класс онлайн-подготовка на Ростелеком Лицей
Введение
Тема урока: «Закон Кулона». Закон Кулона количественно описывает взаимодействие точечных неподвижных зарядов – то есть зарядов, которые находятся в статичном положении друг относительно друга. Такое взаимодействие называется электростатическим или электрическим и является частью электромагнитного взаимодействия.
Электромагнитное взаимодействие
Конечно, если заряды находятся в движении – они тоже взаимодействуют. Такое взаимодействие называется магнитным и описывается в разделе физики, который носит название «Магнетизм».
Стоит понимать, что «электростатика» и «магнетизм» – это физические модели, и вместе они описывают взаимодействие как подвижных, так и неподвижных друг относительно друга зарядов. И всё вместе это называется электромагнитным взаимодействием.
Электромагнитное взаимодействие – это одно из четырех фундаментальных взаимодействий, существующих в природе.
Электрический заряд
Что же такое электрический заряд? Определения в учебниках и Интернете говорят нам, что заряд – это скалярная величина, характеризующая интенсивность электромагнитного взаимодействия тел. То есть электромагнитное взаимодействие – это взаимодействие зарядов, а заряд – это величина, характеризующая электромагнитное взаимодействие. Звучит запутанно – два понятия определяются друг через друга. Разберемся!
Существование электромагнитного взаимодействия – это природный факт, что-то вроде аксиомы в математике. Люди его заметили и научились описывать. Для этого они ввели удобные величины, которые это явление характеризуют (в том числе электрический заряд) и построили математические модели (формулы, законы и т. д.), которые это взаимодействие описывают.
Закон Кулона
Выглядит закон Кулона следующим образом:
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними.
Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.
Коэффициент k в законе Кулона численно равен:
Аналогия с гравитационным взаимодействием
Закон всемирного тяготения гласит: все тела, обладающие массой, притягиваются друг к другу. Такое взаимодействие называется гравитационным. Например, сила тяжести, с которой мы притягиваемся к Земле, – это частный случай именно гравитационного взаимодействия. Ведь и мы, и Земля обладаем массой. Сила гравитационного взаимодействия прямо пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними.
Коэффициент γ называется гравитационной постоянной.
Численно он равен: .
Как видите, вид выражений, количественно описывающих гравитационное и электростатическое взаимодействия, очень похож.
В числителях обоих выражений – произведение единиц, характеризующих данный тип взаимодействия. Для гравитационного – это массы, для электромагнитного – заряды. В знаменателях обоих выражений – квадрат расстояния между объектами взаимодействия.
Обратная зависимость от квадрата расстояния часто встречается во многих физических законах. Это позволяет говорить об общей закономерности, связывающей величину эффекта с квадратом расстояния между объектами взаимодействия.
Эта пропорциональность справедлива для гравитационного, электрического, магнитного взаимодействий, силы звука, света, радиации и т. д.
Объясняется это тем, что площадь поверхности сферы распространения эффекта увеличивается пропорционально квадрату радиуса (см. рис. 1).
Рис. 1. Увеличение площади поверхности сфер
Это будет выглядеть естественным, если вспомнить, что площадь сферы пропорциональна квадрату радиуса:
Физически это означает, что сила взаимодействия двух точечных неподвижных зарядов в 1 Кл, находящихся на расстоянии 1 м друг от друга в вакууме, будет равна 9·109 Н (см.
рис. 2).
Рис. 2. Сила взаимодействия двух точечных зарядов в 1 Кл
Казалось бы, эта сила огромна. Но стоит понимать, что ее порядок связан с еще одной характеристикой – величиной заряда 1 Кл. На практике заряженные тела, с которыми мы взаимодействуем в повседневной жизни, имеют заряд порядка микро- или даже нанокулонов.
Коэффициент и электрическая постоянная
Иногда вместо коэффициента используется другая постоянная, характеризующая электростатическое взаимодействие, которая так и называется – «электрическая постоянная». Обозначается она . С коэффициентом она связана следующим образом:
Выполнив несложные математические преобразования можно ее выразить и вычислить:
Обе константы, конечно, присутствуют в таблицах задачников. Закон Кулона тогда примет такой вид:
Обратим внимание на несколько тонких моментов.
Важно понимать, что речь идет именно о взаимодействии.
То есть если мы возьмем два заряда, то каждый из них будет действовать на другой с силой, по модулю равной. Эти силы будут направлены в противоположные стороны вдоль прямой, соединяющей точечные заряды.
Заряды будут отталкиваться, если они имеют один знак (оба положительные или оба отрицательные (см. рис. 3)), и притягиваться, если имеют разные знаки (один отрицательный, другой положительный (см. рис. 4)).
Рис. 3. Взаимодействие одноименных зарядов
Рис. 4. Взаимодействие разноименных зарядов
Точечный заряд
В формулировке закона Кулона присутствует термин «точечный заряд». Что это означает? Вспомним механику. Исследуя, например, движение поезда между городами, мы пренебрегали его размерами. Ведь размеры поезда в сотни или тысячи раз меньше расстояния между городами (см. рис. 5). В такой задаче мы считали поезд «материальной точкой» – телом, размерами которого в рамках решения некоторой задачи мы можем пренебречь.
Рис.
5. Размерами поезда в данном случае пренебрегаем
Так вот, точечные заряды – это материальные точки, обладающие зарядом. На практике, используя закон Кулона, мы пренебрегаем размерами заряженных тел в сравнении с расстояниями между ними. Если же размеры заряженных тел сопоставимы с расстоянием между ними, то из-за перераспределения заряда внутри тел электростатическое взаимодействие будет носить более сложный характер.
Задача 1
В вершинах правильного шестиугольника со стороной помещены друг за другом заряды . Найдите силу, действующую на заряд , расположенный в центре шестиугольника (см. рис. 6).
Рис. 6. Рисунок к условию задачи 1
Порассуждаем: заряд, находящийся в центре шестиугольника, будет взаимодействовать с каждым из зарядов, находящихся в вершинах шестиугольника. В зависимости от знаков это будет сила притяжения или сила отталкивания. С зарядами 1, 2 и 3, которые являются положительными, заряд, находящийся в центре, будет испытывать электростатическое отталкивание (см.
рис. 7).
Рис. 7. Электростатическое отталкивание
А с зарядами 4, 5 и 6 (отрицательными) заряд в центре будет иметь электростатическое притяжение (см. рис. 8).
Рис. 8. Электростатическое притяжение
Суммарная сила, действующая на заряд, находящийся в центре шестиугольника, будет равнодействующей сил ,,,, и, модуль каждой из которых можно найти с помощью закона Кулона. Приступим к решению задачи.
Решение
Силы взаимодействия заряда, который находится в центре, с каждым из зарядов в вершинах зависит от модулей самих зарядов и расстояния между ними. Расстояние от вершин к центру правильного шестиугольника одинаковое, модули у взаимодействующих зарядов в нашем случае тоже равны (см. рис. 9).
Рис. 9. Расстояния от вершин до центра в правильном шестиугольнике равны
А значит, все силы взаимодействия заряда в центре шестиугольника с зарядами в вершинах будут равны по модулю. Воспользовавшись законом Кулона, мы можем найти этот модуль:
Расстояние от центра до вершины в правильном шестиугольнике равно длине стороны правильного шестиугольника, которая нам известна из условия, поэтому:
Теперь нам необходимо найти векторную сумму – для этого выберем систему координат: ось вдоль силы , а ось перпендикулярно (см.
рис. 10).
Рис. 10. Выбор осей
Найдем суммарные проекции на оси – модуль каждой из них обозначим просто .
Так как силы и сонаправлены с осью , а находятся под углом к оси (см. рис. 11).
Рис. 11. Направление сил относительно оси
Проделаем такие же действия для оси :
Знак «-» – потому что силы и направлены в противоположную сторону оси . То есть проекция суммарной силы на ось , которую мы выбрали, будет равна 0. Получается, что суммарная сила будет действовать только вдоль оси , остается подставить сюда только выражения для модуля сил взаимодействия и и получить ответ. Суммарная сила будет равна:
Задача решена.
Диэлектрическая проницаемость
Еще один тонкий момент заключается вот в чем: в законе Кулона сказано, что заряды находятся в вакууме (см. рис. 12).
Рис. 12. Взаимодействие зарядов в вакууме
Это действительно важное замечание.
Рис. 13. Взаимодействие зарядов в среде, отличной от вакуума
Чтобы учесть этот фактор, в модель электростатики была введена специальная величина, которая позволяет сделать «поправку на среду». Называется она диэлектрической проницаемостью среды. Обозначается, как и электрическая постоянная, греческой буквой «эпсилон», но уже без индекса.
Физический смысл этой величины заключается в следующем.
Сила электростатического взаимодействия двух точечных неподвижных зарядов в среде, отличной от вакуума, будет в ε раз меньше, чем сила взаимодействия таких же зарядов на таком же расстоянии в вакууме.
Таким образом, в среде, отличной от вакуума, сила электростатического взаимодействия двух точечных неподвижных зарядов будет равна:
Значения диэлектрической проницаемости различных веществ давно найдены и собраны в специальных таблицах (см.
рис. 14).
Рис. 14. Диэлектрическая проницаемость некоторых веществ
Мы можем свободно использовать табличные значения диэлектрической проницаемости необходимых нам веществ при решении задач.
Важно понимать, что при решении задач сила электростатического взаимодействия рассматривается и описывается в уравнениях динамики как обычная сила. Решим задачу.
Задача 2
Два одинаковых заряженных шарика подвешены в среде с диэлектрической проницаемостью на нитях одинаковой длины , закрепленных в одной точке. Определите модуль заряда шариков, если нити находятся под прямым углом друг к другу (см. рис. 15). Размеры шариков пренебрежимо малы по сравнению с расстоянием между ними. Массы шариков равны .
Рис. 15. Рисунок к условию задачи 2
Порассуждаем: на каждый из шариков будут действовать три силы – сила тяжести ; сила электростатического взаимодействия и сила натяжения нити (см. рис. 16).
Рис.
16. Силы, действующие на шарики
По условию шарики одинаковые, то есть их заряды равны как по модулю, так и по знаку, а значит, сила электростатического взаимодействия в данном случае будет силой отталкивания (на рис. 16 силы электростатического взаимодействия направлены в разные стороны). Так как система находится в равновесии, будем использовать первый закон Ньютона:
Так как в условии сказано, что шарики подвешены в среде с диэлектрической проницаемостью , а размеры шариков пренебрежимо малы по сравнению с расстоянием между ними, то в соответствии с законом Кулона сила, с которой будут отталкиваться шарики, будет равна:
Решение
Распишем первый закон Ньютона в проекциях на оси координат. Ось направим горизонтально, а ось вертикально (см. рис. 17).
Рис. 17. Выбор направления осей координат
Рис. 18. Силы в проекциях на оси координат
Так как на шарики действуют одинаковые силы тяжести и силы электростатического взаимодействия, нити тоже одинаковые – они отклонятся на одинаковые углы (см.
рис. 19).
Рис. 19. Углы, на которые отклоняются шарики, одинаковые
В сумме эти углы дают нам , это означает, что:
Тогда из прямоугольного треугольника можно найти углом :
Добавим к двум уравнениям, которые мы записали, выражение для модуля силы электростатического взаимодействия:
Расстояние найдем геометрически – найдем прилежащий к углу катет и умножим его на 2:
Мы получили систему из 4-х уравнений:
Математическое решение можно пронаблюдать в свертке.
Ответ:
Решение системы уравнений
Выразим из второго уравнения силу натяжения нити и подставим в первое:
Отсюда выразим силу электростатического взаимодействия:
Приравняем выражение для силы электростатического взаимодействия, которое мы сейчас выразили с третьим уравнением:
Подставим сюда выражение для
Выразим искомый заряд
Так как угол , то , тогда:
На этом наш урок закончен.
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: Учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание – М.: Просвещение, 2010.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «physics.ru» (Источник)
- Интернет-портал «Класс!ная физика» (Источник)
Домашнее задание
- Запишите формулу закона Кулона.
- Как взаимодействуют разноименно заряженные тела?
- Решите задачу: два заряда, 10 нКл и -2 нКл, закреплены на расстоянии 10 см друг от друга. Определите силу, с которой они взаимодействуют.
Закон Кулона — ZNZN📗
Закон Кулона
Взаимодействие неподвижных (в данной инерциальной системе отсчёта) зарядов называется электростатическим.
Раздел электродинамики, в котором изучается взаимодействие неподвижных зарядов, называется электростатикой.
Основной закон электростатики — это закон Кулона.
По внешнему виду закон Кулона удивительно похож на закон всемирного тяготения, который устанавливает характер гравитационного взаимодействия точечных масс. Закон Кулона является законом электростатического взаимодействия точечных зарядов.
Точечный заряд — это заряженное тело, размеры которого много меньше других размеров, характерных для данной задачи.
Точечный заряд — такая же идеализация, как материальная точка, точечная масса и т. д. В случае точечных зарядов мы можем однозначно говорить о расстоянии между ними, не задумываясь о том, между какими именно точками заряженных тел это расстояние измеряется.
Закон Кулона
Сила взаимодействия двух неподвижных точечных зарядов в вакууме прямо пропорциональна произведению абсолютных величин зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила называется кулоновской. Вектор кулоновской силы всегда лежит на прямой, соединяющей заряды. Для кулоновской силы справедлив третий закон Ньютона: заряды действуют друг на друга с силами, равными по модулю и противоположными по направлению.
В качестве примера на рис. 1 показаны силы и , с которыми взаимодействуют два отрицательных заряда.
Рисунок 1. Кулоновская сила
Если заряды, равные по модулю q1 и q2, находятся на расстоянии r друг от друга, то они взаимодействуют с силой
Коэффициент пропорциональности k в системе СИ равен:
Если сравнивать с законом всемирного тяготения, то роль точечных масс в законе Кулона играют точечные заряды, а вместо гравитационной постоянной G стоит коэффициент k. Математически формулы этих законов устроены одинаково. Важное физическое отличие заключается в том, что гравитационное взаимодействие всегда является притяжением, а взаимодействие зарядов может быть как притяжением, так и отталкиванием.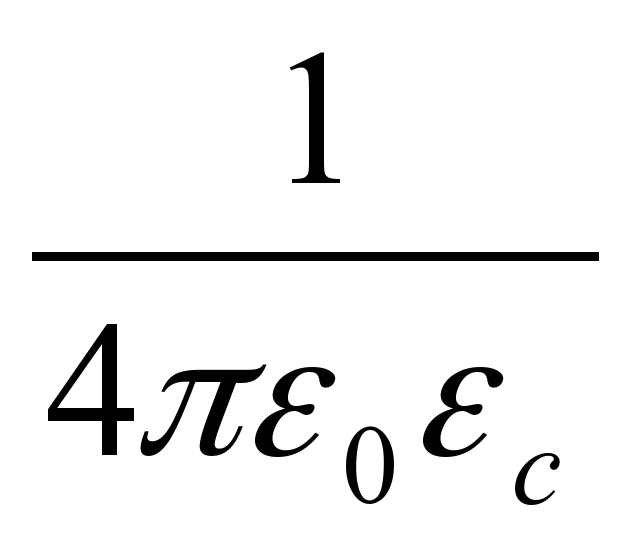
Так уж вышло, что наряду с константой k имеется ещё одна фундаментальная константа ε0, связанная с k соотношением
Константа ε0 называется электрической постоянной. Она равна:
Закон Кулона с электрической постоянной выглядит так:
Закон Кулона в диэлектрике
Отличие электростатического взаимодействия от гравитационного состоит не только в наличии сил отталкивания. Сила взаимодействия зарядов зависит от среды, в которой заряды находятся (а сила всемирного тяготения от свойств среды не зависит).
Диэлектриками, или изоляторами называются вещества, которые не проводят электрический ток.
Оказывается, что диэлектрик уменьшает силу взаимодействия зарядов (по сравнению с вакуумом). Более того, на каком бы расстоянии друг от друга заряды ни находились, сила их взаимодействия в данном однородном диэлектрике всегда будет в одно и то же число раз меньше, чем на таком же расстоянии в вакууме. Это число обозначается ε и называется диэлектрической проницаемостью диэлектрика.
Диэлектрическая проницаемость зависит только от вещества диэлектрика, но не от его формы или размеров. Она является безразмерной величиной и может быть найдена из таблиц.
fДиэлектрическая проницаемость вакуума, как видим, равна единице. Во всех остальных случаях диэлектрическая проницаемость больше единицы. Диэлектрическая проницаемость воздуха настолько близка к единице, что при расчёте сил взаимодействия зарядов в воздухе пользуются формулами для вакуума.
электромагнетизм — Откуда взялась постоянная Кулона, $k_e$?
спросил
Изменено 2 года, 2 месяца назад
Просмотрено 374 раза
$\begingroup$
Я знаком с законом Кулона, $\vec{F} = k_e\frac{q_1q_2}{r^2}$, и знаю, как его применять (много раз использовал его на практике, на экзаменах и т.
2}$ «часть» закона Кулона, по крайней мере, несколько интуитивна, однако я никогда не понимал, откуда именно берется постоянная Кулона, $k_e$. 92}$?
Ищу как «строгий» вывод, так и интуицию (где это возможно).
- электромагнетизм
- заряд
- размерный анализ
- закон кулона
- физические константы
$\endgroup$
2
$\begingroup$
Обратите внимание, что закон Кулона определяется экспериментально, хотя, поскольку уравнения Максвелла описывают все электромагнитные явления, вы можете сделать это следующим образом (чтобы вы могли видеть, как возникает константа $k$): 92}$$
, что соответствует закону Кулона.
Постоянная диэлектрической проницаемости вакуума является мерой того, насколько вакуум пропускает электрическое поле. В большинстве задач мы предполагаем, что в пространстве между изучаемыми зарядами нет ничего, поэтому мы используем $\epsilon_0$.
В тех случаях, когда мы это делаем, мы используем диэлектрическую проницаемость $\epsilon$, которая является мерой того, насколько среда пропускает электрическое поле.
Когда мы манипулируем уравнениями Максвелла, мы приходим к уравнению электромагнитной волны и, как вы можете видеть по ссылке
$$v = \frac{1}{\sqrt{\mu \epsilon }}$$
где $v$ — скорость электромагнитной волны в области с проницаемостью $\mu$ и диэлектрической проницаемостью $\epsilon $. Конечно, если мы находимся в вакууме, это становится
$$c = \frac{1}{\sqrt{\mu_0 \epsilon_0}}$$
, где $c$ — скорость света в вакууме.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электромагнетизм — Закон Кулона: почему $k = \dfrac{1}{4\pi\epsilon_0}$
спросил
Изменено 10 лет, 4 месяца назад
Просмотрено 14 тысяч раз
$\begingroup$
Это должен был быть длинный вопрос, но что-то пошло не так, и все, что я набрал, было потеряно. Вот оно.
Почему $k = \dfrac{1}{4\pi\epsilon_0}$ в законе Кулона?
Это экспериментальный факт?
Если нет, то каково значение этого определения?
92}{2\epsilon_0 d}$, где множитель $4\pi$ получается из разумного применения закона Гаусса.
Если вы разовьете это дальше в теорию емкости, то обнаружите, что из нее следует, что напряжение между пластинами равно $V=Q/C$, где $C=\epsilon_0 A/d$.
Кроме того, если вы хотите вставить диэлектрик между пластинами (как вы часто делаете), тогда емкость изменится на $$C=\epsilon A/d$$, где $\epsilon$ называется диэлектрической проницаемостью диэлектрика. Тогда $\epsilon_0$ естественно понимается как «диэлектрическая проницаемость свободного пространства» (что, конечно, просто определяет, что мы подразумеваем под диэлектрической проницаемостью).
Тогда, конечно, возникает вопрос, почему эта «производная» единица, $\epsilon_0$, считается более «фундаментальной», чем исходная $k$? Ответ заключается в том, что это не так, поскольку они эквивалентны, но диэлектрическую проницаемость свободного пространства гораздо легче измерить (и, безусловно, так было в конце 19-го и начале 20-го веков, когда исследования в области электротехники были в значительной степени ориентированы на технологии, основанные на схемах) , чтобы он вышел победителем, а зачем два символа для эквивалентных величин?
$\endgroup$
$\begingroup$
Единица секунды определяется как продолжительность определенного количества периодов излучения, испускаемого при переходе электронов определенного типа между энергетическими уровнями в изотипе цезия (см.
здесь).
Предполагается, что свет распространяется с постоянной скоростью $c$ независимо от системы отсчета, так что теперь, когда мы зафиксировали единицу времени, мы можем определить единицу длины: метр — это расстояние, которое свет проходит за $1 /292} $$ а также $$ k=\frac{1}{4\pi \varepsilon _0}. $$
Теперь имейте в виду, что вам не нужно исправлять систему единиц, чтобы сделать это (как это делал я раньше). Поскольку приведенные выше определения , они будут выполняться в любой системе единиц. Однако, чтобы увидеть, что эти определения не становятся замкнутыми, полезно увидеть, что мы можем определить $\mu _0$ и $c$ в терминах чисто физических явлений. Другими словами, чтобы приведенные выше определения имели смысл, мы должны были знать, что сначала можем определить $c$ и $\mu _0$ независимо от $\varepsilon _0$ и $k$. Приведенное выше определение единиц СИ поможет вам увидеть, что это можно сделать. 9{-7}H/м$ в единицах СИ.
«Причина» появления «$4\pi$» здесь и в константе Кулона (верите или нет), так что уравнения Максвелла могут быть записаны без множителей $4\pi$!
Чтобы понять это, рассмотрим, как электростатические явления выражаются в законе Кулона как «напряженность поля на квадрате расстояния» по сравнению с (эквивалентным) законом Гаусса, который описывает «поток через замкнутую поверхность, окружающую заряд».
