| ||||||||
План Магнитное поле и его характеристики: магнитная индукция и напряжённость.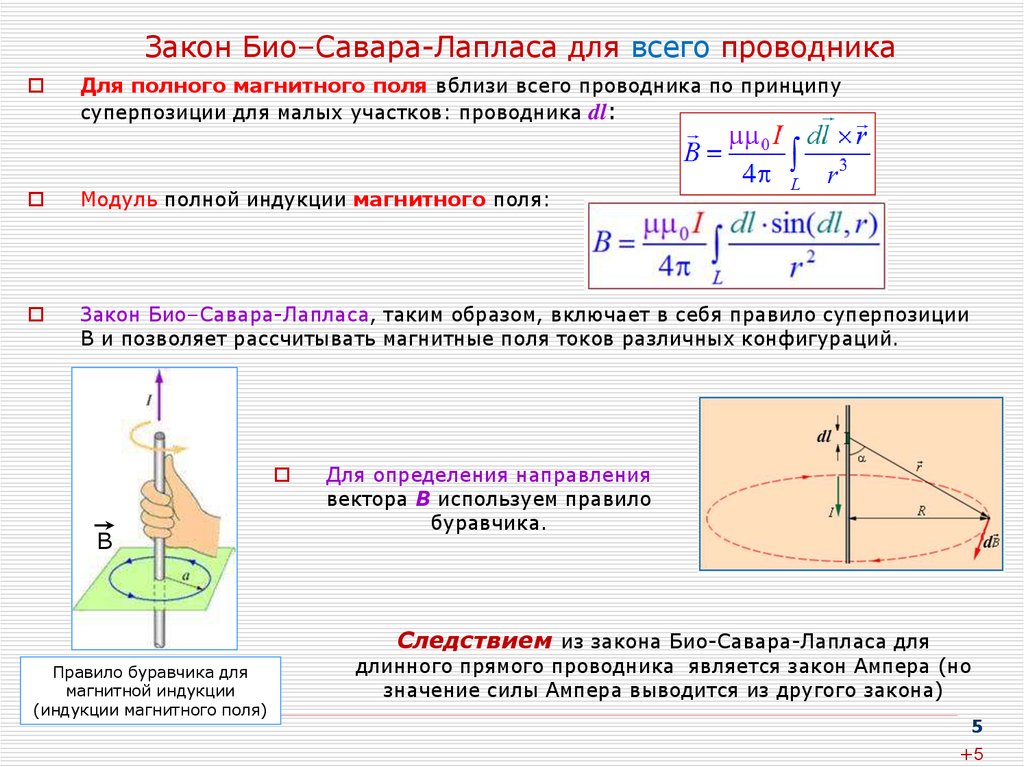 .. ..Закон полного тока для магнитного поля в вакууме. Непотенциальность магнитного поля. Применение закона полного тока для расчёта поля… | Максвеллу пришлось производить подлог и фальсификации, прикрываясь… Кулона, Ампера, Фарадея-Ленца, не существует, а тем более экспериментальных. Напротив, предположения Максвелла, как сейчас увидим… | |||||||
| Закон Био́-Савара-Лапла́са Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постоянным электрическим… | Магнитное поле тока. Магнитная индукция. Магнитный поток. Закон Ампера…. Сформировать представление о магнитном поле как виде материи; ознакомить учащихся с графическим методом представления структуры магнитного… | |||||||
| Решение: F=BIlsin -закон Ампера | 2. Магнитное взаимодействие токов в вакууме. Закон Ампера Диа-, пара- и ферромагнитные вещества. 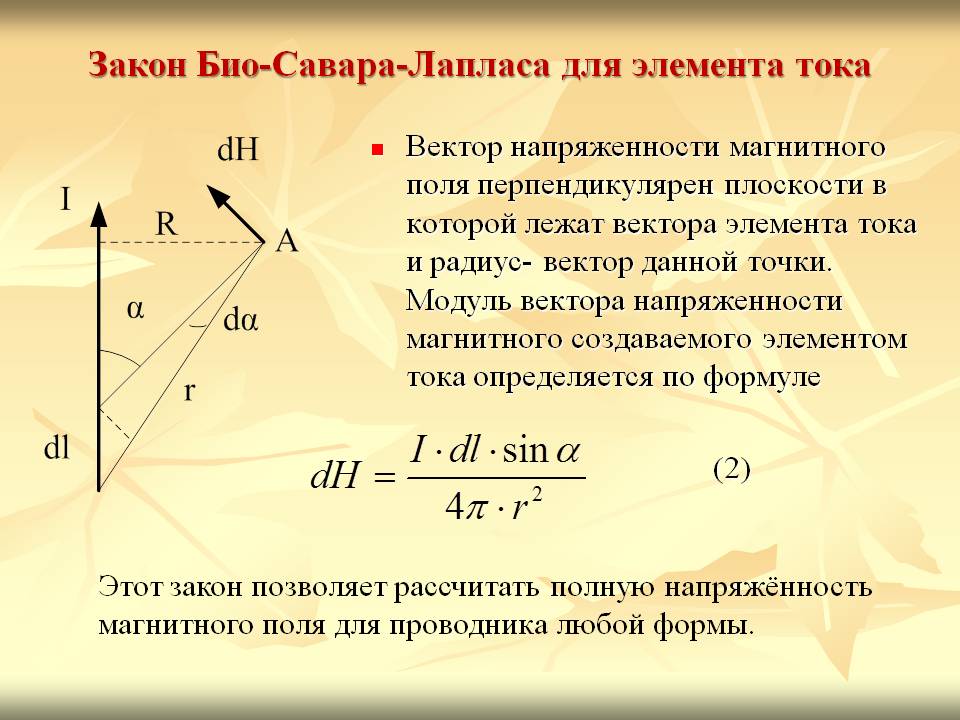 Магнитная проницаемость и магнитная индукция Магнитная проницаемость и магнитная индукция | |||||||
| Тема: магнитный поток. Сила ампера цель урока: изучить действие магнитного… Цель урока: изучить действие магнитного поля на проводник с током, познакомить учащихся с понятием магнитный поток и сила Ампера…. | План Магнитное поле, его характеристики. Силовые линии магнитной… … | |||||||
| Список вопросов к госэкзамену по общей физике: электричество и магнетизм Электрический заряд, его свойства, единицы измерения (Гауссовская система и си). Закон Кулона, потенциал и напряженность электрического… | План Понятие магнитного поля. Закон Ампера. Магнитная индукция. Сила… Циркуляция вектора магнитной индукции. Закон полного тока (теорема о циркуляции магнитного поля в вакууме). Применение закона полного… |
Вопросы и задания для самоконтроля
Что такое магнитное поле (МП)?
Назовите источники МП.

Какие силы действуют между движущимися зарядами?
Во сколько раз магнитная сила меньше электрической для двух движущихся точечных электрических зарядов?
Сформулируйте определение квазинейтральности проводов с током.
Какие силы и почему действуют между проводами с током?
Дайте определение линии индукции МП. Зачем их рисуют?
Запишите закон Био-Савара-Лапласа. В чем он похож на закон Кулона?
Сформулируйте принцип суперпозиции для МП.
Дайте определение циркуляции МП.
Сформулируйте и запишите формулу закона циркуляции МП.
Сформулируйте и запишите формулу для МП прямого провода с током.
Как выглядят линии индукции МП прямого провода с током?
Сформулируйте и запишите формулу для МП на оси кругового витка (контура) с током.
Что такое магнитный момент витка с током?
Какую форму имеет линия индукции, проходящая через центр витка с током?
Что такое соленоид и для чего он используется?
Чему равно магнитное поле в центре соленоида?
Является ли МП внутри соленоида точно однородным?
Как определить протяженность области однородности МП внутри соленоида, если задана точность?
литература
Трофимова Т.

Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2000. Гл. 22, §§ 22.1-22.3.
ЛАБОРАТОРНАЯ РАБОТА
Ознакомьтесь с конспектом лекций и учебником. Запустите программу. Выберите «Электричество и магнетизм» и «Электромагнитная индукция». (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ стр.5 еще раз).
Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. Закройте внутреннее окно, нажав кнопку с крестом справа вверху этого окна.
ЦЕЛЬ РАБОТЫ
КРАТКАЯ ТЕОРИЯ
элементарным Магнитным потоком dФB через физически малый элемент поверхности площадью dS называется скалярное произведение вектора индукции магнитного поля на вектор нормали к данному элементу поверхности и на площадь dS:
dФB = ()dS
.
Магнитным потоком ФB через поверхность площадью S называется сумма всех элементарных потоков через все элементы этой поверхности (интеграл по поверхности):
ФB = .
Анализируя свойства интеграла в правой части данного соотношения, можем получить условия, когда для определения потока не требуется интегрирование.
Простейший вариант: потока нет (ФВ = 0), если 1) В = 0 или 2) вектор магнитной индукции направлен по касательной к поверхности в любой ее точке ().
Второй вариант: поток есть произведение индукции на площадь (ФВ = BS), если , т.е. одновременно выполняются два условия: вектор индукции направлен по нормали и имеет одну и ту же величину в любой точке поверхности.
ИНДУКЦИЕЙ называется явление возникновения одного поля (например, электрического) при изменении другого поля (например, магнитного).
ЭЛЕКТРОМАГНИТНОЙ
ИНДУКЦИЕЙ называется явление возникновения
электрического поля при изменении
магнитного поля.
Закон ЭМИ: циркуляция электрического поля по замкнутому контуру Г0Е пропорциональна быстроте изменения потока магнитного поля Ф0В через замкнутую поверхность S0 (L0), ограниченную контуром L0 , по которому рассчитана циркуляция. Математически:
Г0Е = — , где знак – соответствует «правилу Ленца» (см.учебник).
В расшифрованном виде .
В результате ЭМИ возникает электрическое поле с ненулевой циркуляцией. Поле с ненулевой циркуляцией называется вихревым .
Если в таком поле находится проводящее вещество, то в веществе возникает вихревой электрический ток, величина которого пропорциональна напряженности вихревого электрического поля. Такие токи называются токами Фуко.
Если проводящее вещество имеет форму замкнутого контура, тогда циркуляция электрического поля в нем определяет ЭДС, которая в случае ЭМИ называется ЭДС индукции. Закон ЭМИ для проводящего контура будет выглядеть так ЭДСИНД = —
Ток, который
в этом случае появляется в контуре,
называется индукционным.
Обозначая ЭДС индукции символом инд и используя закон Ома для полной цепи, получим выражение для тока индукции iИНД = инд / R , где R – сопротивление контура.
Если имеется замкнутый контур с переменным током, тогда магнитное поле с изменяющимся потоком создается собственным током в этом контуре, и в соответствии с законом ЭМИ в контуре возникает дополнительная ЭДС, называемая ЭДС самоиндукции.
Явлением САМОИНДУКЦИИ называется возникновение ЭДС самоиндукции при протекании по проводнику переменного тока.
ЗАКОН самоиндукции: ЭДССАМОИНД = -L , где L – индуктивность проводника.
МЕТОДИКА и ПОРЯДОК ИЗМЕРЕНИЙ
Закройте окно теории.
В данной лабораторной работе используется компьютерная модель, в которой изменяющийся магнитный поток возникает в результате движения проводящей перемычки по параллельным проводникам, замкнутым с одной стороны.
Эта система изображена на рисунке:
ЗАДАЧА:
Проводящая
перемычка движется со скоростью V
по параллельным проводам, замкнутым с
одной стороны.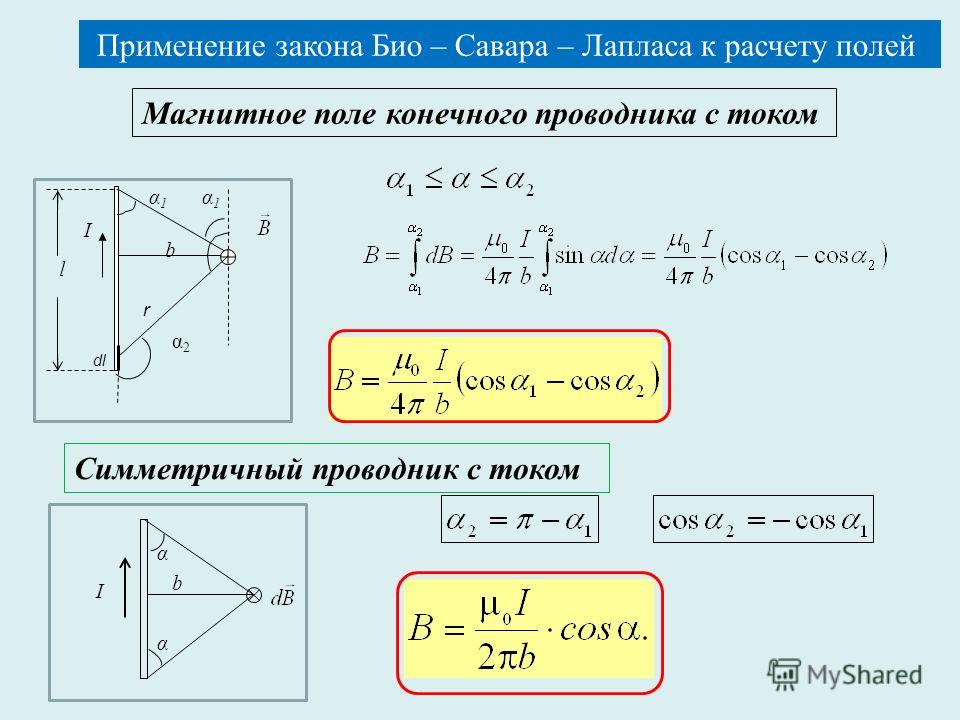 Система проводников
расположена в однородном магнитном
поле, индукция которого равна В и
направлена перпендикулярно плоскости,
в которой расположены проводники. Найти
ток в перемычке, если ее сопротивление
R, а сопротивлением
проводников можно пренебречь.
Система проводников
расположена в однородном магнитном
поле, индукция которого равна В и
направлена перпендикулярно плоскости,
в которой расположены проводники. Найти
ток в перемычке, если ее сопротивление
R, а сопротивлением
проводников можно пренебречь.
Решив задачу в черновике, получите уравнение для тока в общем виде.
Подготовьте таблицу 1, используя образец. Подготовьте также таблицы 3 и 4, аналогичные табл.1.
ТАБЛИЦА 1. результаты измерений (12 столбцов). В = ____ мТл | ТАБЛИЦА 2. Значения характеристик (не перерисовывать) | |||||||||||||
v (м/c) = | -10 | -8 | . | 10 | Бригады | R (Ом) | (мТл) | В2 (мТл) | В3 (мТл) | |||||
ЭДС, В | 1 и 5 | 1 | -30 | 40 | 90 | |||||||||
I, мА | 2 и 6 | 2 | -40 | 20 | 80 | |||||||||
3 и 7 | -50 | 10 | 70 | |||||||||||
4 и 8 | 2 | -60 | -20 | 100 | ||||||||||
Для бригад 1-4 L = 1 м, для бригад 5-8 L = 0. 7 м.
7 м.
Получите у преподавателя допуск для выполнения измерений.
ИЗМЕРЕНИЯ:
Закройте окно теории (если вы ее вызывали), нажав кнопку в правом верхнем углу внутреннего окна. Запустите эксперимент, щелкнув мышью по кнопке «Старт». Наблюдайте движение перемычки и изменение магнитного потока Ф (цифры внизу окна) .
Зацепив мышью, перемещайте движки регуляторов
L –расстояния между проводами,
R – сопротивления перемычки,
В1 – величины индукции магнитного поля
и зафиксируйте значения, указанные в таблице 2 и под ней для вашей бригады.
Установив указанное в табл.1 значение скорости движения перемычки, нажмите левую кнопку мыши, когда ее маркер размещен над кнопкой «Старт». Значения ЭДС и тока индукции занесите в табл.1. Повторите измерения для других значений скорости из табл.1.
Повторите измерения для двух других значений индукции магнитного поля, выбирая их из табл.
 2.
Полученные результаты запишите в табл.3
и 4.
2.
Полученные результаты запишите в табл.3
и 4.
ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЕТА
Постройте на одном листе графики зависимости тока индукции от скорости движения перемычки при трех значениях индукции магнитного поля.
Для каждой прямой определите тангенс угла наклона по формуле
tg() = .
Вычислите теоретическое значение тангенса для каждой прямой по формуле tg()ТЕОР = .
Заполните таблицу результатов измерений
Номер измерения
tg()ЭКСП (Ac/м)
tg()ТЕОР (Ac/м)
Сделайте выводы по графикам и результатам измерений.

Сравнение закона Кулона и закона Био-Савара
Автор ФизикаGoeasy / 13 мая 2021 г. 30 мая 2021 г.
В этой статье мы узнаем о сравнении законов Кулона и законов Био-Савара. Мы рассмотрим как сходства, так и различия между законом Кулона и законом Био-Савара. Один для статических зарядов, а другой для движущихся зарядов. Однако обе силы, объясняемые этими законами, имеют электрическое происхождение. Закон Кулона, который дает электрическую силу между зарядами, может использоваться для определения электростатического поля, а закон Био-Савара определяет магнитное поле из-за проводника с током. 92$ в вакууме Электрическое поле, вызванное точечным зарядом
Что такое закон Био-Савара
Проводник с током I создает вокруг себя магнитное поле. Закон Био-Савара дает нам выражение для магнитного поля в точке из-за элемента тока
Согласно этому закону величина дБ магнитного поля в точке P из-за элемента тока зависит от следующих факторов
- $дБ \propto I$
- $dB\propto dl$
- $dB\propto \frac{1}{r^2}$ 92}$
Как получить скорость из ускорения.
 ..
..Включите JavaScript
Как получить скорость из ускорения?
Приведенное выше уравнение дает величину магнитного поля в точке из-за малого элемента тока $Id\vec{l}$. Элемент электрических токов является векторной величиной. Следует отметить, что этот закон строго выполняется только для постоянного тока.
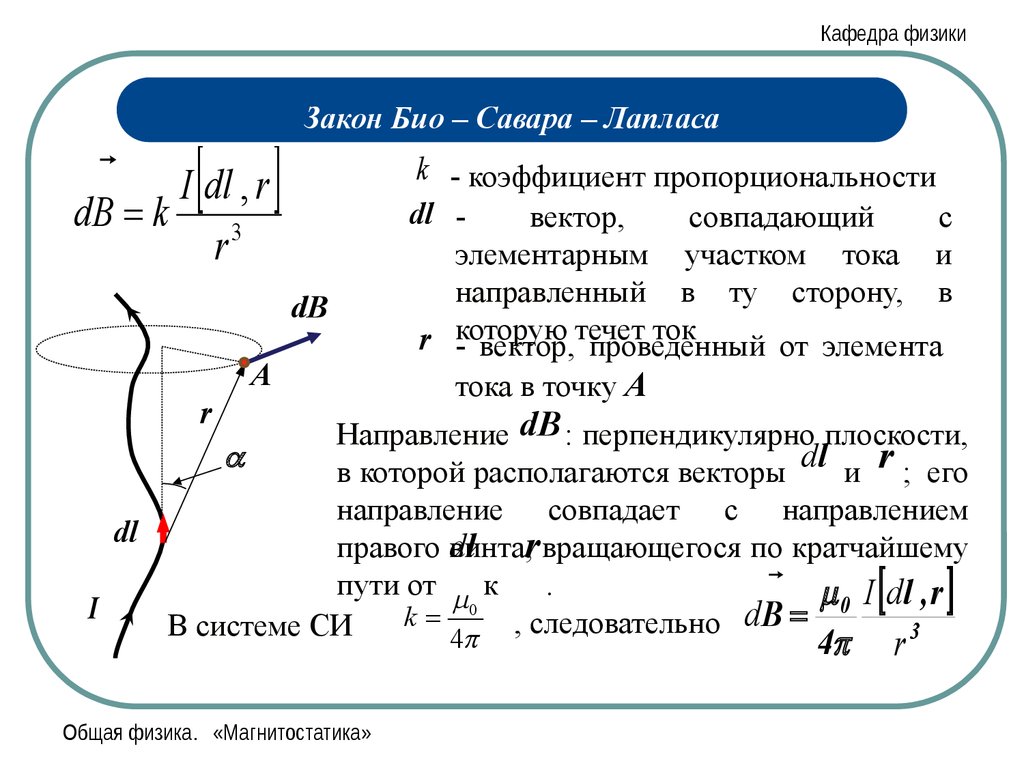
Направление магнитного поля из-за элемента токаСходство между законом Кулона и законом Био-Савара
- И электрическое, и магнитное поля обратно пропорциональны квадрату расстояния между источником поля и рассматриваемыми точками поля.
- Обе силы дальнего действия.
- Оба они подчиняются принципу суперпозиции. Рекламные ссылки
Различия между законом Кулона и законом Био-Савара
- Элемент электрического заряда $dq$, создающий электростатическое поле, является скалярным источником, тогда как элемент электрического тока, создающий магнитное поле $Id\vec{l}$, является вектором источник, имеющий такое же направление, как и поток тока.

- Электрическое поле $E$ действует вдоль вектора смещения, тогда как $B$ действует перпендикулярно $dl\times r$. Согласно закону Кулона, величина электрического поля в любой точке (Р) зависит только от расстояния элемента заряда от любой точки (Р). Согласно закону Био-Савара, направление магнитного поля перпендикулярно элементу тока, а также линии, соединяющей элемент тока с точкой P.
- Электрическое поле $(E)$ не зависит от угла, тогда как магнитное поле $(B)$ зависит от угла $(\theta)$, где $(\theta)$ — угол между $(v)$ (скоростью движущегося заряда) и $(B)$ (магнитным полем) .
Comparison in tabular form
Сравнение закона Кулона и закона Био-СавараBiot-Savart’s Law for Magnetic Field Coulomb’s Law for electrostatic Field Long Range Force Long Range Force Principle of Применяется суперпозиция Применяется принцип суперпозиции Поле создается векторным источником $Id\vec{l}$ Поле создается электрическим зарядом, скалярным В законе Био-Савара есть угловая зависимость В законе Кулона угловая зависимость отсутствует Магнитное поле действует перпендикулярно плоскости, содержащей элемент тока
$Id\vec{l}$ и вектор смещения $\vec{r}$, который находится в направлении их векторного произведения.
Электростатическая сила или поле действуют вдоль линии, соединяющей источник и точку. Соответствующая статья
- Тест по закону Кулона
- Чем закон Кулона похож на закон всемирного тяготения Ньютона? Как это отличается?
сообщить об этом объявлении
сообщите об этом объявлении
Искать на этом сайте
Искать:сообщить об этом объявлении
Категории
Последние сообщения
сообщить об этом объявлении сообщить об этом объявлении
электромагнетизм — Можем ли мы вывести закон Био-Савара из закона Кулона?
Задавать вопрос
спросил
Изменено 4 года, 11 месяцев назад
Просмотрено 885 раз
$\begingroup$
Можем ли мы вывести закон Био-Савара из закона Кулона, установив в данный момент источник тока вместо одного из зарядов? Допустим, $dl$ — это длина проводника с зарядом $dQ$, который прикладывает силу к другому заряду в некоторый момент времени.
 Беря производные с обеих сторон, мы получаем некоторый текущий член. Но как это доказать? 9E производит B, и у вас слева dl/dt, что равно v. Таким образом, вы правы, только нуждаясь в некотором уточнении в рассуждениях и в том, что означает каждая переменная. Еще одно указание на то, что вы правы, заключается в том, что если вы возьмете выражение статической силы Кулона и поместите его в выражение запаздывающего потенциала (с конечной скоростью распространения), вы сможете восстановить все уравнения Максвелла, включая магнетизм и излучение. Так что вы делаете то же самое, по крайней мере, символически. И, как показывают уравнения Эйнштейна, магнитные поля — это электрические поля, наблюдаемые из движущейся системы отсчета.
Беря производные с обеих сторон, мы получаем некоторый текущий член. Но как это доказать? 9E производит B, и у вас слева dl/dt, что равно v. Таким образом, вы правы, только нуждаясь в некотором уточнении в рассуждениях и в том, что означает каждая переменная. Еще одно указание на то, что вы правы, заключается в том, что если вы возьмете выражение статической силы Кулона и поместите его в выражение запаздывающего потенциала (с конечной скоростью распространения), вы сможете восстановить все уравнения Максвелла, включая магнетизм и излучение. Так что вы делаете то же самое, по крайней мере, символически. И, как показывают уравнения Эйнштейна, магнитные поля — это электрические поля, наблюдаемые из движущейся системы отсчета.$\endgroup$
$\begingroup$
вы в основном пытаетесь совершить переход от закона, справедливого для статических зарядов (или нерелятивистских скоростей), к закону, справедливому для установившихся токов.



 Таким образом, измеряя частоту излучения, пришедшего к неподвижному наблюдателю из движущейся системы, по отношению частот можно вычислить скорость системы.
Таким образом, измеряя частоту излучения, пришедшего к неподвижному наблюдателю из движущейся системы, по отношению частот можно вычислить скорость системы. Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :
Сила , с которой магнитное поле действует на элемент объёма dV проводника с током плотности , находящегося в магнитном поле с индукцией :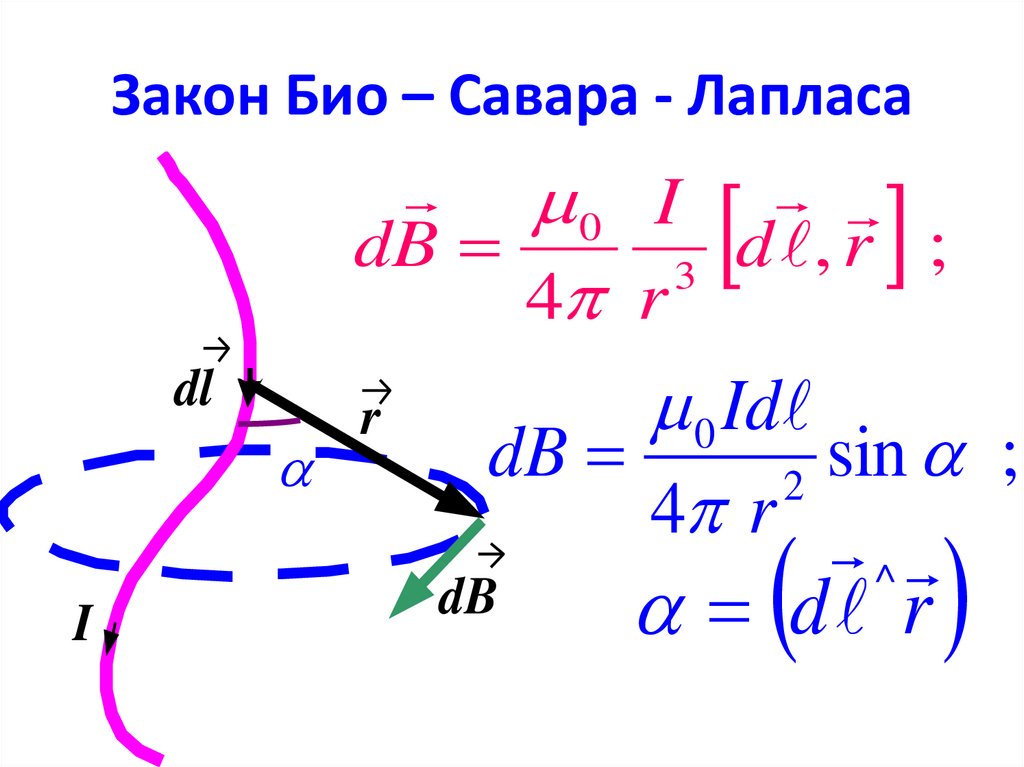 Основными характеристиками электростатического поля являются напряженность и потенциал.
Основными характеристиками электростатического поля являются напряженность и потенциал. Гравитационное поле, как известно, является потенциальным, и, следовательно, аналогичными свойствами должно обладать и электростатическое поле. Работа сил такого поля не зависит от формы траектории, а определяется только начальным и конечным положением перемещаемого заряда. Элементарная работа, совершаемая силой на расстоянии, равна .
Гравитационное поле, как известно, является потенциальным, и, следовательно, аналогичными свойствами должно обладать и электростатическое поле. Работа сил такого поля не зависит от формы траектории, а определяется только начальным и конечным положением перемещаемого заряда. Элементарная работа, совершаемая силой на расстоянии, равна .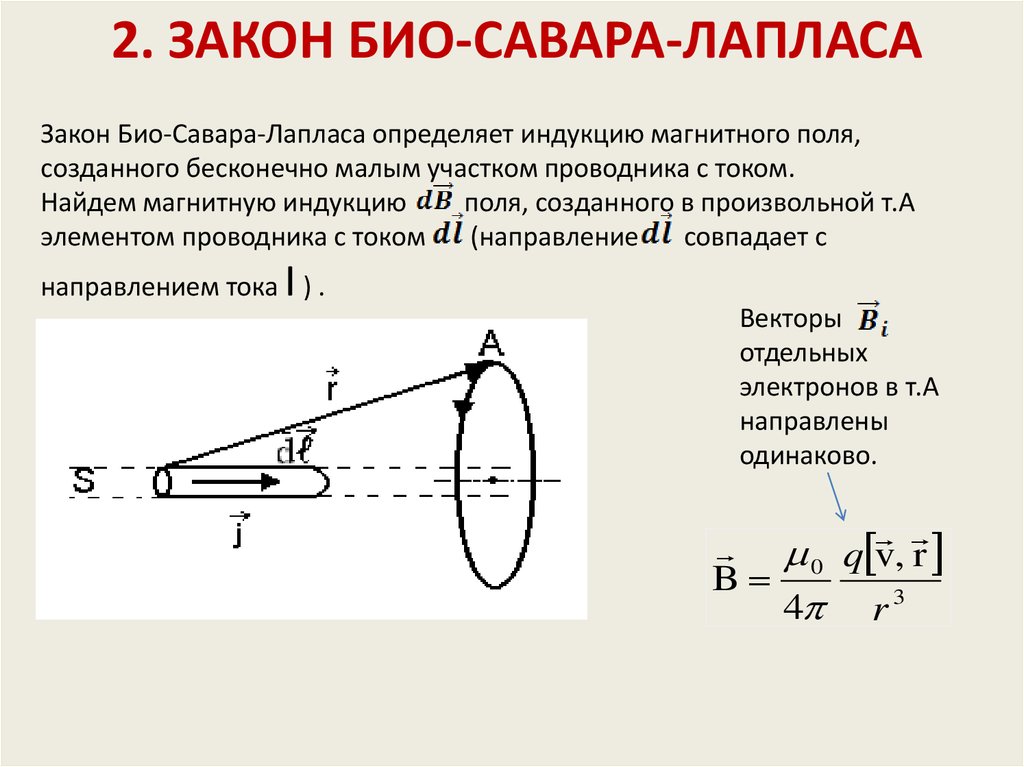
 Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E‘ = E» = E. Поток вектора напряжённости равен 2EΔS.
Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E‘ = E» = E. Поток вектора напряжённости равен 2EΔS.  Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr2). Иными словами, суммарный поток будет равен:
Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr2). Иными словами, суммарный поток будет равен: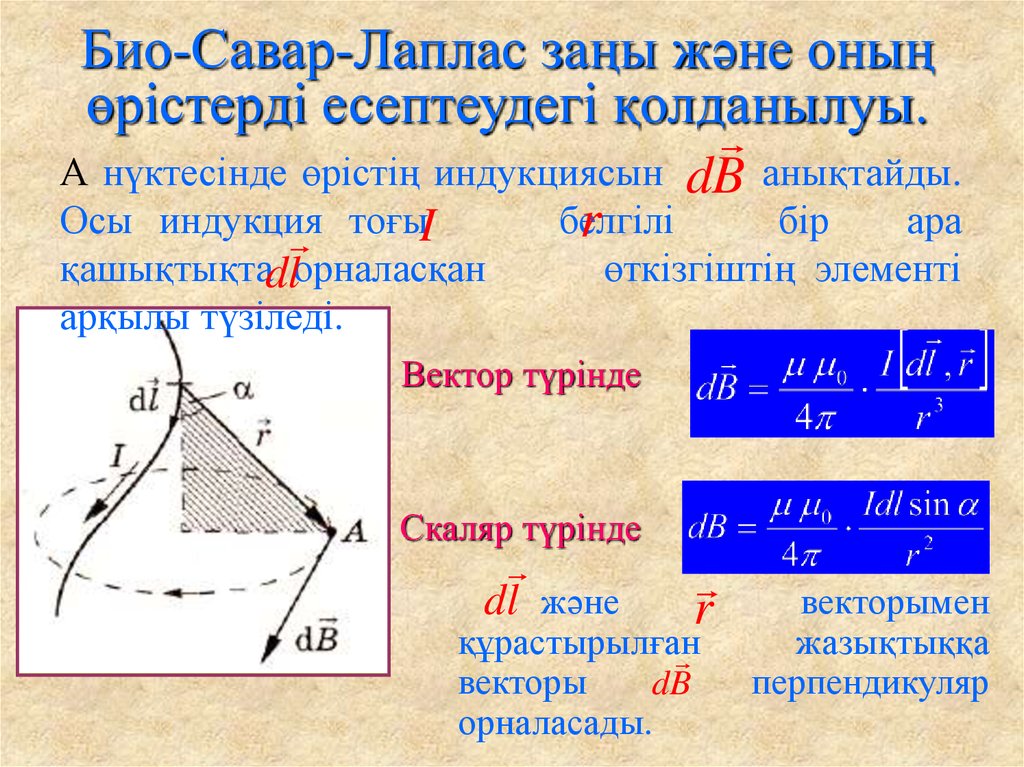
 поле, образующие диполь заряды +q и –q окажутся под действием равных по величине, но противоположных по направлению сил . Эти силы образуют пару, плечо которой равно l·sinα, т.е. зависит от положения диполя относительно поля, также они стремится повернуть диполь так, чтобы электрический момент диполя развернулся вдоль направления поля.
поле, образующие диполь заряды +q и –q окажутся под действием равных по величине, но противоположных по направлению сил . Эти силы образуют пару, плечо которой равно l·sinα, т.е. зависит от положения диполя относительно поля, также они стремится повернуть диполь так, чтобы электрический момент диполя развернулся вдоль направления поля.

 ..
..