Резонансная частота | это… Что такое Резонансная частота?
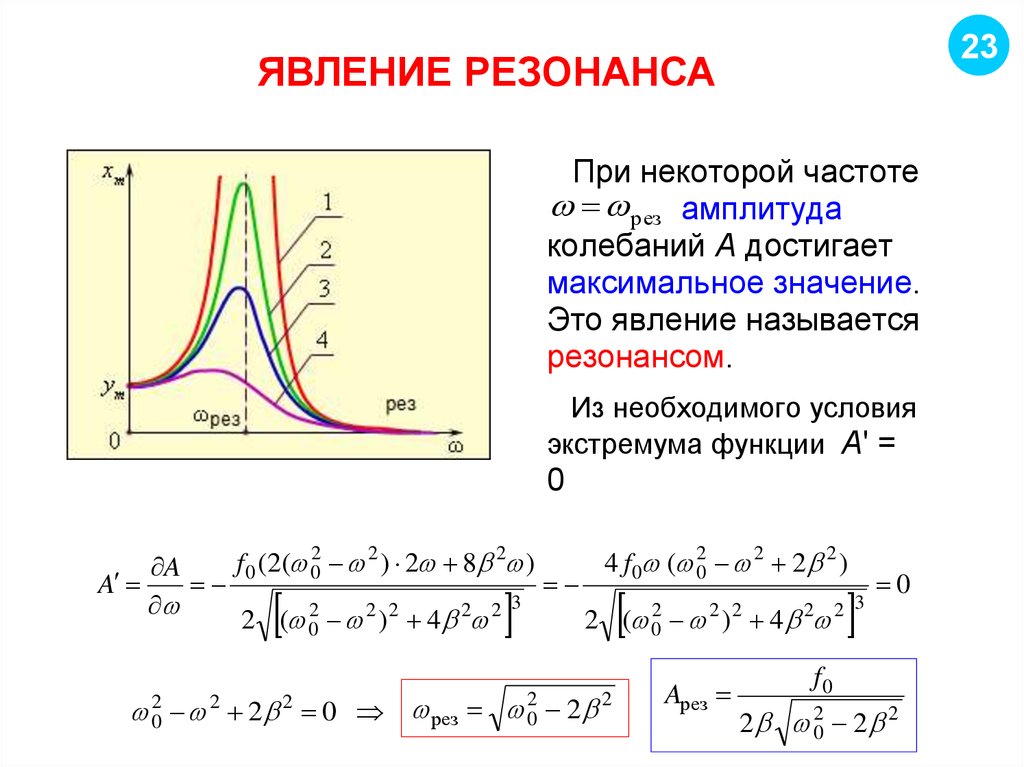
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам.
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы
Содержание
|
Механика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
- ,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс. (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах.
Электроника
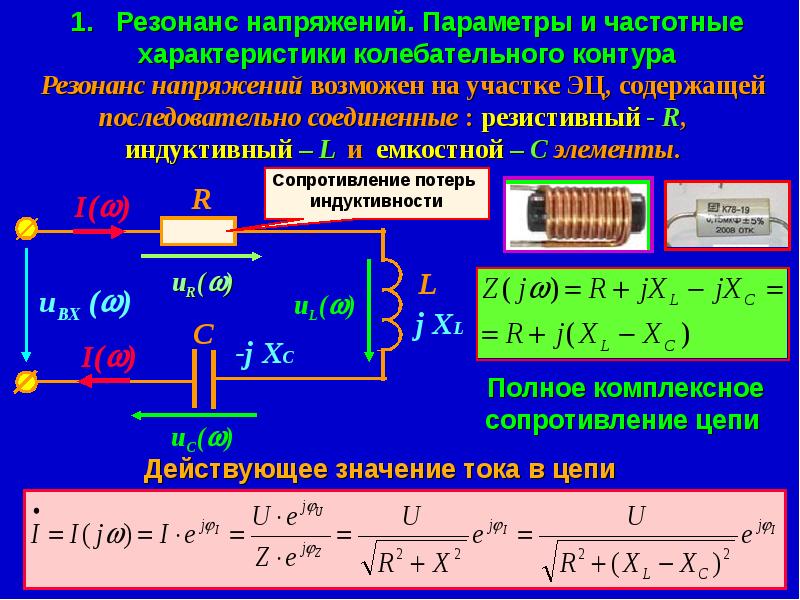
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
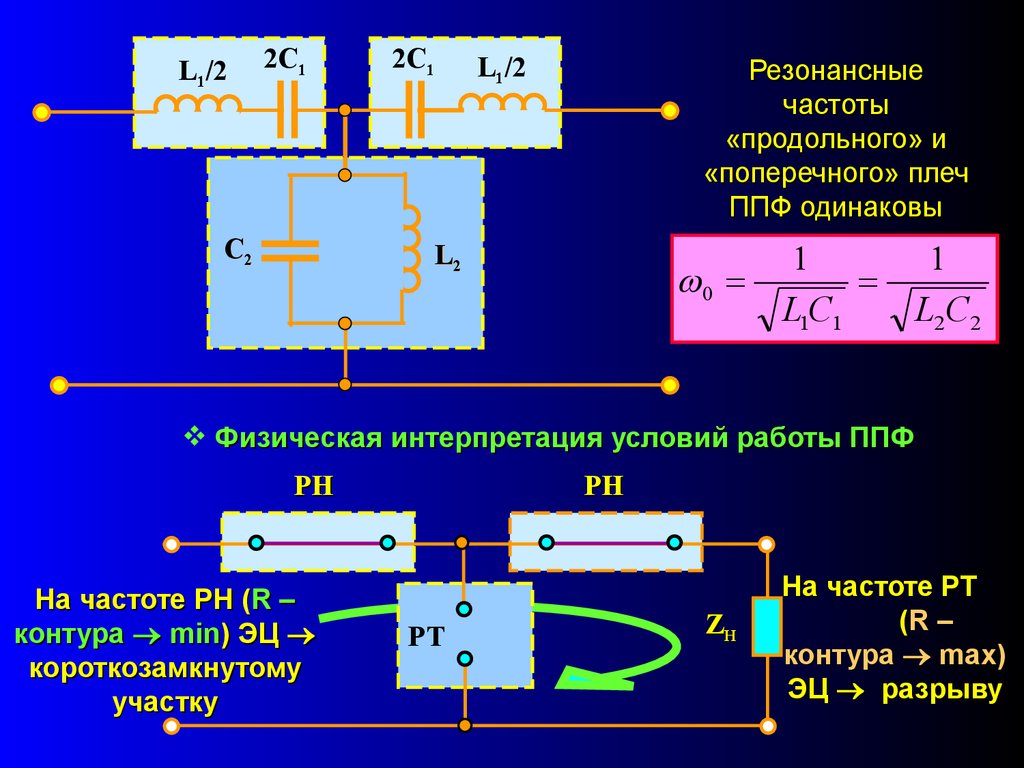
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром. Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
- ,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.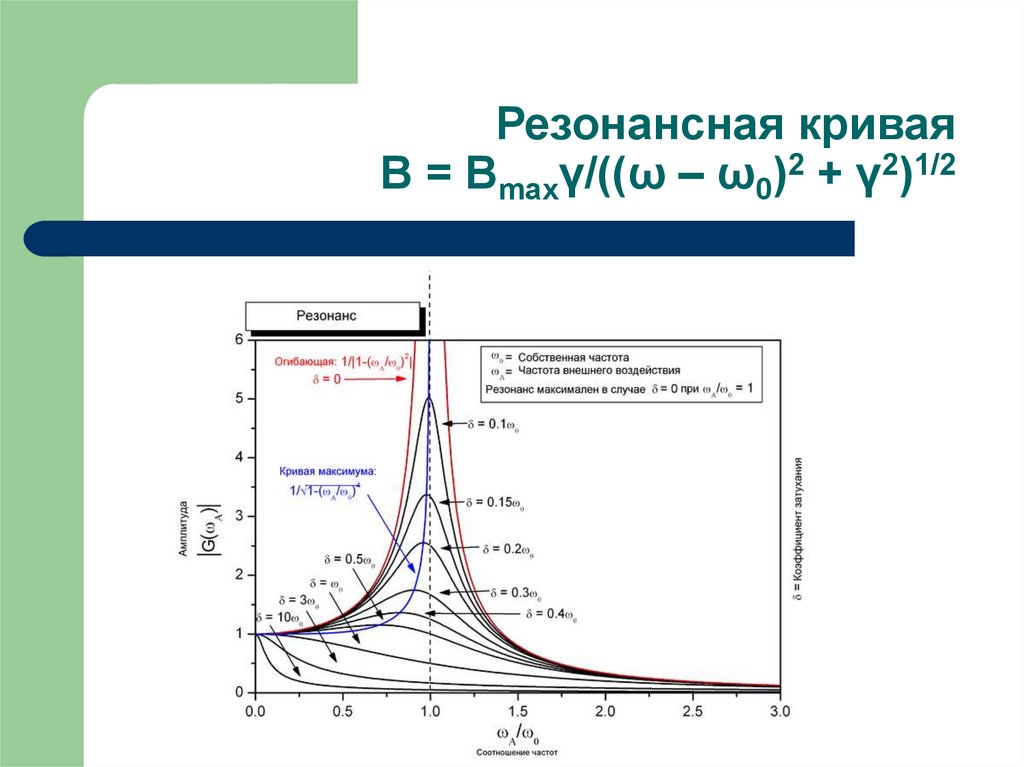
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты
Примечания
См. также
- Диссипативная структура
- Солитон
- Интерференция
- Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))
Ссылки
Richardson LF (1922),
Bretherton FP (1964), Resonant interactions between waves.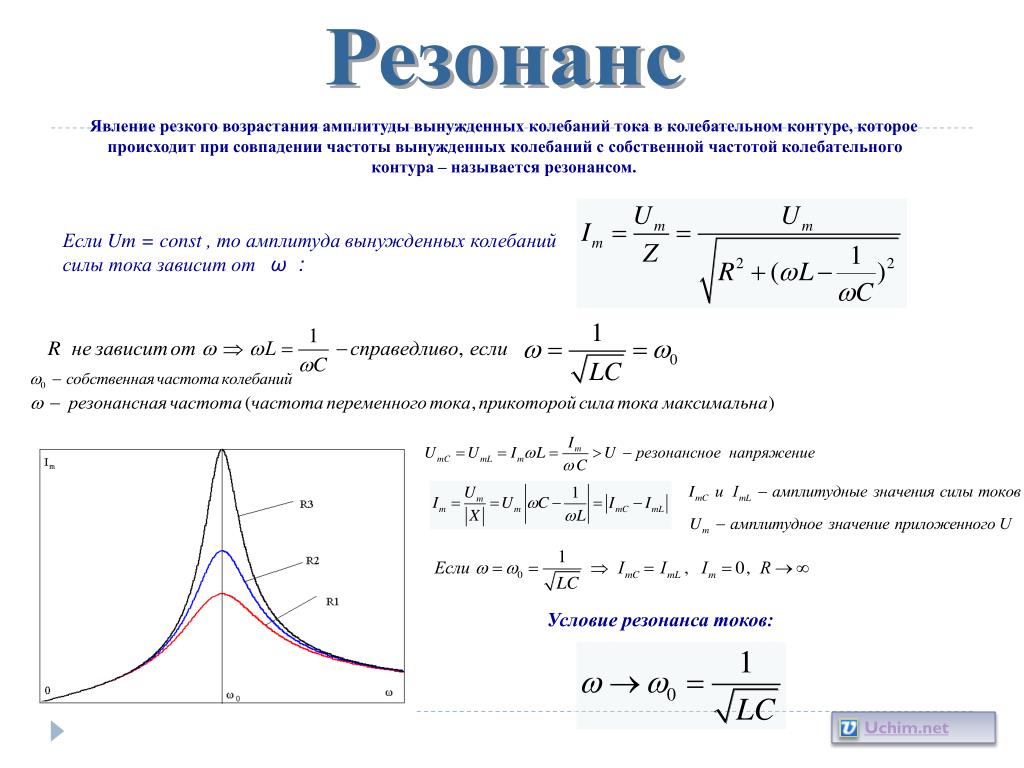 J. Fluid Mech., 20, 457-472.
J. Fluid Mech., 20, 457-472.
Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium,
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М. : Наука — 232 с.
: Наука — 232 с.
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Резонансная частота | это… Что такое Резонансная частота?
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы.
Но это далеко не полное определение явления резонанса. Для более детального восприятия этой категории необходимы некоторые факты из теории дифференциальных уравнений и математического анализа. В теории обыкновенных дифференциальных уравнений известна проблема собственных векторов и собственных значений. Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.
Резонанс в динамической системе, описываемой дифференциальными уравнениями (и не только ими), формально наступает, когда проблема собственных значений приводит к кратным собственным числам. При этом в математическом аспекте не очень существенно, являются ли собственные числа комплексными или действительными. В физическом аспекте явление резонанса обычно связывают только с колебательными динамическими системами. Наиболее ярко понятие явления резонанса развито в современной теории динамических систем. Примером является известная теория Колмогорова-Арнольда-Мозера. Центральная проблема этой теории — вопрос сохранения квазипериодического или условно-периодического движения на торе (теорема КАМ). Эта теорема дала мощный толчок к развитию современной теории нелинейных колебаний и волн. В частности, стало ясно, что резонанс может и не наступить, хоть собственные числа совпадают или близки. Напротив, резонанс может проявиться в системе, где никакие собственные числа не совпадают, а удовлетворяют лишь определенным резонансным соотношениям или условиям синхронизма.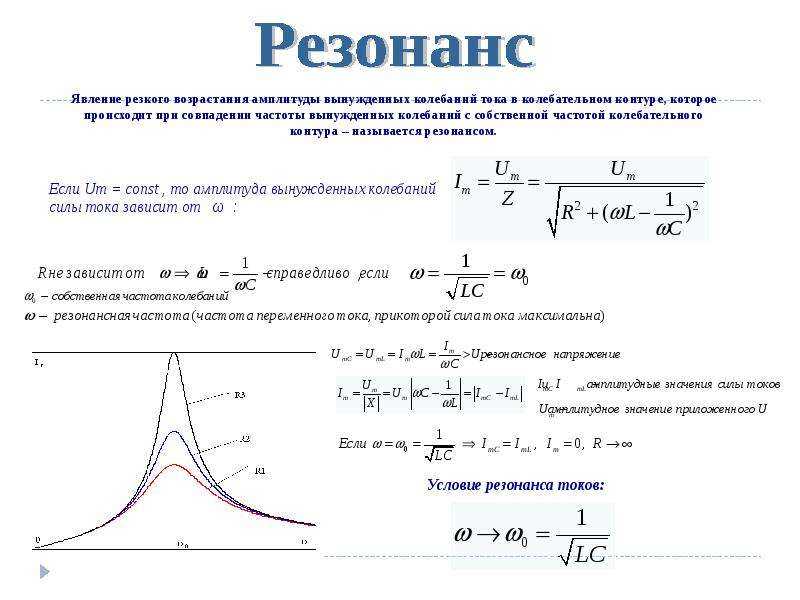
Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы
Содержание
|
Механика
Наиболее известная большинству людей механическая резонансная система — это обычные качели. Если вы будете подталкивать качели в соответствии с их резонансной частотой, размах движения будет увеличиваться, в противном случае движения будут затухать. Резонансную частоту такого маятника с достаточной точностью в диапазоне малых смещений от равновесного состояния, можно найти по формуле:
- ,
где g это ускорение свободного падения (9,8 м/с² для поверхности Земли), а L — длина от точки подвешивания маятника до центра его масс.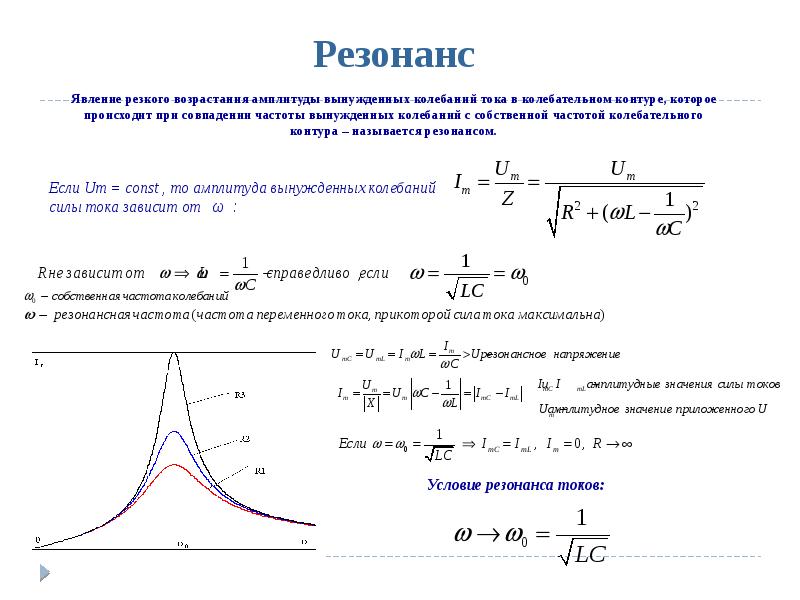 (Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
(Более точная формула довольно сложна, и включает эллиптический интеграл). Важно, что резонансная частота не зависит от массы маятника. Также важно, что раскачивать маятник нельзя на кратных частотах (высших гармониках), зато это можно делать на частотах, равных долям от основной (низших гармониках).
Резонансные явления могут вызвать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США. Чтобы предотвратить такие повреждения существует правило, заставляющее строй солдат сбивать шаг при прохождении мостов.
В основе работы механических резонаторов лежит преобразование кинетической энергии в потенциальную и обратно. В случае простого маятника, вся его энергия содержится в потенциальной форме, когда он неподвижен и находится в верхних точках траектории, а при прохождении нижней точки на максимальной скорости, она преобразуется в кинетическую. Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Потенциальная энергия пропорциональна массе маятника и высоте подъёма относительно нижней точки, кинетическая — массе и квадрату скорости в точке измерения.
Другие механические системы могут использовать запас потенциальной энергии в различных формах. Например, пружина запасает энергию сжатия, которая, фактически, является энергией связи её атомов.
Электроника
В электронных устройствах резонанс возникает на определённой частоте, когда индуктивная и ёмкостная составляющие реакции системы уравновешены, что позволяет энергии циркулировать между магнитным полем индуктивного элемента и электрическим полем конденсатора.
Механизм резонанса заключается в том, что магнитное поле индуктивности генерирует электрический ток, заряжающий конденсатор, а разрядка конденсатора создаёт магнитное поле в индуктивности — процесс, который повторяется многократно, по аналогии с механическим маятником.
Электрическое устройство, состоящее из ёмкости и индуктивности, называется колебательным контуром.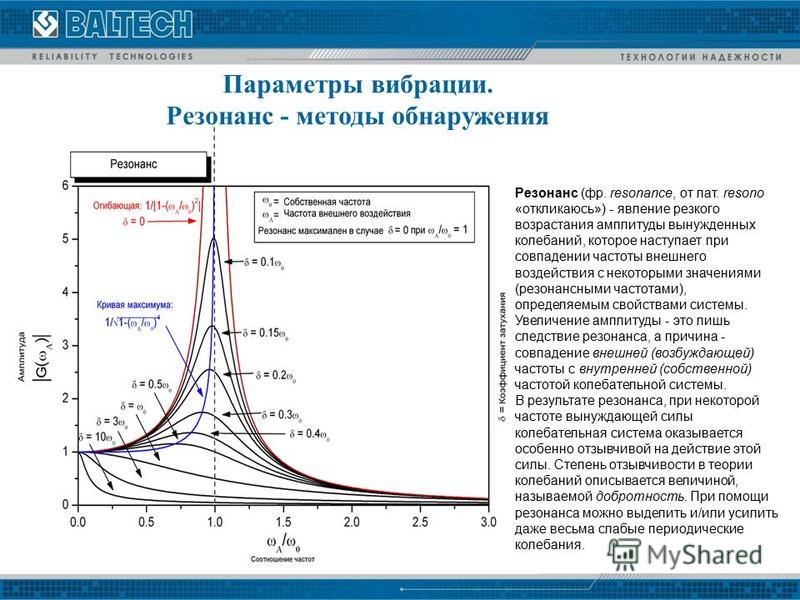 Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Элементы колебательного контура могут быть включены как последовательно, так и параллельно. При достижении резонанса, импеданс последовательно соединённых индуктивности и ёмкости минимален, а при параллельном включении — максимален. Резонансные процессы в колебательных контурах используются в элементах настройки, электрических фильтрах. Частота, на которой происходит резонанс, определяется величинами (номиналами) используемых элементов. В то же время, резонанс может быть и вреден, если он возникает в неожиданном месте по причине повреждения, недостаточно качественного проектирования или производства электронного устройства. Такой резонанс может вызывать паразитный шум, искажения сигнала, и даже повреждение компонентов.
Приняв, что в момент резонанса индуктивная и ёмкостная составляющие импеданса равны, резонансную частоту можно найти из выражения ωL = 1/ωC, где ω = 2πf; f — резонансная частота в герцах; L — индуктивность в генри; C — ёмкость в фарадах. Важно, что в реальных системах понятие резонансной частоты неразрывно связано с полосой пропускания, то есть диапазоном частот, в котором реакция системы мало отличается от реакции на резонансной частоте. Ширина полосы пропускания определяется добротностью системы.
Ширина полосы пропускания определяется добротностью системы.
Акустика
Резонанс — один из важнейших физических процессов, используемых при проектировании звуковых устройств, большинство из которых содержат резонаторы, например, струны и корпус скрипки, трубка у флейты, мембрана у барабанов.
Струна
Струны таких инструментов, как лютня, гитара, скрипка или пианино, имеют основную резонансную частоту, напрямую зависящую от длины и силы натяжения струны. Длина волны первого резонанса струны равна её удвоенной длине. При этом, его частота зависит от скорости v, с которой волна распространяется по струне:
где L — длина струны (в случае, если она закреплена с обоих концов). Скорость распространения волны по струне зависит от её натяжения T и массы на единицу длины ρ:
Таким образом, частота главного резонанса зависит от свойств струны и выражается следующим отношением:
- ,
где T — сила натяжения, ρ — масса единицы длины струны, а m — полная масса струны.
Увеличение натяжения струны и уменьшение её длины увеличивает её резонансную частоту. Помимо основного резонанса, струны также имеют резонансы на высших гармониках основной частоты f, например, 2f, 3f, 4f, и т. д. Если струне придать колебание коротким воздействием (щипком пальцев или ударом молоточка), струна начнёт колебания на всех частотах, присутствующих в воздействующем импульсе (теоретически, короткий импульс содержит все частоты). Однако частоты, не совпадающие с резонансными, быстро затухнут, и мы услышим только гармонические колебания, которые и воспринимаются как музыкальные ноты.
Примечания
См. также
- Диссипативная структура
- Солитон
- Интерференция
- Журавлёв, Виктор Филиппович (см. в кн. «Прикладные методы в теории колебаний» (1988, совместно с Д. М. Климовым))
Ссылки
Richardson LF (1922), Weather prediction by numerical process, Cambridge.
Bretherton FP (1964), Resonant interactions between waves. J. Fluid Mech., 20, 457-472.
J. Fluid Mech., 20, 457-472.
Бломберген Н. (1965), Нелинейная оптика, М.: Мир — 424 с.
Захаров В.Е. (1974), Гамильтонов формализм для волн в нелинейных средах с дисперсией, Изв. вузов СССР. Радиофизика, 17(4), 431-453.
Арнольд В.И. (1979), Потеря устойчивости автоколебаний вблизи резонансов, Нелинейные волны, ред. А.В. Гапонов-Грехов, М.: Наука, 116-131.
Kaup PJ, Reiman A and Bers A (1979), Space-time evolution of nonlinear three-wave interactions. Interactions in a homogeneous medium, Rev. of Modern Phys, 51(2), 275-309.
Haken H (1983), Advanced Synergetics. Instability Hierarchies of Self-Organizing Systems and devices, Berlin, Springer-Verlag.
Филлипс O.М. (1984), Взаимодействие волн. Эволюция идей, Современная гидродинамика. Успехи и проблемы. М.: Мир, 297-314.
Журавлёв В.Ф., Климов Д.М. (1988), Прикладные методы в теории колебаний, М.:Наука
Сухоруков А.П. (1988), Нелинейные волновые взаимодействия в оптике и радиофизике, М. : Наука — 232 с.
: Наука — 232 с.
Брюно А.Д. (1990), Ограниченная задача трех тел, М.:Наука
Резонанс
РезонансВ звуковых приложениях резонансная частота — это собственная частота вибрации, определяемая физическими параметрами вибрирующего объекта. Та же основная идея физически определенных собственных частот применяется во всей физике, в механике, электричестве и магнетизме, и даже во всей области современной физики. Некоторые последствия резонансных частот:
| Индекс Концепции резонанса | ||||||
| Назад |
Легко заставить объект вибрировать на его резонансных частотах, трудно на других частотах. Качели на детской площадке — пример маятника, резонансной системы только с одной резонансной частотой. Слегка толкая качели каждый раз, когда они возвращаются к вам, вы можете продолжать наращивать амплитуду качелей. Если вы попытаетесь заставить его качаться с удвоенной частотой, вам будет очень трудно, и вы можете даже потерять зубы в процессе!
| Индекс Концепции резонанса | |||
| Назад |
Вибрирующий объект будет выделять свои резонансные частоты из сложного возбуждения и вибрировать на этих частотах, по существу «отфильтровывая» другие частоты, присутствующие в возбуждении.
| Индекс Концепции резонанса | |||
| Вернуться назад |
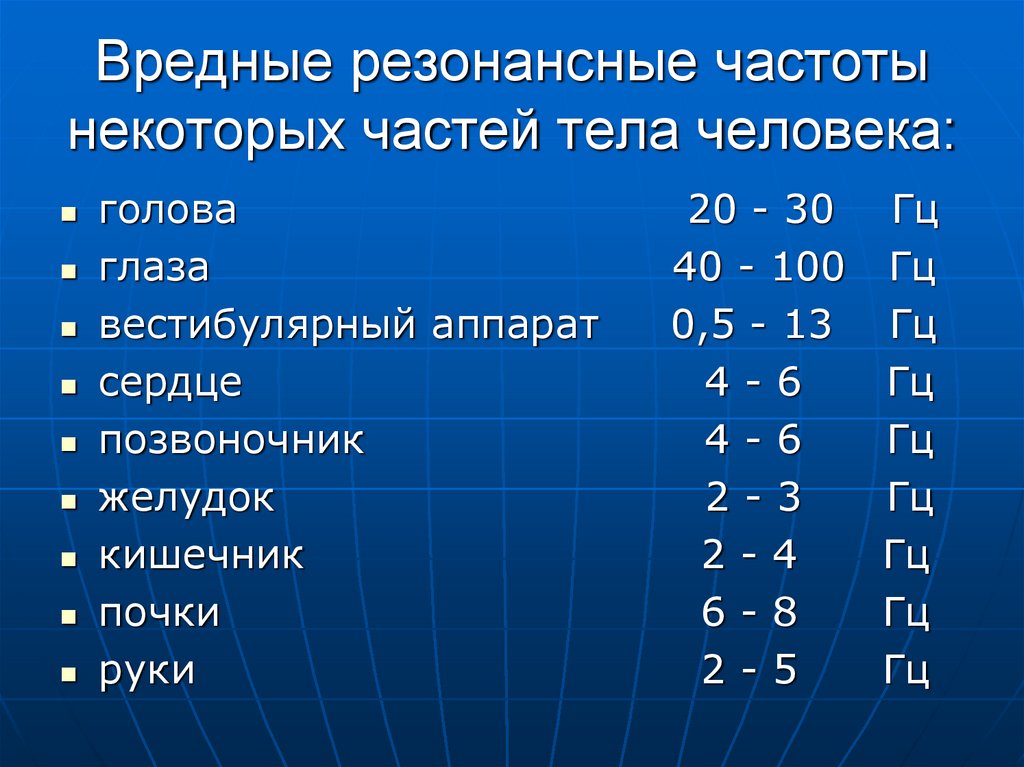
Проверка фактов: воздействие на раковые клетки резонансными частотами не «излечивает» рак
Автор: Reuters Fact Check
9 Min Read
Утверждения социальных сетей о том, что исследования американского изобретателя Рояла Рэймонда Райфа в 1920-х и 1930-х годах, а также современные методы, использующие направленную низкочастотную энергию, представляют собой реальное «лекарство» от рака, выпадают из контекста. что ни один из этих подходов никогда не был продемонстрирован для излечения человека или животного от рака.
что ни один из этих подходов никогда не был продемонстрирован для излечения человека или животного от рака.
Видео TikTok, широко распространенное в Facebook, спрашивает: «Знаете ли вы, что лекарство от рака уже найдено?» а затем переходит к описанию некоторых аспектов работы Рояла Раймонда Райфа, американского инженера и изобретателя микроскопа. Райф разработал теорию о том, что воздействие электромагнитной энергией на бактериальные клетки с частотой, определяемой собственной уникальной энергетической частотой организма, вызовет резонанс, разрушающий клетки. В видео также упоминаются имена двух современных исследователей в качестве примеров современных подходов к терапии рака, основанных на идее клеточных резонансных энергетических частот.
Видео можно увидеть размещенным на Facebook (здесь) (здесь) и (здесь), и оно содержит некоторые неверные детали, поскольку оно фокусируется на использовании Райфом направленной энергии для уничтожения раковых клеток. В видео, например, не отмечено, что Райф считал, что вирусы и бактерии, вызывающие рак, имеют определенные частоты, а не сами раковые клетки, и что уничтожение этих патогенов уничтожит раковую клетку вместе с микробами (здесь).
В видео говорится: «Резонанс может усиливать частоту чего угодно и уничтожать его» и что «Райф создал устройство, которое могло разрушать клетки, подстраиваясь под резонансную частоту… его машина Райфа уничтожала 60% раковых клеток у его пациентов. К сожалению, некоторые жадные люди в то время думали, что это плохо для медицинского бизнеса… поэтому они нашли способы разрушить карьеру Райфа и его новое изобретение…».
Затем спикер в видео предупреждает, что «медицинские новости» называют результаты Райфа мистификацией, добавляя: «В это можно было бы поверить, если бы другие люди не воспроизвели те же результаты, используя частоты и резонанс».
Спикер в видео приводит пример исследователя Энтони Холланда, который, как говорят, «уничтожил клетки лейкемии, а также клетки рака поджелудочной железы с помощью резонанса, также уничтожив 60% клеток, как это сделал Райф, и замедлив рост рака на 65%». …». Затем в видео показано изображение Кристин Гиббонс, в настоящее время генерального директора компании Histosonics, в то время как в повествовании технология компании Гиббонса неверно охарактеризована как использование «звуковых волн для разрушения раковой ткани, также совпадающей с резонансной частотой рака».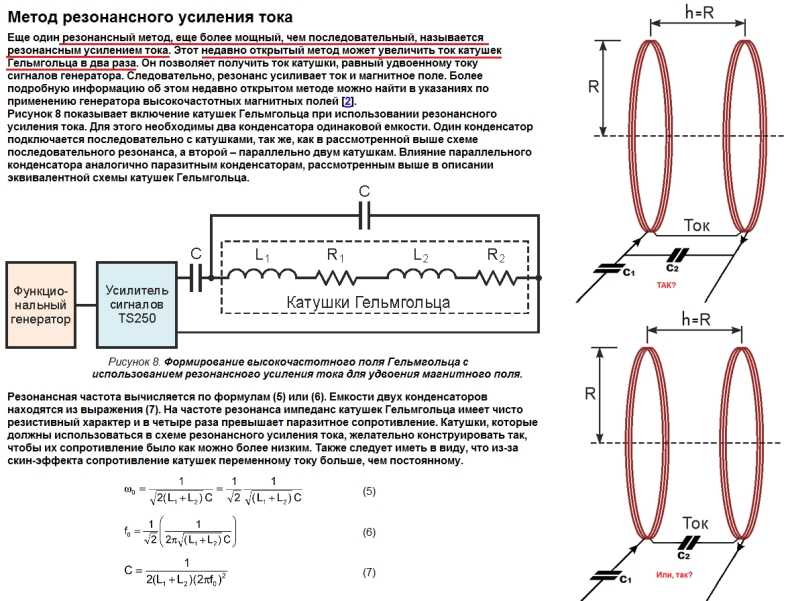
Агентство Reuters ранее проверяло утверждения о том, что современные «машины Райфа», которые позиционируются как основанные на оригинальном устройстве и теории Райфа, могут лечить рак (здесь). Другие источники также обращали внимание на тот факт, что современные машины Райфа и другие энергосберегающие технологии, которые могут показаться похожими, никогда не подвергались научным испытаниям и не демонстрировали «лечения» рака у людей (здесь), (здесь), (здесь) и (здесь). .
Хотя эксперименты Райфа по разрушению клеток в лаборатории хорошо задокументированы, по словам обозревателей, которые искали их (здесь), не было опубликовано никаких клинических испытаний или научных исследований воздействия оригинальных устройств Райфа на рак или другие заболевания у пациентов. и продавцу, продающему принадлежности для Rife Machine и исторические подборки документов и интервью, связанных с Райфом (rifevideos.com/library.html).
Доктор Дэвид Горски, профессор хирургии Медицинской школы государственного университета Уэйна, хирург и исследователь рака груди, сообщил агентству Рейтер по электронной почте, что, кроме анекдотов и отзывов, он не знает никаких доказательств, подтверждающих утверждения или работу Райфа.
Горски, который также является управляющим редактором веб-сайта Science-Based Medicine (sciencebasedmedicine.org/), добавил: «Я не видел доказательств того, что это когда-либо успешно тестировалось на каких-либо моделях рака».
Профессор музыки и композитор Энтони Холланд, цитируемый в видео, размещенном в Facebook, проводил эксперименты с бактериальными и раковыми клетками в лаборатории, которые Холланд описал в выступлении на TEDx в 2013 году (здесь). С тех пор TED пометил это видео с примечанием, в котором говорилось, что «оно, похоже, не соответствует рекомендациям TEDx по содержанию. Эффективность резонансно-частотной терапии не доказана научными исследованиями».
Холланд, который не ответил на запрос Reuters о комментариях, объяснил свой подход в выступлении на TEDx как воздействие на клетки энергией на двух разных частотах для достижения «11-й гармоники», которая вызывает изменение формы и поведения клеток. видны под микроскопом.
Теория Холланда, как он ее описал, отличалась от теории Райфа тем, что типы раковых клеток, которые он тестировал, были названы «уязвимыми» для этой энергии, поставляемой «в диапазоне частот от 100 000 до 300 000 герц», но Холланд не утверждал, что опухолевые клетки имели собственные уникальные частоты. Компания, созданная Холландом для продолжения работы (здесь), никогда не сообщала о дальнейших тестах, объясняющих значение наблюдаемых изменений формы клеток, или каких-либо результатах испытаний на животных или людях.
Компания, созданная Холландом для продолжения работы (здесь), никогда не сообщала о дальнейших тестах, объясняющих значение наблюдаемых изменений формы клеток, или каких-либо результатах испытаний на животных или людях.
Генеральный директор Histosonics доктор Кристин Гиббонс, которая в 2017 году также выступила на TEDx с докладом о технологии, которую она разрабатывала в то время (здесь), не делает никаких заявлений, связанных с Райфом, частотным резонансом или электромагнитными частотами клеток. в своем выступлении на TEDx или где-либо еще. Разработанный компанией метод разрушения опухолей, известный как гистотрипсия, не связан с электромагнитными частотами или резонансом. Он использует ультразвук для разрушения раковых клеток изнутри, воздействуя на них звуковыми волнами на частотах, которые вызывают своего рода турбулентность внутри клетки, известную как кавитация. По данным компании, устройство было протестировано как неинвазивная альтернатива хирургии или процедурам с выделением тепла и проходит клинические испытания в США и Европе.
«Энтузиасты Райфа часто ссылаются на технологии, которые имеют мало или вообще ничего общего с тем, что на самом деле утверждал Райф, или с тем, что на самом деле делали его устройства, например гистотрипсия», — отметил Горски.
«Идея «вибрации» и «частоты» в болезнях и здоровье — очень распространенная тема в альтернативной медицине, как и концепция энергетических полей…», — сказал Горски. «По сути, концепция манипулирования «энергетическими полями» или действия на основе «частоты» «вибраций» имеет тенденцию быть виталистической концепцией».
Тело действительно имеет «много электрохимической активности», добавил он, «Без этого ЭКГ, ЭЭГ и ЭМГ не работали бы». Однако, по словам Горски, такие устройства, как машины Райфа, «не измеряют повседневную электрическую активность, связанную с передачей нервных импульсов и активностью мышц, таких как сердечная мышца».
Вводит в заблуждение. Ройал Рэймонд Райф показал, что может разрушать клетки в лаборатории, и утверждал, что нашел потенциальное лекарство от рака и инфекционных заболеваний, но его теория и метод никогда не подвергались научной проверке и не доказали свою эффективность на людях.


 1 Струна
1 Струна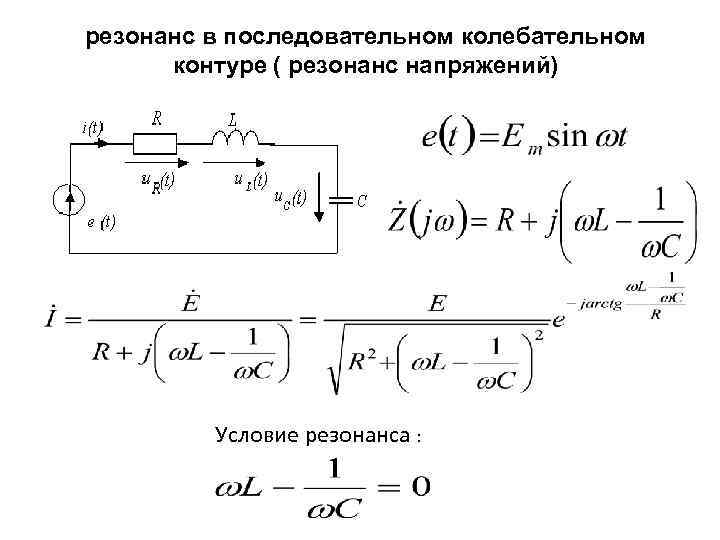 Большинство вибрирующих объектов имеют несколько резонансных частот.
Большинство вибрирующих объектов имеют несколько резонансных частот.