«Частотные характеристики электрических цепей» — конспект лекции

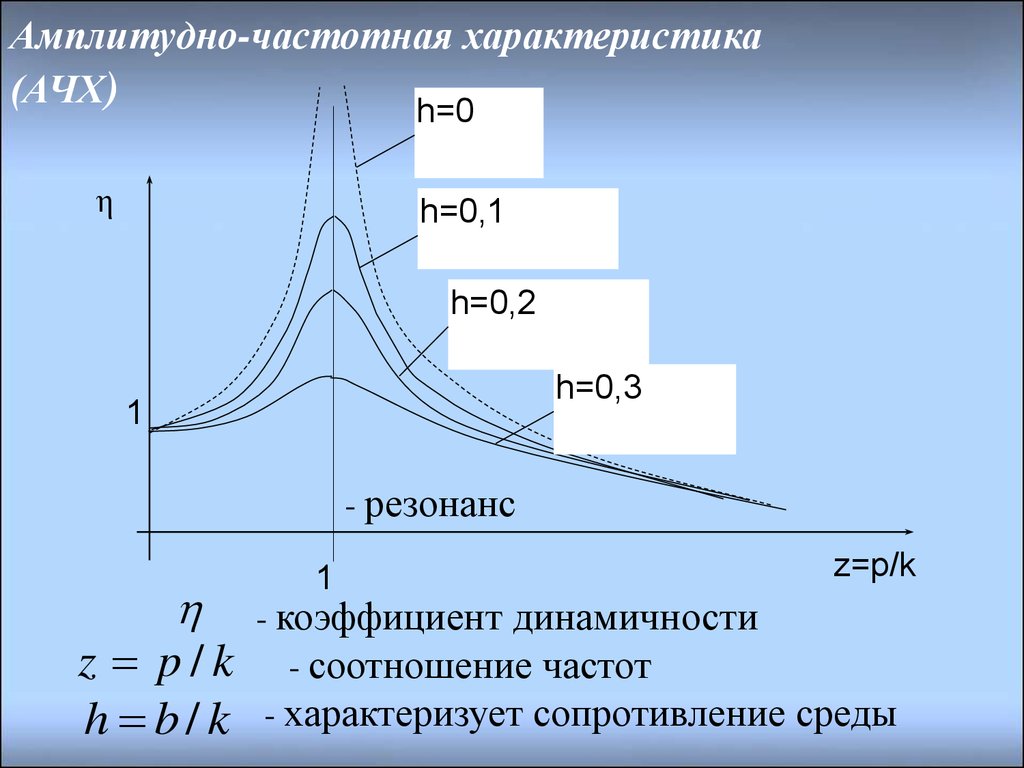
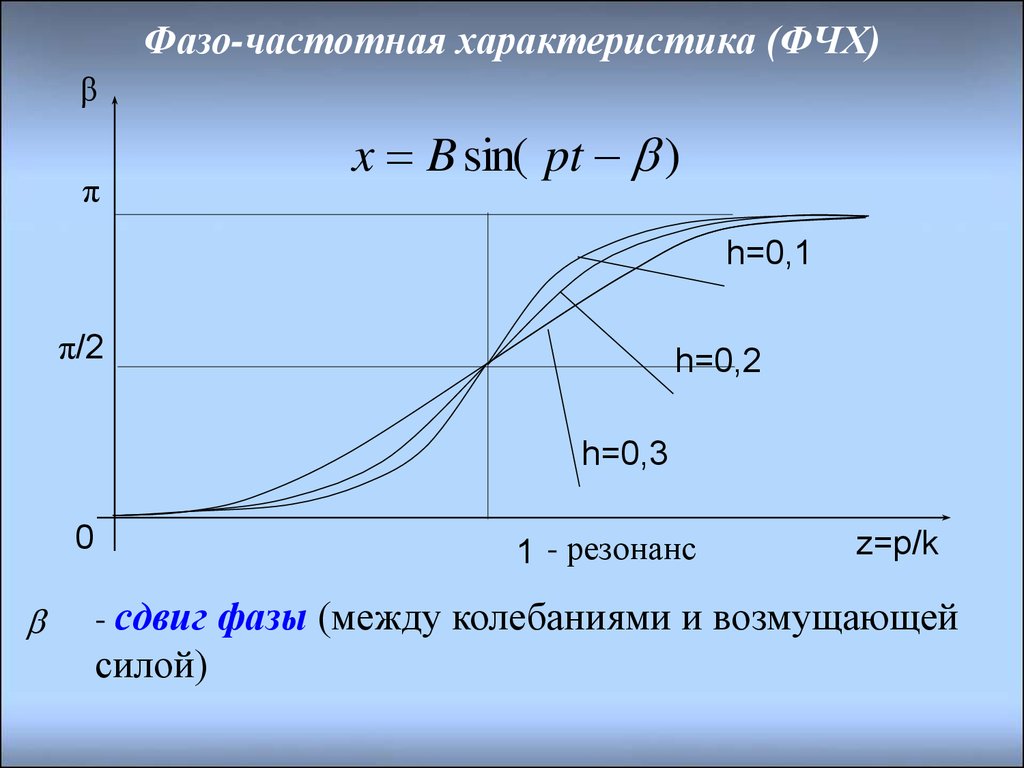
124 Лекция 15 ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ 1. Комплексные передаточные функции. 2. Логарифмические частотные характеристики. 3. Заключение. 1. Комплексные передаточные функции (комплексные частотные характеристики) Сопротивления индуктивных и емкостных элементов являются функциями частоты приложенного напряжения. Поэтому изменение частоты гармонических колебаний входного воздействия приводит к изменению амплитуды и начальной фазы реакции. Частотную зависимость отношений амплитуд реакции и входного воздействия называют амплитудно-частотной характеристикой, а зависимость разности начальных фаз реакции и входного воздействия от частоты – фазочастотной характеристикой. 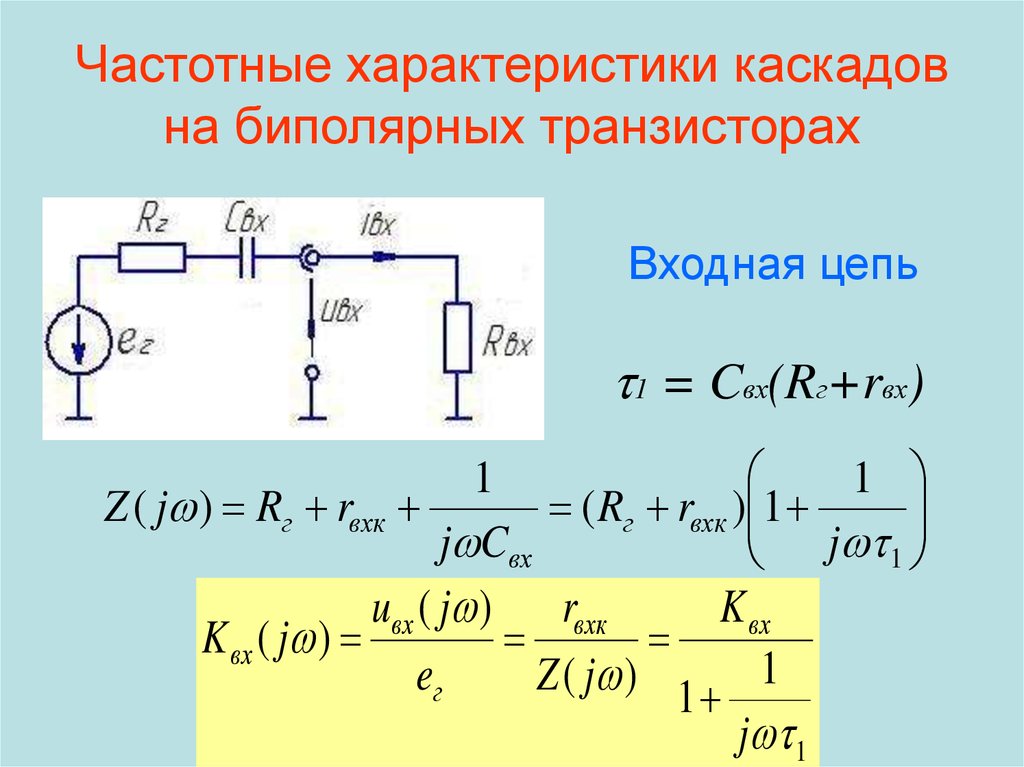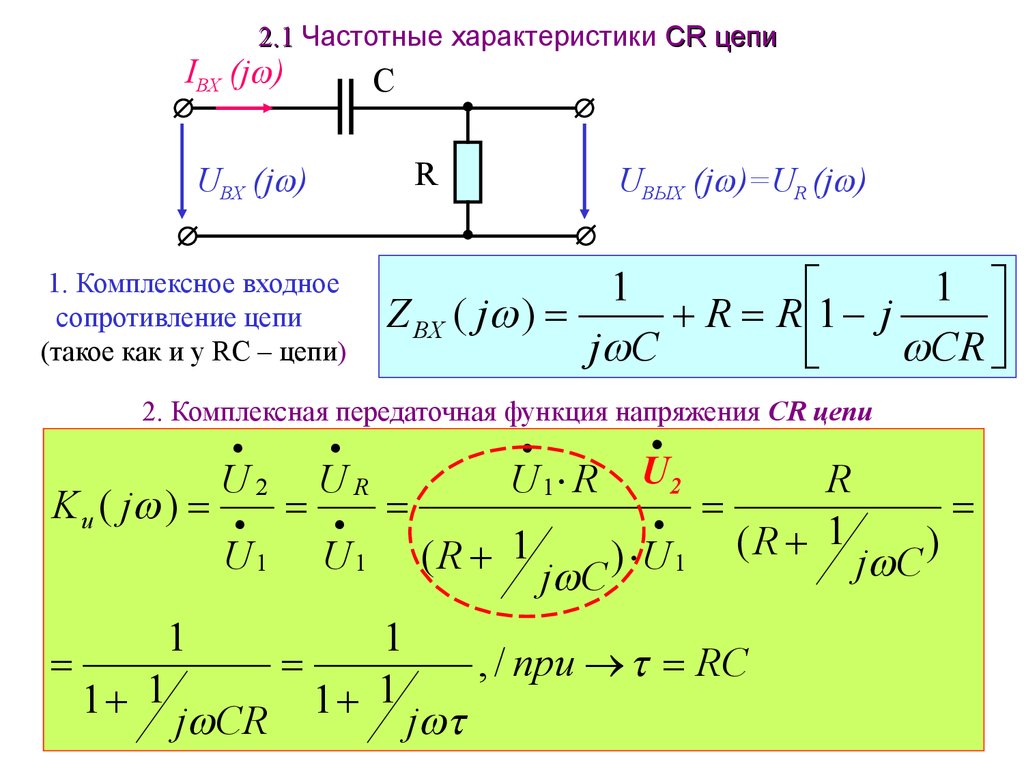Электронные цепи, которые служат для передачи сигналов, имеют обычно две пары внешних зажимов, т. е. являются четырехполюсниками (рис. 15.1). 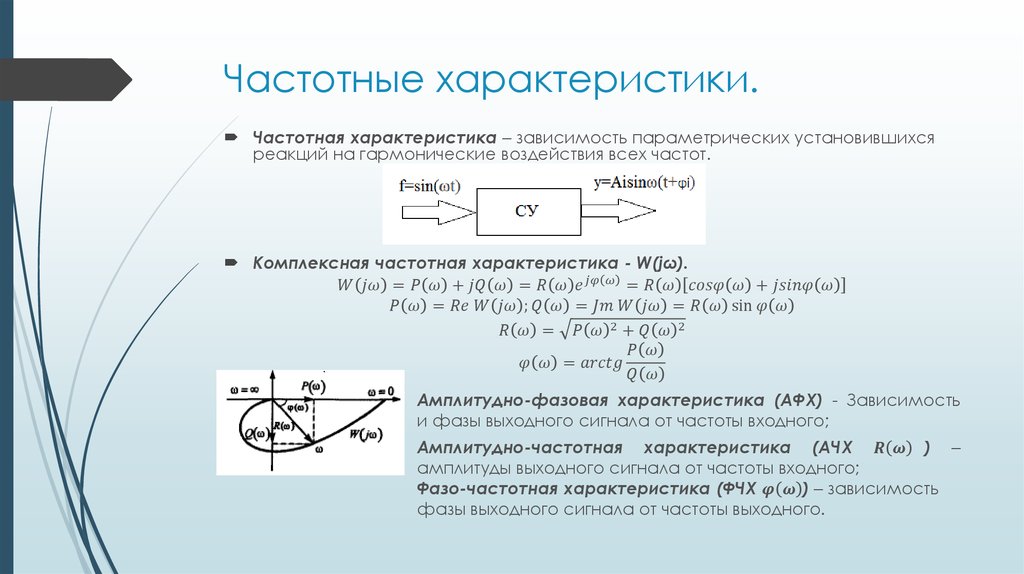Передающие свойства четырехполюсника характеризуют передаточными функциями. Комплексной передаточной функцией называют отношение комплексной амплитуды реакции к комплексной амплитуде входного воздействия.

Поскольку входным воздействием и реакцией могут быть ток или напряжение, различают четыре вида передаточных функций. Рис. 15.1 Функция передачи напряжений равна отношению напряжений на выходе и на входе цепи: 125 H U  j  U  . U  Здесь U  , U  – комплексы напряжений соответственно на входе и выходе цепи. Функция передачи тока равна отношению выходного и входного токов H I  j  Передаточным сопротивлением напряжения U  к входному току I : Z 21  j   I . I называют отношение выходного U 2 . I1 Передаточная проводимость – это отношение выходного тока I к напряжению на входе U  : Y21  j   I2 . U 1 Следует подчеркнуть несколько особенностей передаточных функций. Во-первых, для однозначного определения передаточной функции необходимо указать направления токов и напряжений. Во-вторых, следует помнить, что первый индекс соответствует выходу, а второй – входу. В-третьих, передаточное сопротивление Z  j не является величиной, обратной проводимости Y j.

Передаточные функции принимают комплексные значения при любых значениях частоты jω . Их можно представить в алгебраической форме через вещественные и мнимые части либо в показательной форме через модуль и аргумент. Представим комплексную передаточную функцию в показательной форме записи: H  j H  j e j . Модуль комплексной передаточной функции определяет амплитудночастотную характеристику, а аргумент – фазочастотную характеристику. Запишем комплексную амплитуду входного воздействия в показательной форме U m  U me j . 126 Комплексная амплитуда реакции U m 2  H  j U m1  H  j  e j  U m1e j . 1 Амплитуда реакции равна произведению амплитуды входного воздействия на модуль комплексной передаточной функции: U m   H  j U m . Начальная фаза реакции равна сумме начальной фазы входного воздействия и значения фазочастотной характеристики на частоте :  2   1     . Поскольку H  jω – комплексная величина, ее можно изобразить вектором на комплексной плоскости. Длина вектора равна значению АЧХ на частоте , а угол, который образует вектор с вещественной положительной полуосью – значению ФЧХ. С изменением частоты конец вектора опишет кривую, которую называют годографом комплексной передаточной функции или амплитудно-фазовой частотной характеристикой (АФЧХ). Годограф H  jω строят при изменении частоты  от 0 до ω   . Функции цепи можно найти как отношение определителей и алгебраических дополнений матриц коэффициентов системы узловых или контурных уравнений. В качестве примера рассмотрим четырехполюсную цепь, на входе которой действует источник тока (рис. 15.2). Рис. 15.2 Входным является узел 1, а выходным – узел 2. Напряжения входного и выходного узлов:    D   D   U  ; U  . D D 127 Здесь D – главный определитель системы узловых уравнений, Dij – минор, полученный вычеркиванием i-й строки и j-го столбца. Комплексная передаточная функция   U    D . H  j   U  D В общем случае, если входным является узел номером i, а выходным – узел j, передаточная функция определяется формулой i j U j   Di j . H  j   U i Dii (15.1) Элементы матрицы контурных или узловых уравнений являются рациональными функциями частоты jω . Поскольку суммы, произведения и разности рациональных функций также рациональные функции, комплексные функции линейных цепей являются дробно-рациональными функциями, т. е. отношением полиномов от jω . Все коэффициенты в числителе и знаменателе функции цепи – вещественные числа. Порядок функции цепи равен суммарному числу реактивных элементов. Пример. Определить комплексную передаточную функцию интегрирующей RC-цепи, показанной на рис. 15.3. Рис. 15.3 Комплексная передаточная функция представляет отношение комплексов напряжения на входе и выходе цепи: H  j  U    . U  jCR   Амплитудно-частотная характеристика 128 H  j   1  CR  2 1 . Фазочастотная характеристика     arg H  j   arctg CR . Графики АЧХ и ФЧХ анализируемой цепи показаны на рис. 15.4, а, б. а б Рис. 15.4 Амплитудно-частотная характеристика RC-цепи монотонно убывает с ростом частоты и стремится к нулю при ω   .

Фазочастотная характеристика π также монотонно убывает, изменяясь от 0 при ω  0 до  при ω   . 2 Рис. 15.5 На рис. 15.5 показан график амлитудно-фазовой характеристики цепи. Годограф H  jω представляет кривую, начинающуюся в точке с координатами (1, 0) и заканчивающуюся в точке (0, 0). 2. Логарифмические частотные характеристики В технике связи, теории автоматического регулирования широко используются устройства, у которых значения амплитудно-частотных характе- 129 ристик изменяются в очень широких пределах. Примером являются резонансные контуры, используемые в радиотехнике, электрические фильтры, усилители и т. д. В таких случаях удобнее оперировать логарифмическими частотными характеристиками (ЛАХ), которые пропорциональны логарифму от соответствующей безразмерной АЧХ. Обычно используют аббревиатуры ЛАХ или ЛАЧХ. ЛАХ принято оценивать в децибелах (дБ): Aω  20 lg H ω , где lg – логарифм при основании 10. Переход к логарифмической шкале позволяет существенно «сжать» пределы изменения амплитудно-частотных характеристик. Усилению сигнала в два раза соответствует приращение Aω на 6 дБ; усилению в 10 раз соответствует значение Aω, равное 20 дБ. Величину Aω называют логарифмическим усилением или усилением в децибелах. Усилению сигнала соответствуют положительные значения Aω, ослаблению – отрицательные значения логарифмического усиления. При исследовании ЛАЧХ в широком диапазоне частот изменение частоты также целесообразно оценивать в логарифмических единицах. Отношение частот двух гармонических колебаний называют интервалом, а интервал, соответствующий удвоению частоты, – октавой. Например, изменению частоты в четыре раза соответствует интервал в две октавы, а восьмикратному увеличению частоты – в три октавы. Число октав N  может быть приближенно найдено из формулы N   . lg  .  Интервал, соответствующий изменению частоты в десять раз, называют декадой. Число декад определяется формулой N  lg  .  Изменению частоты в 10 раз соответствует одна декада, в 100 раз – две декады и т. д. Использование логарифмического масштаба позволяет рассмотреть изменение частотных характеристик в широком диапазоне на небольшом графике. Кроме того, умножение передаточных функций отдельных звеньев сложной цепи заменяется суммированием ЛАХ. 3. Заключение 130 1. 2. 3. Комплексной передаточной функцией электрической цепи называют отношение комплексной амплитуды реакции к комплексной амплитуде входного воздействия. Частотную зависимость отношений амплитуд реакции и входного воздействия называют амплитудно-частотной характеристикой. Зависимость разности начальных фаз реакции и входного воздействия от частоты называют фазочастотной характеристикой.

Параметр «Частотная характеристика»

Время публикации:15:46/

31.01.2022

О каком бы Hi-Fi устройстве не шла речь (звукоснимателе, усилителе, колонках), наиболее важной его характеристикой будет диапазон воспроизводимых частот. Если речь идет об акустике, то предпочтительнее выбрать колонки с диапазоном от 20 Гц до 25 кГц, вместо 45 Гц-18 кГц. Однако правда заключается в том, что без учета некоторых других данных эти цифры мало что говорят о качестве звучания Hi-Fi техники.

Итак, читаем параметр «Частотная характеристика» правильно.

Здесь слышу, здесь не слышу

Считается, что человеческий слух способен воспринимать частоты от 20 Гц до 20 кГц (20 000 Гц). Хотя на практике этот диапазон обычно заметно более узкий. Получается, что и колонки, воспроизводящие звук в этом диапазоне, будут самым лучшими? И да, и нет. На самом деле очень важно, чтобы при прослушивании музыки уровень громкости звука во всем этом частотном диапазоне был точно таким же, как и при ее записи. Не случайно данную характеристику называют амплитудно-частотной (АЧХ), отмечая важность того, какую амплитуду имеет сигнал на различных частотах.

Например, равномерность частотной характеристики акустики проверяют следующим образом. Колонки помещают в безэховую камеру, у которой нет собственных резонансов. Затем на акустику с усилителя подается специальный свип-тон (или сигнал «качающейся частоты»). Его частота меняется в заданном интервале — например, от 20 Гц до 20 кГц — но уровень остается постоянным. С помощью помещенного в ту же камеру микрофона измеряется сигнал, который воспроизводит колонка.

Если бы мы жили в идеальном мире, измеренная частотная характеристика колонки была бы такой, как на рис 1.

Рис. 1

Увы, в реальности это невозможно. На самом деле частотная характеристика колонок будет похожа на ту, которая представлена на фото 2.

Рис. 2

Здесь мы видим изменение амплитуды сигнала на различных частотах. Причин этому может быть много — это и характеристики динамиков, и настройка разделительного фильтра, и взаимодействие корпуса и динамиков.

Равномерная частотная характеристика колонки вовсе не означает, что при прослушивании музыки сигналы всех частот через нее будут звучать одинаково. Это значит, что каждая композиция будет звучать именно так, как она была записана, с тем же уровнем сигнала на различных частотах. Поэтому про акустику, которая имеет частотную характеристику, максимально приближенную к линейной, говорят, что она звучит нейтрально и не вносит в звучание музыки собственной окраски.

Все на уровне

Частотная характеристика в спецификациях аудиоустройств обычно сопровождается дополнительным параметром, на который многие меломаны не обращают внимание. А зря! Именно он показывает, насколько точно (близко к оригиналу) будет звучать музыка через колонки. Например, для акустики этот параметр часто представлен как «+/- 3dB». Это значит, что частотная характеристика колонки в указанном частотном диапазоне может отклоняться в вверх или вниз на уровень 3 децибела от центральной. Значение именно в 3 дБ было принято потому, что оно уже позволяет отчетливо определить на слух изменения в уровне сигнала. В то же время изменение (спад) сигнала на какой-либо частоте до 9 дБ сделает его практически неслышимым на фоне общего микса. По современным стандартам неравномерность 3 дБ для частотной характеристики в аудио является очень большой. Например, у усилителей или ЦАП обычно можно видеть ее значение в +/- 0,5 дБ. Однако для электромеханического устройства, которым по сути являются динамики колонок, звукосниматели проигрывателей винила, такой показатель является приемлемым.

Измерение акустики Triangle в безэховой камере

И вот с учетом этого дополнения и можно оценивать частотные характеристики разной акустики. Например, у одной модели показатель частотной характеристики от 40 Гц до 25 кГц указан для значения +/- 1 дБ, а у другой +/- 3 дБ. Соответственно, первая (теоретически) будет звучать более натурально и с более глубоким басом, а также лучшими ВЧ. А если параметры колонки указаны как 20 Гц до 25 кГц с неравномерностью +/- 6 дБ, то она, скорее всего, уступит по звучанию той, которая имеет более скромные 40 Гц — 20 кГц , но по уровню +/- 1,5 дБ. Если же у какой-либо модели этот параметр вообще не оговаривается в спецификациях — есть повод задуматься.

Важное дополнение

Однако на практике и неравномерность частотной характеристики, выраженная в цифрах спецификаций, не дает полной картины о качестве звучания той или иной модели. Например, на рисунках 3 и 4 показаны АЧХ двух колонок, каждая из которых имеет на первый взгляд одинаковую неравномерность характеристики в +/- 3 дБ.

Рис. 3

Рис. 4

Однако неравномерность колонки с рисунка 3 имеет плавный и вполне приемлемый для восприятия характер, в то время как «пила» на рисунке 4 сделает звучание музыки грубым и ненатуральным.

Опираться при выборе Hi-Fi-техники только на ее измеренные характеристики так же опасно, как и полагаться только на субъективные тесты ее звучания. Колонка, которая будет отлично звучать на музыке определенного жанра, на самом деле может иметь не самые лучшие технические характеристики. Просто ту окраску, которую она внесет в звучание композиций, наш слух воспримет как «благозвучную». Но если ваши музыкальные пристрастия изменятся, колонка уже может им и не соответствовать. Измерения позволяют инженерам настроить работу акустики по определенным стандартам, но затем последует ее тонкая настройка с помощью многочисленных сеансов прослушивания. И только после этого колонки поступят в серийное производство, чтобы в дальнейших радовать меломанов не только точным, но и музыкальным звуком.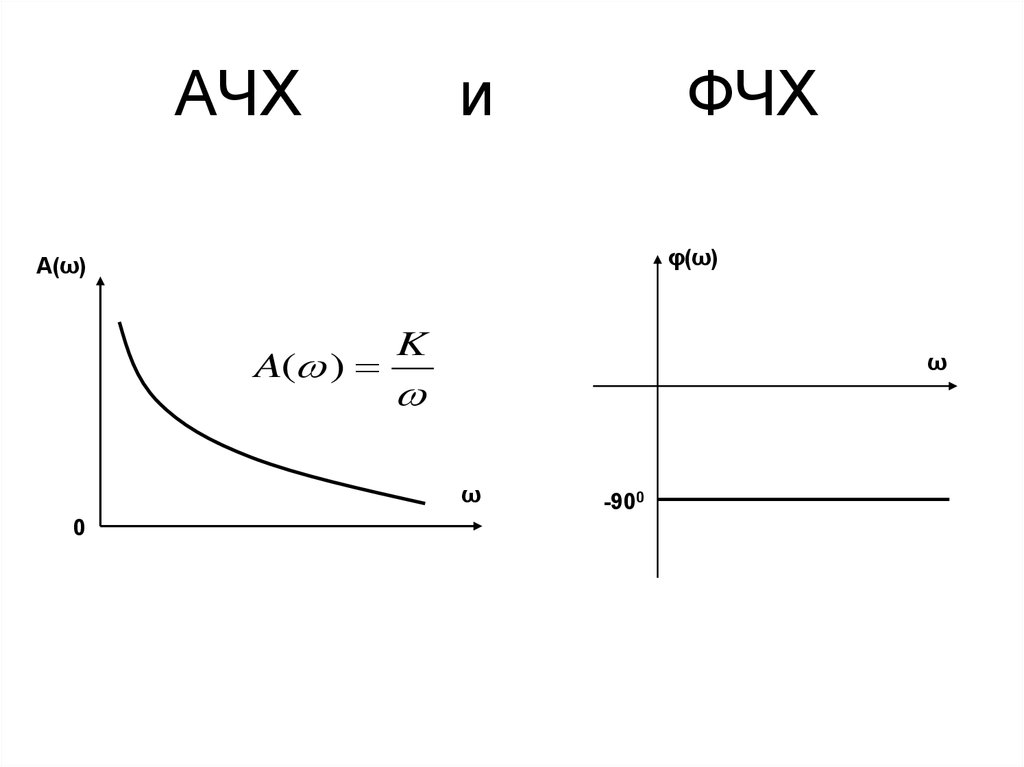

Частотные характеристики сигналов и приборов: значение для исследований биологической обратной связи ЭМГ

Обзор

. 1990 декабрь; 15 (4): 335-52.

дои: 10.1007/BF01000027.

П.А. Матье ¹ , С. Дж. Салливан

принадлежность

• ¹ Центр исследований, Факультет медицины, Университет Монреаля, Квебек, Канада.

• PMID: 2275944
• DOI: 10.1007/BF01000027

Обзор

P A Mathieu et al. Саморегуляция биологической обратной связи. 1990 Декабрь

. 1990 декабрь; 15 (4): 335-52.

дои: 10.1007/BF01000027.

Авторы

П. А. Матье ¹ , С. Дж. Салливан

принадлежность

• ¹ Центр исследований, Факультет медицины, Университет Монреаля, Квебек, Канада.

• PMID: 2275944
• DOI: 10.1007/BF01000027

Абстрактный

Сигналы можно анализировать как во временной, так и в частотной области. Во временной области анализ состоит из манипулирования и измерения одной или нескольких характеристик сигнала, которые могут меняться со временем. Можно, например, исправить сигнал, отфильтровать его, вычислить его среднее значение, отобразить гистограмму его амплитуды и так далее. Частотный анализ менее понятен, потому что он требует длительной математической обработки, которую легче всего выполнить с помощью компьютера. Однако он дает эксклюзивную информацию о сигнале. Например, когда известна частотная составляющая сигнала, легко указать, какими характеристиками должен обладать усилитель, чтобы усиливать сигнал без искажений, или установить частоты среза фильтров для устранения шума. Кроме того, во многих случаях частотные спектры легче интерпретировать, чем исходные необработанные данные. Так обстоит дело с ЭМГ, где случайный аспект сигнала делает некоторую форму обработки (например, исправление, фильтрацию и т. д.) необходимой, но не всегда столь значимой, как хотелось бы. Таким образом, мы представляем здесь основные характеристики частотного анализа и обсуждаем его полезность при анализе сигналов ЭМГ и его применение для биологической обратной связи, клинической практики и исследований.

Похожие статьи

• Методология аппаратуры для записи и обратной связи поверхностных электромиографических (SEMG) сигналов.

  Шерман Р.А. Шерман РА. Приложение «Психофизиология биологической обратной связи». 2003 июнь; 28 (2): 107–19. doi: 10.1023/a:1023806508040. Приложение «Психофизиология биологической обратной связи». 2003. PMID: 12827989 Обзор.

• Оценка и применение амплитуды ЭМГ при динамических сокращениях.

  Клэнси Э.А., Бушар С., Ранкур Д. Клэнси Э.А. и др. IEEE Eng Med Biol Mag. 2001 ноябрь-декабрь; 20(6):47-54. дои: 10.1109/51.982275. IEEE Eng Med Biol Mag. 2001. PMID: 11838258

• Цифровая фильтрация ЭМГ-сигналов.

  Зшорлич В.Р. Зшорлич ВР. Электромиогр Клин Нейрофизиол. 1989 марта; 29(2):81-6. Электромиогр Клин Нейрофизиол. 1989. PMID: 2707144

• Разделение электрокардиографических сигналов от электромиографических с помощью динамической фильтрации.

  Христов И., Райкова Р., Ангелова С. Христов И. и др. мед. инж. физ. 2018 июль; 57: 1-10. doi: 10.1016/j.medengphy.2018.04.007. Epub 2018 24 апр. мед. инж. физ. 2018. PMID: 29699890

• [Использование E.M.G. в стоматологических исследованиях и клинической практике.

  Друкас Б., Антониу Д. Друкас Б. и др. Стоматология (Афины). 1989 г., июль-август; 46(4):233-44. Стоматология (Афины). 1989. PMID: 2701199 Обзор. греческий, современный.

Посмотреть все похожие статьи

Рекомендации

1. 1. Электромиогр Клин Нейрофизиол. 1979 январь-март;19(1-2):183-97 — пабмед
2. 1. Eur J Appl Physiol Occup Physiol. 1978 г., 15 декабря; 40 (1): 45–55. — пабмед
3. 1. Eur J Appl Physiol Occup Physiol. 1982;48(2):147-56 — пабмед
4. 1. Am J Phys Med. 1982 Октябрь; 61 (5): 244-54 — пабмед
5. 1. J Appl Physiol Respir Environ Exerc Physiol. 1979 янв; 46(1):1-7 — пабмед

Типы публикаций

термины MeSH

Характеристики частоты базового стока выбранных водотоков Пенсильвании

Авторы: К. Э. Уайт и Р. А. Слото

https://doi.org/10.3133/wri904160

Твит

Ссылки

• Отчет: ПДФ
• Пластина: Пластина 1 (pdf)
• Индексная страница NGMDB: Индексная страница базы данных национальных геологических карт
• Скачать ссылку как: РИС | Дублин Ядро

Аннотация

Гидрографы речного стока 309 станций речного стока в Пенсильвании были проанализированы с использованием трех компьютеризированных эмпирических методов — локального минимума, фиксированного интервала и скользящего интервала — для разделения компонентов грунтовых вод и поверхностного стока. Для каждой станции были определены 2-, 5-, 10- и 25-летние интервалы повторяемости базового стока. 50- и 100-летние интервалы повторяемости определены для станций с минимумом 25- и 50-летней регистрации соответственно. Все активные и неактивные речные станции Пенсильвании с непрерывной записью с 10 или более годами регистрации по водному году 19.86 были проанализированы. Также были включены станции на реке Делавэр в Нью-Йорке и Нью-Джерси. Компьютерный анализ гидрографа обеспечивает согласованность результатов, устраняя субъективность, присущую ручному анализу, и значительно сокращает время, необходимое для проведения анализа. Оценки 25-летнего интервала повторяемости базового расхода, сделанные с использованием метода локального минимума, который дает наиболее консервативную оценку, колеблются от 0,069 до 0,888 миллиона галлонов в день на квадратную милю. Базовые стоки, рассчитанные с использованием трех компьютерных методов, хорошо сравнимы с опубликованными базовыми стоками, оцененными с использованием ручных методов для трех исследований на юго-востоке Пенсильвании.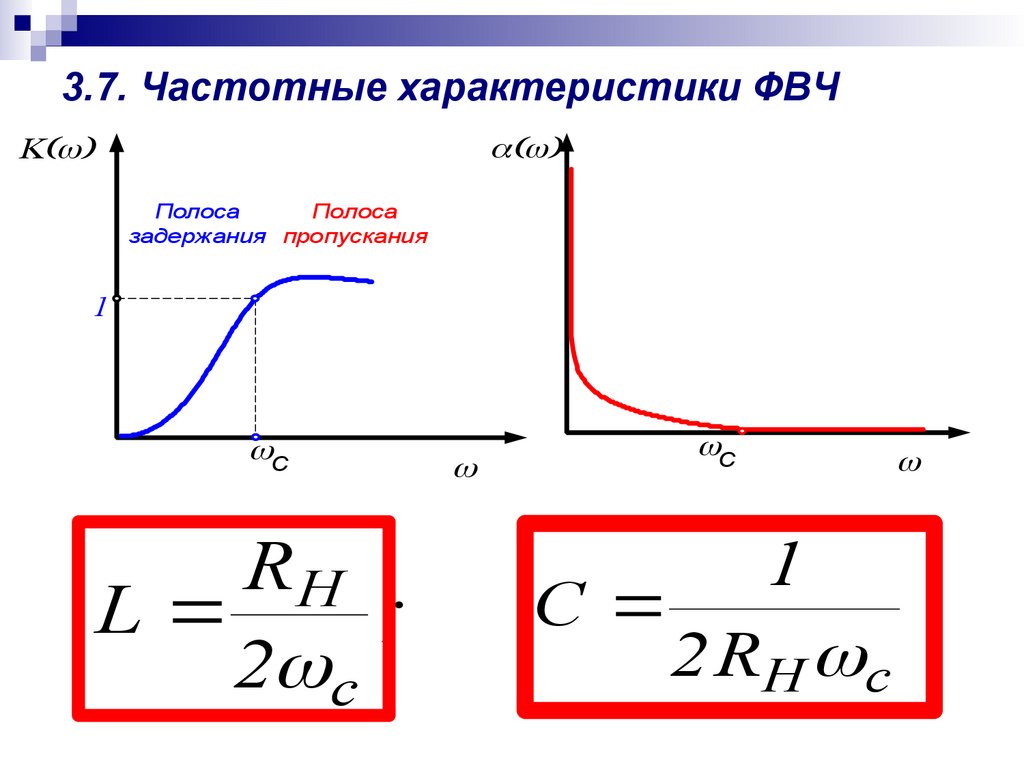 Приведены примеры влияния геологии, климата, регулирования и урбанизации на базовый сток.

Зона исследования

Дополнительная информация о публикации

Тип публикации	Отчет
Подтип публикации	Пронумерованная серия USGS
Титул	Базовые частотные характеристики отдельных водотоков Пенсильвании
Название серии	Отчет об исследованиях водных ресурсов
Серийный номер	90-4160
DOI	10.3133/wri904160
Год публикации	1990
Язык	Английский
Издатель	Геологическая служба США
Предоставляющий(ие) офис(а)	Центр водных наук Пенсильвании
Описание	vi, 67 стр.
Страна	США
Государственный	Пенсильвания
Аналитические метрики Google	Страница показателей

Часть или весь этот отчет представлен в формате Portable Document Format (PDF). Для достижения наилучших результатов при просмотре и печати PDF-документов рекомендуется загрузить документы на свой компьютер и откройте их с помощью Adobe Reader. PDF-документы, открытые с вашего браузер может не отображать или печатать должным образом. Загрузите последнюю версию Adobe Reader бесплатно. Больше информации информацию о просмотре, загрузке и печати файлов отчетов можно найти в разделе часто задаваемых вопросов о проблемах с загрузкой.