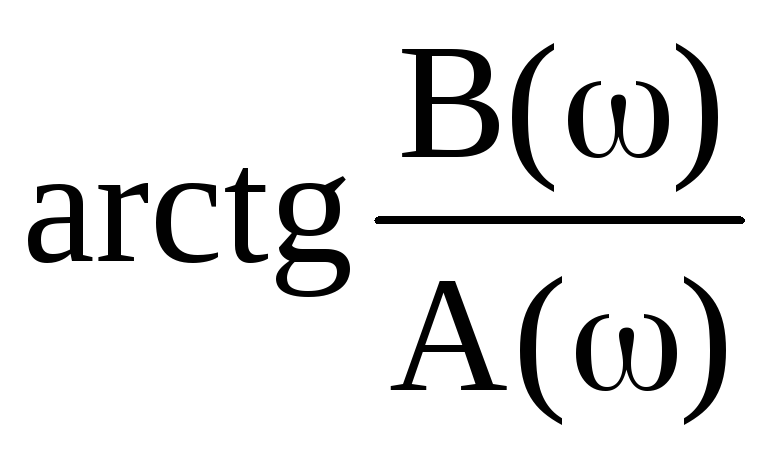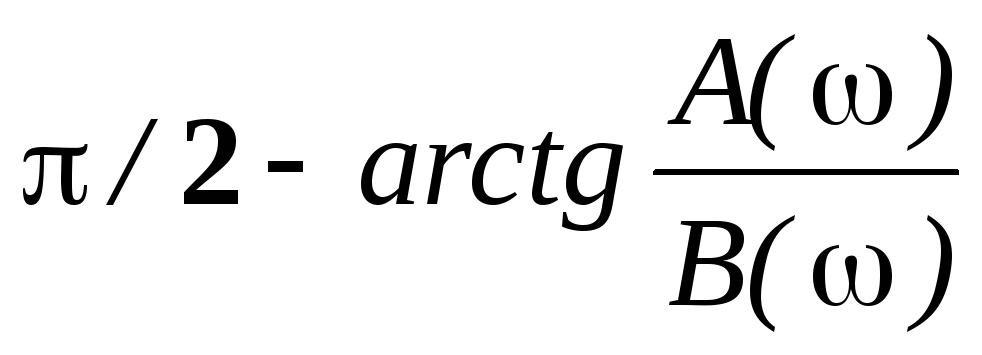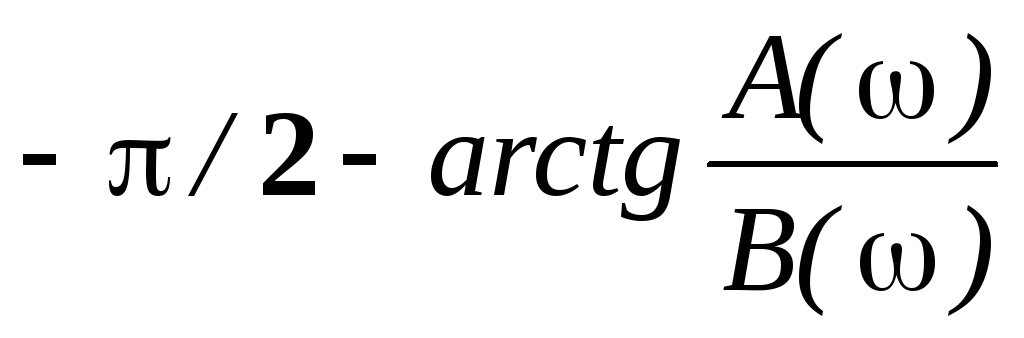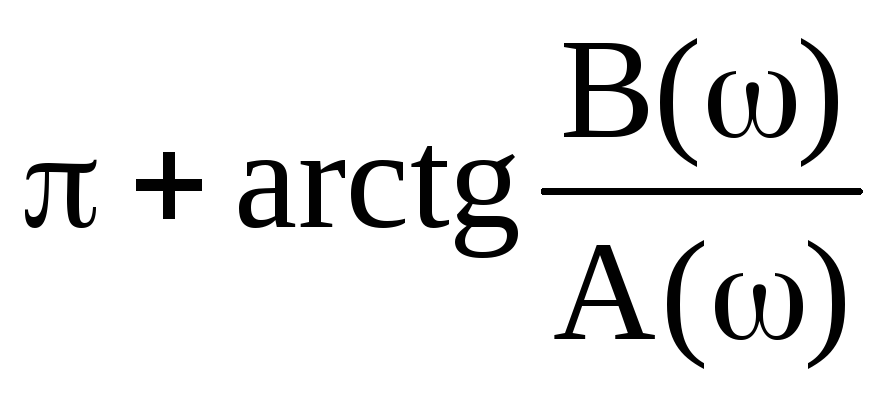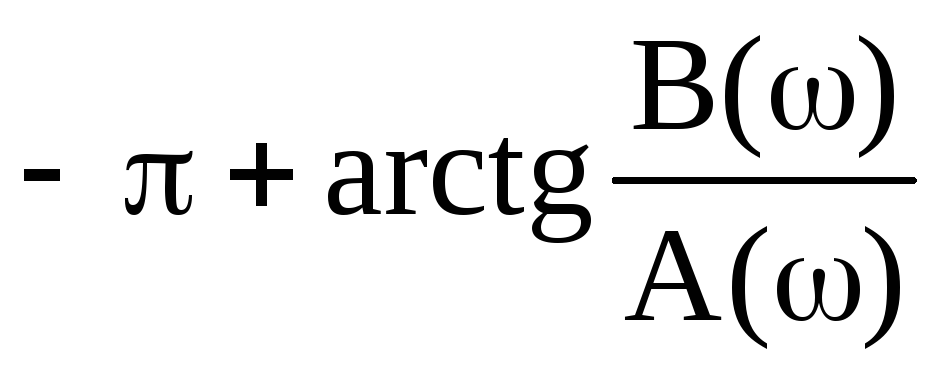Комплексная частотная характеристика

.

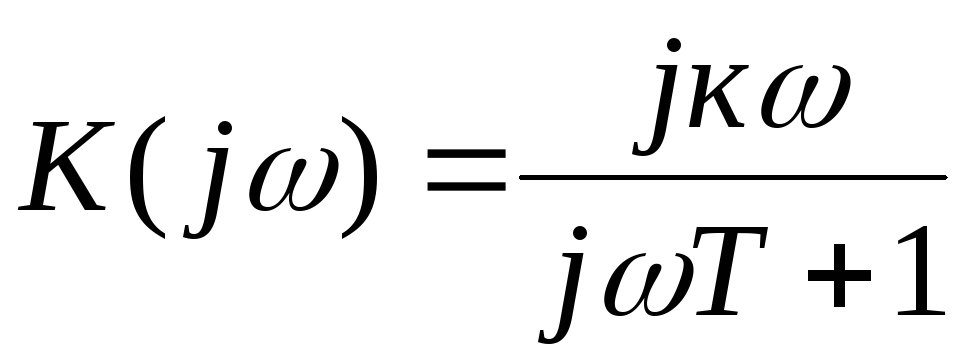Действительная и мнимая частотные характеристики

, .

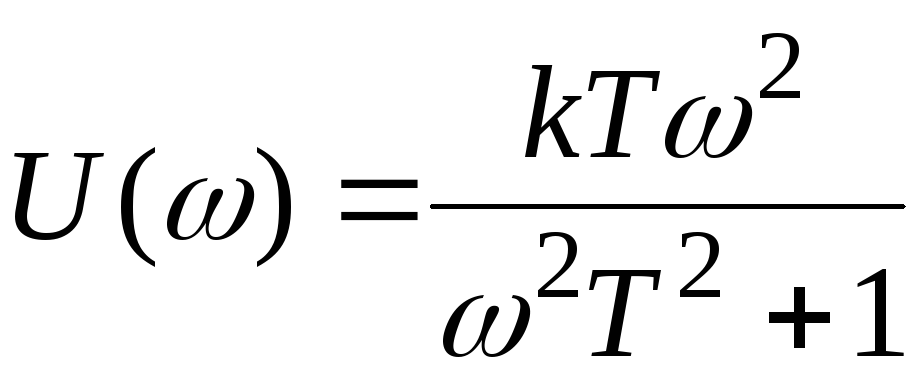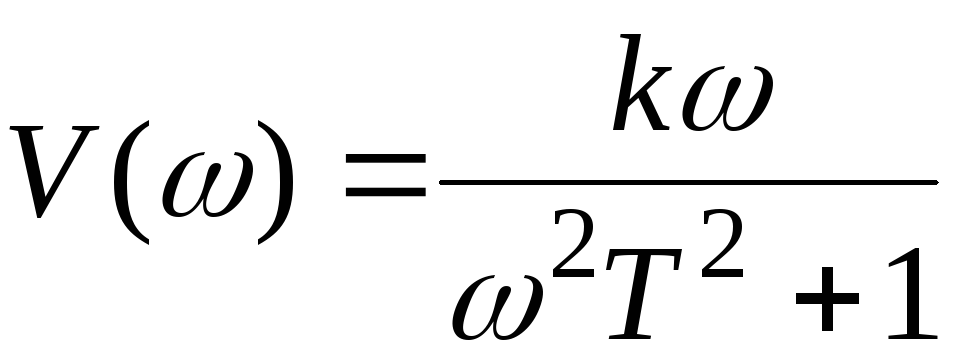Амплитудная частотная характеристика

.

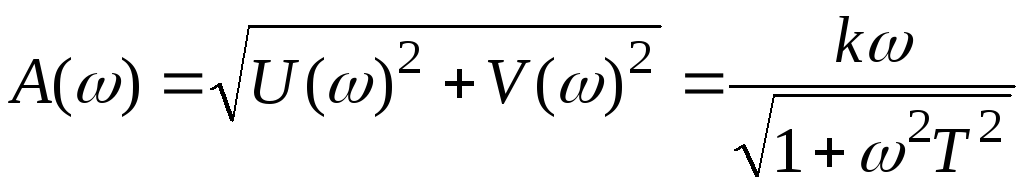У идеального дифференцирующего звена с увеличением  амплитуда линейно возрастает до ∞ . У реального дифференцирующего звена амплитуда возрастает монотонно, стремясь к пределу k / T .

Фазовая частотная характеристика

 () = arctg .

При  = 0,  = 90 , как у идеального дифференцирующего звена. Но мере увеличения частоты опережение по фазе уменьшается до нуля.

Логарифмическая амплитудная частотная характеристика

.

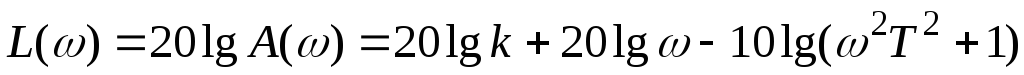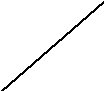
Найдем асимптотические прямые логарифмической амплитудной частотной характеристики. В области < 1 . В области > 1L₂= 20lg(k/T)

Прямая L

₁ пересекает ординату в точке с координатами lg = 0 , L₁ = 20 lg k , абсциссу – в точке с координатами lg = lg(1 / k) , L₁ = 0 . Cледует учесть, что k  1 и потому lg(1 / k) – число отрицательное. Прямая L₂ параллельна оси абсцисс, пересекает ординату в точке lg = 0, L₂ = 20lg(k /T) . Прямые L₁ и L₂ пересекаются в точке с абсциссой lg = lg(1 /T) . График представлен на рис. 3.6.

L()

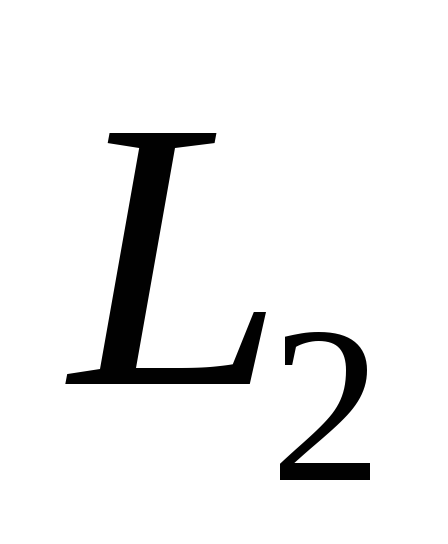
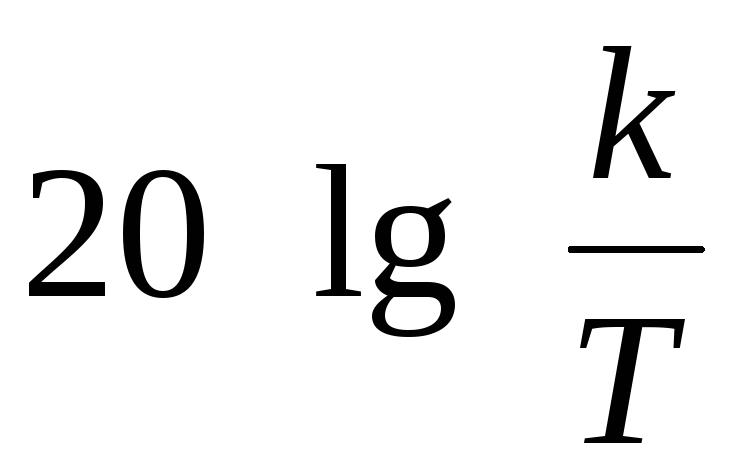
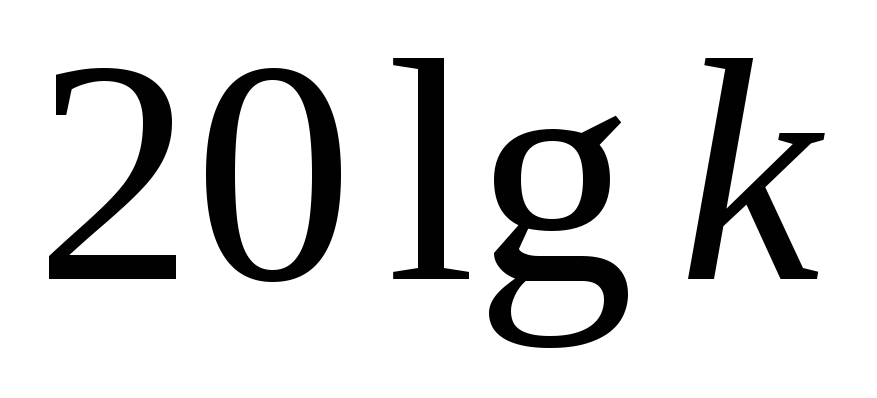
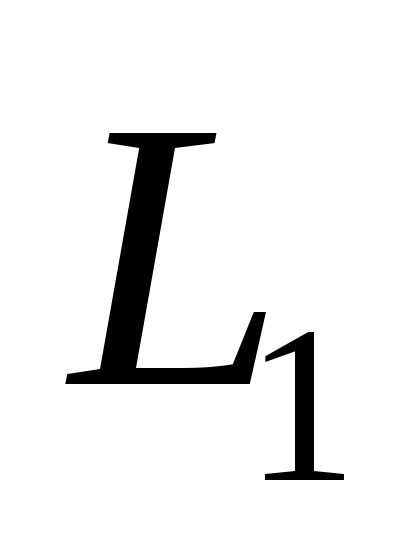
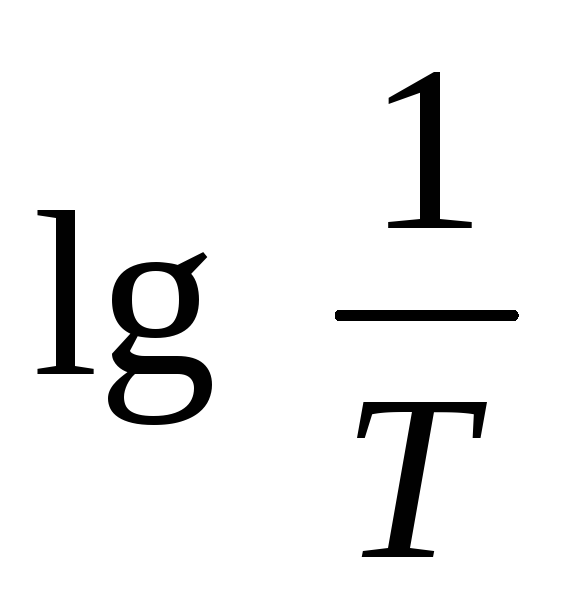
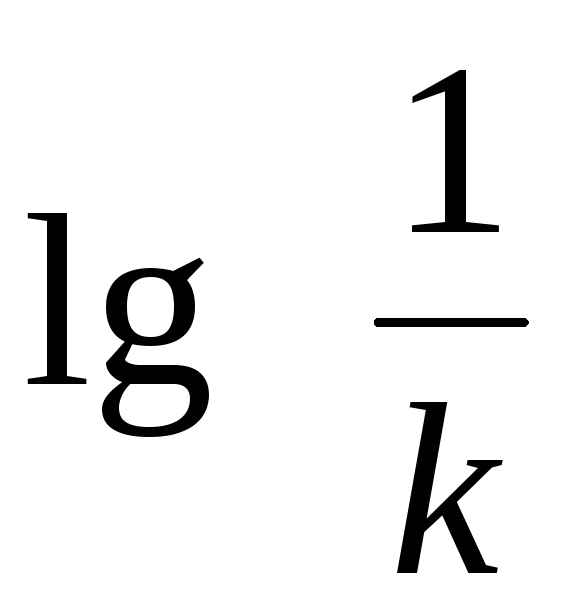
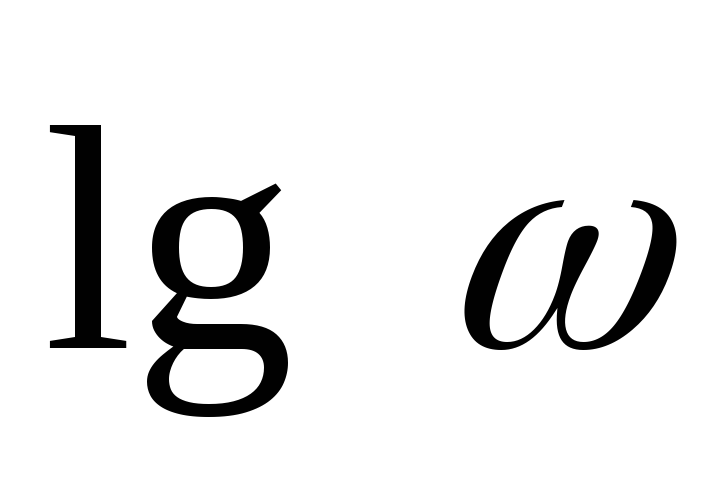0

Рис. 3.6. Асимптоты ЛАЧХ

реального дифференцирующего звена.

Чтобы найти переходную функцию, в операторном уравнении заменим X(p) на 1/ p:

.

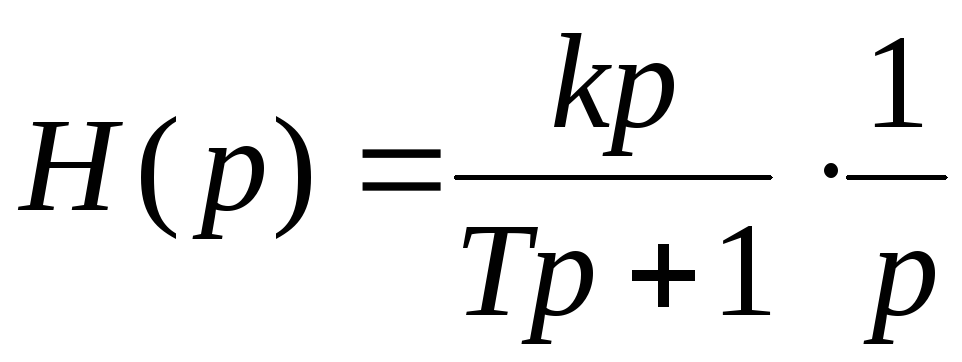Таблица преобразований Лапласа указывает, что

.

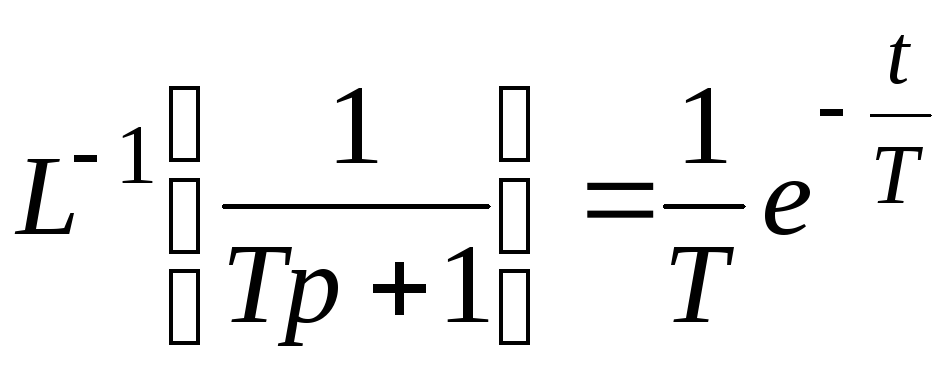
Значит, переходная функция имеет вид

.

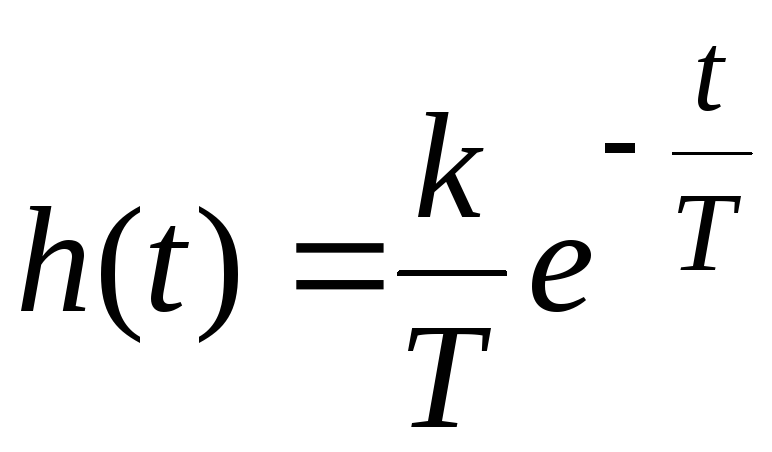В момент t = 0 h(0) = k /T. По мере увеличения t, функция h (t) экспоненциально уменьшается до нуля. Напомним: в идеальном дифференцирующем звене переходная функция имеет вид импульса.

5. Колебательное звено.

Математической моделью колебательного звена является линейное дифференциальное уравнение второго порядка с постоянными коэффициентами

, (3.7)

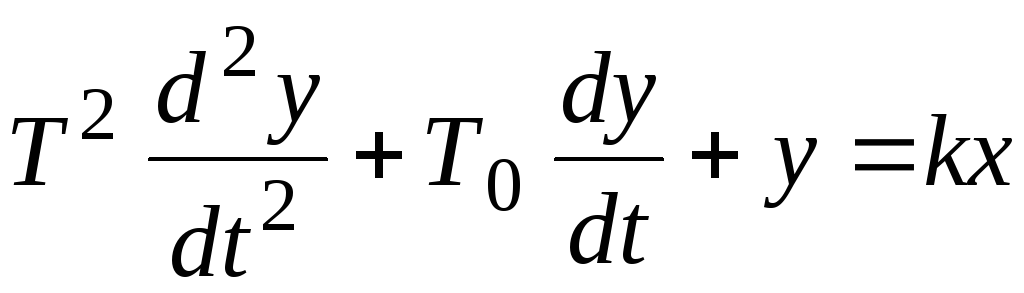
при условии .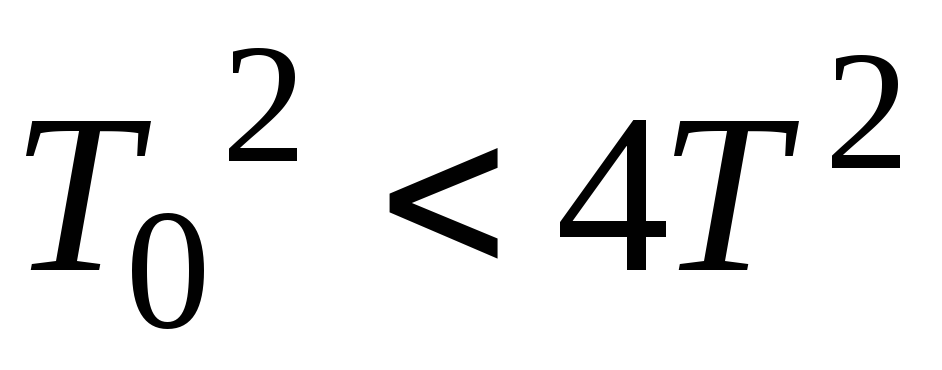

Колебательные процессы характеризуются двумя важными параметрами: коэффициентом затухания  и резонансной частотой ω₀ . Они выражаются через постоянные времени уравнения (3.7):  = Т₀ / 2Т , ω₀ = 1 / Т . Если ввести  в уравнение (3.7) , оно получает вид, более удобный для исследования колебательного процесса:

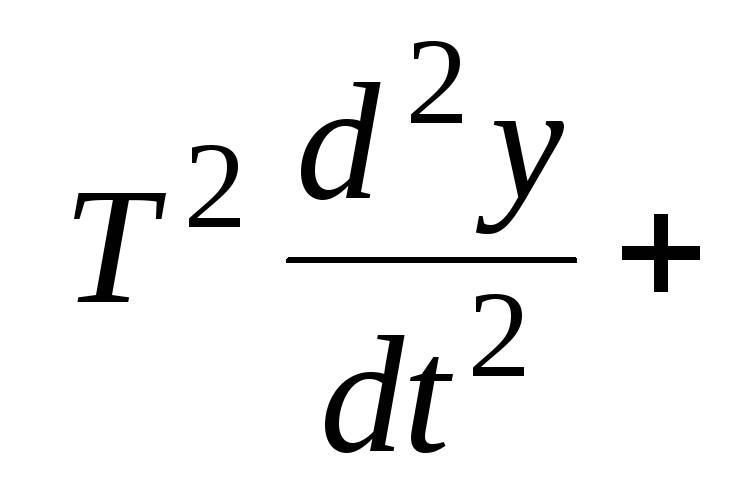
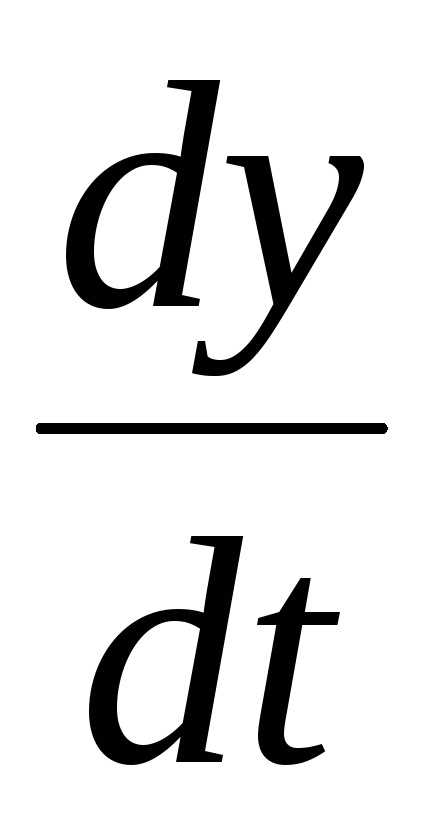2  Т + y = kx. (3.8)

Условие Т₀² < 4Т ² заменяется условием ² < 1 .

Получим описание колебательного звена.

Дифференциальному уравнению (3.8) соответствует операторное уравнение

(T²p² + 2  Tp + 1) Y(p) = kX(p) ,

из которого получается передаточная функция

.

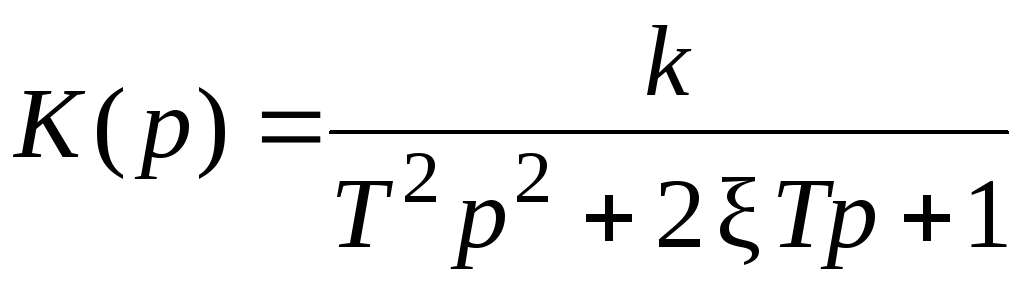Если выходная величина не изменяется (dy/dt = 0, p = 0) передаточная функция вырождается в коэффициент усиления: К(0) = k.

Комплексная частотная характеристика звена

.

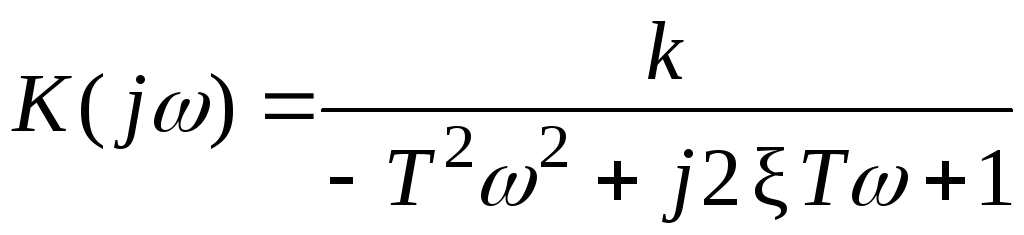Действительная и мнимая частотные характеристики имеют вид:

,

.

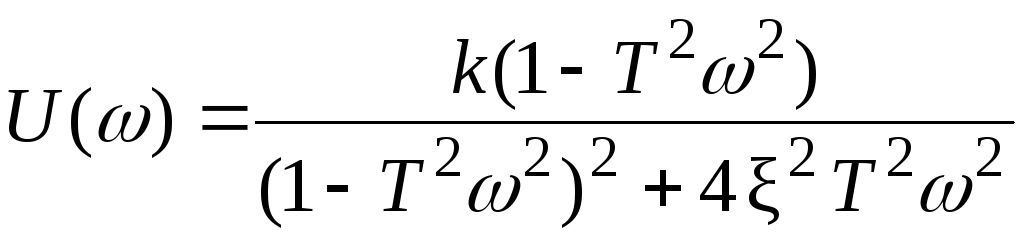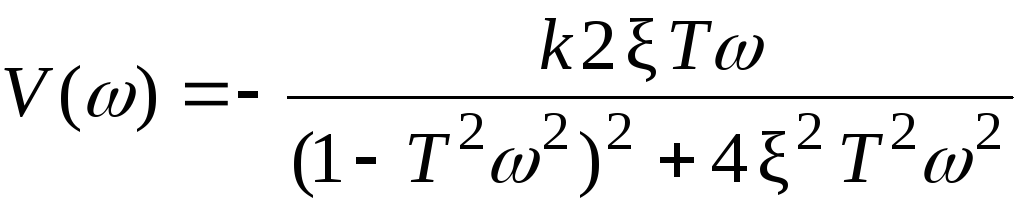
Амплитудная частотная характеристика колебательного звена

.

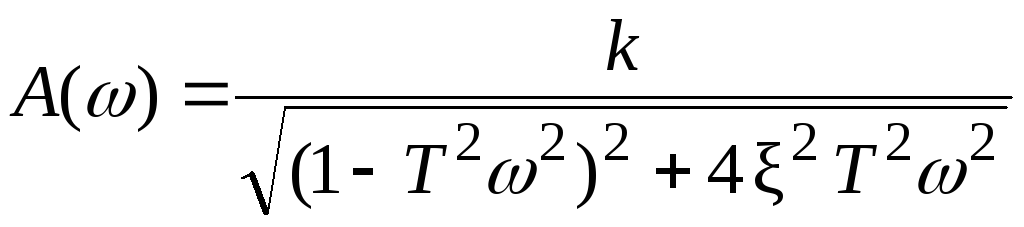У колебательного звена кривая A() имеет пик, вершина которого отвечает частоте₀= 1/T(рис. 3.5). То есть резонансной частоте. Максимальная величина амплитуды равнаk/ 2. Пик выше, если больше коэффициент усиления и меньше коэффициент затухания.

Фазовая частотная характеристика в интервале изменения частоты от = 0 до= 1/Tрассчитывается по формуле

.

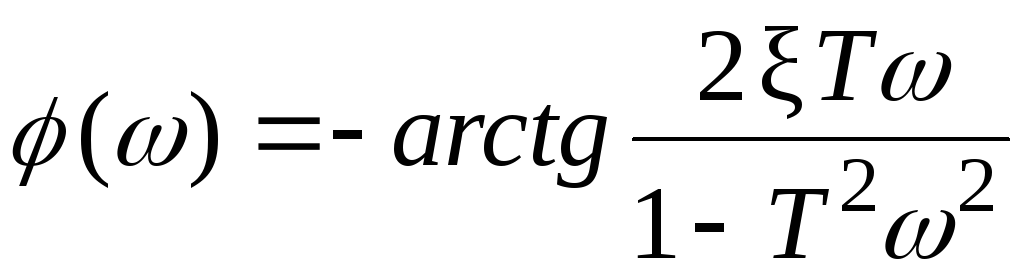
П

2

2

1

ξ

2

)

(











T

T

arctg









ри = 0 () = 0. Значению ₀ = 1/T соответствует запаздывание –90  . С увеличением  запаздывание увеличивается и расчет надо вести по формуле .

Характер кривых показан на рис. 3.6.

Логарифмическая амплитудная частотная характеристика имеет вид:

L() = 20 lg k – 10 lg (1-T²²)² + 4 ²T²² .

Форма этой кривой зависит от коэффициента затухания  . В интервале 0,3    1 приемлемо асимптотическое представление. В области   1 L₁ = 20lgk. В области   1 L₂ = 20lg (k/T²) – 40 lg . Условие сопряжения прямых ₀

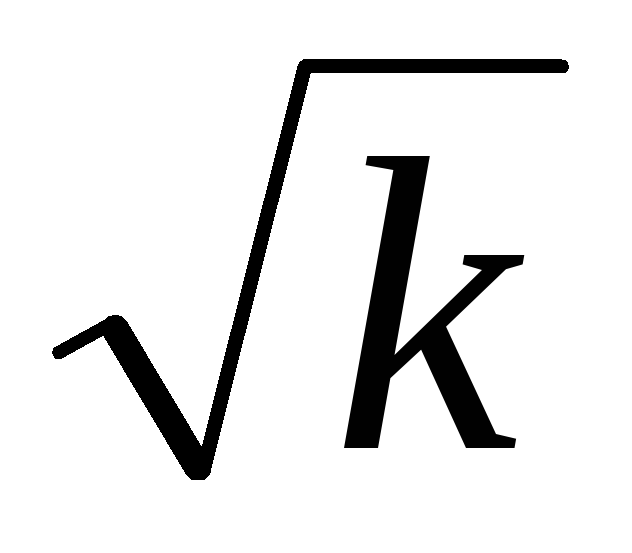= 1/T, т.е. на резонансной частоте. Пересечение прямой L₂ c осью абсцисс при  =/T. Расположение асимптотических прямых показано на рис. 3.7.

1.3. Частотные характеристики электрических цепей

Если в состав цепи входят реактивные элементы( L, C ), то из-за зависимости их сопротивлений от частоты гармонического сигнала параметры цепи становятся частотно-зависимыми. Зависимости параметров цепи от частоты гармонического воздействия называют частотными характеристиками, т.е. для каждого параметра цепи есть своя комплексная частотная характеристика (КЧХ). Названия частотным характеристикам дают в соответствии с названием параметра. Частотная характеристика цепи или комплексная функции цепи есть зависимость от частоты отношения комплексных амплитуд отклика и воздействия. Она может быть записана в показательной и алгебраической форме:

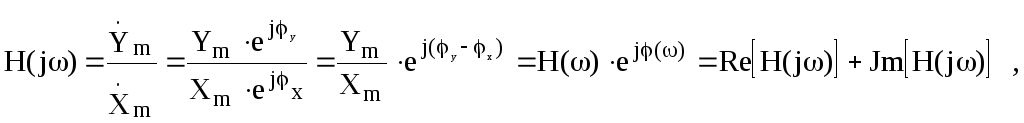где 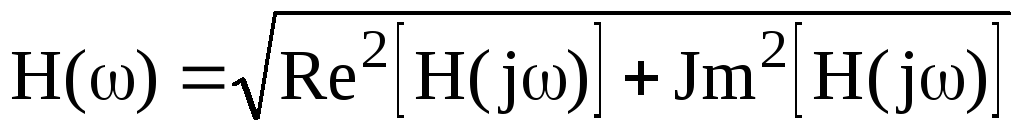— амплитудно-частотная характеристика (АЧХ) (или модуль комплексной функции -H(j)) — есть зависимость от частоты отношения амплитуд выходного и входного гармонических колебаний ;

()=arctg[Jm[H(j)] — фазо-частотная характеристика (ФЧХ) (или аргумент комплексной функции – arg(H(j)) — есть зависимость от частоты разности фаз выходного и входного сигналов т.е. ()=₂-_1.

Re[ H(j)]. Im[H(j)] – реальная и мнимая части комплексной функции.

1.4. Расчет частотных характеристик

В основу расчета частотных характеристик положен метод комплексных амплитуд (МКА). Для простых цепей частотную характеристику находят, используя законы Ома и Кирхгофа. Для сложных функций при расчете частотных характеристик используют методы: эквивалентных преобразований, контурных токов, узловых потенциалов и др. Порядок применения метода МКА следующий:

1. Гармонические токи и напряжения (x(t)=X_mcos(ωt-φ_x)) всех ветвей схемы заменить их комплексными амплитудами (X_m=X_me^—jφx), а от исходной схемы цепи составленной из элементов (R,L,C), перейти к комплексной схеме замещения с комплексными сопротивлениями (Z_R=R,Z_C=1/(jωC),Z_L=jωL).

2. Составить уравнения электрического равновесия цепи для комплексных изображений токов и напряжений с использованием законов Ома и Кирхгофа или используя другие методы.

3. Решить систему составленных уравнений относительно комплексных амплитуд интересующих токов или напряжений (Ý_m=Y_me^—jφx).

4. Для нахождения комплексной частотной характеристики (КЧХ) записать отношение комплексной амплитуды отклика к комплексной амплитуде воздействия.

5. Если необходимо, то перейти от комплексных амплитуд интересующих токов и напряжений к гармоническим функциям времени (y(t)=Y_mcos(ωt-φ_y)).

Для цепи второго порядка КЧХ в общем случае можно записать в виде

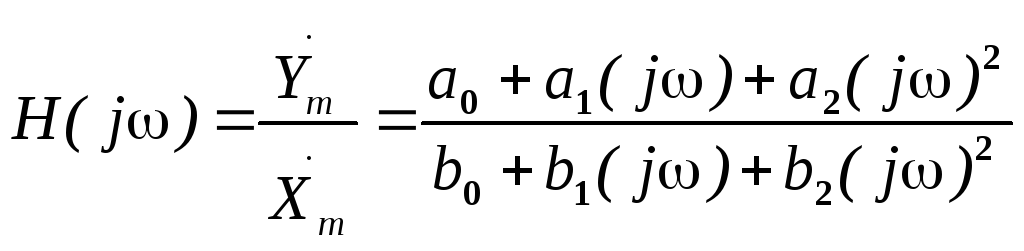. (1.11)

Выделим в числителе и знаменателе действительную и мнимую части, приведем подобные члены, и запишем 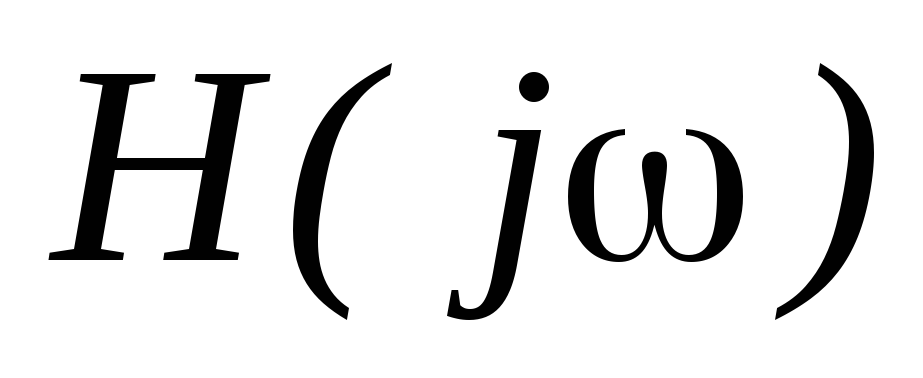в показательной форме

. (1.12)

Отсюда получим выражения для расчета амплитудно-частотных (АЧХ) и фазо-частотных (ФЧХ) характеристик

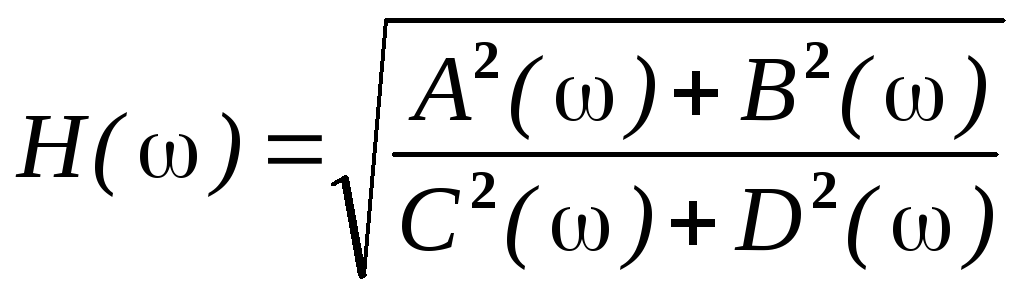
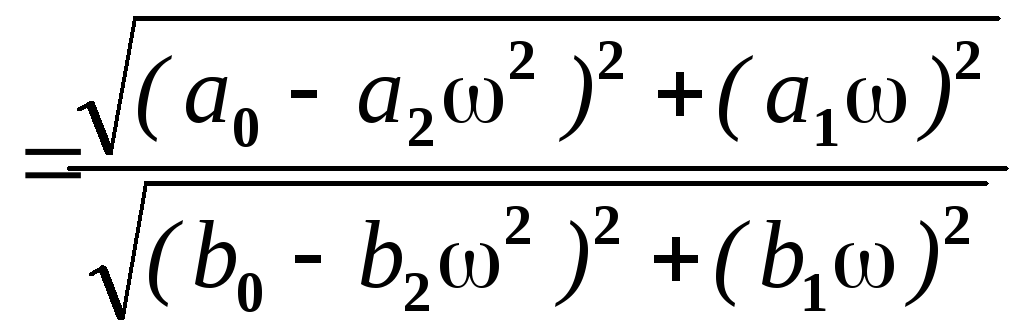(1.13)

φ(ω)=φ_числ(ω)–φ_знам(ω), (1.14)

1.5. Построение графиков частотных характеристик

При графическом изображении частотных характеристик электрической цепи обычно строят отдельные графики АЧХ и ФЧХ цепи. Графики функции, заданной формулой Н(ω) строятся по точкам, в определенном диапазоне частот, в котором проявляются основные свойства электрической цепи, которые затем соединяются плавной линией.

Выбор диапазона частот.

Для оценки частотного диапазона, в котором необходимо построить графики частотных характеристик цепи, определим особые точки операторной передаточной функции. Для этого заменим в формуле (1.11) 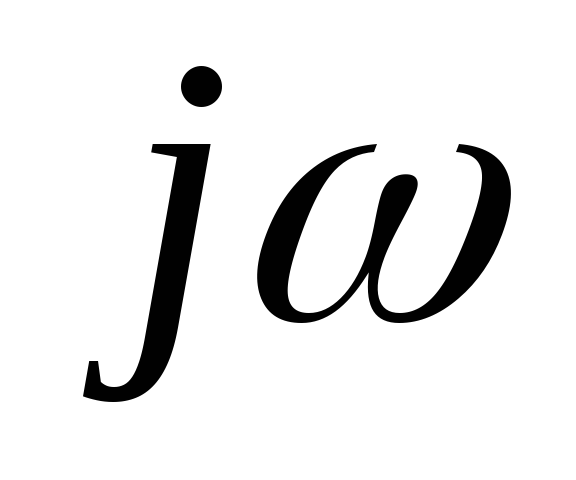=p, получим операторный коэффициент передачи по напряжению

. ()

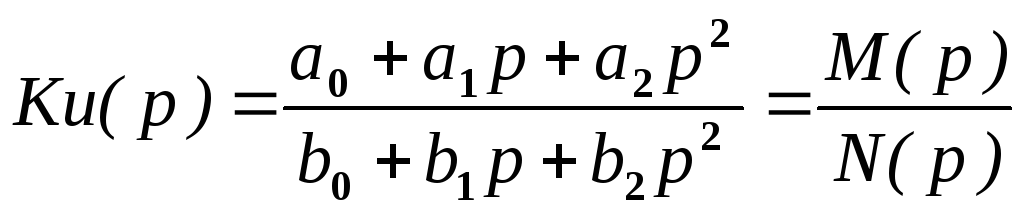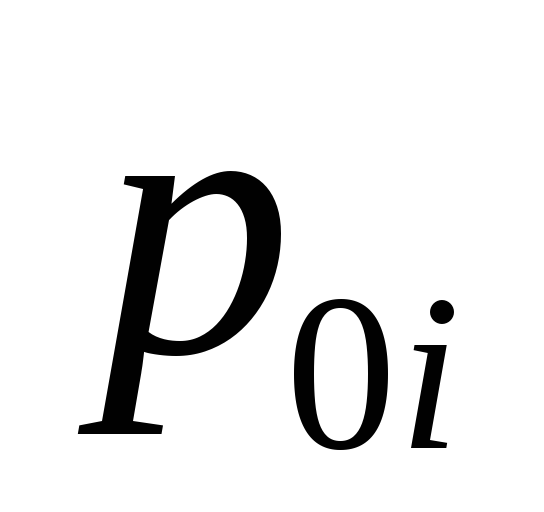Особыми точками (нулями и полюсами) K_u(p) являются значения аргумента (нули), при которых M(p)=0, и значения аргумента (полюсы), при которых N(p)=0, где i=1,2.. порядковый номер особой точки. Для наглядности их изображают в комплексной плоскости, комплексной частоты р=+j. Нули изображают кружочками, а полюсы крестиками.

За частотный диапазон можно принять интервал между 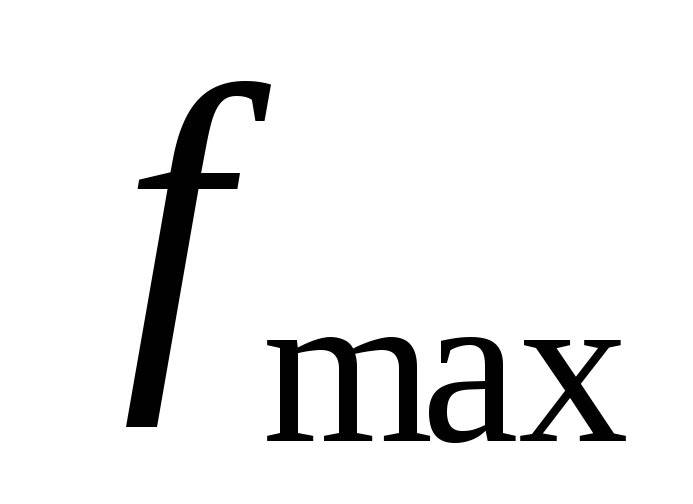и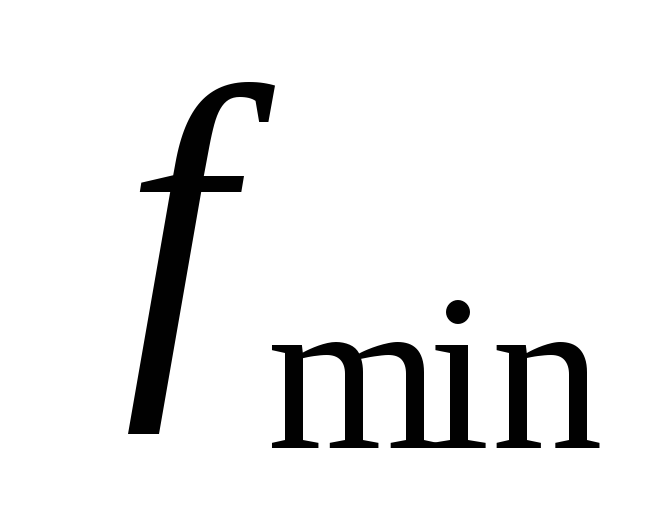

; ,

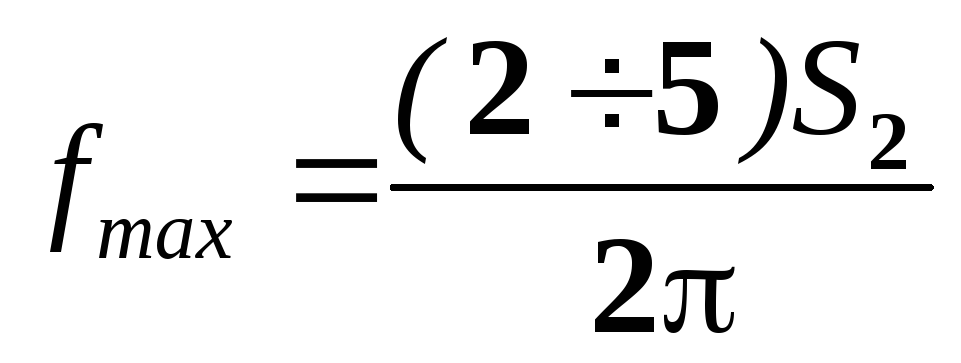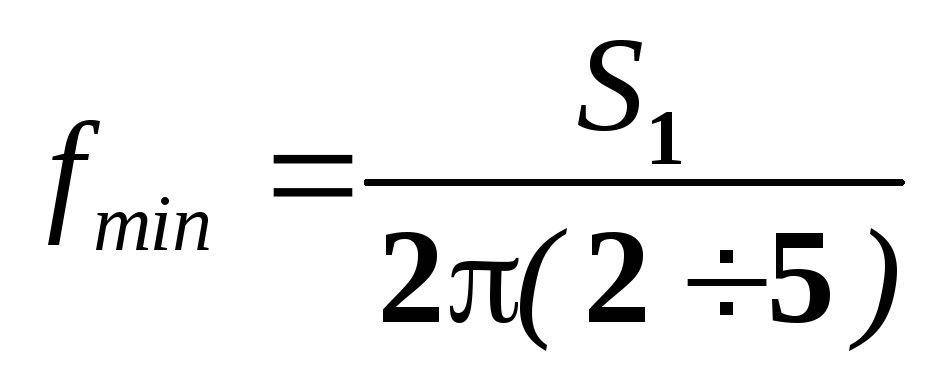где 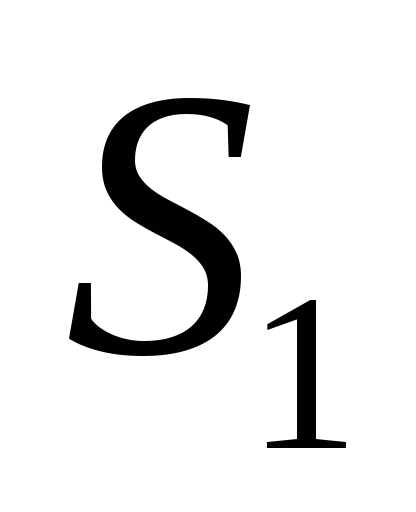— расстояние от начала координат до ближайшей особой точки, которое определяется ее модулем, т.е. 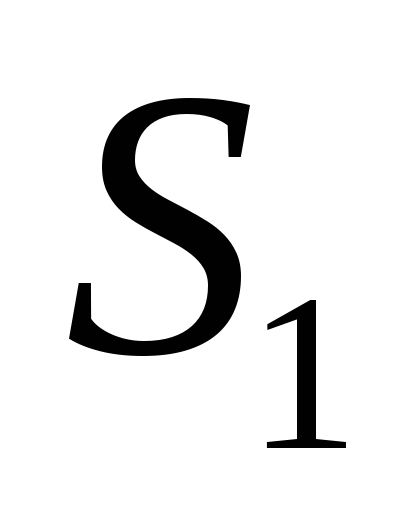=min{|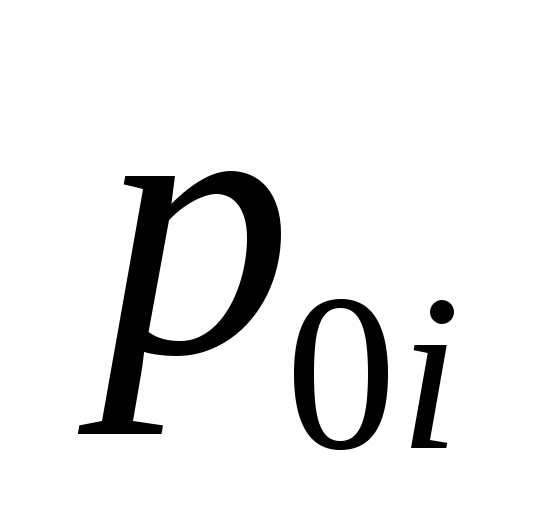|,||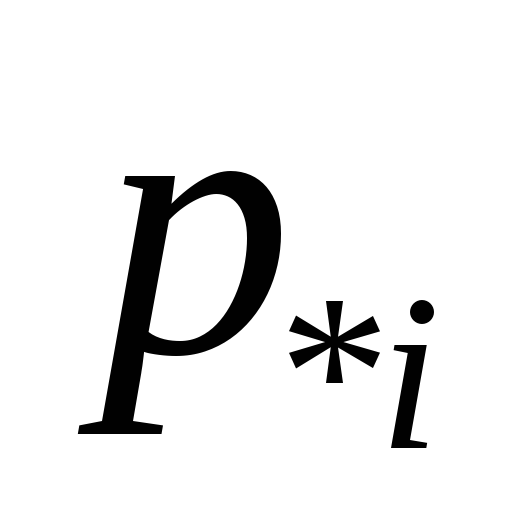}; 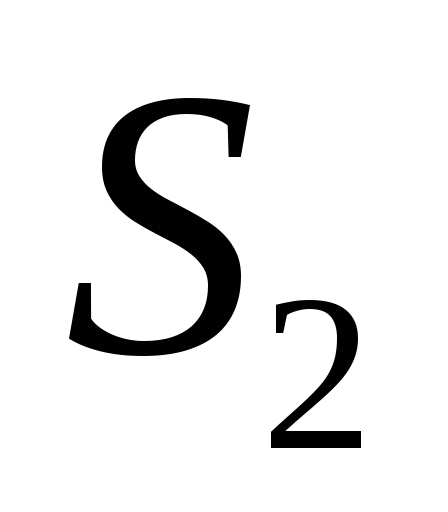— расстояние до самой удаленной особой точки, т.е. 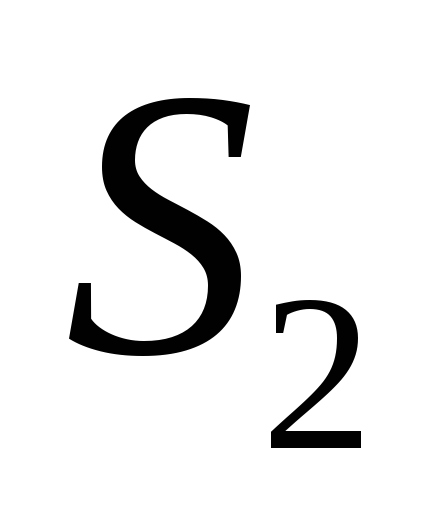=max{|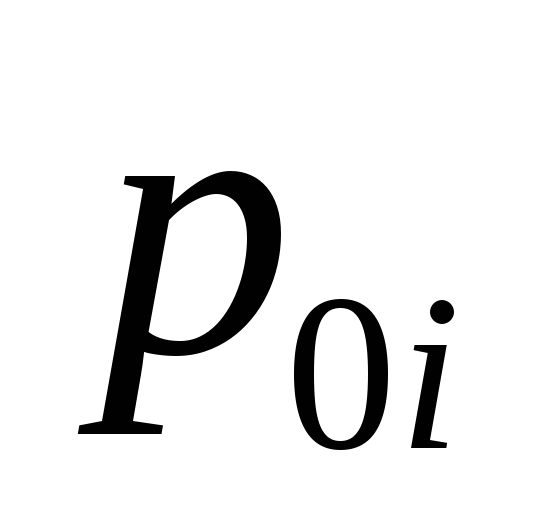|,||}, где модуль комплексной частоты определяют по формуле |p|=.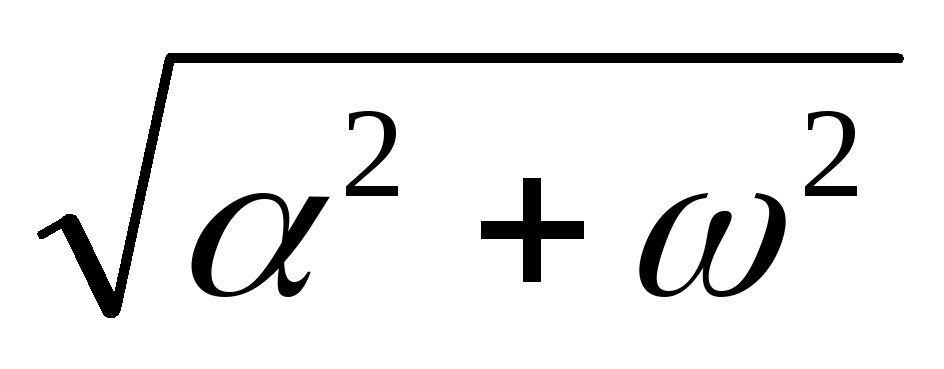

Выбор масштаба построения графиков. При построении графиков частотных характеристик применяют различные масштабы по осям (вертикальной – ось ординат и горизонтальной – ось абсцисс): абсолютный (линейный) масштаб по осям применяют, если диапазон изменения величины не более одной декады, и логарифмический, если диапазон изменения величины составляет две и более декады. На практике часто используется полулогарифмический масштаб, когда по горизонтальной оси берется логарифмический масштаб, а по вертикальной – линейный.

В тех случаях, когда предполагаемая частотная характеристика располагается в широком диапазоне частот, то ее график строят в логарифмическом масштабе по оси частот. Сначала проводят расчет точек на частотах f→0, f→∞, а далее, на частотах в логарифмическом масштабе f =lg(f/f₀), гдеf=1,2, 3 и т.д. – нормированная частота в логарифмическом масштабе; f₀ – частота излома (частота среза) характеристики, выбранная за единицу; f/f₀=f_н — нормированная частота в абсолютном масштабе. Величина f₀ может быть принята любой. В простейшем случае за f₀ можно принять 1Гц, или 1кГц. Однако если анализируется цепь первого порядка, то за f₀ принимают f₀=(2)^-1 (₀=1/), где  — постоянная времени цепи.

Если цепь имеет несколько постоянных времени, то ее ассимптотическая логарифмическая характеристика, состоит из нескольких прямых и имеет несколько точек излома, каждой из которых соответствует своя постоянная времени ₁=1/₁; ₂=1/₂ и т. д. Выбрав одну из них за опорную, можно построить график в масштабе  или lg.

При построении логарифмических частотных характеристик, более подробно, в каждой декаде следует брать по 3 –точки (0, 2, 5). Если необходимо, то проводят уточнение вблизи точек экстремумов — минимума или максимума, взяв по 10 точек вблизи них.

Особенности построения графиков ФЧХ.

Формула ФЧХ (уравнение ФЧХ) выражает зависимость аргумента (фазового угла) комплексной функции Кu(jω) от частоты:

φ(ω)=φ_числ(ω)–φ_знам(ω), (7)

где φ _числ(ω) — аргумент числителя Н(jω), φ _знам(ω) — аргумент знаменателя Н(jω).

При записи формул для φ _числ(ω) и φ _знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа Z=А(ω)+jВ(ω) вычисляется по различным формулам в зависимости от положения комплексного числа на комплексной плоскости (см. табл. 1.1).

Таблица 1.1.

«№	Область расположения числа Z=А+jВ на комплексной плоскости.	Условия	Формула φ (ω)
1)		A(ω) > 0, B(ω) 
2)		B(ω) > 0,A(ω)
3)		B(ω)0,A(ω) .
4)		A(ω) < 0, B(ω)> 0.
5)		A(ω) < 0, B(ω) < 0.

Отсюда следует, что уравнение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.

Рассмотрим первый пример. Для схемы 3 приведенной в табл.3.2 частотная характеристика коэффициента передачи имеет вид:

К(jω)= {(jω)²R₁C₁R₂C₂}/{(1+(jω)²R₁C₁R₂C₂)+ jω(R₁C₁+R₂C₂+R₁C₂)}=

= {А(ω)}/{С(ω)+ jD(ω)},

где А(ω)=-(ω)²А₁; С(ω)= 1-(ω)²А₁; D(ω)= ωВ₁, А₁= R₁C₁R₂C₂, В₁=R₁C₁+R₂C₂+R₁C₂.

Формула ФЧХ вычисляется из выражения

φ(ω)=φ_числ(ω)–φ_знам(ω),

1. Анализ числителя для определения его аргумента.

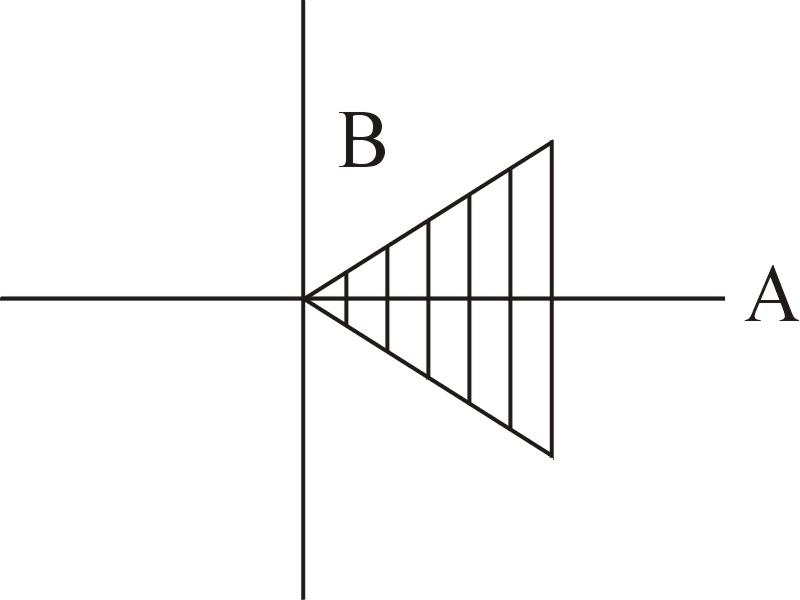
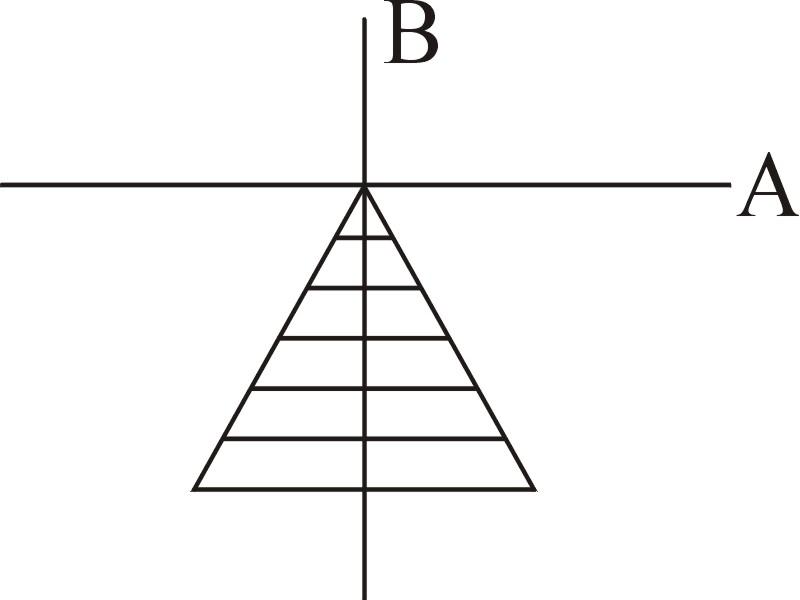
Действительная часть числителя при любой частоте А(ω)=-(ω)²А₁<0 — отрицательна, а мнимая часть отсутствует т.е. всегда равна нулю В(ω)=0. Следовательно, точка отображающая числитель всегда находится на отрицательной части реальной оси т. е.

φ_числ(ω)=π.

2. Анализ числителя для определения его аргумента.

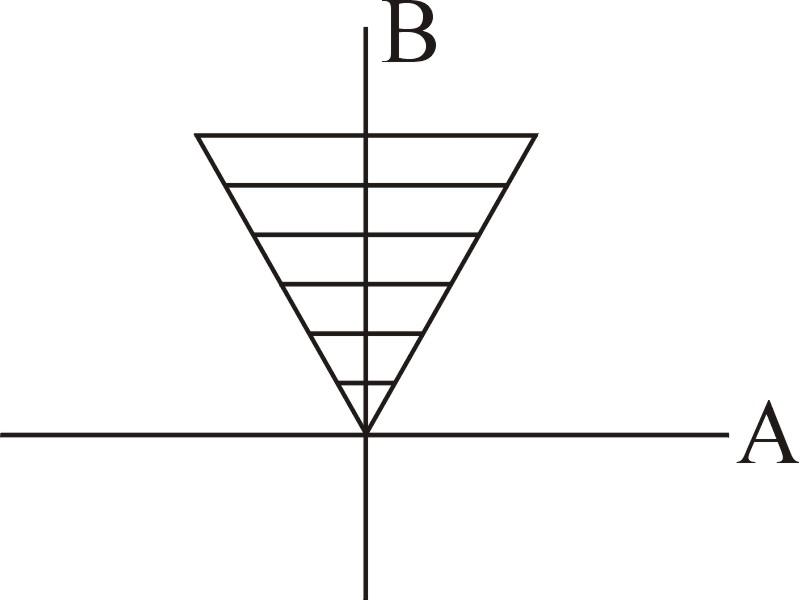
Мнимая часть знаменателя при любой частоте положительна, а действительная знакопеременная, следовательно точка отображающая знаменатель находится в первом или втором квадранте комплексной плоскости и для вычисления аргумента знаменателя нужно использовать формулу 2 из таблицы1.1.

φ_знам(ω)= π/2 — arctg( (1-ω² А₁)/ ω В₁ ).

Таким образом окончательно, ФЧХ коэффициента передачи для нашего примера имеет вид

φ(ω)= π- (π/2 — arctg( (1-ω²А₁)/ ωВ₁))= π/2 + arctg( (1-ω²А₁)/ ωВ₁)).

Рассмотрим второй, более сложный, пример. Частотная характеристика цепи задана выражением

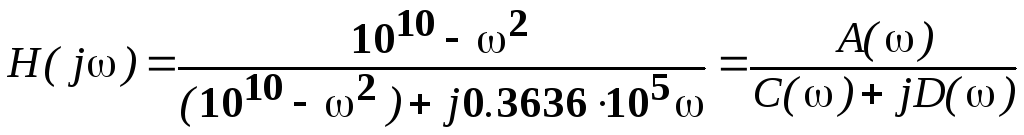. (9)

где A(ω)=(10¹⁰–ω ²) , B(ω)=0, C(ω)=(10¹⁰ –ω ²), D(ω)=0.3636·10⁵ω.

Учитывая (8), получим выражение для АЧХ

(10)

Формула ФЧХ выражает зависимость аргумента (фазового угла) комплексной функции K_U(jω) от частоты и имеет вид:

φ(ω)= φ_числ(ω) –φ_знам(ω) ,

(11)

где φ _числ(ω) – аргумент комплексного числителя H(jω),

φ _знам(ω) – аргумент комплексного знаменателя H(jω).

При записи формул для φ _числ(ω) и φ _знам(ω) следует учитывать, что фазовый угол произвольного комплексного числа Z(jω)=А(ω)+jB(ω) вычисляется различным образом в зависимости от положения комплексного числа на комплексной плоскости (см. таблицу 1.1).

Отсюда следует, что выражение ФЧХ может быть записано несколькими формулами, каждая из которых справедлива в некотором своем диапазоне частот. Граничные частоты диапазонов можно оценить приближенно, так как в точках, близких к биссектрисам координатных квадрантов, можно пользоваться формулами обеих соседних областей.

Для нашего примера действительные A(ω) и C(ω) и мнимая D(ω) части числителя и знаменателя коэффициента передачи (9) зависят от частоты и не только меняют свое значение, но и меняют знак. А это значит, что комплексные числа числителя и знаменателя меняют свое положение на комплексной плоскости. Это обстоятельство требует анализа аргументов числителя φ_числ(ω) и знаменателя φ_знам(ω) при изменении частоты от нуля до бесконечности.

1. Анализ числителя для определения его аргумента.

Действительная часть числителя равна A(ω)=10¹⁰–ω². Если , т.е., числитель представляет собой действительное и положительное число –A(ω) ≥ 0. Поэтому φ_числ(ω)=0 при .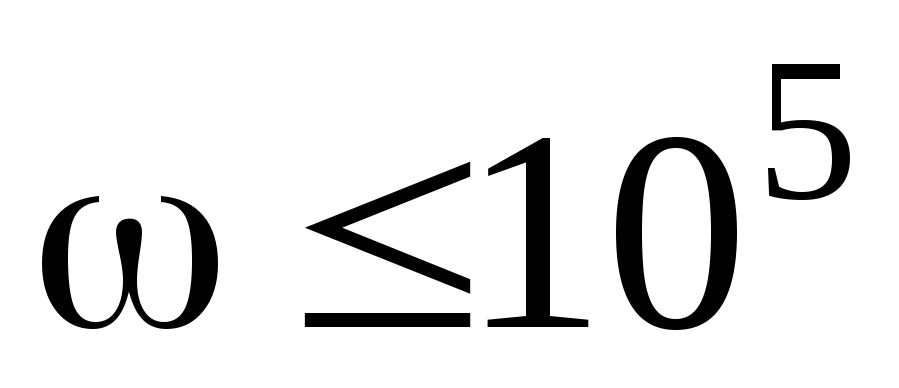

При 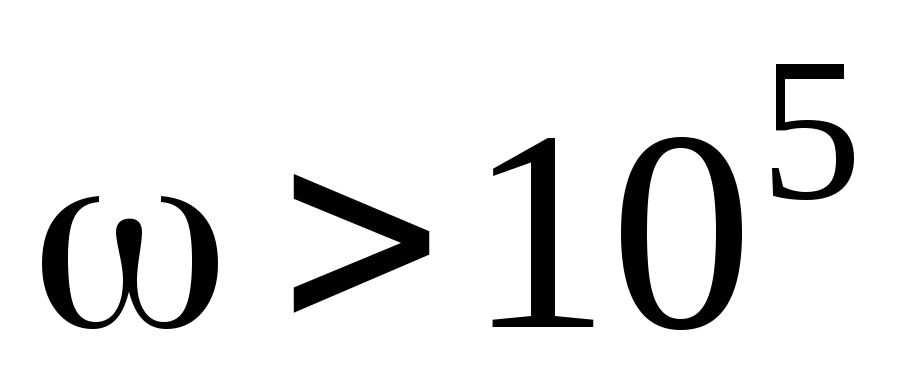,A(ω) < 0. Поэтому φ _числ(ω)=.

2. Анализ знаменателя для определения его аргумента.

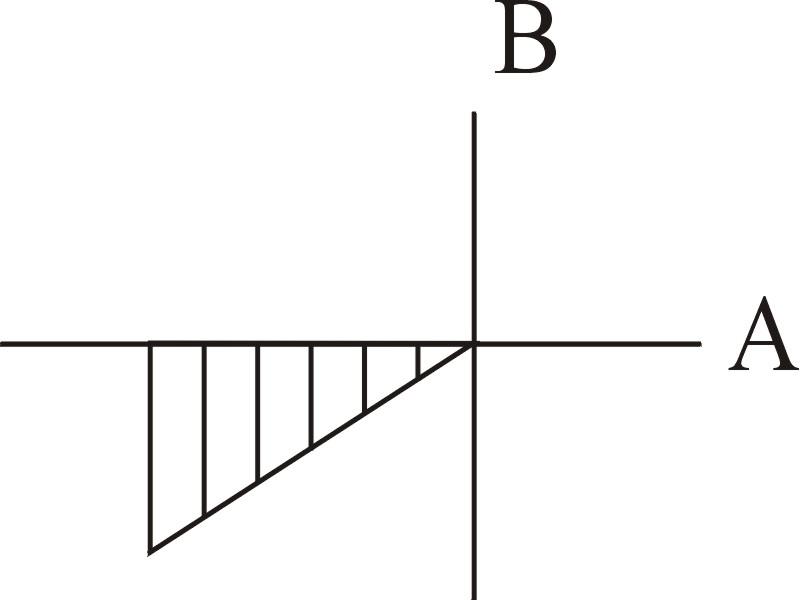
Действительная часть знаменателя равна действительной части числителя C(ω)=A(ω)=10¹⁰–ω² и изменяется с изменением частоты также, как и числитель. Мнимая часть знаменателя D(ω)=0.3636·10⁵ω прямо пропорциональна частоте ω и положительная D(ω)> 0 при ω > 0.

При 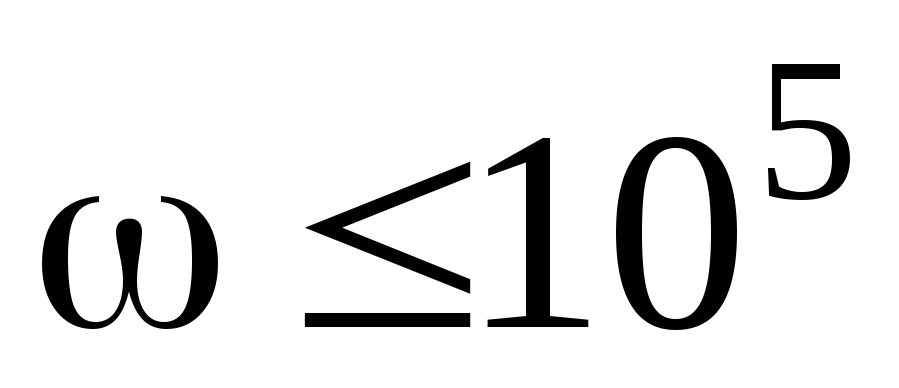точка, отображающая знаменатель, находится в первом квадранте комплексной плоскости, причем при ω>0.8346 10⁵ она пересекает биссектрису первого квадранта. Поэтому в диапазоне 0< ω<0.8346·10⁵ при вычислении фазового угла знаменателя нужно использовать формулу 1 из таблицы 1: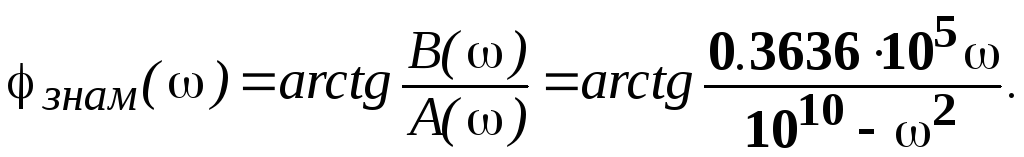

При 0.8346·10⁵ <ω 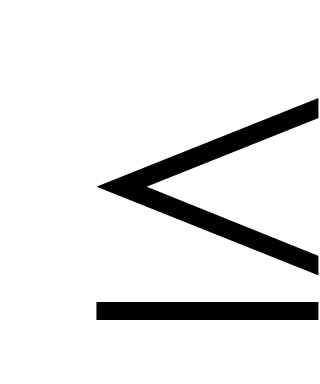1.1982·10⁵ отображающая точка находится в области 2 таблицы 1. Поэтому

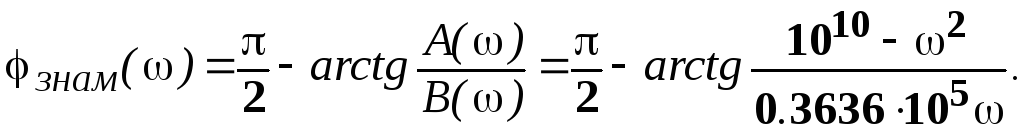
При ω >1.1982·10⁵ точка переходит в область 4 таблицы 1.

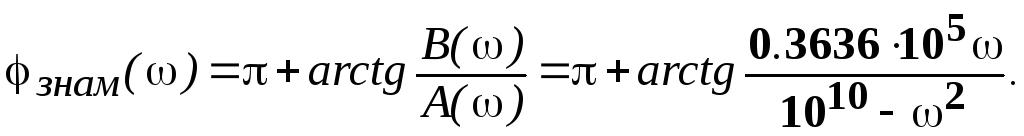
Таким образом, ФЧХ коэффициента передачи в нашем примере будет описываться различными формулами для четырех частотных областей.

1). 0< ω<0.8346·10⁵

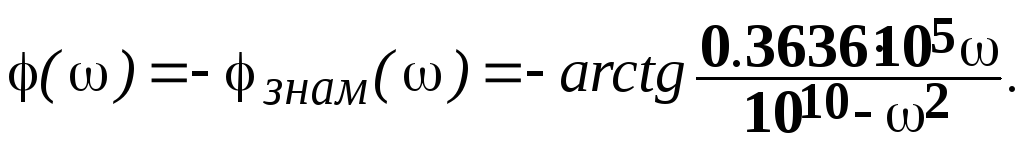
2). 0.8346·10⁵< ω< 10⁵

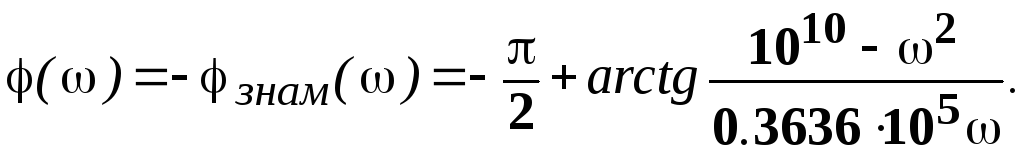
3). 10⁵< ω <1.1982·10⁵

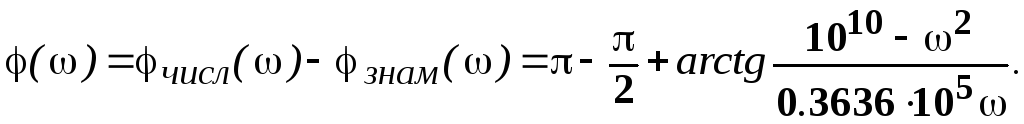
4). 1.1982·10⁵<ω<∞

Комплексная частотная характеристика системы — это… Что такое Комплексная частотная характеристика системы?



Комплексная частотная характеристика системы

77. Комплексная частотная характеристика системы

Характеристика линейной системы, представляющая собой преобразование Фурье импульсной характеристики системы

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

• комплексная структура ЗБИ ЕСФОБД
• комплексно-системный каталог

Смотреть что такое «Комплексная частотная характеристика системы» в других словарях:

• Логарифмическая амплитудная частотная характеристика — ЛАФЧХ фильтра Баттерворта первого порядка Логарифмическая амплитудно фазовая частотная характеристика (ЛАФЧХ)  представление частотного отклика линейной стационарной системы в логарифмическом масштабе. ЛАФЧХ строится в виде двух графиков:… …   Википедия

• Логарифмическая амплитудно-фазовая частотная характеристика — ЛАФЧХ фильтра Баттерворта первого порядка Логарифмическая амплитудно фазовая частотная характеристика (ЛАФЧХ)  представление частотного отклика линейной стационарной системы в логарифмическом масштабе. ЛАФЧХ строится в виде двух графиков:… …   Википедия

• Логарифмическая фазовая частотная характеристика — ЛАФЧХ фильтра Баттерворта первого порядка Логарифмическая амплитудно фазовая частотная характеристика (ЛАФЧХ)  представление частотного отклика линейной стационарной системы в логарифмическом масштабе. ЛАФЧХ строится в виде двух графиков:… …   Википедия

• ГОСТ 21878-76: Случайные процессы и динамические системы. Термины и определения — Терминология ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа: Cross power spectral density function of stationary dependent random processes Определения термина из разных документов: Cross power… …   Словарь-справочник терминов нормативно-технической документации

• Импульсная перезодная характеристика — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… …   Википедия

• Импульсная переходная характеристика — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… …   Википедия

• Импульсная характеристика — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… …   Википедия

• СА 03-002-05: Стандарт ассоциации. Системы мониторинга агрегатов опасных производственных объектов. Общие технические требования — Терминология СА 03 002 05: Стандарт ассоциации. Системы мониторинга агрегатов опасных производственных объектов. Общие технические требования: 2.1. Агрегат : совокупность механически соединенных механизмов, узлов, машин и конструкций, работающих… …   Словарь-справочник терминов нормативно-технической документации

• Импульсная передаточная функция — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… …   Википедия

• Импульсный отклик — Импульсная переходная функция (импульсная переходная характеристика, импульсная характеристика, ИПФ) выходной сигнал динамической системы как реакция на входной сигнал в виде дельта функции Дирака. В цифровых системах входной сигнал представляет… …   Википедия

5. Комплексные передаточные функции (комплексные частотные характеристики)

Будем рассматривать линейную электрическую цепь. На вход цепи подключен гармонический источник (воздействие). На выходе рассматривается реакция цепи (отклик на воздействие).

Под комплексной передаточной функцией понимают отношение комплексного изображения гармонической реакции ЛЭЦ к комплексному изображению воздействия на цепь.

Пусть воздействие 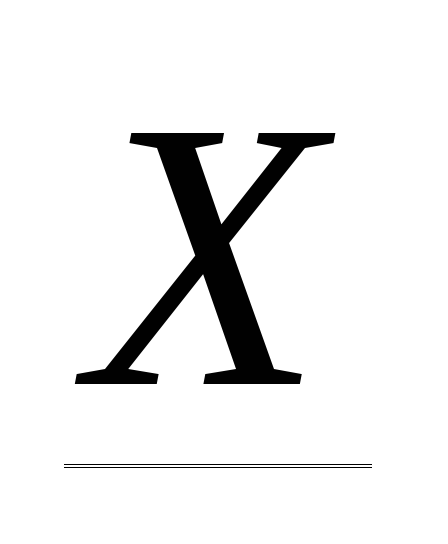, а реакция — ; а комплексная передаточная функция 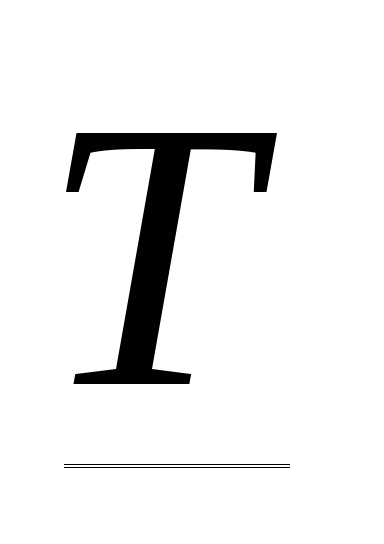. Тогда 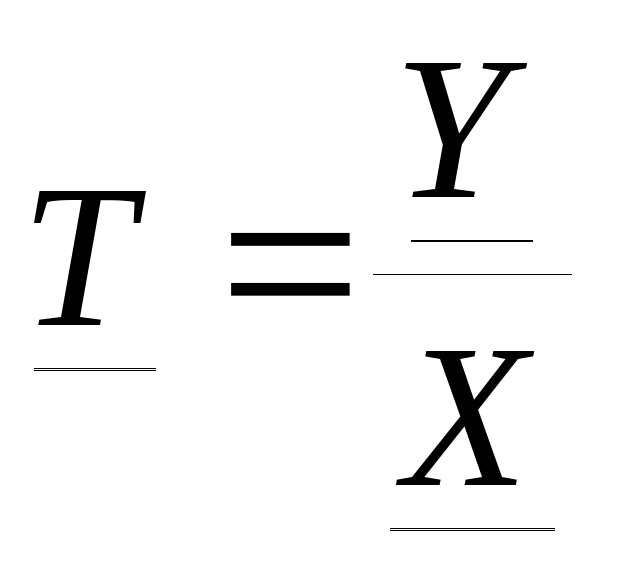. Если воздействие гармоническое и мы будем менять частоту, то получим комплексную частотную характеристику (КЧХ).

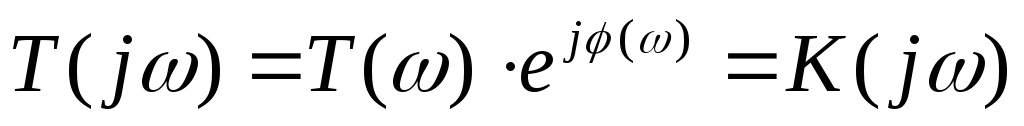
Сокращенно функцию T(jω) называют комплексным коэффициентом передачи. Модуль комплексного коэффициента T(ω) представляет собой амплитудно-частотную характеристику (АЧХ). Аргумент комплексного коэффициента передачи 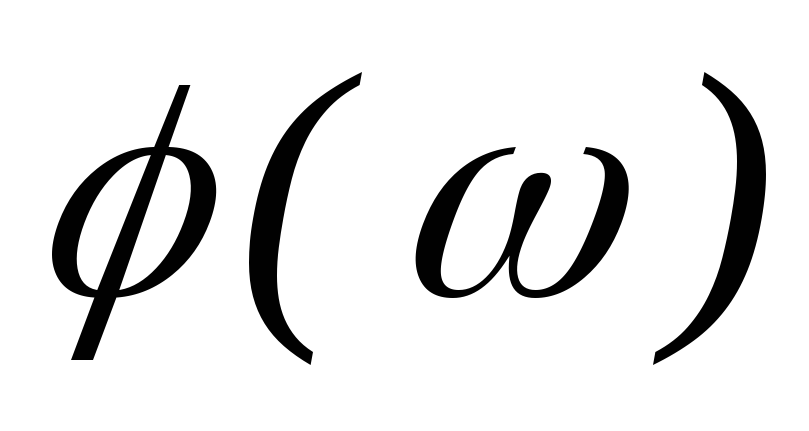— это фазово-частотная характеристика (ФЧХ).

АЧХ – это такая характеристика цепи, которая показывает, как изменяется в зависимости от частоты отношение амплитуды реакции (выходного сигнала) к амплитуде воздействия (входного сигнала) при гармоническом воздействии.

ФЧХ – это такая характеристика цепи, которая показывает, как изменяется сдвиг фаз выходного и входного сигнала в зависимости от частоты при гармоническом воздействии.

Это основные характеристики электрических цепей. Теоретически они рассчитываются с помощью расчетных методов на основе законов Ома и Кирхгофа в комплексной форме. Практически они измеряются с использованием приборов (вольтметров, фазометров, осциллографов).

В зависимости от вида реакции и воздействия различают четыре типа передаточных функций: по напряжению (напряжение / напряжение), по току (ток / ток), по сопротивлению (напряжение / ток), по проводимости (ток /напряжение ).

Для примера рассмотрим колебательный контур:

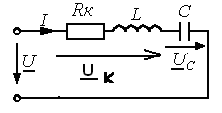
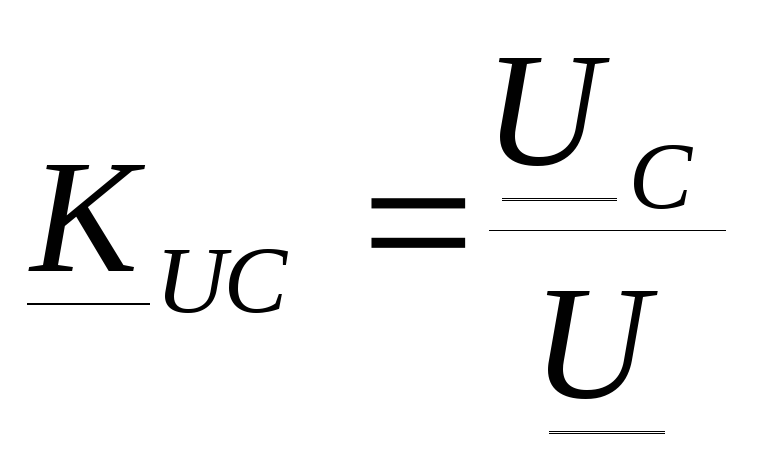
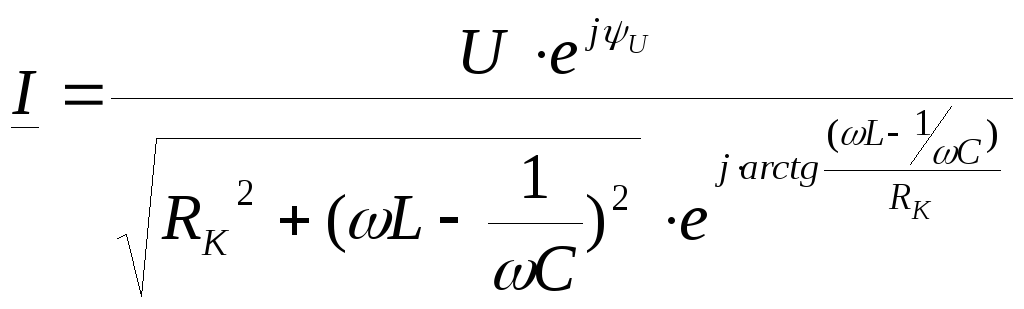
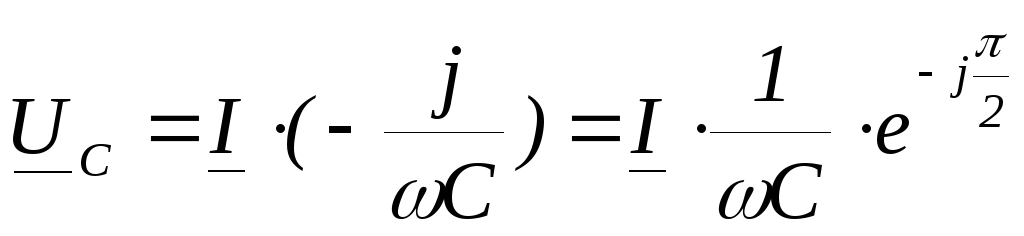
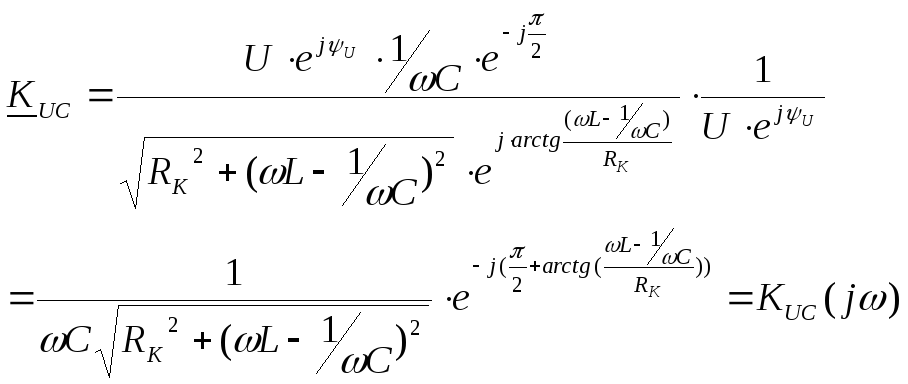
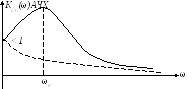
Q>>1

кривая пунктирная при Q<1.,

при ω=ω₀ К₀=Q

С использованием расстройки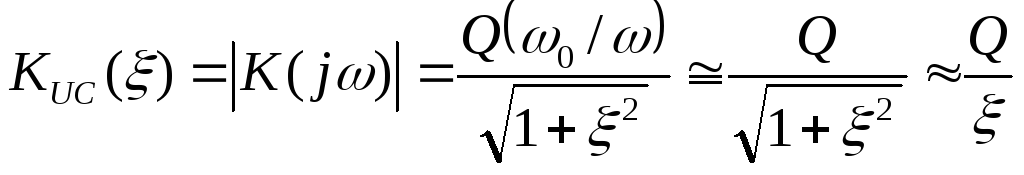

6. Влияние внешних сопротивлений на избирательность контура (на добротность и полосу пропускания)

1) Влияние внутреннего сопротивления источника

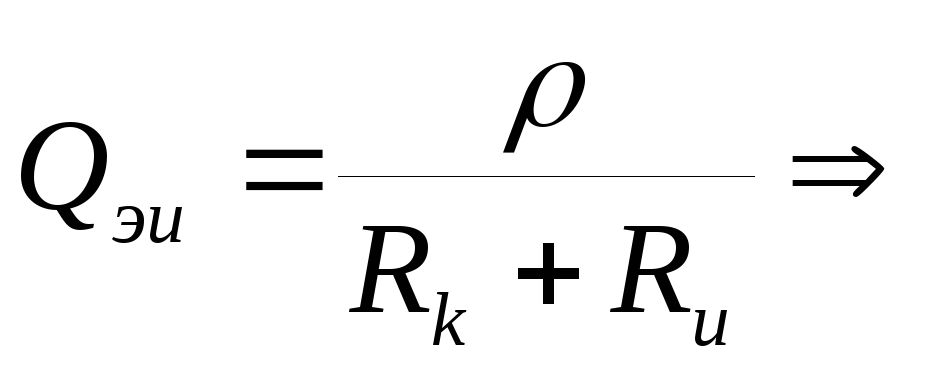
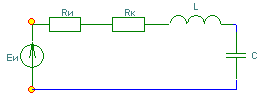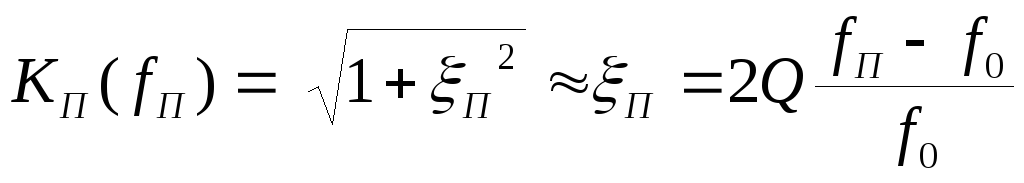добротность уменьшается, коэффициент подавления помехи уменьшается (на той же частоте помехи величина расстройки ξ будет меньше), 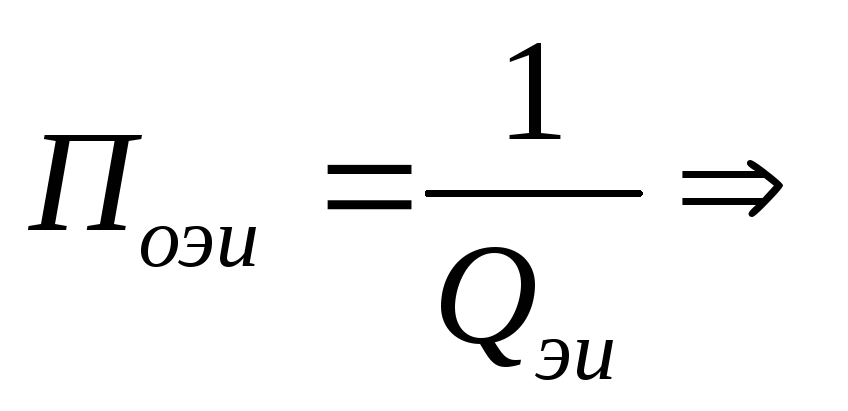полоса пропускания увеличивается. Избирательность (подавление помех) ухудшается.

2) Влияние сопротивления нагрузки

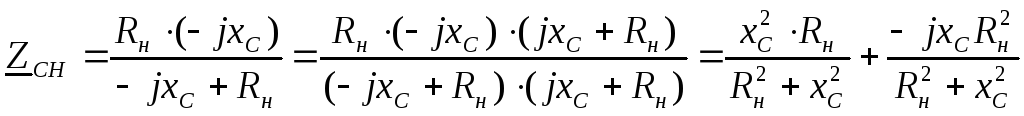
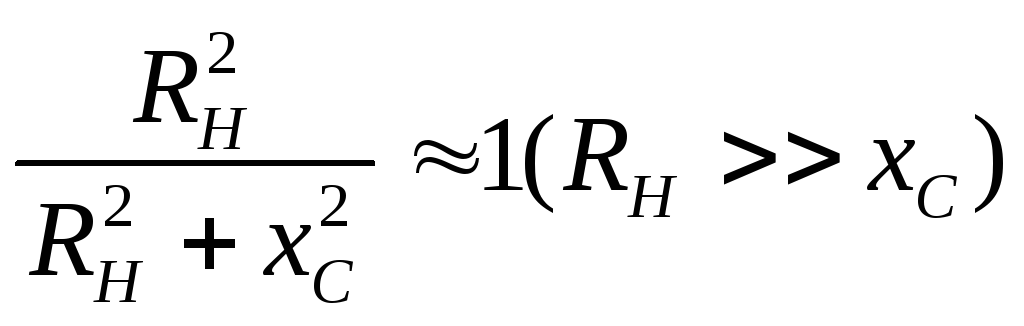
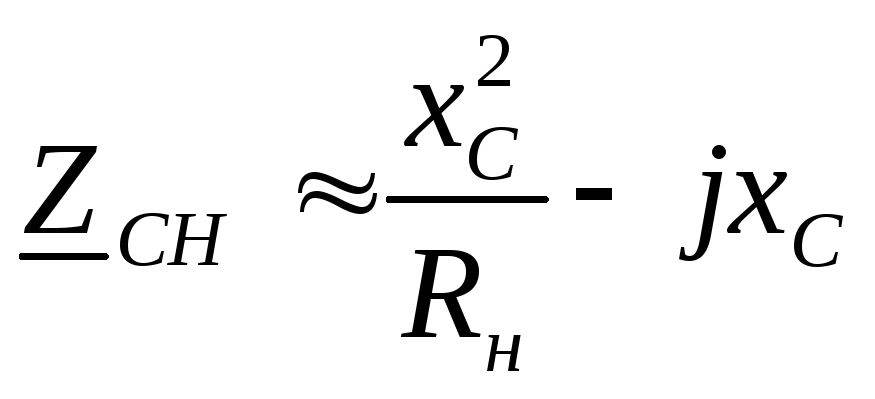Появляется некоторое добавочное сопротивление 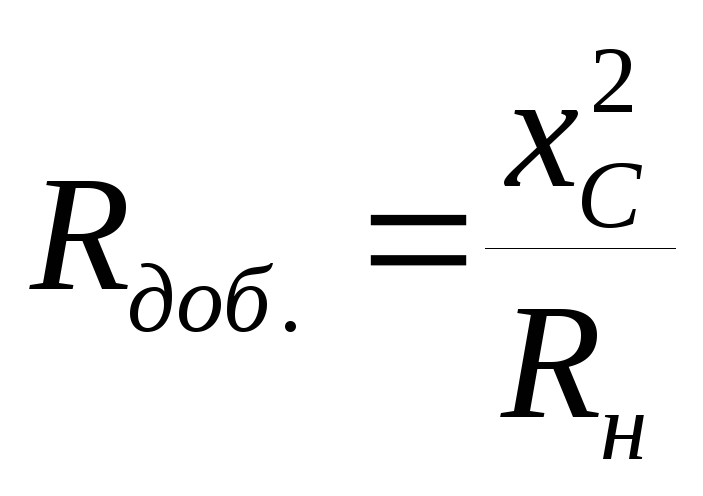. 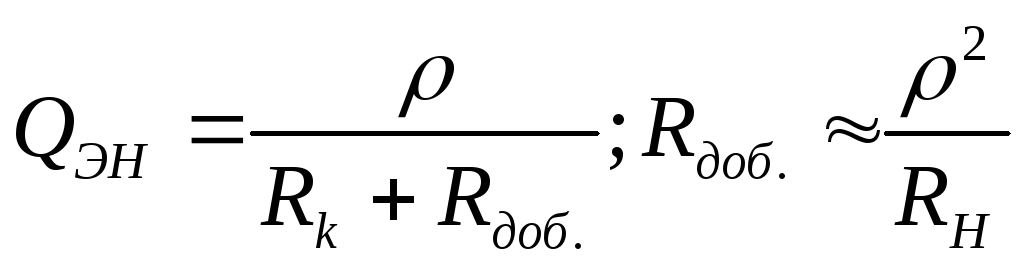, т.к. добротность рассматривается на резонансной частоте. Добротность уменьшается, полоса пропускания возрастает, а коэффициент подавления помехи уменьшается. Избирательность ухудшается. Любое добавочное сопротивление ухудшает избирательность; это надо учитывать на практике.

Пример расчета

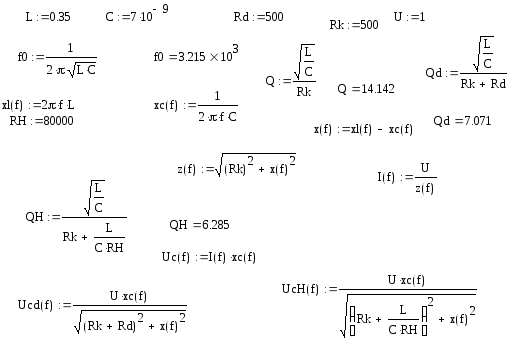
Рассмотрим графики частотной зависимости напряжения на емкости последовательного контура, так же с учетом сопротивления источника сигнала или нагрузки.

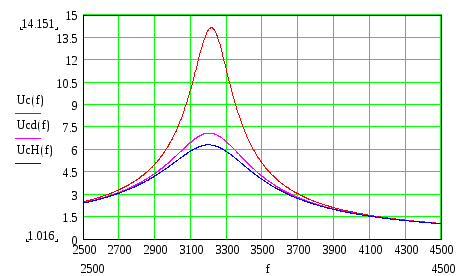Гц

§3. Параллельный колебательный контур

1. Идеализированный контур

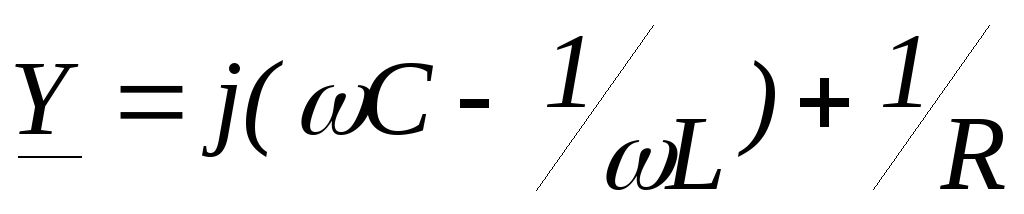— комплексная проводимость.

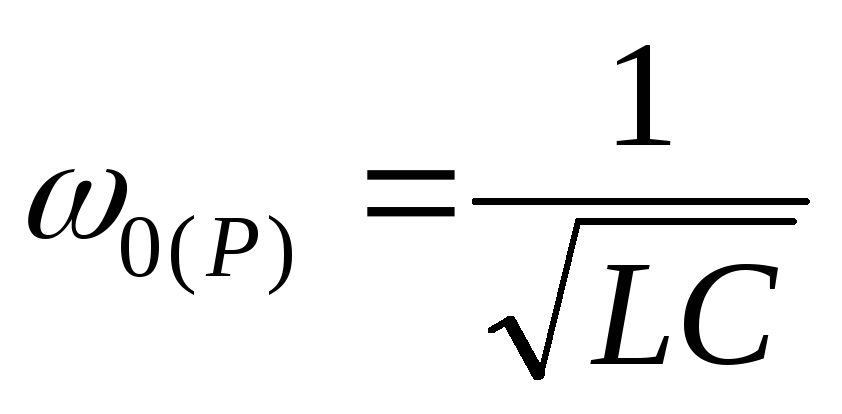— резонансная частота 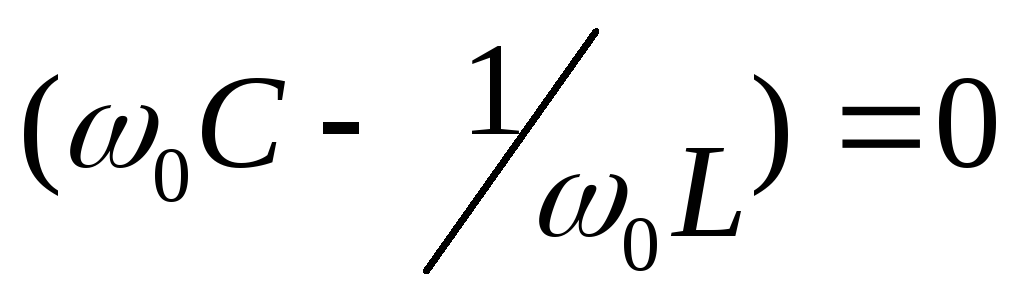— характеристическое сопротивление, сопротивление реактивного элемента на резонансной частоте, На ней Y=1/R

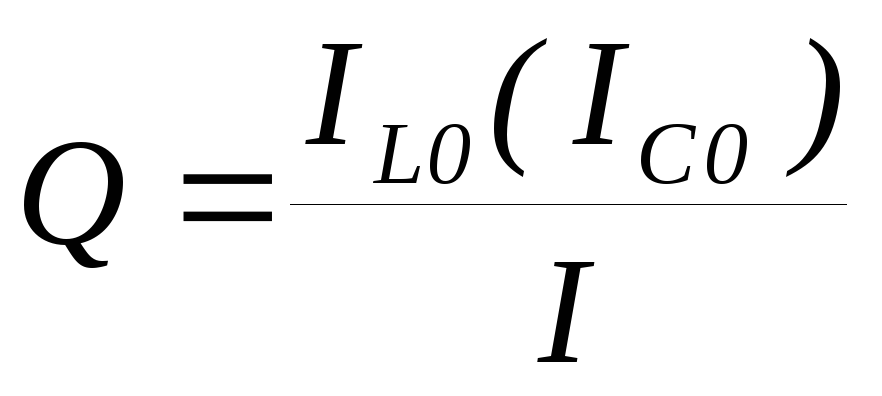, — усилительная способность контура где I_L0, I_C0 – токи на резонансной частоте; I – общий ток. 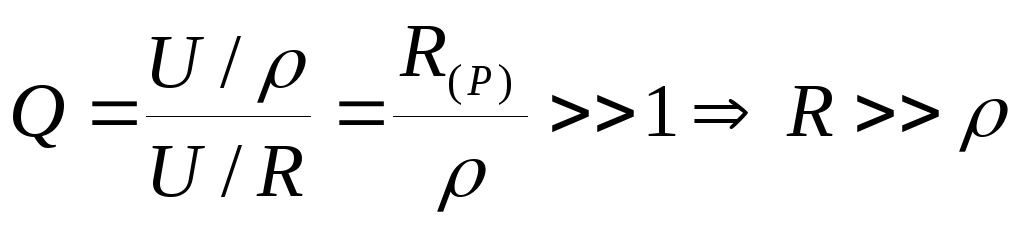Полоса пропускания П определяется аналогично, как для последовательного контура по уровню половинной активной мощности. Коэффициент подавления помехи: 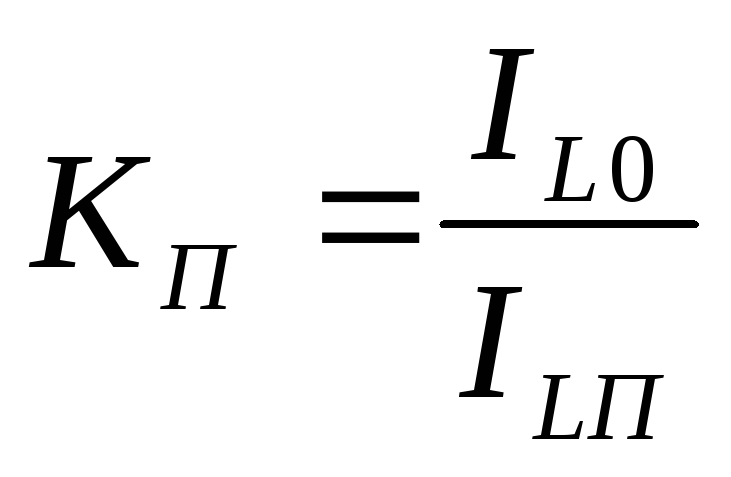Рассчитаем токи в ветвях идеального параллельного контура при резонансе. При резонансе (=_р) токи в ветвях контура равны 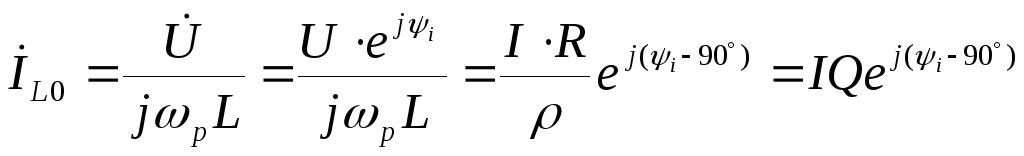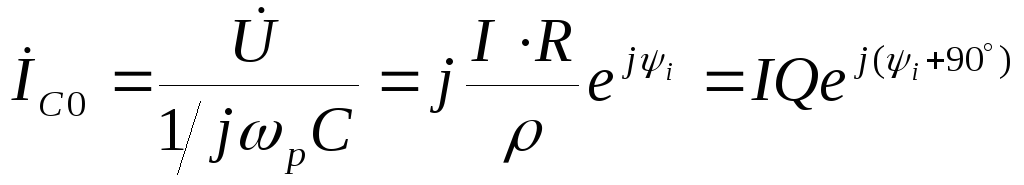и в Q раз больше тока в общей ветви. Поэтому резонанс в параллельном контуре называется резонансом токов.

Векторные диаграммы:

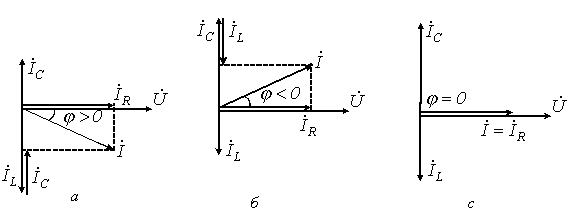
ω < ω₀ ω > ω₀ ω = ω₀

2. Реальный параллельный контур Схема замещения:

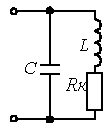
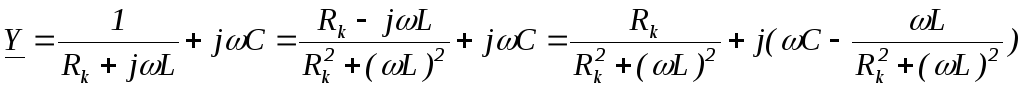
Условие резонанса: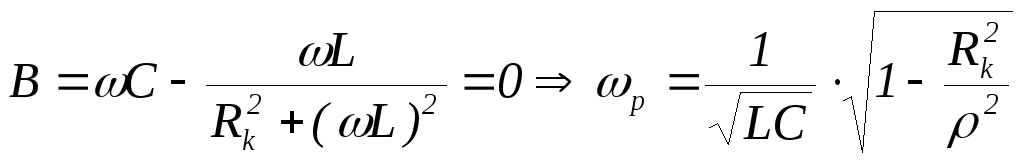

Условие приближения к идеальному контуру: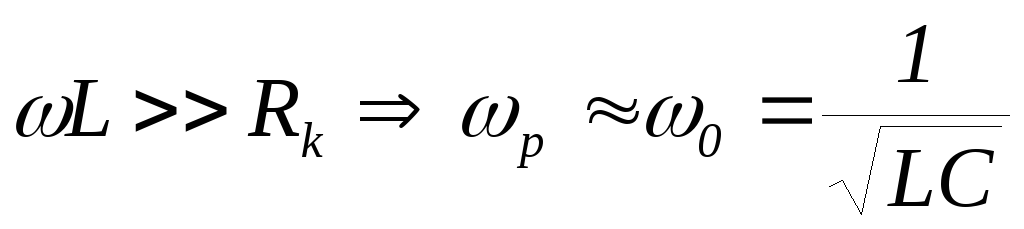

Резонансное сопротивление:

Векторная диаграмма:

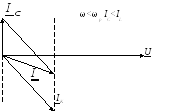
2.3.3. Частотные характеристики Комплексный коэффициент передачи

Применение частотных характеристик приводит к косвенным методам анализа систем. Их преимущество в возможности использования исключительно наглядных графических и графоаналитических методов. Построенные вручную или с применением вычислительной техники эти характеристики используются для предварительного, достаточно приближенного анализа и коррекции системс последующим уточнением полученных результатов с применением цифровой вычислительной техники.

Рассматриваемые ниже частотные характеристики являются характеристиками комплексного коэффициента передачи 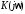. Используются две формы его представления.

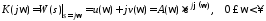, (2.14)

где 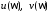– вещественные характеристики,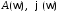– амплитудно-частотная и фазочастотная характеристики системы.

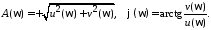
Амплитудно-фазовая характеристика (афх)

Амплитудно-фазовая характеристика системы представляет собой годограф комплексного коэффициента передачи 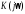, изображенный на комплексной плоскостипри изменении частотыв диапазоне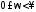(рис. 2.1). Полная характеристика должна быть построена в диапазоне изменения частоты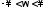_.Но в силу симметричности этой характеристики относительно точки при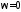изображается только её половина. При необходимости вторая половина характеристики легко восстанавливается.

Годограф строится в декартовой или полярной системах координат в зависимости от формы представления 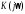в выражении (2.14). В обоих случаях искомая кривая задается в параметрической форме, следовательно, при построении годографатеряется информация об изменении частотыпри движении изображающей точки по годографу. Поэтому должны бытьпредусмотрены способыопределения значения частоты в любой заданной точке годографа. Например, в ряде точек графика АФХ указываются значения соответствующих частот.

Логарифмические частотные характеристики

АФХ несет полную информацию о свойствах системы, но построение графика этой характеристики достаточно трудоемко. Проще построить графики логарифмических частотных характеристик (ЛАХ), и поэтому они чаще используются.

ЛАХ – это совокупность логарифмических амплитудно-частотной 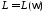и фазочастотной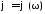характеристик. Графики этих хаактеристик изображаются с применением логарифмического масштаба по оси частот(рис. 2.2).

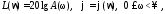
(2.15)

Подробно методы построения ЛАХ будут рассмотрены ниже после изучения типовых звеньев.

Используя графики ЛАХ, для ряда значений 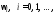на оси частот можно определить значения амплитуды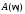и фазы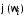. Далее в полярной системе координат изображают точку на графике АФХ. Так можно построить, хотя и приближенно, всю амплитудно-фазовую характеристику.

2.3.4. Временные характеристики

Зависимость от времени выходной величины, т.е. функции 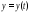, полностью определяет изучаемый динамический режим работы системы. Указанная зависимость определяется как свойствами самой системы, так и видом входного воздействия (функцияx=x(t)). Чтобы отвлечься от влияния последнего,рассматривают реакцию системы на стандартные или пробные входные воздействия. Эта реакция (выходная величина при заданном входном воздействии) зависит только от свойств системы и рассматривается как одна из её характеристик.

Для исследования свойств динамики системы наиболее часто используют две характеристики: импульсно-переходную и переходную характеристики.

Импульсно-переходная характеристика 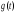–это реакция системы на идеальное импульсное входное воздействие. Математической моделью такого воздействия является дельта-функция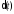. Эта функция равна нулю для всех моментов времени, кроме моментаt= 0. Площадь под этой кривой равна единице. Импульсно-переходная характеристика используется для анализа устойчивости системы.

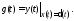(2.16)

Переходная характеристика h(t) – это реакция системы на входное воздействие типа функции включения. Математической моделью функции включения служит единичный скачок 1(t). Эта функция равна нулю для отрицательных моментов времени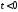,равна единице для положительных моментов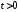и не определена при.

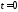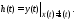(2.17)

Временные характеристики связаны между собой соотношениями 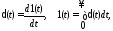следовательно, по одной из этих характеристик всегда можно определить другую

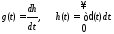(2.18)

Для наглядности в предлагаемой работе в учебных целях используют графики обеих этих характеристик. Они изображаютсяобязательнов масштабе и одна под другой. Переходная характеристикаизображается на фоне единичного скачка(рис. 2.3).

Комплексная частотная характеристика САУ

Количество просмотров публикации Комплексная частотная характеристика САУ — 763

– является преобразованием Фурье от весовой функции :

;

Комплексная частотная характеристика является комплексной величиной.

Комплексная частотная характеристика как и передаточная функция есть отношение выходного гармонического сигнала к гармоническому сигналу на входе комплексном виде, принимающую множество значений исходя из частоты гармонического сигнала .

; .

Представление в полярных координатах:

, где

принято называть амплитудно-частотной характеристикой системы и представляет собой отношение амплитуды гармонического сигнала на выходе к амплитуде гармонического сигнала на входе , при частоте входного сигнала равной , что означает, что если – некоторая амплитуда

, то

сигнал на выходе

зависит от частоты.

.

– фазо-частотная характеристика показывает на сколько выходной сигнал при заданной частоте сдвинут по фазе относительно входного сигнала .

– вещественная часть комплексной частотной характеристики системы;

– мнимая часть комплексной частотной характеристики системы.

и – полярные координаты частотной характеристики.

Между полярными координатами и , существует однозначное соответствие:

;

;

;

.

При каждом фиксированном значении частоты значение однозначно определяет точку на комплексной области … с декартовыми координатами и или полярными координатами и .

можно изобразить на комплексной области в виде годографа вектора в зависимости от частоты , где изменяется от до .

Часть годографа при от до симметрична части годографа при от до .

При экспериментальном определœении комплексной частотной характеристики на вход системы подают гармонический сигнал , то выход системы будет меняться по закону , причем и при неизменной амплитуде будут зависеть от частоты .

Каждому фиксированному значению частоты будут соответствовать определœенные значения и , а следовательно вычисленная для данной частоты

.

Амплитудно-частотная характеристика — Википедия

Амплиту́дно-часто́тная характери́стика (АЧХ) — зависимость амплитуды выходного сигнала некоторой системы от частоты её входного гармонического сигнала^[1][2]. АЧХ — один из видов «частотного отклика» системы (англ. frequency response) наряду c ФЧХ и АФЧХ.

АЧХ в математической теории линейных стационарных систем описывает зависимость модуля комплексной передаточной функции линейной системы от частоты. Значение АЧХ на некоторой частоте указывает, во сколько раз амплитуда сигнала этой частоты на выходе системы отличается от амплитуды выходного сигнала на другой частоте. Обычно используют нормированные к максимуму значения АЧХ.

В математике АЧХ называют модулем комплексной функции. Для построения АЧХ обычно требуется 5-8 точек в рабочем диапазоне частот от ωmin до ωср. Эти характеристики так же, как и временные, содержат информацию о свойствах линейных динамических систем.^[3]

На графике АЧХ в декартовых координатах по оси абсцисс откладывается частота, а по оси ординат — отношение амплитуд выходного и входного сигналов системы.

Обычно для оси частоты используется логарифмический масштаб, так как отображаемый диапазон частот может изменяться в достаточно широких пределах (от единиц до миллионов герц или рад/с). В случае, когда логарифмический масштаб используется и на оси ординат, АЧХ принято называть логарифмической амплитудно-частотной характеристикой.

ЛАЧХ широкое применяется в теории автоматического управления в связи с простотой построения и наглядностью при исследовании поведения систем автоматического регулирования.

АЧХ в радиолокации, связи и других радиотехнических приложениях[править | править код]

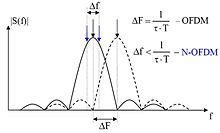
АЧХ приемных каналов средств радиолокации, связи и других радиотехнических систем характеризуют их помехозащищенность. Необходимо учесть, что при цифровой обработке сигналов АЧХ становится периодически повторяющейся, поэтому паразитные полосы приёма (так называемые боковые лепестки АЧХ (side lobe of frequency response) ^[4]) в цифровых средствах должны подавляться на этапе аналоговой обработки сигналов.

В многоканальных системах, например, в цифровых антенных решетках, важную роль имеет также межканальная идентичность АЧХ с коэффициентами межканальной корреляции до 0,999 и выше в области главной полосы пропускания. Чем выше этот показатель и чем шире полоса частот, в которой он соответствует требованиям, тем лучше удается минимизировать мультипликативные помехи, возникающие при межканальной обработке сигналов. Для повышения этой идентичности могут применяться специальные алгоритмы межканальной коррекции АЧХ приемных каналов.

Поскольку коэффициенты коррекции в общем случае зависят от уровня тестирующих сигналов, для многоканальных систем представляет интерес анализ зависимости АЧХ от уровня входного воздействия в пределах всего линейного динамического диапазона устройства. Соответствующий вариант АЧХ будет иметь трехмерную зависимость. Она должна формироваться после проведения коррекции АЧХ анализируемых устройств ^[5].

Классическим методом измерения АЧХ является подача на вход исследуемого объекта гармонического сигнала изменяемой частоты с постоянной или известной для каждой частоты сигнала амплитудой. В этом случае измеряется отношение модулей амплитуды выходного и входного сигналов (коэффициента передачи) исследуемой системы для разных частот .

Для сокращения времени, необходимого для формирования АЧХ, изменение частоты лучше производить с помощью генератора качающейся частоты — измерительного генератора, плавно перестраивающего частоту своего сигнала с неизменной амплитудой во времени. Обычно эти генераторы изменяют плавно свою частоту генерации от низких частот до высоких, затем быстро переключают частоту на низшую, периодически повторяя процесс. Такие генераторы называют генераторами качающейся частоты (ГКЧ) или «свип-генераторами» (от англ. sweep — мести метлой).

Указанные методы последовательной смены частот не пригодны для устройств с работающей автоматической регулировкой усиления (АРУ), выравнивающей различия в значениях АЧХ на разных частотах при времени перехода от одной частоты к другой, превышающем постоянную времени срабатывания АРУ. Они также не позволяют оценить интермодуляционные искажения между действующими одновременно сигналами разных частот. Метод измерения АЧХ с помощью линейно-частотно модулированных сигналов (ЛЧМ) не позволяет осуществлять когерентное накопление во времени напряжений сигнала для частотных компонент, поэтому его точность ограничена условием достаточно больших отношений сигнал-шум. По этой причине метод не пригоден для формирования трехмерных АЧХ, характеризующих зависимость линейного динамического диапазона от частоты, поскольку при слабых отношениях сигнал-шум дает большие погрешности.

Существуют измерители АЧХ, основанные на иных принципах, например, измерители, подающие на вход исследуемой системы широкополосный сигнал, широкополосный импульс с короткими фронтами или измерители с шумовым сигналом, имеющим в полосе частот, существенном для измерения, постоянную спектральную плотность мощности. Отклик системы анализируется с помощью анализатора спектра или фурье-измерителя АЧХ, выполняющего фурье-преобразование отклика системы из временно́й в частотную область для формирования полного вида АЧХ.

Любому методу измерения АЧХ присущи те или иные достоинства или недостатки. Приемлемый способ применения измерения зависит от конкретной задачи.

• Харкевич А.А. Спектры и анализ. — М.: Государственное издательство физико-математической литературы, 1962.
• Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы. — М.: Радио и связь, 1994.
• Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. — М.: Мир. — 1978. — С. 106. — 848 с.